Регрессионный анализ в Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
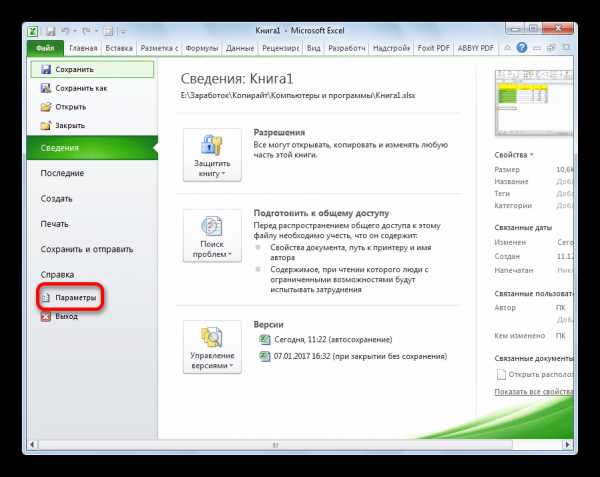
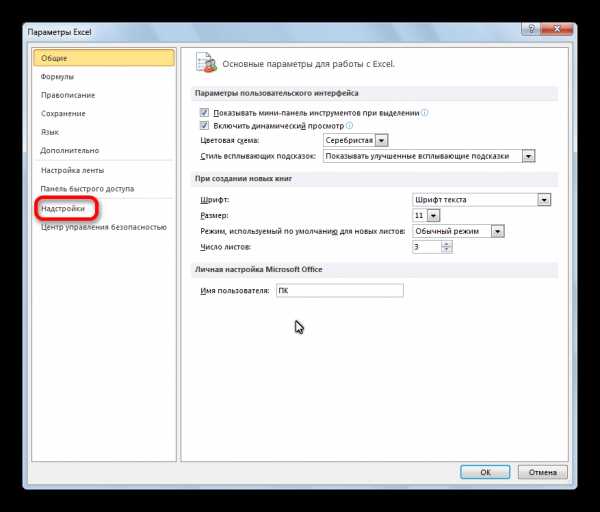
- Переходим в раздел «Параметры».
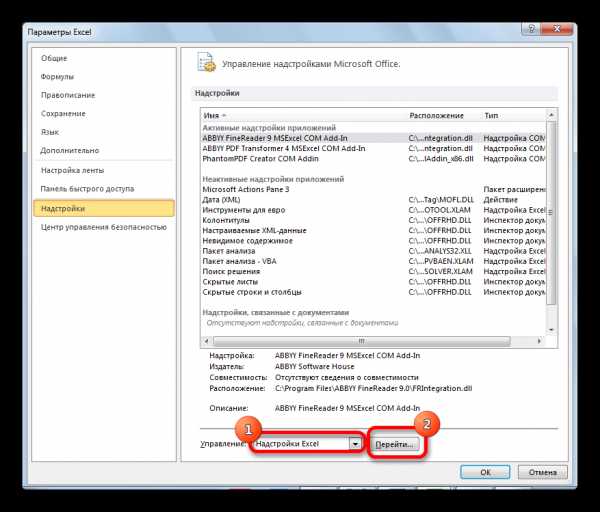
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
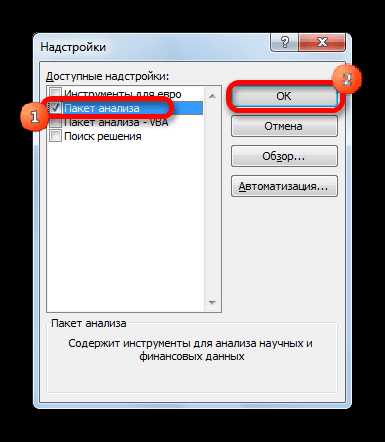
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
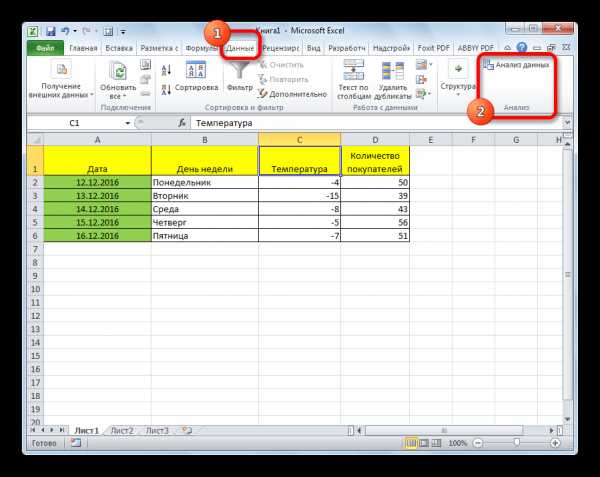
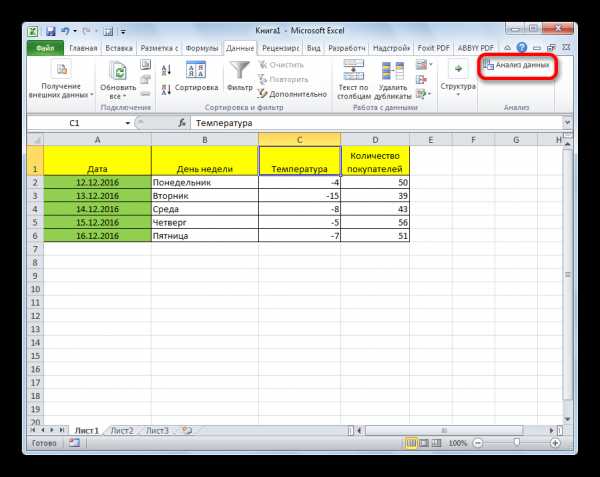
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
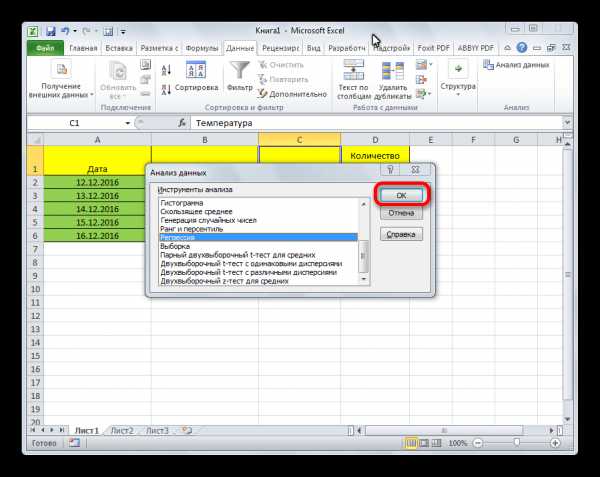
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
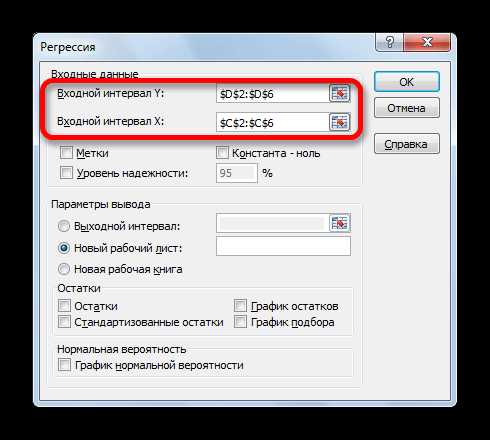
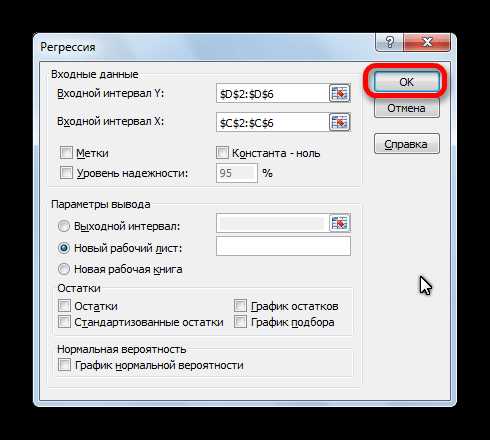
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
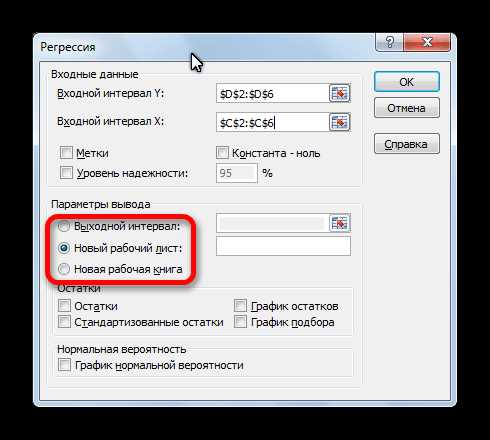
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
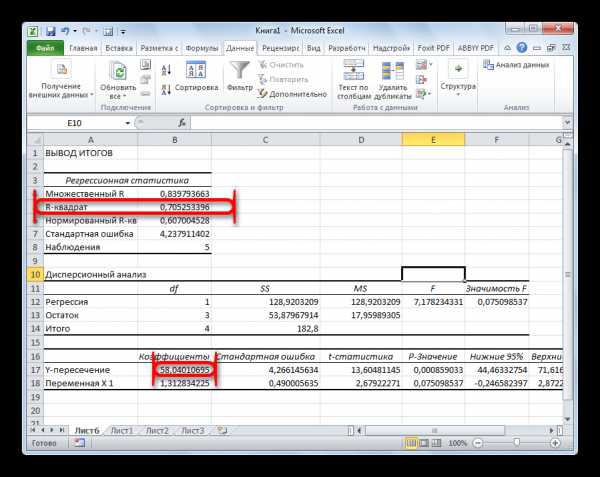
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ1 Построение множественного линейного уравнения регрессии в Excel
В пакете анализа MicrosoftExcelв режиме «Регрессия» реализованы следующие этапы множественной линейной регрессии:
1. Задания аналитической формы уравнения регрессии и определение параметров регрессии
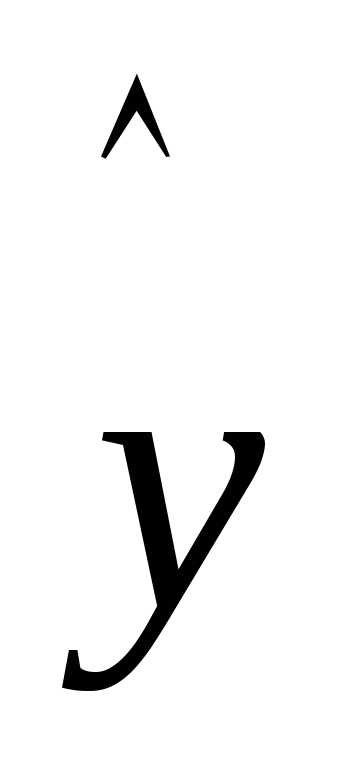= α0+ α1x1+ α2x2+ …+ αmxm,
где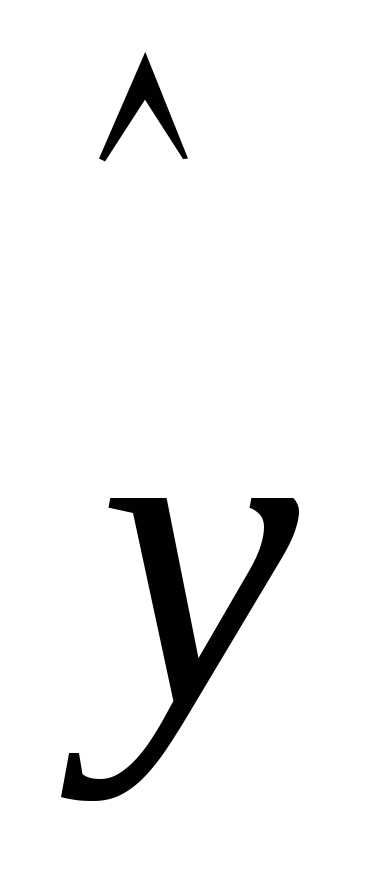 
—
теоретические значения результативного
признака, полученные путем подстановки
соответствующих значений факторных
признаков в уравнении регрессии;x1, x
Эти параметры определяются с помощью
метода наименьших квадратов. Для
нахождения параметров модели (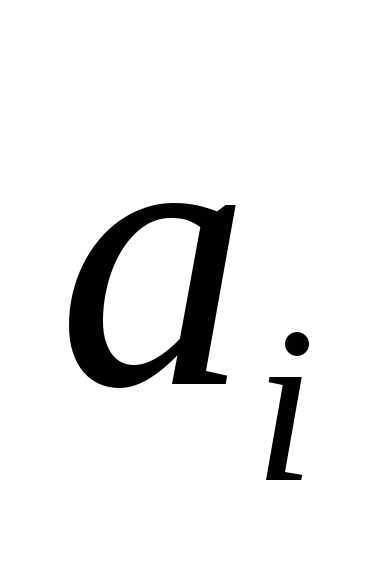
),
минимизируется сумма квадратов отклонений
эмпирических (фактических) значений
результативного признака от теоретических,
полученных по выбранному уравнению
регрессии.
2. Определение в регрессии степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии. Здесь необходимо знать следующие дисперсии:
– общую дисперсию результативного
признака 
,
отображающую влияние как основных, так
и остаточных факторов:
,
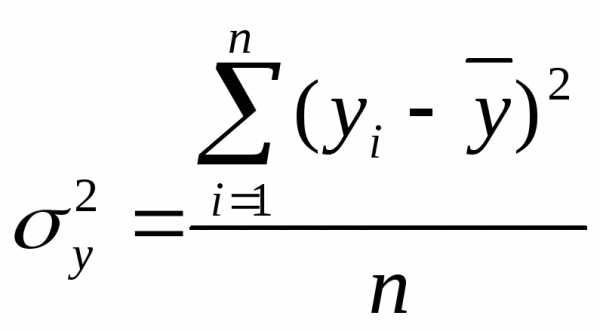где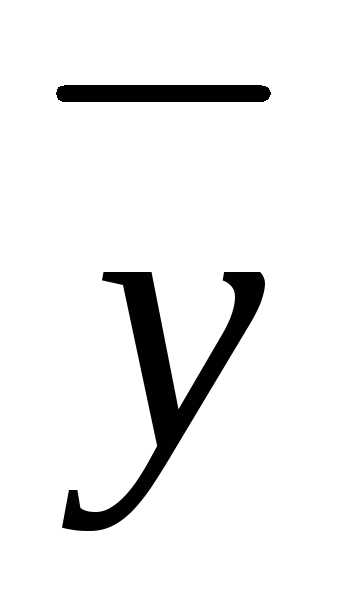 
– среднее значение результативного
признака
;
– факторную дисперсию результативного
признака 
,
отображающую влияние только основных
факторов:
;
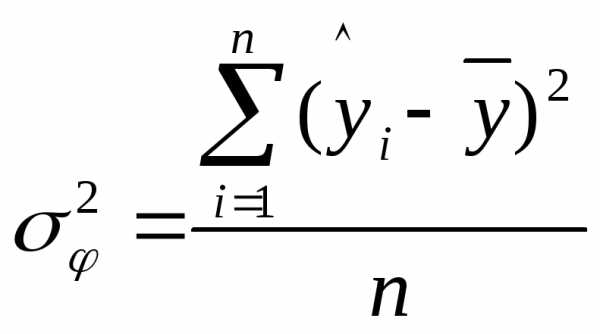– остаточную дисперсию результативного
признака 
,
отображающую влияние только остаточных
факторов:
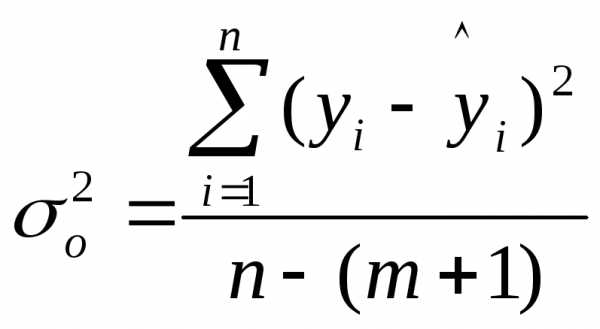
При корреляционной связи результативного признака и факторов выполняется соотношение
,
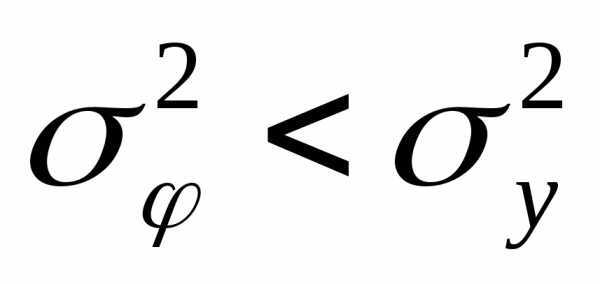при этом.
Для анализа общего качества уравнение
линейной многофакторной регрессии
используют множественный коэффициент
детерминации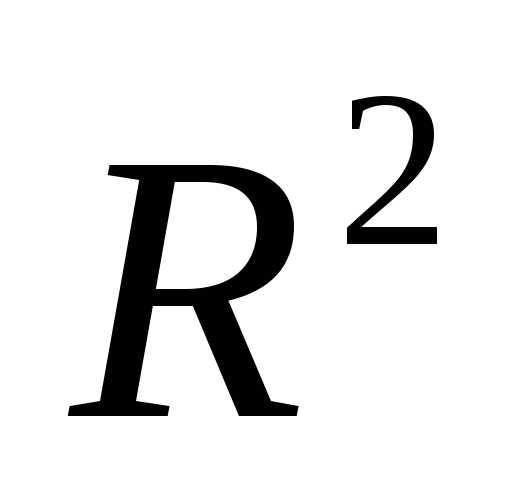 
(квадрат коэффициента множественной
корреляции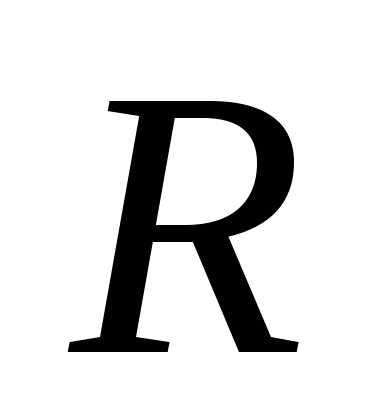
),
которые рассчитываются по формуле
.
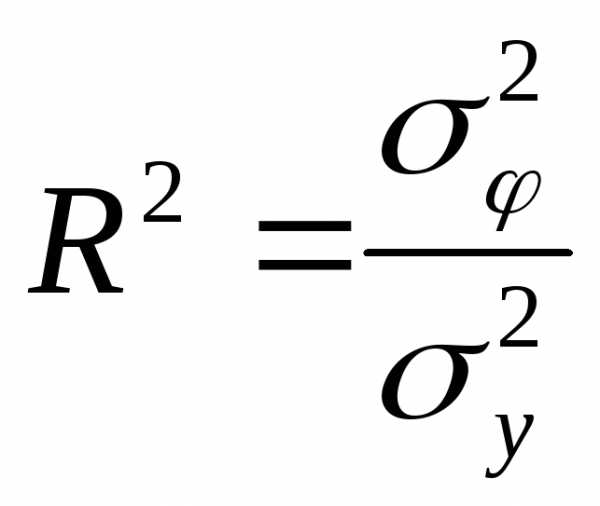Этот коэффициент определяет долю вариации результативного признака, обусловленную изменению факторных признаков, входящих в многофакторную регрессивную модель.
Так как уравнение регрессии строят на
основе выборочных данных, то возникает
вопрос об адекватности построенного
уравнения генеральным данным. Для этого
проверяется статистическая значимость
коэффициента детерминации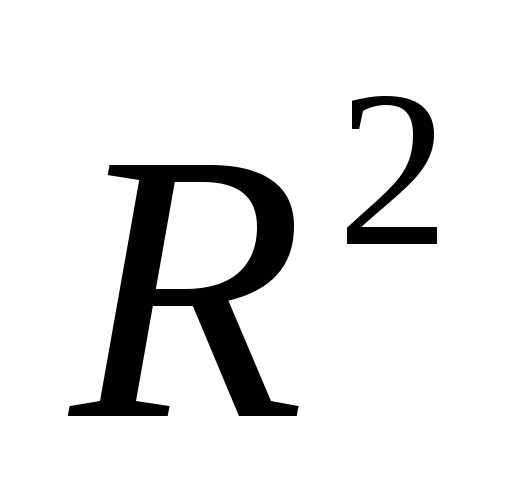 
В математической статистике доказывается,
что если гипотеза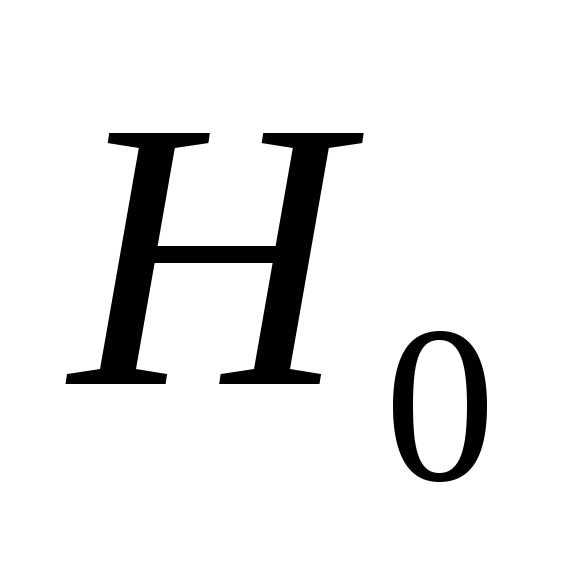 
:
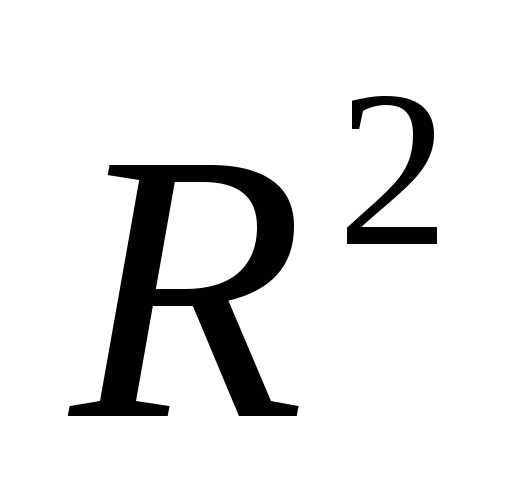=0
выполняется, то величина
,
имеет 
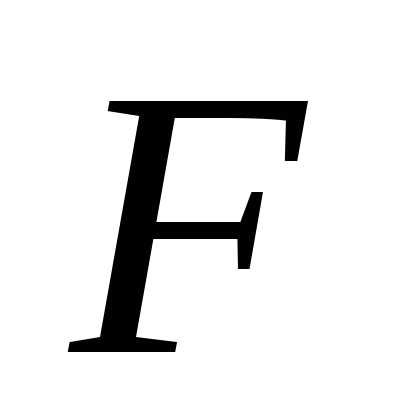распределение
(Фишера) с числом степеней свободы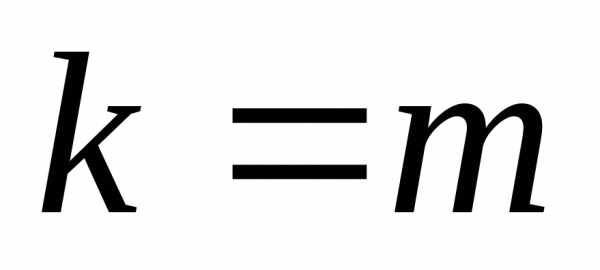
и.
При значениях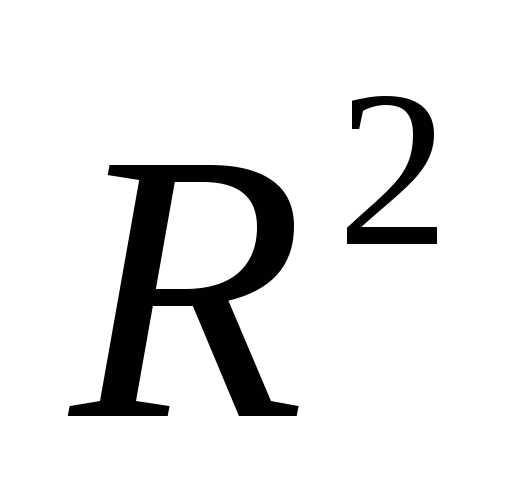 
>
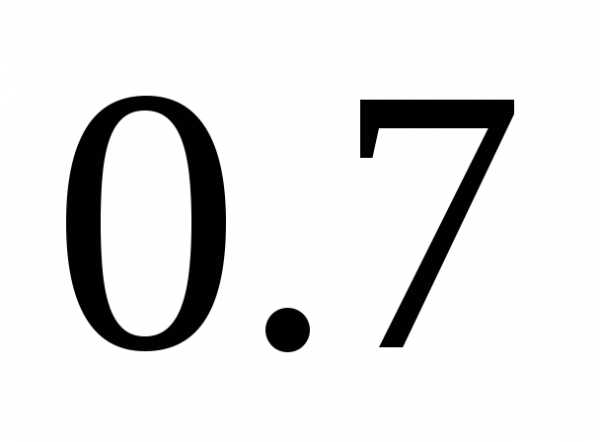считается,
что вариация результативного признака
обусловлена в основном влиянием
включенных в регрессионную модель
факторов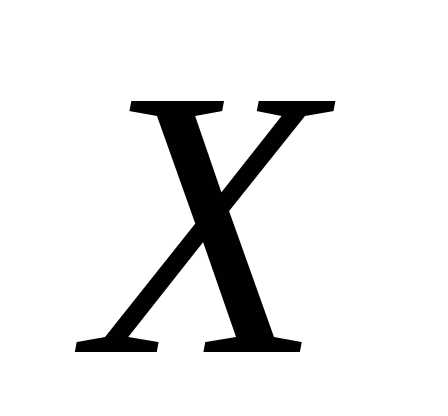
.
Для оценки адекватности уравнения регрессии так же используют показатель средней ошибки аппроксимации:
.
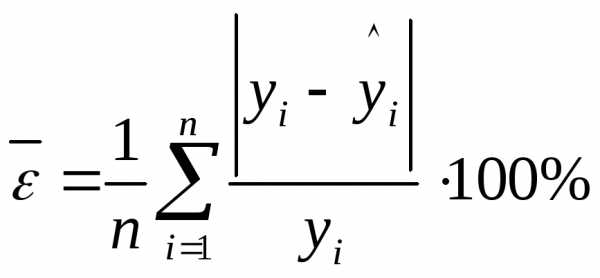3. В тех случаях, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, их исключают из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии включает в себя проверку значимости каждого коэффициента регрессии.
В математической статистике доказывается,
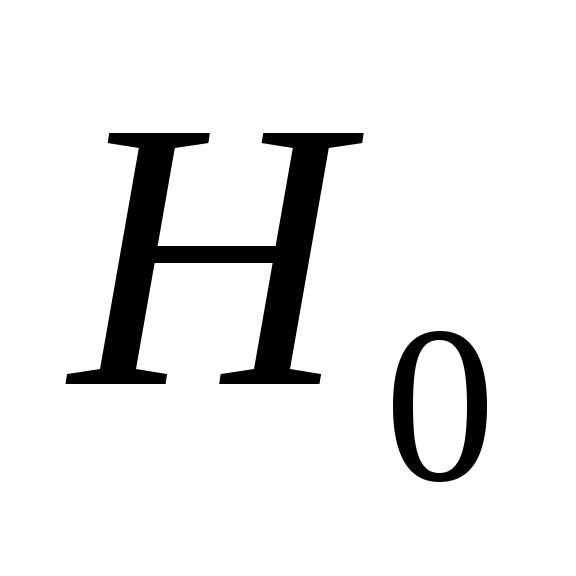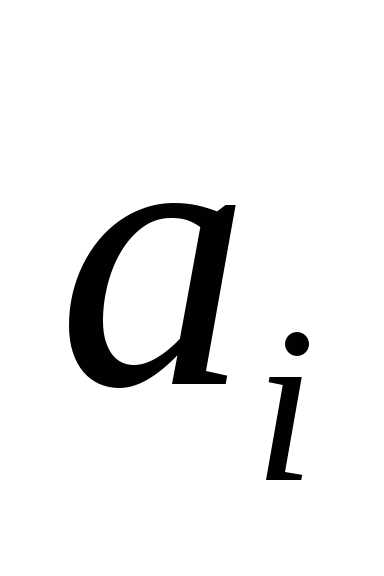что если гипотеза 
:
=0
выполняется, то величина
,
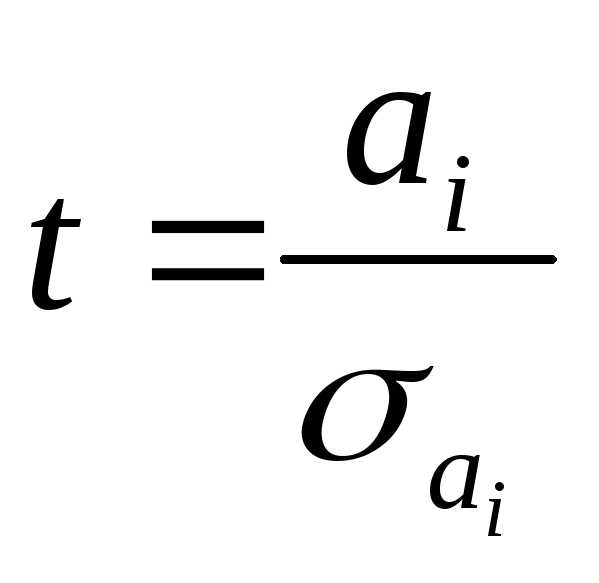имеет распределение Стьюдента с числом
степеней свободы
,
где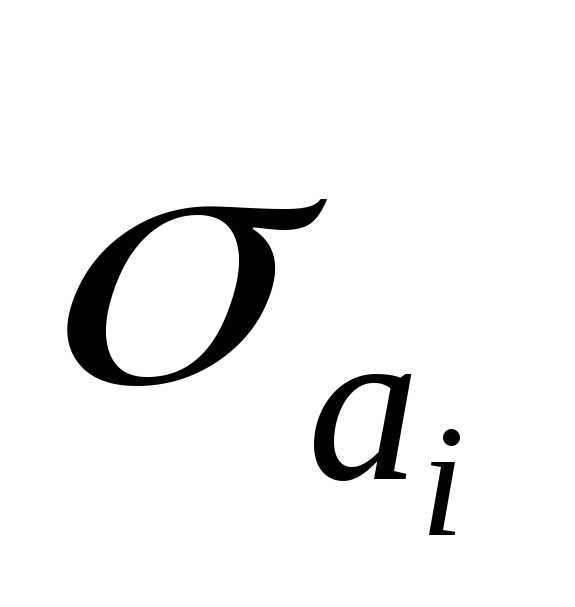
—
стандартное значение ошибки для
коэффициента регрессии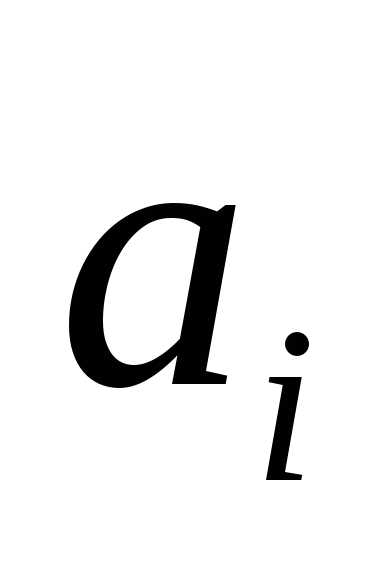
.
Гипотеза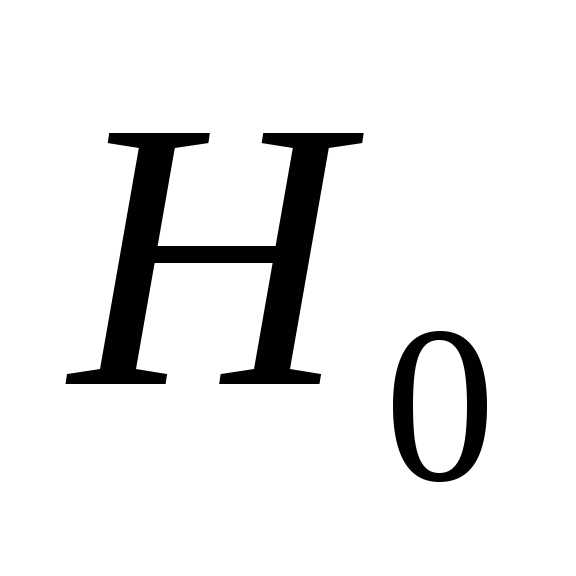 
:
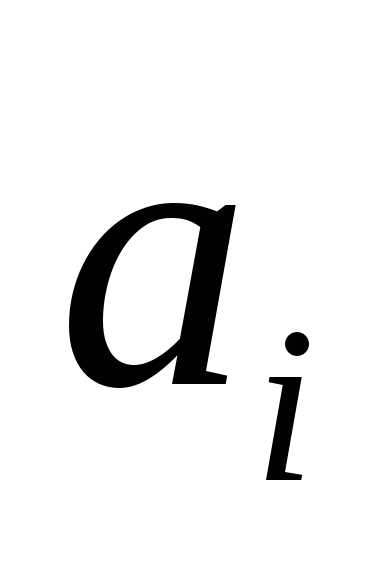=0
о незначимости коэффициента регрессии
отвергается, если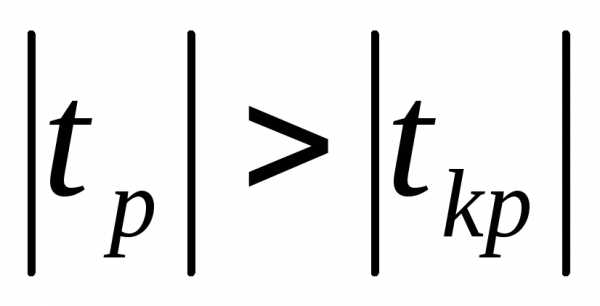
.
Зная значение
можно найти границы доверительных
интервалов для коэффициентов регрессии
(
;
).
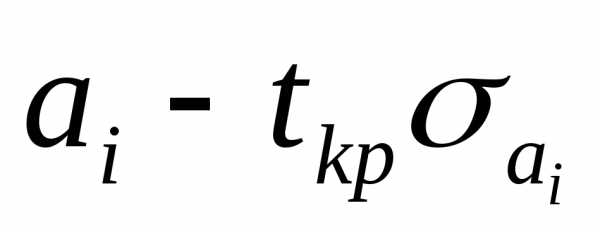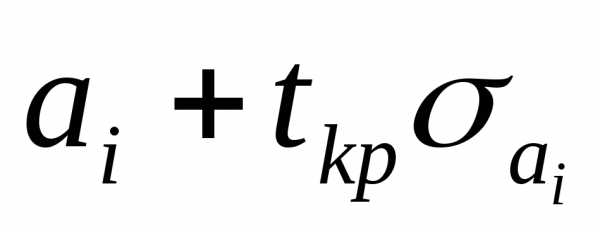При экономической интерпретации уравнения регрессии используются частные коэффициенты эластичности:
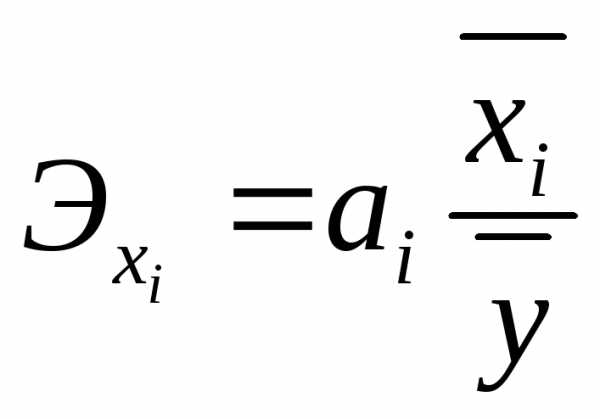
показывающие, насколько процентов в среднем изменится значение результативного признака при изменении значения соответствующего факторного признака на один процент.
В диалоговом окне режима работы «регрессии» задаются следующие параметры:
1. Входной интервал 
– вводятся ссылки на ячейки, содержащие
данные по результативному признаку
(состоят из одного столбца).
2. Входной интервал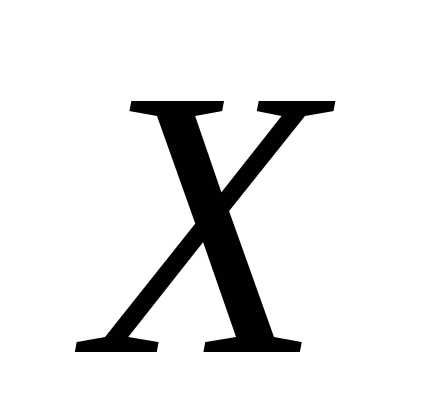 
– вводятся ссылки на ячейки, содержащие
факторные признаки (максимальное число
столбцов — 16).
3. Метки в первой строке/метки в первом столбце – устанавливаются в активное состояние, если первая строка (столбец) в обходном диапазоне содержит заголовки.
4. Уровень надежности – устанавливается в активное состояние, если необходимо ввести уровень надежности отличный от уровня 95 %, применяемого по умолчанию.
5. Константа – ноль – флажок устанавливается
в активное состояние, если требуется
чтобы линия регрессии прошла через
начало координат (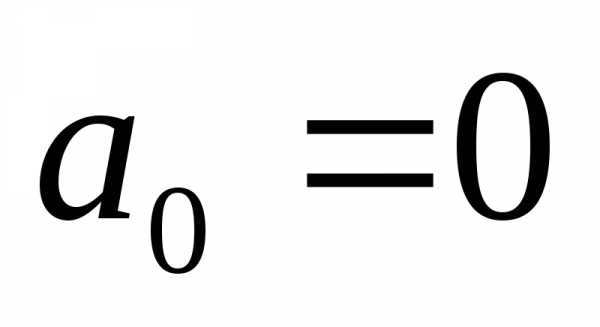
).
6. Выходной интервал/Новый рабочий лист/Новая рабочая книга – указывается, куда необходимо вынести результаты исследования.
7. Остатки – флажок устанавливается в активное состояние, если требуется включить выходной диапазон в столбец остатков.
8. Стандартизованные остатки – флажок устанавливается в активное состояние, если требуется включить выходной диапазон столбец стандартизованных остатков.
9. График остатков – флажок устанавливается
в активное состояние, если требуется
вывести на рабочий лист точечные графики
зависимости остатков от факторных
признаков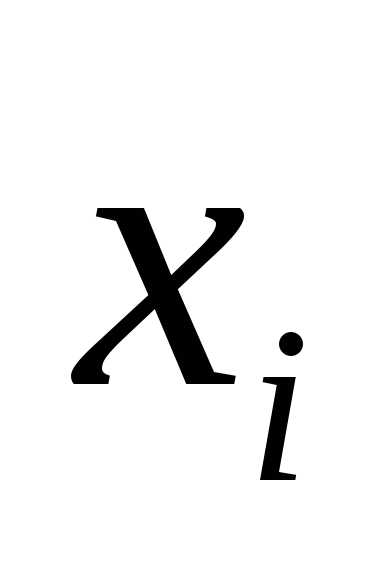 
.
10. График подбора – флажок устанавливается
в активное состояние, если требуется
вывести на рабочий лист точечные графики
зависимости теоретических результативных
значений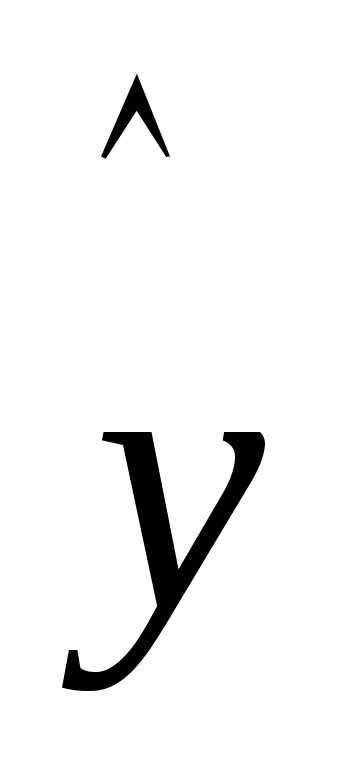 
от факторных признаков
.
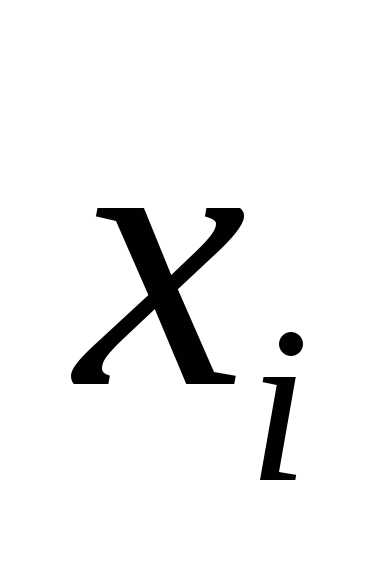11. График нормальной вероятности –
флажок устанавливается в активное
состояние, если требуется вывести
точечный график зависимости, наблюдаемых
значений 
от
автоматически формируемых интервалов
персентилей.
studfiles.net
Построение модели множественной регрессии в MS Excel
скачать (14081.3 kb.)Введение
Целью работы является построение модели множественной регрессии в MS Excel и построение прогнозов, принятие решений о спецификации и идентификации модели, интерпретация результатов.
Задачи:
) Построение системы показателей.
) Проведение корреляционного анализа.
) Нахождение уравнения регрессии зависимости объема продаж от ставки по депозитам и среднегодовой ставки по кредитам.
) Проведение регрессионного анализа. Оценивание качества построенной модели.
) Вычисление коэффициентов детерминации и F-критерия Фишера.
) Оценка статистической значимости коэффициентов уравнения множественной регрессии с помощью t-критерия Стьюдента при уровне значимости ? = 0,05.
1.
Построение системы показателей (факторов)
По десяти объектам экономической эффективности развития банков получены данные, характеризующие зависимость объема прибыли (Y) от среднегодовой ставки (Х1), ставки по депозитам (Х2) и размера внутрибанковских расходов (Х3).
Необходимо:
. Построить систему показателей.
. Провести анализ коэффициентов парной корреляции.
. Выбрать признаки для построения двухфакторной регрессионной модели.
. Выбрать вид модели и оценить ее параметры.
. Применить инструмента Регрессия (Анализ данных в EXCEL).
. Оценить качество модели.
. Определить значение F-критерия Фишера.
. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
Таблица 1. Статистические данные по всем переменным
Приведем промежуточные результаты при вычислении коэффициента корреляции:
Формула для вычисления ry,x1:
Таблица 2
Таблица 3
Таблицы 2-4. Промежуточные результаты при вычислении коэффициента.
Средние значения:
Дисперсия:
Коэффициент корреляции:
2. Анализ матрицы коэффициентов парной корреляции. Выбор факторных признаков для построения двухфакторной регрессионной модели
Использование инструмента Корреляция (Анализ данных в EXCEL):
1. Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.
. Выберем команду Сервис, Анализ данных.
. В диалоговом окне Анализ данных выберем инструмент Корреляция, а затем щелкнем на кнопку ОК.
4. В диалоговом окне Корреляция в поле Входной интервал вводим диапазон ячеек, содержащий исходные данные. Если и выделены и заголовки столбцов, то установим флажок Метки в первой строке.
Таблица 5. Результаты корреляционного анализа
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем прибыли имеет тесную связь с размером внутрибанковских расходов (0,865), с расходами на среднегодовую ставку (0,549) и с наблюдением (0,912). В данном примере n=10, m=4, после исключения незначимых факторов n=10, m=2.
3. Выбор вида модели и оценка ее параметров
Оценка параметров регрессии осуществляется по методу наименьших квадратов. Используем данные, приведенные в таблице.
Таблица 6. Статистические данные по всем переменным.
Уравнение может иметь вид:
Решим данную систему уравнений по формулам Крамера:
Найдем определители матриц:
Таблица 7. Нахождение определителей матриц
Найдем коэффициенты уравнения:=∆1/∆= 18,5158=∆2/∆= 0,185566=∆3/∆= 0,582028
Уравнение регрессии составит:
=18,51583+0,185566×1+0,582028×2
Расчетные значения Y определяются путем последовательной подстановки в эту модель значений, факторов, взятых для каждого наблюдения.
корреляция регрессионный определитель excel
4. Применение инструмента Регрессия (Анализ данных в EXCEL)
Регрессионный анализ — это статистический метод исследования зависимости случайной величины от переменных (аргументов), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения.
Для проведения регрессионного анализа выполним следующие действия:
. Выбираем команду Сервис, Анализ данных.
. В диалоговом окне Анализ данных выбираем инструмент Регрессия, ОК.
. В диалоговом окне Регрессия в поле Входной интервал Y введем адрес одного диапазона ячеек, который представляет зависимую переменную. В поле входной интервал Х введем адрес одного или нескольких диапазонов, которые содержат значения независимых переменных.
. Если выделены и заголовки столбцов, то устанавливаем флажок Метки в первой строке.
. Выбираем параметры вывода.
. В поле Остатки ставим необходимые флажки. ОК.
Таблица 8
Таблица 9
5. Оценка качества модели. Значение F-критерия Фишера
В таблице 10 приведены вычисленные по модели значения Y и значения остаточной компоненты.
Рисунок 1. График остатков
Стандартная ошибка коэффициента корреляции рассчитывается по формуле:
Serk=
к = 0,3162278
Вычисляем для модели коэффициент детерминации:
Он показывает долю вариации результативного признака под воздействием изучаемых факторов, т.е. в 83% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая.
Проверку значимости уравнения регрессии можно произвести на основе вычисления F-критерия Фишера.
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам. Для этого выполняется сравнение полученного значения F и табличного F значения. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
F=9,3
где n — число наблюдений, а m — число параметров при факторе х. F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а=0,05.
Значение F-критерия Фишера можно найти в таблице 4.2 протокола EXCEL.
Табличное значение F-критерия при доверительной вероятности 0,95 при V1=k=2 и V1=n-k=7 составляет 4,74. табличное значение F-критерия можно найти с помощью FРАСПОБР
Рисунок 2. Табличное значение F-критерия Фишера
6. Оценивание с помощью t-критерия Стьюдента статистической значимости коэффициентов уравнения множественной регрессии
Значимость коэффициентов уравнения регрессии а0, а1, а2 оценим с использованием t-критерия Стьюдента.
Наиболее часто t — критерий используется в двух случаях. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящая из разных пациентов, количество которых в группах может быть различно. Во втором же случае используется так называемый парный t-критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными.
Находим обратную матрицу (XTX)-1
| 4.13 | 0.0445 | -0.0696 |
| 0.0445 | 0.00374 | -0.00252 |
| -0.0696 | -0.00252 | 0.00214 |
b11=4.13
b22=0.00374
b33=0,00214
ta0=20,669/15,03=1.375
ta1=0,176/0,384=0.458
Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии а1, а2 приведены в четвертом столбце 4.3 протокола EXCEL. Табличное значение t-критерия при 5% уровне значимости и степенях свободы 7 составляет 2,36, его можно найти с помощью СТЬЮДРАСПОБР.
Рисунок 3. Табличное значение t-критерия Стьюдента
Заключение
Делаем следующие выводы:
1) Коэффициент множественной корреляции показывает на весьма сильную связь всего набора факторов с результатом
2) Сравнивая Fтабл. и Fфакт мы видим, что Fтабл. =4,74Fфакт. = 9.3. С вероятностью 0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты , которые сформировались под неслучайным воздействием факторов x1 и x2..
) Общий вывод состоит в том, что множественная модель с факторами x1 и x2 с = 0,83 содержит информативный фактор х1 и х2.
) Уравнение регрессии зависимости объема продаж от ставки по депозитам и среднегодовой ставки по кредитам:
=18,51583+0,185566×1+0,582028×2.
Список литературы
1) Кремер, Н.Ш. Эконометрика / Н.Ш. Кремер, Б.А. Путко. — М.: ЮНИТИ-ДАНА, 2005.
) Под ред. И.И. Елисеевой — М. — Финансы и статистика, 2003.
) В.П. Носко Эконометрика — «Дело» РАНХиГС, 2011
) Практикум по эконометрике / Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2005.
) Магнус Я.Р. — Эконометрика, 2009
) Айвазян С.А., Бухштабер В.М., Енюков С.А., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности. — М.: Финансы и статистика, 1989.
) Мартьянова М.Н., Сафронова Т.П. Основы статистики промышленности: Учебное пособие. — М.: Финансы и статистика, 1983
ref.rushkolnik.ru