Уравнение окружности в полярной системе координат – Окружность в полярных координатах | Формулы и расчеты онлайн

Окружность в полярных координатах | Формулы и расчеты онлайн

Уравнение окружности в полярных координатах выглядит очень просто

\[ ρ = R = \const \]

Это уравнение показывает, что ρ вообще не зависит от угла φ.

Построение окружности по простому уравнению в полярной системе координат

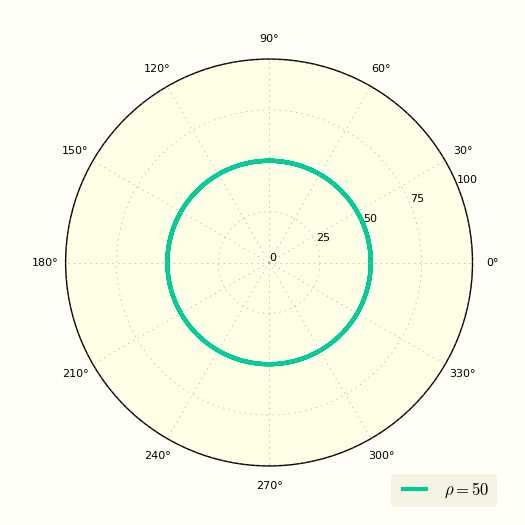
Еще одно уравнение окружности в полярных координатах

Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.

Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:

\[ (x-R)^2 + y^2 = R^2 \]

Также известны формулы перевода декартовых координат в полярные

Используя эти формулы и подставив их в (1) мы получим:

Уравнение окружности в полярных координатах

Изначально после подстановки имеем

\[ ρ^2-2Rρ\cos(φ) = 0 \]

И этого уравнения получается система

\[ \lvbig ρ = 0
ρ = 2R\cos(φ) \r.\]

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

\[ ρ = 2R\cos(φ) \]

Построение окружности в полярной системе координат

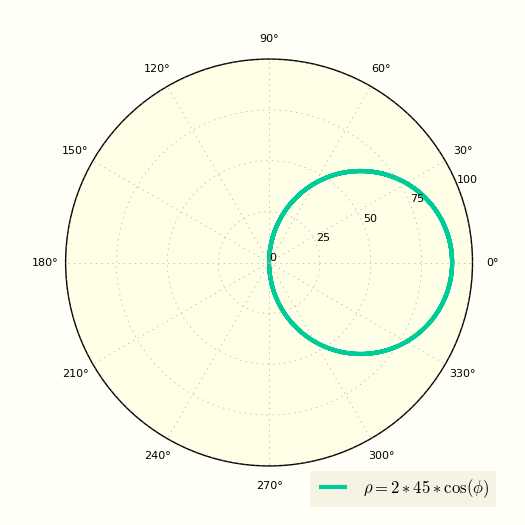
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах

В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.

При таком смещении окружность описывается уравнением:

\[ x^2 + (y-R)^2 = R^2 \]

Снова используем формулы перевода декартовых координат в полярные

получаем:

\[ ρ^2-2Rρ\sin(φ) = 0 \]

И этого уравнения получается система

\[ \lvbig ρ = 0
ρ = 2R\sin(φ) \r.\]

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

\[ ρ = 2R\sin(φ) \]

Построение окружности в полярной системе координат смещенной вверх относительно полюса

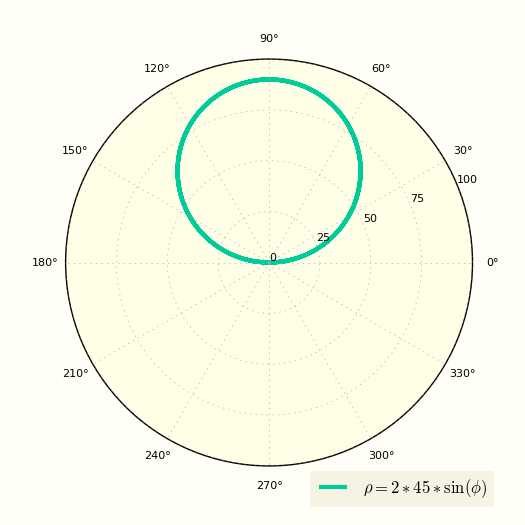
www.fxyz.ru

Уравнение кривых в полярных координатах

Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат были бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.

Окружность

Круг, заданный уравнением .

Общее уравнение окружности с центром в () и радиусом имеет вид:

Это уравнение может быть упрощено для частных случаев, например

является уравнением, определяющим окружность с центром в полюсе и радиусом .^[15]

Прямая

Радиальные прямые (те, которые проходят через полюс) определяются уравнением

где  — угол, на который прямая отклоняется от полярной оси, то есть, где  — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением

Полярная роза

Полярная роза задана уравнением .

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:

для произвольной постоянной (включая 0). Если  — целое число, то это уравнение будет определять розу с лепестками для нечётных , либо с лепестками для чётных . Если  — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь — лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

Спираль Архимеда

Одна из ветвей спирали Архимеда, задаваемая уравнением для .

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

Изменения параметра приводят к повороту спирали, а параметра  — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для а другую для . Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

Конические сечения

Эллипс.

Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

где  — эксцентриситет, а  — фокальный параметр. Если , это уравнение определяет гиперболу; если , то параболу; если , то эллипс. Отдельным случаем является , определяющее окружность с радиусом .

86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.

Вычисление площадей и длин дуг кривых в декартовых координатах

Пусть на плоскости x0y задана область, ограниченная снизу кривой y=f₁(x) , заданной в декартовых координатах, сверху – кривой  y=f₂(x) , слева – прямой x=a (ее может и не быть, если f₁(a)=f₂(a) ), справа – прямой  x=b.

Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле

Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, f₁(x)<0, то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.

Пусть на отрезке [a,b] уравнением  y=f(x) задана плоская кривая. Ее длина вычисляется по формуле

Пример 1 ::  Вычисление площадей и длин дуг в декартовых координатах

Вычислим площадь области, ограниченной кривыми   и длину границы этой области.

Вычисление площадей и длин дуг при параметрическом задании кривых

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть

при этом   x₁()=b, x₁()=b,  а сверху – кривой

Тогда площадь такой плоской фигуры вычисляем по формуле

Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что x'(t)dt=dx.

Пусть кривая на плоскости задана параметрически

Тогда длина этой кривой вычисляется по формуле

Пример 2 ::  Вычисление площадей и длин дуг при параметрическом задании кривых.

Вычислим площадь фигуры, ограниченной кривыми   ,   , . Вычислим длину дуги циклоиды  ,  .

Вычисление площадей и длин дуг кривых в полярных координатах

Когда кривая, ограничивающая область, задана в полярных координатах  =(), то площадь этой области вычисляем по формуле

Основная трудность в использовании этой формулы заключается в определении пределов интегрирования   ,  . Здесь нужно понимать, что кривая  =() определена только, если  >0. Поскольку в формуле присутствует ² , то она учтет и не существующую площадь, когда . Решив уравнение ()=0 , найдем пределы интегрирования.

Если кривая, ограничивающая область, задана в полярных координатах  =(), то ее длина вычисляется по формуле

Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.

studfiles.net

в полярной системе координат уравнение окружности

Вы искали в полярной системе координат уравнение окружности? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и окружность в полярных координатах, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «в полярной системе координат уравнение окружности».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как в полярной системе координат уравнение окружности,окружность в полярных координатах,уравнение окружности в полярной системе координат,уравнение окружности в полярных координатах,формула окружности в системе координат. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и в полярной системе координат уравнение окружности. Просто введите задачу в окошко и нажмите «решить» здесь или введите в окно ввода ниже свой запрос (например, уравнение окружности в полярной системе координат).

Где можно решить любую задачу по математике, а так же в полярной системе координат уравнение окружности Онлайн?

Решить задачу в полярной системе координат уравнение окружности вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на этой странице.

www.pocketteacher.ru

7 ВОПРОС

7. Полярная система координат. Уравнения некоторых линий в полярной системе координат.

Положение точки на плоскости можно определять не только в декартовой системе координат, но и в так называемой полярной системе координат.

Полярная система координат задается: точкой

O, называемой полюсом, и выходящей из этой точки полупрямой, называемой полярной осью с выбранной на ней единицей масштаба

Положение точкиM на плоскости определяется двумя числами: числом , выражающим расстояние точки M от полюса, и числом – величиной угла, образованного отрезком OM с полярной осью. Положительным направлением отсчета угла  считается направление против хода часовой стрелки. Числа  и  называют полярными координатами точки M и обозначают М(,).

Полярный угол определен с точностью до слагаемого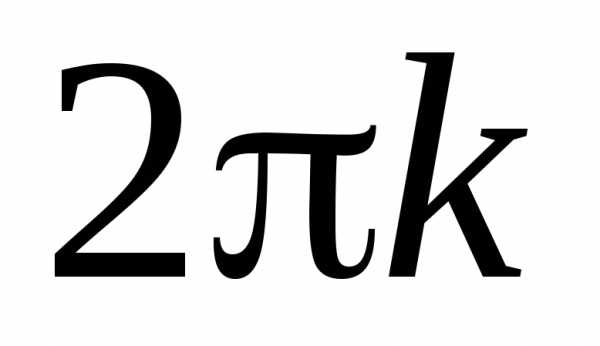,. Положение любой точки на плоскости (кроме полюса) однозначно соответствует координатам и , если 0≤≤∞, 0≤≤2k, (или -≤). Для полюса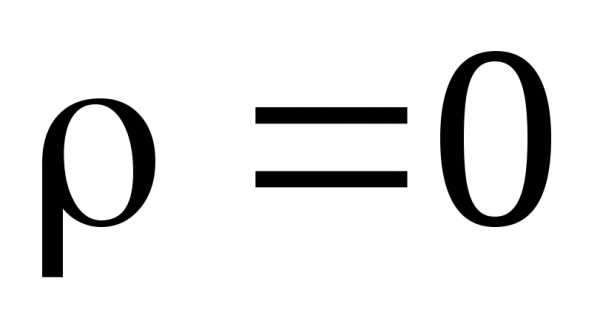

,– произвольное. В дальнейшем полярное расстояниебудем всегда считать положительным.

Cвязь между полярными и прямоугольными декартовыми координатами. 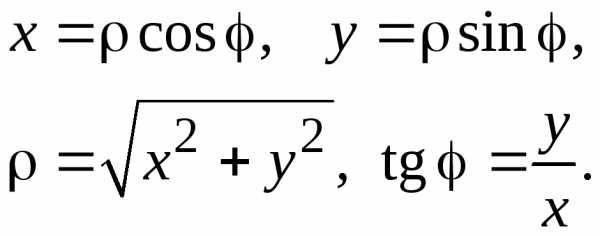(2)

В последней формуле при определении нужно учитывать, в какой четверти находится точка.

Рис. 4

Уравнения некоторых линий в полярной системе координат

1.Прямая линия,

А) проходящая через полюс:.y=kx, x=r*cos , y= r*sin  k*r*cos = r*sin k=tg

B) не проходящая через полюс: Ах+Ву+С=0r=/cos(-£), где -расстояние от прямой до полюса, £ — угол наклона нормального вектора прямой n(А,В)

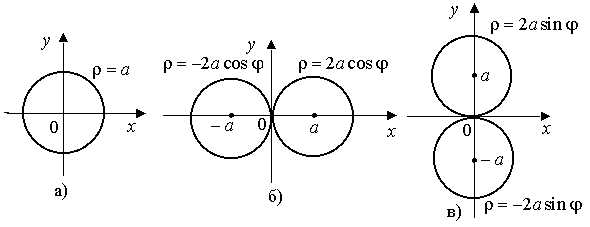
2. Окружность.

а) Окружность с центром в начале координат (рис а) .

б) Окружность с центром, смещенным по оси Ox (рис. б)

, .

в) Окружность с центром, смещенным по оси Oy (рис. в)

, .

3. Линии второго порядка (эллипс, гипербола, парабола)

Уравнение эллипса, гиперболы и параболы в полярной системе координат имеет вид

,

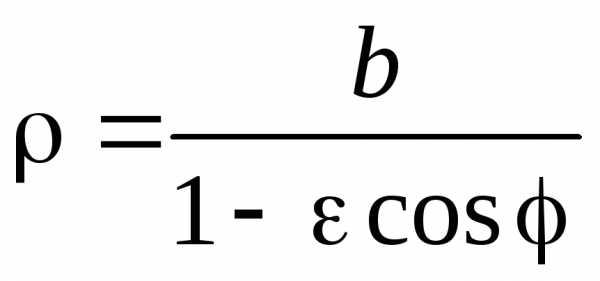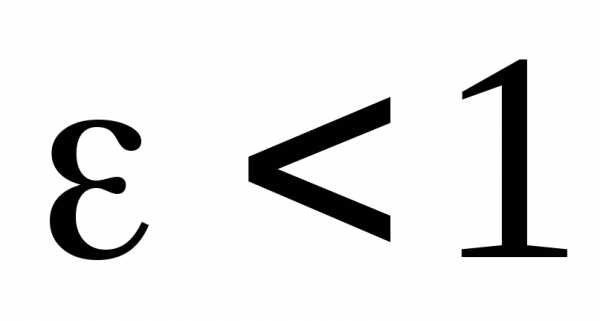где b – параметр, – эксцентриситет. При— эллипс при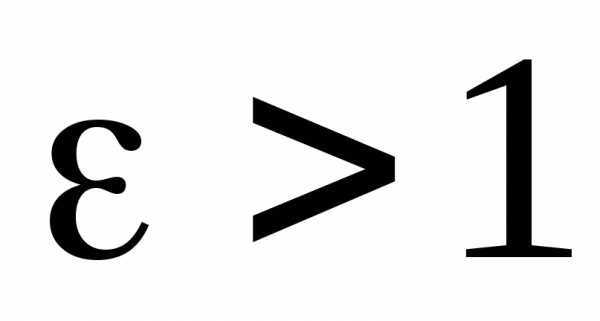– гипербола, при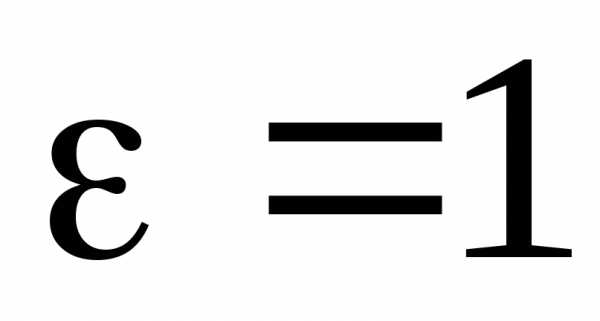– парабола.

Переход к декартовым координатам:

r=(x²+y²)^1/2, cos=x/ (x²+y²)^1/2

Розы. Розами называются семейство кривых, уравнение которых в полярных координатах имеет вид:

или ,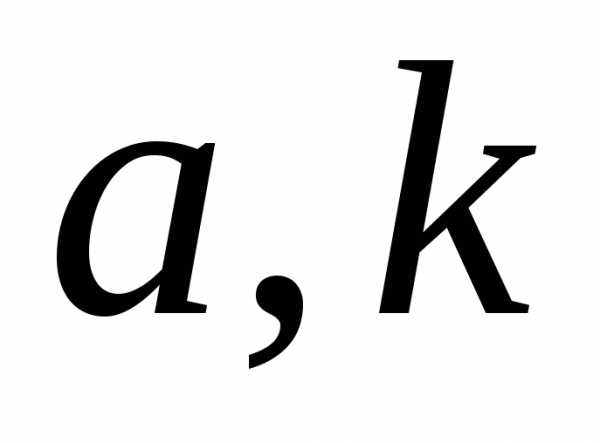– положительные числа.

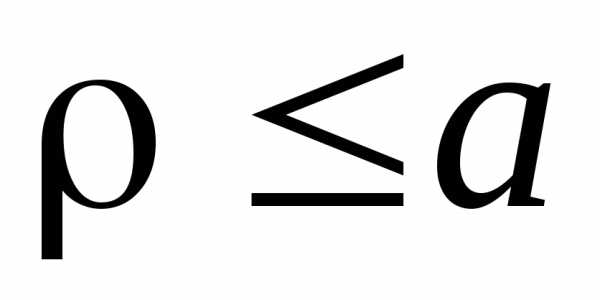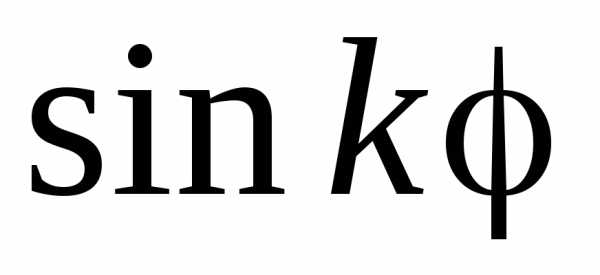Так как , то кривые находятся внутри круга радиусаa. Вследствие периодичности функций и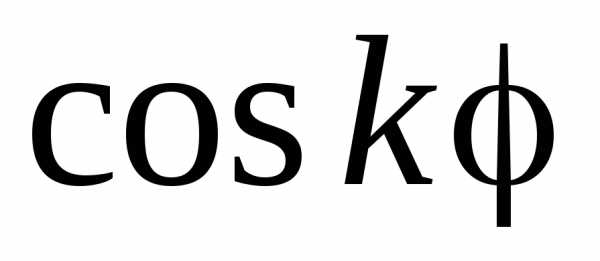розы состоят из конгруэнтных лепестков, симметричных относительно наибольших радиусов, каждый из которых равенa. Если 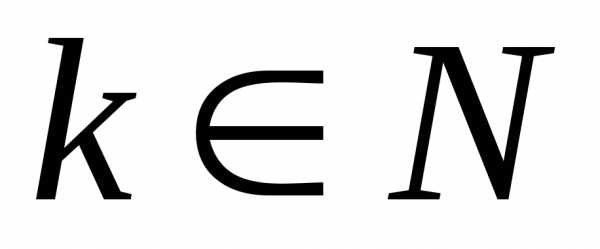, то роза состоит изk лепестков (если кривая строится для ).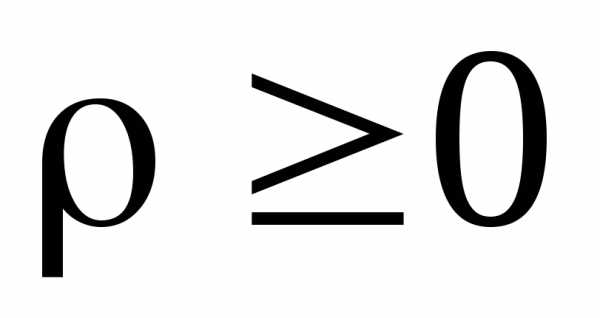

, .

5.Спираль Архимеда определяется как траектория точки, движущейся из точки O с постоянной скоростью v по лучу, вращающемуся около полюса O с постоянной угловой скоростью . Уравнение в полярных координатах имеет вид

, .

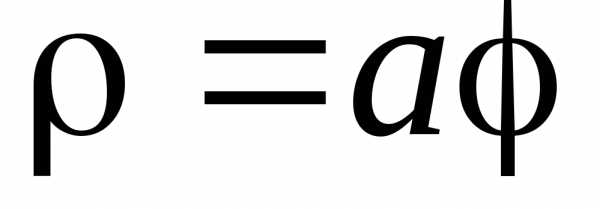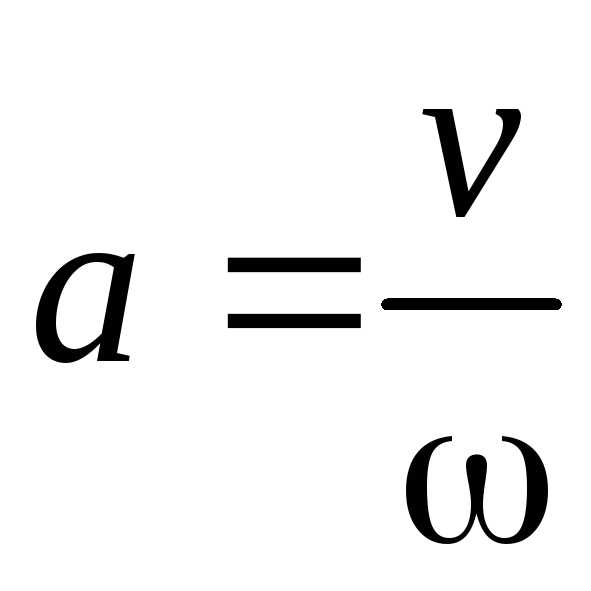studfiles.net

18. Полярные координаты. Параметрические уравнения линии

Наиболее важной после прямоугольной системы является полярная система координат.

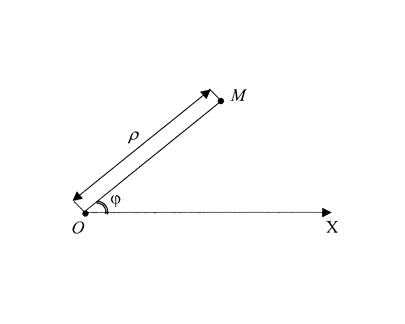Возьмем на плоскости точку , которая называется полюсом. Проведем из полюса направленную полупрямую , называемую полярной осью (рис.18). Пусть — произвольная точка плоскости. Соединим точку С полюсом Отрезком . Длина отрезка , т. е. расстояние точки от полюса, называется Полярным радиусом точки , а угол , отсчитываемый от полярной оси к отрезку Против движения часовой стрелки, Полярным углом.

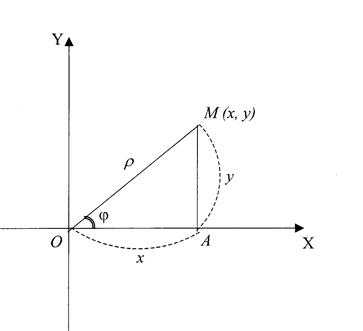Полярный радиус и полярный угол и Составляют Полярные координаты точки , и записывается следующим образом .

Рассмотрим переход от полярных координат к прямоугольным и обратно.

Пусть полюс полярной системы совпадает в началом прямоуголь­ной системы координат , а по­лярная ось является положительной полуосью (рис.19). Тогда для произвольной точки имеем:

Считая угол острым, из прямоугольного находим

Или

Полученные формулы справедливы для любого угла и выражают прямоугольные координаты точки через ее полярные координаты.

Выразим полярные координаты точки через прямоугольные координаты из того же прямоугольника

Или

Пример 1. Найти полярное уравнение прямой

Решение. Так как , то или . Это и есть уравнение данной прямой в полярных координатах.

Пример 2. Написать уравнение линии в полярных координатах.

Решение. Так как , а Подставим эти выражения в данное уравнение линии

или

Это уравнение данной линии в полярных координатах.

Иногда бывает удобнее вместо уравнения линии в прямоугольных координатах, рассматривать параметрические уравнения линии, дающие выражения текущих координат и в виде функций от некоторой переменной величины (параметра).

Пример 1. Выведем параметрическое уравнение окружности.

Решение. Пусть — произвольная точка окружности радиуса с центром в начале координат (рис.20). В прямоугольном треугольнике обозначим угол через . Будем иметь равенства

Или

(1)

Это и есть параметрическое урав­нение окружности.

Пример 2. Параметрическое уравнение эллиса.

Решение. Эллипс с полуосями и можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса , где коэффициент сжатия . Пусть — точка эллипса и — соответствующая точка окружности (рис.21), где

. (1)

За параметр Примем угол, образованный радиусом окружности с положительным направлением оси : Используя формулы (1) имеем

Таким образом, параметрические уравнения эллипса с полуосями и есть

. (2)

< Предыдущая		Следующая >

matica.org.ua

Полярная система координат.

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из точки лучаl, называемогополярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными. Обычно считают положительными повороты против часовой стрелки.

Определение.Точка О называетсяполюсом, а луч l –полярной осью.

Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол называетсяполярным углом.

М

r

r =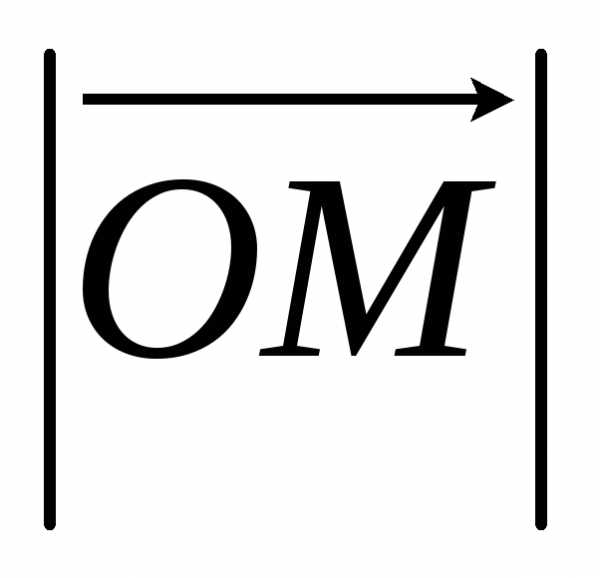



0

l

Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.

Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:

x = rcos; y = rsin; x² + y² = r²

Пример.Уравнение кривой в полярной системе координат имеет вид:

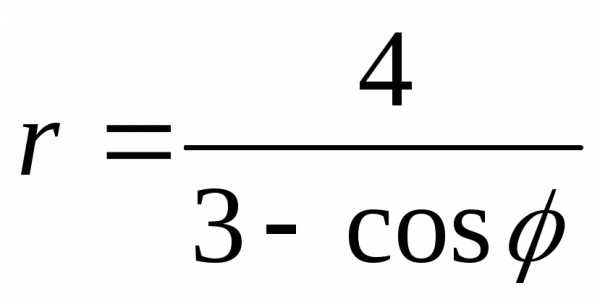. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.

Воспользуемся связью декартовой прямоугольной и полярной системы координат: ;

Получили каноническое уравнение эллипса. Из уравнения видно, что центр эллипса сдвинут вдоль осиОхна 1/2 вправо, большая полуосьa равна 3/2, меньшая полуосьb равна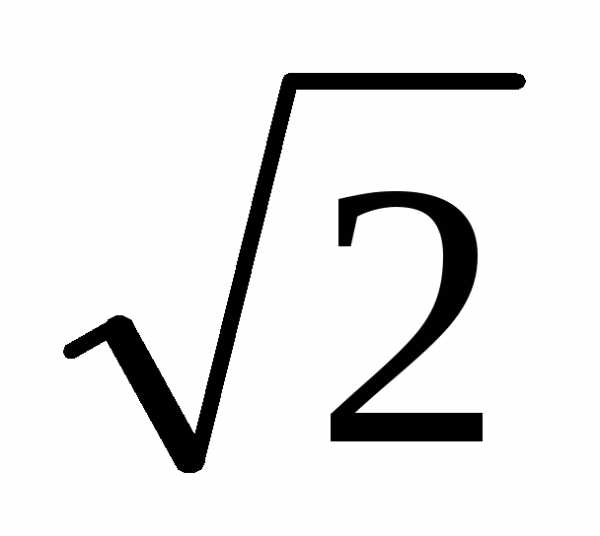, половина расстояния между фокусами равнос =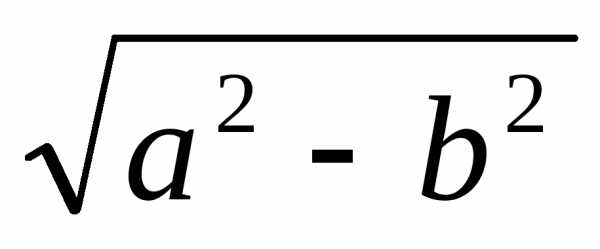= 1/2. Эксцентриситет равене = с/a= 1/3. ФокусыF₁(0; 0) иF₂(1; 0).

y

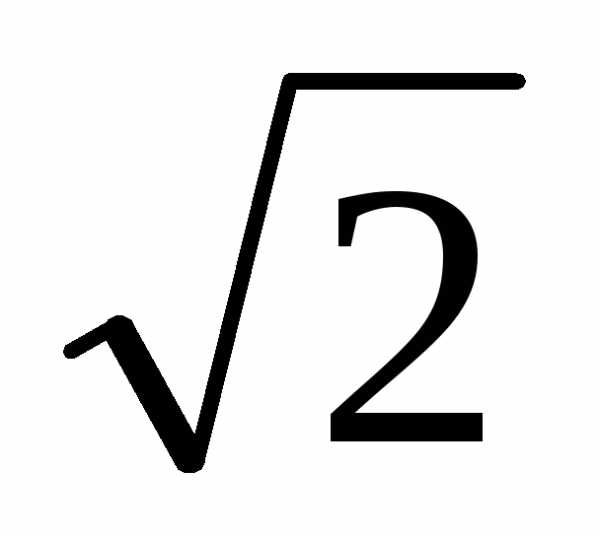
F₁F₂

-1 0 ½ 1 2 x

—

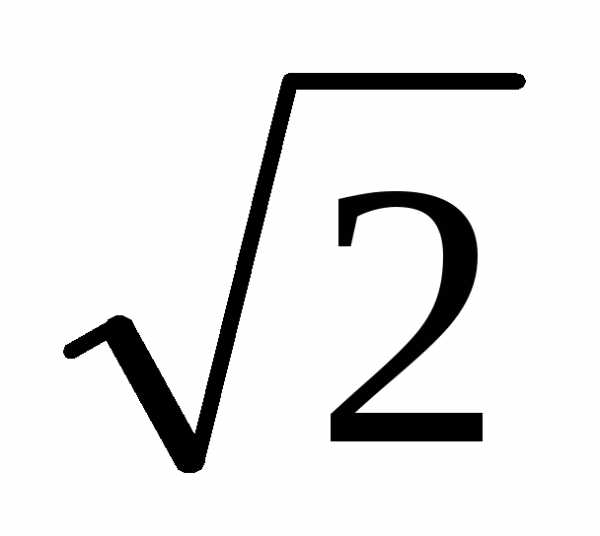
Пример.Уравнение кривой в полярной системе координат имеет вид:

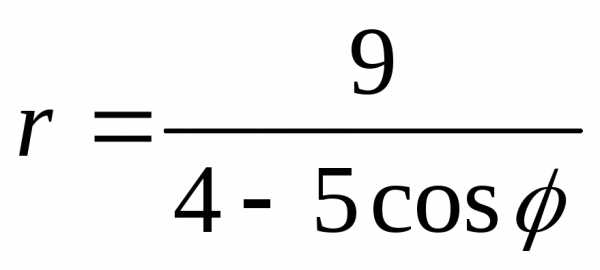. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.

Подставим в заданное уравнение формулы, связывающие полярную и декартову прямоугольную системы координат.

Получили каноническое уравнение гиперболы. Из уравнения видно, что гипербола сдвинута вдоль оси Ох на 5 влево, большая полуось а равна 4, меньшая полуосьbравна 3, откуда получаемc²=a²+b²;c= 5;e=c/a= 5/4.

Фокусы F₁(-10; 0),F₂(0; 0).

Построим график этой гиперболы.

y

3

F₁-9 -5 -1 0F₂x

-3

§5. Аналитическая геометрия в пространстве.

Уравнение поверхности и линии в пространстве.

Определение.Пусть в прямоугольной системе координатOXYZ координатыx, y, z связаны уравнениемF(x,y,z) = 0 (1.1).

Любое уравнение, связывающее координаты x, y, z(1.1.), является уравнением поверхностиS в заданной системе координат, если ему удовлетворяют координаты любой точкиM(x,y,z), принадлежащейS и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

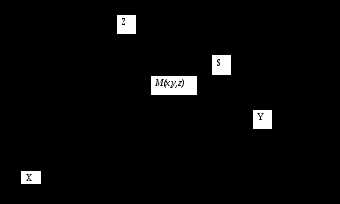
Линию в пространстве L можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0– уравнения поверхностей, пересекающихся по линииL.

Тогда систему двух уравнений

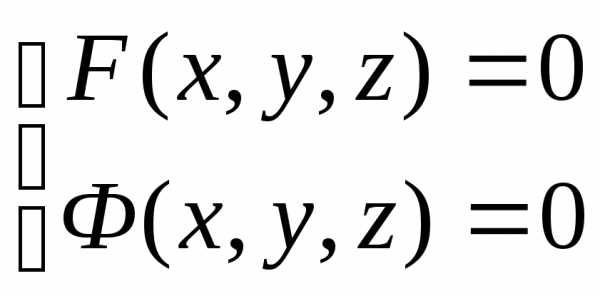
назовем уравнением линии L в пространстве.

studfiles.net

Связь между декартовыми координатами и полярными

Часто можно легко выписать формулу, показывающую, как изменятся координаты точки М, если от одной системы координат перейти к другой. Выведем формулы связи между декартовыми координатами (x,y) и полярными r и φ.

Пусть даны: декартова система координат и полярная с полюсом в начале координат и полярной осью, совпадающей с осью X (рис. 7а), x и y – декартовы координаты точки, r и φ – ее полярные координаты. Из треугольника, образованного точками О, М и х, видно, что зависимость между полярными координатами r и φ точки М и ее прямоугольными координатами x и y выражается формулами, известными из тригонометрии:

y=rsinj, x=rcosj — вычисление декартовых координат по полярным

— вычисление полярных координат по декартовым (одной формулы для определения угла недостаточно).

То есть, зная декартовы координаты точки, мы можем определить ее полярные координаты. И наоборот. Зная ее полярные координаты, можно определить декартовы координаты.

 

Пример

Чему равны полярные координаты точки М, имеющей декартовы координаты один и минус один?

Подставив значения декартовых координат в формулы, которые задают выражение полярных координат через декартовы, получаем, что:

Так как точка М находится в четвертой четверти, то j=315° (рис. 7б)

 

Линии и их уравнения

Итак, при наличии системы координат каждой точке плоскости соответствует пара действительных чисел и, наоборот, каждой паре чисел соответствует определенная точка плоскости. Можно установить, что линиям на плоскости соответствует некоторое уравнение с двумя переменными x и y в декартовой системе координат и переменными r и j в полярной. Связь между уравнениями и линиями позволяет свести изучение геометрических свойств линий к исследованию аналитических свойств соответствующих им уравнений. Линии на плоскости соответствует некоторое уравнение с двумя переменными, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней. Такое уравнение называют уравнением данной линии. Входящие в него координаты x и y (или r и j) произвольной точки линии называются текущими координатами.

Уравнение линии на плоскости может быть аналитически задано в явном виде — y=f(x), r=f(j) или неявном виде — F(x,y)=0, F(r,j)=0. Полярную систему координат удобно использовать, когда длина радиуса-вектора точек, лежащих на линии, связана аналитической зависимостью со значением угла поворота j.

 

Примеры уравнений линий в декартовой и полярной системе координат

1.Уравнение прямой, отсекающей на оси Y отрезок величины b: y=kx+b, где k — значение tg угла наклона прямой к оси ОХ; параметр k называется угловым коэффициентом прямой. Уравнение линии задано в явном виде (рис. 8).

2.Уравнение линии, являющейся геометрическим местом точек, для которых расстояние до некоторой точки О с координатами а и b есть величина постоянная (обозначим ее через R). Выпишем условие равенства константе R расстояния от любой точки М(x,y) до точки O(a,b): . Возведя обе части равенства в квадрат, получаем каноническое уравнение окружности:

(x-a)²+(y-b)²=R²

Если система координат выбрана так, что центр окружности совпадает с началом координат, то a=0, b=0 и уравнение окружности принимает вид:

x²+y²=R²

Уравнение линии в этих примерах задано в неявном виде.

3.Уравнение окружности в полярной системе координат.

Введем полярную систему координат, центр которой совпадает с центром окружности, а направление полярной оси, например, горизонтальное. Окружность определяется, как геометрическое место точек, для которых расстояние до некоторой точки О есть величина постоянная (эту величину мы обозначали через R). Следовательно, уравнение окружности в полярных координатах: r=R

Окружность дает простейший пример линии, уравнение которой от перехода к полярной системе координат упрощается.

 

 

На рисунке 9 приведена окружность и ее уравнение в разных системах координат. Одновременно мы показали на этом простом примере, что вид линии не зависит от того, в какой системе координат написано ее уравнение. От выбора системы координат зависит лишь вид уравнения.

Рассмотрим примеры еще 2 кривых, длина радиуса-вектора которых связана аналитической зависимостью со значением его угла поворота j. Уравнения этих кривых удобно задавать именно в полярной системе координат.

 

Уравнение спирали Архимеда

Пусть по лучу, вращающемуся около полюса О с постоянной угловой скоростью w, движется точка М с постоянной скоростью v. Тогда точка М опишет линию, которая называется спиралью Архимеда. Для того чтобы вывести уравнение этой линии, введем полярную систему координат, центр которой совпадает с точкой О, тогда расстояние от точки М до полюса О r=ОМ пропорционально углу j (рис 10а). Это означает, что уравнение спирали Архимеда можно записать в виде:

r=kj.

В предыдущих главах мы строили опорные точки графика спирали Архимеда, руководствуясь именно этим свойством спирали – при изменении угла на величину nΔφ длину радиуса-вектора мы меняли на nΔr.

 

Из уравнения видно, что если j=2p (точка М совершила полный оборот вокруг центра О), то r₁=k×2p, после второго оборота r₂=k×4p=2r₁, после третьего r₃=k×6p=3r₁ и т.д. Величина k×2p=а называется шагом спирали. Шаг спирали — это величина смещения вдоль луча, соответствующее повороту луча на 2p.

Так как шаг спирали имеет ясный физический смысл, уравнение спирали Архимеда принято задавать в терминах именно шага спирали: . Коэффициент пропорциональности k и шаг спирали а связаны соотношением: и а=2pk.

 



infopedia.su