Методы решения показательных уравнений
Разделы: Математика
Методы решения показательных уравнений
1. Простейшие показательные уравнения
Примеры.
Пример 1. Решите уравнение: 34x-5 = 3x+4 .
Решение.
34x-5 = 3x+4 <=> 4x 5 = x+4 <=> 3x=9<=> x = 3 .
Ответ:3
Пример 2. Решите уравнение: 2x-4 = 3 .
Решение.
2x-4 = 3 <=> x- 4 = x = + 4 <=> x = + <=> x = .
Ответ:.
Пример 3. Решите уравнение:-3x = -7 .
Решение.
-3x = -7 , решений нет, так как -3x > 0 для x R .
Ответ: .
2. Методы преобразования показательных уравнений к простейшим.
A. Метод уравнивания оснований.
Примеры.
Пример 1. Решите уравнение: 27- = 0 .
Решение.
27- = 0 <=> 3334x-9— (32)x+1 = 0 <=> 33+ (4x-9)— 32(x+1) = 0<=> 34x-6-32x+2 = 0 <=> 34x-6 = 32x+2<=> 4x-6=2x+2 <=> 2x = 8 <=> x=4.
Ответ: 4.
Пример 2. Решите уравнение: .
Решение.
0 <=> (22)x3x
5x = 604x-15 <=> 4x3x5x = 604x-15 <=> (4x = 604x-15 <=> 60x=604x-15 <=> <=>x=4x-15 <=> 3x=15 <=> x=5.Ответ: 5.
В. Уравнения, решаемые разложением на множители.
Примеры.
Пример 1. Решите уравнение: x2x = 22x + 8x-16.
Решение.
x2x = 22x + 8x-16 <=> x2x — 22x = 8x-2) <=> 2x(x-2) — 8<=> (x-2) x — 8) = 0 <=> <=> <=> <=> .
Ответ:
Пример 2 . Решите уравнение:
52x — 7x — 52x35 +7x = 0 <=> (52x — 7x)((
Ответ: 0.
С. Уравнения, которые с помощью подстановки f(x) = t, t>0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).
Пусть , где А, В, С — некоторые числа. Сделаем замену: >0, тогда A2 + B + C = 0
Решаем полученное уравнение, находим значения t, учитываем условие t >0 , возвращаемся к простейшему показательному уравнению f(x) = t, решаем его и записываем ответ.
Примеры.
Пример 1 . Решите уравнение: 22+x — 22-x = 5.
Решение.
22+x — 22-x
= 5 <=> 222x — = 15 <=> 4(2x)2 — 4 = 15xДелаем замену t = 2x, t > 0. Получаем уравнение 42 — 4 = 15t <=> 4t2 — 15t — 4=0
<=> , t = не удовлетворяет условию t > 0.
Вернемся к переменной х:
2х = 4<=> 2x = 22 <=> x=2.
Ответ: 2
Пример 2. Решите уравнение:
Решение.
5
Делаем замену: , тогда Получаем уравнение:
5 , t = не удовлетворяет условию t
Вернемся к переменной Х:
Ответ: 2.
D. Уравнения, левая часть которых имеет вид A
nx + B kx bmx + С bnx
Для решения уравнения такого типа необходимо обе части уравнения разделить либо на nx, либо на nx и получится уравнение типа С).
Примеры.
Пример 1. Решите уравнение: 222x — 5x + 332x = 0.
Решение.
222x — 5x + 332x = 0 <=> 22x — 5x3x + 332x = 0 <=> 2 — + 3 = 0 <=>
<=> 22x — 5x + 3 = 0
Пусть t = x, t>0 , тогда 2t- 5t + 3 = 0 <=> , оба значения t удовлетворяют условию t Вернемся к переменной х:
<=> <=> .Ответ:
Пример 2. Решите уравнение: 8 x + 18x — 227x = 0 .
Решение.
8x + 18x — 227x = 0 <=> + — 2 = 0 <=> 23x + 2x 32x — 233x = 0<=>
<=> + — 2 = 0 <=> + — 2 = 0.
Пусть = t, t>0 , тогда t3 + t — 2 = 0<=> (t3 — 1) + (t -1 )= 0 <=> (t-1) (t2 +t +1) + (t — 1) <=> (t — 1) (t2 + t +2) = 0 <=> <=> t - 1= 0 <=> t=1. (t>0)
Вернемся к переменной х: = 1 <=> = x = 0 .
Ответ: 0.
К данному типу уравнений относятся уравнения , левая часть которых имеет вид , где А, В, С -некоторые числа, причем .
Уравнения такого типа решаются с помощью подстановки :
Пример 3. Решите уравнение:
Решение.
Заметим, что произведение оснований степени равно единице:
(. Поэтому можно ввести новую переменную: , причем . Получим уравнение:
t ,оба корня удовлетворяют условию :.
Вернемся к переменной х:
.Ответ: .
Е. Уравнения, имеющие вид Aam = Bbm.
Для решения необходимо обе части уравнения разделить либо на am, либо на bm. В результате получается простейшее уравнение.
Примеры.
Пример 1. Решите уравнение: 7х = 5х.
Решение.
7х = 5х <=> = 1 <=> = <=> x = 0.
Ответ: 0.
Пример 2. Решите уравнение: .
Решение.
.
Ответ: 2.
F. Метод, основанный на использовании свойства монотонности показательной функции .
Примеры.
Пример 1. Решите уравнение: .
Решение.
Заметим, что при х=1 уравнение обращается в тождество. Следовательно, х=1 — корень уравнения. Перепишем уравнение в виде
(*)Так как при основании, меньшем единицы, показательная функция убывает на R, то при хлевая часть уравнения (*) больше единицы, то есть
Если то левая часть уравнения меньше единицы, то есть
Ответ: 1.
Пример 2. Решите уравнение: .
Решение.
Это уравнение также обращается в тождество при х=1.
Перепишем уравнение в виде:
.При основании, меньшем единицы, показательная функция убывает на R.
Поэтому при ха при х: . Таким образом, других корней, кроме х=1 , уравнение не имеет.
Ответ: 1.
G. Графический способ решения уравнений вида f(x).Чтобы графически решить уравнение такого вида, необходимо построить графики функций y=f(x) в одной системе координат и найти (точно или приближенно) абсциссы точек (если они есть) пересечения этих графиков. Абсциссы этих точек — корни данного уравнения (точность результатов определяем только после подстановки в уравнение ).
Примеры.
Пример 1. Решите уравнение: .
Решение.
1.Рассмотрим две функции: f(x) = и g(x) = x+1.
2.Графиком функции f(x) = является кривая, расположенная в верхней полуплоскости, графиком функции g(x) = x+1 является прямая.
3. Зададим таблицы значений этих функций:
х -1 0 1 2 3 f(x) = 1 2 4 х 0 3 g(x)= x+1 1 4
4. Из рисунка видно, что прямая и кривая пересекаются в двух точках- в точке А и в точке В. По графику определяем абсциссы этих точек: . Значит, уравнение имеет два корня: х=3 и х= . Число х=3 — точный корень заданного уравнения, так как при подстановке в это уравнение получается верное числовое равенство:
Ответ: 3; .
Пример 2. Решите уравнение: .
Решение.
1. Рассмотрим две функции f(x) = и g(x) = .Используем свойства степени и преобразуем выражение :
= , тогда вторую формулу можно переписать в виде: f(x) = .2. Функция f(x) = — показательная по основанию и ее графиком является кривая, расположенная в верхней полуплоскости.
Функция g(x) =- прямая пропорциональность и ее график - прямая, проходящая через точку .
3. Зададим таблицы значений этих функций и затем построим их графики в одной системе координат.
4. Графики пересекаются в одной точке — в точке А, ее абсцисса равна единице.Значит, х=1 — корень заданного уравнения.
Примечание:
Если одна часть уравнения содержит убывающую функцию f(x) , а другая часть -возрастающую функцию g(x), и уравнение имеет корень х=, то он -единственный.
В примере 2. : f(x) = убывающая на R функция, а g(x = - возрастающая на R функция, х=1- корень уравнения и он единственный.
Ответ: 1.
Приложение к статье «Методы решения показательных уравнений»
22.05.2011
urok.1sept.ru
повторение. 11 класс. Алгебра. Показательная функция.
Что является обязательным при решении системы показательных уравнений? Конечно, преобразование данной системы в систему простейших уравнений.
Примеры.
Решить системы уравнений:
Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы.
Решаем (2) -ое уравнение полученной системы:
2х+2x+2=10, применяем формулу: ax+y=ax∙ay.
2x+2x∙22=10, вынесем общий множитель 2х за скобки:
2х(1+22)=10 или 2х∙5=10, отсюда 2х=2.
2х=21, отсюда х=1. Возвращаемся к системе уравнений.
Ответ: (1; 2).
Решение.
Представляем левую и правую части (1) -го уравнения в виде степеней с основанием 2, а правую часть (2) -го уравнения как нулевую степень числа 5.
Если равны две степени с одинаковыми основаниями, то равны и показатели этих степеней — приравниваем показатели степеней с основаниями 2 и показатели степеней с основаниями 5.
Получившуюся систему линейных уравнений с двумя переменными решаем методом сложения.
Находим х=2 и это значение подставляем вместо х во второе уравнение системы.
Находим у.
Ответ: (2; 1,5).
Решение.
Если в предыдущих двух примерах мы переходили к более простой системе приравнивая показатели двух степеней с одинаковыми основаниями, то в 3-ем примере эта операция невыполнима. Такие системы удобно решать вводом новых переменных. Мы введем переменные u и v, а затем выразим переменную u через v и получим уравнение относительно переменной v.
Решаем (2) -ое уравнение системы.
v (v+63)=64;
v2+63v-64=0. Подберем корни по теореме Виета, зная, что: v1+v2=-63; v1∙v2=-64.
Получаем: v1=-64, v2=1. Возвращаемся к системе, находим u.
Так как значения показательной функции всегда положительны, то уравнения 4x=-1 и 4y=-64 решений не имеют.
Представляем 64 и 1 в виде степеней с основанием 4.
Приравниваем показатели степеней и находим х и у.
Ответ: (3; 0).

Ответ: (2; 1).
Запись имеет метки: системы показательных уравнений.
www.mathematics-repetition.com
повторение. 11 класс. Алгебра. Показательная функция.
Уравнения, содержащие переменную в показателе степени, называются показательными уравнениями.
Простейшие показательные уравнения — это уравнения вида: ax=ay. Отсюда следует равенство: х=у. В самом деле, степени с одинаковыми основаниями могут быть равными только в том случае, если равны показатели этих степеней.
Примеры.
Решить уравнение:
1) 5x=125. Представим число 125 в виде степени числа 5:
5x=53; Степени равны, их основания равны, значит, и показатели степеней будут равны:
x=3.
2) 4x=32. Представим левую и правую части в виде степеней с основанием 2:
(22)x=25; используем формулу возведения степени в степень: (ax)y=axy
22x=25;
2x=5 |:2
x=2,5.
3) 32x-1=81. Число 81 представим в виде степени числа 3:
32x-1=34; приравняем показатели степеней с одинаковыми основаниями:
2x-1=4; решаем простейшее линейное уравнение:
2x=4+1;
2x=5 |:2;
x=2,5.
К правой части применяем формулу: (a/b)-x=(b/a)x. Получим равенство степеней с одинаковыми основаниями.
Приравниваем показатели степеней и находим х из полученного линейного уравнения.
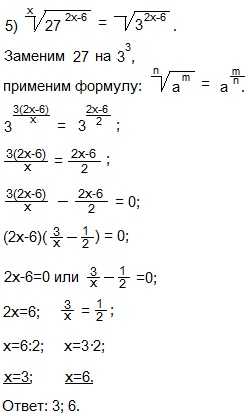
Приравняем показатели степеней с одинаковыми основаниями.
Переносим степень из правой части уравнения в левую.
Вынесли общий множитель (2х-6) за скобки. Произведение двух или нескольких множителей равно нулю, если один из множителей равен нулю, а другие при этом значении не теряют смысла. Содержимое каждой из скобок приравниваем к нулю и решаем простейшие уравнения.
6) 7∙5x-5x+1=2∙53.
Показатели степеней складываются, если степени перемножаются ( ax∙ay=ax+y ), поэтому:
7∙5x-5x∙51=2∙53;
5x(7-5)=2∙53; вынесли общий множитель за скобки.
5x∙2=2∙53 |:2
5x=53; отсюда следует:
x=3.
7) 3x+2+4∙3x+1=21. Применим формулу: ax+y=ax∙ay (При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают):
3x∙32+4∙3x∙31=21; вынесем общий множитель за скобки:
3x(9+12)=21;
3x∙21=21 |:21
3x=1; число 1 можно представлять в виде нулевой степени с любым основанием.
3x=30;
x=0.
51+2x+52x+3=650. Решаем аналогично.
51∙52x+52x∙53=650;
52x(5+125)=650;
52x∙130=650 |:130
52x=5; приравняем показатели равных степеней с основаниями 5.
2x=1 |:2
x=0,5.
Запись имеет метки: показательные уравнения
www.mathematics-repetition.com
Решение показательных уравнений. Видеоуроки
В этой статье вы познакомитесь со всеми типами показательных уравнений и алгоритмами их решения, научитесь распознавать, к какому типу принадлежит показательное уравнение, которое вам надо решить, и применять для его решения соответствующий метод. Подробное решение примеров показательных уравнений каждого типа вы сможете посмотреть в соответствующих ВИДЕОУРОКАХ.
Показательным уравнением называется уравнение, в котором неизвестное содержится в показателе степени.
Прежде чем начать решать показательное уравнение, полезно сделать несколько предварительных действий, которые могут значительно облегчить ход его решения. Вот эти действия:
1. Разложите все основания степеней на простые множители.
2. Корни представьте в виде степени.
3. Десятичные дроби представьте в виде обыкновенных.
4. Смешанные числа запишите в виде неправильных дробей.
Пользу этих действий вы осознаете в процессе решения уравнений.
Рассмотрим основные типы показательных уравнений и алгоритмы их решения.
1. Уравнение вида
Это уравнение равносильно уравнению
Посмотрите в этом ВИДЕОУРОКЕ решение уравнения этого типа.
2. Уравнение вида
В уравнениях этого типа:
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени равны.
Чтобы решить это уравнение, нужно вынести за скобку множитель в наименьшей степени.
Пример решения уравнения этого типа:
посмотрите в ВИДЕОУРОКЕ.
3. Уравнение вида
Уравнения этого типа отличаются тем, что
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени разные.
Уравнения такого типа решаются с помощью замены переменных. Прежде чем вводить замену, желательно освободиться от свободных членов в показателе степени. (, , и т.д)
Посмотрите в ВИДЕОУРОКЕ решение уравнения этого типа:
4. Однородные уравнения вида
Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями.
Однородные уравнения решаются по сходному алгоритму.
Чтобы решить уравнение такого типа, разделим обе части уравнения на (можно разделить на или на )
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
В нашем случае, поскольку выражение не равно нулю ни при каких значениях неизвестного, мы можем делить на него без опаски. Разделим левую часть уравнения на это выражение почленно. Получим:
Сократим числитель и знаменатель второй и третьей дроби:
Введем замену:
, причем при всех допустимых значениях неизвестного.
Получим квадратное уравнение:
Решим квадратное уравнение, найдем значения , которые удовлетворяют условию , а затем вернемся к исходному неизвестному.
Смотрите в ВИДЕОУРОКЕ подробное решение однородного уравнения:
5. Уравнение вида
При решении этого уравнения будем исходить из того, что
Исходное равенство выполняется в двух случаях:
1. Если , поскольку 1 в любой степени равна 1,
или
2. При выполнении двух условий:
Посмотрите в ВИДЕОУРОКЕ подробное решение уравнения
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Как решить уравнения со степенями 🚩 решение уравнений с степенями 🚩 Математика
Автор КакПросто!
Навыки решения уравнений со степенями требуются от учащихся всех учебных организаций, будь то школа, вуз или колледж. Решать степенные уравнения нужно как сами по себе, так и для решения других задач (физических, химических). Научиться решать такие уравнения довольно несложно, главное учитывать ряд небольших тонкостей и соблюдать алгоритм.
Статьи по теме:
Вам понадобится
Инструкция
Сперва нужно определить, к какому виду относится имеющееся степенное уравнение. Оно может быть квадратным, биквадратным или уравнением с нечетными степенями. Важно посмотреть на высшую степень. Если она вторая — то уравнение квадратное, если первая — линейное. Если высшая степень уравнения — четвертая, а дальше имеется переменная во второй степени и коэффициент, то уравнение — биквадратное.Если в уравнении имеется два слагаемых: переменная в какой-либо степени и коэффициент, то уравнение решается очень просто: переносим переменную в одну часть уравнения, а число в другую. Далее извлекаем корень такой степени из числа, в какой стоит переменная. Если степень нечетная, то вы можете записывать ответ, если же четная, то решения два — посчитанное число, и посчитанное число с противоположным знаком.
Решить квадратное уравнение тоже довольно просто. Квадратное уравнение — это уравнение вида: a*x^2+b*x+c=0. Сначала считаем дискриминант уравнения по формуле: D=b*b-4*a*c. Дальше все зависит от знака дискриминанта. Если дискриминант меньше нуля, то у нас нет решений. Если дискриминант больше или равен нулю, то считаем корни уравнения по формуле x=(-b-корень(D))/(2*a).
Биквадратное уравнение типа: a*x^4+b*x^2+c=0 решается так же быстро, как и предыдущие два вида степенных уравнений. Для этого используем замену x^2=y, и решаем биквадратное уравнение как квадратное. Мы получим в результате два y и перейдем обратно к x^2. То есть, мы получим два уравнения вида x^2=a. Как решить такое уравнение упоминалось выше.
Полезный совет
Если в уравнениях есть нечетные степени, попробуйте привести их к уравнениям с четными. Для этого нужно разделить уравнение на переменную один или несколько раз. Если в нем нет коэффициентов,не забудьте включить в число корней 0.
Источники:
- Материалы по математике
Решение уравнений со степенями входит как в школьную программу, так и в вузовскую. Чтобы научиться решать подобные уравнения, необходимо уметь их классифицировать, и в зависимости от их типа, применять определенный алгоритм.

Вам понадобится
- — тетрадь;
- — ручка
Инструкция
Определите, к какому виду относится степенное уравнение. Оно может являться квадратным или биквадратным, а также уравнением с нечетными степенями. Обратите внимание на высшую степень. В случае если она вторая — уравнение квадратное, если же первая — линейное. Если высшей степенью уравнения является четвертая, а также есть коэффициент и переменная во второй степени, то уравнение является биквадратным. Обратите внимание на структуру уравнения. Если в нем имеется два слагаемых, которыми являются переменная в какой-либо из степеней и коэффициент, уравнение решается достаточно просто: перенесите переменную в одну из частей уравнения, а числовое значение в другую. Извлеките корень той степени из числа, в какой находится переменная. Если степень нечетная, можно сразу записывать ответ, если четная, то уравнение имеет два решения — посчитанное число, и оно же, только с противоположным знаком.Учитывайте, что квадратное уравнение имеет вид: a*x^2+b*x+c=0. Посчитайте дискриминант уравнения, применив формулу: D=b*b-4*a*c. Обратите внимание на получившийся в ответе знак. Если дискриминант меньше нуля, уравнение решений не имеет. Если дискриминант равен нулю или больше нуля, считайте корни уравнения по известной формуле: x= (-b-корень(D))/(2*a).
Чтобы решить биквадратное уравнение вида: a*x^4+b*x^2+c=0 используйте замену x^2= y, и решайте биквадратное уравнение как и квадратное. В результате, в данном случае, получится два y, переходите обратно к x^2. То есть, образуется два уравнения вида x^2=a. Чтобы решить подобное уравнение, воспользуйтесь вышеприведенной инструкцией.
Если в уравнениях имеются нечетные степени, попытайтесь привести их к уравнениям, имеющим четные степени. Для этого разделите уравнение на переменную либо один, либо несколько раз. Если оно не содержит коэффициентов, включите в число корней 0.
Обратите внимание
Знак ^ в данном контексте обозначает — процесс возведения в степень и стоит перед степенным показателем.
Знак * равносилен знаку умножить, / — разделить.
www.kakprosto.ru
Уравнения со степенями | Логарифмы
Рассмотрим показательные уравнения со степенями, содержащими две степени с разными основаниями и одинаковыми показателями:
(где a и b — положительные числа, отличные от единицы).
Уравнения такого вида называются однородными показательными уравнениями первой степени. Однородные уравнения решаются делением на одну из степеней:
(так как b>0, то
при любом показателе f(x), то есть деление на степень не приводит к потере корней).
В результате деление получаем с одной стороны частное степеней с одинаковыми показателями, с другой — единицу:
По свойству степеней,
а единицу можно представить как степень с любым основанием и показателем 0:
Приравниваем показатели:
Рассмотрим примеры решений такого вида уравнений со степенями.
ОДЗ: x∈R.
Разделим обе части уравнения на степень, стоящую в правой части уравнения:
Преобразуем левую часть уравнения
и представим единицу в виде степени с таким же основанием, что и степень в левой части
Из равенства степеней с одинаковыми основаниями следует равенство показателей этих степеней:
Ответ: 2,5.
ОДЗ: x∈R.
Делим обе части уравнения на степень, стоящую в правой части:
Приравняв показатели степеней, приходим к квадратному уравнению
корни которого —
Ответ: 1; 5.
ОДЗ: x∈R.
Это — простейшее тригонометрическое уравнение, корни которого
Ответ: πn, n∈Z.
www.logarifmy.ru
Как решать уравнения высших степеней
Автор КакПросто!
Решение большинства уравнений высших степеней не имеет четкой формулы, как нахождение корней квадратного уравнения. Однако существует несколько способов приведения, которые позволяют преобразовать уравнение высшей степени к более наглядному виду.
Статьи по теме:
Инструкция
Наиболее распространенным методом решения уравнений высших степеней является разложение на множители. Этот подход представляет собой комбинацию подбора целочисленных корней, делителей свободного члена, и последующее деление общего многочлена на двучлен вида (x – x0).Например, решите уравнение x^4 + x³ + 2·x² – x – 3 = 0.Решение.Свободным членом данного многочлена является -3, следовательно, его целочисленными делителями могут быть числа ±1 и ±3. Подставьте их по очереди в уравнение и выясните, получится ли тождество:1: 1 + 1 + 2 – 1 – 3 = 0.
Итак, первый же предположительный корень дал правильный результат. Разделите многочлен уравнения на (x — 1). Деление многочленов выполняется столбиком и отличается от обычного деления чисел только наличием переменной.Перепишите уравнение в новом виде (x — 1)·(x³ +2·x² + 4·x + 3) = 0. Наибольшая степень многочлена уменьшилась до третьей. Продолжите подбор корней уже для кубического многочлена:1: 1 + 2 + 4 + 3 ≠ 0;-1: -1 + 2 – 4 + 3 = 0.
Второй корень x = -1. Поделите кубический многочлен на выражение (x + 1). Запишите получившееся уравнение (x — 1)·(x + 1)·(x² + x + 3) = 0. Степень понизилась до второй, следовательно, уравнение может иметь еще два корня. Чтобы найти их, решите квадратное уравнение:x² + x + 3 = 0D = 1 – 12 = -11
Дискриминант – отрицательная величина, значит, действительных корней у уравнения больше нет. Найдите комплексные корни уравнения:x = (-2 + i·√11)/2 и x = (-2 – i·√11)/2.
Запишите ответ:x1,2 = ±1; x3,4 = -1/2 ± i·√11/2.
Другой метод решения уравнения высшей степени – замена переменных для приведения его к квадратному. Такой подход используется, когда все степени уравнения четные, например:x^4 – 13·x² + 36 = 0
Это уравнение называется биквадратным. Чтобы привести его к квадратному, сделайте замену y = x². Тогда:y² – 13·y + 36 = 0D = 169 – 4·36 = 25y1 = (13 + 5)/2 = 9; y2 = (13 — 5)/2 = 4.
Теперь найдите корни исходного уравнения:x1 = √9 = ±3; x2 = √4 = ±2.
www.kakprosto.ru
