Уравнения с дробными степенями как решать – Показательные уравнения. Метод логарифмирования.

Показательные уравнения

    Показательные уравнения. Как известно — в состав ЕГЭ входят простые уравнения. Некоторые мы уже рассмотрели – это логарифмические, тригонометрические, рациональные. Здесь представлены показательные уравнения.

В недавней статье мы поработали с показательными выражениями, посмотрите, будет полезно. Сами уравнения решаются просто и быстро. Требуется лишь знать свойства показателей степени и…  Об этом далее.

Перечислим свойства показателей степени:

Нулевая степень любого числа равна единице.

Далее:

Следствие из данного свойства:

Ещё немного теории.

Показательным уравнением называется уравнение содержащее переменную в показателе, то есть  это уравнение вида:

f(x)  выражение, которое содержит переменную

Методы решения показательных уравнений

1. В результате преобразований уравнение можно привести к виду:

Тогда применяем свойство:

2. При получении уравнения вида  a ^f(x) = b  используется определение логарифма, получим:

3. В результате преобразований можно получить уравнение вида:

Применяется логарифмирование:

Далее применяем свойство логарифма степени:

Выражаем и находим х.

В задачах вариантов ЕГЭ достаточно будет использовать первый способ.

То есть, необходимо представить левую и правую части в виде степеней с одинаковым основанием, а далее приравниваем показатели и решаем обычное линейное уравнение.

Рассмотрим уравнения:

Найдите корень уравнения 4^1–2х = 64.

Необходимо сделать так, чтобы в левой и правой частях были показательные выражения с одним основанием. 64 мы можем представить как 4 в степени 3. Получим:

4^1–2х = 4³

Основания равны, можем приравнять показатели:

1 – 2х = 3

– 2х = 2

х =  – 1

Проверка:

4^1–2(–1) = 64

4¹⁺² = 64

4³ = 64

64 = 64

Ответ: –1

Найдите корень уравнения 3^х–18 = 1/9.

Известно, что

Значит  3^х-18 = 3^-2

Основания равны, можем приравнять показатели:

х – 18 = – 2

х = 16

Проверка:

3^16–18 = 1/9

3^–2 = 1/9

1/9 = 1/9

Ответ: 16

Найдите корень уравнения:

Представим дробь 1/64 как  одну четвёртую в третьей степени:

Теперь можем приравнять показатели:

2х – 19 = 3

2х = 22

х = 11

Проверка:

Ответ: 11

Найдите корень уравнения:

Представим 1/3 как  3^–1, а 9 как 3 в квадрате, получим:

(3^–1)^8–2х = 3²

3^{–1∙(8–2х)} = 3²

3^–8+2х = 3²

Теперь можем приравнять показатели:

 – 8+2х = 2

2х = 10

х = 5

Проверка:

Ответ: 5

26654. Найдите корень уравнения:

Решение:

Ответ: 8,75

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Посмотреть решение

Что хочется отметить обсобо!!!

Как бы  вы не были уверены в правильности решения — ОБЯЗАТЕЛЬНО делайте проверку.

Ещё теория (чуть-чуть):

Самое простейшее показательное уравнение:

При данных условиях уравнение всегда имеет решение, при том единственное.

Действительно, при а > 1 показательная функция монотонно возрастает, а при 0 < а < 1 — монотонно убывает. В любом случае, она принимает каждое своё значение ровно один раз (видно по графику):

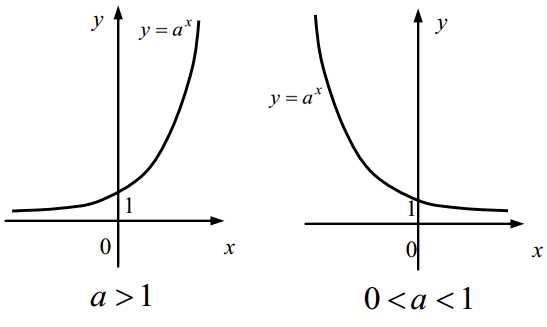
А вот если b < 0, то уравнение не имеет решений, ведь показательная функция может принимать только положительные значения.

Действительно, в какую бы степень мы не возвели положительное число a, мы никак не можем получить число отрицательное.

Любое показательное уравнение после соответствующих преобразований сводится к реше­нию одного или нескольких простейших.В данной рубрике мы ещё рассмотрим решение некоторых уравнений, не пропустите! На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Показательные уравнения. Более сложные случаи. Видеоурок. Алгебра 11 Класс

На данном уроке мы рассмотрим решение более сложных показательных уравнений, вспомним основные теоретические положения касательно показательной функции.

Напомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.

Показательная функция – это функция вида , где основание степени  и  Здесь х – независимая переменная, аргумент; у – зависимая переменная, функция.

Рис. 1. График показательной функции

На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно.

Обе кривые проходят через точку (0;1)

Свойства показательной функции:

Область определения: ;

Область значений: ;

Функция монотонна, при  возрастает, при  убывает.

Монотонная функция принимает каждое свое значение при единственном значении аргумента.

При  когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности. При  наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно.

Напомним, как решать простейшие показательные уравнения. Их решение основано на монотонности показательной функции. К таким уравнениям сводятся практически все сложные показательные уравнения.

Равенство показателей степени при равных основаниях обусловлено свойством показательной функции, а именно ее монотонностью.

Методика решения:

Уравнять основания степеней;

Приравнять показатели степеней.

Перейдем к рассмотрению более сложных показательных уравнений, наша цель – свести каждое из них к простейшему.

Пример 1:

Освободимся от корня в левой части и приведем степени к одинаковому основанию:

Для того чтобы свести сложное показательное уравнение к простейшим, часто используется замена переменных.

Пример 2:

Воспользуемся свойством степени:

Вводим замену. Пусть , тогда . При такой замене очевидно, что у принимает строго положительные значения. Получаем:

Умножим полученное уравнение на два и перенесем все слагаемые в левую часть:

Первый корень не удовлетворяет промежутку значений у, отбрасываем его. Получаем:

Пример 3:

Приведем степени к одинаковому показателю:

Вводим замену:

Пусть , тогда . При такой замене очевидно, что у принимает строго положительные значения. Получаем:

Решать подобные квадратные уравнения мы умеем, выпишем ответ:

Чтобы удостовериться в правильности нахождения корней, можно выполнить проверку по теореме Виета, т. е. найти сумму корней и их произведение и сверить с соответствующими коэффициентами уравнения.

Получаем:

Изучим следующий важный тип показательных уравнений:

Уравнения такого типа называют однородными второй степени относительно функций f и g. В левой его части стоит квадратный трехчлен относительно f с параметром g или квадратный трехчлен относительно g с параметром f.

Методика решения:

Данное уравнение можно решать как квадратное, но легче поступить по-другому. Следует рассмотреть два случая:

1.

2.

В первом случае получаем

Во втором случае имеем право разделить на старшую степень  и получаем:

Следует ввести замену переменных , получим квадратное уравнение относительно у:

Обратим внимание, что функции f и g могут быть любыми, но нас интересует тот случай, когда это показательные функции.

Пример 4:

Перенесем все слагаемые в левую часть уравнения:

Воспользуемся свойствами степени и приведем все степени к простым основаниям:

Несложно заметить функции f и g:

Поскольку показательные функции приобретают строго положительные значения, имеем право сразу делить уравнение на , не рассматривая случай, когда :

Получаем:

Вводим замену:  (согласно свойствам показательной функции)

Получили квадратное уравнение:

Определяем корни по теореме Виета:

Первый корень не удовлетворяет промежутку значений у, отбрасываем его, получаем:

Пример 5:

Воспользуемся свойствами степени и приведем все степени к простым основаниям:

Несложно заметить функции f и g:

Поскольку показательные функции приобретают строго положительные значения, имеем право сразу делить уравнение на , не рассматривая случай, когда :

Получаем:

Вводим замену:  (согласно свойствам показательной функции)

Получили квадратное уравнение:

Определяем корни:

Первый корень не удовлетворяет промежутку значений у, отбрасываем его, получаем:

Решение отдельных показательных уравнений является ключом к решению систем показательных уравнений.

Пример 6 – решить систему:

В обоих уравнениях приведем основания степеней к простым числам:

Получили систему двух линейных уравнений относительно двух неизвестных, такие системы мы умеем решать, например, методом подстановки:

Ответ: (1;3)

Итак, мы рассмотрели решение разнообразных сложных показательных уравнений, вывели методики их сведения к простейшим показательным уравнениям. На следующем уроке перейдем к решению показательных неравенств.

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Mathematics-repetition.com (Источник).
2. Terver.ru (Источник).
3. Yourtutor.info (Источник).

 

Домашнее задание

1.      Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 465, 471;

2.      Решить уравнение:

3.      Решить систему уравнений:

interneturok.ru

Простейшие показательные уравнения

5 февраля 2012

Если взять обычную степень и «засунуть» в показатель переменную x , получим показательное уравнение. Таких уравнений великое множество, и для них есть собственные методы решения.

Сегодня мы познакомимся с простейшими конструкциями. Они так и называются — простейшие показательные уравнения (кэп?). Все остальные, как бы сложно они ни выглядели, в итоге сводятся к простейшим. Но это уже материал следующих уроков.

Простейшее показательное уравнение — это уравнение вида:

a ^x = b , где a > 0, a ≠ 1

Такое уравнение не имеет корней при b ≤ 0, а при b > 0 имеет единственный корень: x = log _a b . Более сложные показательные уравнения решаются по следующей схеме:

1. Перевести все степени к одинаковому основанию. Желательно, чтобы оно было целым и минимальным. Например, вместо 4 ^x лучше писать 2^{2 x} , а вместо 0,01 ^x — вообще 10^{−2 x} . Почему — узнаете из примеров;
2. В уравнениях, где есть умножение или деление, надо выполнить эти действия. Напомню: при умножении степеней с одинаковым основанием показатели складываются, при делении — вычитаются;
3. Если все сделано правильно, получим уравнение вида a ^{f ( x )} = a ^{g ( x )}, где a — просто число. Его можно отбросить, поскольку показательная функция монотонна. Получим уравнение f ( x ) = g ( x ), которое легко решается.

Помните, что корни — тоже степени, но с дробным основанием:

Задача. Решите уравнение:

Итак, приведем все степени к основанию 2:

4 ^x = (2²) ^x = 2^{2 x} ; 1 = 2⁰; 256 = 2⁸

Теперь перепишем исходное уравнение и выполним деление:

Получили простейшее показательное уравнение. Отбрасываем основание — получаем:

2 x = −8 ⇒ x = −4

Задача. Решите уравнение:

Снова приводим все степени к наименьшему целому основанию:

9^{2 x} = (3²)^{2 x} = 3^{4 x} ; 1 = 3⁰; 27 = 3³

Обратите внимание: число 27 не является целой степенью девятки. Именно поэтому надо приводить все степени к основанию 3, а не 9. Возвращаемся к исходному уравнению:

Осталось избавиться от основания степени:

4 x = −3 ⇒ x = −3/4 = −0,75

Задача. Решите уравнение:

В уравнении присутствуют сразу 4 множителя, которые надо перевести в степени с одинаковым основанием:

Учитывая эти факты, перепишем исходное уравнение:

Избавимся от основания — и после приведения дробей к общему знаменателю получим классическую пропорцию:

Дальше все стандартно: произведение крайних элементов пропорции равно произведению средних. Имеем:

14 + 4 x − 4 = −35 ⇒ 4 x = −45 ⇒ x = −45 : 4 = −11,25

Ниже даны 12 тренировочных задач. Если что-то не получается — ничего страшного, потому что есть второй вариант этого теста (см. «Простейшие показательные уравнения — 2 вариант»). Попробуйте решить его.

Смотрите также:

1. Тест: простейшие показательные уравнения (2 вариант)
2. Показательные уравнения с логарифмами
3. Тест на тему «Значащая часть числа»
4. Сводный тест по задачам B12 (1 вариант)
5. Задача 18: метод симметричных корней
6. Задача B4: Скачать файл на разной скорости

www.berdov.com

Решение показательных уравнений. Основы. | Александр Будников

Что такое показательное уравнение? Примеры.

        Итак, показательное уравнение… Новый уникальный экспонат на нашей общей выставке самых разнообразных уравнений!) Как это почти всегда бывает, ключевым словом любого нового математического термина является соответствующее прилагательное, которое его характеризует. Так и тут. Ключевым словом в термине «показательное уравнение» является слово

«показательное». Что оно означает? Это слово означает, что неизвестное (икс) находится в показателях каких-либо степеней. И только там! Это крайне важно.

        Например, такие простые уравнения:

        3^x+1 = 81

        5^x + 5^x+2 = 130

        4·2^2x-17·2^x+4 = 0

 

        Или даже такие монстры:

        2^sinx = 0,5

        

        

        И так далее, и тому подобное…

        Прошу сразу обратить внимание на одну важную вещь: в основаниях степеней (снизу) – только числа. А вот в показателях степеней (сверху) – самые разнообразные выражения с иксом. Совершенно любые.) Всё от конкретного уравнения зависит. Если, вдруг, в уравнении вылезет икс где-нибудь ещё, помимо показателя (скажем, 3^x = 18+x²), то такое уравнение будет уже уравнением смешанного типа. Такие уравнения не имеют чётких правил решения. Поэтому в данном уроке мы их рассматривать не будем. На радость ученикам.) Здесь мы будем рассматривать только показательные уравнения в «чистом» виде.

        Вообще говоря, даже чистые показательные уравнения чётко решаются далеко не все и не всегда. Но среди всего богатого многообразия показательных уравнений есть определённые типы, которые решать можно и нужно. Вот именно эти типы уравнений мы с вами и рассмотрим. И примеры обязательно порешаем.) Так что устраиваемся поудобнее и – в путь! Как и в компьютерных «стрелялках», наше путешествие будет проходить по уровням.) От элементарного к простому, от простого – к среднему и от среднего — к сложному. По пути вас также будет ждать секретный уровень – приёмы и методы решения нестандартных примеров. Те, о которых вы не прочитаете в большинстве школьных учебников… Ну, а в конце вас, разумеется, ждёт финальный босс в виде домашки.)

 

Уровень 0. Что такое простейшее показательное уравнение? Решение простейших показательных уравнений.

        Для начала рассмотрим какую-нибудь откровенную элементарщину. С чего-то же надо начинать, верно? Например, такое уравнение:

        2^х = 2²

        Даже безо всяких теорий, по простой логике и здравому смыслу ясно, что х = 2. Иначе же никак, верно? Никакое другое значение икса не годится… А теперь обратим наш взор на запись решения этого крутого показательного уравнения:

        2^х = 2²

        х = 2

        Что же у нас произошло? А произошло следующее. Мы, фактически, взяли и… просто выкинули одинаковые основания (двойки)! Совсем выкинули. И, что радует, попали в яблочко!

        Да, действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, то эти числа можно отбросить и просто приравнять показатели степеней. Математика разрешает.) И дальше можно работать уже отдельно с показателями и решать куда более простое уравнение. Здорово, правда?

        Вот и ключевая идея решения любого (да-да, именно любого!) показательного уравнения: с помощью тождественных преобразований необходимо добиться того, чтобы слева и справа в уравнении стояли одинаковые числа-основания в различных степенях. А дальше можно смело убрать одинаковые основания и приравнять показатели степеней. И работать с более простым уравнением.

        А теперь запоминаем железное правило: убирать одинаковые основания можно тогда и только тогда, когда в уравнении слева и справа числа-основания стоят в гордом одиночестве.

        Что значит, в гордом одиночестве? Это значит, безо всяких соседей и коэффициентов. Поясняю.

        Например, в уравнении

        3·3^x-5 = 3^2x+1

        тройки убирать нельзя! Почему? Потому что слева у нас стоит не просто одинокая тройка в степени, а произведение 3·3^x-5. Лишняя тройка мешает: коэффициент, понимаешь.)

        То же самое можно сказать и про уравнение

        5^3x = 5^2x+5^x

        Здесь тоже все основания одинаковые – пятёрка. Но справа у нас не одинокая степень пятёрки: там – сумма степеней!

        Короче говоря, убирать одинаковые основания мы имеем право лишь тогда, когда наше показательное уравнение выглядит так и только так:

        a^f(x) = a^g(x)

        Такой вид показательного уравнения называют простейшим. Или, по-научному, каноническим. И какое бы накрученное уравнение перед нами ни было, мы его, так или иначе, будем сводить именно к такому простейшему (каноническому) виду. Или, в некоторых случаях, к совокупности уравнений такого вида. Тогда наше простейшее уравнение можно в общем виде переписать вот так:

        f(x) = g(x)

        И всё. Это будет эквивалентным преобразованием. При этом в качестве f(x) и g(x) могут стоять совершенно любые выражения с иксом. Какие угодно.

        Возможно, особо любознательный ученик поинтересуется: а с какой такой стати мы вот так легко и просто отбрасываем одинаковые основания слева и справа и приравниваем показатели степеней? Интуиция интуицией, но вдруг, в каком-то уравнении и для какого-то основания данный подход окажется неверным? Всегда ли законно выкидывать одинаковые основания? К сожалению, для строгого математического ответа на этот интересный вопрос нужно довольно глубоко и серьёзно погружаться в общую теорию устройства и поведения функций. А чуть конкретнее – в явление строгой монотонности. В частности, строгой монотонности показательной функции y=a^x. Поскольку именно показательная функция и её свойства лежат в основе решения показательных уравнений, да.) Развёрнутый ответ на этот вопрос будет дан в отдельном спецуроке, посвящённом решению сложных нестандартных уравнений с использованием монотонности разных функций.)

        Объяснять подробно этот момент сейчас – это лишь выносить мозг среднестатистическому школьнику и отпугивать его раньше времени сухой и грузной теорией. Я этого делать не буду.) Ибо наша основная на данный момент задача – научиться решать показательные уравнения! Самые-самые простые! Посему – пока не паримся и смело выкидываем одинаковые основания. Это можно, поверьте мне на слово!) А дальше уже решаем эквивалентное уравнение f(x) = g(x). Как правило, более простое, чем исходное показательное.

        Предполагается, конечно же, что решать хотя бы линейные, квадратные и дробные уравнения, уже без иксов в показателях, народ на данный момент уже умеет.) Кто до сих пор не умеет – смело закрывайте эту страницу, гуляйте по соответствующим ссылочкам и восполняйте старые пробелы. Иначе несладко вам придётся, да…

        Я уж молчу про иррациональные, тригонометрические и прочие зверские уравнения, которые также могут всплыть в процессе ликвидации оснований. Но не пугайтесь, откровенную жесть в показателях степеней мы с вами пока рассматривать не будем: рано ещё. Будем тренироваться лишь на самых простых уравнениях.)

        Теперь рассмотрим уравнения, которые требуют некоторых дополнительных усилий для сведения их к простейшим. Для отличия назовём их простыми показательными уравнениями. Итак, двигаемся на следующий уровень!

 

Уровень 1. Простые показательные уравнения. Распознаём степени! Натуральные показатели.

        Ключевыми правилами в решении любых показательных уравнений являются правила действий со степенями. Без этих знаний и умений ничего не получится. Увы. Так что, если со степенями проблемы, то для начала милости прошу сюда. Кроме того, ещё нам понадобятся базовые тождественные преобразования уравнений. Эти преобразования (целых два!) – основа решения всех уравнений математики вообще. И не только показательных. Так что, кто забыл, тоже прогуляйтесь по ссылочке: я их не просто так ставлю.

        Но одних только действий со степенями и тождественных преобразований мало. Необходима ещё личная наблюдательность и смекалка. Нам ведь требуются одинаковые основания, не так ли? Вот и осматриваем пример и ищем их в явном или замаскированном виде!

        Например, такое уравнение:

        3^2x – 27^x+2 = 0

        Первый взгляд на основания. Они… разные! Тройка и двадцать семь. Но паниковать и впадать в отчаяние рано. Самое время вспомнить, что

        27 = 3³

        Числа 3 и 27 – родственнички по степени! Причём близкие.) Стало быть, имеем полное право записать:

        27^x+2 = (3³)^x+2

        А вот теперь подключаем наши знания о действиях со степенями (а я предупреждал!). Есть там такая очень полезная формулка:

        (a^m)ⁿ = a^mn

        Если теперь запустить её в ход, то вообще отлично получается:

        27^x+2 = (3³)^x+2 = 3^3(x+2)

        Исходный пример теперь выглядит вот так:

        3^2x – 3^3(x+2) = 0

        Отлично, основания степеней выровнялись. Чего мы и добивались. Полдела сделано.) А вот теперь запускаем в ход базовое тождественное преобразование – переносим 3^3(x+2) вправо. Элементарных действий математики никто не отменял, да.) Получаем:

        3^2x = 3^3(x+2)

        Что нам даёт такой вид уравнения? А то, что теперь наше уравнение сведено к каноническому виду: слева и справа стоят одинаковые числа (тройки) в степенях. Причём обе тройки — в гордом одиночестве. Смело убираем тройки и получаем:

        2х = 3(х+2)

        Решаем это линейное уравнение и получаем:

        x = -6

        Вот и все дела. Это правильный ответ.)

        А теперь осмысливаем ход решения. Что нас спасло в этом примере? Нас спасло знание степеней тройки. Как именно? Мы опознали в числе 27 зашифрованную тройку! Этот приёмчик (шифровка одного и того же основания под разными числами) – один из самых популярных в показательных уравнениях! Если только не самый популярный. Да и в логарифмах тоже, кстати. Именно поэтому в показательных уравнениях так важна наблюдательность и умение распознавать в числах степени других чисел!

        Практический совет:

        Степени популярных чисел надо знать. В лицо!

        Конечно, возвести двойку в седьмую степень или тройку в пятую может каждый. Не в уме, так хотя бы на черновике. Но в показательных уравнениях гораздо чаще надо не возводить в степень, а наоборот — узнавать, какое число и в какой степени скрывается за числом, скажем, 128 или 243. А это уже посложнее, чем простое возведение, согласитесь. Почувствуйте разницу, что называется!

        Поскольку умение распознавать степени в лицо пригодится не только на этом уровне, но и на следующих, вот вам небольшое задание:

        Определить, какими степенями и каких чисел являются числа:

        4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.

        Ответы (вразброс, естественно):

        27²; 2¹⁰; 3⁶; 7²; 2⁶; 9²; 3⁴; 4³; 10²; 2⁵; 3⁵; 7³; 16²; 2⁷; 5³; 2⁸; 6²; 3³; 2⁹; 2⁴; 2²; 4⁵; 25²; 4⁴; 6³; 8²; 9³.

        Да-да! Не удивляйтесь, что ответов побольше, чем заданий. Например, 2⁸, 4⁴ и 16² – это всё 256.

        А теперь движемся дальше.)

 

Уровень 2. Простые показательные уравнения. Распознаём степени! Отрицательные и дробные показатели.

        На этом уровне мы уже используем наши знания о степенях на полную катушку. А именно – вовлекаем в сей увлекательный процесс отрицательные и дробные показатели! Да-да! Нам же надо наращивать мощь, верно?

        Например, такое страшное уравнение:

        Опять первый взгляд – на основания. Основания – разные! Причём на этот раз даже отдалённо не похожие друг на друга! 5 и 0,04… А для ликвидации оснований нужны одинаковые… Что же делать?

        Ничего страшного! На самом деле всё то же самое, просто связь между пятёркой и 0,04 визуально просматривается плохо. Как выкрутимся? А перейдём-ка в числе 0,04 к обычной дроби! А там, глядишь, всё и образуется.)

        0,04 = 4/100 = 1/25

        Ух ты! Оказывается, 0,04 – это 1/25! Ну кто бы мог подумать!)

        Ну как? Теперь связь между числами 5 и 1/25 легче углядеть? Вот то-то и оно…

        А теперь уже по правилам действий со степенями с отрицательным показателем можно твёрдой рукой записать:

        Вот и отлично. Вот мы и добрались до одинакового основания – пятёрки. Заменяем теперь в уравнении неудобное нам число 0,04 на 5^-2 и получаем:

Опять же, по правилам действий со степенями, теперь можно записать:

(5^-2)^x-1 = 5^-2(x-1)

        На всякий случай, напоминаю (вдруг, кто не в курсе), что базовые правила действий со степенями справедливы для любых показателей! В том числе и для отрицательных.) Так что смело берём и перемножаем показатели (-2) и (х-1) по соответствующему правилу. Наше уравнение становится всё лучше и лучше:

        

        Всё! Кроме одиноких пятёрок в степенях слева и справа больше ничего нет. Уравнение сведено к каноническому виду. А дальше – по накатанной колее. Убираем пятёрки и приравниваем показатели:

        x²–6x+5=-2(x-1)

        Пример практически решён. Осталась элементарная математика средних классов – раскрываем (правильно!) скобки и собираем всё слева:

        x²–6x+5 = -2x+2

        x²–4x+3 = 0

        Решаем это квадратное уравнение и получаем два корня:

        x₁ = 1; x₂ = 3

        Вот и всё.)

        А теперь снова поразмышляем. В данном примере нам вновь пришлось распознать одно и то же число в разной степени! А именно — увидеть в числе 0,04 зашифрованную пятёрку. Причём на этот раз – в отрицательной степени! Как же нам это удалось? С ходу – никак. А вот после перехода от десятичной дроби 0,04 к обыкновенной дроби 1/25 всё и высветилось! И дальше всё решение пошло как по маслу.)

        Поэтому очередной зелёный практический совет.

        Если в показательном уравнении присутствуют десятичные дроби, то переходим от десятичных дробей к обыкновенным. В обыкновенных дробях гораздо проще распознать степени многих популярных чисел! После распознавания переходим от дробей к степеням с отрицательными показателями.

        Имейте в виду, что такой финт в показательных уравнениях встречается очень и очень часто! А человек не в теме. Смотрит он, например, на числа 32 и 0,125 и огорчается. Неведомо ему, что это одна и та же двойка, только в разных степенях… Но вы-то ведь уже в теме!)

        Дальше – больше! Развлекаться, так развлекаться.)

        Решить уравнение:

        

        Во! На вид – тихий ужас… Однако внешность обманчива. Это простейшее показательное уравнение, несмотря на его устрашающий внешний вид. И сейчас я вам это покажу.)

        Конечно, возиться да считать побольше придётся, но ведь и наш с вами уровень тоже растёт, не правда ли? Итак, ничего не боимся и приступаем.)

        Во-первых, разбираемся со всеми чиселками, сидящими в основаниях и в коэффициентах. Они, ясное дело, разные, да. Но мы всё же рискнём и попробуем сделать их одинаковыми! Попробуем добраться до одного и того же числа в разных степенях. Причём, желательно, числа самого возможно малого. Итак, начинаем расшифровку!

        Ну, с четвёркой сразу всё ясно – это 2². Так, уже кое-что.)

        С дробью 0,25 – пока непонятно. Проверять надо. Используем практический совет – переходим от десятичной дроби к обыкновенной:

        0,25 = 25/100 = 1/4

        Уже гораздо лучше. Ибо теперь уже отчётливо видно, что 1/4 – это 2^-2. Отлично, и число 0,25 тоже сроднили с двойкой.)

        Пока всё идёт хорошо. Но осталось самое нехорошее число из всех – корень квадратный из двух! А с этим перцем что делать? Можно ли его тоже представить как степень двойки? А кто ж его знает…

        Что ж, снова лезем в нашу сокровищницу знаний о степенях! На этот раз дополнительно подключаем наши знания о корнях. Из курса 9-го класса мы с вами должны были вынести, что любой корень, при желании, всегда можно превратить в степень с дробным показателем. 

        Вот так:

        

        В нашем случае:

        

        Во как! Оказывается, корень квадратный из двух – это 2^1/2. Вот оно что!

        Вот и прекрасно! Все наши неудобные числа на самом деле оказались зашифрованной двойкой.) Не спорю, где-то весьма изощрённо зашифрованной. Но и мы ведь тоже повышаем свой профессионализм в разгадке подобных шифров! А дальше уже всё очевидно. Заменяем в нашем уравнении числа 4, 0,25 и корень из двух на степени двойки:

        Всё! Основания всех степеней в примере стали одинаковыми – двойка. А теперь в ход идут стандартные действия со степенями:

        a^m·aⁿ = a^m+n

        a^m:aⁿ = a^m-n

        (a^m)ⁿ = a^mn

        Для левой части получится:

        2^-2·(2²)^5x-16 = 2^-2+2(5x-16)

        Для правой части будет:

        И теперь наше злое уравнение стало выглядеть вот так:

        Кто не врубился, как именно получилось это уравнение, то тут вопрос не к показательным уравнениям. Вопрос – к действиям со степенями. Я же просил срочно повторить тем, у кого проблемы!

        Вот и финишная прямая! Получен канонический вид показательного уравнения! Ну как? Убедил я вас, что не всё так страшно? 😉 Убираем двойки и приравниваем показатели:

        Осталось всего лишь решить это линейное уравнение. Как? С помощью тождественных преобразований, вестимо.) Дорешайте, чего уж там! Умножайте обе части на двойку (чтобы убрать дробь 3/2), переносите слагаемые с иксами влево, без иксов вправо, приводите подобные, считайте – и будет вам счастье!

        Должно всё получиться красиво:

        x = 4

        А теперь снова осмысливаем ход решения. В данном примере нас выручил переход от квадратного корня к степени с показателем 1/2. Причём только такое хитрое преобразование нам помогло везде выйти на одинаковое основание (двойку), которое и спасло положение! И, если бы не оно, то мы бы имели все шансы навсегда зависнуть и так и не справиться с этим примером, да…

        Поэтому не пренебрегаем очередным практическим советом:

        Если в показательном уравнении присутствуют корни, то переходим от корней к степеням с дробными показателями. Очень часто только такое преобразование и проясняет дальнейшую ситуацию.

        Конечно же, отрицательные да дробные степени уже гораздо сложнее натуральных степеней. Хотя бы с точки зрения визуального восприятия и, особенно, распознавания справа налево!

        Понятно, что напрямую возвести, например, двойку в степень -3 или же четвёрку в степень -3/2 не такая уж и большая проблема. Для знающих.)

        А вот поди, например, с ходу сообрази, что

        0,125 = 2^-3

        или

        

        Тут только практика и богатый опыт рулят, да. И, конечно же, чёткое представление, что такое отрицательная и дробная степень. А также – практические советы! Да-да, те самые зелёные.) Надеюсь, что они всё-таки помогут вам лучше ориентироваться во всём разношёрстном многообразии степеней и значительно увеличат ваши шансы на успех! Так что не пренебрегаем ими. Я не зря зелёным цветом пишу иногда.)

        Зато, если вы станете на «ты» даже с такими экзотическими степенями, как отрицательные и дробные, то ваши возможности в решении показательных уравнений колоссально расширятся, и вам уже будет по плечу практически любой тип показательных уравнений. Ну, если не любой, то процентов 80 всех показательных уравнений – уж точно!  Да-да, я не шучу!

        Итак, наша первая часть знакомства с показательными уравнениями подошла к своему логическому завершению. И, в качестве промежуточной тренировки, я традиционно предлагаю немного порешать самостоятельно.)

 

        Задание 1.

        Чтобы мои слова о расшифровке отрицательных и дробных степеней не пропали даром, предлагаю сыграть в небольшую игру!

        Представьте в виде степени двойки числа:

      

        Ответы (в беспорядке):

 

        Получилось? Отлично! Тогда делаем боевое задание – решаем простейшие и простые показательные уравнения!

 

        Задание 2.

        Решить уравнения (все ответы – в беспорядке!):

        5^2x-8 = 25

        2^5x-4 – 16^x+3 = 0

        

       

        Ответы:

        x = 16

        x₁ = -1; x₂ = 2

        x = 5

       Получилось? Действительно, уж куда проще-то!

       

        Тогда решаем следующую партию:

        

        (2^x+4)^x-3 = 0,5^x·4^x-4

        35^1-x = 0,2^—x·7^x

       

        Ответы:

        x₁ = -2; x₂ = 2

        x = 0,5

        x₁ = 3; x₂ = 5

       

        И эти примеры одной левой? Отлично! Вы растёте! Тогда вот вам на закуску ещё примерчики:

        

 

        Ответы:

        x = 6

        x = 13/31

        x = -0,75

        x₁ = 1; x₂ = 8/3

 

        И это решено? Что ж, респект! Снимаю шляпу.) Значит, урок прошёл не напрасно, и начальный уровень решения показательных уравнений можно считать успешно освоенным. Впереди – следующие уровни и более сложные уравнения! И новые приёмы и подходы. И нестандартные примеры. И новые сюрпризы.) Всё это – в следующем уроке!

        Что-то не получилось? Значит, скорее всего, проблемы в действиях со степенями. Или в тождественных преобразованиях. Или в том и другом сразу. Тут уж я бессилен. Могу в очередной раз предложить лишь одно – не лениться и прогуляться по ссылочкам.)

        Продолжение следует.)

abudnikov.ru

Как решать примеры со степенями и дробями: калькулятор возведения в квадрат

Нулевая, отрицательная и дробная степень

Нулевой показатель

Возвести данное число в некоторую степень значит повторить его сомножителем столько раз, сколько единиц в показателе степени.

Согласно этому определению, выражение: a0 не имеет смысла. Но чтобы правило деления степеней одного и того же числа имело значение и в том случае, когда показатель делителя равен показателю делимого, введено определение:

a0 = 1

Нулевая степень любого числа будет равна единице.

Отрицательный показатель

Выражение a-m, само по себе не имеет смысла. Но чтобы правило деления степеней одного и того же числа имело значение и в том случае, когда показатель делителя больше показателя делимого, введено определение:

Пример 1. Если данное число состоит из 5 сотен, 7 десятков, 2 единиц и 9 сотых долей, то его можно изобразить так:

5 × 102 + 7 × 101 + 2 × 100 + 0 × 10-1 + 9 × 10-2 = 572,09

Пример 2. Если данное число состоит из a десятков, b единиц, c десятых и d тысячных долей, то его можно изобразить так:

a × 101 + b × 100 + c × 10-1 + d × 10-3

Действия над степенями с отрицательными показателями

При умножении степеней одного и того же числа показатели складываются.

При делении степеней одного и того же числа из показателя делимого вычитается показатель делителя.

Чтобы возвести в степень произведение, достаточно возвести в эту степень каждый сомножитель отдельно:

Чтобы возвести в степень дробь, достаточно возвести в эту степень отдельно оба члена дроби:

При возведении степени в другую степень показатели степеней перемножаются.

Дробный показатель

Если k не есть число кратное n, то выражение: не имеет смысла. Но чтобы правило извлечения корня из степени имело место при любом значении показателя степени, введено определение:

Благодаря введению нового символа, извлечение корня всегда может быть заменено возведением в степень.

Действия над степенями с дробными показателями

Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для целых показателей.

При доказательстве этого положения, будем сначала предполагать, что члены дробей: и , служащих показателями степеней, положительны.

В частном случае n или q могут равняться единице.

При умножении степеней одного и того же числа дробные показатели складываются:

При делении степеней одного и того же числа с дробными показателями из показателя делимого вычитается показатель делителя:

Чтобы возвести степень в другую степень в случае дробных показателей, достаточно перемножить показатели степеней:

Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:

Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.

Справка по контенту:

1. Сложность работы инженерного калькулятора

2. Инструкции по функциям инженерного калькулятора

3. Как использовать инженерный калькулятор — например

4. Тригонометрический калькулятор онлайн — примеры

Комплекс компьютерной инженерии

интегрированный математический калькулятор это поможет вам выполнить простейшие вычисления: умножение и сложение, вычитание и деление.

Онлайн-калькулятор быстро и точно построить любое количество на выбранном вами уровне.

Представленный калькулятор калькулятора содержит в себе все возможные версии веб-программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, замки), логарифмы (Вход) факториалов (N!), расчет корней, пазух и arktangenti, kosinusov, касательныйонлайн — набор тригонометрических функций, а не только.

С помощью компьютерной программы вы можете работать на любом устройстве, в любом случае размер интерфейса будет персонализирован для вашего устройства, или вы можете настроить его на свой вкус.

Номера вводятся в двух версиях:

• с мобильных устройств — запись с дисплеем телефона или планшета, программируемые клавиатуры
• с персонального компьютера — используя дисплей электронного интерфейса или с помощью компьютерной клавиатуры с любым номером

Инструкции для функций инженерного калькулятора

Чтобы понять возможности программы, дадим вам краткую инструкцию, см. примеры веб-расчетов.

Принцип работы научного калькулятора: введите номер, по которому производится расчет, затем нажмите функциональную клавишу или операцию, а затем, при необходимости, другое изображение, например, скорость, в конце — знак равенства.

Как использовать MR MC M + M-MS

Как использовать инженерный калькулятор — например

Как добраться до власти

Например, если вы хотите построить 12 ^ 3, введите следующую последовательность:

12 [ху] 3 [=]

12, клавиша «x в игровом уровне» [xy], 3, знак равенства [=]

Ответ: 1728

Как найти корни кубика

Предположим, что мы вытащили корень куба 729, щелкните в следующем порядке:

729 [3√x] [=]

729, [3√x] «кубический корень X» равен [=]

Как найти корень на вашем компьютере

Проблема: найдите квадратный корень из 36.

Решение: все просто, просто нажмите:

36 [Y√х] 2 [=]

36, [y√x] «корень X, скорость воспроизведения», требуемый уровень 2, [=]

Ответ: 6

С помощью этой функции вы можете найти корень на любом этапе, а не только квадрат.

Как квадрат

Существует две функции для квадратной калькуляции веб-программы:

[Х] «X на стадии воспроизведения», [X2] «X в квадрате»,

входная последовательность данных такая же, как и раньше, — первое начальное значение, затем «x ^ 2» и равные, или если нет квадратов, но любое число, нажмите «x ^ y», а затем укажите соответствующий уровень и в том же самом принте равняется символу.

Например: 45 [xy] 6 [=]

Ответ: Сорок пять на шестом шаге.

Трехграмотный калькулятор онлайн — примеры

Как сделать веб-расчет синусов и косинусов, касательных

Обратите внимание, что kalkpro.ru может работать с обоими уровнями, радианами и градом.

1 рад = 57,3 °; 360 ° = 2π, 1 градус = 0,9 градуса или 1 град = 0,015708 радианов.

Чтобы активировать определенный режим измерения, нажмите нужную кнопку:

где Deg — градусы, Rad — измерение в радианах, Град — в граде.

Метод расчета по умолчанию находится в градусах.

В качестве простейшего примера шаг синуса составляет 90 градусов. нажмите:

90 [sin] [=]

Ответ: единица

Мы также вычисляем другие тригонометрические функции, например, вычисляем косинус 60 °:

60 [cos] [=]

Решение: 0,5

Аналогичным образом, наоборот тригонометрические функции онлайн на CALPRO — арксин, дуговый косинус, арктангенс и гиперболические функции sinh, cosh, tanh.

Чтобы войти, вы должны включить интерфейс, нажав [Inv], будут отображаться новые кнопки — asin, acos, atan.

Порядок ввода данных одинаков: сначала значение, затем символ желаемой функции, будь то акросин или дуговый косинус.

Преобразование с помощью кнопок Dms и Deg на калькуляторе

[Deg] позволяет конвертировать, как в градусах, минутах и ​​секундах в формате, в десятичные точки для вычисления. [Dms] создает обратный перевод — в виде «градусов, минут, секунд».

К примеру, как 35 ° 14 минут 04 секунды 53 десятых секунды переводятся на десятки:

35, 140, 4553 [Deg] [=] 35, 23, 44, 45, 46, 66, 66, 66, 66, 66,

Перейдем к предыдущей форме: 35,23459166666666666666 [Dms] [=] 35,140453

Десятичный логарифм онлайн

Десятичный логарифм калькулятора вычисляется следующим образом, например, если вы ищете журналы для базы 10, log10 (1) или lg1:

1 [log] [=]

В результате получилось 0.

Чтобы вычислить lg100, нажмите:

100 [log] [=]

решение: два. Как проверить себя?

как решать дела с фракциями и полномочиями

Что такое логарифмический логарифм на базе 10. В нашем примере есть 2-ступенчатый уровень, на который вы должны ввести базу логарифмов, т. Е. 10, чтобы получить 100.

Также вычисляется натуральный логарифм, но с ключом [ln].

Как использовать память на компьютере

Существующие кнопки памяти: M +, M-, МР, МС, MC.

Добавьте данные в память программы, чтобы MS впоследствии помогала в дальнейших вычислениях.

MR отобразит данные, хранящиеся в памяти.

MC удалит все данные из памяти. M — вычитает номер на веб-дисплее из памяти, хранящейся в памяти.

пример:. В память о программе мы сделаем сто сорок пять:

145 [MR]

После выполнения других вычислений нам пришлось внезапно вернуть сохраненный номер на экран электронного калькулятора, просто нажав:

[MR]

Экран появится снова 145.

Затем снова мы верим, что мы верим, а затем решили добавить, например, 85 с памятью 145, для которой мы нажимаем [M +], или [М] для подсчета 85 из 145 сохраненных.

В первом случае, после возврата окончательного номера из памяти, оказывается, что кнопка [MR] 230, а во втором, после нажатия [M-] и [MR], получается, что 60.

Инженерный калькулятор kalkpro.ru быстро и точно выполняет сложные вычисления, которые значительно упрощают ваши задачи.

Список калькуляторов и функциональных возможностей будет расширен, просто добавьте сайт в закладки и расскажите своим друзьям!

Как подсчитать градусы

Мы часто сталкиваемся с уровнями в разных сферах жизни и даже в повседневной жизни.

Когда дело доходит до квадратных метров или кубических, он сказал, что число на 2-м или 3-м этапах, когда мы видели отметку пленного штрафа или в больших количествах, часто использует 10 ^ n.

И, наконец, есть много формул, которые включают ставки. И какой уровень действия разрешен и как они учитываются?

инструкции

первый Начнем с основ, с определением. Ставка — это продукт тех же факторов. Множитель называется базой, а число факторов называется показателем.

Как уменьшить долю сил

Действие, созданное силой, называется степенью возведения в степень. Показатель может быть положительным и отрицательным, целочисленным или частичным, правила обработки ставок остаются прежними. Если основание силы — с отрицательным знаком, а экспоненциальный странный, то результат потенцирования отрицательный, но если показатель является даже результатом, то в автономии отрицательного или положительного знака до уровня фундамента всегда будет знак плюса.

второй Все свойства, которые мы сейчас пишем, считаются одной и той же.

Однако, если основы ставок отличаются, добавление или вычитание разрешено только после определения. Так же, как они размножаются и делятся. Поскольку построение мощности в соответствии с установленным порядком выполнения расчетных операций имеет преимущество перед умножением и делением, а также сложение и вычитание, выполненные в последней строке. И для метаморфоза этой серьезной последовательности действий есть скобки, в которых завершены основные меры.

третий Какие конкретные правила для арифметических операций существуют для примерно одинаковых оснований?

Помните следующие свойства мощности. Если они работают до 2-градусных выражений, например, ^ n * s ^ m, то пусть это будет свернуто в той мере, в какой это потому, что ^ (n + m). Точно так же они работают с частными, но ставка вычитается из других. a ^ n / a ^ m = a ^ (n-m).

четвёртая В случае, когда требование меньше (a ^ n) ^ m, экспоненты умножаются и получаются ^ (n * m).

пятые Следующее более важное правило, если оно допустимо в качестве основы для представления в виде произведения, может быть преобразовано из (a * b) ^ n в n ^ n * b ^ n.

Также разрешено преобразовывать часть. (a / b) ^ n = a ^ n / b ^ n.

шестые Заключительные инструкции. Если показатель степени равен нулю, результат экспоненциальности всегда является единицей. Если показатель отрицательный, то это частичное выражение.

Это означает a ^ -n = 1 / a ^ n. Наконец, если показатель является частичным, извлечение корня важно, так как a ^ (n / m) = m? A ^ n.

Похожие видео

Правила обработки ставок

1. Уровень произведения двух или более факторов равен произведению мощности этих факторов (с одинаковым показателем):

(abc …) n = anbncn …

Пример 1.

(7 • 2 • 10) 2 = 72 • 22 • 102 = 49 • 4 • 100 = 19600.
Пример 2 (x2 -a2) 3 = [(x + a) (x-a)] 3 = (x + a) 3 (x-a) 3

Обратное преобразование важнее:

anbncn … = (abc …) n

то есть.

Произведение равных количеств нескольких величин равно одинаковому уровню произведения этих величин.

Пример 3.
Пример 4.

(A2 — ab + b2) 2 = (a3 + b3) 2 = [(a + b2) 2

2. Коэффициент распределения (дробь) равен коэффициенту деления той же степени деления с той же степенью дивиденда:

Пример 5.
Пример 6.

Обратное преобразование:.
Пример 7..
Пример 8..

третий

При умножении ставок с одинаковыми основаниями мы добавляем показатель:

aman = am + n

Пример 9.22 • 25 = 22 + 5 = 27 = 128.
Пример 10.

(a — 4c + x) 2 (a — 4c + x) 3 = (a — 4c + x) 5.

четвёртая

Меры с разрешениями и корнями

При делении ставок с одинаковыми основаниями счетчики дивидендов вычитаются из величины дивиденда

Пример 11 125: 123 = 125-3 = 122 = 144.
Пример 12. (x-y) 3: (x-y) 2 = x-y.

5. Когда уровень поднят до мощности, показатели умножаются:

Пример 13 (23) 2 = 26 = 64.
Пример 14.

Выражения власти (члены с полномочиями) и их трансформация

← Вернуться назад на «Калькуляторы онлайн»

Будет решение …

Этот калькулятор поможет вам окончил онлайн, как целое, так и десятичное число.

Наш калькулятор позволяет вам поднимать не только положительные, но и отрицательные числа.

Степень, в которой мы можем построить число, может быть отрицательный.

Инструкции для калькулятора

Помните правила округления десятичного знака в соответствующем уроке.

К небольшим номерам (до 20) мы советуем вам узнать сердце, передавая «таблицу градусов» в разделе «Для изучения».

Важно!

Администрация веб-сайта math-prosto.ru указывает, что вы можете освежить свои знания предмета уровня аудитории для 7-го и 8-го классов.

Уменьшение фракций со степенями

Это онлайн-калькулятор, предназначенный для облегчения задачи увеличения количества мощностей. Введенные числа могут быть отрицательными. В десятичных дробях вы можете вводить разделитель, точка и запятая одинаковы.

Вы также можете ввести число «e» в формах полей калькулятора (введите латинский алфавит).

Имейте в виду, что число с отрицательным значением будет размещено на нецелого этапа (диплом с дробным компонентом, поскольку отрицательные числа не определены), ничто не может поднять его до отрицательной энергии.

Использование калькулятора степеней очень просто: когда вы вводите в первом поле слева, укажите базовую мощность (номер, который должен быть установлен для питания), а другой — значение его индекса.

Затем нажмите кнопку «Расчет», чтобы вычислить, результат будет отображаться одним и тем же символом. Чтобы сбросить форму, нажмите кнопку «Сброс».

Например, если вы хотите рассчитать, сколько 5 в 5 степеней, заполните форму следующим образом:

vipstylelife.ru

Степень уравнения

Кроме разделения уравнений по количеству неизвестных, уравнения так же разделяются по степеням неизвестных: уравнения первой степени, уравнения второй степени и так далее.

Чтобы определить степень данного уравнения, в нём нужно предварительно сделать следующие преобразования:

• раскрыть скобки,
• освободить уравнение от дробных членов,
• перенести все неизвестные члены в одну из частей уравнения,
• сделать приведение подобных членов.

После выполнения всех этих преобразований, степень уравнения определяется по следующим правилам:

Степенью уравнения с одним неизвестным называется показатель при неизвестном в том члене уравнения, в котором этот показатель наибольший.

Примеры:

10 — x = 2 – уравнение первой степени с одним неизвестным
x² + 7x = 16 – уравнение второй степени с одним неизвестным
x³ = 8 – уравнение третьей степени с одним неизвестным

Степенью уравнения с несколькими неизвестными называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.

Для примера возьмём уравнение

3x²y + xy + 25 = 0

Для наглядности расставим показатели первой степени (которые обычно не ставят):

3x²y¹ + x¹y¹ + 25¹ = 0

Теперь посчитаем суммы показателей для тех членов уравнения, в которых присутствуют неизвестные:

3x²y¹ – сумма показателей равна 2 + 1 = 3
x¹y¹ – сумма показателей равна 1 + 1 = 2

Сумма показателей у первого члена уравнения больше чем у второго, значит при определении степени уравнения будем ориентироваться на сумму показателей первого члена. Это значит что про данное уравнение можно сказать, что это уравнение третьей степени с двумя неизвестными.

Ещё примеры:

2xy — x = 25 – уравнение второй степени с двумя неизвестным
xy² — 2xy + 8y = 0 – уравнение третьей степени с двумя неизвестным

naobumium.info

Показательные уравнения. Решения

Решение множества показательных уравнений не обходится без замен, квадратных уравнений и сложных преобразований. Приведенные ниже примеры помогут Вам в этом быстро разобраться и научат решать самые сложные из них. Также Вы сможете выучить некоторые свойства логарифмов без которых показательные уравнения в простой способ не решить. Начнем с самых азов — теоретического материала об уравнениях.
Показательными называют уравнения в которых неизвестная величина содержится в показателе степени, при этом основа степени не содержит неизвестной величины. Самое простое показательных уравнения a^x=b решают логарифмированием x=log[a](b).

При решении показательных уравнений используют свойство показателей: если в уравнение степени с одной и той же основой то равные показатели степени или основание равно единице.
Из равенства следует или .

Некоторые уравнения требуют замены переменной и сводится к решению степенного уравнения. Например уравнения
легко сводится к квадратному если сделать замену
При этом исходное уравнение примет вид
После его решения нужно вернуться к замене и решить полученное уравнение.
Если показательной уравнение содержит две различные показательные функции ( основы не сводятся к одной) , то выполняют деления уравнения на одну из основ в соответствующей степени и переход до показательного уравнения которое содержит функцию с дробной основой.
Находя решения показательных уравнений следует помнить что показательная функция принимает только положительные значения. Отрицательные значения или нули замененной переменной не принимаются к рассмотрению.

На этом необходимый теоретический материал заканчивается и переходим к рассмотрению распространенных примеров.

Пример 1.Решить показательное уравнение

Решение. Перепишем уравнение к следующему виду

Второе слагаемое распишем как произведение

и сделаем замену в уравнении

Исходное уравнение преобразуем к следующему

Областью допустимых значений будет действительная ось за исключением точки y=0.
Умножим его на y и переносим все в левую сторону

Получили квадратное уравнение корни которого находим по теореме Виета. Нетрудно убедиться что они принимают значения

Возвращаемся к замене и находим решения


Выполняем проверку


Итак оба решения удовлетворяют уравнению.

 

Пример 2. Решить показательное уравнение

Решение. Используя одну из свойств логарифма записываем правую сторону уравнения в виде

Приравнивая показатели находим

 

Пример 3. Решить уравнение

Решение. Такого сорта примеры решают логарифмированием обеих сторон что приводит к сведению показательного уравнения к простому виду.


Полученное уравнение относительно переменной решаем через дискриминант

Корни уравнения приобретут значения



Другого метода позволяющего аналитически получить решения Вы не найдете ни в интернете, ни на форумах.

 

Пример 4. Решить уравнение

Решение. Выполним некоторые преобразования с показателями чтобы упростить уравнение

Эквивалентные значения подставим в уравнение, в результате получим

Выполняем замену

Уравнение превратится к квадратному


Вычисляем дискриминант

Найденное значение подставляем в формулу корней


Возвращаемся к замене и находим


Задача решена.

 

Пример 5.Решить уравнение

Решение. Такого типа уравнения решают с постоянной основой . За основу классически берут 10 , однако , если взять другую (для данного примера 5 или 9 ) то решение примет компактный вид
Рассмотрим оба метода.
1. Прологарифмируем обе части равенства

Раскрываем скобки и группируем слагаемые при неизвестных


Такой интересный результат.

2. Прологарифмируем обе части равенства по основанию 9

Группируя слагаемые содержащие переменную получим


Оба метода достаточно быстрые и эффективные, для себя выбирайте который Вам больше подходит.

 

Пример 6.Решить уравнение

Решение.Такого рода задачи решают по следующей схеме. Показательное уравнения превращают к виду

Все слагаемые разделяем на величину чтобы свести к дробному виду

После этого выполняем замену

Уравнение переписываем в виде

Умножаем на переменную и решаем квадратное уравнение


Дискриминант принимает нулевое значение, при етом корни уравнения совпадают

Возвращаемся к замене и решаем


Итак x=2 — единственное решение.
Используйте приведенную схему в подобных задач и гарантированно получите верный результат.

 

Пример 7. Решить уравнение

Решение. На первый взгляд уравнения достаточно сложное и неизвестно как его упрощать, однако схема решения данного примера и подобных довольно проста и интересна. Выполним над уравнением преобразования

Нужно это уравнение преобразовать к квадратному



Выполним замену

и перепишем уравнение в виде следуещого

Вычисляем дискриминант

и корни уравнения

Возвращаемся к совершенной замене

Такое уравнение сводим к квадратному, выполнив замену

В результате получим

Решаем через дискриминант


Возвращаемся к замене и определяем переменную x

Второе значение рассматривать не будем, поскольку оно отрицательное, а показательная функция всюду положительная.
Решаем вторую половину задачи

Используя предыдущую замену получим

Дискриминант примет значение

Находим корни уравнения

Первый корень имеет место бить, второй — отрицательный и не подходит.

Получили два решения показательного уравнения

Хорошо разберитесь с приведенными методами решения показательных уравнений, возможно некоторые из них пригодятся при прохождении ВНО, экзамене или контрольной работе. Будьте внимательны при упрощении, первое время используйте подстановку для проверки результатов.

Похожие материалы:

yukhym.com