Тема урока: «Четырехугольники (параллелограммы, прямоугольники, ромбы, квадраты, трапеции, дельтоиды) в окружающем нас мире» | План-конспект урока по геометрии (8 класс):
Разумова Галина Владимировна, учитель математики
Тема урока: «Четырехугольники (параллелограммы, прямоугольники, ромбы, квадраты, трапеции, дельтоиды) в окружающем нас мире»
Тип урока: обобщающий и систематизирующий урок по теме «Четырехугольники» с интеграцией в предметную область «Технология».
Цель деятельности учителя:
- систематизировать в памяти обучающихся знания о четырёхугольниках, их видах, свойствах, признаках;
- отработать умение решать задачи по данной теме;
- обнаружить связь между геометрией и технологией;
- обозначить область практического применения полученных знаний в жизни.
Цели деятельности учащихся:
- уметь находить примеры использования четырехугольников в жизни и применять полученные на уроке знания на практике;
- умение добывать информацию из разных источников, осмысливать и анализировать её;
- умение работать в команде, высказывать свою точку зрения, принимать чужую, развивать связную речь;
- расширить свои знания, математический кругозор, интуицию, логику.

Планируемые результаты:
Предметные:
- знать виды четырёхугольников, их свойства и признаки;
- уметь решать задачи на нахождение неизвестных величин и на доказательство;
- умение выстраивать логичную последовательность действий.
Метапредметные:
Познавательные УУД:
- самостоятельно формулируют познавательные цели;
- применяют методы информационного поиска;
- обосновывают выбор эффективного способа решения задачи;
- строят логическую цепочку утверждений.
Регулятивные УУД:
- формулируют учебные задачи на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно;
- составляют план и последовательность действий, оценивают правильность выполнения действий;
- адекватно воспринимают оценку учителя и одноклассников.
Коммуникативные УУД:
- учитывают позиции других людей;
- участвуют в коллективном обсуждении проблемы;
- умеют работать в группе, формулируют собственное мнение, задают вопросы.

Личностные УУД:
- адекватная самооценка учебной деятельности;
- осознание границ собственного знания и незнания;
- стремление к речевому совершенствованию;
- развитие творческих способностей.
Цель: Создать условия для систематизации знаний по теме «Четырехугольники»
Задачи:
Образовательные: развивать предметные компетенции:
- систематизировать знания по теме «Четырехугольники»;
- анализировать различные свойства четырёхугольников;
- формировать умения решать задачи;
- применять полученные знания в нестандартной ситуации, в повседневной жизни.
Развивающие:
- развивать учебно-познавательную компетенцию через учебно-логические умения: анализ, синтез, обобщение и классификацию;
- развивать информационную компетенцию ;
- развивать ценностно-смысловую компетенцию через умения определять цель урока, высказывать оценочные суждения;
- развивать коммуникативную компетенцию через умения работать в парах и группе.

Воспитательные:
- прививать интерес к предмету;
- воспитывать у учащихся внимание и аккуратность в решении задач;
- развивать чувство коллективизма, умение выслушивать ответы одноклассников.
Оборудование: компьютер, проектор, раздаточный материал, ножницы.
Ход урока:
1.Организационный этап.
Здравствуйте, ребята, здравствуйте уважаемые гости, я рада приветствовать Вас на нашем уроке. Сегодня у нас необычный урок. Я надеюсь, что он пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – это интересный и нужный предмет. Потому что как сказал ученый — математик, физик, философ Александр Данилович Александров «Окружающий нас мир – это мир геометрии».
Прежде, чем мы начнем, мне бы хотелось, чтобы вы, ребята, взялись за руки и пожелали друг другу хорошего настроения на сегодняшний урок.
Тренинг «Пожелание»: учащиеся берутся за руки и по очереди произносят пожелания одноклассникам. (Удачи, легких задач, смелости, решительности, везения, собранности и т.д.).
(Удачи, легких задач, смелости, решительности, везения, собранности и т.д.).
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Учитель: «Природа говорит языком математики, буквы этого языка — круги, треугольники и иные геометрические фигуры» так сказал Галилео Галилей, ученый математик, физик, философ.
Скажите, какие геометрические фигуры чаще всего встречаются в природе?
Ответы учащихся: цилиндры, конусы, пирамиды, треугольники, круги, овалы, шары, полушары — птичьи гнезда, шестиугольники – соты, снежинки.
Учитель: Часто ли в природе встречаются четырехугольники?
Ответы учащихся.
Учитель: Оглянитесь вокруг. Какие геометрические фигуры чаще всего окружают нас? Приведите примеры.
Ответы учащихся.
Учитель: Почему в жизни людей четырехугольники встречаются чаще, чем в природе? Подумайте над этим вопросом. Готовы отвечать? Пожалуйста, от каждого из вас один ответ, просьба не повторяться.
Ответы учащихся: четырёхугольниками проще всего эффективно заполнять пространство, удобны в применении, при применении четырехугольников больше полезной площади, экономия материала, упрощаются вычисления.
Учитель: А от чего это зависит?
Ученики: От свойств четырёхугольников.
Учитель: итак, сформулируем тему сегодняшнего урока.
Ответы учащихся.
Учитель: Правильно, тема нашего урока «Четырехугольники в окружающем нас мире». (Записываем тему урока в тетрадях).
Учитель: Каковы ваши ожидания от сегодняшнего урока? Попробуйте, исходя из ваших ожиданий, сформулировать вашу личную цель урока и записать ее в тетрадь. (Цель урока формулируют несколько учеников)
Учитель: Сформулируем общую цель урока.
(Систематизировать знания о четырехугольниках и отработать умение решать геометрические задачи практической направленности, где встречаются четырехугольники в окружающем мире).
3.Актуализация знаний. (Фронтальная работа и проверка домашнего задания).
Перед вами на слайде геометрические фигуры — четырехугольники:
2) 3) 4)
1)
5) 6) 7) 8)
- Видите ли вы на рисунке параллелограммы? (да) Сколько их? (5) Назовите, под какими они номерами? (2;4;5;6;7) Почему вы думаете, что каждая из этих фигур параллелограмм? (у этих четырехугольников противоположные стороны попарно параллельны).
 Дайте определение и перечислите свойства параллелограмма.
Дайте определение и перечислите свойства параллелограмма. - Есть ли на рисунке прямоугольники? (да) Сколько вы их видите? (2) На каких рисунках они изображены? (2;4) Докажите, что эти фигуры прямоугольники? (это параллелограммы, у которого все углы прямые). Дайте определение и перечислите свойства прямоугольника.
- Видите ли вы на рисунке ромбы? (да) Под какими они номерами? (2;6;7) Что называется ромбом? (параллелограмм, у которого все стороны равны, называется ромбом). Дайте определение и перечислите свойства ромба.
- Найдите на рисунке квадраты. (2) Обоснуйте, почему это квадрат? (это прямоугольник, у которого все стороны равны или это ромб, у которого все углы прямые). Дайте определение и перечислите свойства ромба.
- На каком рисунке изображены трапеции? (1) Как вы определили, что это трапеция? (это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны). Дайте определение и перечислите свойства равнобедренной трапеции.
- А какие фигуры мы ни разу не назвали? (3 и 8)
Что это за четырехугольники?
Это четырехугольники, у которых нет параллельных сторон. У таких четырехугольников нет специальных названий?
У таких четырехугольников нет специальных названий?
На дом вам было задание узнать самостоятельно, почему так называются знакомые нам четырехугольники и где они нашли применение в окружающем нас мире. (Заслушиваем сообщения учащихся).
1 ученик: Слово «параллелограмм» пришло к нам из Древней Греции и связано с самым известным в истории математиком – Евклидом. Оно состоит из двух греческих слов – «Parallelos», что означает «параллельный», и «Gramme» — линия. Таким образом, параллелограмм можно перевести как параллельные линии. Этот принцип и заложен в определение параллелограмма.
Параллелограмм даёт определения прямоугольнику, ромбу; в жизни параллелограмм – это рамы велосипедов, мотоциклов, где для жёсткости проведена диагональ, в орнаментах мы можем увидеть параллелограммы. В физике параллелограмм применяется при изучении разложения сил, при нахождении равнодействующих сил.
2 ученик: Слово «ромб» тоже греческого происхождения, «rombos» — бубен. Если сейчас бубны делают круглой формы, то раньше их делали в виде квадратов или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходят еще с тех времен, когда бубны не были круглыми.
Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходят еще с тех времен, когда бубны не были круглыми.
Реечный домкрат для легковых автомобилей имеет форму ромба. Плиточники укладывают плитку в виде ромба, квадрата – из них получаются красивые узоры. Ромб часто используется в орнаментах и паркетах. Аргайл (шотландское слово) – узор из ромбов или квадратов расположенных в шахматном порядке и образующих параллельные и поперечные полосы разных цветов. Название происходит от имени шотландского клана Камбел в графстве Аргайл. Особую популярность этого орнамент получил в 20 веке. С тех пор этот рисунок не выходит из моды. Особенно популярен на свитерах, жилетах, кардиганах платьях, шарфах, носках, гетрах. И в вашем гардеробе, я уверена, что-нибудь да найдется с таким рисунком.
Логотип автомобиля «Рено» французской марки – ромб, «Mitsubishi» (Мицубиси) – японский автомобиль, логотип – три ромба, что в переводе с японского и означает слово мицубиси (три ромба/бубна).
3 ученик: Слово «квадрат» заимственное слово в 17 веке из латинского языка – делать четырёхугольным. «Слово круг вошло в геометрию, — писал В.Г.Белинский, — но для квадрата не нашлось русского слова, ибо хотя каждый квадрат есть четвероугольник, но не каждый четвероугольник – квадрат…»
Ни наука, ни техника, ни искусство не обходятся без квадрата. И в хозяйственных делах его тоже используют.
В основании мраморных колонн лежит квадрат. Играя в шахматы, фигуры по квадратам передвигают. Тетрадки разрисованы голубыми квадратиками.
В хирургическом отделении для пересадки кожи применяют специальную машинку, которая вырезает кожу в виде квадратов. Их располагают на обожжённом участке в шахматном порядке.
В сельском хозяйстве применяют квадратно – гнездовой способ посадки культур – урожай при этом лучше, этот способ хорош тем, что можно применять механизированную обработку.
«Черный квадрат» Казимира Малевича, русского художника, — одна из самых интересных картин, которая «прославляет» квадрат. Казалось бы, что может быть проще: на белом фоне черный квадрат. Любой человек, наверное, может нарисовать такое. Но вот загадка этот шедевр, созданный в начале 20 века, до сих пор притягивает к себе и исследователей и любителей живописи.
Казалось бы, что может быть проще: на белом фоне черный квадрат. Любой человек, наверное, может нарисовать такое. Но вот загадка этот шедевр, созданный в начале 20 века, до сих пор притягивает к себе и исследователей и любителей живописи.
(В классе организована выставка рисунков «Геометрические фигуры».) Учитель: Обратите внимание, на выставку своих работ по мотивам К. Малевича. Ребята, вы очень постарались, все работы интересны, хороши.
4 ученик: Прямоугольник – четырехугольник, у которого все углы прямые. В евклидовой геометрии для того, чтобы четырехугольник был прямоугольником, достаточно, чтобы, хотя бы три его угла были прямые.
Прямоугольник несёт красоту, чёткость, стройность.
Оглянитесь вокруг: стены, пол, потолок, поверхность стола, футбольное поле, грани карандашей, банковские карточки, даже сотовый телефон – все это прямоугольники.
Попробуйте построить дом или сделать раму для картины, не зная свойств прямоугольника.
5 ученик: Трапеция – слово греческое, означавшее в древности «столик». Геометрическая фигура названа так по сходству с маленьким столом. Как тут не вспомнить греческое слово трапеза, переводимое как стол с яствами и используемое в церковных текстах и поэтической речи.
Геометрическая фигура названа так по сходству с маленьким столом. Как тут не вспомнить греческое слово трапеза, переводимое как стол с яствами и используемое в церковных текстах и поэтической речи.
В «Началах», книге Евклида, термин «трапеция» применяется не в современном, а в другом смысле: любой четырёхугольник (не параллелограмм), лишь в 18 веке приобретает современный смысл.
Созвездие Орион – звезды образуют трапецию, в биологии используется геометрическая фигура трапеции: мышца спины, трапециевидная кость, для пошива одежды: платья, юбки, используется трапециевидная форма, в цирке есть снаряд трапеция.
4. Обобщение и систематизация знаний. Подготовка учащихся к обобщенной деятельности. Воспроизведение на новом уровне.
Итак, все четырехугольники можно классифицировать следующим образом (на экране)
Четырехугольники
Выпуклые четырехугольники Невыпуклые четырехугольники
Дельтоид
Параллелограмм Трапеция Остальные
четырехугольники
прямоугольник ромб
квадрат Равнобедренная Прямоугольная
В таблице есть одно нераскрытое место. Что это означает?
Что это означает?
В школьном курсе геометрии изучаются только 5 видов четырехугольников. Сегодня на уроке предлагаю выйти за рамки школьной программы и познакомиться с еще одним четырехугольником. Этот четырехугольник мы часто встречаем в природе, например, крона деревьев, тело рыбы, человеческий мозжечок, соединенные человеческие руки, лист дерева, а также форма носа и глаз, а также изобретение человека воздушный змей имеют его форму.
Проведем небольшое исследование.
Перед вами четырехугольник, который называется ромбоид или дельтоид. Ваша задача: изучить свойства данного четырехугольника (изучаем стороны, углы, диагонали). (На столе у каждого дельтоид)
Давайте обсудим ваши предположения и запишем его определение и свойства в тетрадь.
1. Возьмите линейки и измерьте его стороны. Что можете сказать? Дайте определение этому четырехугольнику.
Ромбоид ( дельтоид )– это четырехугольник, у которого две стороны, прилежащие к одной вершине, попарно равны.
2. Проведите диагональ ВД, что можете сказать о треугольниках АВД и ВДС.
Вывод:
- Углы между неравными сторонами равны.
- Большая диагональ является биссектрисой углов.
3.Проведите диагональ АС, что можете сказать о треугольниках АВС и АДС.
Вывод:
3) Меньшая диагональ делит дельтоид на 2 равнобедренных треугольника.
4) Диагонали взаимно перпендикулярны.
5) Меньшая диагональ точкой пересечения делится пополам.
Свойства:
- Меньшая диагональ точкой пересечения делится пополам.
- Диагонали перпендикулярны.
- Большая диагональ является биссектрисой углов.
- Меньшая диагональ делит его на два равнобедренных треугольника.
Ребята, скажите, пожалуйста, в каких известных вам четырехугольниках стороны, прилежащие к одной вершине равны?
(Квадрат, ромб) Правильно, это говорит о том, что квадрат и ромб являются дельтоидами, у которых все стороны равны.
5. Физкультминутка («истинно — ложно»):
Я скажу несколько предложений. Если предложение ложное, то вы встаете, если верное, то поднимаете руку.
Если предложение ложное, то вы встаете, если верное, то поднимаете руку.
1. Диагонали прямоугольника равны.
2. Все углы квадрата прямые.
3. Диагонали параллелограмма равны.
4. В ромбе все стороны равны.
5. Диагонали прямоугольника перпендикулярны.
6. В параллелограмме противоположные стороны равны.
7. Диагонали ромба равны.
6. Применение знаний и умений в новой ситуации
Работа в группе по решению практических задач, интеграция в предметную область технология. Девиз: “Думаем много, пишем мало”.
Вы все на уроках технологии, готовите себя к дальнейшей жизни, к взрослой жизни.
Сейчас мы перевоплотимся в бригаду плотников (работа с деревом). Назовите их необходимый инструмент (ножовка, угольник, рулетка, ). Решаем задачи:
Ситуация первая: Заготовлены одинаковые по длине и ширине рейки в форме прямоугольников. Как обрезать концы реек под углом в 45 , не используя углоизмерительного инструмента, чтобы из них можно было сложить раму?
Решение:
Сначала надо отметить равные отрезки AB, BC и CD, затем провести диагональ BD, и по ней обрезать на два равных угла квадрат ABCD. Следова-тельно ⦟ABD ⦟CBD. Вот мы и обрезали концы реек под углом в 45ᵒ, не используя углоизмерительного инструмента так, чтобы из них можно было сложить раму.
Следова-тельно ⦟ABD ⦟CBD. Вот мы и обрезали концы реек под углом в 45ᵒ, не используя углоизмерительного инструмента так, чтобы из них можно было сложить раму.
Ситуация вторая: Плотник, вырезая квадраты из дерева, проверял их так: он сравнивал длины сторон, и если все четыре стороны были равны, то считал квадрат вырезанным правильно. Надежна ли такая проверка?
(Такая проверка недостаточна. Четырехугольник мог выдержать такое испытание, не будучи квадратом, ромб тоже имеет равные стороны).
Ситуация третья: В прямоугольной дощечке нужно просверлить круглое отверстие на равном расстоянии от ее вершин. Как найти центр этого отверстия. (Центр отверстия – точка пересечения диагоналей).
А теперь мы перевоплотимся в бригаду укладчиков паркета. Решаем задачи:
Ситуация четвертая: Мастерская получила заказ на изготовление партии паркета прямоугольной формы. Параллельность противолежащих сторон пластин технология изготовления гарантирует. Как проверить, располагая лишь линейкой, будет ли элемент паркета иметь форму прямоугольника?
(Располагая лишь линейкой, мы измерили и сравнили диагонали пластины (если у пластины диагонали равны (по теореме), то пластина будет иметь форму прямоугольника)).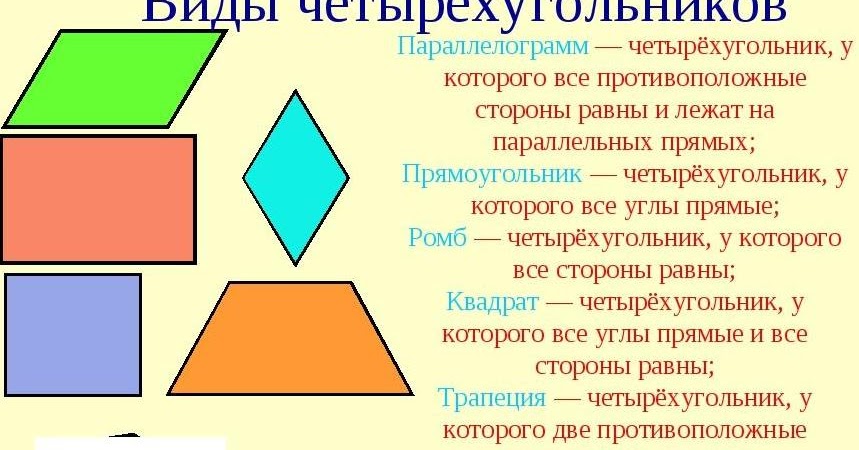
Ситуация пятая: паркетчик, вырезая квадраты из дерева, проверял свою работу так: он мерил диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат вырезанным правильно. Вы тоже так думаете?
(Эта проверка ненадежна. В квадрате, конечно, диагонали равны, но не всякий четырехугольник с равными диагоналями есть квадрат. Равные диагонали могут быть у прямоугольника и у равнобокой трапеции).
Паркетчику следовало бы применить к каждому вырезанному четырехугольнику две проверки сразу (проверить стороны и диагонали), тогда он был бы уверен, что работа сделана правильно.
А теперь мы перевоплотимся в бригаду портных. Решаем задачи:
Ситуация шестая: портной сложил кусок материи пополам по диагонали, убедился, что получившиеся половинки совпали. Затем сложил по другой диагонали и снова убедился в совпадении. Достаточно ли этого, чтобы утверждать, что кусок имеет форму квадрата?
(нет, этого не достаточно, кусок материи может иметь и форму ромба).
Перевоплощаемся в строителей. Решаем задачи:
1.Вам выделили участок для строительства дома и хотите начать строительство. С чего вы начнёте? Конечно, же, с фундамента. А как вы считаете, какой геометрической формой должен быть фундамент? Как построить прямоугольник на земле при помощи веревки?
Обсудите ваши версии и предложите способ построения прямоугольника на участке. Кто готов показать и объяснить свою версию? Какое свойство прямоугольника вам пригодилось?
2. На участке вы решили разбить красивую клумбу в форме ромба. Как построить ромб на участке? Обсудите и эту задачу в группах. Кто догадался и может показать, как построить ромб на участке?
Учитель проводит оценку деятельности учащихся на втором этапе урока, а также интеллектуальную рефлексию, используя следующие вопросы:
Можно ли предложенные в задачах приемы использовать в жизненных ситуациях?
Какой геометрический материал помогает решить эти задачи? (Признаки и свойства четырехугольников).
Достаточен ли уровень ваших знаний по теме “Четырехугольники”, для решения подобных проблем?
7. Контроль усвоения, обсуждения допущенных ошибок и их коррекция
Учитель: Посмотрим, как свойства и признаки параллелограммов помогут нам решить задачи на разрезание.
У каждого из вас на столах пакет с цветной бумагой и ножницами. Каждый вытягивает пакет с заданием и готовит решение
Ситуация первая: из листа бумаги неправильной формы необходимо вырезать прямоугольник без использования чертежных инструментов (с помощью перегибания).
Ситуация вторая: из прямоугольника вырезать квадрат, сделав при этом только один разрез.
Ситуация третья: перегнув лист бумаги неправильной формы, вырезать из нее квадрат, сделав только один разрез.
Ситуация четвертая: перегнув лист бумаги неправильной формы вырезать из нее ромб, сделав только один разрез.
Ситуация пятая: из прямоугольника вырезать равнобедренную трапецию , сделав при этом один разрез.
Ситуация шестая: получите из ромба конверт.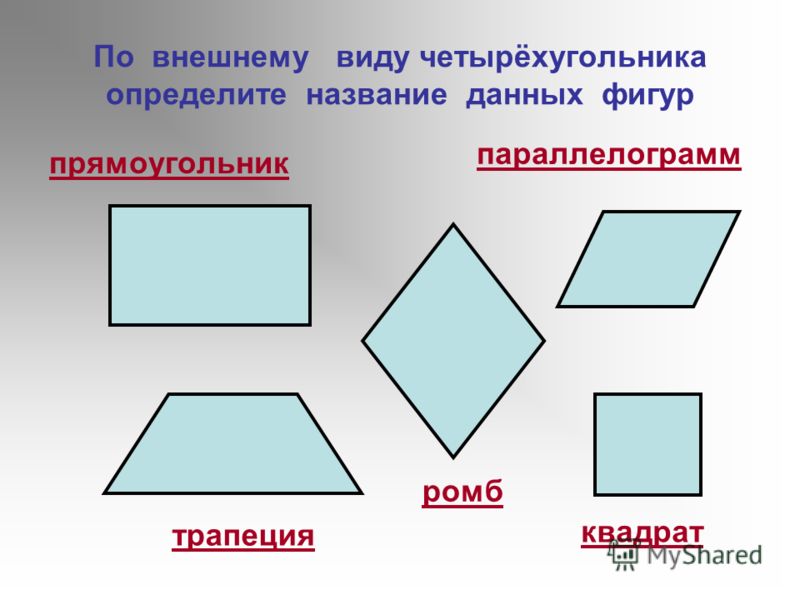
Каждый ученик показывает, как он справился с заданием.
8. Рефлексия
В завершении урока мне бы хотелось обратить ваше внимание на слова великого ученого математика Николая Ивановича Лобачевского «Математике должно учить в школе еще с той целью, чтобы познания здесь приобретаемые были достаточными для потребностей в жизни».
-Как вы думаете, что означают эти слова? (Мы должны учить математику и уметь знания, полученные на уроках применять в жизни.)
Попробуем разрешить простую жизненную ситуацию: Ваши родители решили изменить ландшафтный дизайн своего участка. Подумайте и скажите, какую посильную помощь вы сможете оказать им при этом? Свои ответы вы можете начать со слов…
Какие знания нам потребовались для решения этих задач?
Значит, нужно нам изучать геометрию? Она вам пригодится в жизни? А в учебе? При сдаче экзаменов?
Я должен…
На уроке я научился…, и поэтому…
Я смогу…
Я открыл для себя…
Думаю, что знания, умения и навыки, полученные при изучении темы «Четырехугольники», обязательно пригодятся вам в жизни.
Оценки за урок.
9. Домашнее задание – творческая работа: продолжить сказку и ответить на вопросы. Подготовиться к контрольной работе по теме «Четырехугольники», пробный вариант к/р.
Сказка
В некотором царстве, в некотором государстве с названием Эквадрия, жили – были граждане Четырехугольники. Были они все, как и положено, разные. Только обязательно у всех должно было быть 4 стороны, 4 вершины и 4 угла. А ежели у кого чего было не четыре – так он у них иностранцем считался. Конституция была своя, где все законы записаны, права, обязанности, свойства, признаки… «Если ты четырехугольник – то сумма углов в тебе 360 градусов», например. Или «быть у всех по 2 диагонали!».
И был в той стране царь, как и положено. И было у него, понятно, 3 сына. Все в отца красавцы: и стороны у них попарно параллельны, и противоположные стороны равны, и противоположные углы равны, и диагонали пересекаются и точкой пересечения делятся пополам. А если пройдет биссектриса, то непременно отсечет от любого из братьев равнобедренный треугольник. И биссектрисы — то не простые: коли выходят из противоположных углов, то параллельны, а коли из смежных – то непременно взаимно перпендикулярны.
И биссектрисы — то не простые: коли выходят из противоположных углов, то параллельны, а коли из смежных – то непременно взаимно перпендикулярны.
Гордился отец сыновьями, любовался.
Зовет как — то их к себе и спрашивает: «Как же, сыны, мне вас различать? Больно уж вы на меня все похожи!»
Говорит старший: «Я, батюшка, такой как все, да все же особенный: имею я все четыре угла прямые. А коли приглядитесь ко мне, то увидите, что диагонали мои равные! Нет такого у царя самого!»
Говорит средний: «Нет у меня, царь – батюшка ни одного прямого угла. Но зато все стороны у меня равны, не то, что у некоторых. А диагонали мои тоже особенные: взаимно перпендикулярны и делят углы пополам».
Подошла очередь младшенького. «Не на что мне жаловаться! И углы у меня прямые, и стороны все равны, и диагонали равны и взаимно перпендикулярны, да и биссектрисами углов являются. А еще ребята в школе меня самого первого изучают, в первом классе еще! Так что по всему видать, любимчик я в нашем царстве-государстве».
И была у царя сестрица любимая. Две стороны у нее были параллельны, как у брата, значит, а две другие – не параллельные. И имя красивое у нее было, с латинского «трапеза». И такая переменчивая особа! Коли равны у нее боковые стороны – назовется равнобедренной, коли угол появится прямой – она тогда прямоугольная. Пойди, угадай. Да только все в стране наловчились: коли у царевны, с утра, углы при основании равны, тогда понятно, она сегодня равнобедренная, тогда и диагонали у нее равные. Ну а если нет… ну да ладно.
Продолжите сказочку, добавив нового героя дельтоида.
Ответьте на вопросы:
- Как звали царя, старшего, среднего и младшего царевичей?
- Нарисуйте их «портреты».
- Определите родство дельтоида с параллелограммом, прямоугольником, ромбом и квадратом, трапецией.
- Как звали царевну? Нарисуйте портрет равнобедренной и прямоугольной трапеции
- Изобразите «генеалогическое древо» царской семьи.
.
Дополнительный материал
Учитель: «Ребята! Я прочитаю вам отрывок из повести «Алисы в стране чудес» писателя Кэрролла.
«…в нескольких шагах от нее сидел на ветке кот.
-Скажите, пожалуйста, куда мне отсюда идти?
-А куда ты хочешь попасть? — ответил кот.
-Мне все равно… — сказала Алиса.
-Тогда и все равно «куда и идти» — заметил кот».
О чем хочет поведать этими словами кот Алисе и зачем я вам эти строчки прочитала в самом начале урока? (ответы учеников)
Да! Надо знать цель своей работы (у Алисы должна была быть цель, куда именно она должна была идти).
3. Ребята решили заняться озеленением своего двора. Кате и Мите было поручено сделать две клумбы в форме четырехугольников с равными сторонами длиной 1 м. Клумбы у них получились такие как на рисунке. Почему они оказались разными? Быть может, кто-нибудь из ребят неверно понял описание или дело в самом описании? Подумай над этими вопросами и постарайся дать правильный ответ.
-Вернемся к вопросу, почему у Мити и Кати получились разные клумбы. Оба они правильно поняли описание и точно ему следовали. Дело в том, что само описание было неточно, двусмысленно: следуя ему можно получить клумбу и в форме квадрата – как у Кати, и в форе ромба – как у Мити. Неточное описание повлекло неточности, нарушив план озеленения.
Неточное описание повлекло неточности, нарушив план озеленения.
Домашнее задание 7-четырехугольники и другие специальные теоремы о треугольниках
Домашнее задание 7-четырехугольники и другие специальные теоремы о треугольникахЧАСТЬ I
Четырехугольники
Четырехугольник представляет собой совокупность четырех точек A, B, C и D ( вершин четырехугольника) вместе с четырьмя отрезками AB, BC, CD и DA (т. сторон четырехугольника), такие, что никакие три вершины не
коллинеарный. Примечание. Стороны AB и CD могут пересекаться или стороны AD и BC могут пересекаться.
могут пересекаться. Следующие рисунки являются примерами трех четырехугольников.
Мы хотим исследовать следующие два вопроса:
1.
2. Какова связь площади этой фигуры с площадью четырехугольника?
Какая фигура получится, если середины сторон четырехугольника присоединяются по порядку?
На основе следующего эскиза GSP, когда середины сторон четырехугольник, обозначенный буквами E, F, G и H, соединены по порядку, образуя параллелограмм сформирован.
Для полной анимации различных примеров четырехугольников и их
соответствующие параллелограммы, нажмите здесь .
Наблюдение:
Обратите внимание, что параллелограмм становится прямой линией (параллелограмм вырожден).
когда одна пара противоположных сторон четырехугольника становится параллельной (пунктирная
синие линии обозначают параллельные линии).
Далее мы хотим доказать соотношение: когда середины сторон
четырехугольника, обозначенного как E, F, G и H, соединены по порядку, параллелограмм формируется, а именно EFGH.
Сначала построим четырехугольник ABCD. Затем построить середины
стороны четырехугольника, обозначенные как E, F, G и H, по порядку.
Поскольку E — середина AB, а F — середина BC, AE=EB и БФ=ФК. По теореме, которая гласит, что в треугольнике прямая делит две стороны треугольника, она параллельна третьей стороне, можно сделать вывод что ЭФ || переменного тока. Точно так же, поскольку H — середина AD, а G — середина DC, мы знаем, что AH=HD и CG=DG. По той же теореме, упомянутой ранее, HG || переменного тока. Используя транзитивное свойство, EF || ХГ. Теперь повторяем этот процесс снова, чтобы показать, что EH || ФГ. Следовательно, мы показали, что EF || ГГ и ЭГ || ФГ. Следовательно, по определению параллелограмма имеем показано, что EFGH является параллелограммом.
Каково отношение площади этой фигуры к площади четырехугольника?
Далее мы обратим наше внимание на обнаружение взаимосвязи между площадь четырехугольника и площадь параллелограмма.
 На основе ВСП
На рисунках ниже мы видим, что площадь четырехугольника ABCD равна , умноженному на .
площадь параллелограмма EFGH. Нажмите здесь для анимации, показывающей разные четырехугольники и соответствующие им параллелограммы
и их расчетные площади.
На основе ВСП
На рисунках ниже мы видим, что площадь четырехугольника ABCD равна , умноженному на .
площадь параллелограмма EFGH. Нажмите здесь для анимации, показывающей разные четырехугольники и соответствующие им параллелограммы
и их расчетные площади. Теперь кажется естественным доказать взаимосвязь между площадями; что то есть площадь четырехугольника ABCD равна , удвоенной по площади четырехугольника. параллелограмм EFGH или, что то же самое, площадь параллелограмма EFGH составляет и половину площади четырехугольника ABCD.
Начнем с построения четырехугольника ABCD с серединой каждой стороны, соединенной
по порядку, ЕФГХ. Постройте диагонали четырехугольника ABCD, AC и BD.
Наконец, постройте диагональ параллелограмма FXYZ, FY. Мы знаем, что FXYZ
является параллелограммом, основанным на предыдущем доказательстве, показывающем, что EFGH был параллелограммом.
На основании предыдущей теоремы (стр. 12, №14), которую мы уже доказали, имеем
УХ=ХС. YX — основание треугольника FXY, а XC — основание треугольника.
ФКХ. FP также является высотой двух треугольников FXY и FCX. Следовательно,
площадь этих двух треугольников будет равна, так как формула площади для
треугольник равен 1/2 bh, и оба треугольника имеют одно и то же основание и одинаковую высоту.
Если мы проделаем те же шаги для треугольников FZY и FZB, мы можем показать, что
их площади равны. Если мы подумаем о площади треугольника FCX и треугольника
FXY равны x и, аналогично, площади треугольника FZY и треугольника
FZB оба равны y, тогда общая площадь треугольника BCY = 2x +2y. Упрощение
это алгебраически, мы имеем площадь треугольника BCY = 2 (x + y). Следовательно,
площадь треугольника BCY вдвое больше площади параллелограмма FXYZ, так как
площадь параллелограмма FXYZ = x + y. Если мы повторим этот процесс в течение трех
больше раз на каждую секцию четырехугольника; то есть треугольник DYC, BYA,
и DYA, то естественно следует, что полная площадь четырехугольника
ABCD будет в два раза больше параллелограмма EFGH.
12, №14), которую мы уже доказали, имеем
УХ=ХС. YX — основание треугольника FXY, а XC — основание треугольника.
ФКХ. FP также является высотой двух треугольников FXY и FCX. Следовательно,
площадь этих двух треугольников будет равна, так как формула площади для
треугольник равен 1/2 bh, и оба треугольника имеют одно и то же основание и одинаковую высоту.
Если мы проделаем те же шаги для треугольников FZY и FZB, мы можем показать, что
их площади равны. Если мы подумаем о площади треугольника FCX и треугольника
FXY равны x и, аналогично, площади треугольника FZY и треугольника
FZB оба равны y, тогда общая площадь треугольника BCY = 2x +2y. Упрощение
это алгебраически, мы имеем площадь треугольника BCY = 2 (x + y). Следовательно,
площадь треугольника BCY вдвое больше площади параллелограмма FXYZ, так как
площадь параллелограмма FXYZ = x + y. Если мы повторим этот процесс в течение трех
больше раз на каждую секцию четырехугольника; то есть треугольник DYC, BYA,
и DYA, то естественно следует, что полная площадь четырехугольника
ABCD будет в два раза больше параллелограмма EFGH.
Интересная теорема
Мы хотим исследовать следующие два вопроса:
1. Как соотносятся отношения BX/CX, CY/AY и AZ/BZ?
2. Если соотношение выполняется, должны ли X, Y и Z быть коллинеарными?
Какая связь между соотношениями BX/CX, CY/AY и AZ/BZ?
Мы можем использовать GSP для расчета отношений BX/CX, CY/AY и AZ/BZ и определить их
отношение.
Ясно, что когда вы перемножаете коэффициенты вместе, соотношение между
коэффициенты равны 1.
Для демонстрации, которая показывает, что это соотношение выполняется, когда X, Y и Z
коллинеарно, нажмите здесь .
Мы можем доказать эту связь. Начните со следующей картинки, где мы
построил линию AD, параллельную линии CB. Используя эту параллельную линию и
подобных треугольников, мы докажем, что соотношение выполняется.
Во-первых, мы хотим показать, что треугольник CXY подобен треугольнику ADY. Начиная с нашей эры||до нашей эры,
угол A равен углу C, а угол ADY равен углу CXY, потому что
эти углы являются чередующимися внутренними углами, мы знаем чередующиеся внутренние
углы равны. Угол AYD равен CYX, так как оба угла
вертикальные и вертикальные углы равны. Поэтому мы показали
что треугольник CXY подобен ADY .
Итак, у нас есть CY/AY=CX/AD.
Во-вторых, мы хотим показать, что треугольник ZAD подобен треугольнику ZBX. С
AD||BC, угол ZAD равен углу ZBX, а угол ZDA равен углу
угол ZXB, так как эти углы являются соответствующими углами и соответствующими
углы равны. Мы также знаем, что угол AZD равен углу
BZX, так как эти углы общие между собой. Следовательно, мы имеем это
треугольник ZAD подобен треугольнику ZBX.
Следовательно, мы имеем это
треугольник ZAD подобен треугольнику ZBX.
Итак, у нас есть XB/BZ=DA/AZ. Мы также знаем, что ZA/ZB=AD/BX=ZD/ZX.
CY/AY=CX/AD эквивалентно CY/AY * AD/CX = 1.
XB/BZ=DA/AZ эквивалентно BX/BZ * AZ/AD = 1.
Тогда имеем CY/AY * AD/CX * BX/BZ * AZ/AD = CY/AY * BX/CX *AZ /БЗ = 1.
Таким образом, мы показали, что связь между отношениями всегда
1.
Следовательно, если X, Y и Z коллинеарны, то отношение между отношениями равно 1. Теперь давайте посмотрим на обратную сторону этого утверждения.
Если отношение сохраняется, должны ли X, Y и Z быть коллинеарными?
№ Например:
Мы можем найти пример, который показывает, что отношение равно 1, если мы построим точек X, Y и Z таким образом, что три прямые, проходящие через эти три точки и вершины треугольника ABC совпадают. Например, у нас есть следующая схема.
Для демонстрации, которая показывает, что это соотношение выполняется, когда X, Y и Z
не коллинеарно, нажмите здесь .
Мы хотим показать, что если выполняется это соотношение,
, то X, Y и Z — три неколлинеарные точки.
Это доказательство является доказательством контрпримера для следующего:
Если X, Y и Z коллинеарны, то отношение равно 1.
Используется аналогичный аргумент с использованием параллельных прямых и подобных треугольников. чтобы доказать, что это соотношение выполняется, даже если точки X, Y и Z не лежат на одной прямой.
Начните доказательство с построения двух прямых, BD и CE, параллельных прямой
АКС.
Покажем следующие треугольники, похожие друг на друга:
Треугольник ECY похож на Треугольник KAY
Треугольник DBC похож на Треугольник KXC
Треугольник BEC аналогичен треугольнику BKX
Треугольник ДБЗ подобен треугольнику КАЗ :
Сначала мы хотим показать, что треугольник ДБЗ подобен треугольнику КАЗ.
Треугольник ECY подобен треугольнику KAY:
Мы можем показать, что эти два треугольника подобны, используя одно и то же точное рассуждение.
как указано выше (я избавлю вас от подробностей) и заключаю, что
Треугольник DBC подобен треугольнику KXC:
Далее мы хотим показать, что треугольник DBC подобен треугольнику KXC. С
DB||KX, угол DBC равен углу KXC, а угол BDC равен углу
угол XKC, потому что эти углы являются соответствующими углами и соответствующими
углы равны.
Треугольник BEC подобен треугольнику BKX:
Мы также можем показать, что эти два треугольника подобны, используя те же точные
аргумент, как указано выше (я избавлю вас от деталей), и заключаю, что
Подводя итог, мы показали, что выполняются следующие пропорции:
CY/AY = EC/AK
БК/СХ = БД/КХ
ВХ/ВС = КХ/ЕС
Отсюда следует следующее:
AZ/BZ * CY/AY * BC/CX * BX/BC = AK/BD * EC/AK * BD/KX * KX/EC
и это эквивалентно
Для демонстрации и доказательства этой теоремы нажмите здесь .
 Эта теорема также была доказана в рамках моего последнего проекта на ЕМТ 668.
класса осенью 1997 года. На самом деле я предпочитаю иллюстрации в этом оттиске.
но вроде того, как я доказал теорему в этом доказательстве. Вам решать.
Эта теорема также была доказана в рамках моего последнего проекта на ЕМТ 668.
класса осенью 1997 года. На самом деле я предпочитаю иллюстрации в этом оттиске.
но вроде того, как я доказал теорему в этом доказательстве. Вам решать. Возврат
5.1 Треугольники, четырехугольники, окружности и др. | Геометрия фигур
В этой главе вы узнаете о различных видах 2D-фигур. Вы узнаете имена, данные разные формы. Вы также узнаете о различных свойствах, которые разные типы фигур имеют по отношению к своим сторонам и углам.
Треугольники, четырехугольники, окружности и др.
Решите, что есть что, и нарисуйте несколько фигур
Треугольник представляет собой замкнутую фигуру с тремя прямыми сторонами и тремя углами.
Четырехугольник имеет четыре прямые стороны и четыре угла.
Круг круглый, и край всегда находится на одном и том же расстоянии от центра.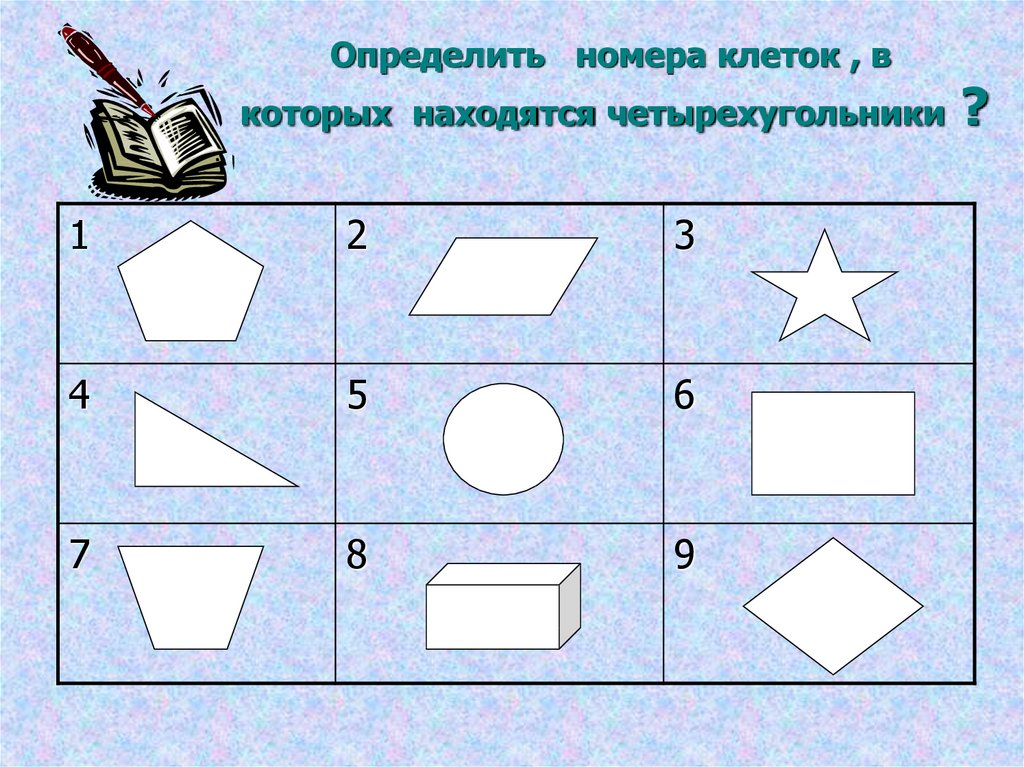
Какие фигуры на противоположной странице круги?
Какие фигуры на противоположной странице треугольники?
Какие фигуры на противоположной странице четырехугольники?
Используйте линейку, чтобы сделать следующее:
Сделать рисунок одного треугольника с тремя острыми углами и другого треугольника с одним тупой угол.
Нарисуйте четырехугольник с двумя тупыми углами.
Можете ли вы начертить треугольник с двумя тупыми углами?
Нарисуйте треугольник с одним прямым углом и треугольник без прямых углов.

Можете ли вы нарисовать треугольник с двумя прямыми углами?
Можешь нарисовать четырехугольник с четырьмя прямыми углами?
Эти четыре линии образуют четырехугольник АВСD.
Две красные стороны, ВС и AD, называются противоположными сторонами четырехугольника ABCD.
Какие две другие стороны ABCD также являются противоположными сторонами?
Линии DA и AB на рисунке в вопрос 7 называются смежных сторон . Они встречаются в точке, которая является одной из вершины (угловые точки) четырехугольника.
Назовите еще двоих смежные стороны в ABCD.
AB примыкает к DA в четырехугольнике ABCD.
 Какая другая сторона ABCD также примыкает к DA?
Какая другая сторона ABCD также примыкает к DA?
Уильям говорит:
«Каждая сторона четырехугольника имеет две смежные стороны.
Каждая сторона четырехугольника также имеет две противоположные стороны.»
Уильям прав? Обоснуйте свой ответ.
Уильям также говорит:
«В треугольнике каждая сторона смежна со всеми остальными сторонами.»
Это правда? Обоснуйте свой ответ.
В каждом случае укажите, две стороны являются противоположными сторонами или смежными сторонами четырехугольника PQRS.
КП и ПС
КП и СР
PQ и RQ
PS и QR
SR и QR
Равнобедренные, равнобедренные, разносторонние и прямоугольные треугольники
Треугольник с двумя равными сторонами называется равнобедренным треугольником .
Треугольник с тремя равными сторонами называется равносторонний треугольник .
Треугольник с прямым углом называется прямоугольным треугольником .
Треугольник с тремя сторонами разной длины и без прямого угла называется разносторонним треугольником .
Измерьте каждый угол в каждом из равнобедренных треугольников , данных выше. Делать вы заметили что-нибудь особенное? Если вы не уверены, нарисуйте больше равнобедренных треугольников. в вашей тетради.
Измерьте углы и стороны следующие треугольники.
 Что особенного в этих треугольниках? Другими словами, что
чем эти треугольники отличаются от других треугольников?
Что особенного в этих треугольниках? Другими словами, что
чем эти треугольники отличаются от других треугольников?Эти треугольники называются равносторонними треугольниками .
Измерьте каждый угол в каждом из следующих треугольников. Вы заметили что-то особенное в этих углах?
Определить самый длинный стороны в каждом из треугольников. Если вы не уверены, какой из них самый длинный сторону, измерьте стороны. Что вы заметили относительно самой длинной стороны в каждом из эти треугольники?
Эти треугольники называются прямоугольными треугольниками .
Сравнение и описание треугольников
w3.org/1999/xhtml»> Когда две или более сторон фигуры имеют одинаковую длину, мы показываем это короткими линиями на равных сторонах.Используйте следующие треугольники, чтобы ответить на следующие вопросы:
Который у треугольника только две равные стороны?
Как называется этот тип треугольника?
В каком треугольнике есть все три стороны равны?
Как называется этот тип треугольника?
Какой треугольник имеет угол равен 90°?
Как называется этот тип треугольника?
Запишите тип каждого из следующих треугольников в пространстве при условии:
w3.org/1999/xhtml»> Нахождение неизвестных сторон в треугольниках
Назовите каждый тип треугольника ниже.
Используйте данную информацию для определить длину следующих сторон:
АБ:
до н.э.:
ЭФ:
Можете ли вы определить длины GH и HI? Поясните свой ответ.
Квадрат в углу ул. \(\triangle\)JKL показывает, что это прямой угол. Назовите причину каждого вашего ответы ниже.
Это треугольник разносторонний, равнобедренный или равносторонний?
Назовите две стороны треугольника, которые равный.

Какова длина JK?
Назовите два равных угла в этом треугольнике.
Какой размер \(\шляпа{J}\) и \(\шляпа{L}\) ?
Различные типы четырехугольников
Исследование четырехугольников
Двое на следующих страницах показаны различные группы четырехугольников.
В котором группы обе пары противоположных сторон параллельны?
В каких группах только некоторые смежные стороны равны?
В каких группах все четыре углы равны?
В каких группах находятся все стороны в каждом четырехугольнике равны?
В каких группах все четыре стороны равны?
В каких группах находится каждая сторона перпендикулярно примыкающим к ней сторонам?
В каких группах противоположны стороны равны?
В каких группах есть хотя бы один пара смежных сторон равны?
В каких группах есть хотя бы один пара противоположных сторон параллельна?
В каких группах находятся все углы прямые?
Цифры в группе 1 называются параллелограммов .

Что вы наблюдаете о противоположных сторонах параллелограмма?
Что вы заметили относительно углов параллелограммы?
Цифры в группе 2 называются воздушных змеев .
Что вы наблюдаете о боках воздушных змеев?
Что еще вы заметили в воздушных змеях?
Группа 1
Группа 2
Группа 3
Группа 4
Группа 5
Группа 6
Цифры в группа 3 называется ромб .

Что вы наблюдаете о сторонах ромба?
Что еще вы заметили в ромбах?
Примечание: один ромб ; два или более ромбов .
Цифры в группе 4 называются прямоугольники .
Что вы наблюдаете о противоположных сторонах прямоугольников?
Что вы заметили относительно углов прямоугольники?
Что вы наблюдаете на соседних сторонах прямоугольники?
Цифры в группе 5 называются трапеции . Что вы наблюдаете о противоположных сторонах трапеции?
Стрелки показывают, какие стороны параллельны друг другу.

Цифры в группе 6 называются квадратов .
Что вы наблюдаете о сторонах квадратов?
Что вы заметили относительно углов квадраты?
Сравнение и описание форм
Имя каждой формы в каждой группе.
Группа А
Группа Б
Каким способом(ами) одинаковы ли цифры в каждой группе?
Группа А:
Группа B:
Каким образом (способами) одна из фигур в каждой группе отличаются от двух других цифр в группе?
Группа А:
Группа B:
Используйте свои знания о сторонах и углах четырехугольников, чтобы ответить на следующие вопросы. Обоснуйте свои ответы.
Четырехугольник ABCD какого типа?
Назовите сторону, равную АВ.
Какова длина BC?
Какой тип четырехугольника EFGH?
Какова длина следующих сторон?
ЭФ:
Цвет:
Какой тип четырехугольника JKLM?
Какова длина JK?
Фигура PQRS — воздушный змей с PQ = 4 см и QR = 10 см.
 Завершите следующий чертеж:
Завершите следующий чертеж:маркировка вершин воздушного змея
показывает на чертеже, какие стороны равны
с указанием длины каждой стороны.
Круги
Поставьте точку в середине круга справа. Напишите букву М рядом с точкой. Если ваша точка находится в середине круга, она называется средней точкой или центром .
Проведите линии MA, MB и MC от M до красных точек A, B и C.
три красные точки находятся на окружности с серединой M.
Прямая линия, такая как AC, проведенная через окружности и проходящей через ее середину, называется диаметром круг.

Измерение MA, MB и MC.
Если MA, MB и MC равны по длине, вы правильно выбрали среднюю точку. Если они не равны, вы можете улучшить набросок круга и его частей.
Прямая линия из середины окружности в точка на окружности называется радиусом окружности.
Синяя линия, MA, представляет собой радиус . Любая прямая, идущая от центра к окружности, радиус.
Черная линия AB соединяет две точки окружности. Мы называем это аккордом круг.
В на следующих двух диаграммах цветные секции сегментов круг. Сегмент – это площадь между хордой и дугой.
В круге справа красная часть называется сектором круга. Как видите, сектор — это область между двумя радиусами и дугой.
w3.org/1999/xhtml»> Подобные и конгруэнтные фигурыНа этой и следующей странице показаны три группы четырехугольников.
Чем каждая группа отличается от других групп, кроме цвета?
Группа А:
Группа Б:
Группа С:
Группа А
Группа Б
Группа С
Фигуры одинаковой формы, такие как синие фигуры на предыдущей странице, считаются равными 9.0017 похожи друг на друга. Похожие фигуры могут отличаться по размеру, но всегда будут иметь одинаковую форму.
Пример похожих форм
Пример конгруэнтных форм
Фигуры одинаковой формы и размера, такие как красные фигуры на предыдущей странице, называются конгруэнтными друг другу.




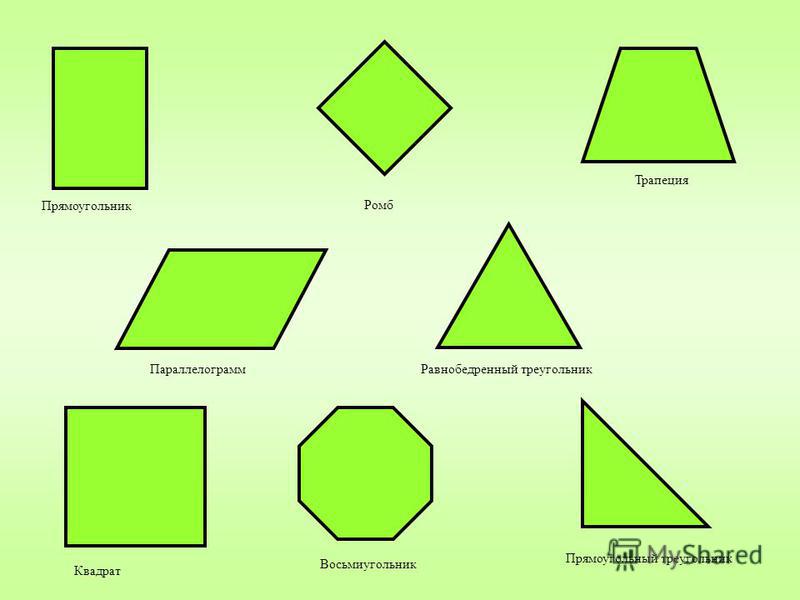
 Дайте определение и перечислите свойства параллелограмма.
Дайте определение и перечислите свойства параллелограмма.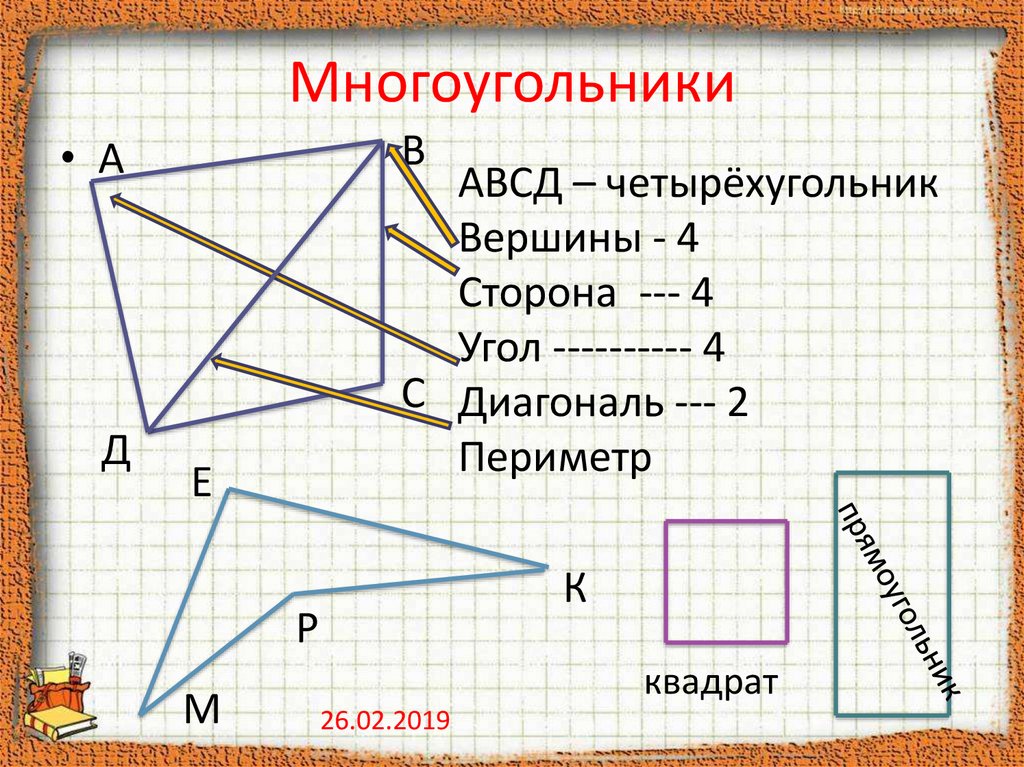
 Какая другая сторона ABCD также примыкает к DA?
Какая другая сторона ABCD также примыкает к DA? Что особенного в этих треугольниках? Другими словами, что
чем эти треугольники отличаются от других треугольников?
Что особенного в этих треугольниках? Другими словами, что
чем эти треугольники отличаются от других треугольников?



 Завершите следующий чертеж:
Завершите следующий чертеж:
