Виды уравнений, формулы и примеры
Определение и основные виды уравнений
Например.
Некоторые классы уравнений решаются аналитически (среди алгебраических это линейные, квадратные, кубические уравнения и уравнения четвертой степени), то есть решение записывается в виде формулы. Алгебраические уравнения высших степеней (более, чем четвертая) в общем случае аналитического решения не имеют, хотя некоторые сводятся к уравнениям низших степеней.
В общем случае, если аналитическое решение не существует, применяют численные методы.
Алгебраические уравнения
Алгебраическим уравнением называется уравнение вида
где — многочлен переменных , которые называются переменными или неизвестными.
Например.
Степенью алгебраического уравнения называется степень многочлена .
Линейным уравнением от неизвестных называется уравнение вида
Например. — линейное уравнение с одной переменной.
Квадратным уравнением (уравнением второй степени)
Здесь — переменная, — старший или первый коэффициент, — второй коэффициент, — свободный коэффициент.
Например.
Квадратное уравнение называется приведенным, если старший коэффициент равен единице.
Например.
Уравнением с параметрами называется математическое равенство, внешний вид и решение которого зависит от значений одного или нескольких параметров.
Например.
Уравнение, содержащее трансцендентные функции, называется трансцендентным.
Например.
Трансцендентная функция — это аналитическая функция, не являющаяся алгебраической. Алгебраической называется элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения.
Функциональным называется уравнение, которое определяет связь между значением функции (или функций) в одной точке с её значениями в других точках.
Например.
Уравнение, в котором неизвестная функция стоит под знаком производной, называется дифференциальным.
Например.
Интегральным уравнением называется уравнение, в котором неизвестная функция находится под знаком интеграл.
Например.
ru.solverbook.com
УРАВНЕНИЯ | Энциклопедия Кругосвет
Содержание статьиУРАВНЕНИЯ. Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида (x – 1)2 = (x – 1)(x – 1) выполняется при всех значениях переменной x. Для обозначения тождества часто вместо обычного знака равенства = пишут знак є, который читается «тождественно равно». Тождества используются в алгебре при записи разложения многочленов на множители (как в приведенном выше примере). Встречаются они и в тригонометрии в таких соотношениях, как sin
Если уравнение, содержащее переменную x, выполняется только при определенных, а не при всех значениях x, как в случае тождества, то может оказаться полезным определить те значения x, при которых это уравнение справедливо. Такие значения x называются корнями или решениями уравнения. Например, число 5 является корнем уравнения 2x + 7= 17.
Уравнения служат мощным средством решения практических задач. Точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Неизвестные величины, обозначаемые в задаче символами, например x, можно найти, сформулировав задачу на математическом языке в виде уравнений. Методы решения уравнений составляют в основном предмет того раздела математики, который называется теорией уравнений.
ТИПЫ УРАВНЕНИЙ
Алгебраические уравнения.
Уравнения вида fn = 0, где fn – многочлен от одной или нескольких переменных, называются алгебраическими уравнениями. Многочленом называется выражение вида
fn = a0 xiyj … vk + a1 xlym … vn + ј + asxpyq … vr,
где x, y,…, v – переменные, а i, j,…, r – показатели степеней (целые неотрицательные числа). Многочлен от одной переменной записывается так:
f(x) = a0xn + a1xn – 1 +… + an – 1x + an
или, в частном случае, 3x4 – x3 + 2x2 + 4x – 1. Алгебраическим уравнением с одним неизвестным называется любое уравнение вида f(x) = 0. Если a0 № 0, то n называется степенью уравнения. Например, 2x + 3 = 0 – уравнение первой степени; уравнения первой степени называются линейными, так как график функции y = ax + b имеет вид прямой. Уравнения второй степени называются квадратными, а уравнения третьей степени – кубическими. Аналогичные названия имеют и уравнения более высоких степеней.
Трансцендентные уравнения.
Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными. Примером могут служить следующие уравнения:
где lg – логарифм по основанию 10.
Дифференциальные уравнения.
Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы. См. также ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Интегральные уравнения.
Уравнения, содержащие неизвестную функцию под знаком интеграла, например, f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.
Диофантовы уравнения.
Диофантовым уравнением называется алгебраическое уравнение с двумя или более неизвестными с целыми коэффициентами, решение которого ищется в целых или рациональных числах. Например, уравнение 3x – 5y = 1 имеет решение x = 7,
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
Линейные уравнения.
Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом.
1. Если равные величины увеличить на одно и то же число, то результаты будут равны.
2. Если из равных величин вычесть одно и то же число, то результаты будут равны.
3. Если равные величины умножить на одно и то же число, то результаты будут равны.
4. Если равные величины разделить на одно и то же число, то результаты будут равны.
Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Квадратные уравнения.
Решения общего квадратного уравнения ax2 + bx + c = 0 можно получить с помощью формулы
Таким образом, существуют два решения, которые в частном случае могут совпадать.
Другие алгебраические уравнения.
Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находит корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удается легко решить, факторизуя их левую часть, т.е. разлагая ее на множители.
Например, уравнение x3 + 1 = 0 можно записать в факторизованном виде (x + 1)(x2 – x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:
Таким образом, корни равны x = –1, , т.е. всего 3 корня.
Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
Системы линейных уравнений.
Два линейных уравнения с двумя неизвестными можно записать в видеРешение такой системы находится с помощью определителей
Оно имеет смысл, если Если же D = 0, то возможны два случая. (1) По крайней мере один из определителей и отличен от нуля. В этом случае решения уравнений не существует; уравнения несовместны. Численный пример такой ситуации – система
(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное число решений.
Общая теория рассматривает m линейных уравнений с n переменными:
Если m = n и матрица (aij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:
где Aji – алгебраическое дополнение элемента aijв матрице (aij). В более общем плане существуют следующие теоремы. Пусть r – ранг матрицы (
www.krugosvet.ru
| Вида ax2+bx = 0
|
| Имеет вид:
| Способы: |
| Имеет вид:
|
infourok.ru
Виды уравнений и способы их решения
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (8,2 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Обучающие:
- Обобщить знания по всем видам уравнений, подчеркнуть значимость всех способов, применяемых при решении уравнений.
- Активизирование работы учащихся за счет, разнообразных приемов на уроке.
- Проверить теоретические и практические навыки при решении уравнений.
- Заострить внимание на том, что, одно уравнение можно решить несколькими способами
Развивающие:
- Повысить интерес учащихся к предмету, через использование ИКТ.
- Ознакомление учащихся с историческим материалом по теме.
- Развитие мыслительной деятельности при определении вида уравнения и способов его решения.
Воспитательные:
- Воспитать дисциплину на уроке.
- Развитие способности к восприятию прекрасного, в себе самом, в другом человеке и в окружающем мире.
Тип урока:
- Урок обобщения и систематизации знаний.
Вид урока:
- Комбинированный.
Материально-техническое оснащение:
- Компьютер
- Экран
- Проектор
- Диск с презентацией темы
Методы и приемы:
- Использование презентации
- Фронтальная беседа
- Устная работа
- Игровые моменты
- Работа в парах
- Работа у доски
- Работа в тетрадях
План урока:
- Организационный момент (1минуты)
- Расшифровка темы урока (3минуты)
- Сообщение темы и цели урока (1минута)
- Теоретическая разминка (3минут)
- Исторический экскурс (3минуты)
- Игра “Убери лишнее” (2минуты)
- Творческая работа (2минуты)
- Задание “Найди ошибку” (2минуты)
- Решение одного уравнения несколькими способами (на слайде) (3минуты)
- Решение одного уравнения несколькими способами (у доски) (24 минут)
- Самостоятельная работа в парах с последующим объяснением (5минут)
- Индивидуальное домашнее задание(1минуты)
- Итог урока рефлексия (1минута)
Эпиграф урока:
“Учиться можно только весело, чтобы переваривать знания, нужно поглощать их с аппетитом”.
А.Франс
Конспект урока
Организационная часть
Проверяю готовность учащихся к уроку, отмечаю отсутствующих на уроке. Ребята, Французский писатель 19 века А.Франс однажды заметил “ Учиться можно только весело, чтобы переваривать знания, нужно поглощать их с аппетитом”. Так давайте на нашем уроке следовать совету, писателя и переваривать знания с большим аппетитом, ведь они пригодятся в нашей жизни.
Расшифровка темы урока
Для того, чтобы перейти к более сложном заданием, давайте разомнем свои мозги простыми заданиями. Тема нашего урока зашифрована, решив устные задания и найдя к ним ответ, зная, что каждый ответ имеет свою букву, мы раскроем тему урока. Презентация слайд 3
Сообщение темы и цели урока
Вы, сегодня сами назвали тему урока
“Виды уравнений и способы их решения”. Презентация слайд 4
Цель: Вспомнить и обобщить все виды уравнений и способы их решения. Решить одно уравнение всеми способами. Презентация слайд 5 Прочитать высказывание Эйнштейна Презентация слайд 5
Теоретическая разминка
Вопросы Презентация слайд 7
Ответы
- Равенство, содержащее переменную величину, обозначенную какой-то буквой.
- Это значит найти все его корни, или доказать, что корней нет.
- Значение переменной, при котором уравнение обращается в верное равенство.
- После этого определения прочесть стихотворение об уравнении Презентация слайд 12,13,14
Ответы на 2 последних вопроса Презентация слайд 9,10,11
Исторический экскурс
Историч
xn--i1abbnckbmcl9fb.xn--p1ai
«Уравнения. Их виды, типы и методы решений»
Уравнения. Их виды, типы и методы решений
Учебный материал, связанный с уравнениями составляет значительную часть школьного курса математики. Это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач. Отметим, что с уравнениями впервые мы встречаемся еще в начальной школе.
Значимость уравнений определяется как теоретико-математической направленностью (здесь уравнения выступают как самостоятельный объект для изучения), так и с точки зрения развития научного мировоззрения учащихся (здесь на первый план выходит применение уравнений к решению различного рода задач самой математики, а также к анализу явлений реального мира) [1].
Существуют следующие типы уравнений и неравенств (рис. 1)
Рис. 1
Для того чтобы решить любое уравнение с одной переменной, учащийся должен знать: во-первых, правило, формулы или алгоритмы решения простейших уравнений данного вида и, во-вторых, правила выполнения тождественных и равносильных преобразований, с помощью которых данное уравнение можно привести к простейшим.
Таким образом, решение каждого уравнения складывается из двух основных частей: 1) преобразования данного уравнения к простейшим; 2) решения простейших уравнений по известным правилам, формулам или алгоритмам.[2]
При этом если вторая часть решения является алгоритмической, то первая — в значительной степени (и тем I большей, чем сложнее уравнение) — эвристической [3]. Именно правильный выбор необходимых тождественных и равносильных преобразований, как и всякий поиск решения задачи, представляет наибольшую трудность для учащихся.
При обучении учащихся решению определенного класса уравнений следует выделять общий прием решения, который можно представить следующими этапами:
1. Определить вид уравнения.
2. Определить стандартное оно или нет.
3. Если стандартное, то решить в соответствии с известным правилом, алгоритмом.
4. Если нестандартное, то выяснить, какие преобразования необходимо выполнить, чтобы свести его к стандартному, либо перейти к использованию искусственных приемов решения.
5. Выполнить эти преобразования.
6. Сделать проверку.
7. Записать ответ.
Алгебраическое уравнение первой степени с одной неизвестной – это уравнение, левая и правая части которого есть многочлены первой степени относительно одной переменной. В некоторых учебниках все такие уравнения называют линейными. Однако чаще к линейным относят лишь уравнения вида , либо уравнения вида . Алгоритм решения линейных уравнений и сводящихся к ним основан на приведении подобных слагаемых и на двух основных свойствах уравнений: первое о переносе слагаемых из одной части в другую, второе – о делении обеих частей уравнения на ненулевое число. Этот алгоритм прочно осваивается учащимися и в дальнейшем воспринимается как единственный метод решения таких уравнений.
Пусть тогда получаем квадратное уравнение относительно переменной t
D= (-6)2 – 4×5×1=16
t1==1 t3= =
t1= 1, cosx=1, x1=2πn, n€Z
t1= , сosx=, x2=±аrccos +2 πn, n€Z
Ответ: x1=2πn, n€Z, x2=±аrccos +2 πn, n€Z
Каким бы методом ученик не решал уравнение или систему, необходимо выполнять проверку. Рассмотрим типичные, часто встречающиеся ошибки, которые допускают ученики.
1. Ошибки в тождественных преобразованиях выражений в одной из частей;
2. Неодинаковость и неправомерность действий, выполняемых в левой и правой части;
3. Упрощение левой и правой частей в отдельности, в результате чего может измениться ОДЗ;
4. Деление/умножение обеих частей на одно и то же выражение;
5. Извлечение квадратного корня из обеих частей с неумением поставить после этого правильный знак;
6. Возведение в квадрат обеих частей, что может привести к расширению ОДЗ;
7. При замене переменной не определяется ОДЗ новой переменной и др.
Учителю следует на простых примерах показывать учащимся суть каждого подхода, его преимущества и недостатки. Выбор же того или иного подхода определяется каждым конкретным решаемым уравнением. [1] На наш взгляд, прежде чем начинать выполнять преобразования самого уравнения, следует установить систему неравенств, задающих область допустимых значений уравнения, оценить трудоемкость ее решения, а уже потом делать выводы: выполнять ли преобразования уравнения с последующей проверкой корней подстановкой, либо свести решение уравнения к решению равносильной ему системе.
Костюченко Р.Ю. Обучение учащихся решению иррациональных неравенств // Электронный научный журнал «Вестник Омского государственного педагогического университета» — 2007
Кудрявцев Л.Д. Современная математика и ее преподавание – М, Наука, 1985 –230c
Колягин Ю.М. Методика преподавания математике в средней школе. Частные методики. – М.: Просвещение, 1977
infourok.ru
Виды уравнений и способы их решения
ТЕМА: ВИДЫ УРАВНЕНИЙ И СПОСОБЫ ИХ РЕШЕНИЯ.
ЦЕЛЬ: Привести в систему знания учащихся по этой теме:
повторить теорию решения уравнений;
выработать умение определять вид уравнения,
выбирать наиболее рациональный способ решения данного уравнения.
Развитие интереса к предмету, активизация мыслительной деятельности, развитие творческого мышления, математической речи.
Формирование навыков самостоятельной деятельности, воспитание коллективизма, духа соревнования.
ХОД УРОКА
Даю историческую справку о том, что наука «алгебра» возникла в связи с решением разнообразных задач при помощи уравнений.
Повторяем теорию по решению уравнений.
Задаю ученикам вопросы:
— Что называется уравнением?
— Что значит решить уравнение?
— Что называется корнем уравнения?
— Какие существуют способы решения уравнений?
— Какие существуют виды уравнений?
— Как определяется степень уравнения?
— Каков общий вид линейного уравнения? Квадратного?
— Дайте определение рационального, дробно-рационального уравнения, уравнения, содержащего модуль?
— Что называется областью допустимых значений уравнения?
3. Предлагаю учащимся решить уравнения, объясняя, какого вида уравнения, способ решения каждого уравнения, теоретически обосновывая каждый шаг.
1) Линейные уравнения
а) 3х + (20 – х) = 35,2,
б) 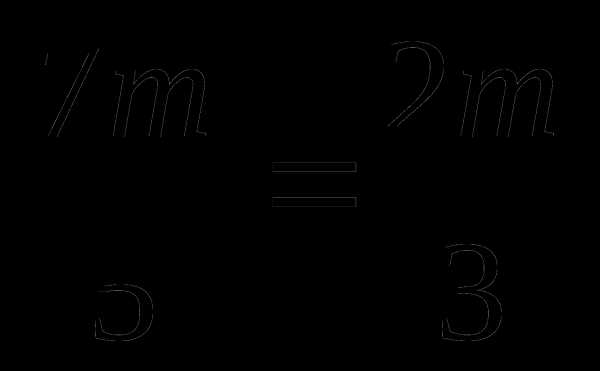 ,
,
в)(х – 3)- х= 7 – 5х.
2) Квадратные и приводимые к квадратным
а) z- 10 = 29,
б) — х = 13,
в) (х – 4) — 5(х – 4) + 6 = 0,
г) х — 13х + 36 = 0,
д) (х + 2) — 11(х + 2)= 12.
3) Уравнения высших степеней
а) х = х,
б) 3у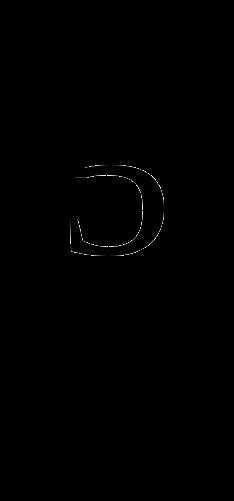 = 96,
= 96,
в) х + х + х + 1 = 0,
г) – 5,5n(n
– 1)(n
+ 2,5)(n
—  )
=0.
)
=0.
4) Дробно- рациональные уравнения
а)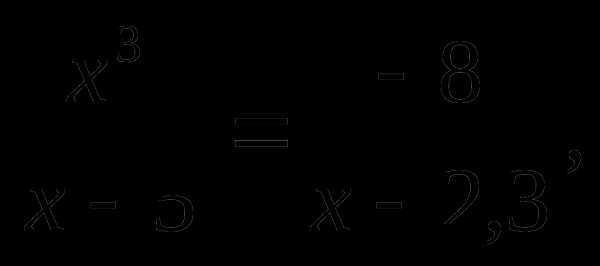
б)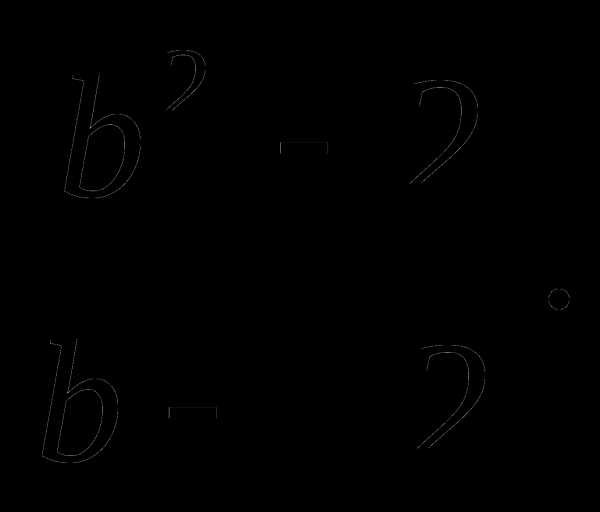
5) Иррациональные уравнения
а)2 + 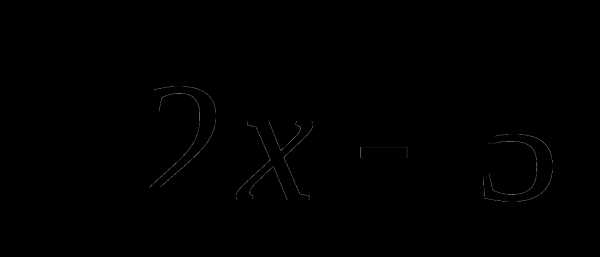 =4,
=4,
б)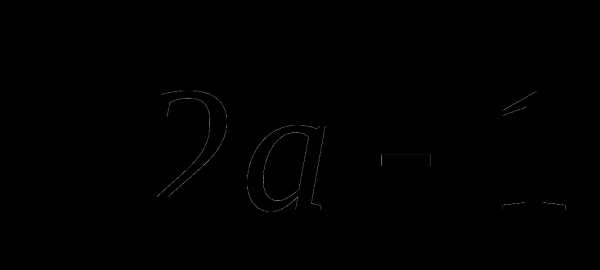 =-5,
=-5,
в)  = — x.
= — x.
6) Уравнения с модулем
а) 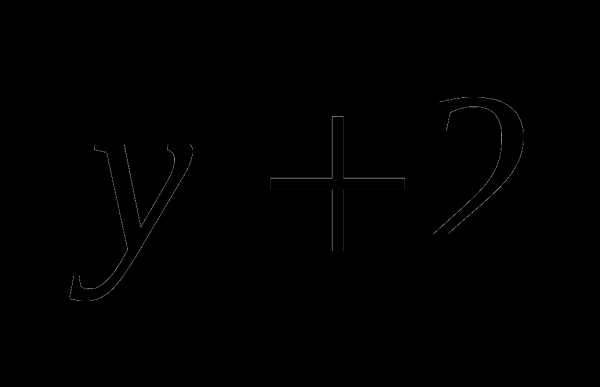 =
=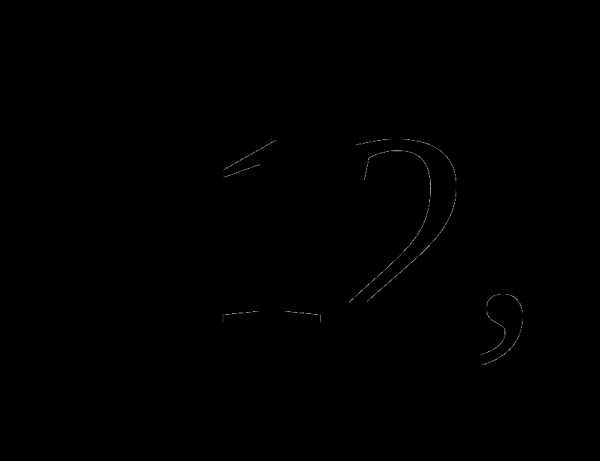
б)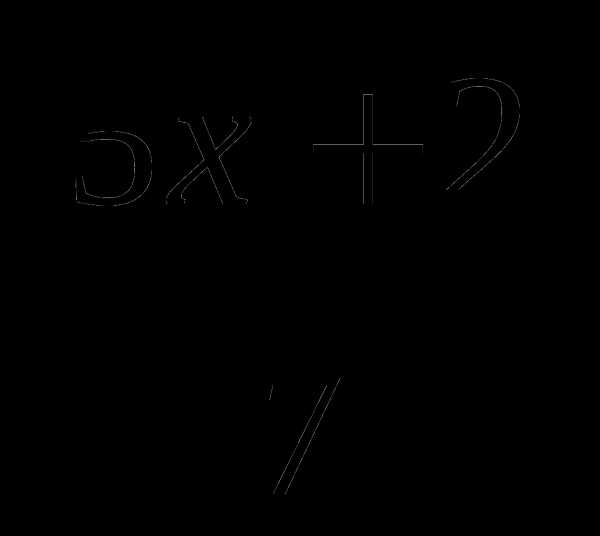 =
-2,
=
-2,
в) х—
5 =
0.
=
0.
7) Уравнения с параметром
а) aх = 10,
б)2ах – 5 = 17.
4. Даю устную самостоятельную работу с последующей проверкой. Например, в виде теста в двух вариантах.
Найти наибольший (наименьший ) корень уравнения
См. Приложение 1
Решаем кроссворд.
См. Приложение 2.
5. Подвожу итог урока. Отмечаю:
что повторили с ребятами,
какие виды уравнений существуют,
какие существуют способы решения уравнений,
чему научились,
кто был самым активным, кому нужно быть поактивнее.
Даю оценку устной работы и оценку устной самостоятельной работы каждого ученика.
6. Домашнее задание.
а) х + 2х — 15=0;
б) (х- 4х)- 7(х- 4х) +12=0;
в) х +9х
+9х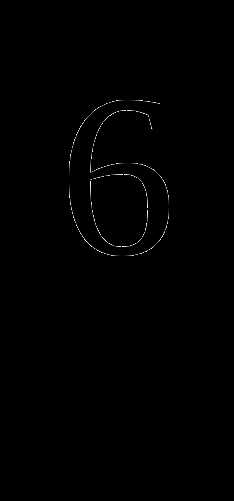 —
х-9=0;
—
х-9=0;
г) у-15 =0;
=0;
д) х- 625=0.
gigabaza.ru
что такое? Определение термина, примеры
В курсе школьной математики, ребенок впервые слышит термин «уравнение». Что такое это, попробуем разобраться вместе. В данной статье рассмотрим виды и способы решения.

Математика. Уравнения
Для начала предлагаем разобраться с самим понятием, что это такое? Как гласят многие учебники математики, уравнение — это некоторые выражения, между которыми стоит обязательно знак равенства. В этих выражениях присутствуют буквы, так называемые переменные, значение которых и необходимо найти.
Что такое переменная? Это атрибут системы, который меняет свое значение. Наглядным примером переменных являются:
- температура воздуха;
- рост ребенка;
- вес и так далее.
В математике они обозначаются буквами, например, х, а, b, с… Обычно задание по математике звучит следующим образом: найдите значение уравнения. Это значит, что необходимо найти значение данных переменных.
Разновидности

Уравнение (что такое, мы разобрали в предыдущем пункте) может быть следующего вида:
- линейные;
- квадратные;
- кубические;
- алгебраические;
- трансцендентные.
Для более подробного знакомства со всеми видами, рассмотрим каждый в отдельности.
Линейное уравнение
Это первый вид, с которым знакомятся школьники. Они решаются довольно-таки быстро и просто. Итак, линейное уравнение, что такое? Это выражение вида: ах=с. Так не особо понятно, поэтому приведем несколько примеров: 2х=26; 5х=40; 1,2х=6.

Разберем примеры уравнений. Для этого нам необходимо все известные данные собрать с одной стороны, а неизвестные в другой: х=26/2; х=40/5; х=6/1,2. Здесь использовались элементарные правила математики: а*с=е, из этого с=е/а; а=е/с. Для того чтобы завершить решение уравнения, выполним одно действие (в нашем случае деление) х=13; х=8; х=5. Это были примеры на умножение, теперь просмотрим на вычитание и сложение: х+3=9; 10х-5=15. Известные данные переносим в одну сторону: х=9-3; х=20/10. Выполняем последнее действие: х=6; х=2.
Также возможны варианты линейных уравнений, где используется более одной переменной: 2х-2у=4. Для того чтобы решить, необходимо к каждой части прибавить 2у, у нас получается 2х-2у+2у=4-2у, как мы заметили, по левую часть знака равенства -2у и +2у сокращаются, при этом у нас остается: 2х=4-2у. Последним шагом делим каждую часть на два, получаем ответ: икс равен два минус игрек.
Задачи с уравнениями встречаются даже на папирусах Ахмеса. Вот одна из задач: число и четвертая его часть дают в сумме 15. Для ее решения мы записываем следующее уравнение: икс плюс одна четвертая икс равняется пятнадцати. Мы видим еще один пример линейного уравнения, по итогу решения, получаем ответ: х=12. Но эту задачу можно решить и другим способом, а именно египетским или, как его называют по-другому, способом предположения. В папирусе используется следующее решение: возьмите четыре и четвертую ее часть, то есть единицу. В сумме они дают пять, теперь пятнадцать необходимо разделить на сумму, мы получаем три, последним действием три умножаем на четыре. Мы получаем ответ: 12. Почему мы в решении пятнадцать делим на пять? Так узнаем, во сколько раз пятнадцать, то есть результат, который нам необходимо получить, меньше пяти. Таким способом решали задачи в средние века, он стал зваться методом ложного положения.
Квадратные уравнения

Кроме рассмотренных ранее примеров, существуют и другие. Какие именно? Квадратное уравнение, что такое? Они имеют вид ax2+bx+c=0. Для их решения необходимо ознакомиться с некоторыми понятиями и правилами.
Во-первых, нужно найти дискриминант по формуле: b2-4ac. Есть три варианта исхода решения:
- дискриминант больше нуля;
- меньше нуля;
- равен нулю.
В первом варианте мы можем получить ответ из двух корней, которые находятся по формуле: -b+-корень из дискриминанта разделенные на удвоенный первый коэфициент, то есть 2а.
Во втором случае корней у уравнения нет. В третьем случае корень находится по формуле: -b/2а.
Рассмотрим пример квадратного уравнения для более подробного знакомства: три икс в квадрате минус четырнадцать икс минус пять равняется нулю. Для начала, как и писалось ранее, ищем дискриминант, в нашем случае он равен 256. Отметим, что полученное число больше нуля, следовательно, мы должны получить ответ состоящих из двух корней. Подставляем полученный дискриминант в формулу нахождения корней. В результате мы имеем: икс равняется пяти и минус одной третьей.
Особые случаи в квадратных уравнениях

Это примеры, в которых некоторые значения равны нулю (а, b или с), а возможно и несколько.
Для примера возьмем следующее уравнение, которое является квадратным: два икс в квадрате равняется нулю, здесь мы видим, что b и с равны нулю. Попробуем его решить, для этого обе части уравнения делим на два, мы имеем: х2=0. В итоге получаем х=0.
Другой случай 16х2-9=0. Здесь только b=0. Решим уравнение, свободный коэфициент переносим в правую часть: 16х2=9, теперь каждую часть делим на шестнадцать: х2= девять шестнадцатых. Так как у нас х в квадрате, то корень из 9/16 может быть как отрицательным, так и положительным. Ответ записываем следующим образом: икс равняется плюс/минус три четвертых.
Возможен и такой вариант ответа, как у уравнения корней вовсе нет. Посмотрим на такой пример: 5х2+80=0, здесь b=0. Для решения свободный член перекидываете в правую сторону, после этих действий получаем: 5х2=-80, теперь каждую часть делим на пять: х2= минус шестнадцать. Если любое число возвести в квадрат, то отрицательное значение мы не получим. По этому наш ответ звучит так: у уравнения корней нет.
Разложение трехчлена
Задание по квадратным уравнениям может звучать и другим образом: разложить квадратный трехчлен на множители. Это возможно осуществить, воспользовавшись следующей формулой: а(х-х1)(х-х2). Для этого, как и в другом варианте задания, необходимо найти дискриминант.

Рассмотрим следующий пример: 3х2-14х-5, разложите трехчлен на множетели. Находим дискриминант, пользуясь уже известной нам формулой, он получается равным 256. Сразу отмечаем, что 256 больше нуля, следовательно, уравнение будет иметь два корня. Находим их, как в предыдущем пункте, мы имеем: х= пять и минус одна третья. Воспользуемся формулой для разложения трехчлена на множетели: 3(х-5)(х+1/3). Во второй скобке мы получили знак равно, потому что в формуле стоит знак минуса, а корень тоже отрицательный, пользуясь элементарными знаниями математики, в сумме мы имеем знак плюса. Для упрощения, перемножим первый и третий член уравнения, чтобы избавиться от дроби: (х-5)(х+1).
Уравнения сводящиеся к квадратному
В данном пункте научимся решать более сложные уравнения. Начнем сразу с примера:
(x2 – 2x)2 – 2(x2 – 2x) – 3 = 0. Можем заметить повторяющиеся элементы: (x2 – 2x), нам для решения удобно заменить его на другую переменную, а далее решать обычное квадратное уравнение, сразу отмечаем, что в таком задании мы получим четыре корня, это не должно вас пугать. Обозначаем повторение переменной а. Мы получаем: а2-2а-3=0. Наш следующий шаг — это нахождение дискриминанта нового уравнения. Мы получаем 16, находим два корня: минус один и три. Вспоминаем, что мы делали замену, подставляем эти значения, в итоге мы имеем уравнения: x2 – 2x=-1; x2 – 2x=3. Решаем их в первом ответ: х равен единице, во втором: х равен минусу одному и трем. Записываем ответ следующим образом: плюс/минус один и три. Как правило, ответ записывают в порядке возрастания.
Кубические уравнения
Рассмотрим еще один возможный вариант. Речь пойдет о кубических уравнениях. Они имеют вид: ax 3 + b x 2 + cx + d =0. Примеры уравнений мы рассмотрим далее, а для начала немного теории. Они могут иметь три корня, так же существует формула для нахождения дискриминанта для кубического уравнения.
Рассмотрим пример: 3х3+4х2+2х=0. Как его решить? Для этого мы просто выносим х за скобки: х(3х2+4х+2)=0. Все что нам остается сделать — это вычислить корни уравнения в скобках. Дискриминант квадратного уравнения в скобках меньше нуля, исходя из этого, выражение имеет корень: х=0.
Алгебра. Уравнения

Переходим к следующему виду. Сейчас мы кратко рассмотрим алгебраические уравнения. Одно из заданий звучит следующим образом: методом группировки разложить на множетели 3х4+2х3+8х2+2х+5. Самым удобным способом будет следующая группировка: (3х4+3х2)+(2х3+2х)+(5х2+5). Заметим, что 8х2 из первого выражения мы представили в виде суммы 3х2 и 5х2. Теперь выносим из каждой скобки общий множитель 3х2(х2+1)+2х(х2+1)+5(х2+1). Мы видим, что у нас есть общий множитель: икс в квадрате плюс один, выносим его за скобки: (х2+1)(3х2+2х+5). Дальнейшее разложение невозможно, так как оба уравнения имеют отрицательный дискриминант.
Трансцендентные уравнения
Предлагаем разобраться со следующим типом. Это уравнения, которые содержат трансцендентные функции, а именно логарифмические, тригонометрические или показательные. Примеры: 6sin2x+tgx-1=0, х+5lgx=3 и так далее. Как они решаются вы узнаете из курса тригонометрии.
Функция
Завершающим этапом рассмотрим понятие уравнение функции. В отличии от предыдущих вариантов, данный тип не решается, а по нему строится график. Для этого уравнение стоит хорошо проанализировать, найти все необходимые точки для построения, вычислить точку минимума и максимума.
fb.ru
