Задачи для самостоятельного решения
1. Векторы  и
и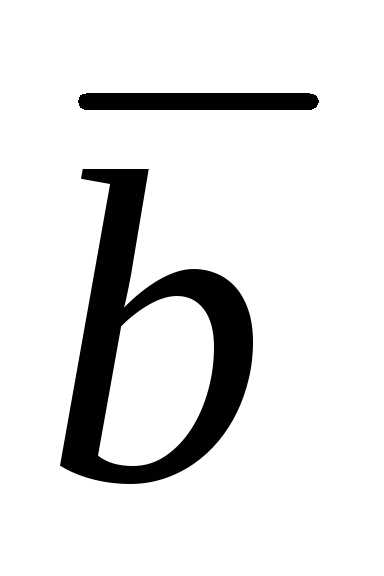 образуют угол
образуют угол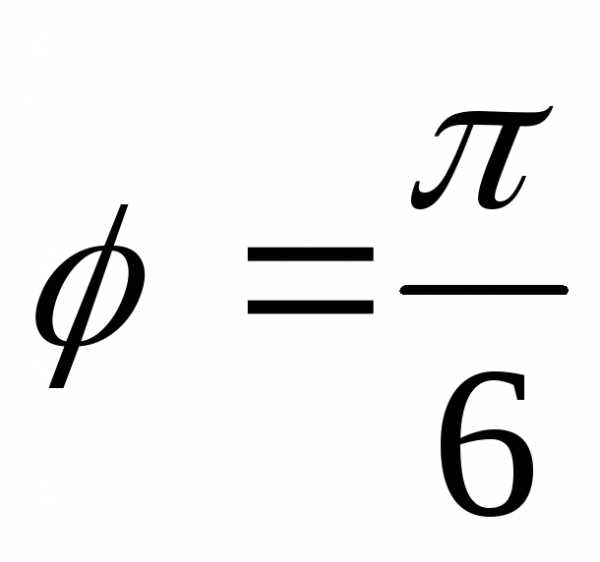 .
Зная, что
.
Зная, что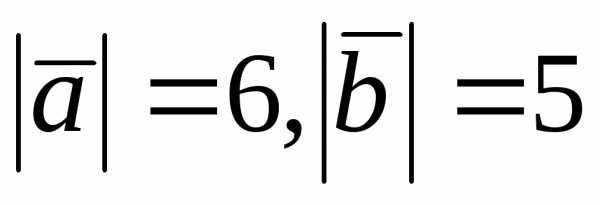 вычислить
вычислить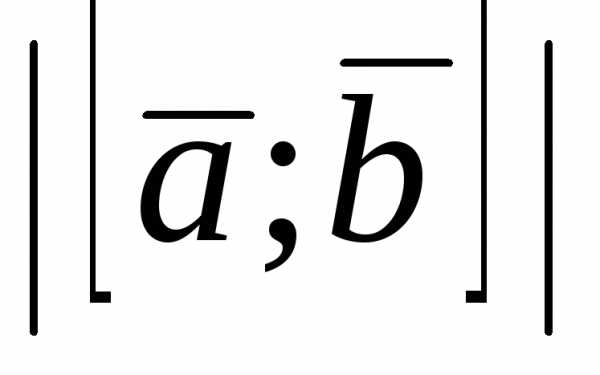 .
.
Ответ. 15.
2. Даны
,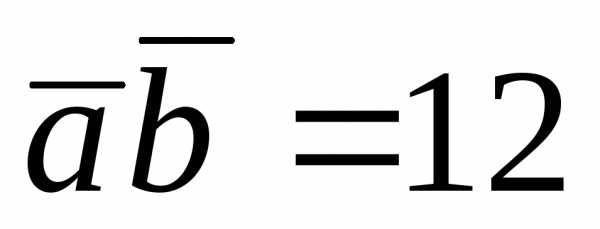 .
Вычислить
.
Вычислить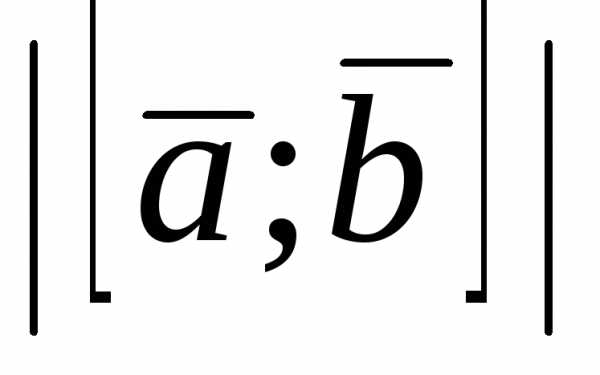 .
.
Ответ. 16.
3. Векторы  и
и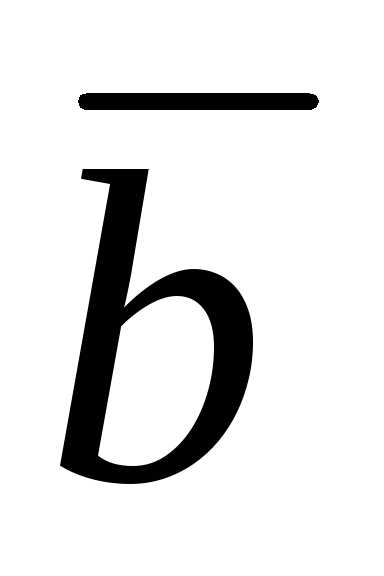 взаимно перпендикулярны. Зная, что,
вычислить
взаимно перпендикулярны. Зная, что,
вычислить
1), 2).
Ответ. 1) 24, 2) 60.
4. Векторы  и
и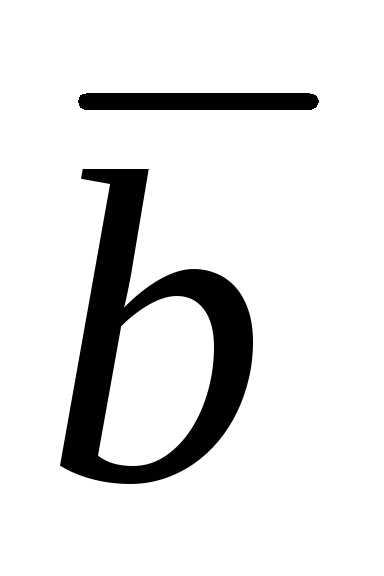 образуют угол
образуют угол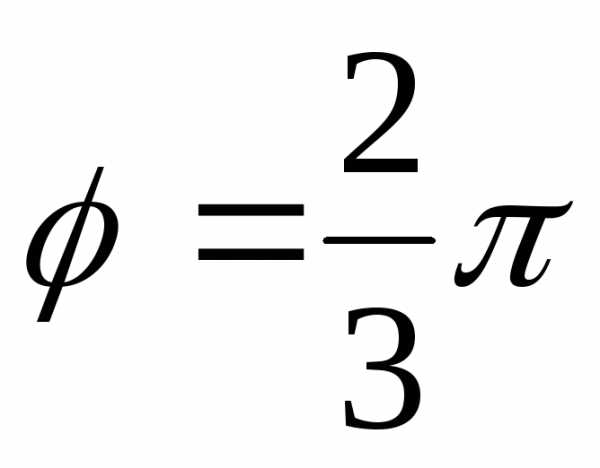 .
Зная, что
.
Зная, что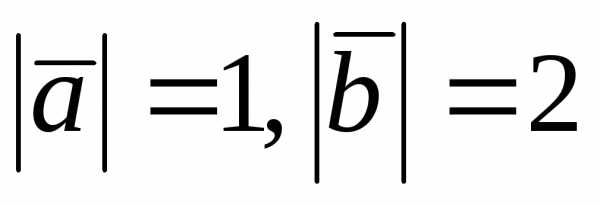 ,
вычислить
,
вычислить
1) 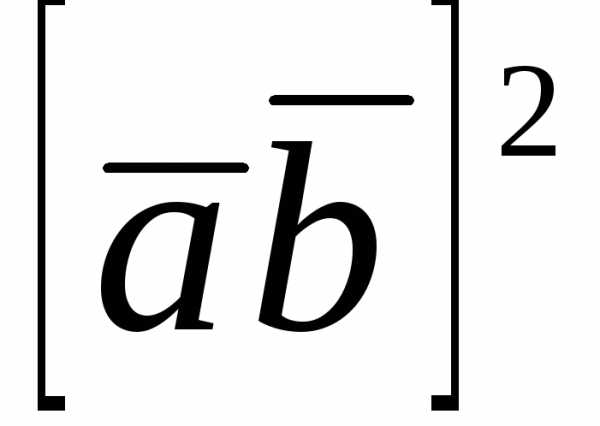 , 2), 3).
, 2), 3).
Ответ. 1) 3, 2) 27, 3) 300.
5. Найти орт 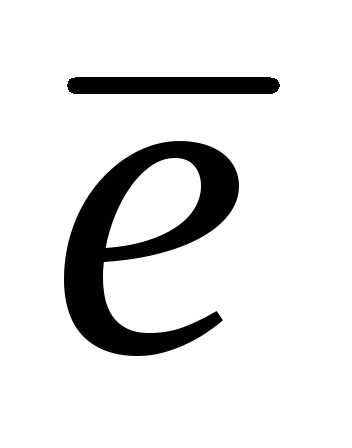 ,
перпендикулярный векторами.
,
перпендикулярный векторами.
Ответ. .
6. Вычислить площадь
треугольника с вершинами 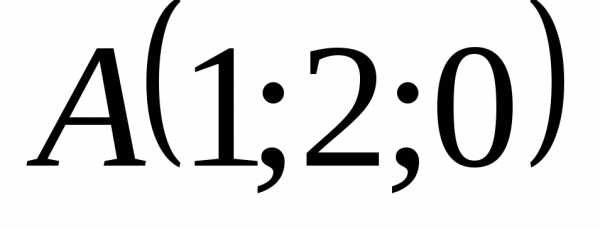 ,и
,и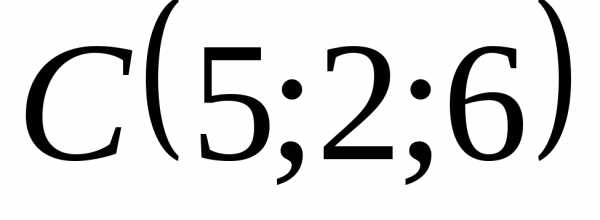 .
.
Ответ. 14 кв. ед.
7. Сила приложена к точке. Найти момент этой силы относительно начала координат.
Указание: если  –
сила, прилаженная к точкеМ,
то момент этой силы относительно точки А равен векторному произведению векторов
–
сила, прилаженная к точкеМ,
то момент этой силы относительно точки А равен векторному произведению векторов 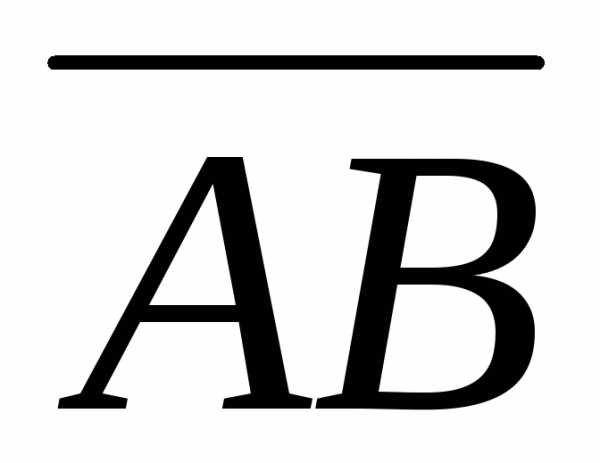
 .
.Ответ. .
8. Дана сила
и точки ее приложения.
Найти момент этой силы относительно
точки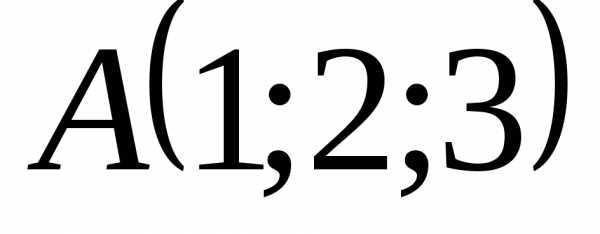 и углы, составляемые им с координатными
осями.
и углы, составляемые им с координатными
осями.
Ответ. 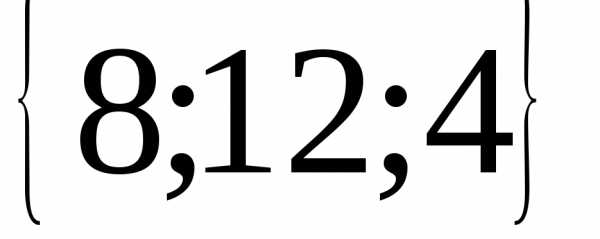 ;
;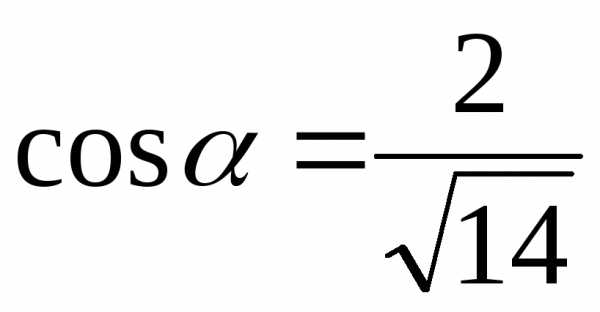 ,
,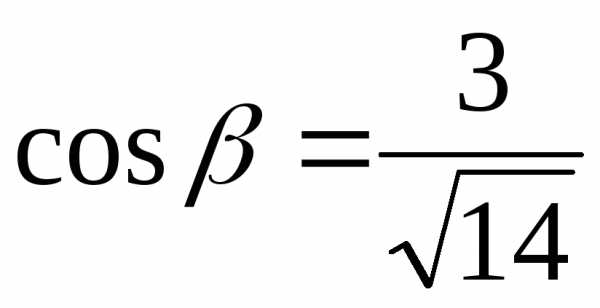 ,
,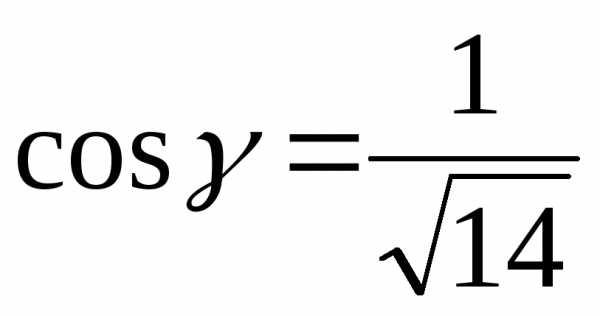 .
.
9. Даны векторы и. Найти векторное произведение.
Ответ. .
10. Дан треугольник с вершинами ,и. Найти длину его высоты, проведенной из вершиныС.Ответ. 10.
§ 4. Смешанное произведение векторов
Основные теоретические сведения
Смешанным
произведением упорядоченной тройки
векторов 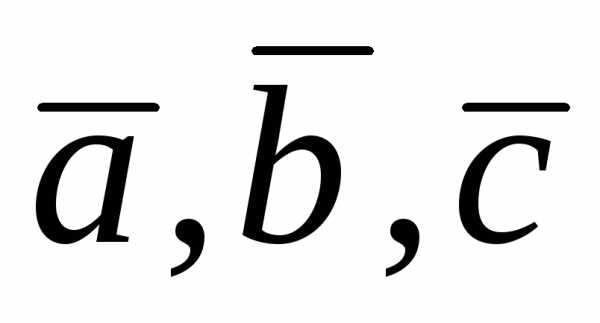 называют число
называют число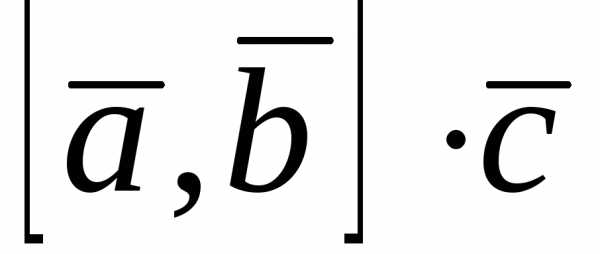 (векторно-скалярное произведение).
(векторно-скалярное произведение).
Свойства смешанного произведения:
1.
.
Это свойство позволяет ввести для
смешанного произведения обозначение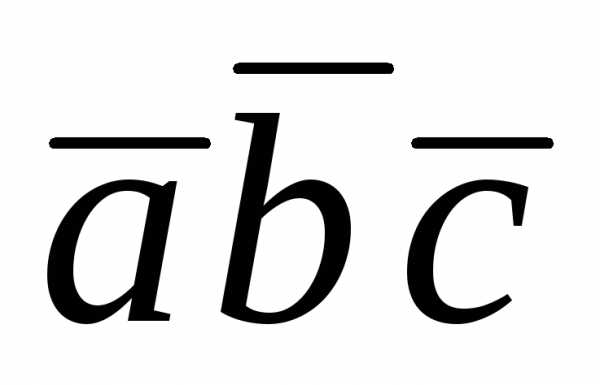 .
.
2. Циклическая перестановка векторов не меняет величины смешанного произведения, т.е.
3. 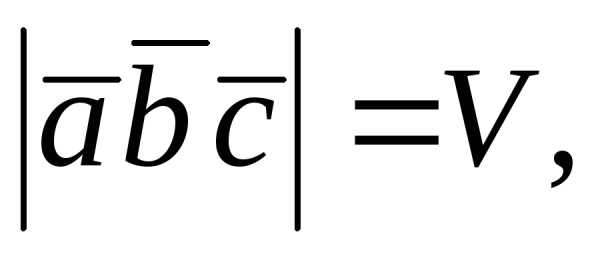
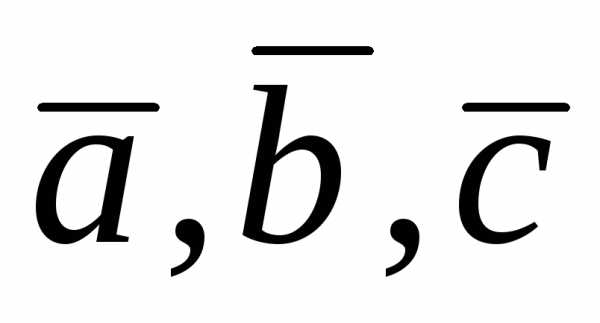 ,
а
,
а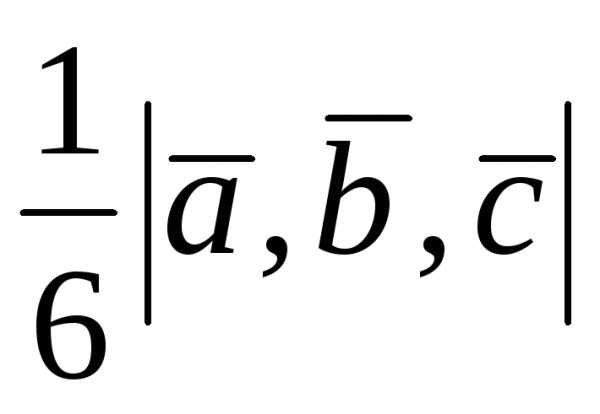 – объем пирамиды, построенной на векторах
– объем пирамиды, построенной на векторах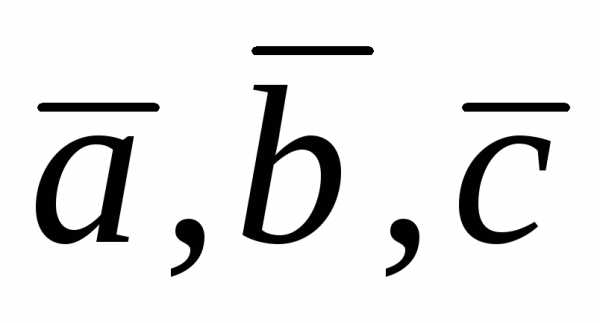 .
. 4. Для того чтобы
векторы 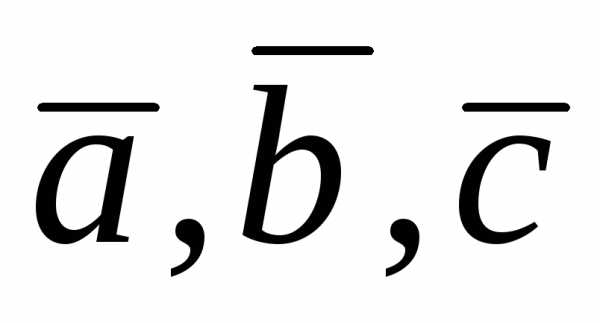 были компланарны, необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю.
были компланарны, необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю.
Замечание. Из определения смешанного произведения следует, что смешанное произведение равно нулю, если среди сомножителей хотя бы два вектора коллинеарны.
Если векторы заданы
своими координатами в ортонормированном
базисе 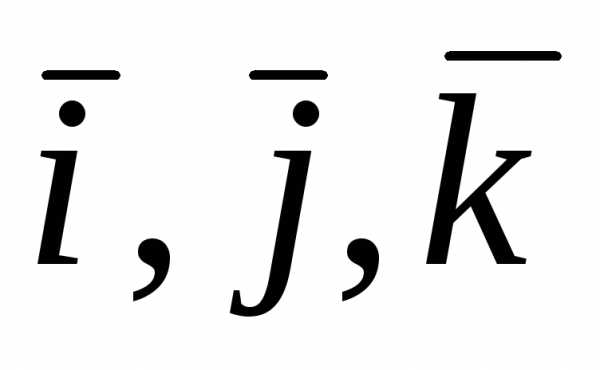
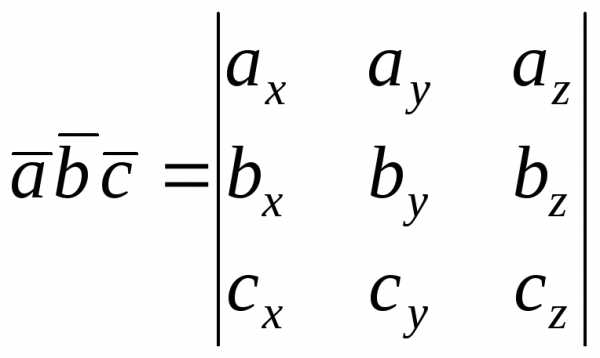 .
.
5. Если – тройка векторов называется правой,– левой.
Примеры решения задач
Задача 4.1. Вычислить смешанное произведение
векторов 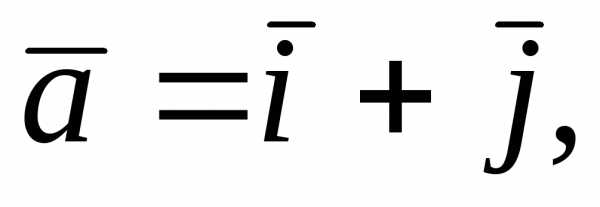
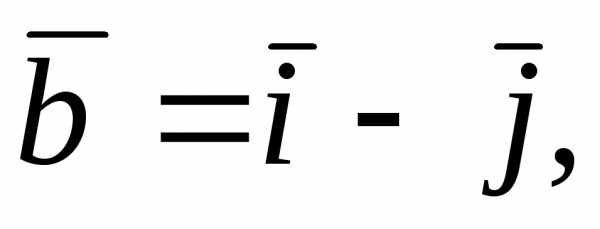
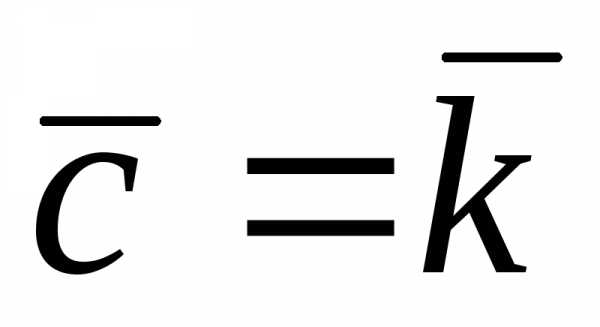 .
.
Решение. Способ 1.
или
Способ 2.

Ответ. –2
Задача 4.2. Упростить выражение:
Решение.
Ответ. 3.
Задача 4.3. Векторы 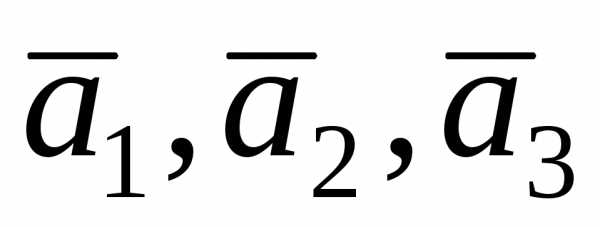 образуют правую тройку, взаимно
перпендикулярны иВычислить
образуют правую тройку, взаимно
перпендикулярны иВычислить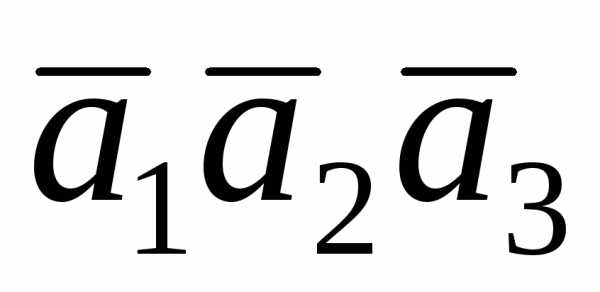 .
.
Решение. по определению скалярного произведения
векторов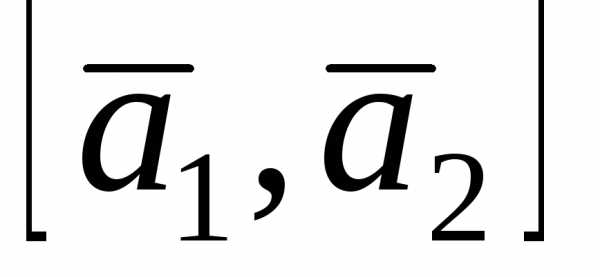 и
и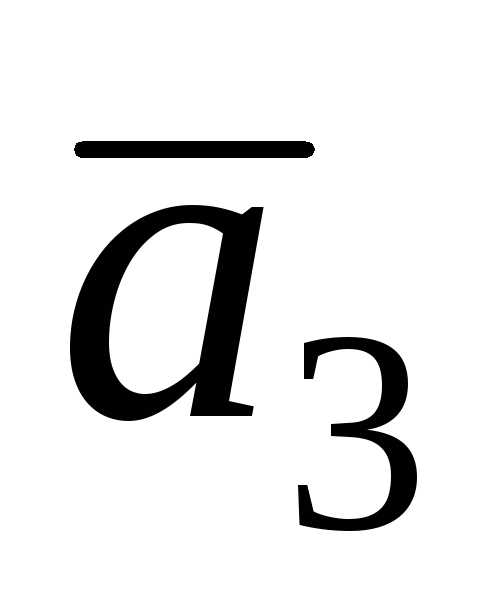 .
.
Из определения
векторного произведения векторов 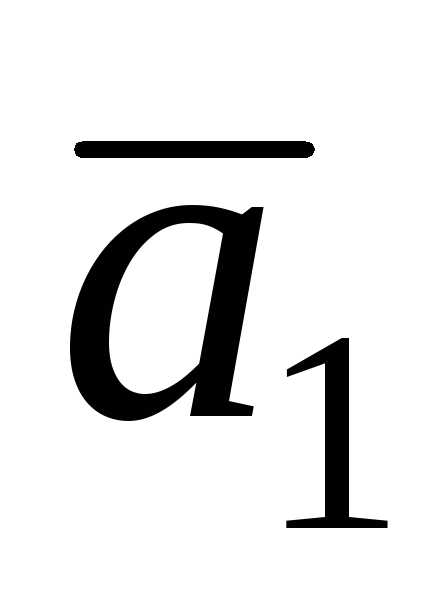
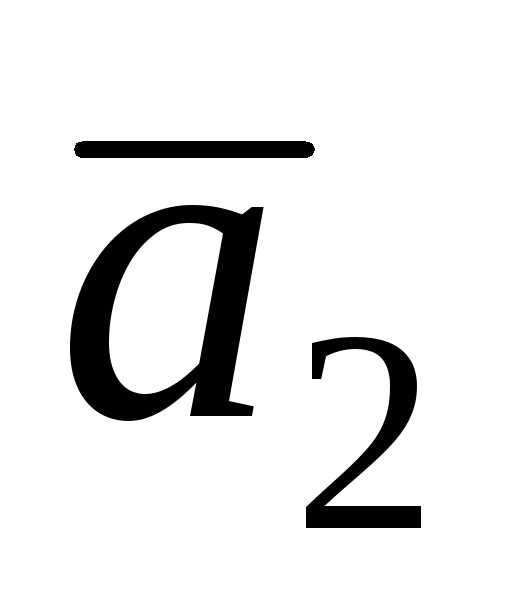 следует, что.
Следовательно, угол между векторами
следует, что.
Следовательно, угол между векторами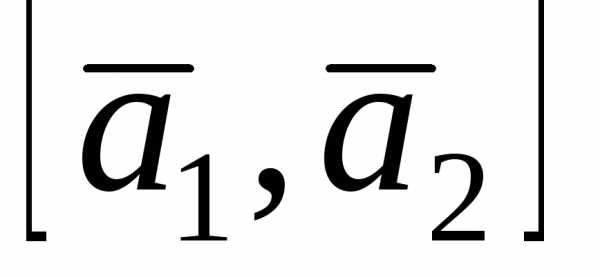 и
и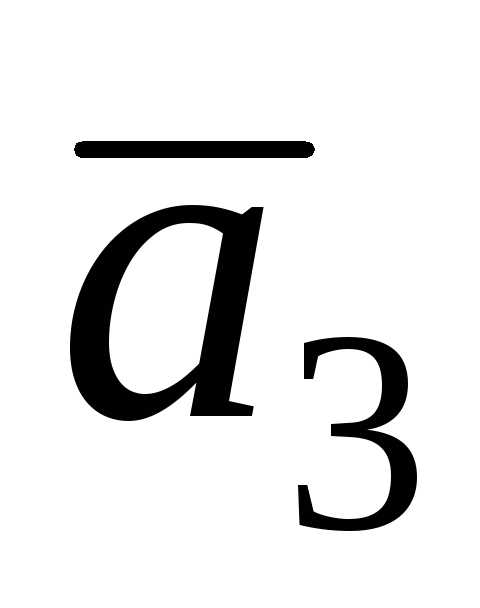 равен нулю и косинус этого угла равен
1. Тогда
равен нулю и косинус этого угла равен
1. ТогдаОтвет. 24.
Задача 4.4. Дано:
и.
Вычислить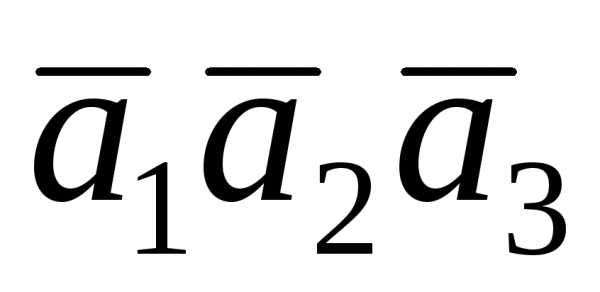 .
.
Решение.
.
Ответ. –7.
Замечание. Векторы 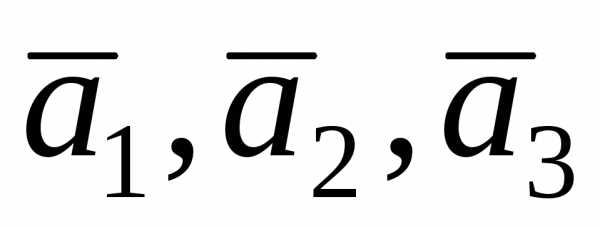 образуют левую тройку.
образуют левую тройку.
Задача 4.5. Установить, образуют ли векторы ибазис в множестве всех векторов.
Решение.
Смешанное
произведение векторов 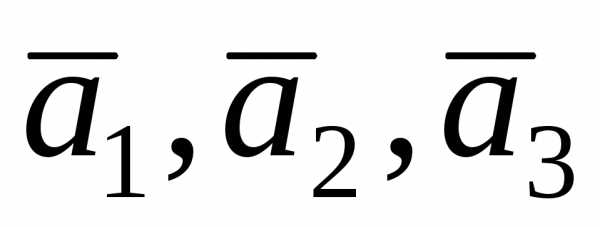 оказалось равным нулю, следовательно,
эти вектора компланарны, а значит,
базисом в множестве всех векторов они
быть не могут.
оказалось равным нулю, следовательно,
эти вектора компланарны, а значит,
базисом в множестве всех векторов они
быть не могут.
Ответ. Не образуют.
Задача 4.6. Доказать тождество .
Решение.
Все слагаемые – смешанные произведения; те из слагаемых, в которых два вектора совпадают, равны нулю.
Задача 4.7. Доказать, что если
,
причем хотя бы одно из чисел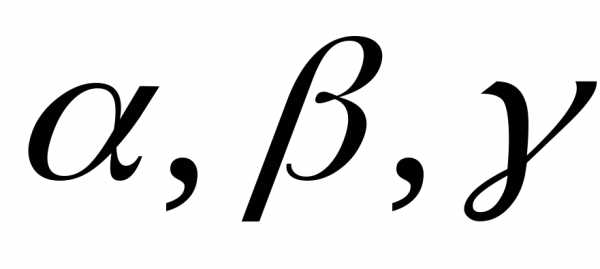 отлично от нуля, то векторы
отлично от нуля, то векторы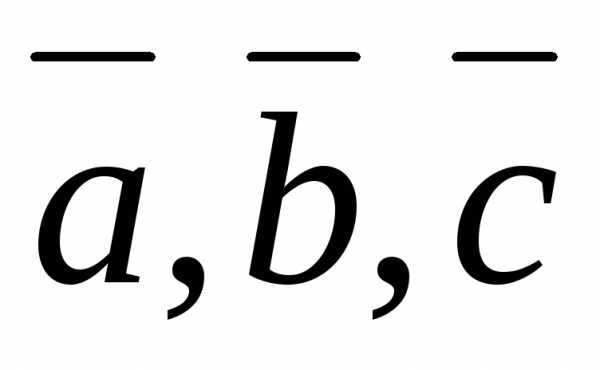 –
компланарны.
–
компланарны.
Решение. Пусть 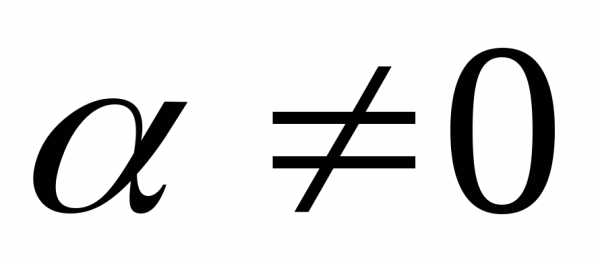 .
Умножим обе части данного равенства
скалярно на вектор
.
Умножим обе части данного равенства
скалярно на вектор .
Получим–
компланарны. Что и требовалось доказать.
.
Получим–
компланарны. Что и требовалось доказать.
Задача 4.8. Вычислить объем тетраэдра OABC, если
.
Решение. Объем тетраэдра равен шестой части объема параллелепипеда, следовательно:
Ответ. 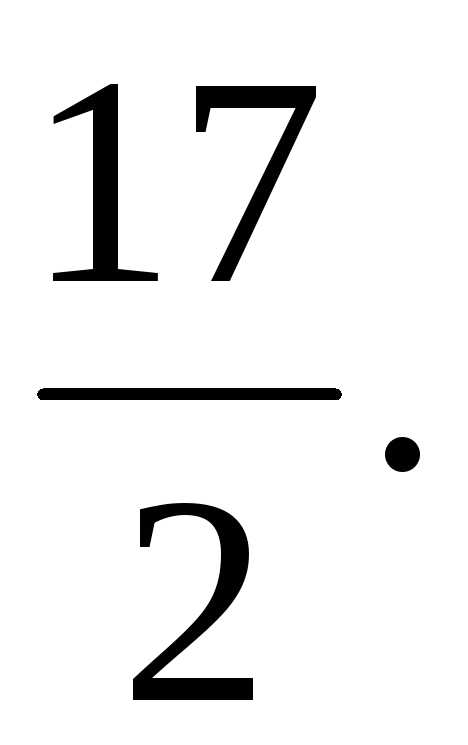
Задача 4.9. В тетраэдре с вершинами в точках A(1,1,1) B(2,0,2), C(2,2,2)
и D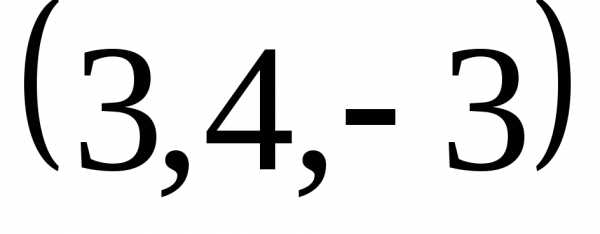 вычислить высоту
вычислить высоту
Решение. (рис. 1.19).С другой стороны, Таким образом | Рис. 1.19 |
Ответ. 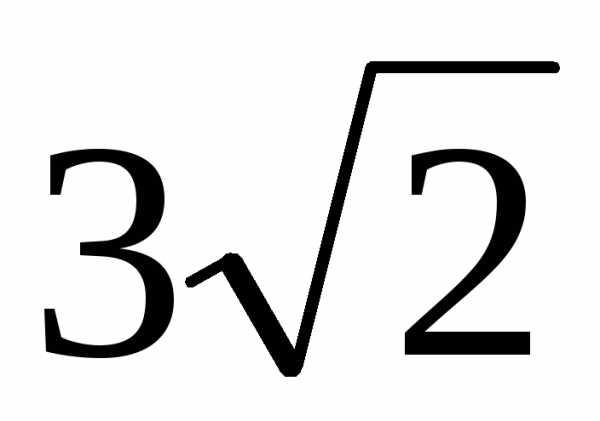 .
.
Задача 4.10. Доказать, что четыре точки A(1,2,–1), B(0,1,5), C(–1,2,1) и D(2,1,3) лежат в одной плоскости.
Решение. Достаточно убедиться в том, что, например,
векторы 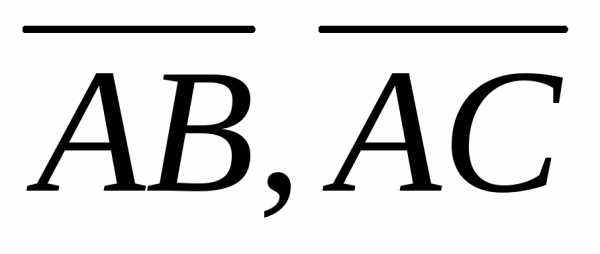 и
и компланарны:
компланарны:
Что и требовалось доказать.
studfiles.net
Правая и левая тройки векторов
ОПРЕДЕЛЕНИЕ Упорядоченная тройка векторов называется правой, если из конца третьего вектора поворот от вектора к вектору по наименьшему углу происходит против часовой стрелки (рис. 1), и левой – если поворот по наименьшему углу происходит по ходу часовой стрелки (рис. 2).Замечание. Правая тройка векторов также называется еще положительно ориентированной, а левая – отрицательно ориентированной.
Замечание. Перестановка двух соседних векторов в рассматриваемой тройке меняет ее ориентацию.
Замечание. Циклическая перестановка или ориентацию тройки не меняет.
Утверждение. Тройка векторов является правой тогда и только тогда, когда смешанное произведение этих векторов больше нуля; и левой – если смешанное произведение меньше нуля.
Примеры решения задач
ПРИМЕР| Задание | Выяснить ориентацию тройки векторов . |
| Решение |
Вычислим смешанное произведение заданных векторов. Для этого составим определитель, по строкам которого записаны координаты векторов и :
Поскольку смешанное произведение векторов и положительно, то тройка векторов является правой. |
| Ответ | Правая тройка векторов. |
ru.solverbook.com
§ 4. Векторное и смешанное произведения векторов.
Векторным
произведением двух векторов  и
и 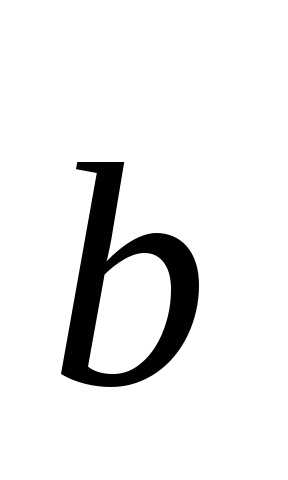 называется вектор
называется вектор  ,
обозначаемый символом
,
обозначаемый символом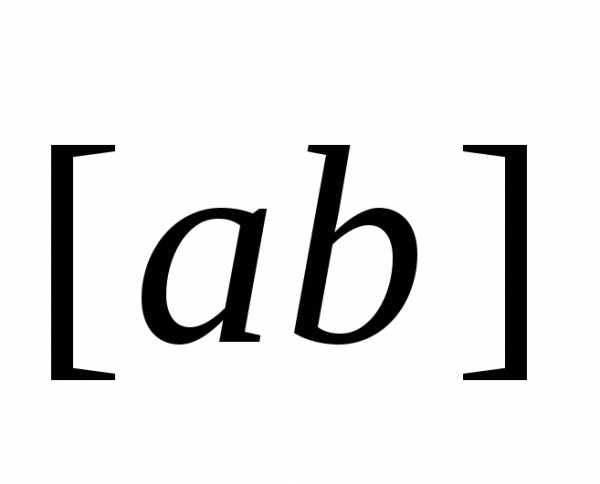 ,
или
,
или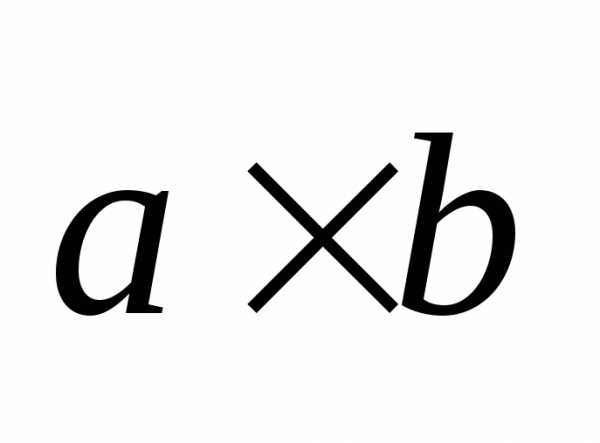 и определяемый следующими тремя
условиями:
и определяемый следующими тремя
условиями:
1)
где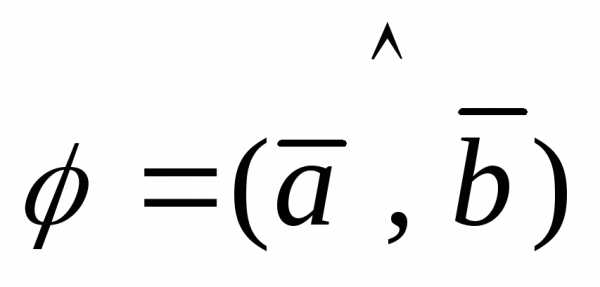 , (1)
, (1)
т.е.
длина векторного произведения равна
площади параллелограмма, построенного
на векторах  и
и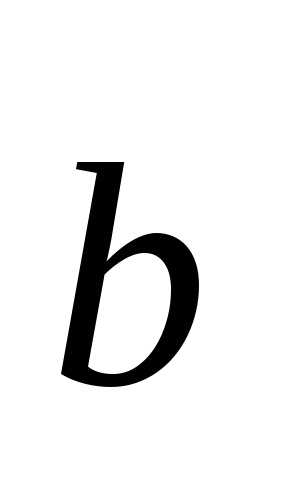 ;
;
2)
т.е. вектор перпендикулярен плоскости парал-лелограмма,
построенного на
перпендикулярен плоскости парал-лелограмма,
построенного на и
и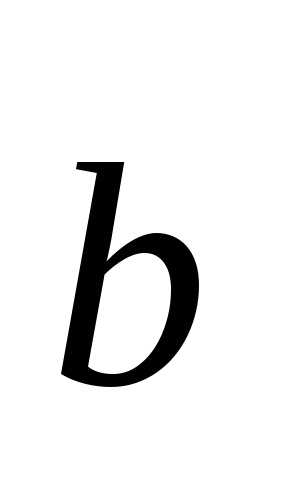 ;
;
3)
векторы
и ,
взятые в указанном порядке, составляютправую
тройку векторов.
,
взятые в указанном порядке, составляютправую
тройку векторов.
Если 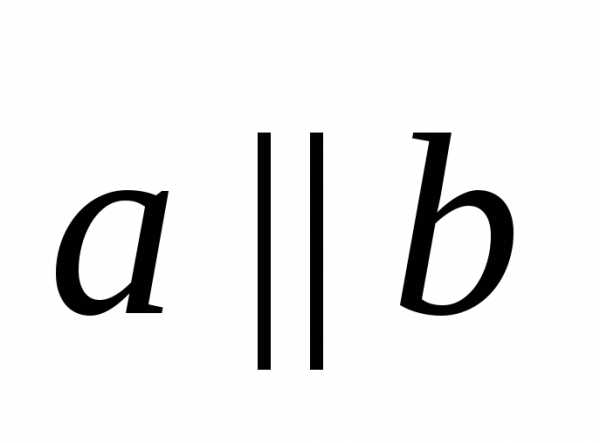 ,
тов частности,
,
тов частности,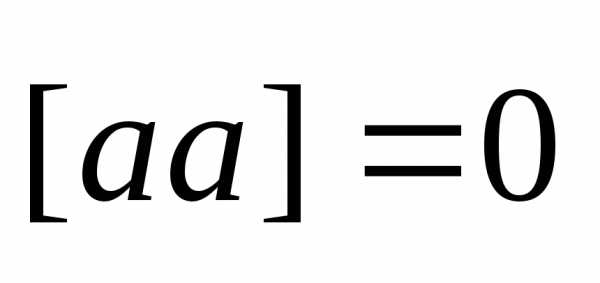 ; (2)
; (2)
если 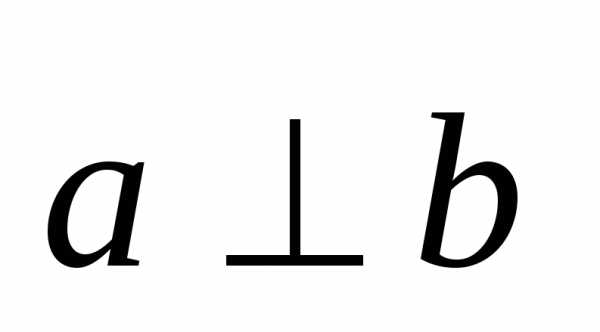 ,
то
,
то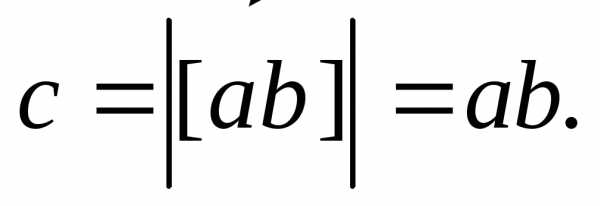
Свойства векторного произведения:
1) (3)
2) (4)
3) (5)
Если то
(6)
Смешанным
произведением трех
векторов 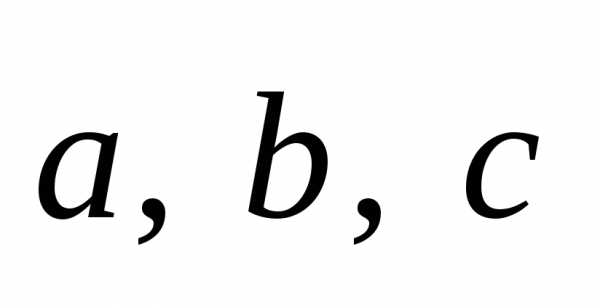 называетсячисло,
равное векторному произведению
называетсячисло,
равное векторному произведению 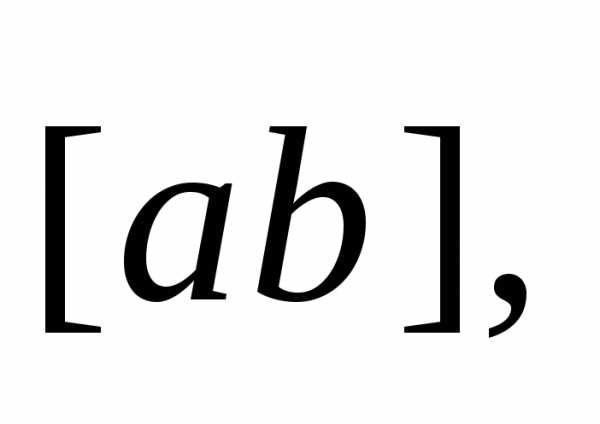 умноженному скалярно на вектор
умноженному скалярно на вектор ,
т.е.
,
т.е.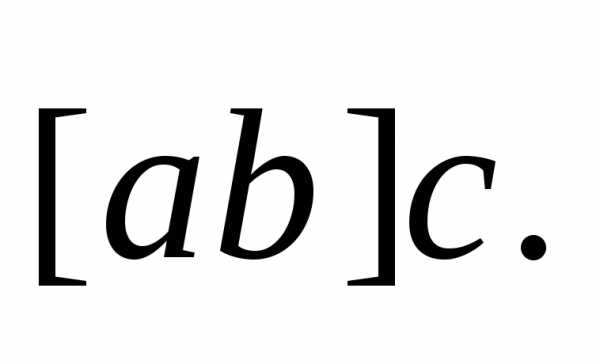
Смешанное произведение равно объему параллелепипеда, построенного на данных трех векторах, взятому со знаком плюс, если тройка правая, и со знаком минус, если эта тройка векторов левая.
Смешанное произведение обладает тем свойством, что оно не меняется при круговой перестановке сомножителей и меняет знак при всякой перестановке, меняющей последовательность сомножителей:
(7)
Поэтому
смешанное произведение векторов 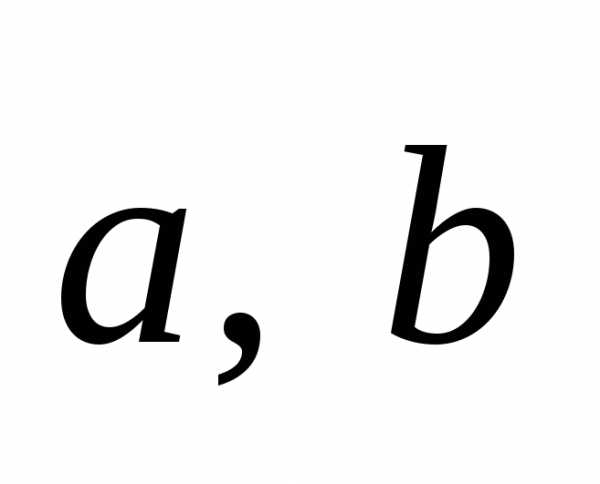 и
и обозначают проще:
обозначают проще:
, или .
Если
векторы 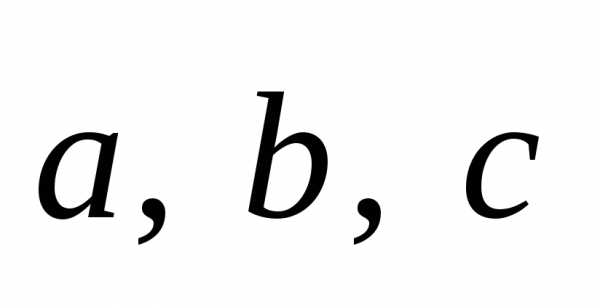 компланарны, их смешанное произведение
равно нулю; т.е. равенство
компланарны, их смешанное произведение
равно нулю; т.е. равенство
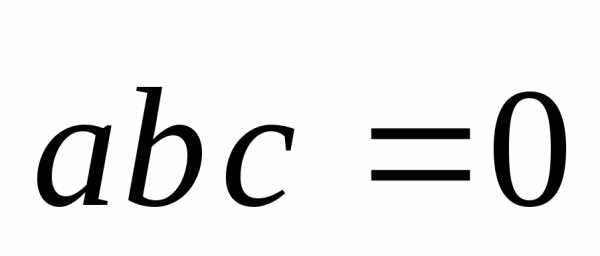 (8)
(8)
есть
необходимое и достаточное условие
компланарности (линейной зависимости) векторов 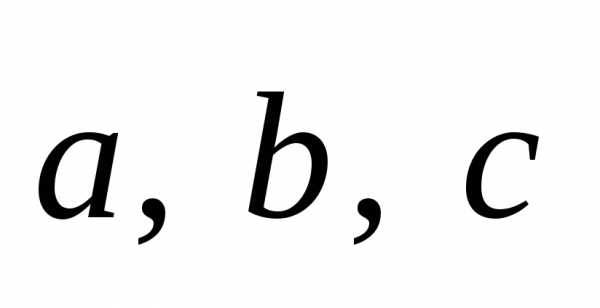 .
.
Если то
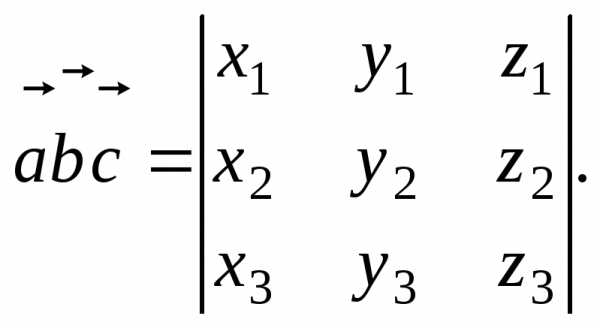 (9)
(9)
Примеры решения типичных задач.
Задача.
Векторы 
 и
и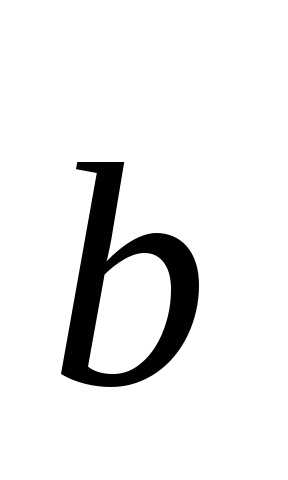 образуют угол
образуют угол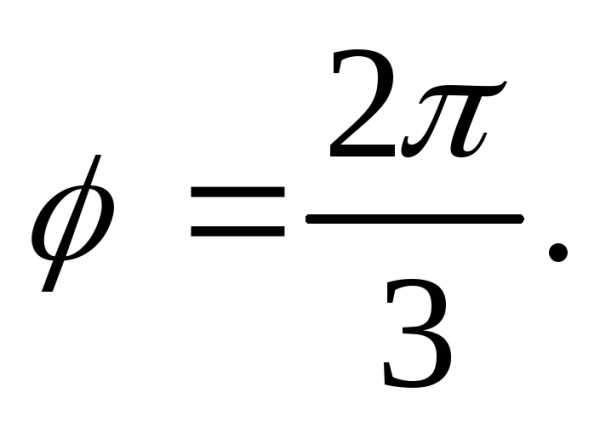 Зная, чтовычислить:
1)
Зная, чтовычислить:
1)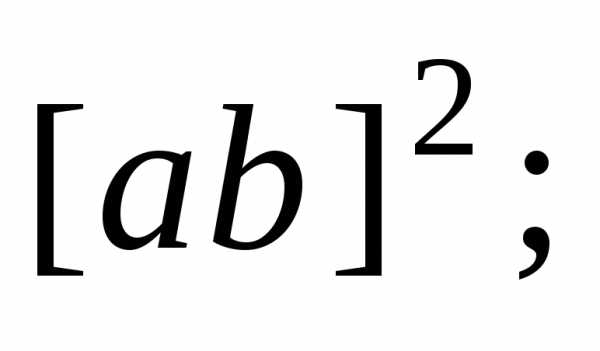 2)3)
2)3)
Решение.
1)
— скалярный квадрат вектора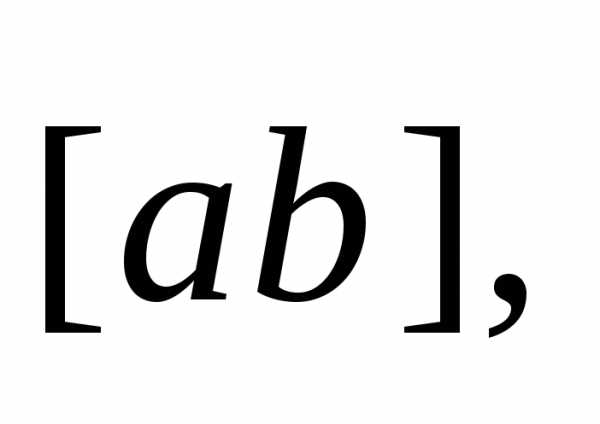 т.е.
квадрат длины этого вектора:
т.е.
квадрат длины этого вектора:
2) вычислим сначала векторное произведение , опираясь на свойства (2)-(5):
,
т.е.
3)
Задача. Даны точки А(1;2;0), В(3;0;-3) и С(5;2;6). Вычислить площадь треугольника АВС.
Решение. Достроим 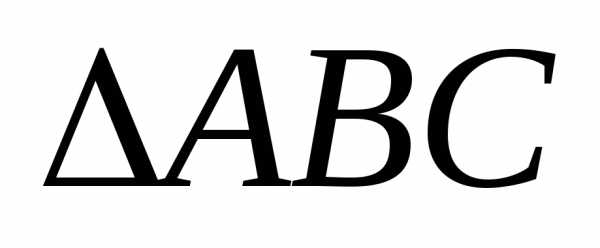 до параллелограмма. Тогда пло-щадь
до параллелограмма. Тогда пло-щадь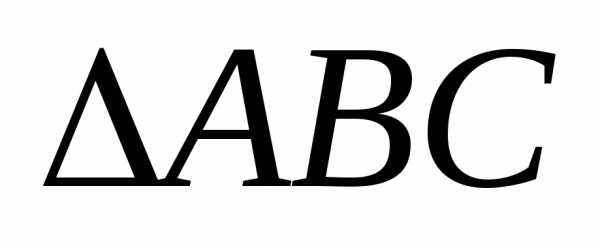 ,
построенного на векторах
,
построенного на векторах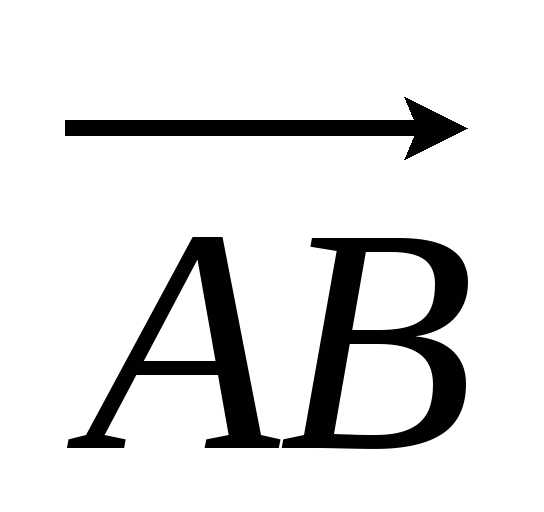 и
и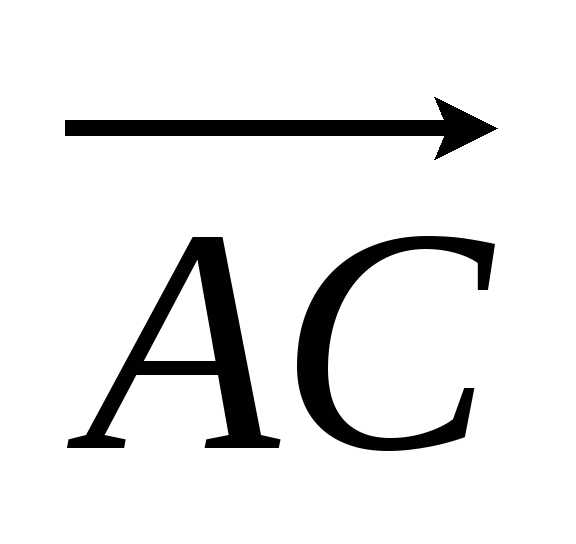 ,
равна половине площади параллелограмма,
построенного на тех же векторах, т.е.
,
равна половине площади параллелограмма,
построенного на тех же векторах, т.е.
.
Найдем
координаты векторов
и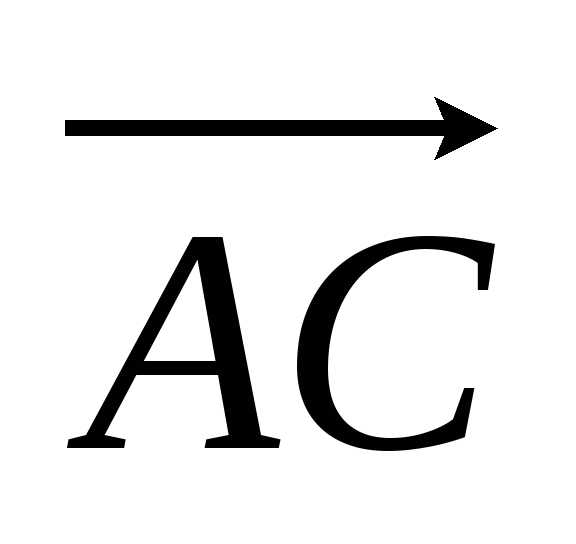 :
:
Применяя формулу (6), получим:
Находим
длину вектора 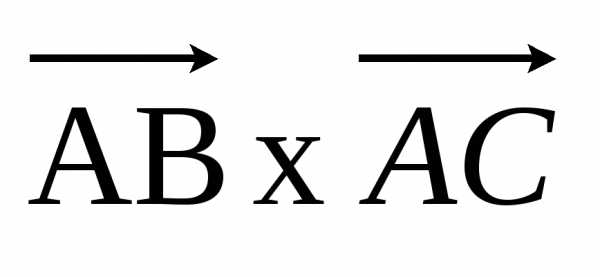 ,
т.е.
,
т.е. :
:
кв.ед.
Таким образом, кв.ед.
Задача. Найти вектор 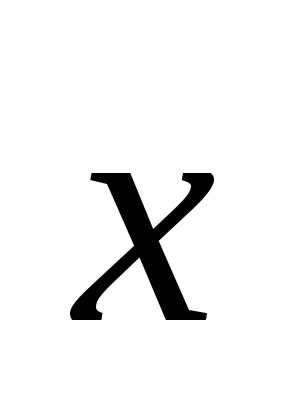 ,
зная, что он перпендикулярен к векторами
,
зная, что он перпендикулярен к векторами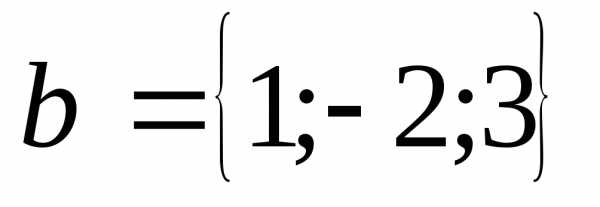 и удовлетворяет условию
и удовлетворяет условию
Решение. Т.к. 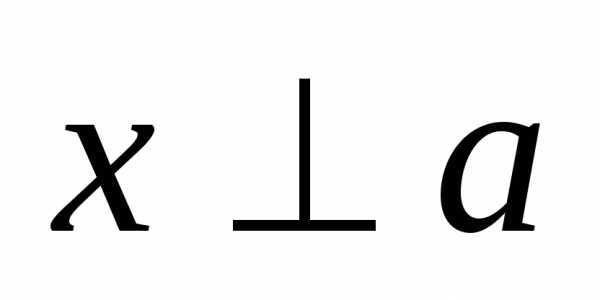 и
и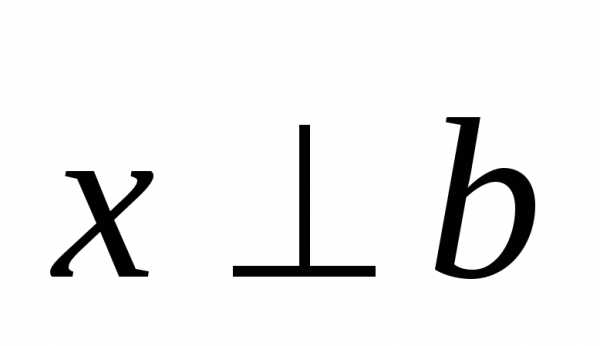 ,
то из определения векторного произведения
следует, что
,
то из определения векторного произведения
следует, что
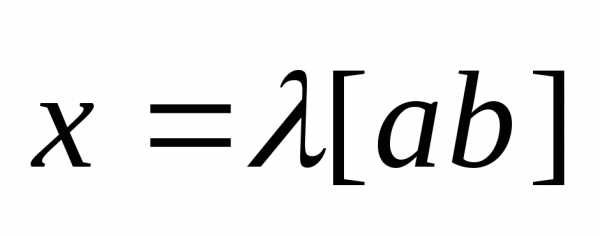 .
.
Т.е.
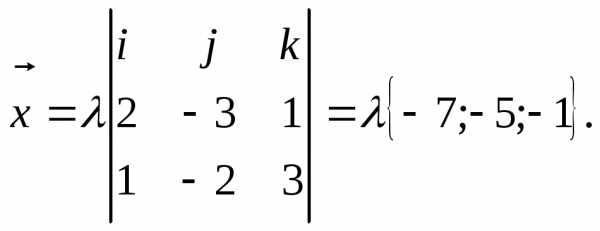
Условие
задачи:
означает, что скалярное произведение
вектора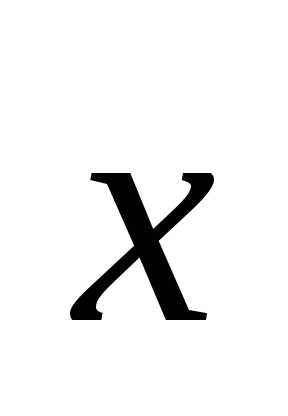 на векторравно 10. Тем самым получаем уравнение
относительно переменной
на векторравно 10. Тем самым получаем уравнение
относительно переменной :
:
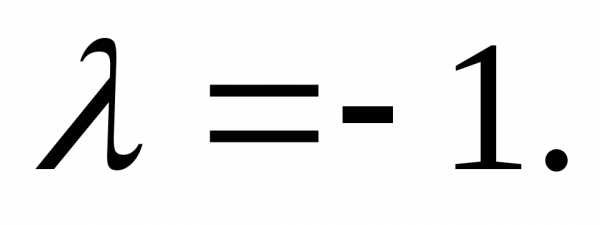
Таким образом,
Задача. Вычислить объем V параллелепипеда, построенного на векторах и
Решение. Найдем смешанное произведение векторов 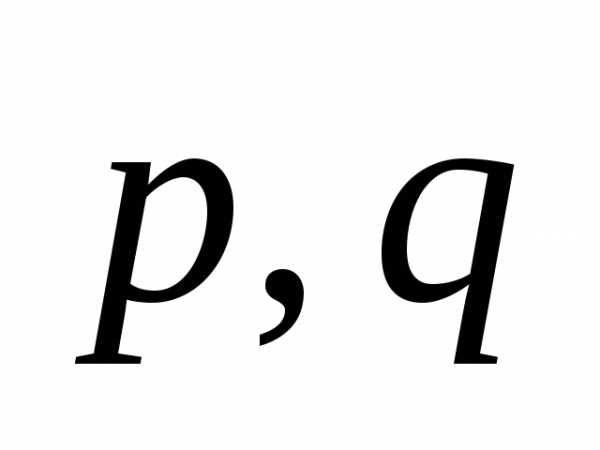 и
и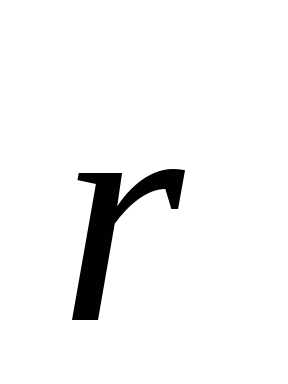 ,
опираясь на определение:
,
опираясь на определение:
;
очевидно, что
Поэтому,
Учитывая свойство (7), получаем: Т.е.
Задача. Даны вершины тетраэдра А(2;3;1), В(4;1;-2), С(6;3;7),
D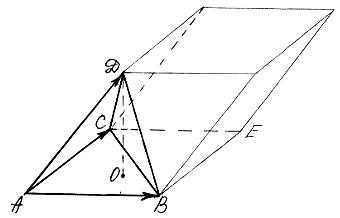 (-5;-4;8). Найти длину его высоты, опущенной из
вершины D.
(-5;-4;8). Найти длину его высоты, опущенной из
вершины D.
Решение: Рассмотрим векторы 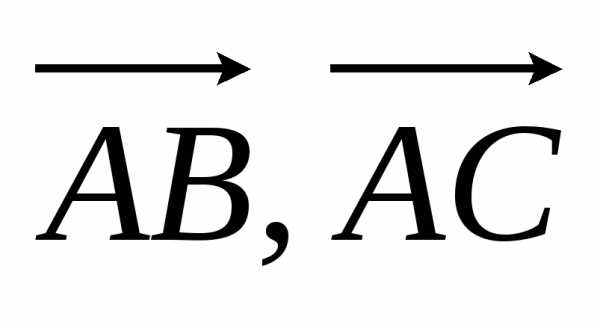 и
и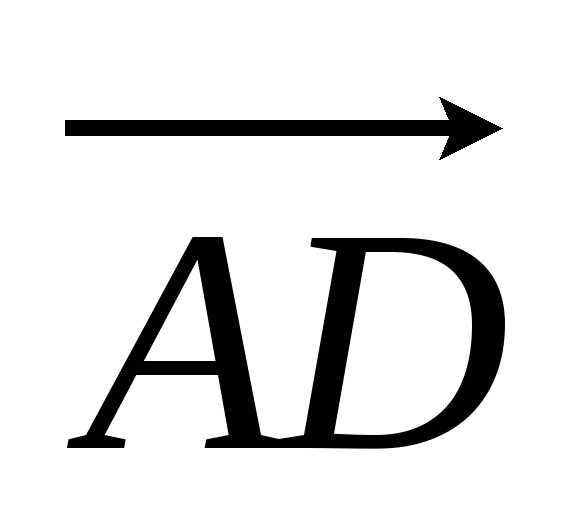 ,
на которых построен тетраэдрABCD.
Объем тетраэдра
,
на которых построен тетраэдрABCD.
Объем тетраэдра
равен одной трети произведения площади основания на высоту:
Параллелепипед,
построенный на тех же векторах, что и
тетраэдр 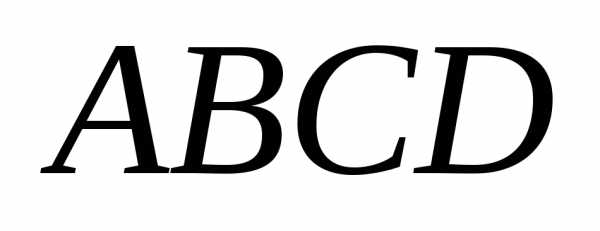 ,
имеет ту же высотуDO,
а площадь основания (параллелограмма)
– в два раза больше, т.е.
,
имеет ту же высотуDO,
а площадь основания (параллелограмма)
– в два раза больше, т.е.
.
Для нахождения высоты тетраэдра (параллелепипеда) получим формулу:
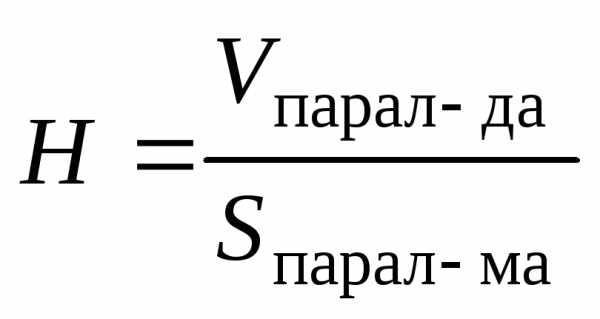 ,
,
или 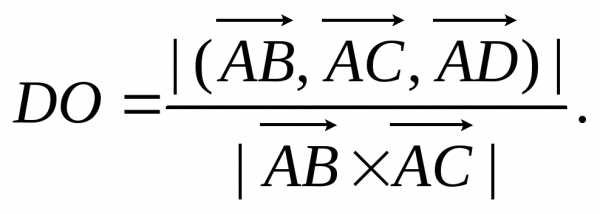
Найдем
координаты векторов 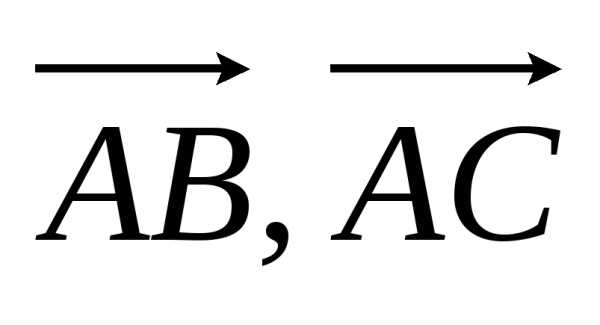 и
и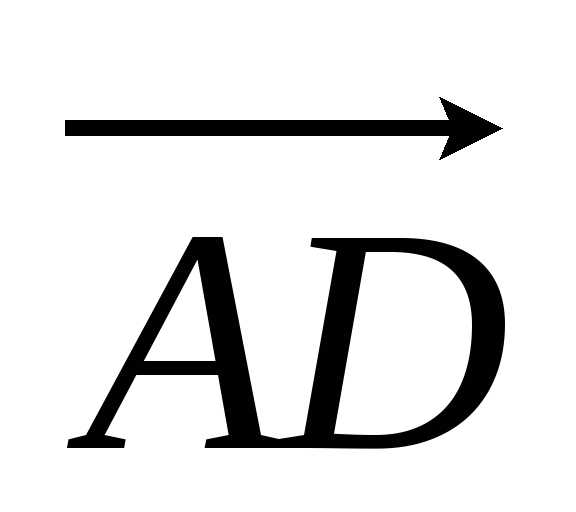 :
:
По формуле (9):
т.е. .
Вычислим
т.е.
Тогда
высота DO тетраэдра ABCD будет равна 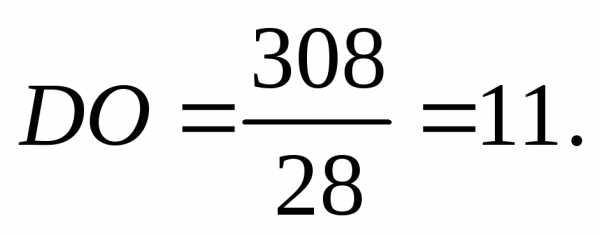
Задачи для самостоятельного решения.
1.
Даны
.
Вычислить 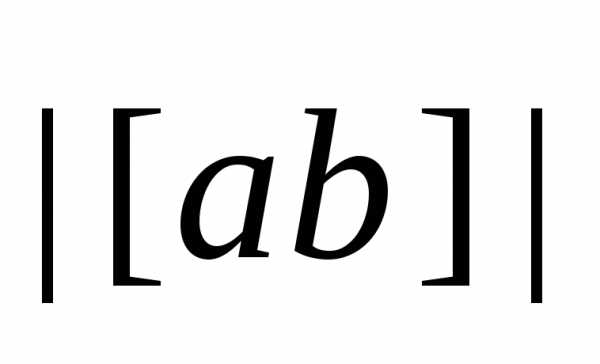 .
(Ответ: 16)
.
(Ответ: 16)
2.
Векторы  и
и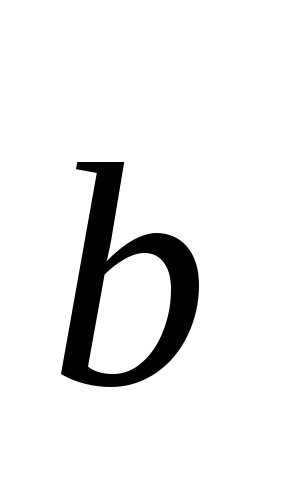 взаимно перпендикулярны. Зная, чтовычислить: 1)2).
(Ответ: 1)24;
2) 60)
взаимно перпендикулярны. Зная, чтовычислить: 1)2).
(Ответ: 1)24;
2) 60)
3.
Какому условию должны удовлетворять
векторы 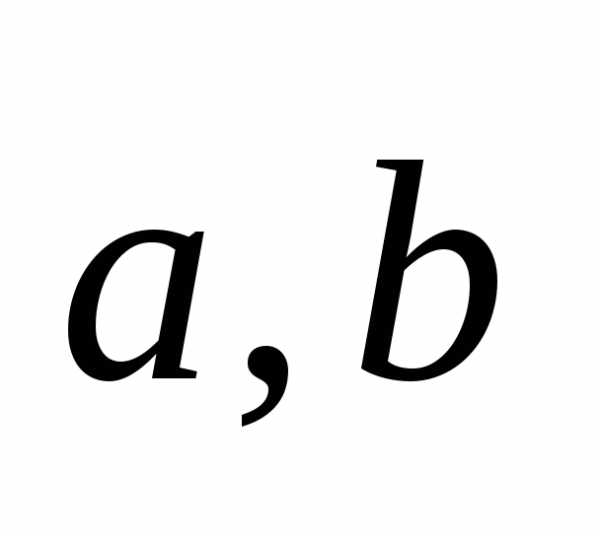 ,
чтобы векторы
,
чтобы векторы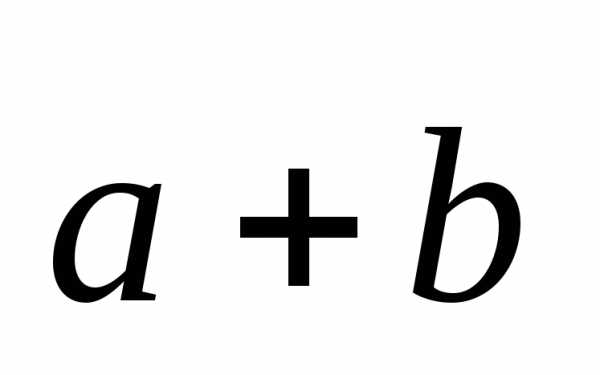 и
и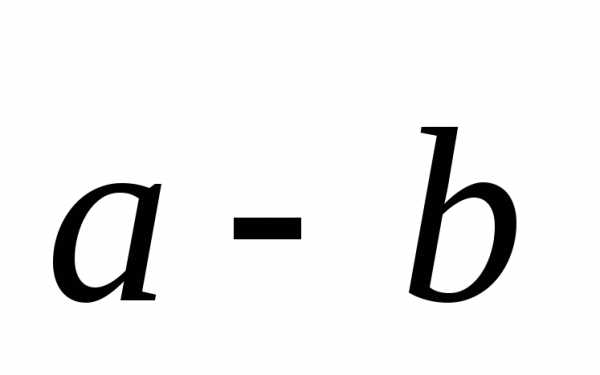 были
коллинеарны? (Ответ:
были
коллинеарны? (Ответ: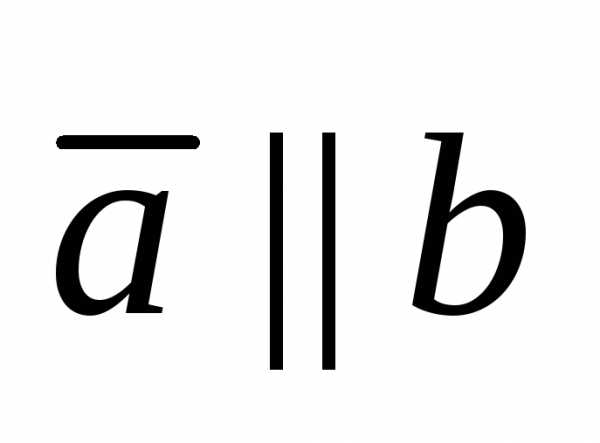 )
)
4.
Вычислить площадь параллелограмма,
построенного на векторах
и,
где и
и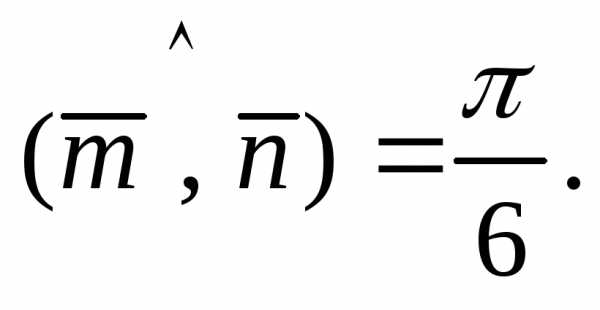 (Ответ: 37,5 кв.ед.)
(Ответ: 37,5 кв.ед.)
5.
Разложить вектор
по взаимно перпендикулярным ортам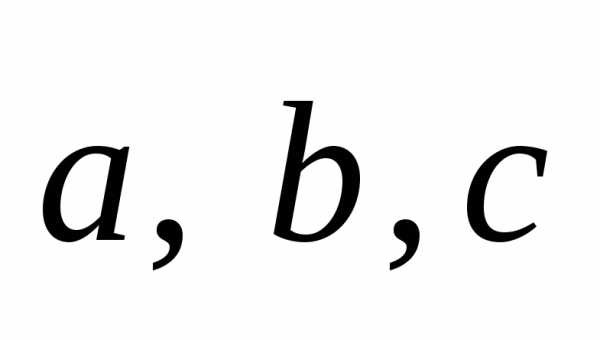 ,
образующим правую тройку. (Ответ:)
,
образующим правую тройку. (Ответ:)
6.
Зная векторы, совпадающие с двумя
сторонами треугольника
и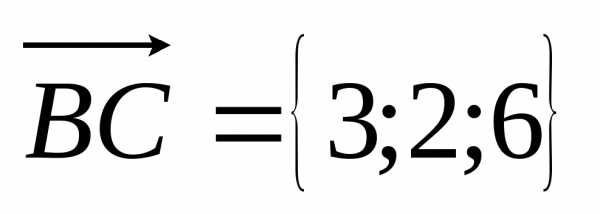 ,
вычислить площадь треугольника.
,
вычислить площадь треугольника.
(Ответ: 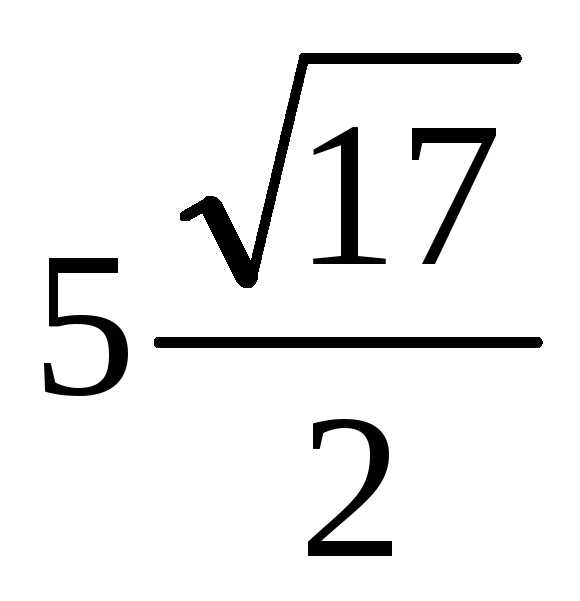 кв.ед.)
кв.ед.)
7.
Даны вершины треугольника
и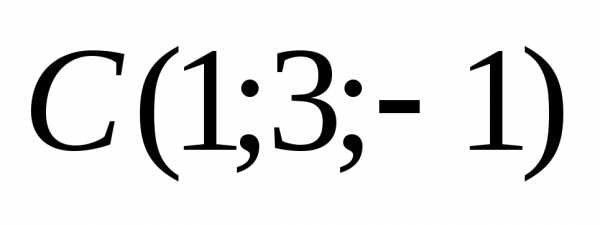 .
Вычислить длину его высоты, опущенной
из вершиныВ на сторону АС.
(Ответ: 5)
.
Вычислить длину его высоты, опущенной
из вершиныВ на сторону АС.
(Ответ: 5)
8.
Вычислить синус угла между диагоналями
параллелограмма, построенного на данных
векторах
и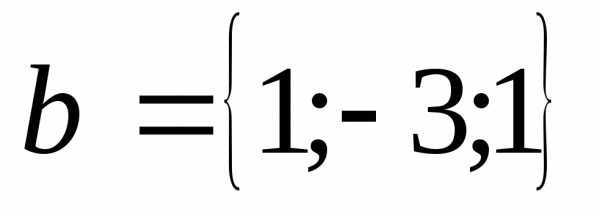 .
.
(Ответ: 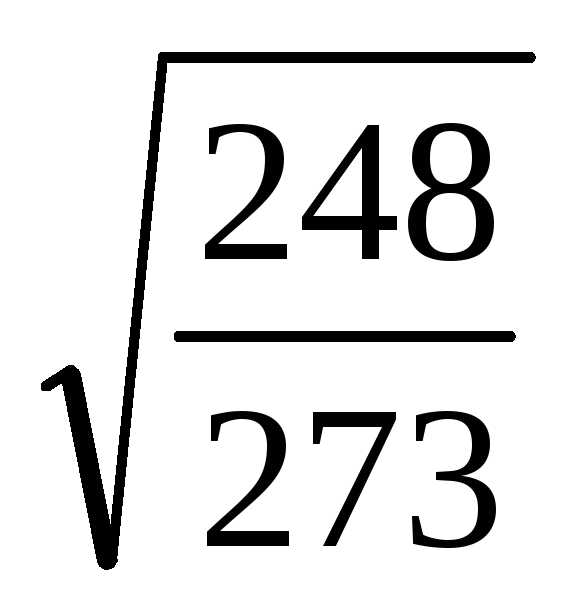 )
)
9.
Вектор 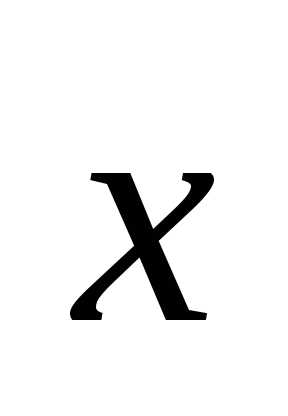 ,
перпендикулярный к векторами
,
перпендикулярный к векторами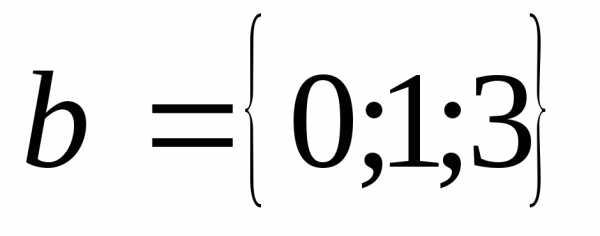 ,
образует с осьюОу тупой угол. Зная, что
,
образует с осьюОу тупой угол. Зная, что 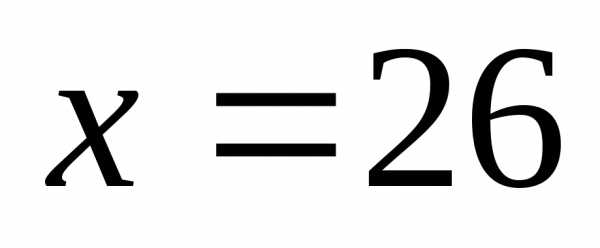 ,
найти его координаты. (Ответ:
)
,
найти его координаты. (Ответ:
)
10.
Вектор 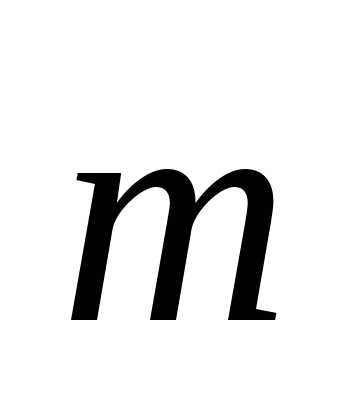 ,
перпендикулярный к осиOz и к вектору
,
образует острый угол с осьюОх.
Зная, что
,
перпендикулярный к осиOz и к вектору
,
образует острый угол с осьюОх.
Зная, что 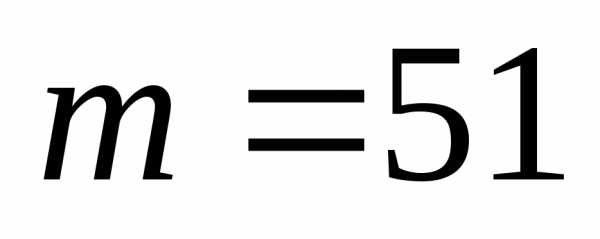 ,
найти его координаты. (Ответ:)
,
найти его координаты. (Ответ:)
11.
Векторы 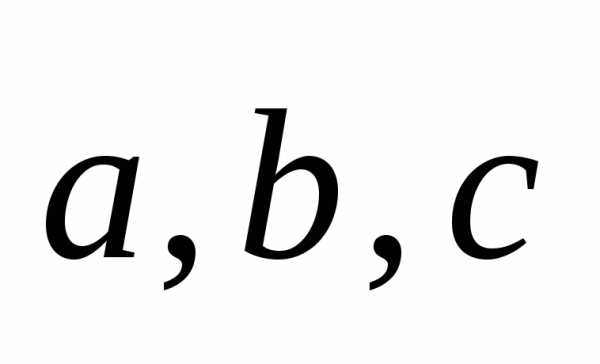 ,
образующие правую тройку, взаимно
перпендикулярны. Зная, что,
вычислить
,
образующие правую тройку, взаимно
перпендикулярны. Зная, что,
вычислить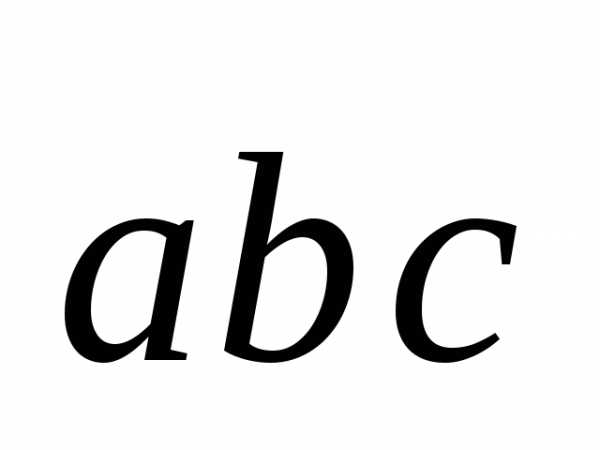 .
.
(Ответ: 24)
12.
Вектор  перпендикулярен к векторам
перпендикулярен к векторам и
и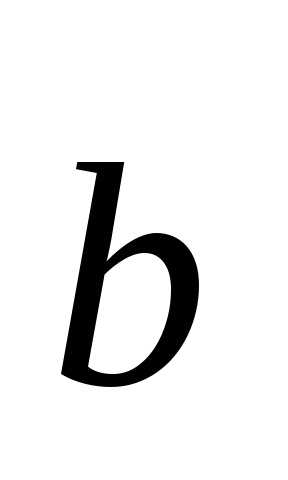 ,
угол между
,
угол между и
и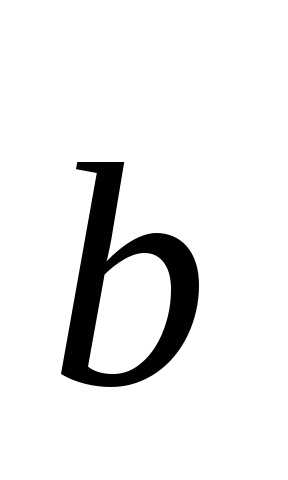 равен 30о.
Зная, что
,
вычислить
равен 30о.
Зная, что
,
вычислить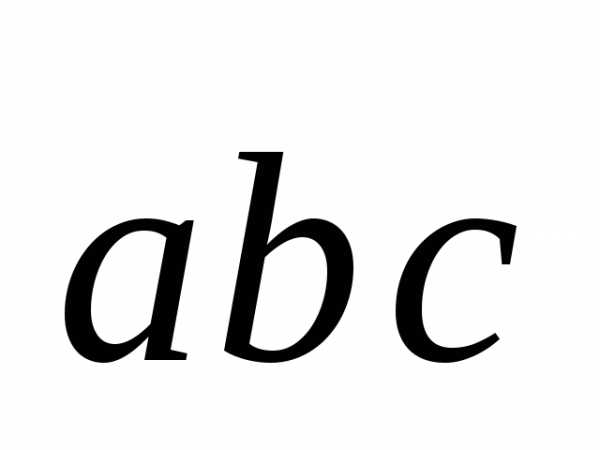 .
(Ответ:
.
(Ответ: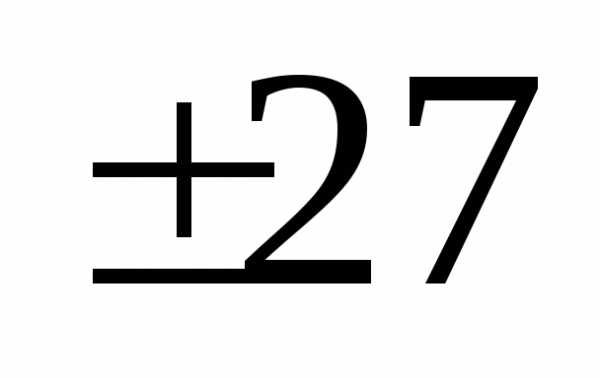 )
)
13. Доказать тождество
14.
Доказать, что векторы 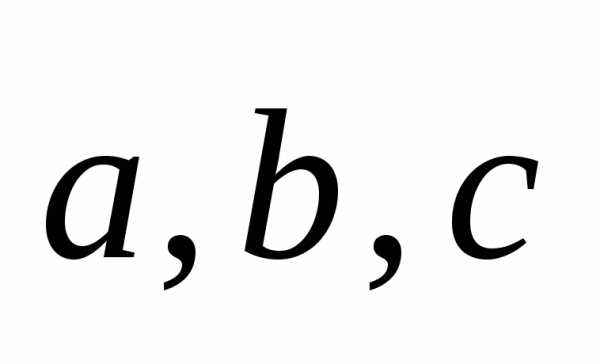 ,
удовлетворяющие условию,
компланарны.
,
удовлетворяющие условию,
компланарны.
15. Доказать, что точки А(1;2;-1), В(0;1;5), С(-1;2;1), D(2;1;3) лежат в одной плоскости.
16.
Вычислить объем параллелепипеда,
построенного на трех данных векторах
и,
и исследовать, образуют ли векторы левую
или правую тройку. (Ответ: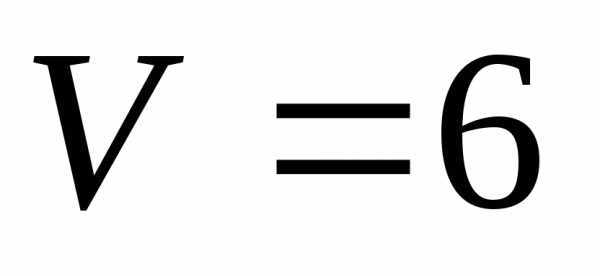 куб.ед., левая тройка)
куб.ед., левая тройка)
17.
Объем тетраэдра 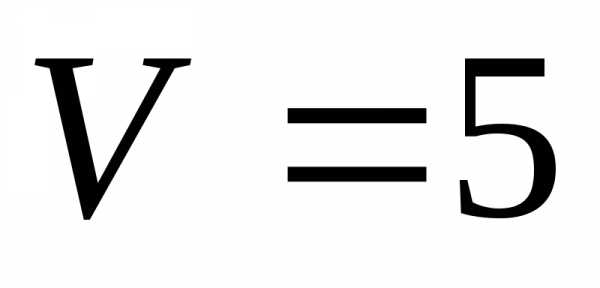 ,
три его вершины находятся в точкахА(2;1;-1),
В(3;0;1), С(2;-1;3). Найти координаты четвёртой вершины D,
если
известно, что она лежит на оси Оу.
(Ответ:
)
,
три его вершины находятся в точкахА(2;1;-1),
В(3;0;1), С(2;-1;3). Найти координаты четвёртой вершины D,
если
известно, что она лежит на оси Оу.
(Ответ:
)
18.
Найти вектор 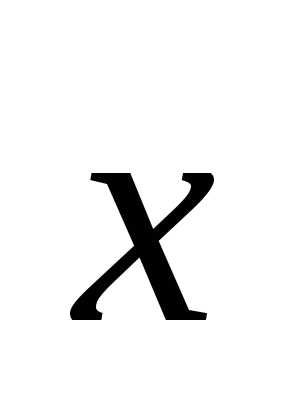 ,
одновременно удовлетворяющий трем
уравнениям:
,
одновременно удовлетворяющий трем
уравнениям: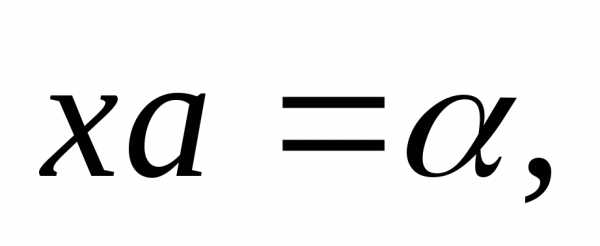
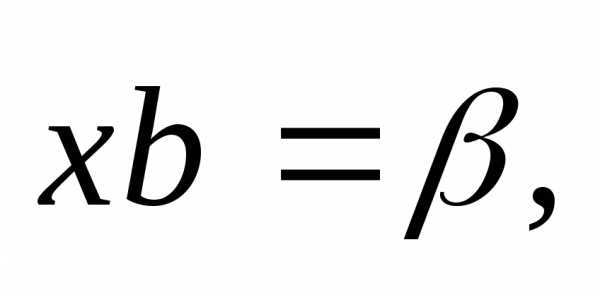
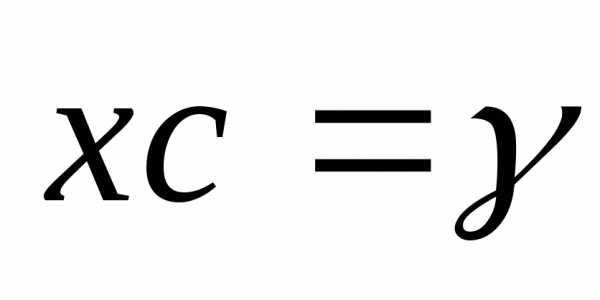 .
(Ответ:)
.
(Ответ:)
studfiles.net
I уровень
1.1.Даны векторы и
и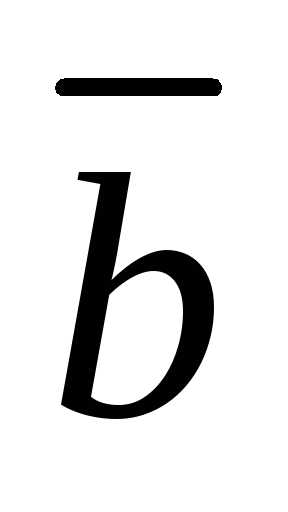 такие, что
такие, что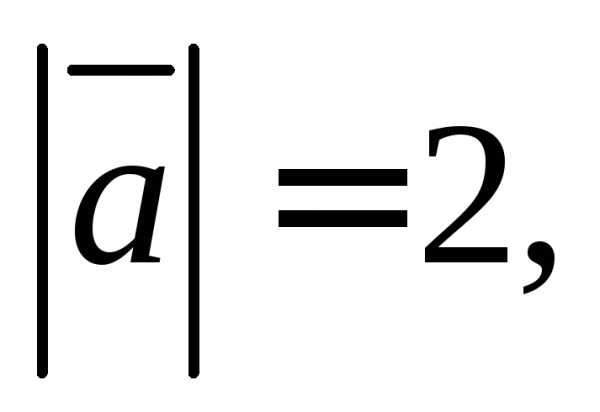
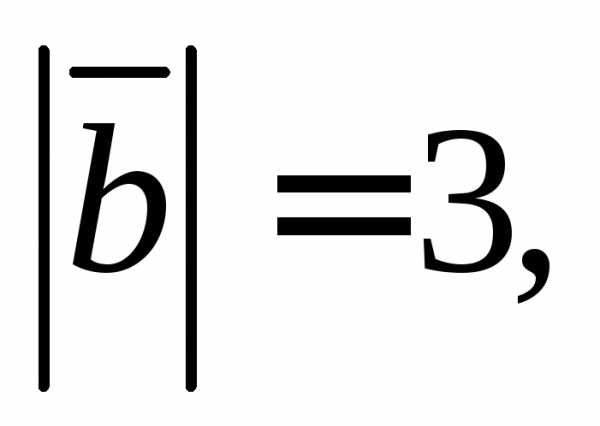
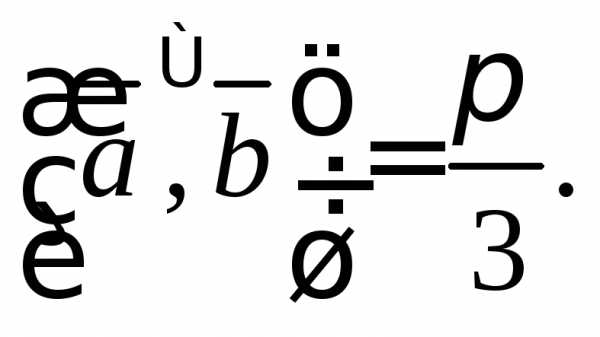 Вычислите:
Вычислите:
1)  2)3)
2)3)
1.2.Для векторовинайдите:
1) 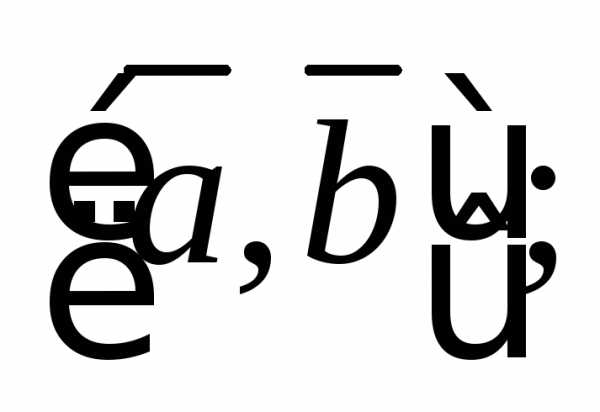 2)3)
2)3)
1.3.Вычислите
площадь параллелограмма, построенного
на векторахи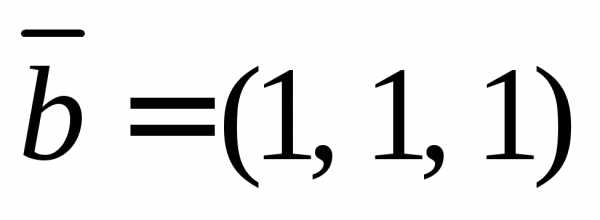 .
.
II уровень
2.1.Докажите, чтои выясните геометрический смысл этого тождества.
2.2.Какому
условию должны удовлетворять векторы и
и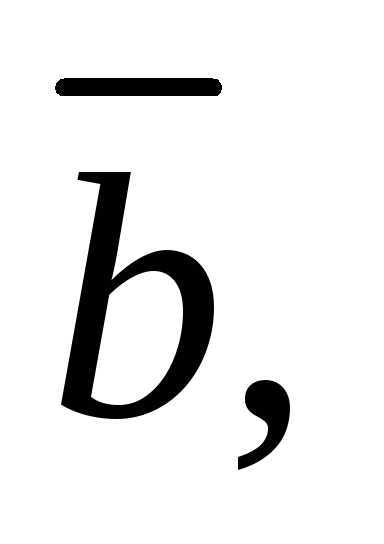 чтобы векторы
чтобы векторы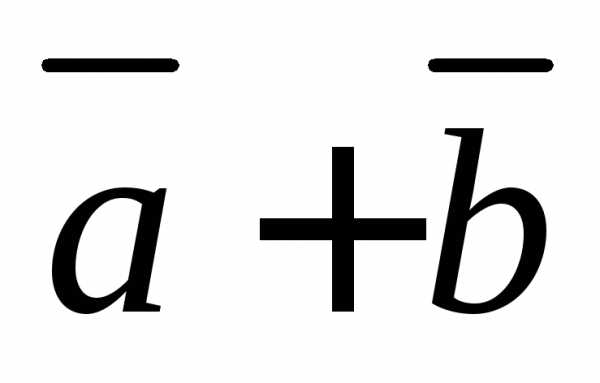 и
и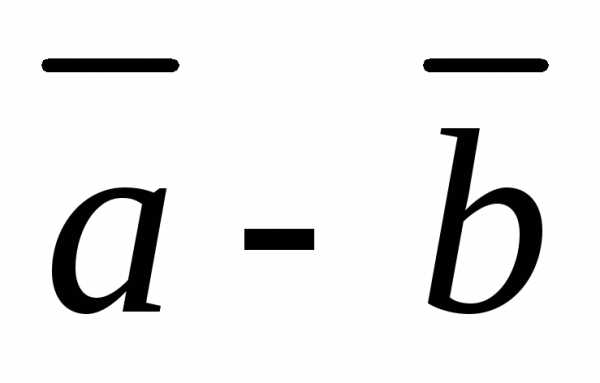 были коллинеарными?
были коллинеарными?
2.3.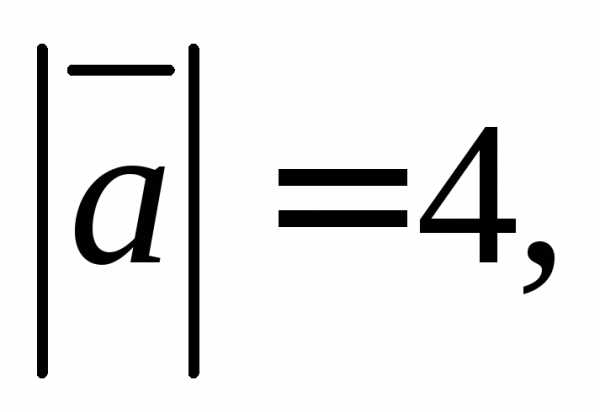
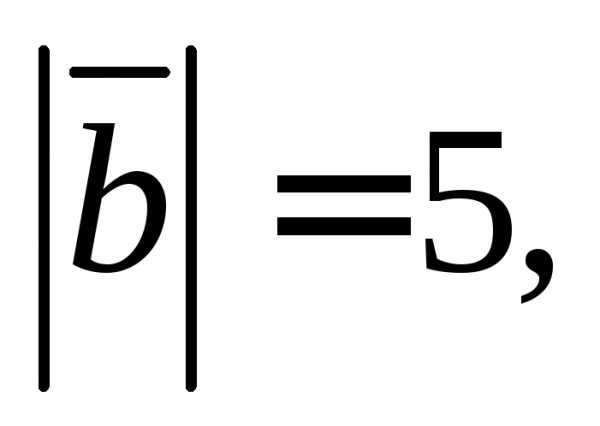
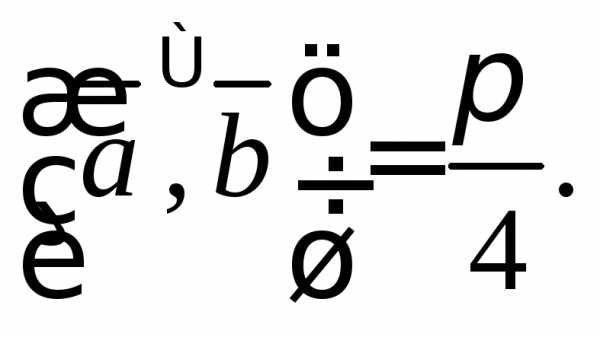 Вычислите площадь треугольника,
построенного на векторах
Вычислите площадь треугольника,
построенного на векторах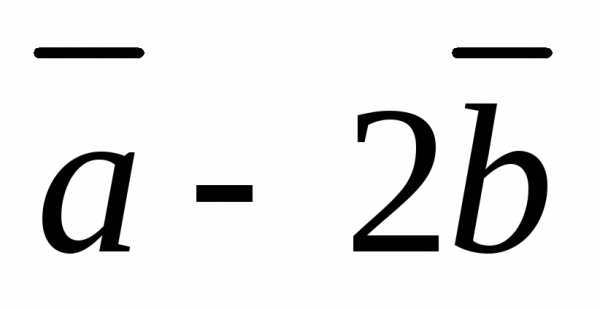 и
и
2.4. 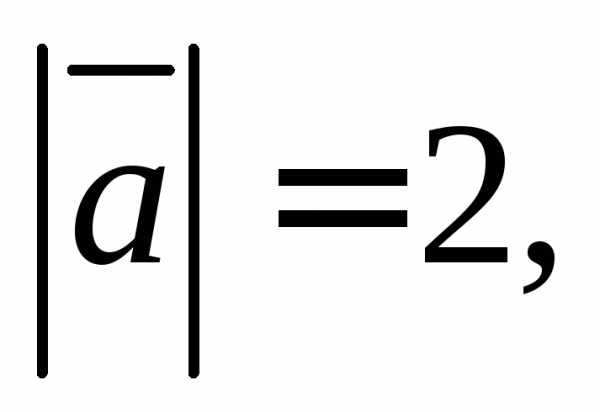
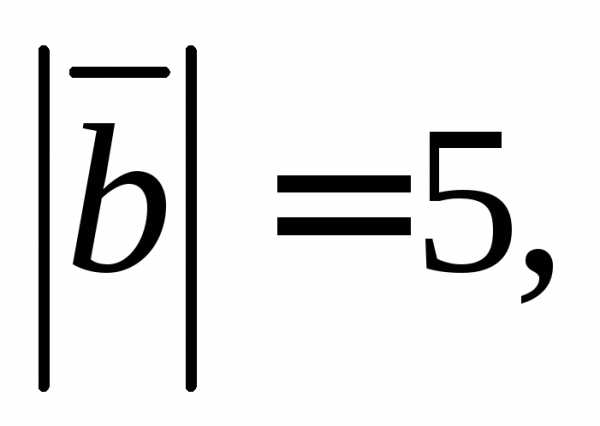
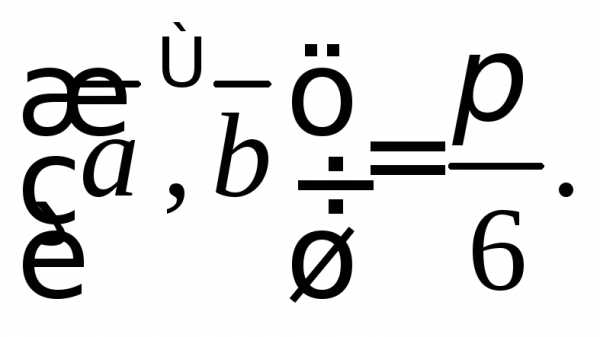 Выразите через векторы
Выразите через векторы и
и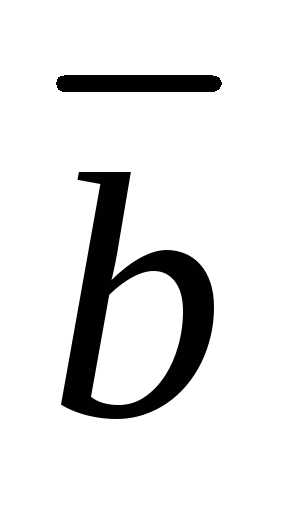 единичный вектор
единичный вектор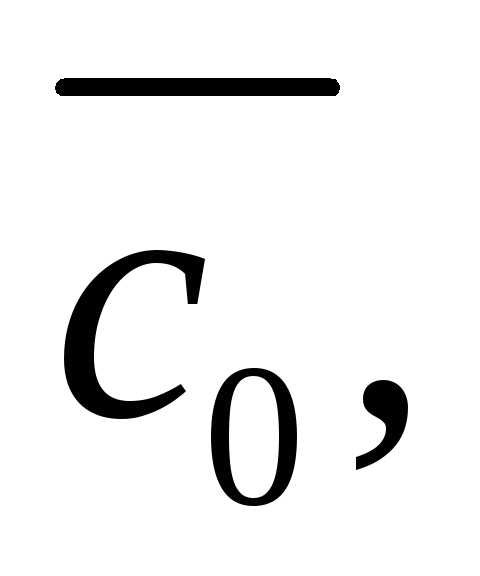 перпендикулярный векторам
перпендикулярный векторам и
и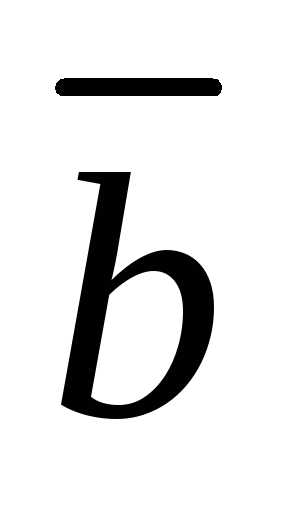 и такой, что:
и такой, что:
1) тройка векторов 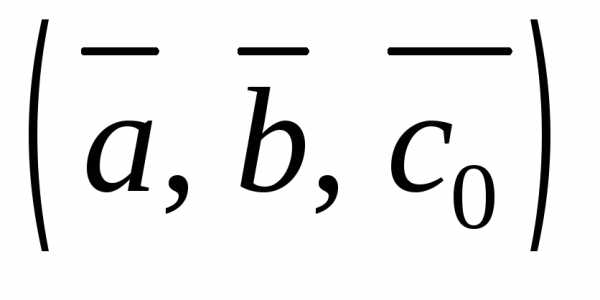 – правая;
– правая;
2) тройка векторов 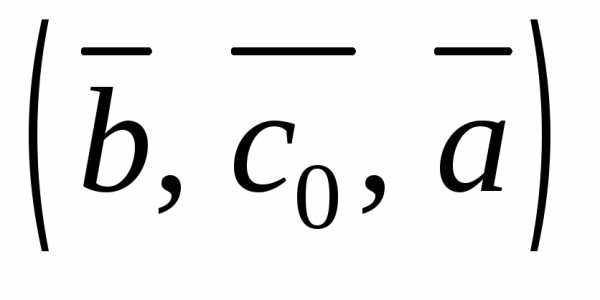 – левая.
– левая.
2.5.Вычислите площадь треугольника с вершинами в точкахA(1, 1, 1),B(2, 3, 4),C(3, 4,2).
2.6.Силаприложена к точкеA(4,
2, –3). Вычислите величину момента
момента этой силы относительно точкиO(2, 4, 0).
этой силы относительно точкиO(2, 4, 0).
III уровень
3.1.Вычислите
длины диагоналей и площадь параллелограмма,
построенного на векторах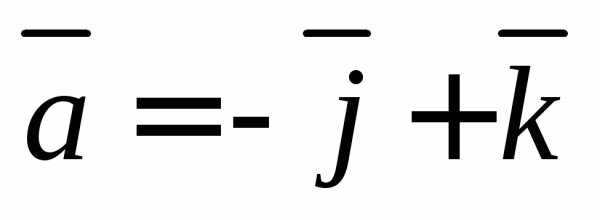 иДокажите, что этот параллелограмм
является прямоугольником.
иДокажите, что этот параллелограмм
является прямоугольником.
3.2.Найдите составляющую вектораперпендикулярную плоскости векторови
3.3.Найдите синус угла между диагоналями параллелограмма, построенного на векторахи
3.4.Сила приложена к точкеB(2,
–3, 4) и перпендикулярна осиOx.
Момент
приложена к точкеB(2,
–3, 4) и перпендикулярна осиOx.
Момент этой силы относительно точкиA(4, 0, –2)
равенНайдите
этой силы относительно точкиA(4, 0, –2)
равенНайдите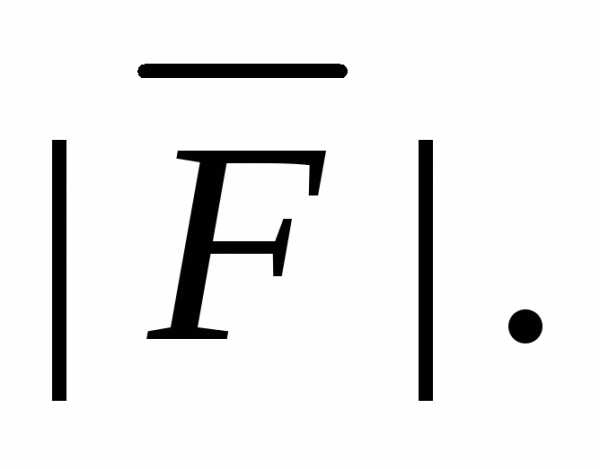
3.5.Докажите,
что для вектора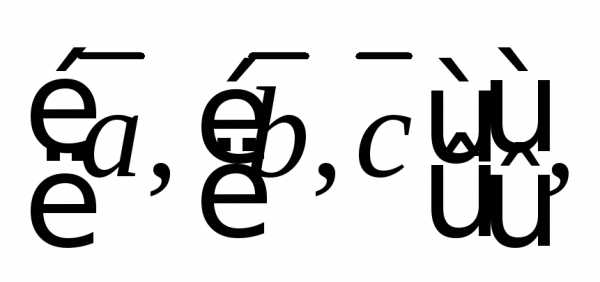 который называется двойным векторным
произведением, справедливо отношение
который называется двойным векторным
произведением, справедливо отношение
3.6.Найдитеесли
У к а з а н и е. Можно воспользоваться формулой из предыдущей задачи 3.5.
14.4. Смешанное произведение векторов
Смешанным
произведением 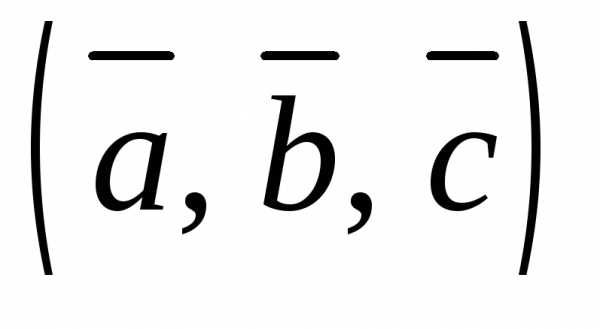 трех векторов
трех векторов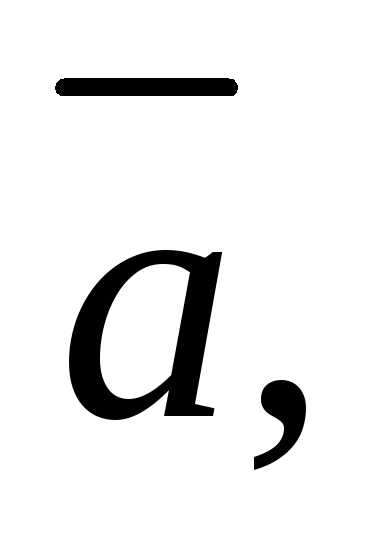
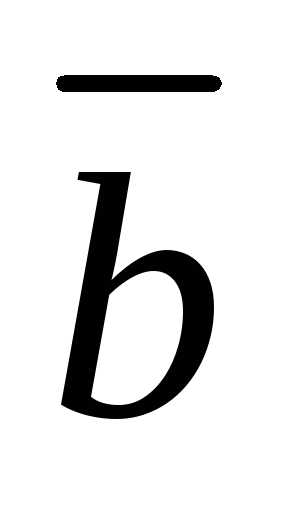 и
и называется число, определяемое
соотношением
называется число, определяемое
соотношением
Если хотя бы один
из векторов 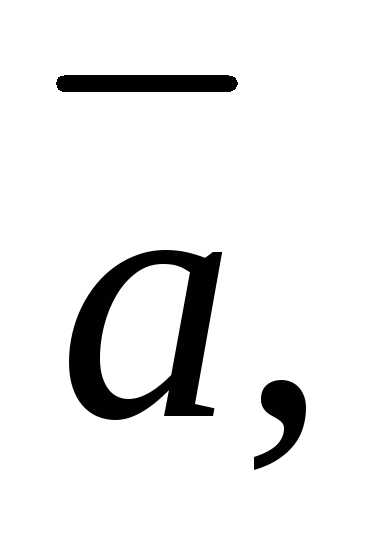
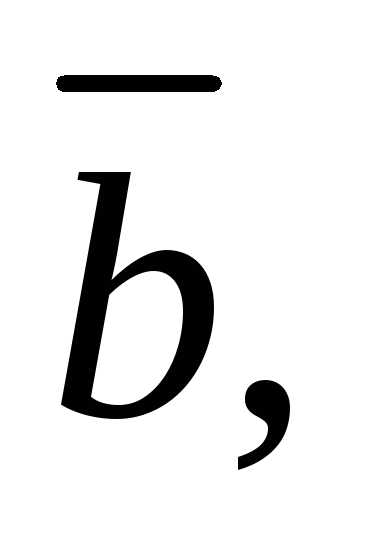
 – нулевой, то их смешанное произведение
равно нулю.
– нулевой, то их смешанное произведение
равно нулю.
Геометрический
смысл смешанного произведения векторов 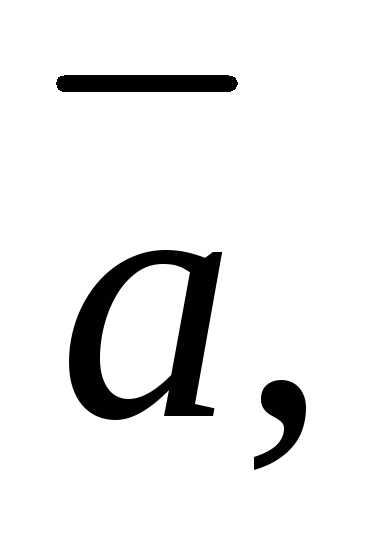
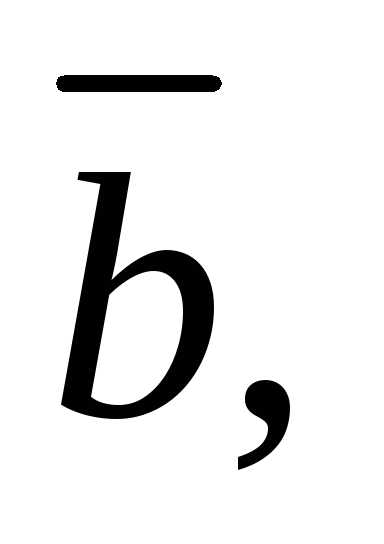
 состоит в том, что его абсолютное значение
равно объемуVпараллелепипеда, построенного на
векторах
состоит в том, что его абсолютное значение
равно объемуVпараллелепипеда, построенного на
векторах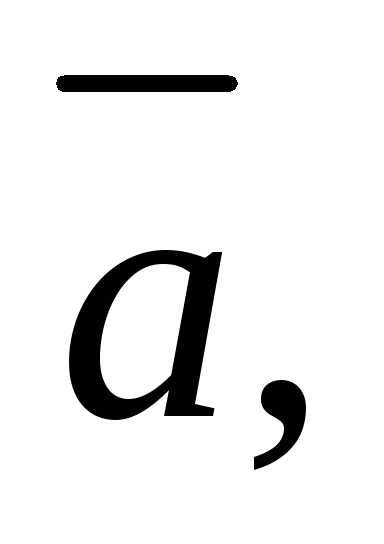
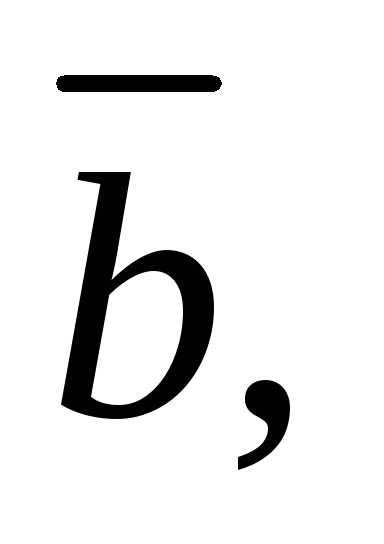
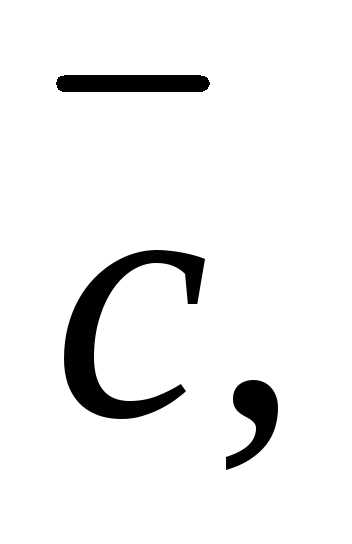 приведенных к общему началу:
приведенных к общему началу:
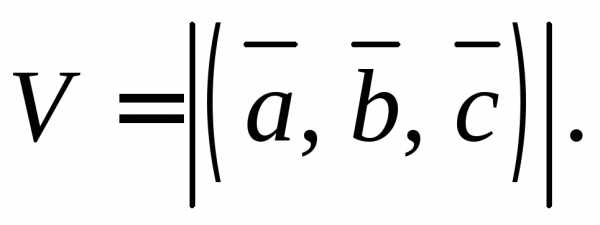
Свойства смешанного произведения
1.
2.
3. , где
4. 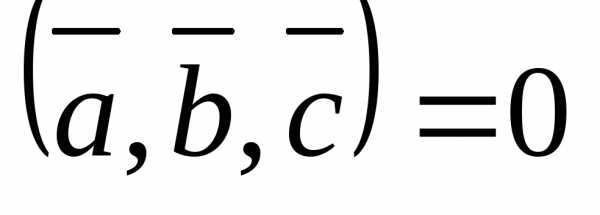 при
при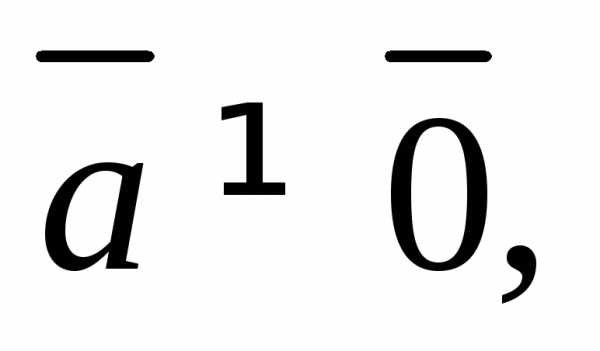
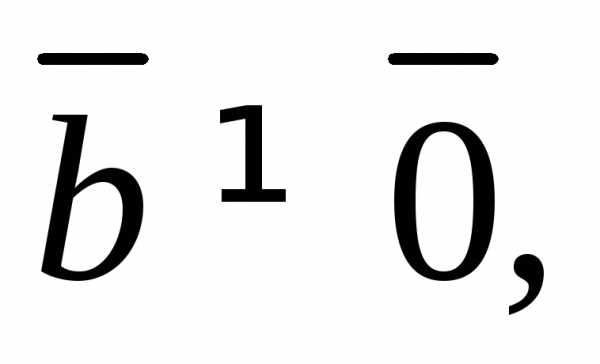
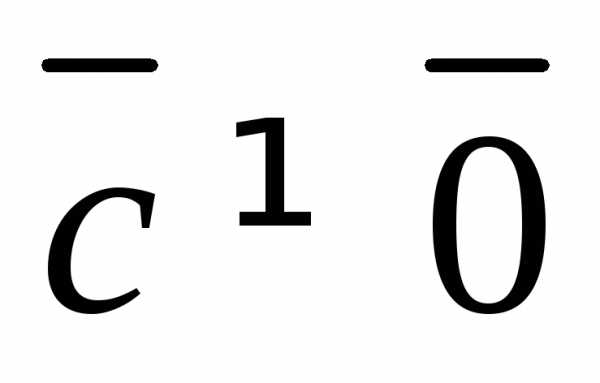 тогда и только тогда, когда
тогда и только тогда, когда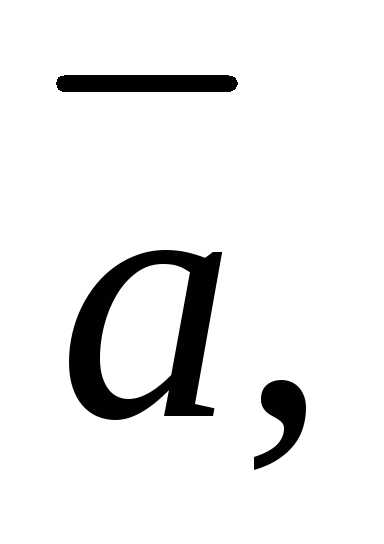
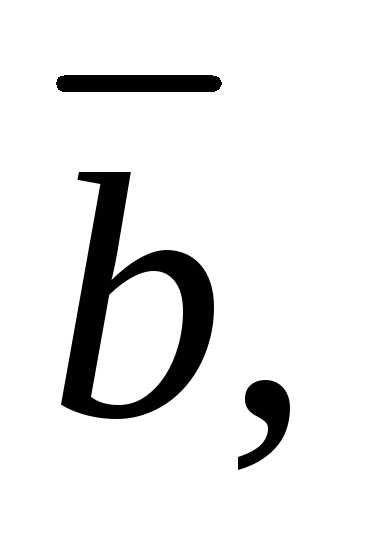
 – компланарные векторы;
– компланарные векторы;
5. векторы 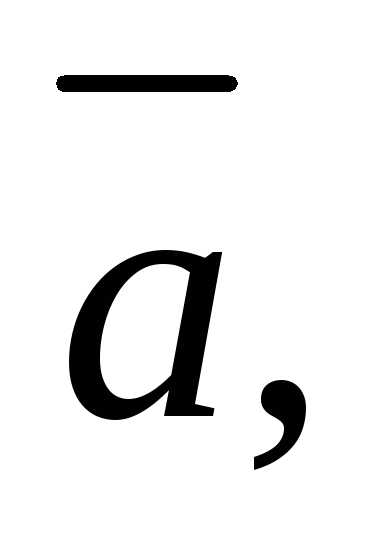
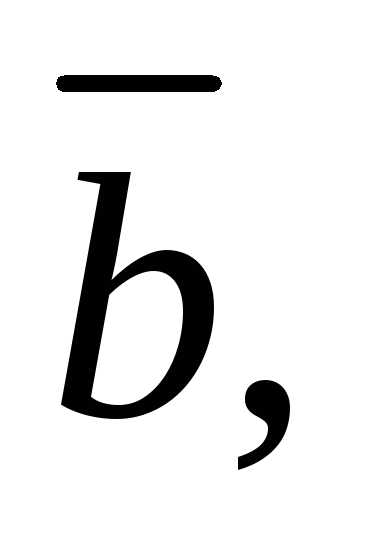
 образуют базис в трехмерном пространстве
при условии
образуют базис в трехмерном пространстве
при условии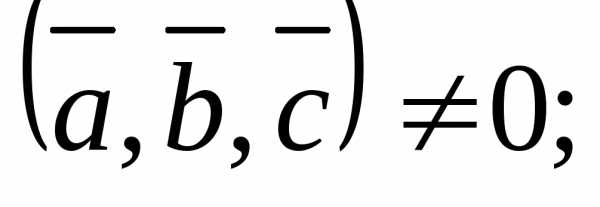
6. если
то векторы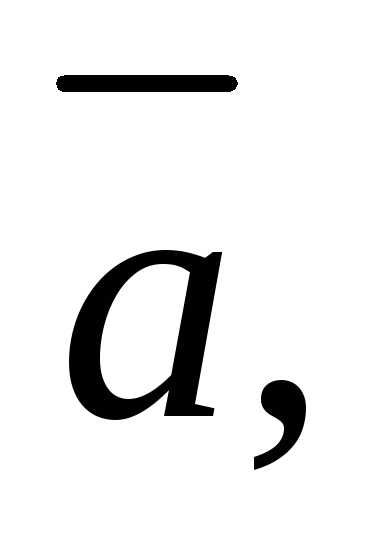
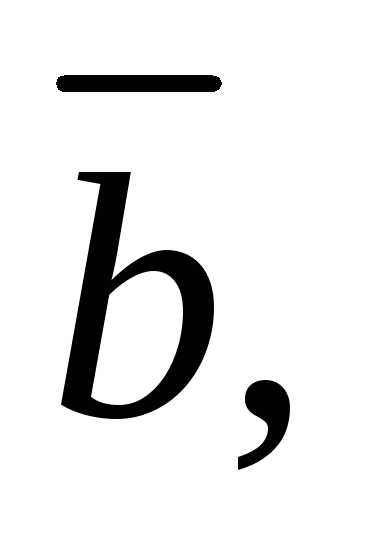
 образуют правую тройку; если– левую.
образуют правую тройку; если– левую.
В
случае, когда векторы 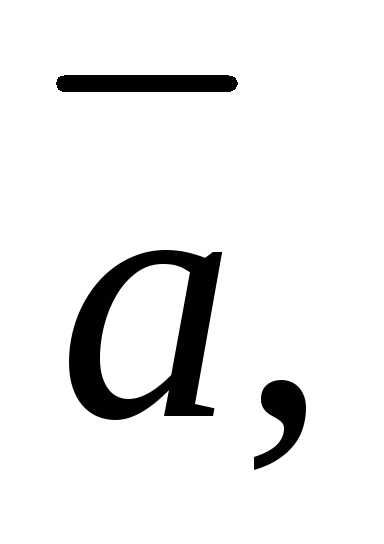
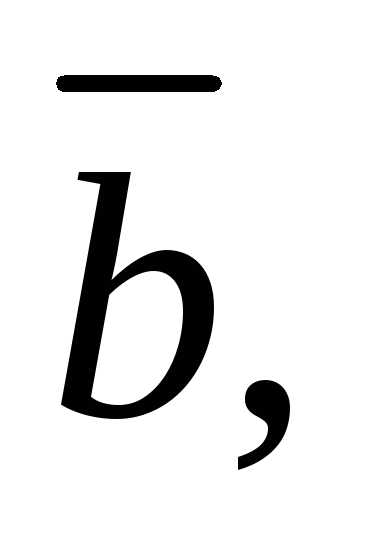
 заданы в ортонормированномбазисе
координатамииих смешанное произведение может быть
найдено по формуле
заданы в ортонормированномбазисе
координатамииих смешанное произведение может быть
найдено по формуле
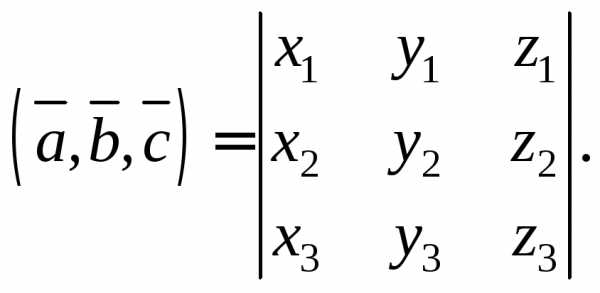 (14.11)
(14.11)
Пример
1. Векторы 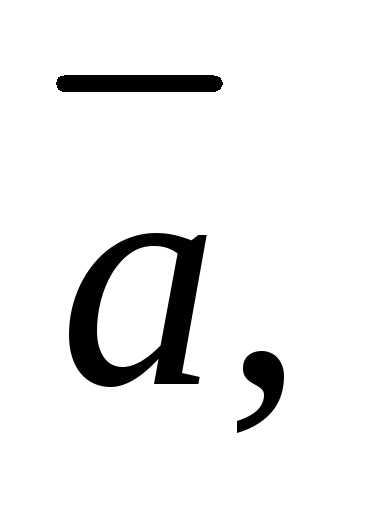
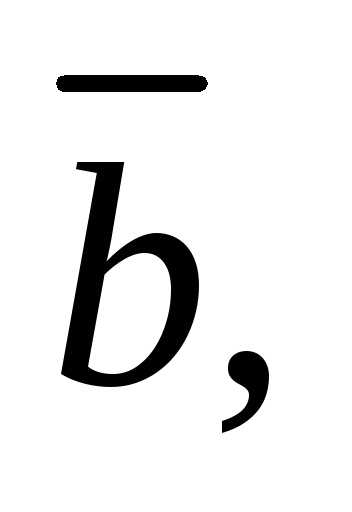
 образуют правую тройку, взаимно
перпендикулярны и
образуют правую тройку, взаимно
перпендикулярны и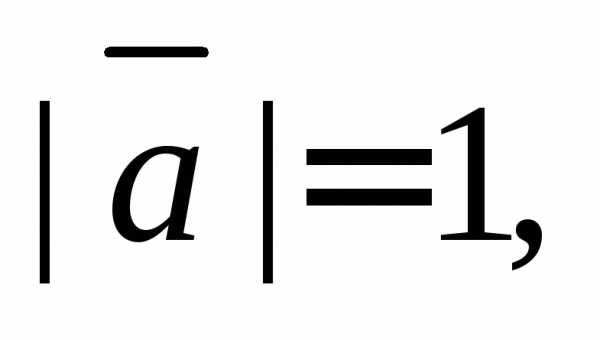
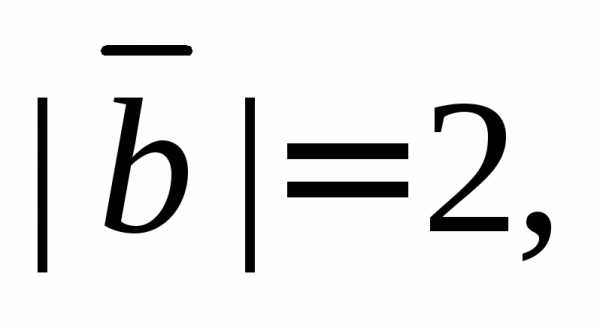
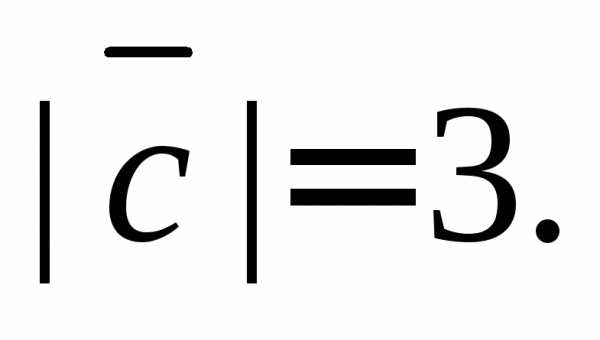 Вычислить их смешанное произведение.
Вычислить их смешанное произведение.
Решение. По определению
.
Вектор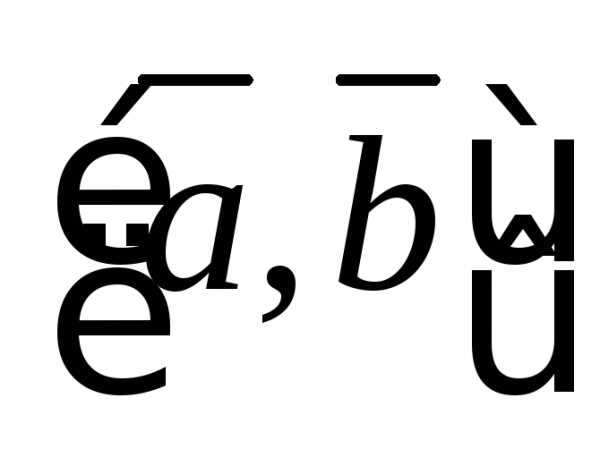 образует с
образует с и
и правую тройку, причем
правую тройку, причем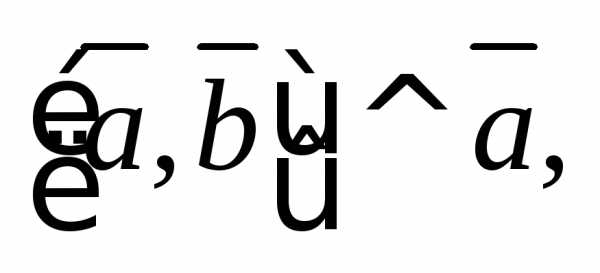
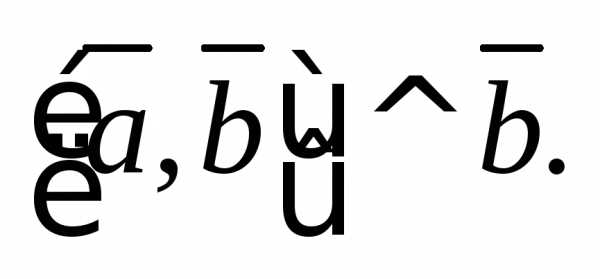 Значит,
Значит,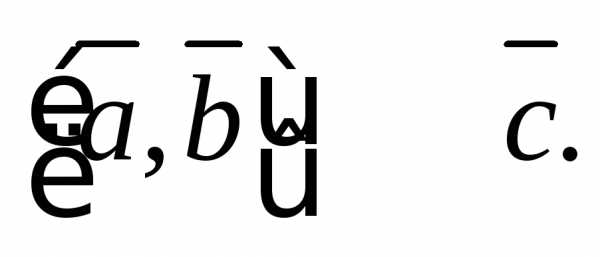 Кроме того,Тогда
Кроме того,Тогда
Пример
2. Для векторов
инайти объем параллелепипеда, построенного
на векторах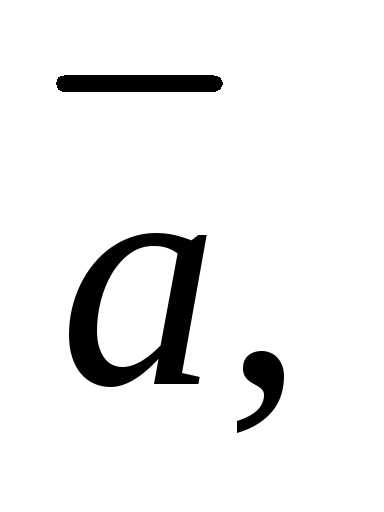
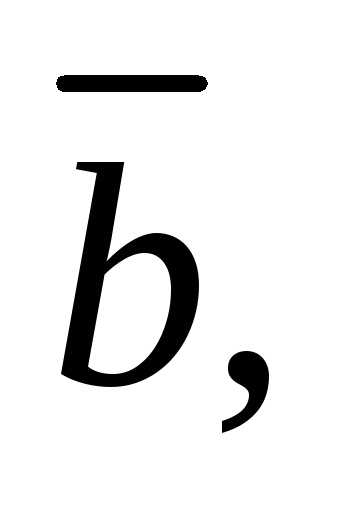
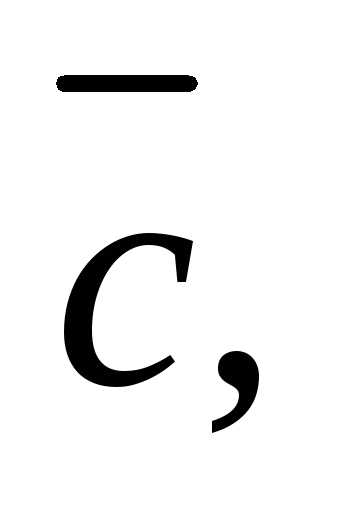 приведенных к общему началу, и определить
ориентацию этой тройки векторов.
приведенных к общему началу, и определить
ориентацию этой тройки векторов.
Решение. Используем формулу (4.11) для вычисления смешанного произведения в координатной форме:
Поскольку
получили отрицательное значение, то
тройка векторов 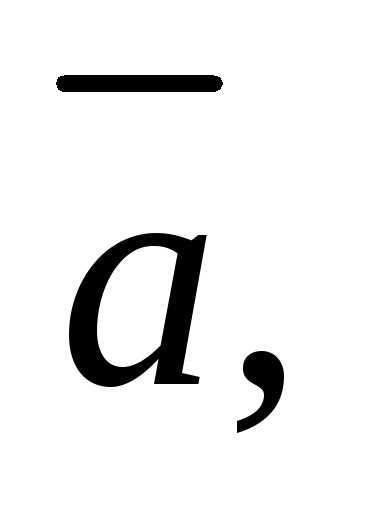
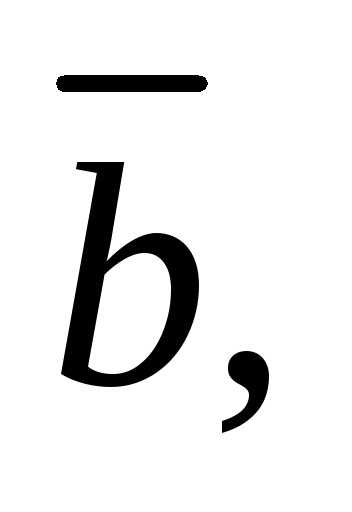
 является левой, а объем параллелепипеда
равен модулю смешанного произведения,
т. е.
является левой, а объем параллелепипеда
равен модулю смешанного произведения,
т. е.
Пример 3. Доказать, что точки A(1, 2, –1), B(0, 1, 5), C(–1, 2, 1) и D(2, 1, 3) лежат в одной плоскости.
Решение. Рассмотрим три вектора:
Вычисляем их смешанное произведение:
Поскольку оно равно нулю, то это значит, что векторы – компланарны. Они лежат в одной плоскости, так как имеют общее начало. Таким образом, точкиA, B, C и D лежат в одной плоскости.
Пример 4. Вычислить объем тетраэдра OABC, если
Решение. Используем формулу
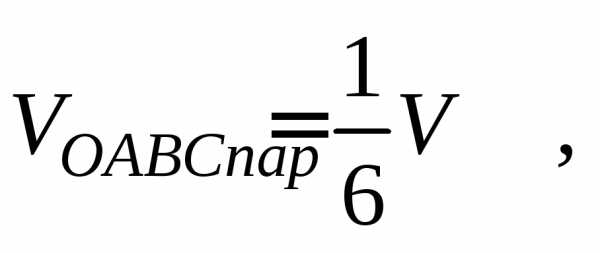
где  – объем
параллелепипеда, построенного на
векторах
– объем
параллелепипеда, построенного на
векторах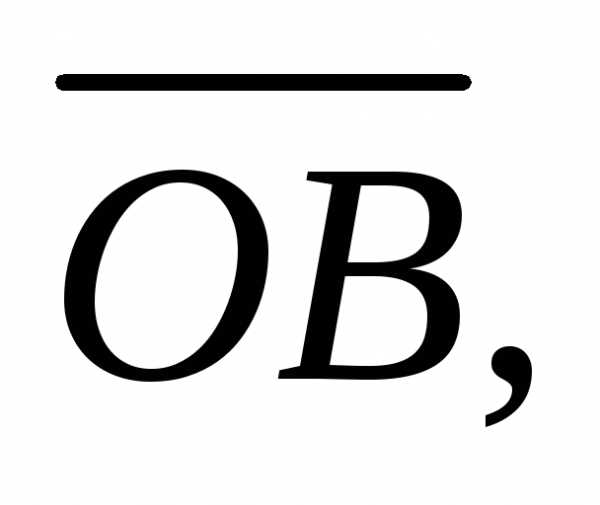
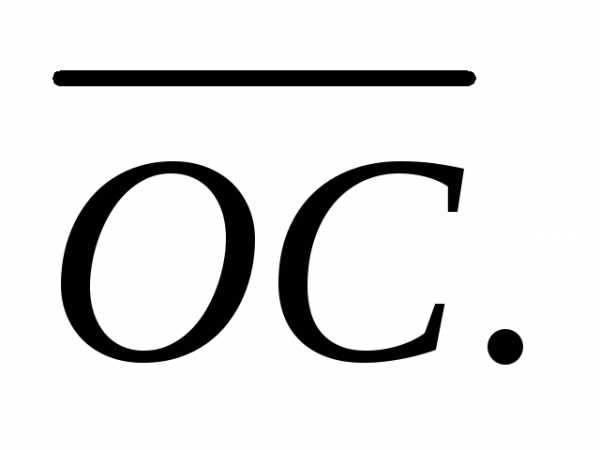 Объем параллелепипеда вычисляется
через смешанное произведение
Объем параллелепипеда вычисляется
через смешанное произведение
Поскольку
то
Пример
5. Вершины треугольника расположены в
точках A(1, 1, 1), B(2, 3, 2)
и C(4,
2, 5). Найти расстояние от точки D(5,
3, 6) до плоскости 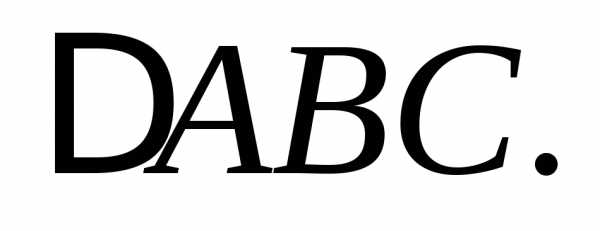
Решение. Убедимся, что точка D не лежит в одной плоскости с точками A, B и C, для чего найдем смешанное произведение векторов . Если оно будет не нулевым, то тем самым будет доказано, что векторыне являются компланарными, а значит, точкиA, B, C, D не лежат в одной плоскости.
Так как то смешанное произведение равно
Значит,
Поскольку
расстояние h от точки D до плоскости  численно равно высоте параллелепипеда,
опущенной из вершиныD на основание, в котором лежит
численно равно высоте параллелепипеда,
опущенной из вершиныD на основание, в котором лежит 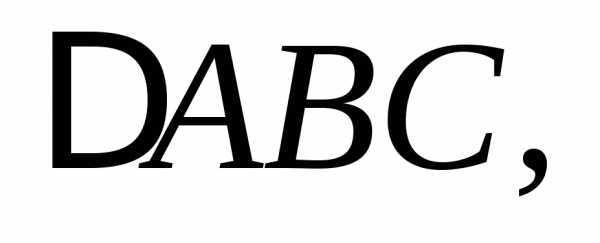 то из формулынаходим
то из формулынаходим
Найдем 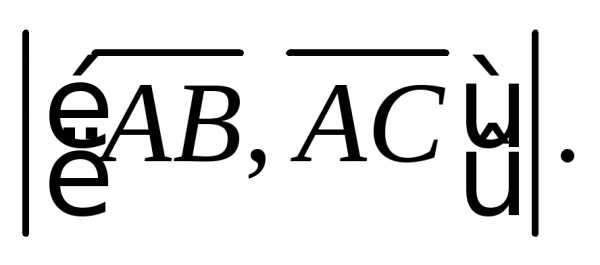 Поскольку
Поскольку
то
Таким
образом, 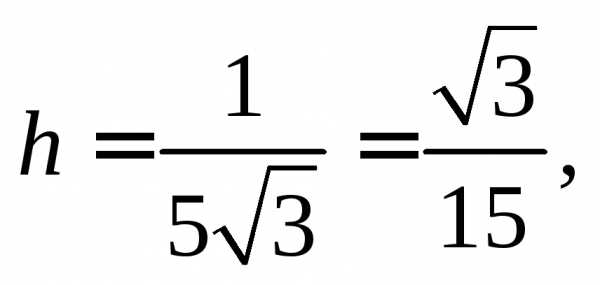 т. е. искомое расстояние равно
т. е. искомое расстояние равно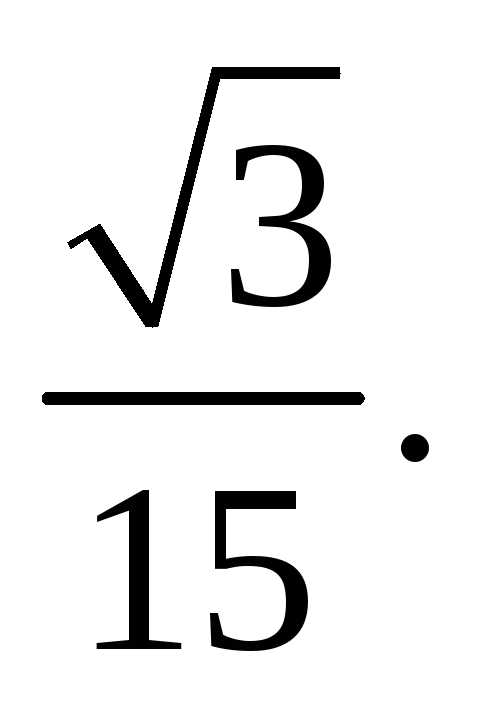
Пример
6. Доказать,
что векторы 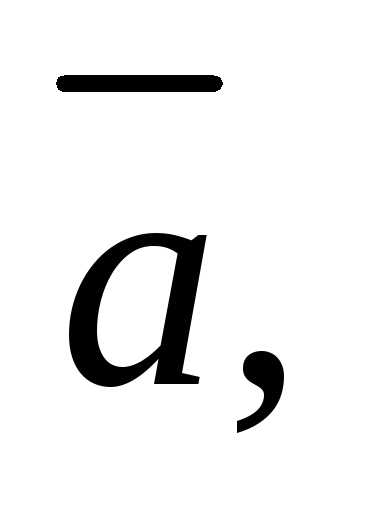
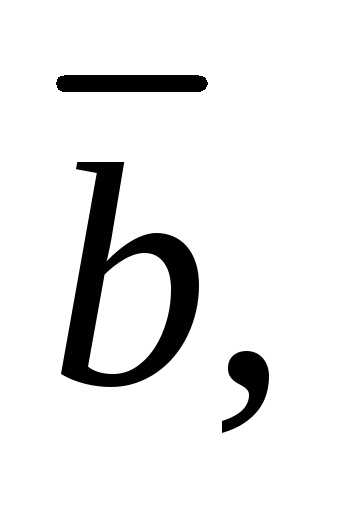
 компланарны, если.
компланарны, если.
Решение. Умножим скалярно данное равенство на
вектор 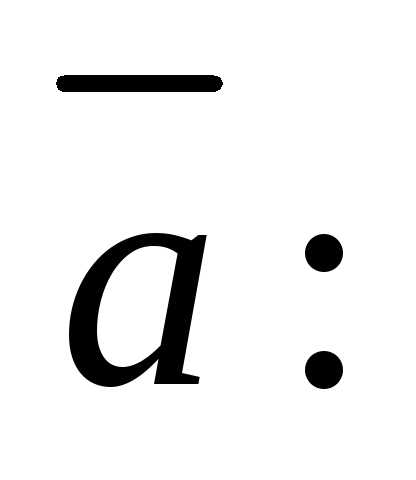
Так
как
то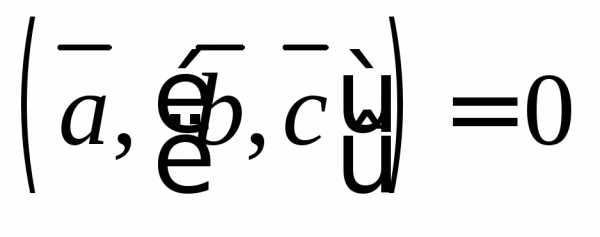 или векторы
или векторы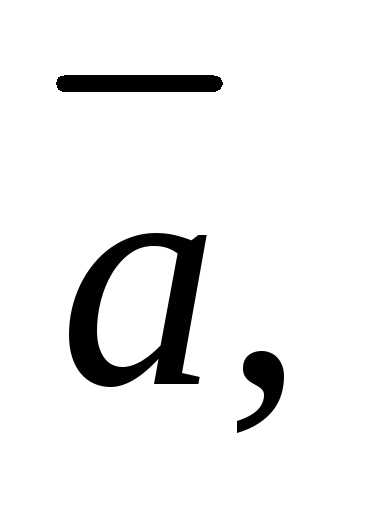
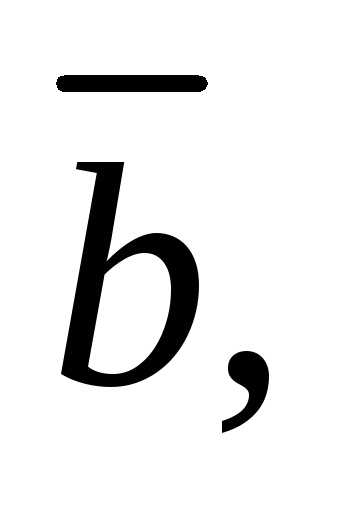
 компланарны.
компланарны.
Доказанное
можно обобщить на случай, когда задано
равенство
где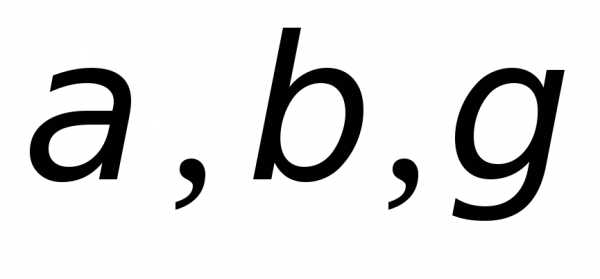 – числа, среди которых, по крайней мере,
есть одно ненулевое.
– числа, среди которых, по крайней мере,
есть одно ненулевое.
Задания
studfiles.net
§ 5. Смешаноё произведение трёх векторов
Литература: (1, с. 78-80; 2, с. 69-71; 3, с. 239-241; 4, с. 40-43)
Определение и свойства смешанного произведения трёх векторов.
Смешанным
произведением трёх векторов 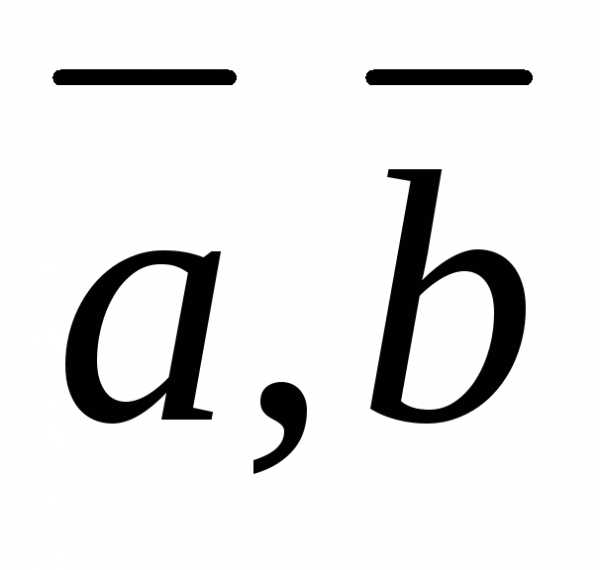 и
и называется их векторно-скалярное
произведение:
называется их векторно-скалярное
произведение:
(24)
Свойства смешанного произведения:
Смешанное произведение не изменяется, если переставлять перемножаемые векторы в круговом порядке: .
При перестановке любых двух векторов смешанное произведение изменяет только знак.
Если векторы заданы своими координатами ,,, то
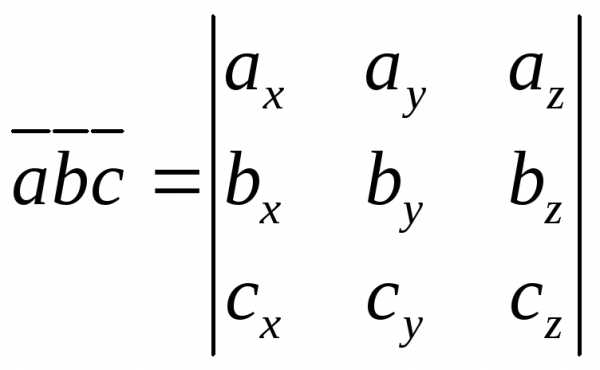 (25)
(25)
Если 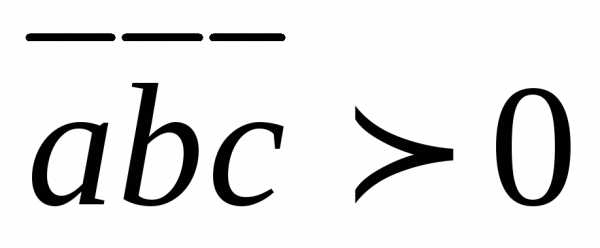 ,
то тройка векторов правая; если
,
то тройка векторов правая; если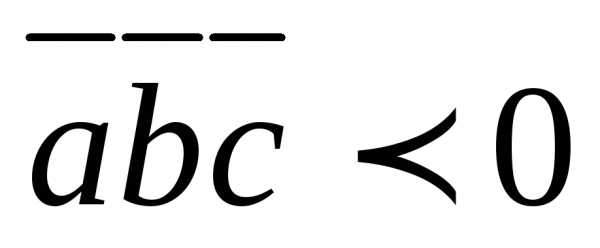 ,
то – левая.
,
то – левая.
Необходимым и достаточным условием компланарности трёх векторов служит условие:
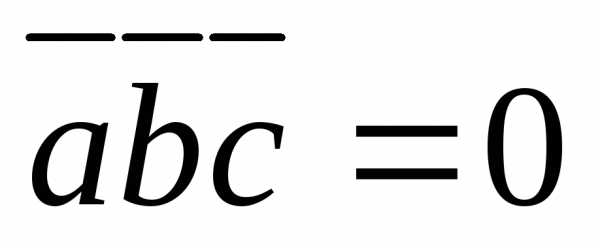 (26)
(26)
Объект  параллелепипеда, построенного на
векторах
параллелепипеда, построенного на
векторах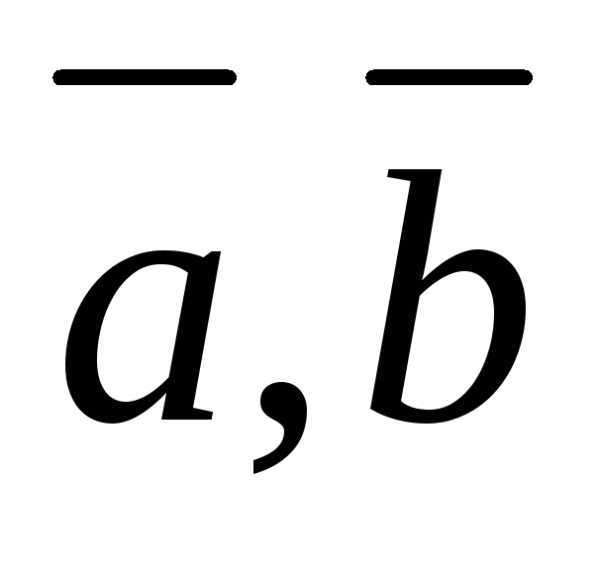 и
и и объём
и объём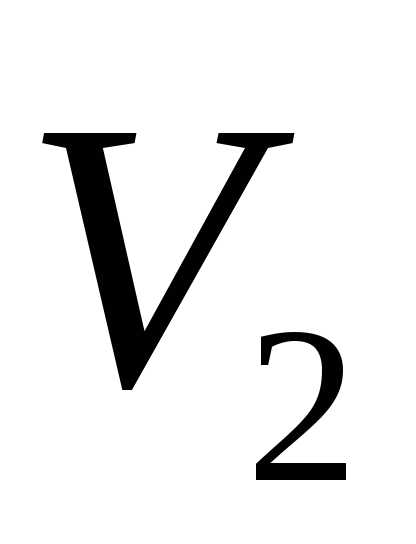 образованный ими треугольной пирамиды
находится по формулам:
образованный ими треугольной пирамиды
находится по формулам:
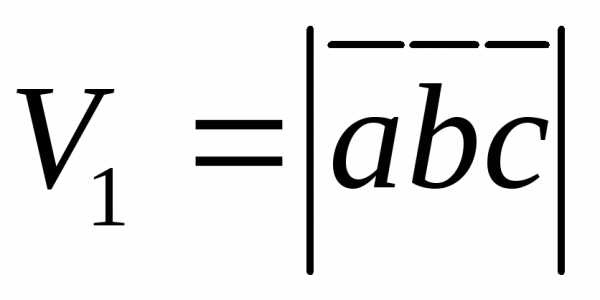 (27)
(27)
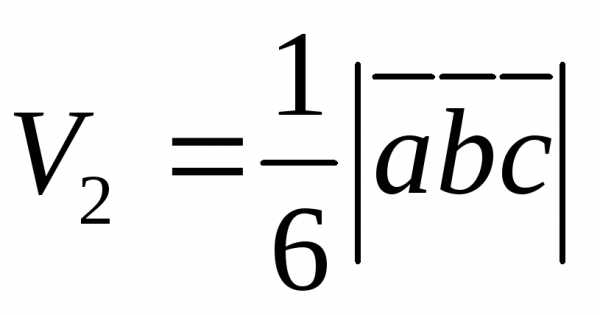 (28)
(28)
Эти формулы выражают геометрический смысл смешанного произведения.
Примеры
5.2.1. Доказать, что векторы ,икомпланарны.
Решение. Вычислим смешанное произведение векторов по формуле (25)
Так как 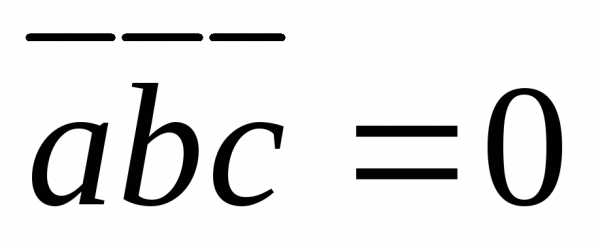 ,
то векторы
,
то векторы 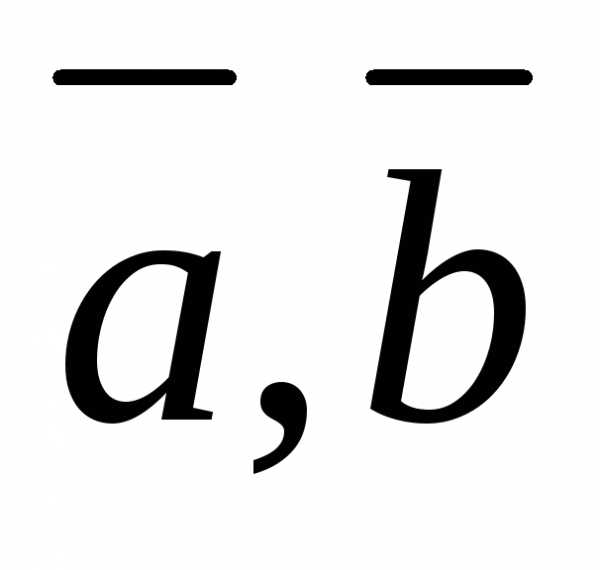 и
и — компланарны.
— компланарны.
5.2.2. Вычислить
объём тетраэдра, вершины которого
находятся в точках 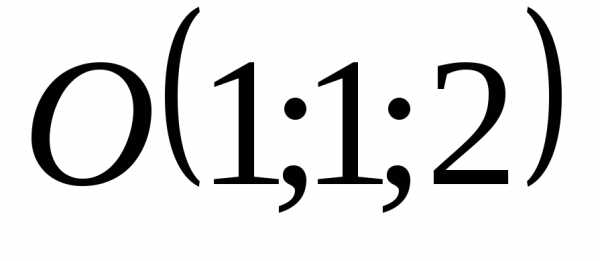 ,
,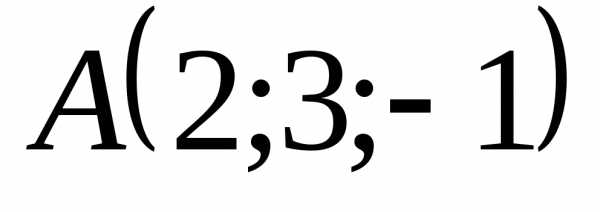 ,
,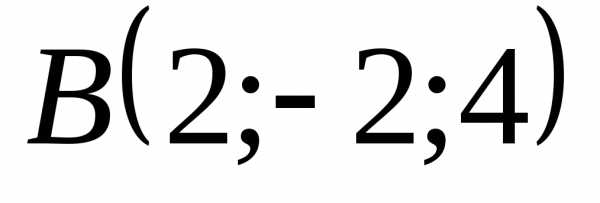 ,
,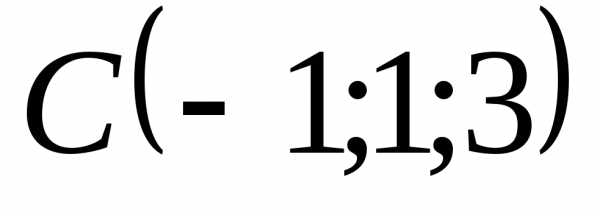
Решение. Введём
векторы
,,,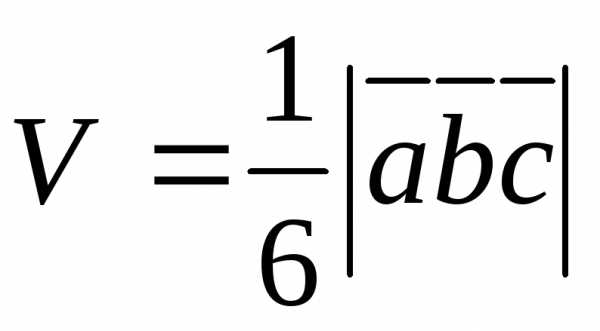 .
.
Найдём
Следовательно, 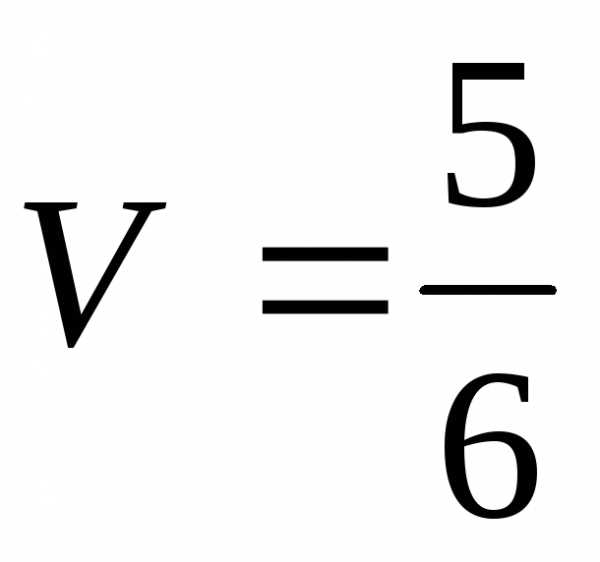 (куб.ед.)
(куб.ед.)
5.2.3. Вычислить 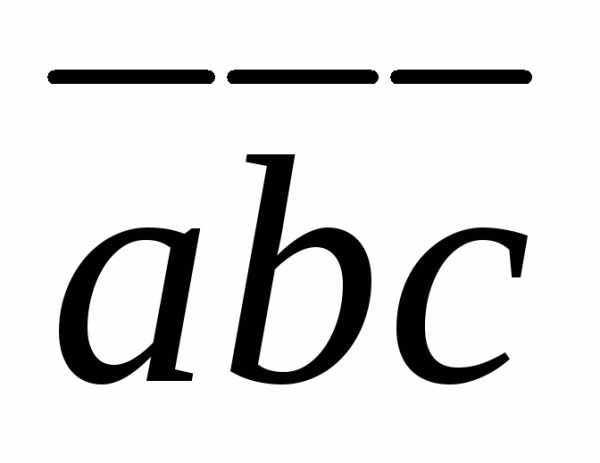 ,
зная, что
,
зная, что 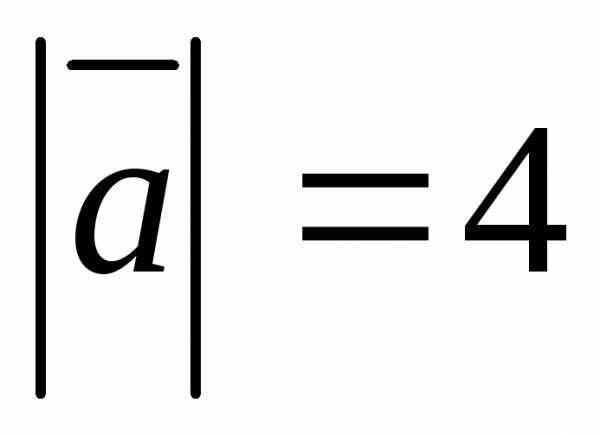 ,
,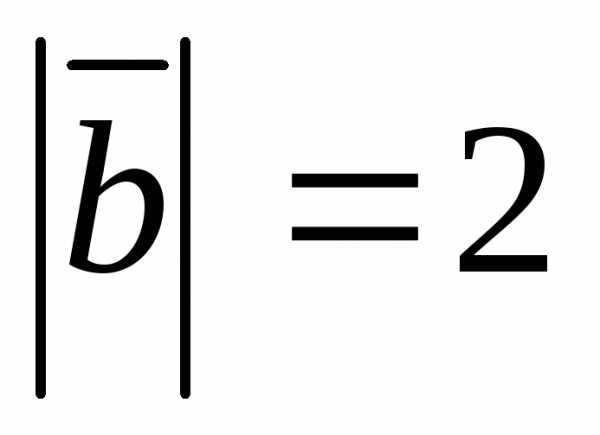 ,
,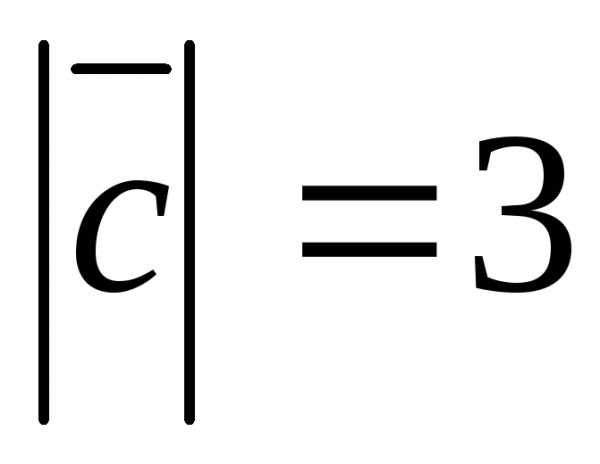 .Векторы
.Векторы 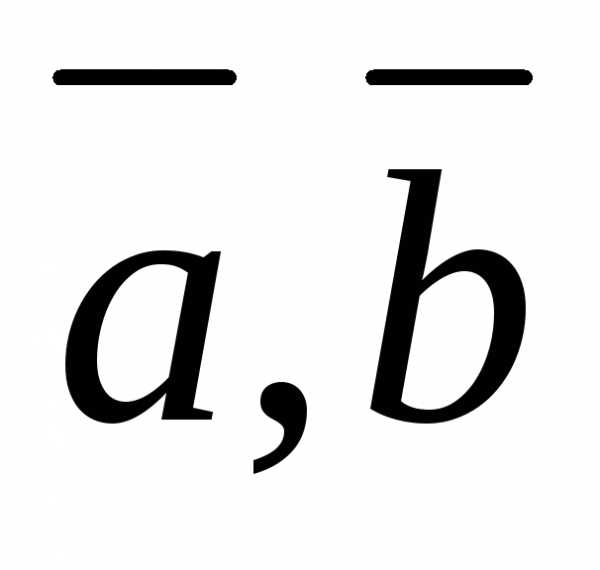 и
и образуют правую тройку и взаимно
перпендикулярны.
образуют правую тройку и взаимно
перпендикулярны.
Решение.
,
где — угол между вектором
— угол между вектором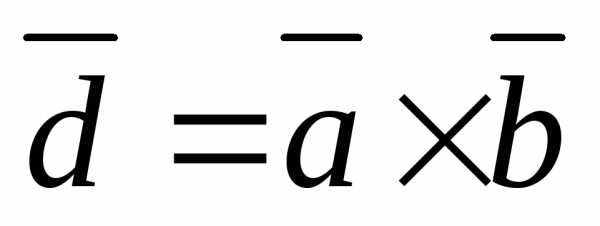 и вектором
и вектором .
Векторы
.
Векторы и
и коллинеарны, поэтому.
Так как по условию векторы
коллинеарны, поэтому.
Так как по условию векторы ,
,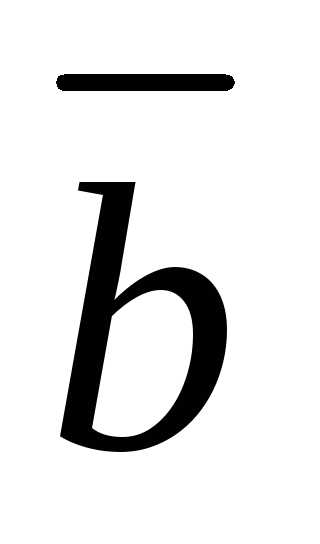 и
и образуют правую тройку, то
образуют правую тройку, то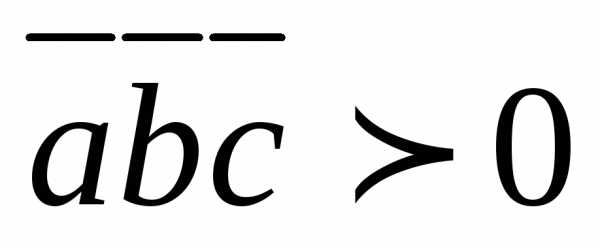 .
Следовательно,.
Найдём.
Тогда.
.
Следовательно,.
Найдём.
Тогда.
Вопросы для самопроверки
Что называется смешанным произведением векторов? Как оно обозначается?
Каковы свойства смешанного произведения?
Как считается смешанное произведение векторов, заданных своими координатами?
Каково условие компланарности векторов?
Каков геометрический смысл смешанного произведения?
Примеры для самостоятельного решения
5.4.1. Найти смешенное произведение векторов ,,
5.4.2. Найти смешанное
произведение векторов 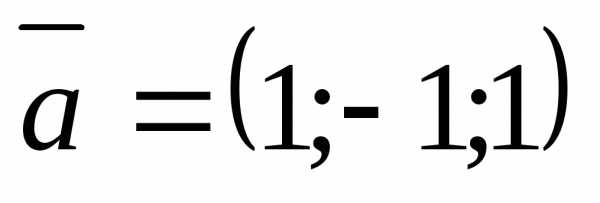 ,
,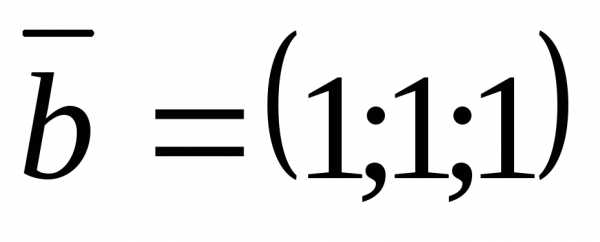 ,
,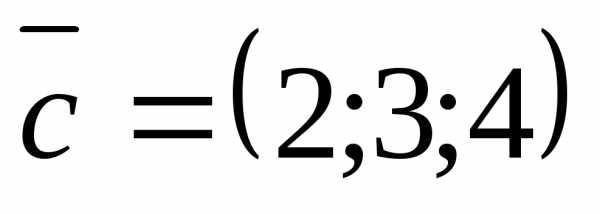
5.4.3. Установить, компланарны ли векторы:
а) ,,
б) 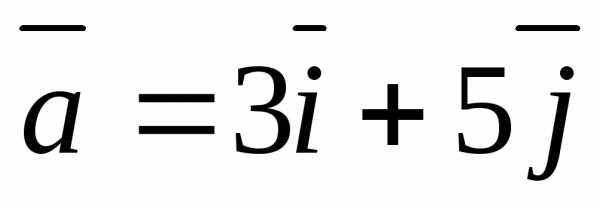 ,,
,,
в) ,,
5.4.4. Показать, что
точки 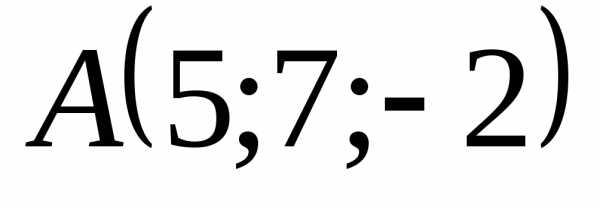 ,
,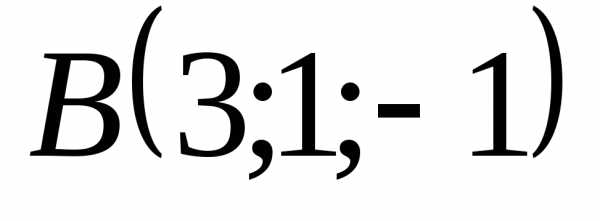 ,
,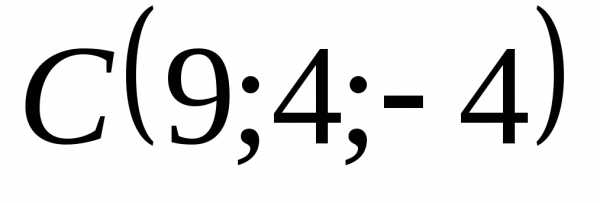 и
и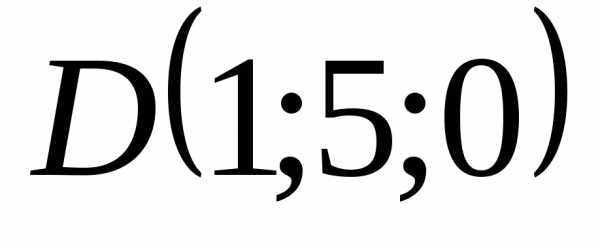 лежат в одной плоскости
лежат в одной плоскости
5.4.5. Определить,
какой является тройка векторов  ,
,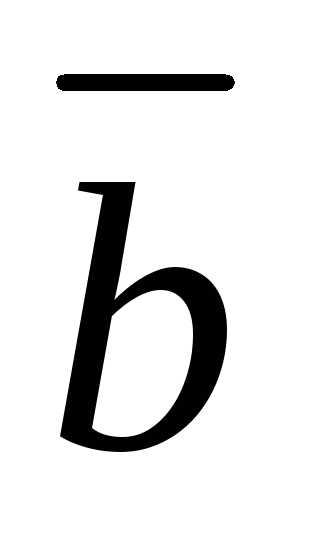 ,
, (правой или левой), если:
(правой или левой), если:
а) 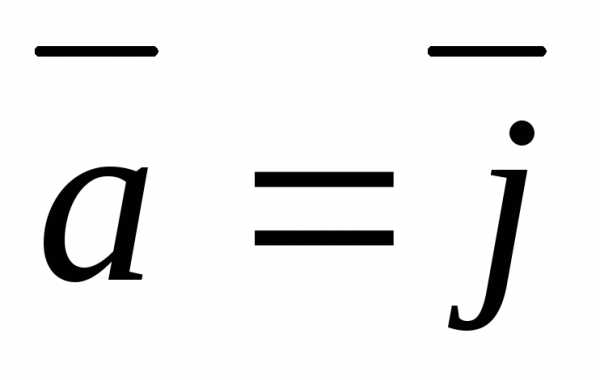 ,
,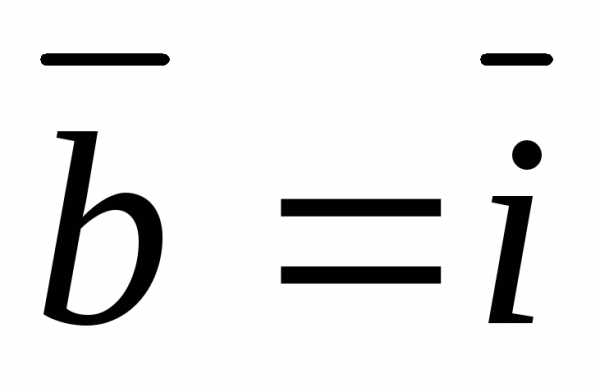 ,
,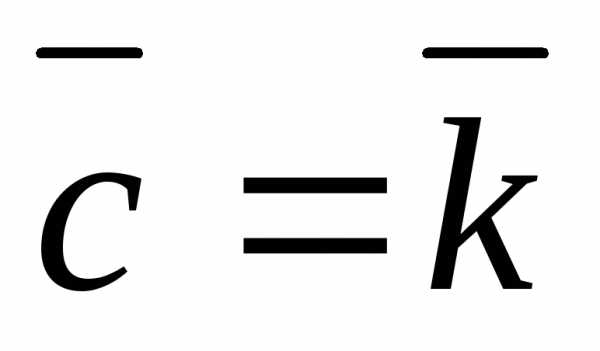 ;
;
б) 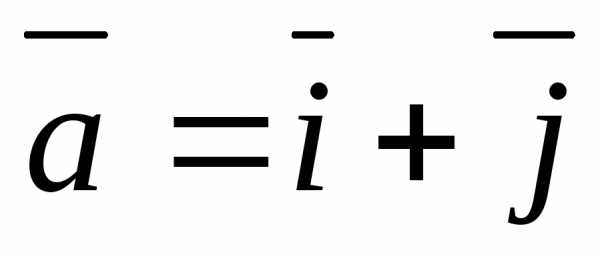 ,
,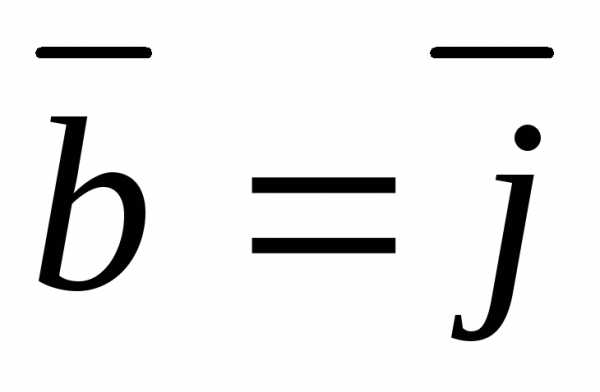 ,
,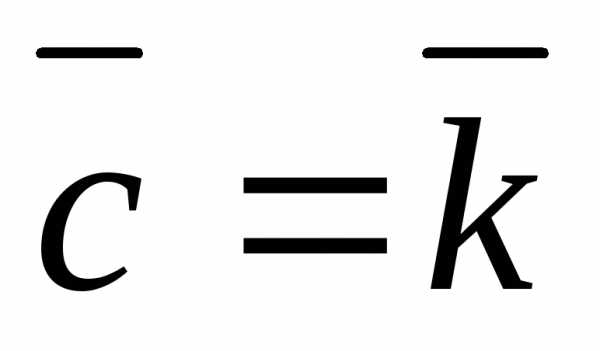 ;
;
в) 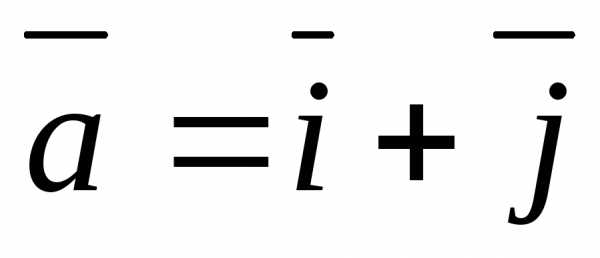 ,
,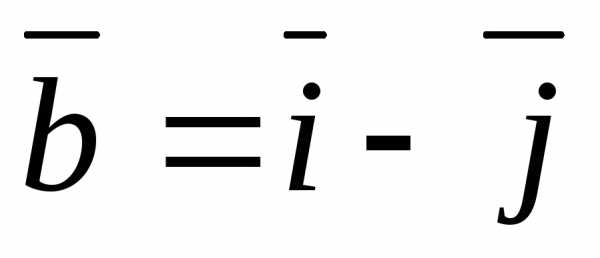 ,
,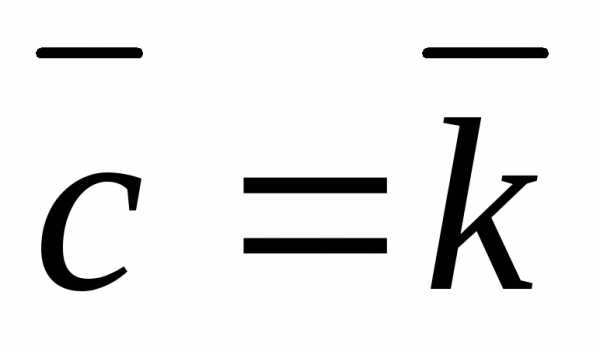 .
.
5.4.6. Векторы  ,
,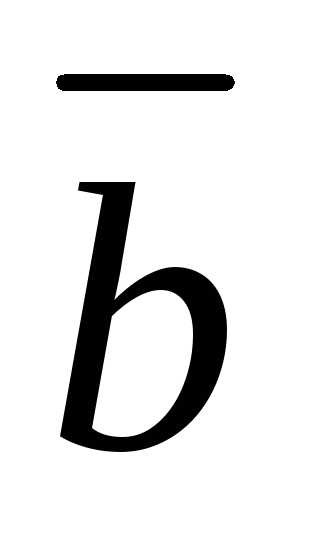 ,
, ,
образующие правую тройку векторов,
взаимно перпендикулярны. Зная, что
,
образующие правую тройку векторов,
взаимно перпендикулярны. Зная, что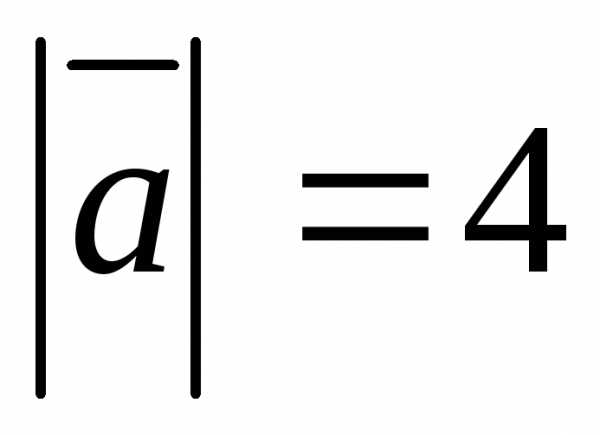 ,
,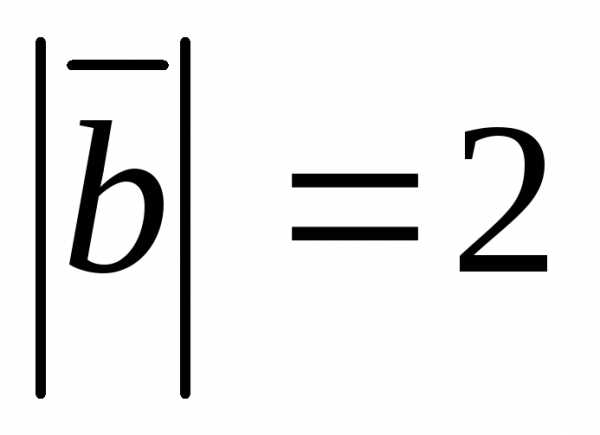 ,
,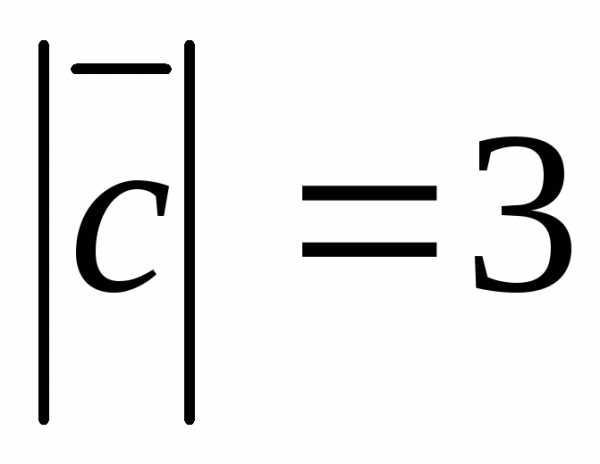 ,
вычислить
,
вычислить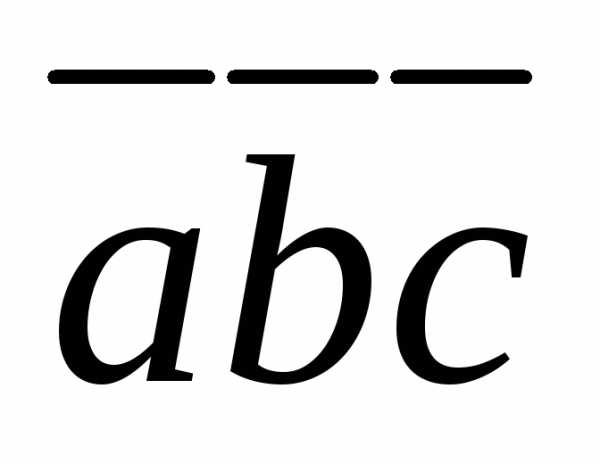 .
.
5.4.7. Вектор  перпендикулярен к векторам
перпендикулярен к векторам и
и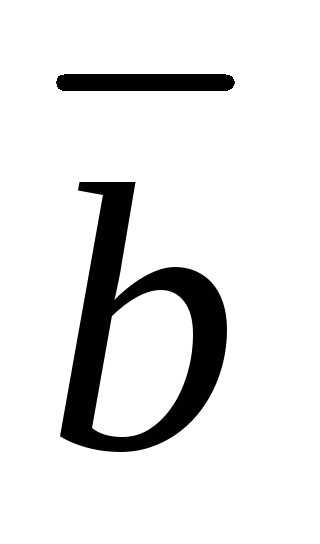 ,
угол между векторами
,
угол между векторами и
и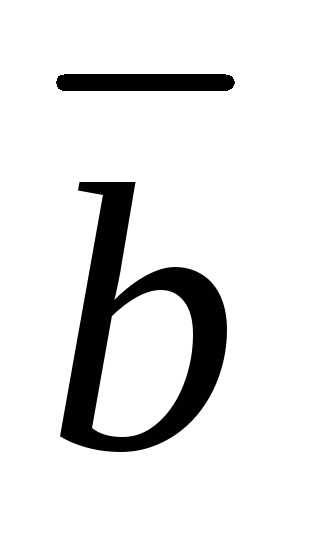 равен
равен .
Зная, что
.
Зная, что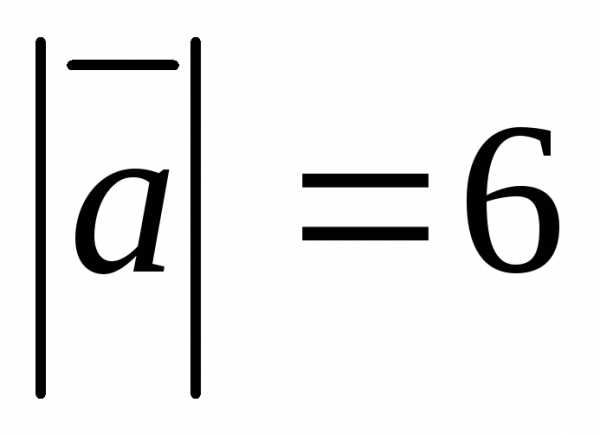 ,
,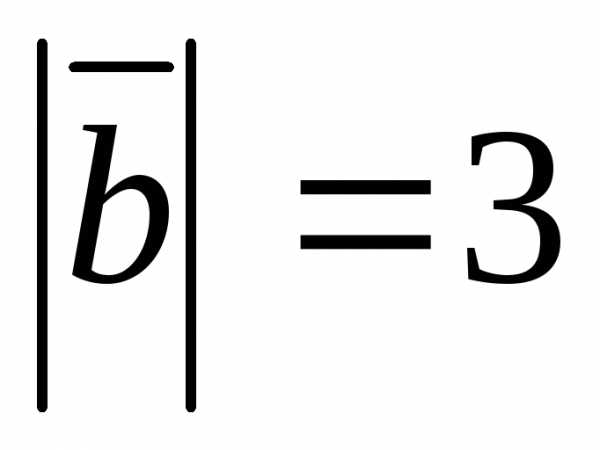 ,
,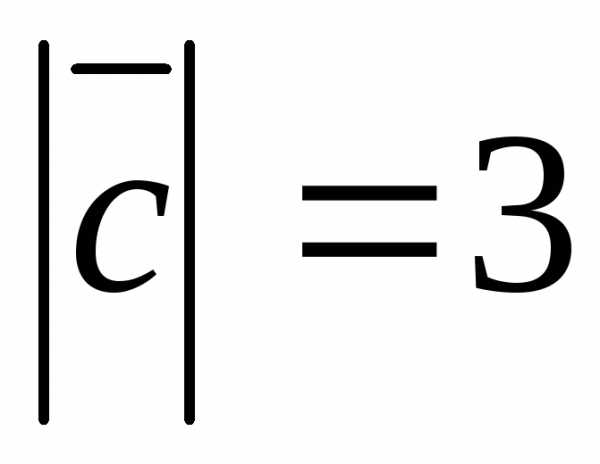 ,
вычислить
,
вычислить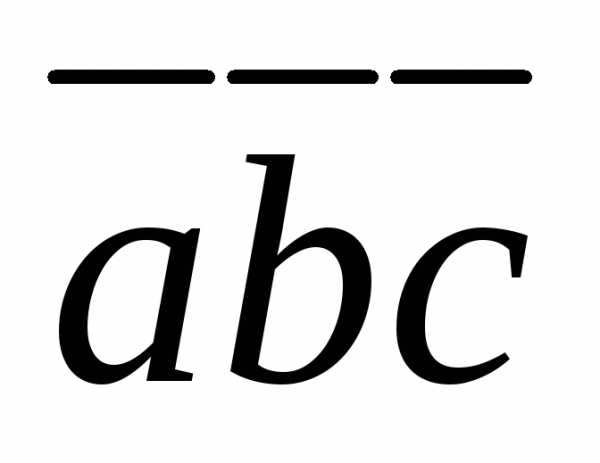 .
.
5.4.8. Найти объём
параллелепипеда, построенного на
векторах
,,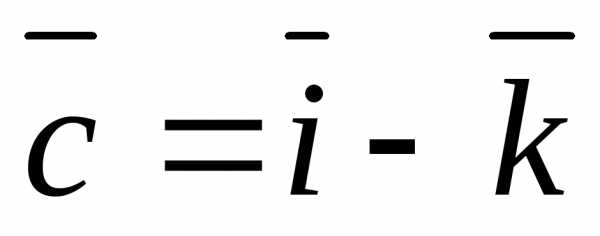 .
.
5.4.9. Вычислить
объём тетраэдра, вершины которого
находятся в точках 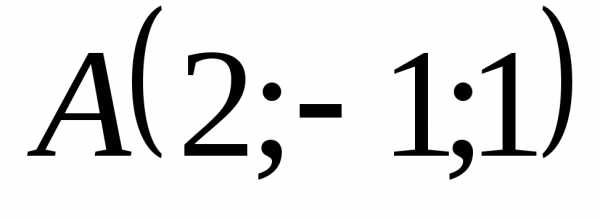 ,
, ,
, и
и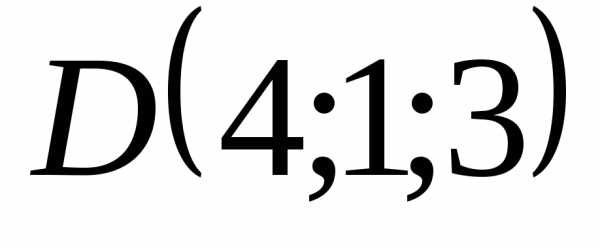
5.4.10. Вычислить
объём треугольной пирамиды с вершинами 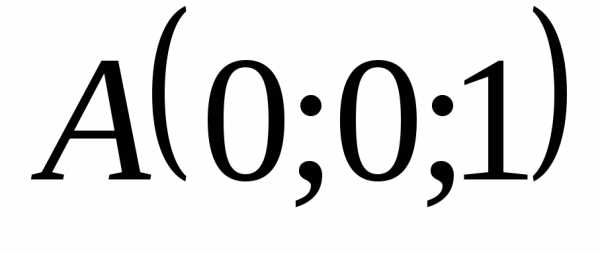 ,
,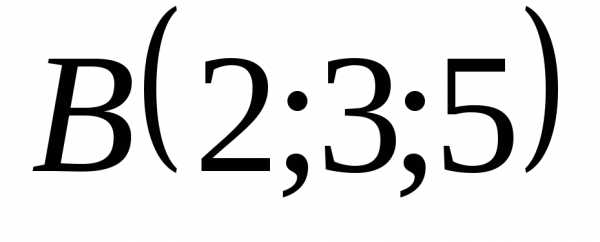 ,
,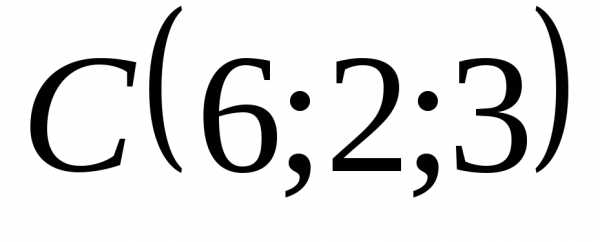 и
и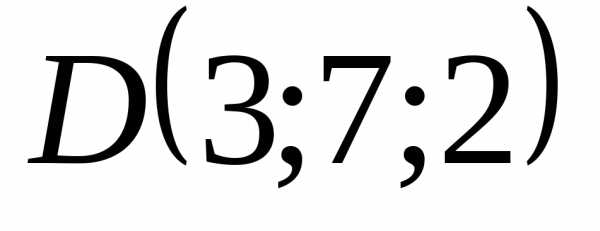 .
.
5.4.11. Даны вершины
тетраэдра 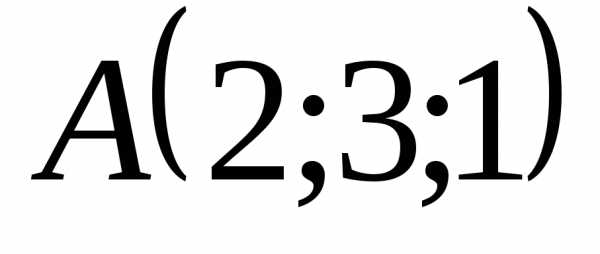 ,
,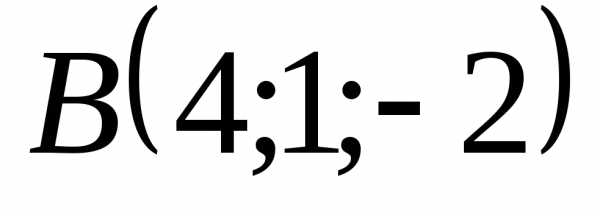 ,
,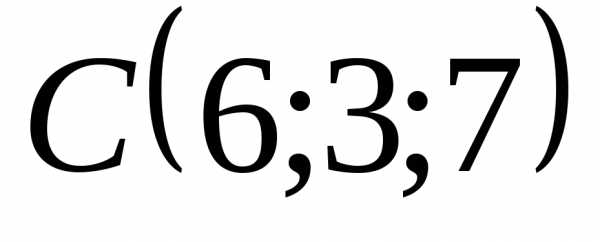 ,.
Найти длину его высоты, опущенной из
вершины
,.
Найти длину его высоты, опущенной из
вершины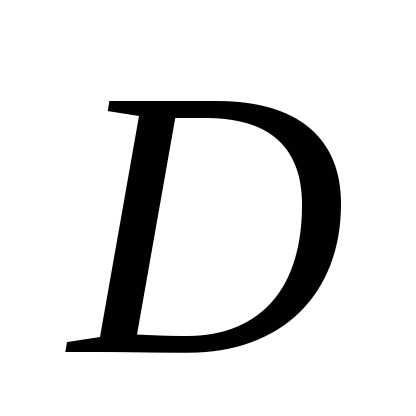 .
.
Ответы к примерам
5.4.1. 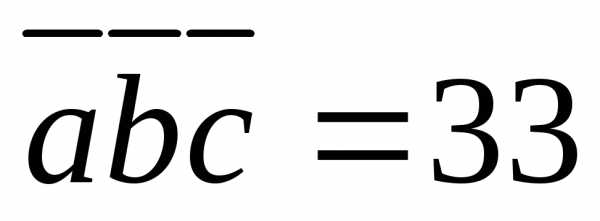 5.4.2.
5.4.2.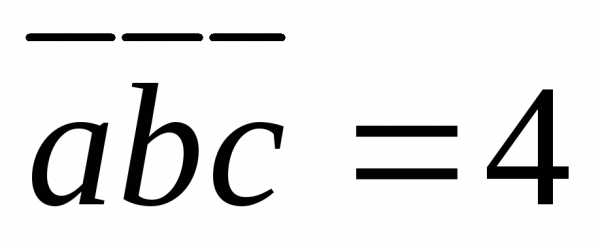
5.4.3. а) нет; б) да; в) да. 5.4.5. а) левая; б) правая; в) левая
5.4.6. 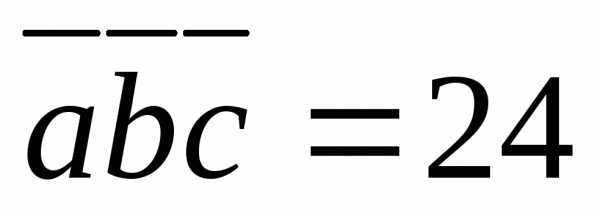 5.4.7.
5.4.7.
5.4.8. 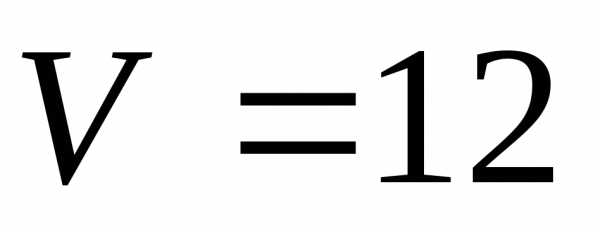 5.4.9.
5.4.9.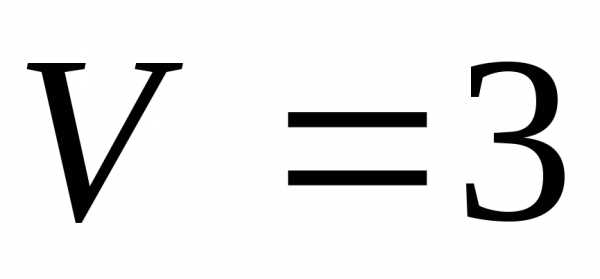
5.4.10. 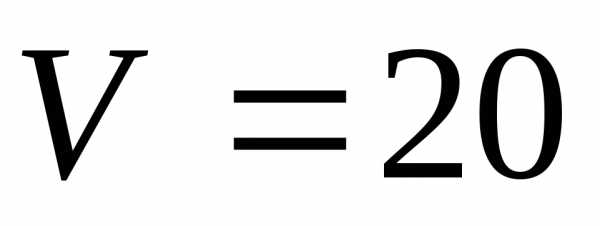 5.4.11.
5.4.11.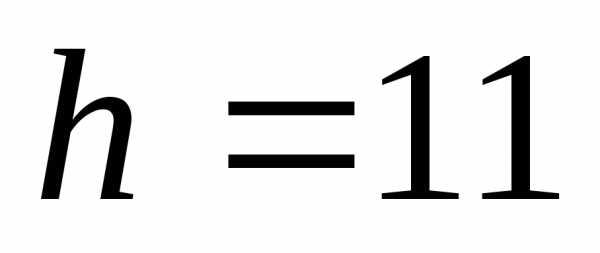
Часть 3. Аналитическая геаметрия на плоскости и в пространстве
§ 1. Предмет аналитической геометрии. Простейшие задачи. Преобразование координат
Литература: (1, с.38-41, 105-108; 2, с. 12-20; 3, с. 33-41; 4, с. 34-40)
Аналитическая геометрия рассматривает изучение геометрических задач средствами алгебры на основе метода координат
Простейшие задачи аналитической геометрии
Расстояние между двумя точками иопределяется по формуле:
(1)
Деление отрезка в данном отношении
Если точка
лежит на прямой, проходящей через данные
точкии,
и делит отрезок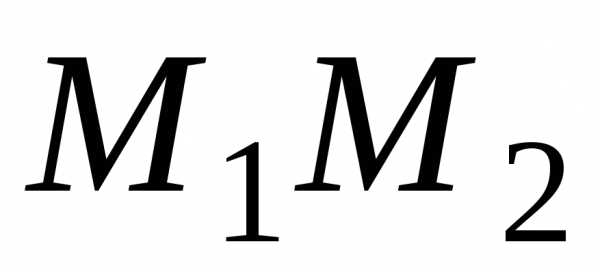 в отношении
в отношении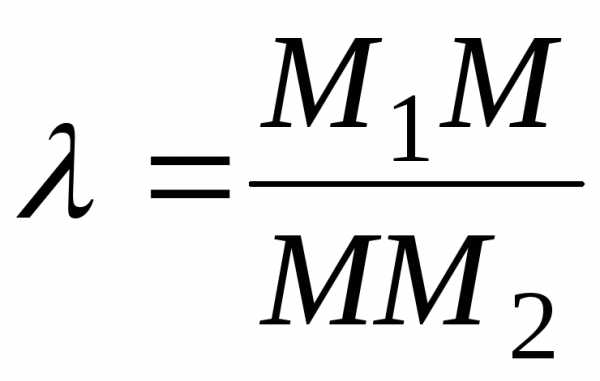 ,
то координаты точки М определяются по
формулам:
,
то координаты точки М определяются по
формулам:
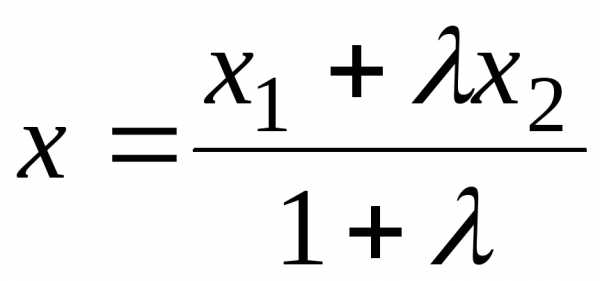 ;
; 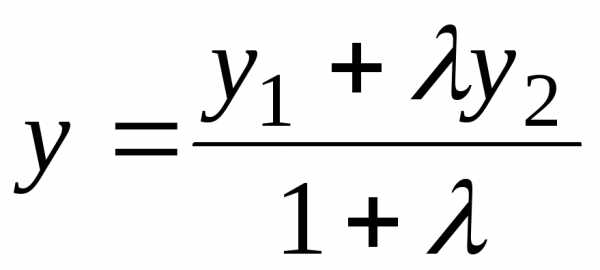 ;
;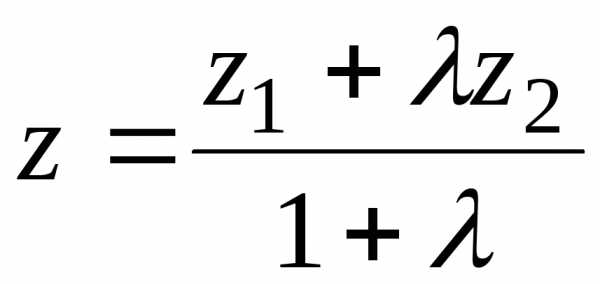 .(2)
.(2)
В частности, если
точка
делит отрезок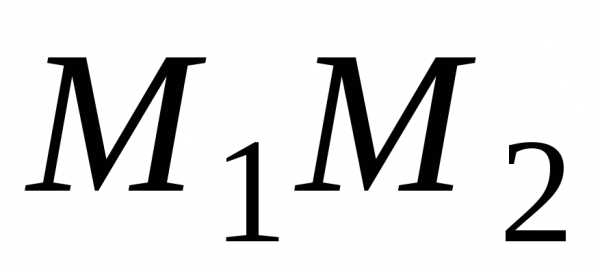 пополам, то
пополам, то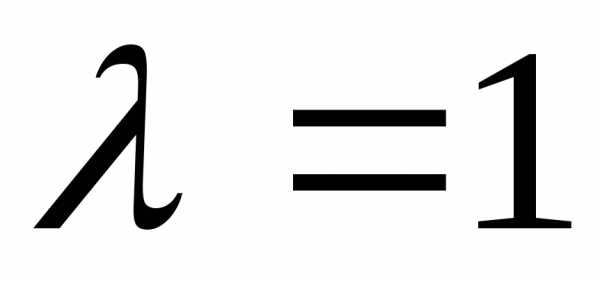 ,
,
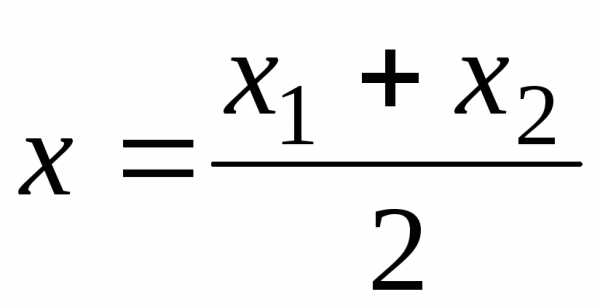 ;
; 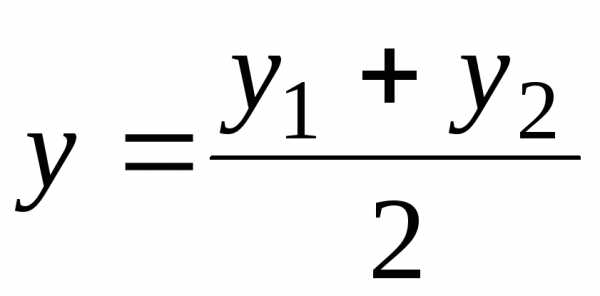 ;
;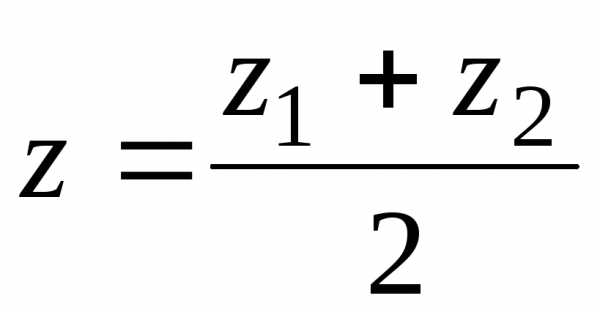 .
.
Пример 1. На оси ординат найти точку, равно удалённую от точек и.
Решение. Искомая
точка М имеет координаты 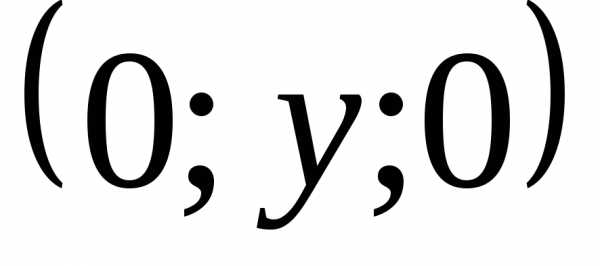 .
Найдём её расстояния до точек А и В по
формуле (1)
.
Найдём её расстояния до точек А и В по
формуле (1)
;
;
По условию , т.е., или. Итак, искомая точка
Пример 2. Даны вершины треугольника ,,. Вычислить длину биссектрисы его внутреннего угла при вершине В.
Решение.
Чтобы найти длину биссектрисы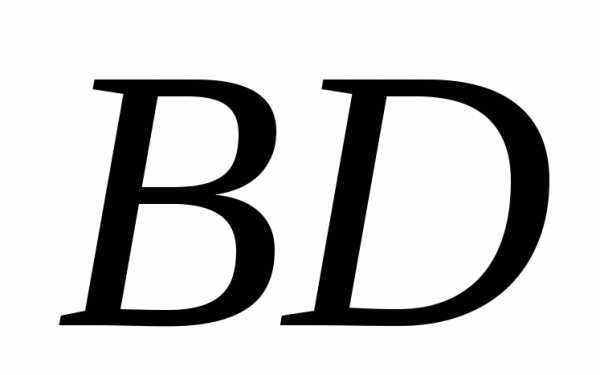 нужно знать координаты точки
нужно знать координаты точки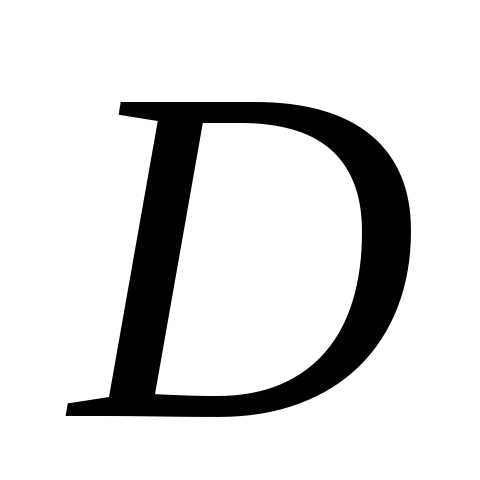 .
Воспользуемся тем, что биссектриса
делит противоположную сторону на части,
пропорциональные прилежащим сторонам,
т.е.
.
Воспользуемся тем, что биссектриса
делит противоположную сторону на части,
пропорциональные прилежащим сторонам,
т.е.
Найдём длинны сторон АВ и ВС по формуле (1):
;
.
Тогда.
По формуле (2)
определим координаты т. 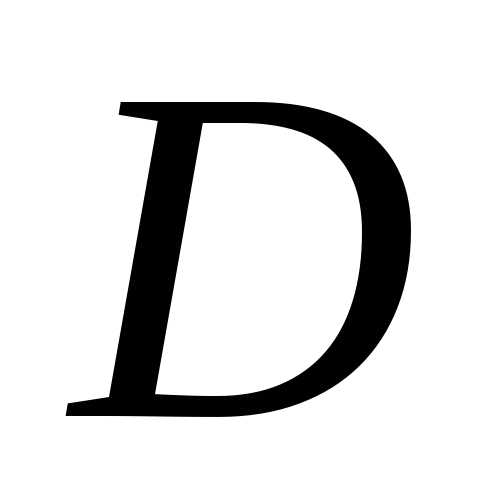 :
:
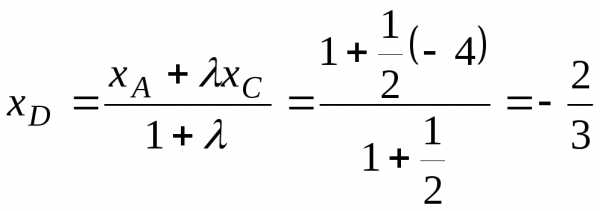 ;
;
;
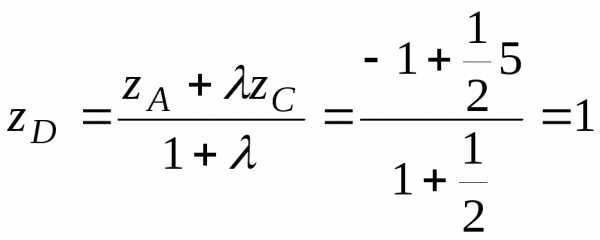 ,
,
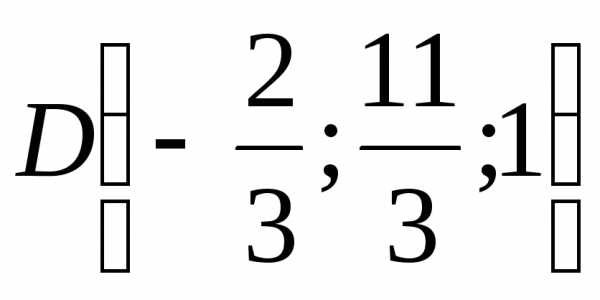 .
.
Следовательно,
.
Полярная система координат
Полярная система координат определяется заданием некоторой точки О, называемой полюсом луча, исходящего из этой точки, называемого полярной осью, и масштаба для изменения длинны.
Полярными
координатами произвольной точки М
называются числа 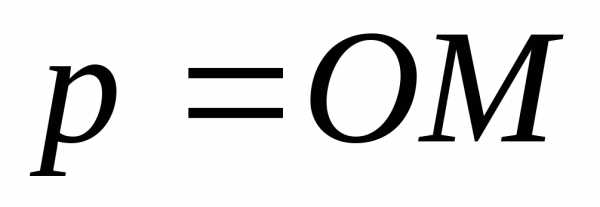 — полярный радиус, и- полярный угол (рис 1).
— полярный радиус, и- полярный угол (рис 1).
Обычно
положительным считается поворот против
часовой стрелки. Исходя из определения,
полярный радиус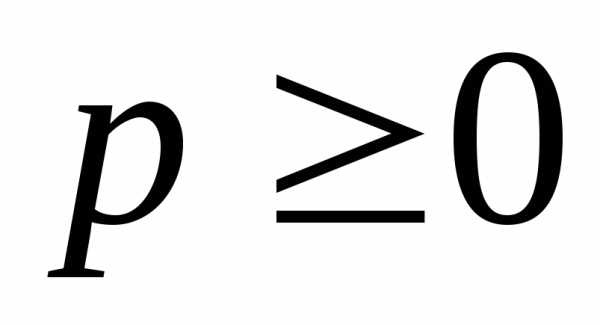 ,
а полярный угол имеет бесконечно много
возможных значений.
,
а полярный угол имеет бесконечно много
возможных значений.
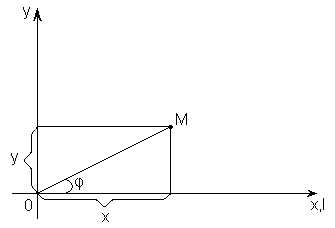
Связь между декартовыми и полярными координатами определяются формулами:
; (3)
; 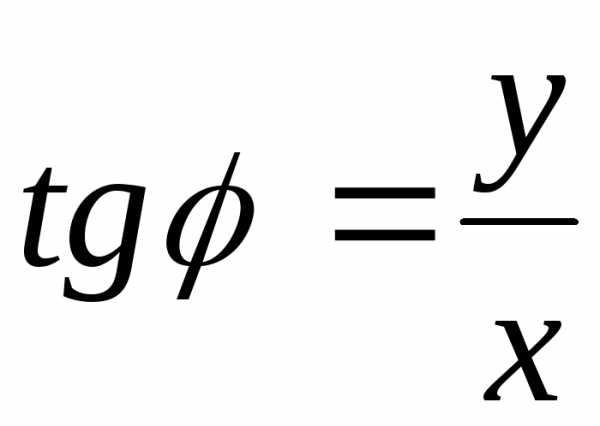 (4)
(4)
При этом предполагается, что полярность ось совпадает с положительным направлением оси абсцисс, начало координат – с полюсом, и все три оси имеют общую единицу масштаба (рис. 2).
Пример 3. В
полярной системе координат даны точки 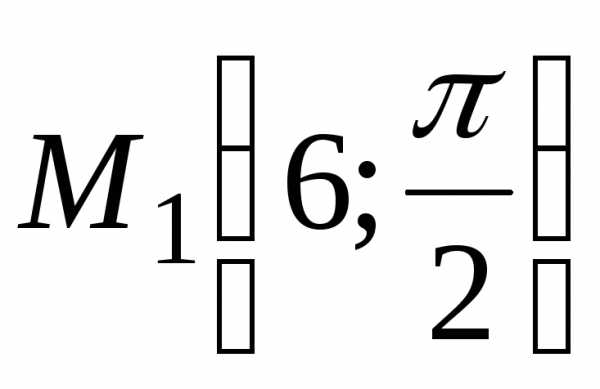 ,
,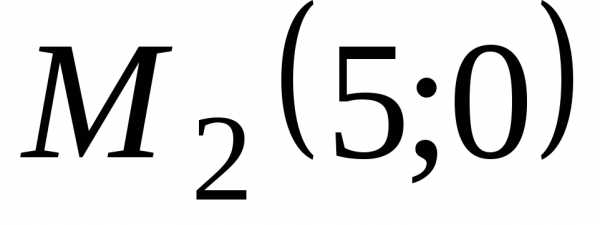 ,
,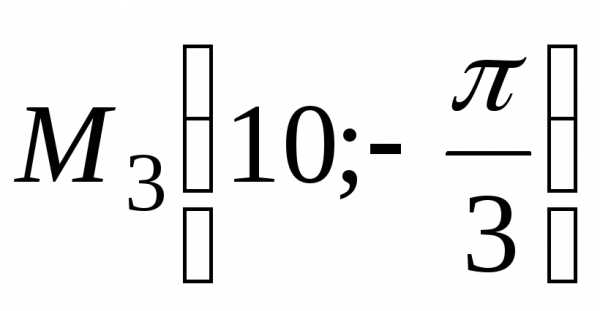 .
Определить декартовы координаты этих
точек.
.
Определить декартовы координаты этих
точек.
Решение. Воспользуемся формулой (3) ;.
Для данных точек имеем:
 ;
; 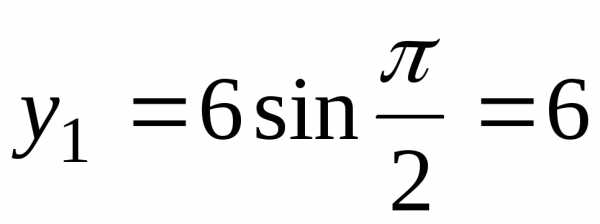 ;
;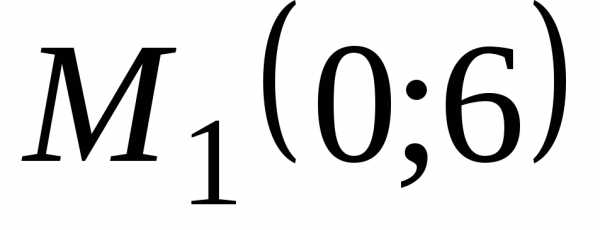 ;
;
;
;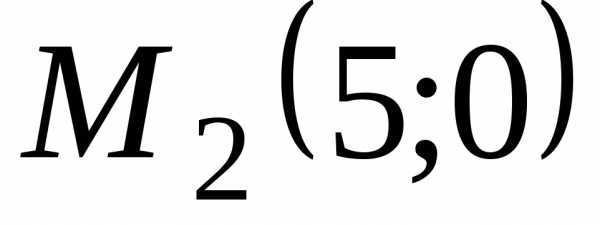 ;
;
; ;;
Преобразование координат
Формулы , выражающие координаты в одной системе через её координаты в другой системе, называются формулами преобразования координат.
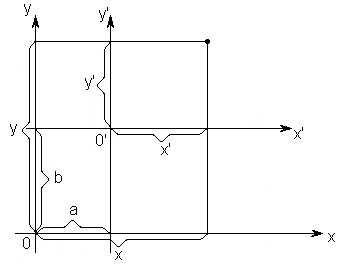
Преобразование декартовых координат при параллельном сдвиге осей определяется по формулам:
, 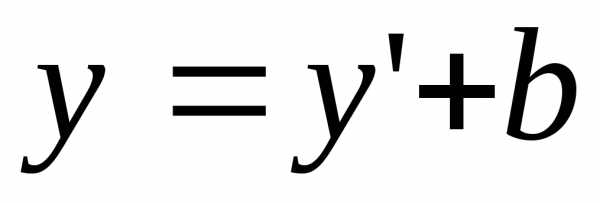 (5)
(5)
где 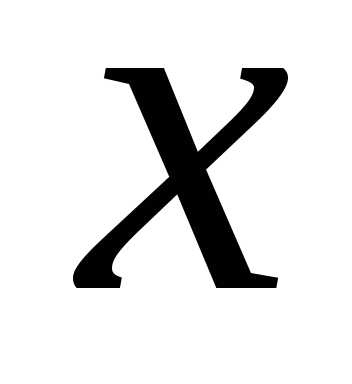 и
и — координаты произвольной точки М
плоскости относительно старых осей:
— координаты произвольной точки М
плоскости относительно старых осей: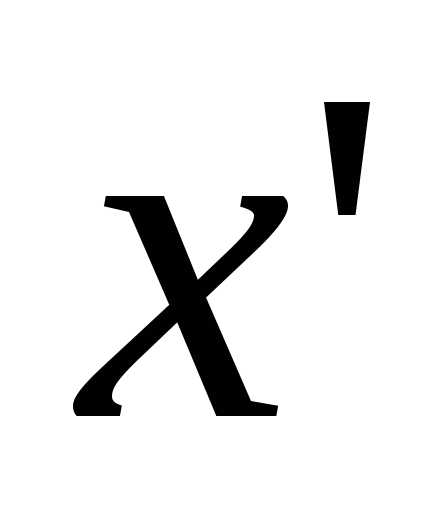 ,
,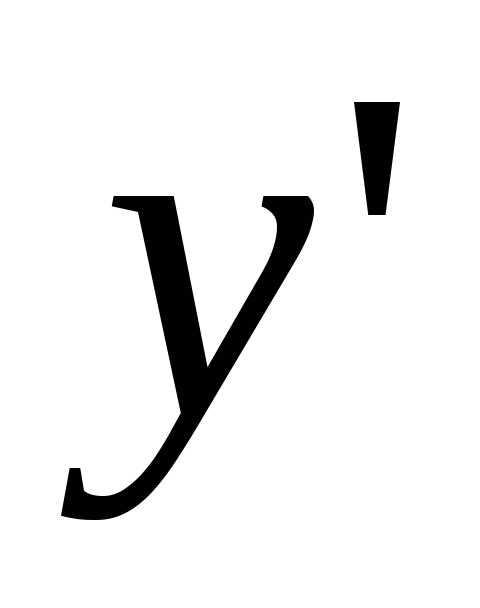 — координаты той же точки относительно
новых осей;
— координаты той же точки относительно
новых осей;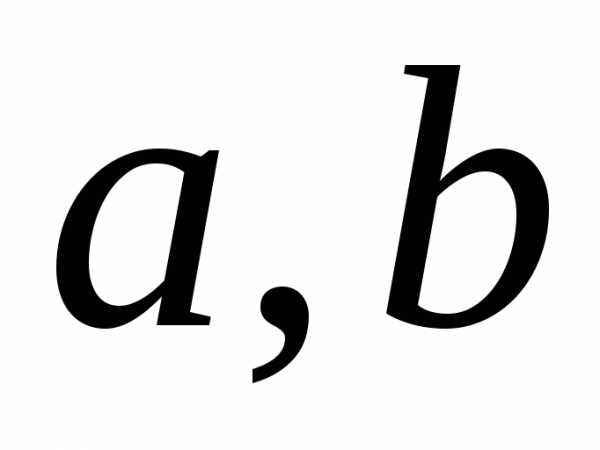 — координаты нового начала
— координаты нового начала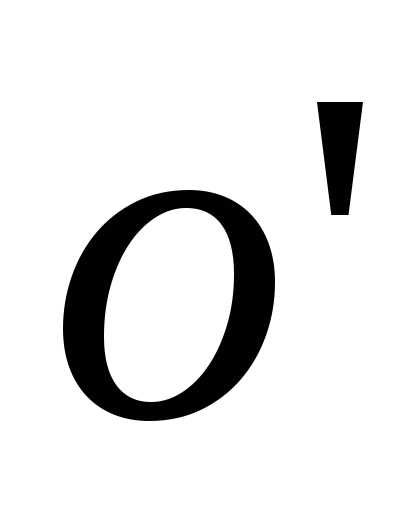 старых осей (рис. 3).
старых осей (рис. 3).
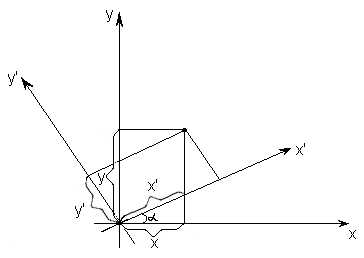
Преобразование
декартовых прямоугольных координат
при повороте осей на угол  (рис. 4) определяется по формулам:
(рис. 4) определяется по формулам:
; .(6)
Пример 4. Оси
координат повёрнуты на угол 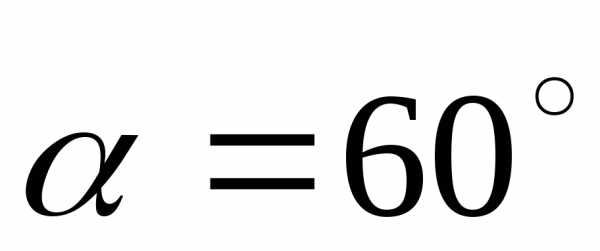 .
Координаты точекиопределены в новой системе. Вычислить
координаты этих же точек в старой системе
координат.
.
Координаты точекиопределены в новой системе. Вычислить
координаты этих же точек в старой системе
координат.
Решение. Воспользуемся
формулами (6)
;,
где — угол поворота,
— угол поворота,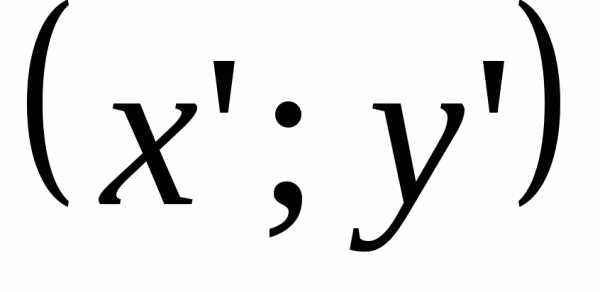 — координаты точек в новой системе,
— координаты точек в новой системе,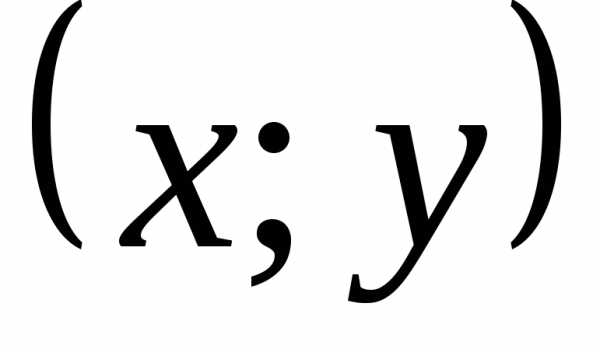 — координаты точки в старой системе.
— координаты точки в старой системе.
Тогда для точки А получим:
;
.
Следовательно, 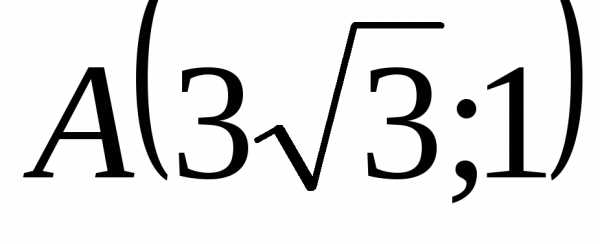 .
.
Аналогично для точки В имеем: ;
.
Следовательно, 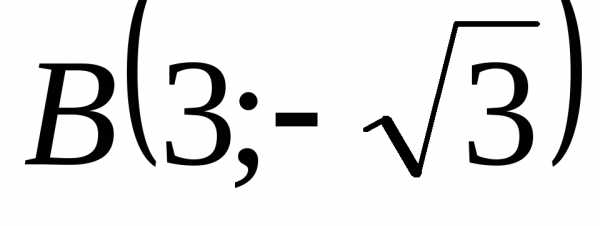 .
.
Вопросы для самопроверки
Как определяется расстояние между двумя точками?
Как находятся координаты точки, делящей отрезок в данном отношении?
Как задаётся полярная система координат?
Какая существует связь между декартовыми и полярными координатами?
Как определяются параллельный перенос и поворот декартовых прямоугольных осей координат?
Примеры для самостоятельного решения
Даны точки ,,,. Вычислить расстояние между: а) А и С; б) В и
 .
.Доказать, что треугольник с вершинами ,иравнобедренный.
На оси абсцисс найти точку, расстояние которой от точки равно 12.
Даны вершины треугольника ,,. Вычислить длину его медианы
 ,
проведённой из вершины А.
,
проведённой из вершины А.Даны три вершины параллелограмма ;и. Найти его четвёртую вершину
 ,
противоположную В.
,
противоположную В.Определить координаты концов отрезка АВ, который точками
 иразделён на три равные части.
иразделён на три равные части.Построить точки
 ,
, ,
, .
.Даны полярные координаты точки
 .
Найти её прямоугольные координаты.
.
Найти её прямоугольные координаты.Сделан параллельный перенос осей координат в точку
 .
Известны старые координаты точки
.
Известны старые координаты точки .
Определить новы координаты этой же
точки.
.
Определить новы координаты этой же
точки.На плоскости
 дана точка
дана точка .
Систему координат повернули вокруг
начала координат так, что новая ось
прошла через точку М. Определить старые
координаты точки А, если известны её
новые координаты
.
Систему координат повернули вокруг
начала координат так, что новая ось
прошла через точку М. Определить старые
координаты точки А, если известны её
новые координаты ,
, .
.
Ответы к примерам
1.5.1. а) АС=7; б) 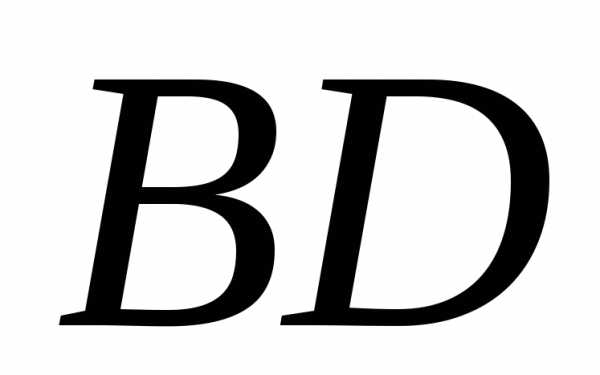 =13. 1.5.3.
=13. 1.5.3.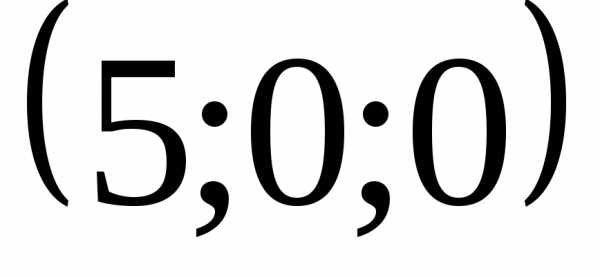 и.
и.
1.5.4. . 1.5.5..
1.5.6.
,. 1.5.8.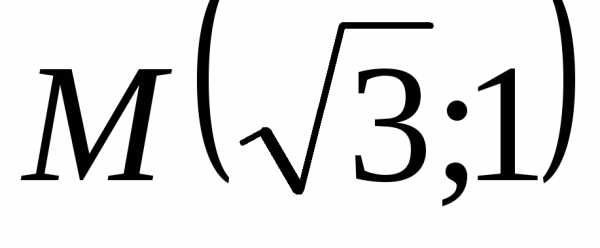 .
.
1.5.9. 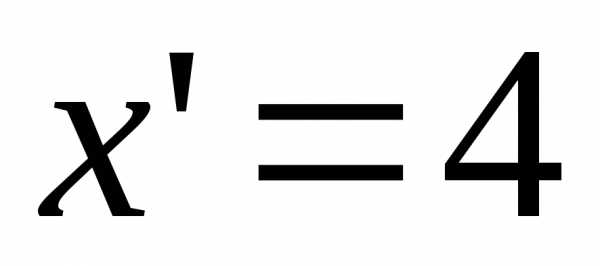 ;
;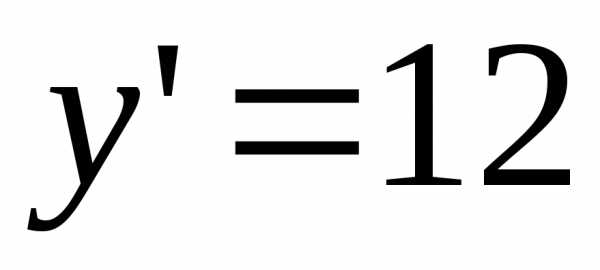 . 1.5.10.
. 1.5.10.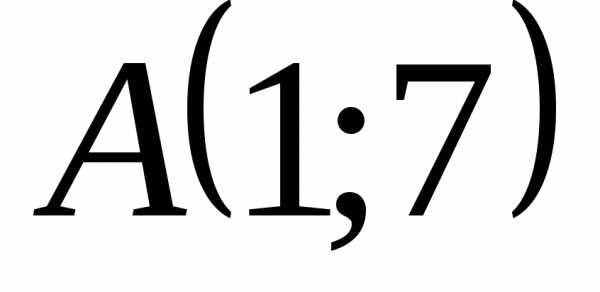 .
.
studfiles.net
Тема 5
Курс “Алгебра и Геометрия”
(специальность прикладная математика, информатика, 1 курс, 1 семестр)
Тема 5. Векторное и смешанное произведения. – 4 часа.
Содержание: вычисление векторного и смешанного произведения; геометрический смысл векторного и смешанного произведений; свойства этих произведений; применение.
Цель: выработать навыки вычисления векторного и смешанного произведений и применения их при решении геометрических задач.
Форма контроля: опрос.
Задачи
Задача 1 ([9], 1062). Упростить
произведения 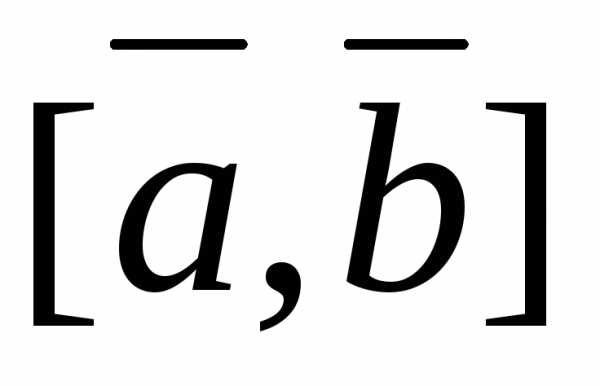 ,
, 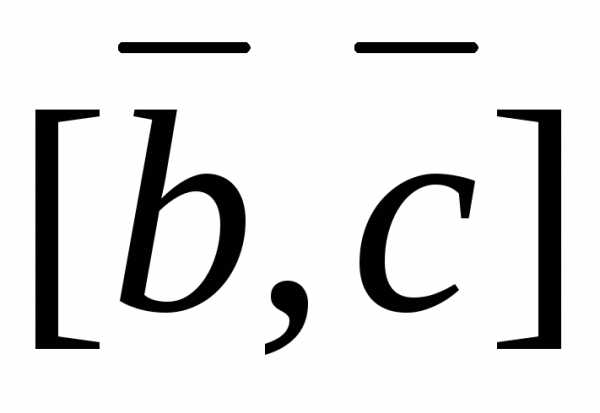 и
и 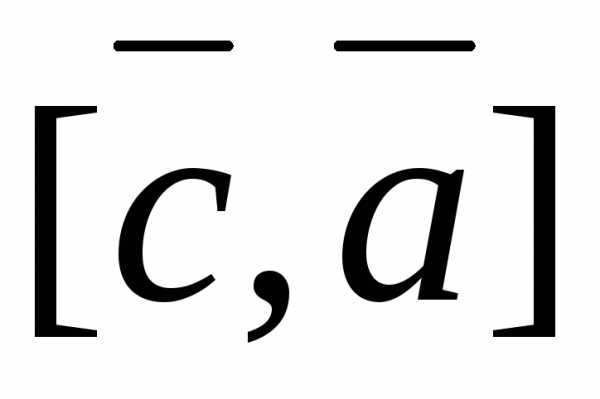 ,
зная, что
,
зная, что  ,
,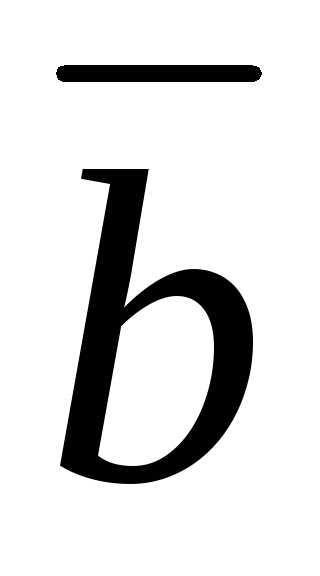 и
и — взаимно перпендикулярные орты,
образующие правую тройку.
— взаимно перпендикулярные орты,
образующие правую тройку.
Задача 2 ([9], 1063). Решить задачу
1 в предположении, что орты  ,
,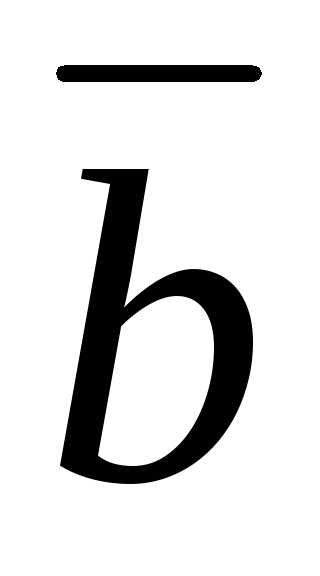 и
и образуют левую тройку.
образуют левую тройку.
Задача 3 ([9], 1064). При каком
значении коэффициента  векторыи
векторыи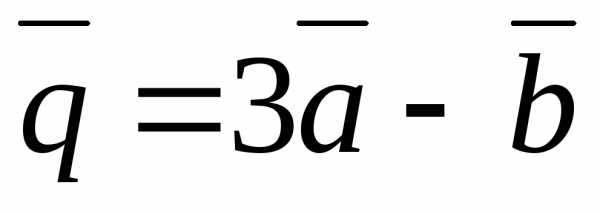 окажутся коллинеарными, если
окажутся коллинеарными, если и
и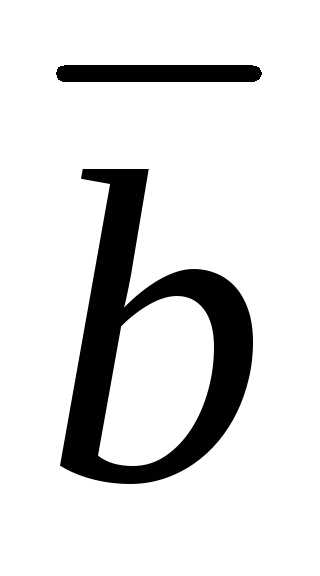 не коллинеарны?
не коллинеарны?
Задача 4 ([9], 1071). Проверить, имеют ли место в векторной алгебре тождества:
1) ;
2) ;
3) .
Задача 5 ([9], 1073). Вычислить скаляр .
Задача 6 ([9], 1074). Вычислить площадь параллелограмма,
построенного на векторах
и,
где и
и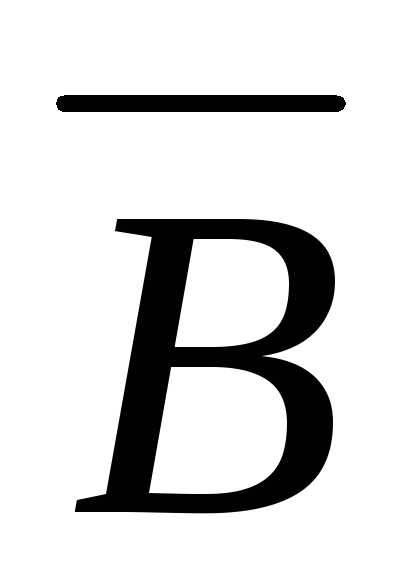 — единичные взаимно перпендикулярные
векторы.
— единичные взаимно перпендикулярные
векторы.
Задача 7 ([9], 1075). Вычислить
площадь параллелограмма, построенного
на векторах
и,
где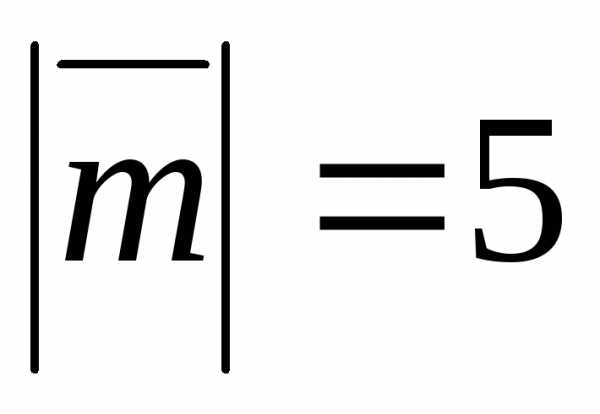 ,
,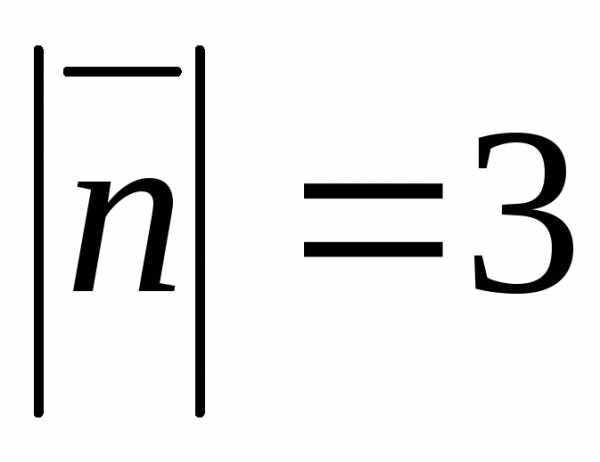 и.
и.
Задача 8 ([9], 1076). Зная две
стороны треугольника
и,
вычислить длину его высоты при условии, что
при условии, что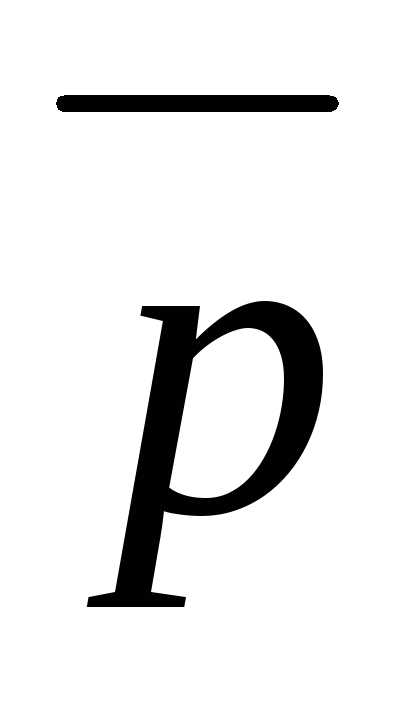 и
и — перпендикулярные друг другу орты.
— перпендикулярные друг другу орты.
Задача 9 ([9], 1077). Разложить
вектор
по взаимно перпендикулярным ортам ,
,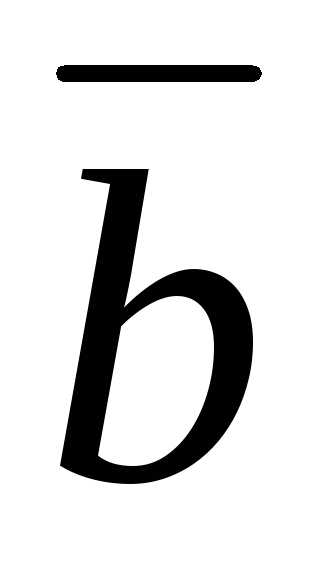 ,
, ,
образующим правую тройку.
,
образующим правую тройку.
Задача 10 ([9],
1078). Дан
вектор
,
где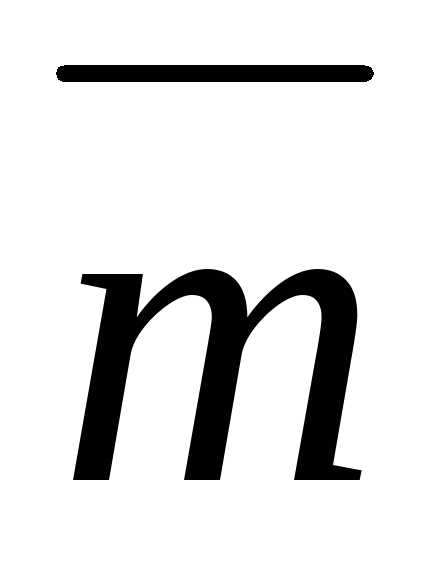 ,
,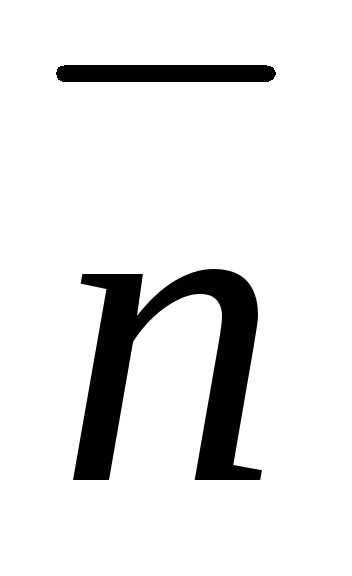 ,
,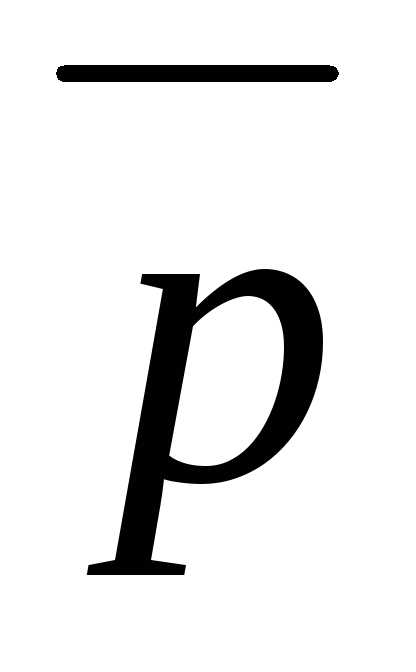 — взаимно перпендикулярные орты,
образующие левую тройку. Вычислить его
длину.
— взаимно перпендикулярные орты,
образующие левую тройку. Вычислить его
длину.
Задача 11 ([9],
1079). Вычислить
синус угла между диагоналями
параллелограмма, построенного на данных
векторах
и,
где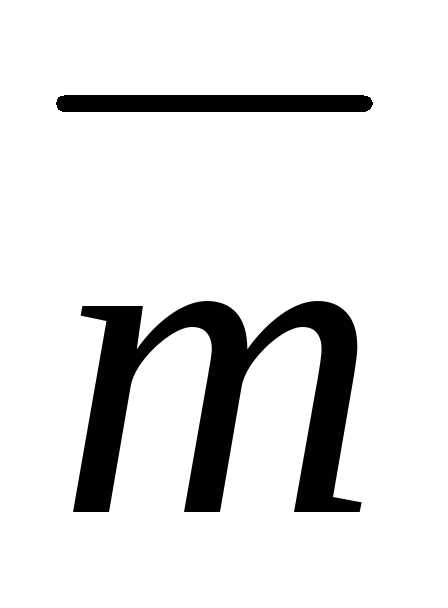 ,
,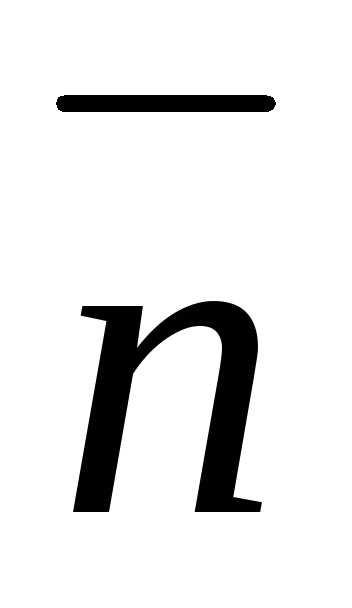 и
и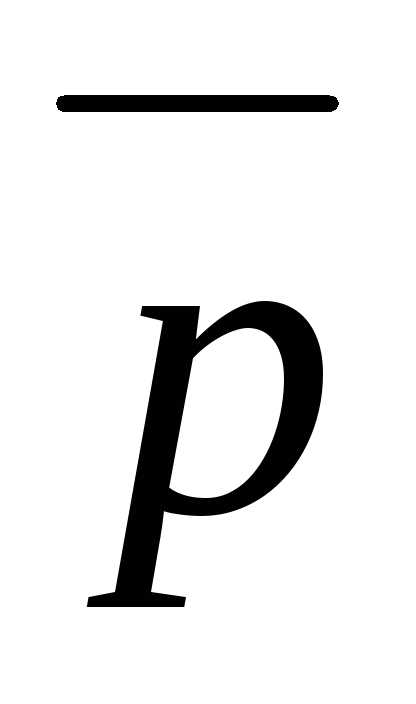 — взаимно перпендикулярные орты.
— взаимно перпендикулярные орты.
Задача 12 ([9],
1080). Вычислить
проекцию вектора
на ось, имеющую направление вектора,
если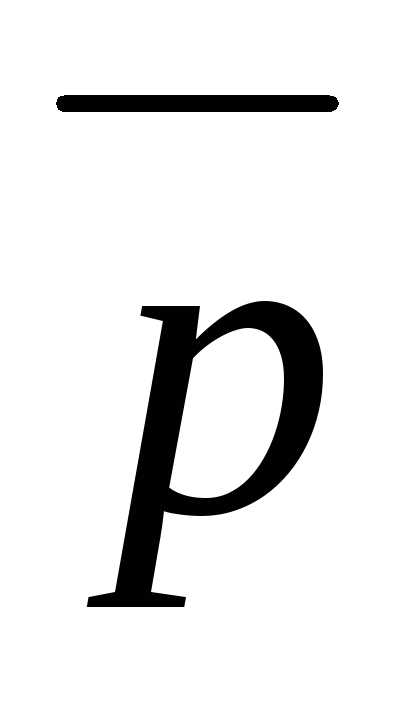 ,
, и
и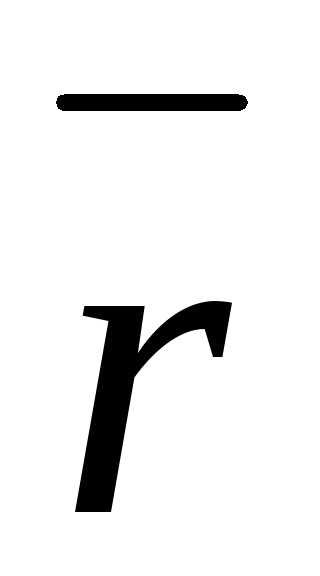 — взаимно перпендикулярные орты.
— взаимно перпендикулярные орты.
Задача 13 ([9],
1084). Вычислить
объем параллелепипеда, построенного
на векторах  ,
,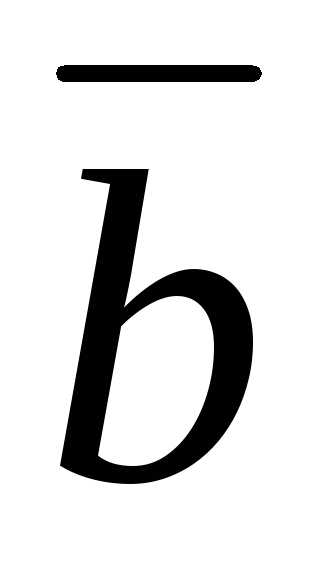 и
и ,
если:
,
если:
1) ,и,
где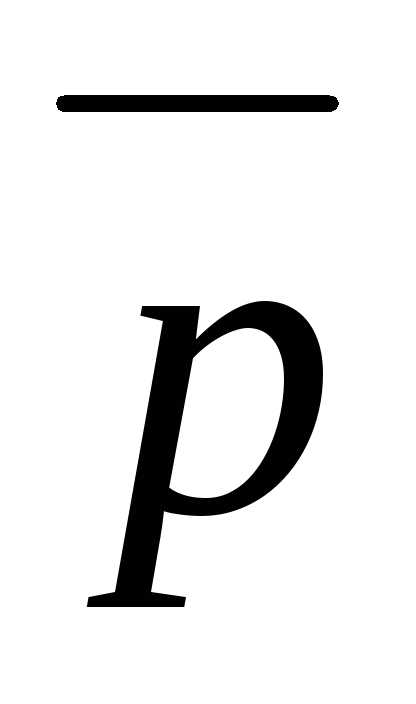 ,
, и
и 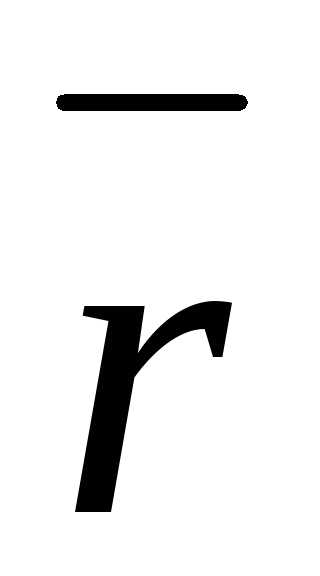 — взаимно перпендикулярные орты;
— взаимно перпендикулярные орты;
2) ,
,,
где 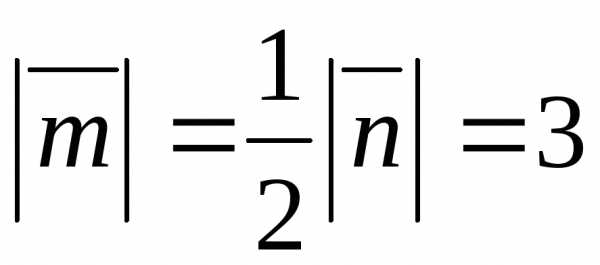 , .
, .
Задача 14 ([9],
1085). Вычислить
высоту параллелепипеда, построенного
на трех векторах: ,и
,
если за основание взят параллелограмм,
построенный на и
и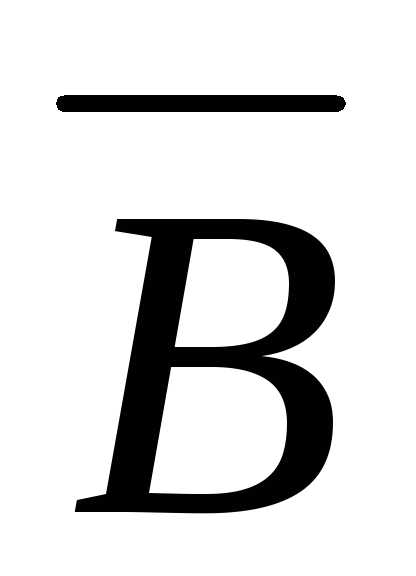 .
Кроме того, известно, что
.
Кроме того, известно, что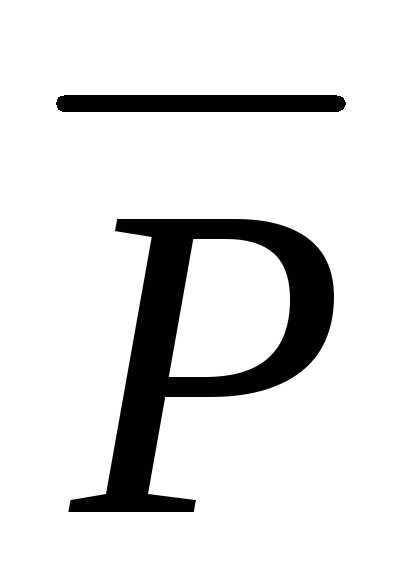 и
и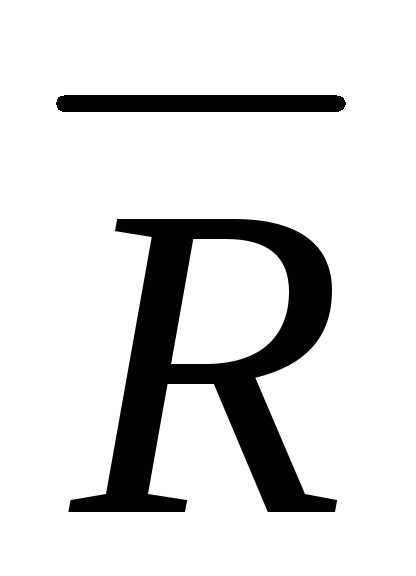 — взаимно перпендикулярные орты.
— взаимно перпендикулярные орты.
Задача 15 ([9],
1091). Зная,
что
,
найти соотношение между векторами ,
,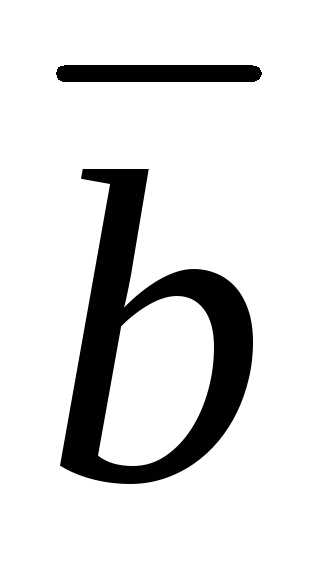 и
и , не содержащее
коэффициентов
, не содержащее
коэффициентов  и
и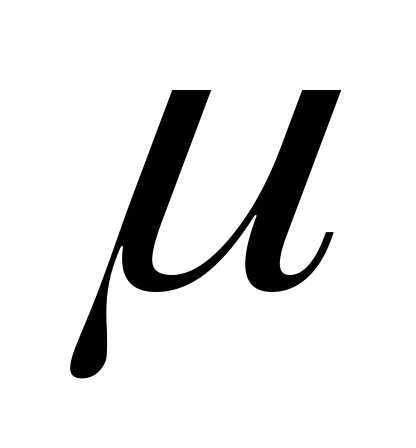 .
.
Задача 16 ([9], 1092). Можно
ли найти вектор 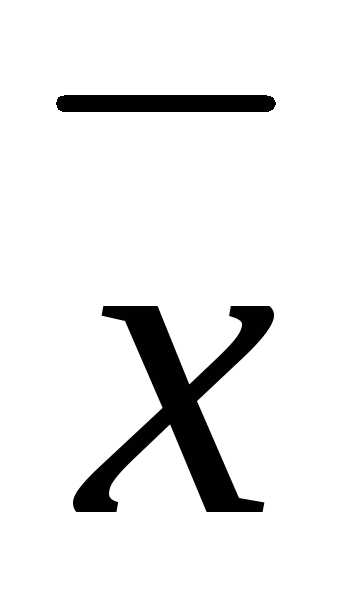 ,
одновременно удовлетворяющий двум
уравнениям:
,
одновременно удовлетворяющий двум
уравнениям: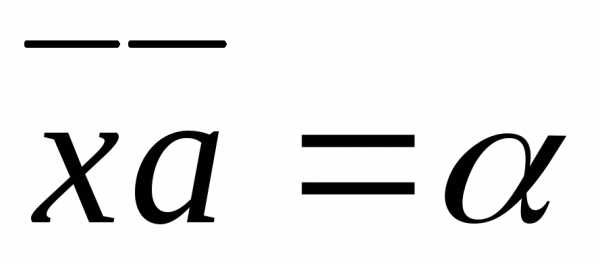 и
и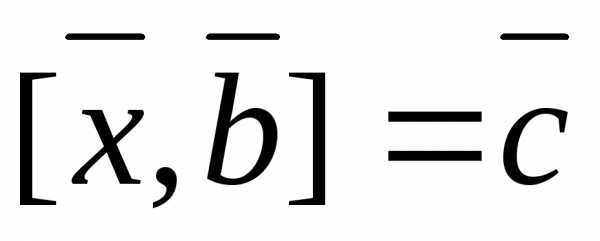 ,
где
,
где ,
,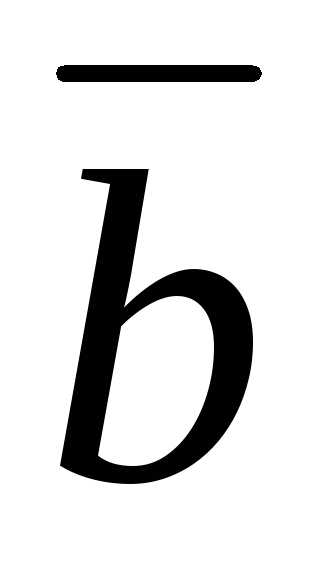 ,
, — данные векторы и
— данные векторы и  — данный
скаляр.
— данный
скаляр.
Задача 17 ([8], 857). Даны точки
,и. Вычислить площадь треугольника 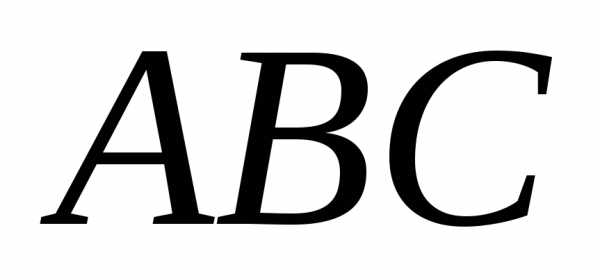 .
.
Задача 18 ([8], 858). Даны вершины
треугольника:
,,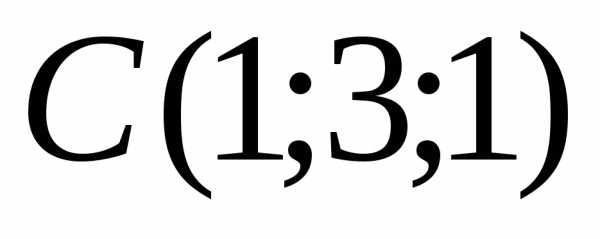 .
Вычислить длину его высоты, опущенной
из вершины
.
Вычислить длину его высоты, опущенной
из вершины на сторону
на сторону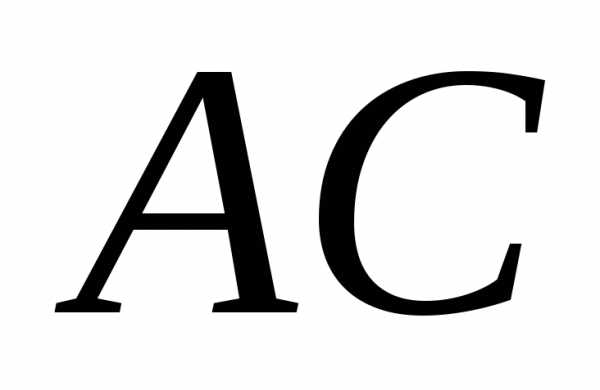 .
.
Задача 19 ([8], 859). Вычислить
синус угла, образованного векторами
,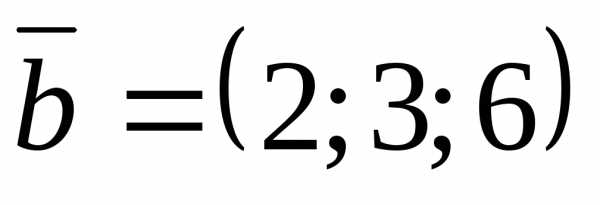 .
.
Задача 20 ([8], 860). Вектор 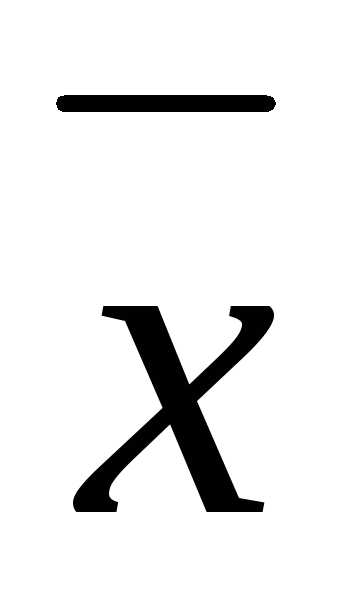 ,
перпендикулярный к векторам,
,
перпендикулярный к векторам,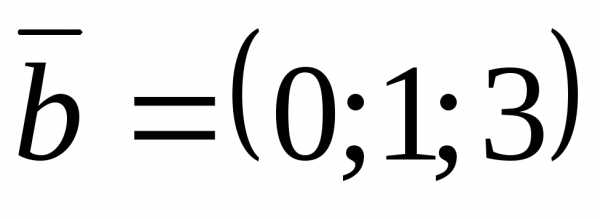 образует с осью Оу тупой угол. Зная что
образует с осью Оу тупой угол. Зная что 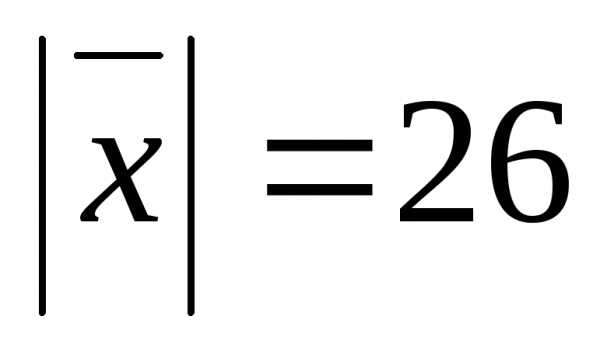 ,
найти его координаты.
,
найти его координаты.
Задача 21 ([8], 861). Вектор  ,
перпендикулярный к оси Oz и к вектору
,
образует острый угол с осью Ох.
Зная что
,
перпендикулярный к оси Oz и к вектору
,
образует острый угол с осью Ох.
Зная что 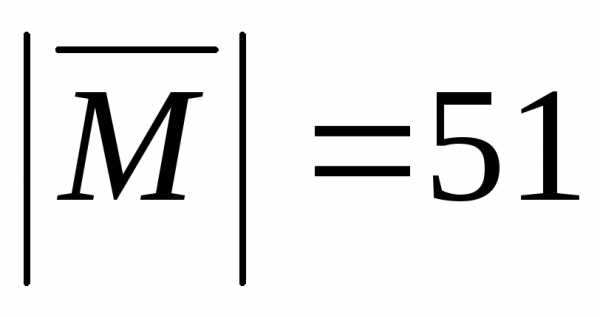 ,
найти его координаты.
,
найти его координаты.
Задача 22 ([8], 862). Найти вектор 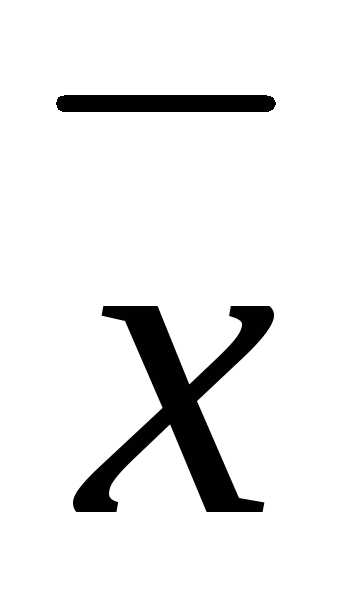 ,
зная, что он перпендикулярен векторуи,
и удовлетворяет условию.
,
зная, что он перпендикулярен векторуи,
и удовлетворяет условию.
Задача 23 ([8], 864). Даны вектора
,и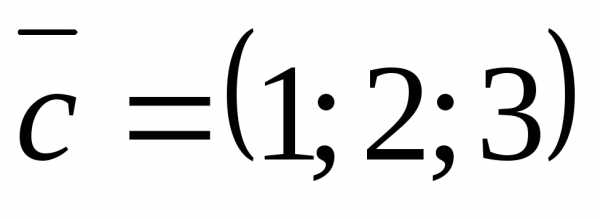 .
Вычислить
.
Вычислить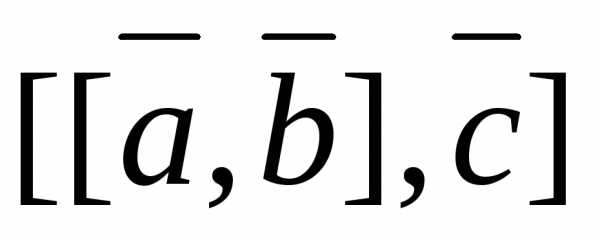 и
и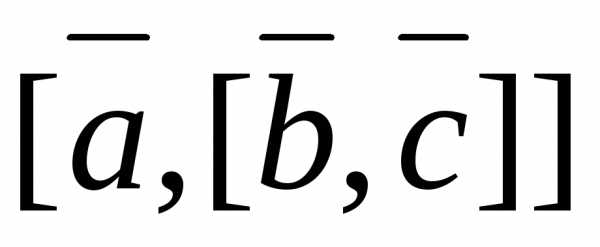 .
.
Задача 24 ([8], 867). Вектор  перпендикулярен к векторам
перпендикулярен к векторам и
и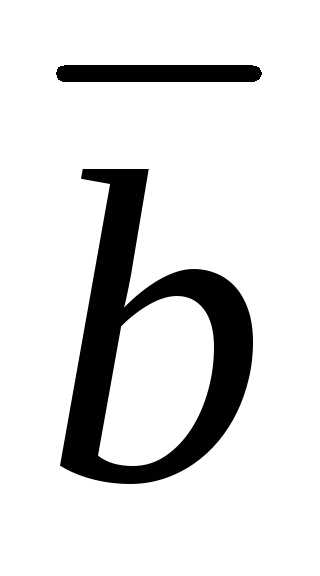 ,
угол между
,
угол между и
и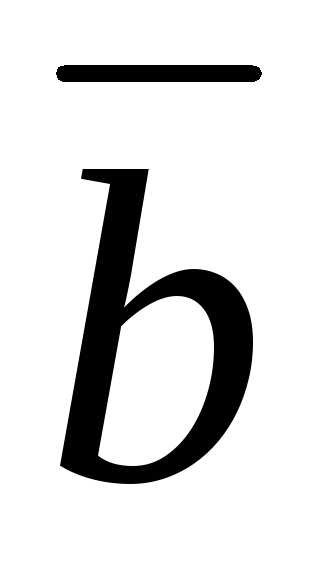 равен
равен . Зная, что
. Зная, что 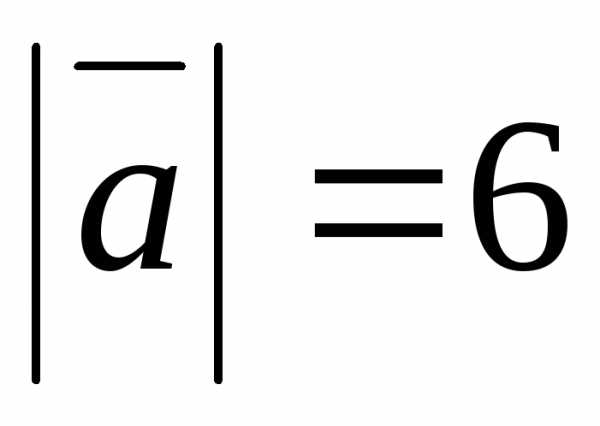 ,
,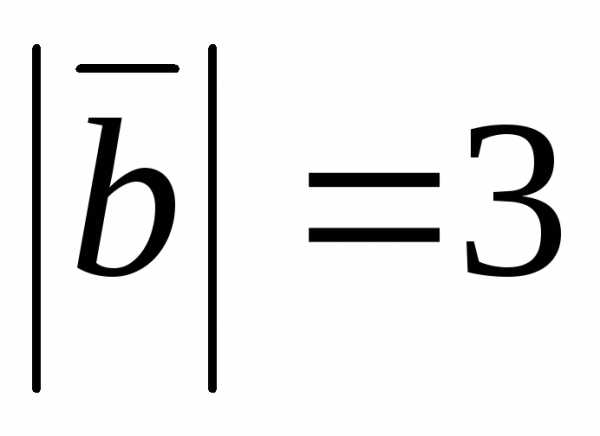 и
и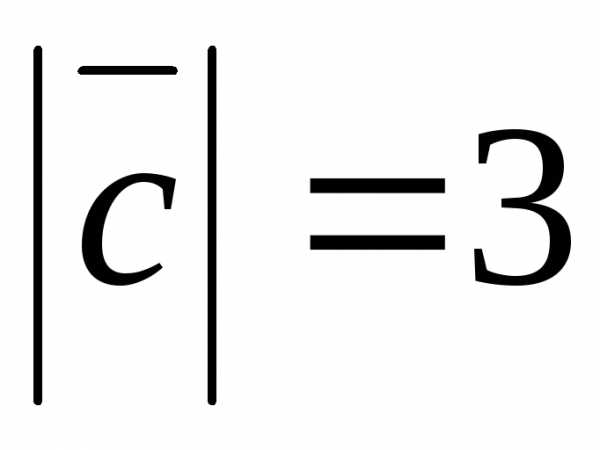 ,
вычислить
,
вычислить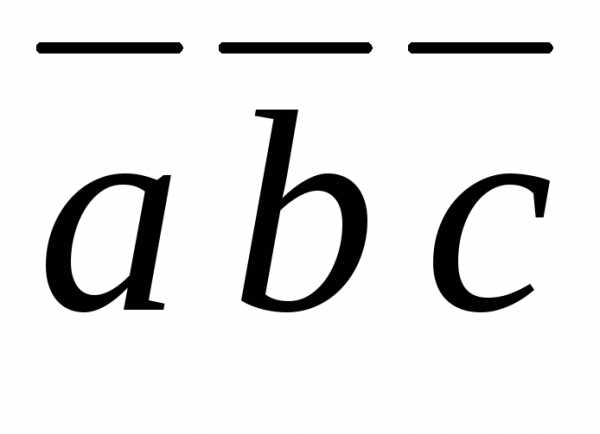 .
.
Задача 25 ([8], 871). Доказать,
что векторы  ,
,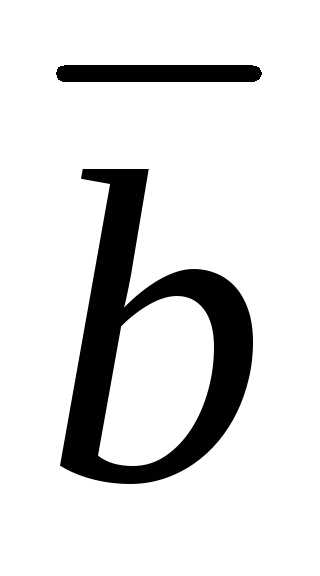 ,
, ,
удовлетворяющие условию.
,
удовлетворяющие условию.
Задача 26 ([8], 873). Даны вектора
,,.
Вычислить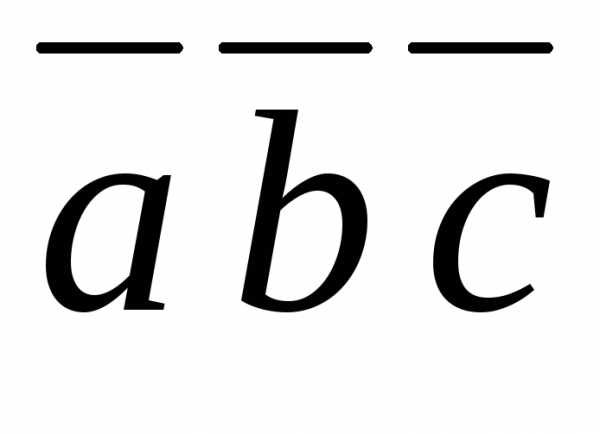 .
.
Задача 27 ([8], 876). Вычислить
объем тетраэдра, вершины которого
находятся в точках
,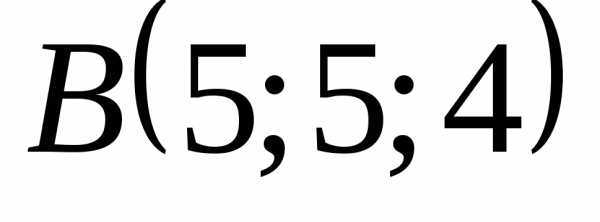 ,,
,,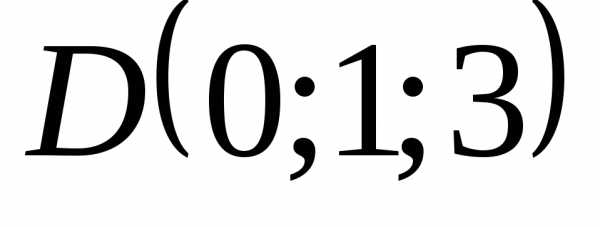 .
.
Задача 28 ([8], 877). Даны вершины
тетраэдра: 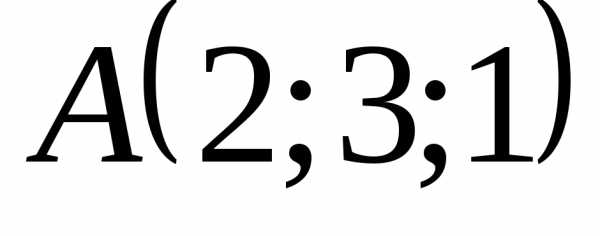 ,,
,,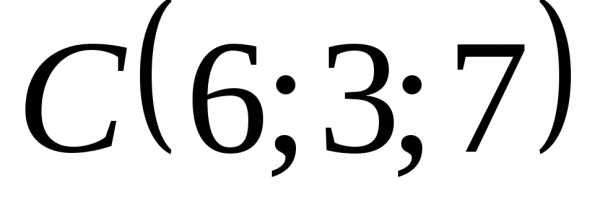 ,.
Найти длину его высоты опущенной из
вершиныD.
,.
Найти длину его высоты опущенной из
вершиныD.
Задача 29 ([8], 878). Объем
тетраэдра равен пяти, три его вершины
находятся в точках: ,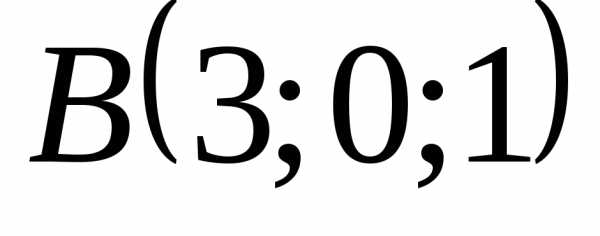 ,.
Найти координату вершиныD,
если известно, что она лежит на оси Оу.
,.
Найти координату вершиныD,
если известно, что она лежит на оси Оу.
Тема 3. Векторное и смешанное произведения.
Ответы
Задача 1. 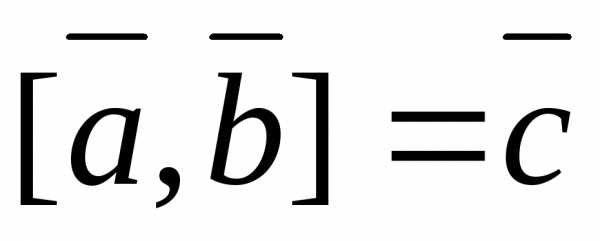 ; ;
; ; 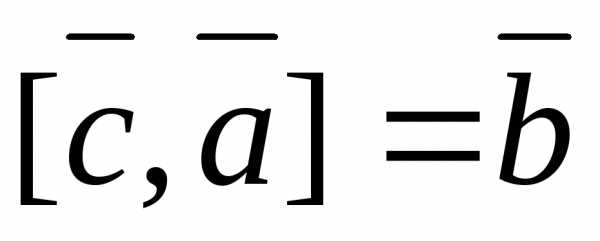 .
.
Задача 2. 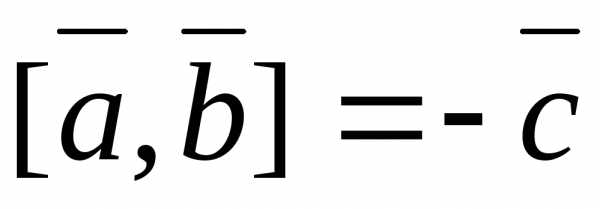 ;
; 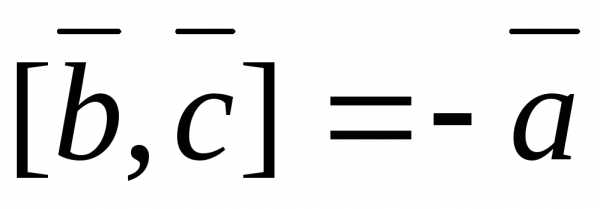 ;
; 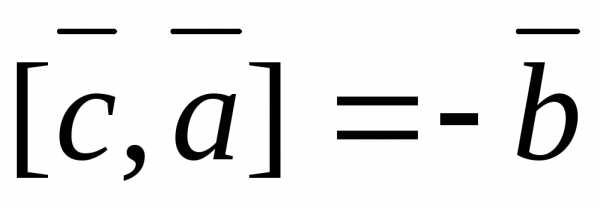 .
.
Задача 3. .
Задача 4. Равенства 1) и 2) неверны
так как
.
Равенство3) справедливо лишь в случае, когда  перпендикулярно
перпендикулярно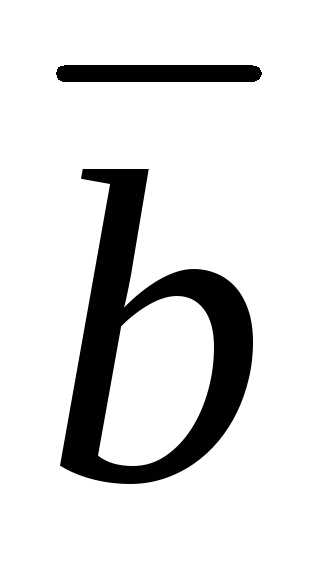 .
.
Задача 5. 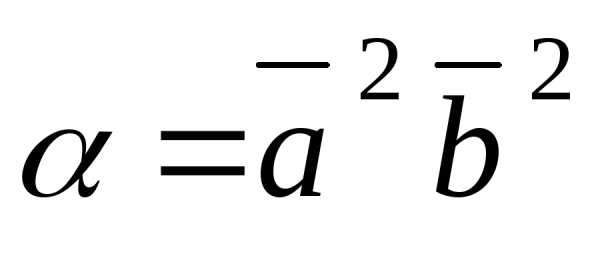 .
.
Задача 6. 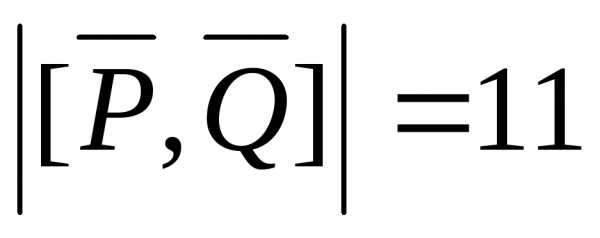 .
.
Задача 7. 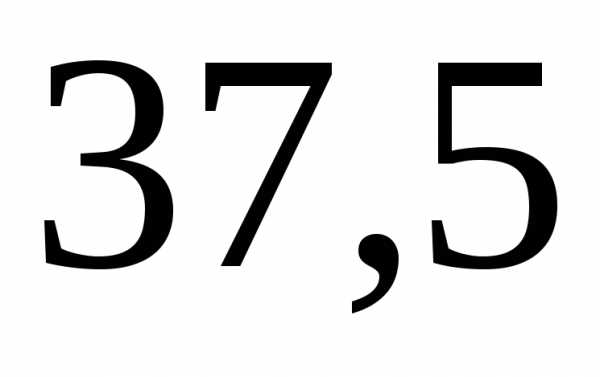 кв.ед.
кв.ед.
Задача 8.
Задача 9. .
Задача 10. 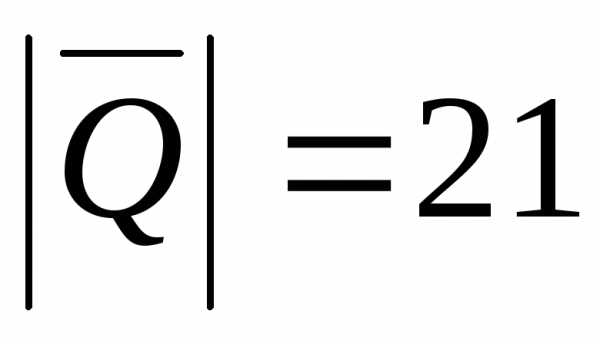 .
.
Задача 11. .
Задача 12. ,
если 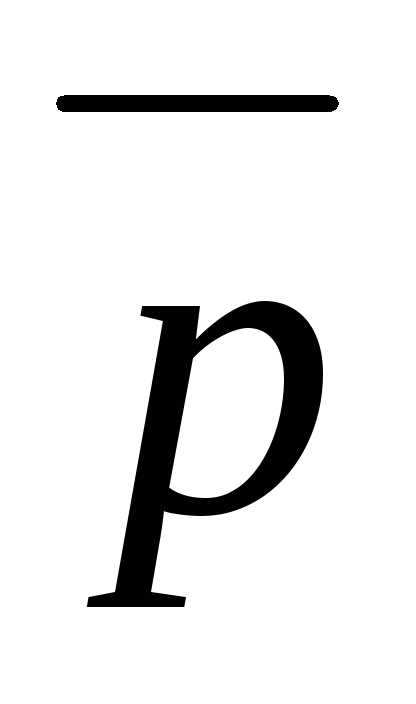 ,
, и
и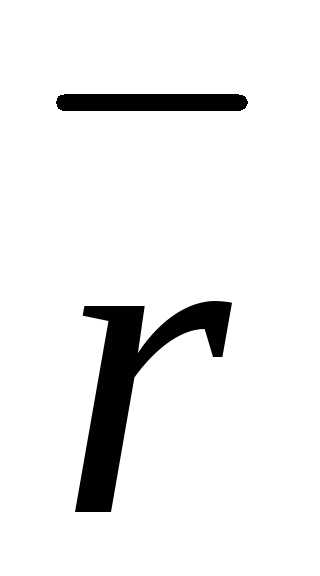 составляют правую тройку;,
если
составляют правую тройку;,
если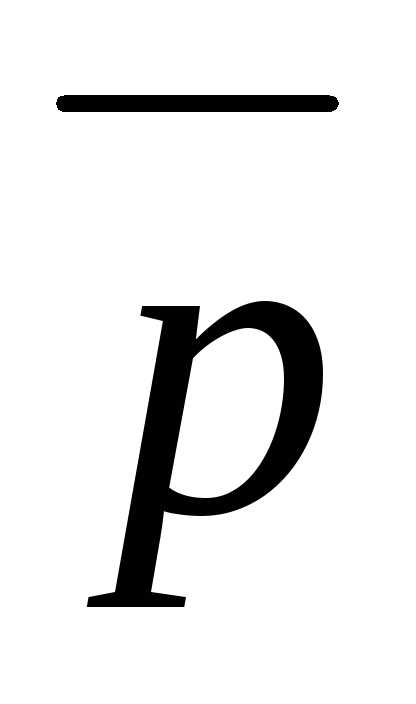 ,
, и
и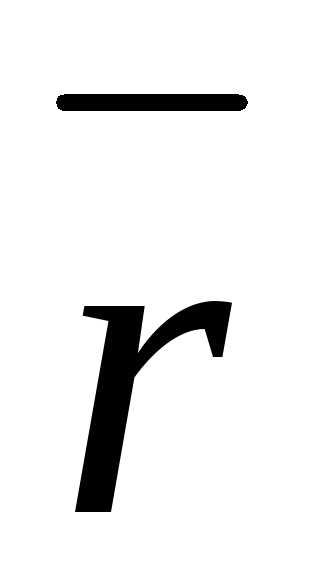 составляют
левую тройку.
составляют
левую тройку.
Задача 13. 1) V = 25 куб. ед.; 2) V = 0. Указание. Второй ответ
очевиден, так как из разложения
соответствующих векторов  ,
,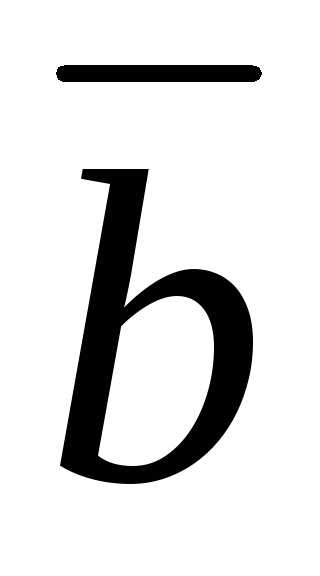 ,
, видно, что они компланарны.
видно, что они компланарны.
Задача 14. .
Задача 15. 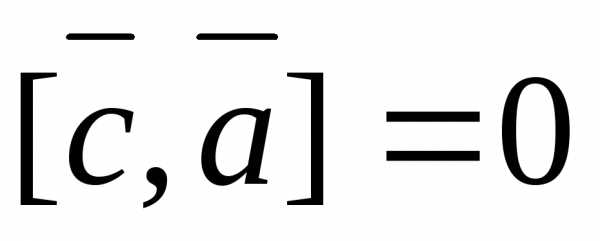 .
.
Задача 16. 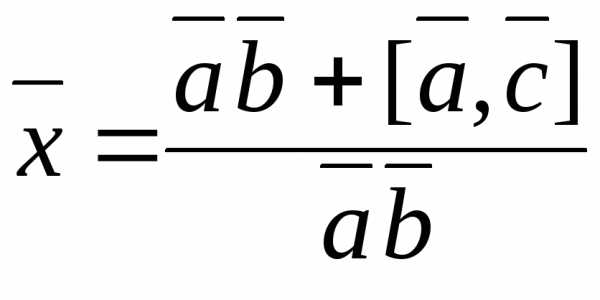 .
.
Задача 17. 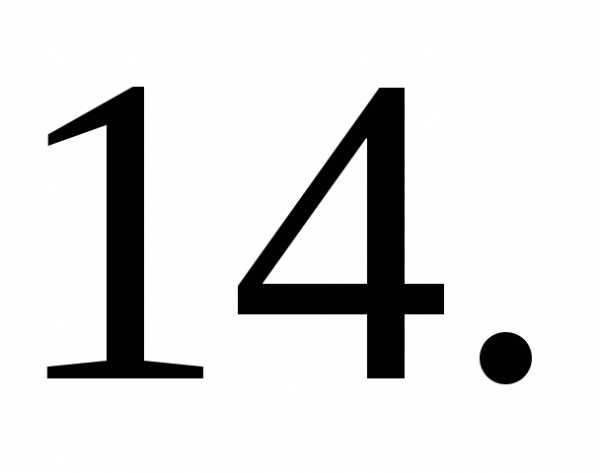
Задача 18. 
Задача 19. .
Задача 20. .
Задача 21. .
Задача 22. 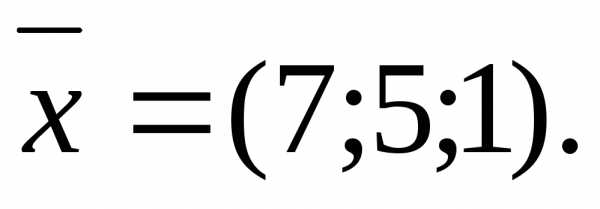
Задача 23. ; .
Задача 24. ;
знак плюс – в том случае, когда тройка
векторов  ,
,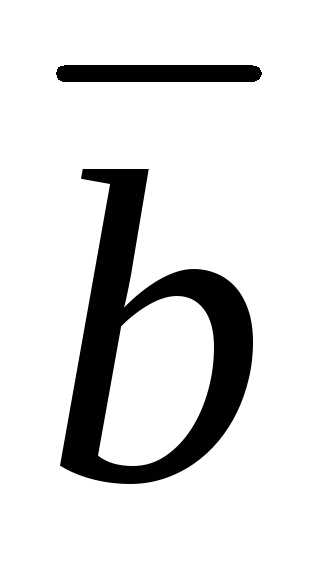 ,
, правая, и минус, когда эта тройка левая.
правая, и минус, когда эта тройка левая.
Задача 26. 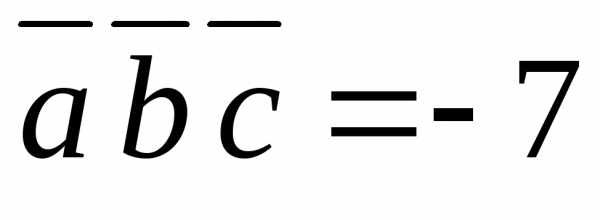 .
.
Задача 27. 
Задача 28. 
Задача 29. , .
studfiles.net
Векторное и смешанное произведения векторов, их вычисление, свойства и применения
Векторное произведение векторов
1. Векторы ивзаимно перпендикулярны. Зная, что, вычислить:
1.1. .1.2. .
2. Даны координаты и. Найти координаты векторных произведений:
2.1. .2.2. .2.3. .
3. Сила приложена к точке. Определить момент этой силы относительно точки, величину и направляющие косинусы момента.
4. Вычислить синус угла, образованного векторами и.
5. Даны точки ,и. Вычислить площадь треугольника.
6. Даны вершины треугольника ,и. Вычислить длину его высоты, опущенной из вершинына сторону.
7. Вектор , перпендикулярный к осиOz и к вектору , образует острый угол с осьюOx. Зная, что , найти его координаты.
Смешанное произведение векторов
8. Доказать, что четыре точки ,,,лежат в одной плоскости.
9. Установить, компланарны ли векторы если:
9.1.
9.2.
9.3.
10. Даны вершины треугольной пирамиды: . Найти объем пирамиды и длину его высоты, опущенной из вершины.
11. Объем треугольной пирамиды три его вершины находятся в точкахНайти координаты четвертой вершины, если известно, что она лежит на осиOy.
12. Какую тройку векторов (правую, левую) образуют векторы: ?
13. Образуют ли базис векторы ?
Дополнительные задания
Д-1. Найти пр.
Д-2. Найти орт вектора , где,
Д-3. Найти площадь параллелограмма , если его тремя последовательными вершинами являются точки
Д-4. Векторы иявляются сторонами параллелограмма. Найти площадь параллелограмма, построенного на его диагоналях.
Д-5. Найти длину опущенной на сторону высоты треугольника, если
Д-6. Найти значение , при котором четыре точкиилежат в одной плоскости.
Д-7. При каких значениях тройка векторов,будет левой и объем параллелепипеда, на них построенного, равен 5 ед3?
Д-8. При каком значении если?
Д-9. Найти значение , при которомесли
Д-10. Найти значение , при которомесли
Д-11. На векторах ипостроен параллелепипед. Найти длину его высоты, опущенной из вершинына грань векторов
Д-12. Объем треугольной пирамиды равен 12. Найти координаты вершины, еслиа точкалежит на осиOz, причем векторы образуют левую тройку.
Д-13. Вектор , перпендикулярный векторами, образует с осьюOy тупой угол. Зная, что найти его координаты.
Д-14. Найти единичный вектор, перпендикулярный векторам и
Д-15. Векторы имеют равные длины и образуют попарно равные углы. Найти вектор, если,
Д-16. Доказать, что при любых векторах векторыикомпланарны.
Д-17. Показать, что векторы имогут быть взяты за ребра куба. Найти третье ребро куба.
Д-18. Векторы иобразуют угол 45о. Найти площадь треугольника, построенного на векторах иесли
Д-19. Дана пирамида с вершинами в точках Найти:
Д-19.1. Длины ребер Д-19.2. Площадь грани Д-19.3. Угол между ребрами иД-19.4. Объем пирамиды.
Д-19.5. Длину высоты, опущенной на грань
Итоговый самоконтроль
С-1. Как построить вектор, перпендикулярный двум векторам и?
С-2. Чему равна проекция ?
С-3. Векторы ,Какому условию удовлетворяют векторыи?
С-4. Как установить компланарность трех векторов, заданных своими координатами?
С-5. Как установить коллинеарность двух векторов, заданных своими координатами?
С-6. Как установить, образуют ли базис в R3 три вектора, заданные своими координатами?
С-7. Доказать, что векторы икомпланарны тогда и только тогда, когда среди чиселиесть равные.
С-8. Пусть — некомпланарные векторы. Как связаны между собой числаесли векторыикомпланарны?
С-9. Векторы удовлетворяют условиюДоказать, что векторыкомпланарны.
С-10. Доказать, что если векторы удовлетворяют равенствуто
С-11. Даны единичные векторы Зная, что, доказать равенство
С-12. Зная, что , найти соотношение между векторамине содержащее коэффициентови
С-13. Чему равно смешанное произведение векторов и, гдеи— произвольные числа?
С-14. Чему равно:
1. .2. .
3. .4. .
С-15. Какому условию должны удовлетворять векторы и, чтобы векторыибыли коллинеарны?
С-16. При каких значениях ивекторыиколлинеарны?
С-17. Чему равно векторное произведение противоположных векторов?
С-18. Изменится ли векторное произведение, если к одному из сомножителей прибавить вектор, коллинеарный другому сомножителю?
С-19. Верны ли утверждения:
а) б)
в) г) .
Ответы поясните.
С-20. Доказать, что
studfiles.net

 .
. ,
проведённой из вершины А.
,
проведённой из вершины А.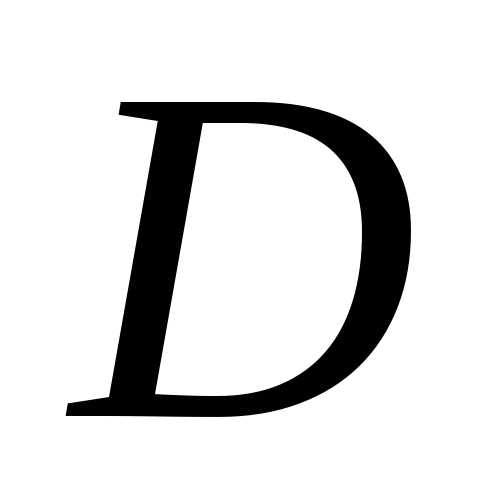 ,
противоположную В.
,
противоположную В.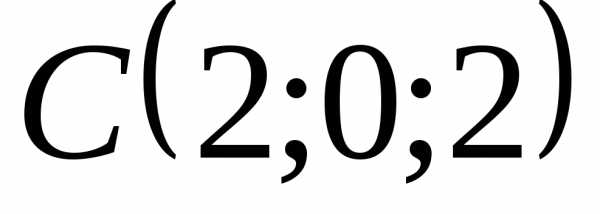 иразделён на три равные части.
иразделён на три равные части.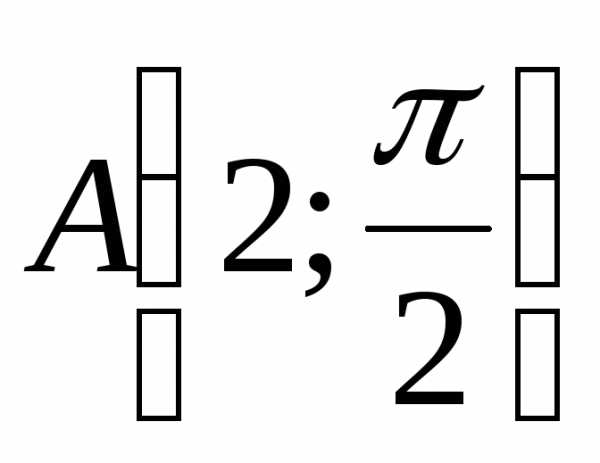 ,
,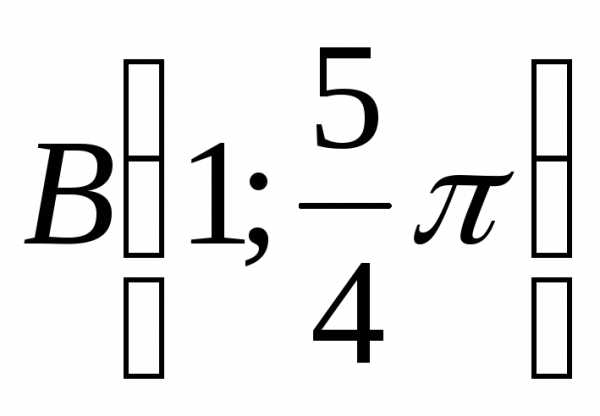 ,
,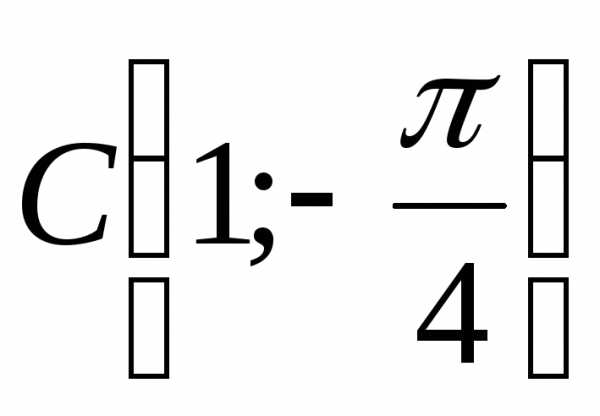 .
.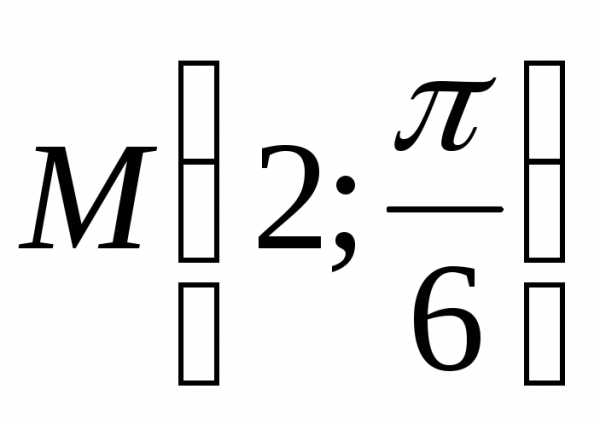 .
Найти её прямоугольные координаты.
.
Найти её прямоугольные координаты.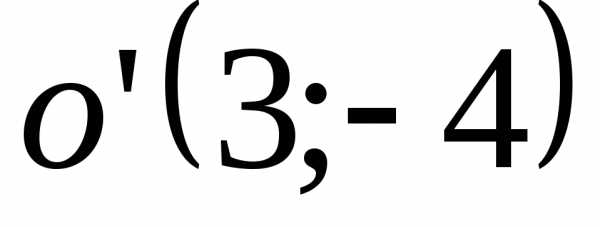 .
Известны старые координаты точки
.
Известны старые координаты точки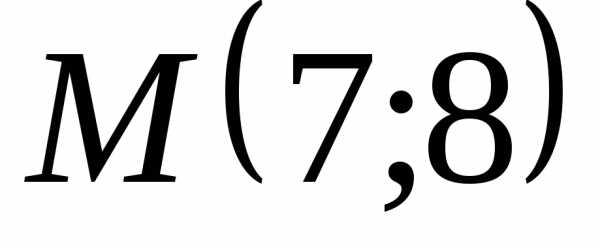 .
Определить новы координаты этой же
точки.
.
Определить новы координаты этой же
точки.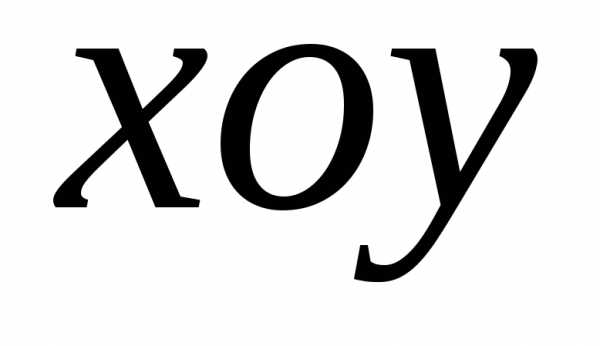 дана точка
дана точка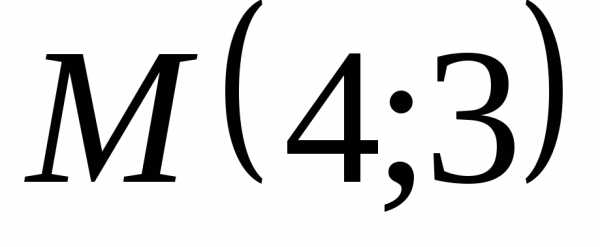 .
Систему координат повернули вокруг
начала координат так, что новая ось
прошла через точку М. Определить старые
координаты точки А, если известны её
новые координаты
.
Систему координат повернули вокруг
начала координат так, что новая ось
прошла через точку М. Определить старые
координаты точки А, если известны её
новые координаты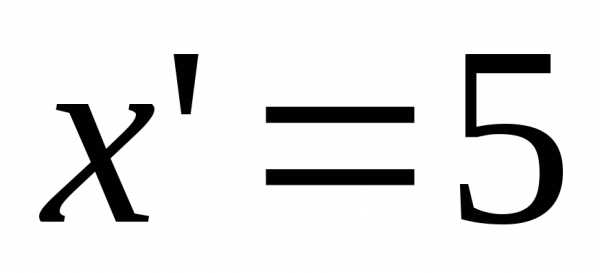 ,
,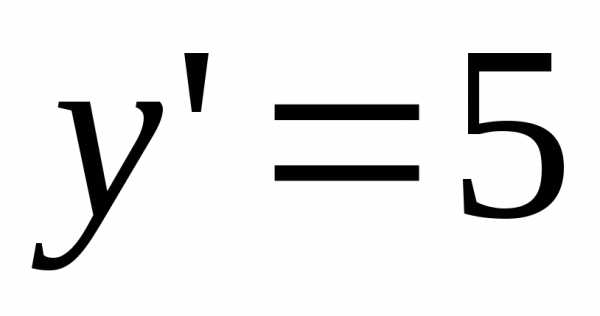 .
.