ВЕКТОРЫ
ВЕКТОРЫ. ДЕЙСТВИЯ НАД ВЕКТОРАМИ. СКАЛЯРНОЕ,
ВЕКТОРНОЕ, СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
1. ВЕКТОРЫ, ДЕЙСТВИЯ НАД ВЕКТОРАМИ.
Основные определения.
Определение 1. Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.
(Масса тела, объем, время и т.д.)
Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.
(Перемещение, сила, скорость и т.д.)
Обозначения: , или , .
Для вектора – точка А – начало, точка В – конец вектора.
Определение 3. Модуль вектора – это длина отрезка AB.
Определение 4. Вектор, модуль которого равен нулю, называется нулевым, обозначается .
Определение 5. Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.
Определение 6. Два вектора считаются равными, если они сонаправлены и равны по модулю.
Действия над векторами.
1) Сложение векторов.
Опр. 6. Суммой двух векторов и является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
Рис.1.
Опр. 7. Суммой трех векторов , , называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Опр. 8. Если А, В, С – произвольные точки, то + = (правило треугольника).
рис.2
Свойства сложения.
1о. + = + (переместительный закон).
3о. + (–) + .
2) Вычитание векторов.
Опр. 9. Под разностью векторов и понимают вектор = – такой, что + = .
В параллелограмме – это другая диагональ СД (см.рис.1).
3) Умножение вектора на число.
Опр. 10. Произведением вектора на скаляр k называется вектор
= k
= k,имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора , если k > 0;
2. противоположно направлению вектора , если k < 0;
3. произвольно, если k = 0.
Свойства умножения вектора на число.
1о. (k + l) = k + l.
k( + )
= k + k
2o. k(l) = (kl).
3o. 1 = , (–1) = – , 0 = .
Свойства векторов.
Опр. 11. Два вектора и называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
Нулевой вектор коллинеарен любому вектору.
Теорема 1. Два ненулевых вектора и коллинеарны, когда они пропорциональны т.е.
= k, k – скаляр.
Опр. 12. Три вектора , , называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
Теорема 2. Три ненулевых вектора , , компланарны, когда один из них является линейной комбинацией двух других, т.е.
= k + l, k ,l – скаляры.
Проекция вектора на ось.
Теорема
3. Проекция
вектора на
ось (направленная прямая) l равна
произведению длины вектора на
косинус угла между направлением вектора
и направлением оси, т.е.
рис.3.
2. КООРДИНАТЫ ВЕКТОРА
Опр. 13. Проекции вектора на координатные оси Ох, Оу, Оz называются координатами вектора. Обозначение: ax,ay, az.
Длина вектора:
Пример: Вычислить длину вектора .
Решение:
Расстояние между точками и вычисляется по формуле:.
Пример: Найти расстояние между точками М (2,3,-1) и К (4,5,2).
Действия над векторами в координатной форме.
Даны векторы =ax, ay, az и =bx, by, bz.
1. ( )=ax bx, ay by, az bz.
2. =ax, ay, az, где – скаляр.
Скалярное произведение векторов.
Определение: Под
скалярным произведением двух векторов
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е. =, — угол между векторами и .
Свойства скалярного произведения:
1. =
2. ( + ) =
3.
4.
5. , где – скаляры.
6. два вектора перпендикулярны (ортогональны), если .
7. тогда и только тогда, когда .
Скалярное произведение в координатной форме имеет вид: , где и .
Пример: Найти скалярное произведение векторов и
Решение:
Векторное проведение векторов.
Определение: Под векторным произведением двух векторов и понимается вектор, для которого:
-модуль равен площади параллелограмма, построенного на данных векторах, т.е. , где угол между векторами и
-этот вектор перпендикулярен перемножаемым векторам, т.е.
-если векторы неколлинеарны, то они образуют правую тройку векторов.
Свойства векторного произведения:
1.При
изменении порядка сомножителей векторное
произведение меняет свой знак на
обратный, сохраняя модуль, т.е.
2.Векторный квадрат равен нуль-вектору, т.е.
3.Скалярный множитель можно выносить за знак векторного произведения, т.е.
4.Для любых трех векторов справедливо равенство
5.Необходимое и достаточное условие коллинеарности двух векторов и :
Векторное произведение в координатной форме.
Если известны координаты векторов и , то их векторное произведение находится по формуле:
.
Тогда из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах и , вычисляется по формуле:
Пример: Вычислить площадь треугольника с вершинами (1;-1;2), (5;-6;2), (1;3;-1).
Решение: .
, , тогда площадь треугольника АВС будет вычисляться следующим образом:
,
Смешанное произведение векторов.
Определение: Смешанным (векторно-скалярным) произведением векторов называется число, определяемое по формуле: .
Свойства смешанного произведения:
1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. .
2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е. .
3.Необходимое и достаточное условие компланарности трех векторов : =0.
4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. .
Если известны координаты векторов , то смешанное произведение находится по формуле:
Пример: Вычислить смешанное произведение векторов .
Решение:
3. Базис системы векторов.
Определение. Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространствуR.
Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами.
Пример.
Определение. Любой вектор вида = называется линейной комбинацией векторов . Числа — коэффициентами линейной комбинации.
Пример. .
Определение. Если вектор является линейной комбинацией векторов , то говорят, что вектор линейно выражается через векторы .
Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой.
Пример. Система векторов линейно-зависима, т. к. вектор .
Определение базиса. Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример 1. Базис пространства : .
2. В системе векторов базисом являются векторы: , т.к. линейно выражается через векторы .
Замечание. Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
studfiles.net
Векторы: определение и основные понятия
Графически вектор изображается в виде направленного отрезка прямой определенной длины. Вектор, начало которого находится в точке , а конец – в точке , обозначается как (рис. 1). Также вектор можно обозначать одной маленькой буквой, например, .
Если в пространстве задана система координат, то вектор можно однозначно задать набором своих координат. То есть под вектором понимается объект, который имеет величину (длину), направление и точку приложения (начало вектора).
Начала векторного исчисления появились в работах в 1831 году в работах немецкого математика, механика, физика, астронома и геодезиста Иоганна Карла Фридриха Гаусса (1777-1855). Работы, посвященные операциям с векторами, опубликовал ирландский математик, механик и физик-теоретик, сэр Уильям Роуэн Гамильтон (1805-1865) в рамках своего кватернионного исчисления. Ученый предложил термин «вектор» и описал некоторые операции над векторами. Векторное исчисление получило свое дальнейшее развитие благодаря работам по электромагнетизму британского физика, математика и механика Джеймса Клерка Максвелла (1831-1879). В 1880-х годах увидела свет книга «Элементы векторного анализа» американского физика, физикохимика, математика и механика Джозайя Уилларда Гиббса (1839-1903). Современный векторный анализ был описан в 1903 году в работах английского ученого-самоучки, инженера, математика и физика Оливера Хевисайда (1850-1925).
Длина (модуль) вектора
Основные виды векторов
Нулевым вектором называется вектор , у которого начальная точка и конечная точка совпадают. Длина нулевого вектора равна нулю.
Вектора, параллельные одной прямой или лежащие на одной прямой, называют коллинеарными (рис. 2).
Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
На рисунке 2 – это векторы и . Сонаправленность векторов обозначается следующим образом: .
Два коллинеарных вектора называются противоположно направленными, если их направления противоположны.
На рисунке 3 – это векторы и . Обозначение: .
Три вектора, параллельные одной плоскости или лежащие в одной плоскости, называют компланарными (рис. 3).
Два вектора и называются равными, если они являются сонаправленными и их длины равны (рис. 4):
Единичным вектором или ортом называется вектор единичной длины.
ru.solverbook.com
Понятие вектора
Существуют величины, которые характеризуются помимо своей величины ещё и направленностью. Это скорость, ускорение, сила, смещение материальной точки и т.п. Можно абстрагироваться от конкретной физической величины и считать, что вектор — это направленный отрезок. Определение: вектор — это направленный отрезок.
Будем обозначать вектор AB . А — начало вектора, В — конец вектора.
— означает длина вектора (символ модуля).
Вектор называется нулевым, если его начало и конец совпадают.
Важное свойство векторов — коллинеарность. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Теперь сформулируем понятие равенства двух векторов: два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление. Два нулевых вектора считаются равными.
равные неравные
Из определения равенства векторов следует, что мы не различаем двух равных векторов, имеющих разные точки приложения. Иными словами, точка приложения вектора может быть произвольной. В соответствии с этим векторы в геометрии называются свободными.
Определим линейные операции над векторами.
Сложение. Суммой 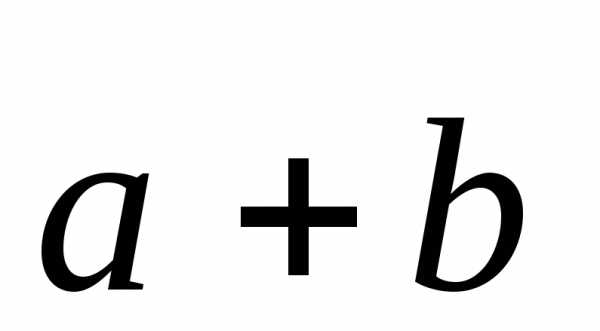 двух векторов
двух векторов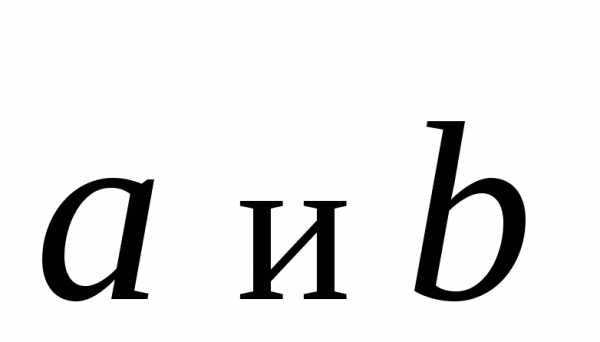 называется
вектор, идущий из начала вектора
называется
вектор, идущий из начала вектора в конец вектора
в конец вектора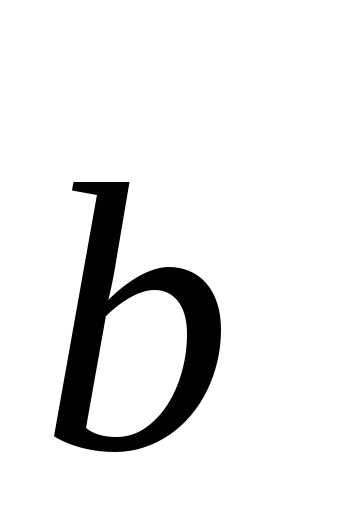 при условии, что начало
при условии, что начало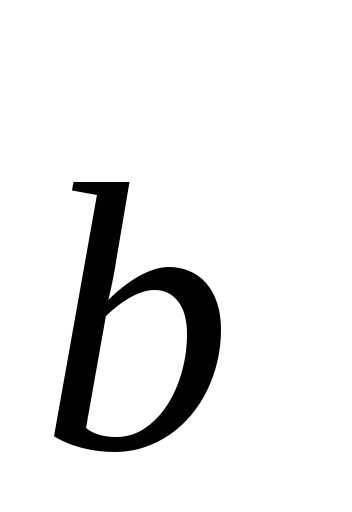 приложено к концу вектора
приложено к концу вектора .
.
Геометрически это можно изобразить правилом треугольника:
Правило сложения векторов обладает теми же четырьмя свойствами, что и правило сложения вещественных чисел:
1. (переместительное свойство).
2. (сочетательное свойство).
3. Существует нулевой вектор, такой, что .
4. Для каждого  существует такой
существует такой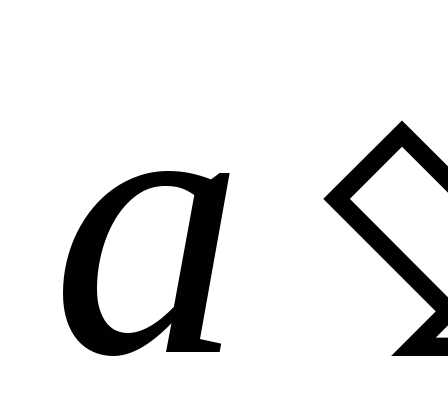 что.
что.
Эти свойства доказываются геометрическими построениями. К примеру свойство 1:
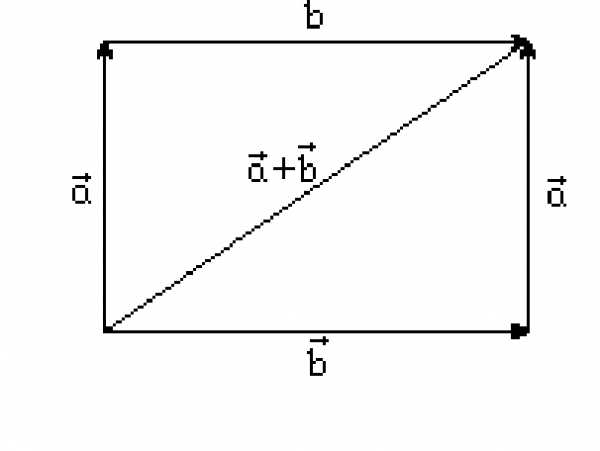
Эти свойства позволяют оперировать с векторами так же как и с вещественными числами.
Определим
разность векторовкак сумму где
где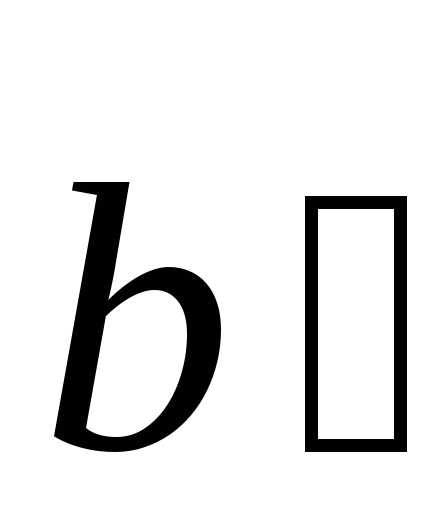 —
противоположный вектор вектору
—
противоположный вектор вектору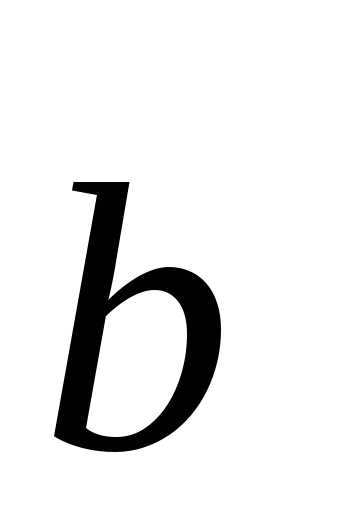 .
.
Определим, наконец, операцию умножения вектора на вещественное число.
Произведением  называется вектор
называется вектор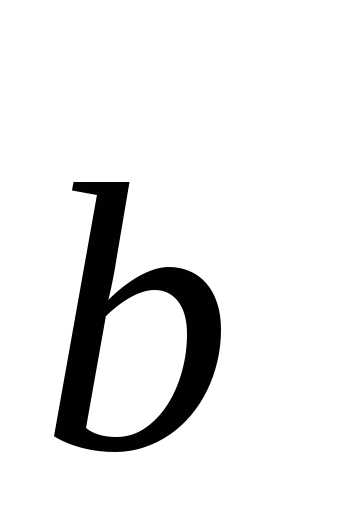 ,
коллинеарный
,
коллинеарный ,
имеющий длину
,
имеющий длину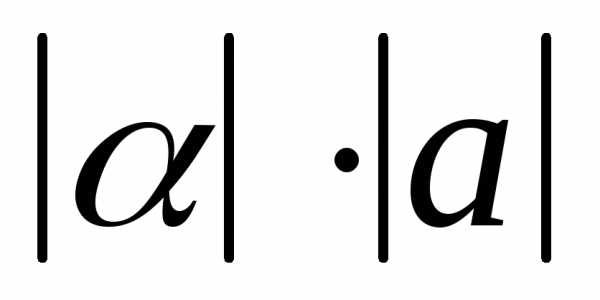 и имеющий направление, совпадающее с
и имеющий направление, совпадающее с еслии
противоположное, если.
еслии
противоположное, если.
Геометрический
смысл умножения — вектор  растягивается враз.
растягивается враз.
Операция умножения обладает тремя свойствами:
5. (распределительное свойство относительно суммы векторов).
6. (распределительное свойство относительно суммы чисел).
7. (сочетательное свойство).
Доказываются эти свойства тоже графически.
Рассмотрим теорему
1. Если вектор 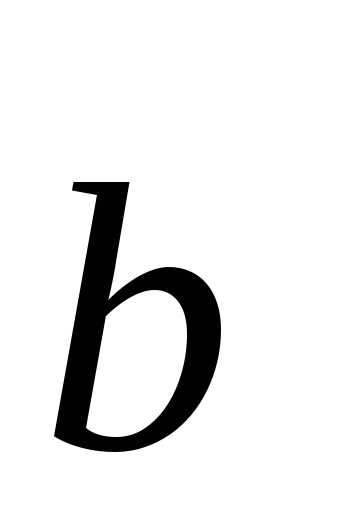 коллинеарен
вектору
коллинеарен
вектору ,
то существует такое вещественное число,
что
,
то существует такое вещественное число,
что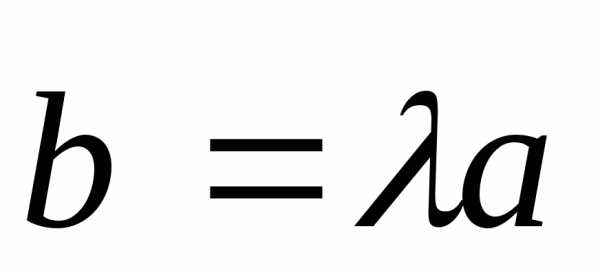 .
.
Совместим 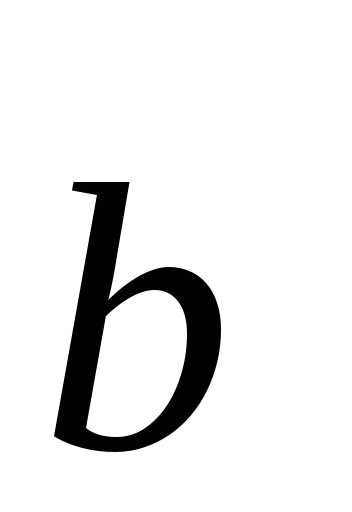 и
и .
В силу коллинеарности они окажутся на
одной прямой. Т. е.
.
В силу коллинеарности они окажутся на
одной прямой. Т. е.
O
(*)
Докажем, что 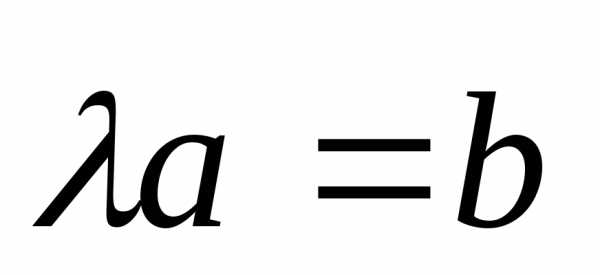 .
Т.е. что длины их равны, направления
совпадают, коллинеарны.
.
Т.е. что длины их равны, направления
совпадают, коллинеарны.
Коллинеарность
вытекает из определения произведения 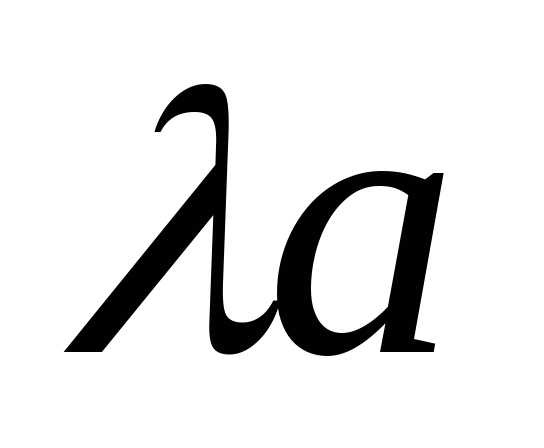 и
коллинеарности
и
коллинеарности и
и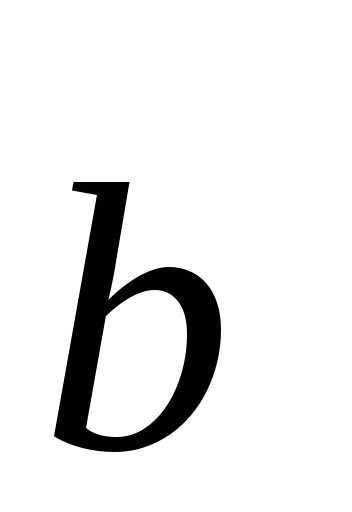 ,
равенство длин непосредственно из
определения произведения и (*). Наконец,
опять из определения произведения
следует, что если,
направления совпадают, и если,
то
,
равенство длин непосредственно из
определения произведения и (*). Наконец,
опять из определения произведения
следует, что если,
направления совпадают, и если,
то и
и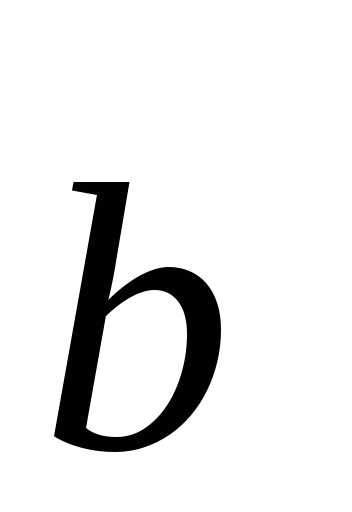 —
противоположно направлены.
—
противоположно направлены.
Определение 1. Линейной комбинацией n векторов мы называем сумму вида
где  —
вещественные числа.
—
вещественные числа.
Определение 2.
Векторы 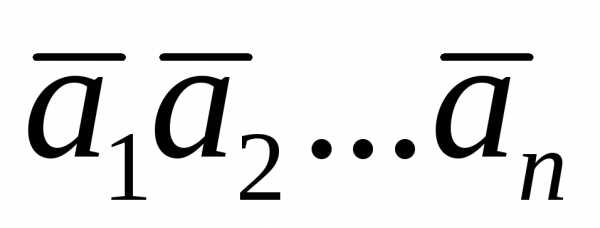 называются линейно зависимыми, если
существуют такие, хотя бы одно из которых отлично от
нуля, что имеет место равенство:
называются линейно зависимыми, если
существуют такие, хотя бы одно из которых отлично от
нуля, что имеет место равенство:
Если все 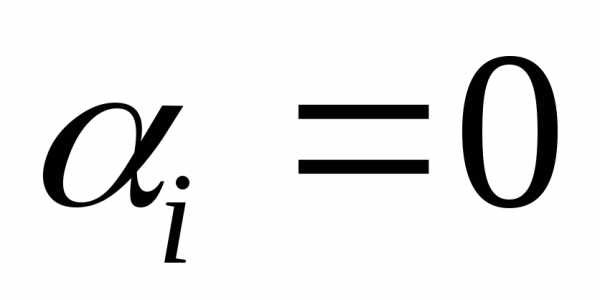 ,
то такие векторыназываются линейно независимыми.
,
то такие векторыназываются линейно независимыми.
Докажем теорему
2. Если среди n векторов
хотя бы один нулевой, то эти векторы
являются линейно зависимы. Доказательство:
пусть для определённости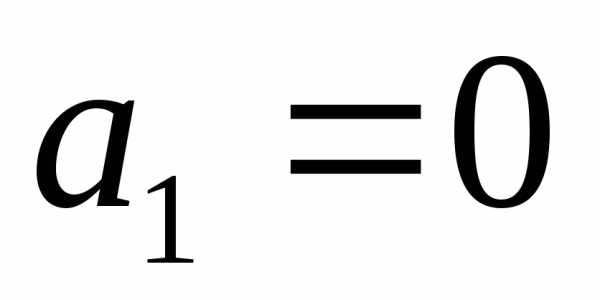 .
Тогда выполняется равенство:
.
Тогда выполняется равенство:
где .
и по определению линейной зависимости эти векторы линейно зависимы.
Теорема номер
три: если
среди п векторов 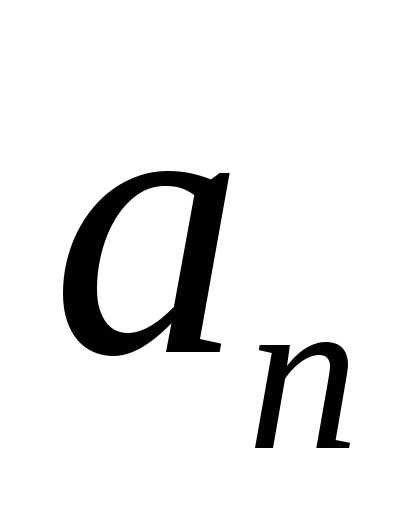 какие
либо (п-1)
линейно зависимы, то и все п являются линейно зависимы.
какие
либо (п-1)
линейно зависимы, то и все п являются линейно зависимы.
Действительно: линейная зависимость (п-1) векторов означает:
Добавим сюда равное
0 слагаемое 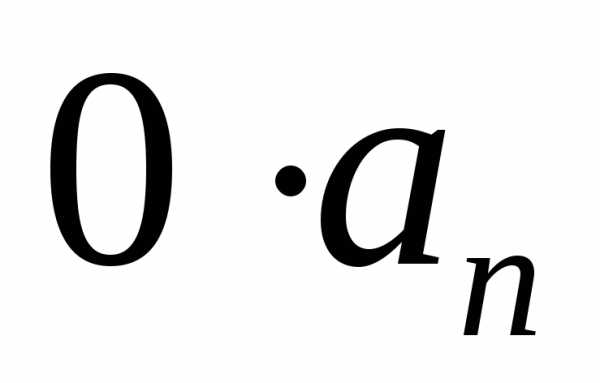 и получим,
и получим,
где не все равны нулю, т.е. теорема доказана.
Линейные комбинации двух векторов.
Теорема 4. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Доказательство
необходимости: предположим, что  и
и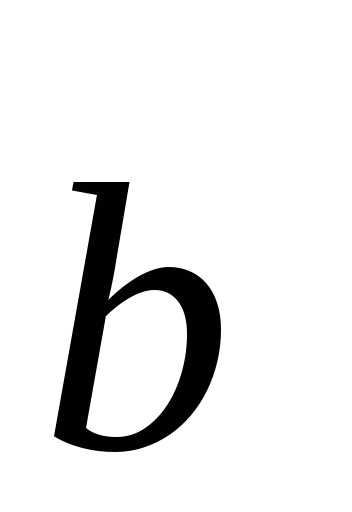 линейно зависимы. Т.е.
линейно зависимы. Т.е.
положим, что
.
Тогда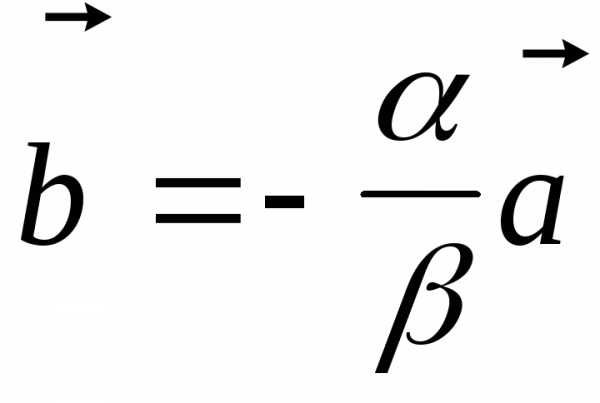 или
или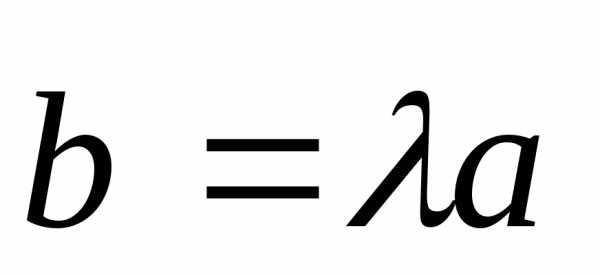 .
По определению произведения
.
По определению произведения и
и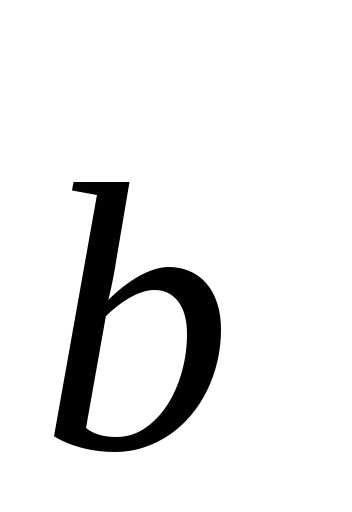 коллинеарны.
коллинеарны.
Достаточность:
предположим,  и
и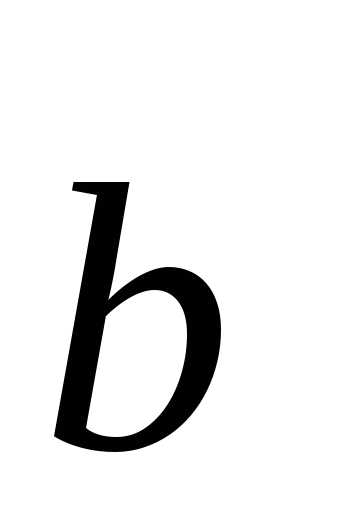 коллинеарны.
Если
коллинеарны.
Если или
или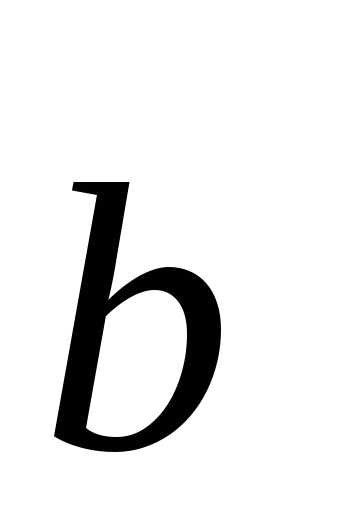 равно
нулю, то они линейно зависимы в силу
теоремы 2. Если
равно
нулю, то они линейно зависимы в силу
теоремы 2. Если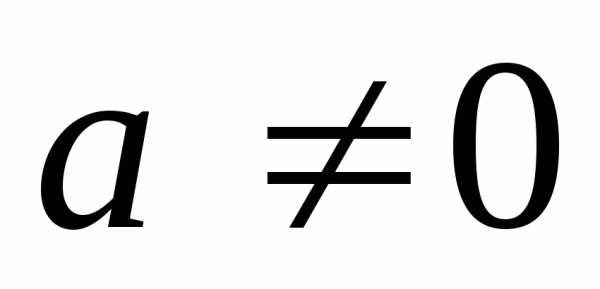 и
и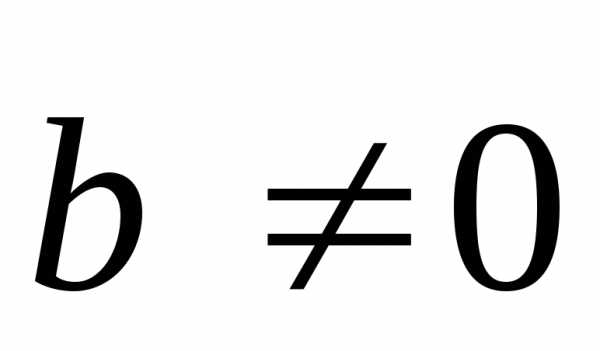 то в силу теоремы 1 имеем:
то в силу теоремы 1 имеем:
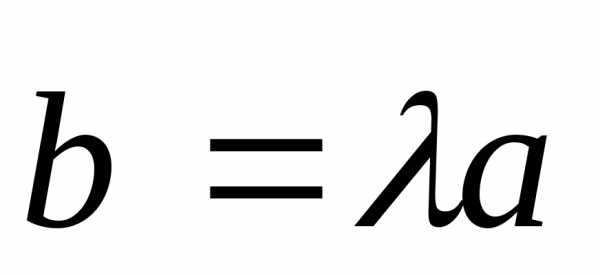 ,
или
.
,
или
.
Т. к. здесь заведомо
(-1) не равно 0, то равенство доказывает
линейную зависимость векторов  и
и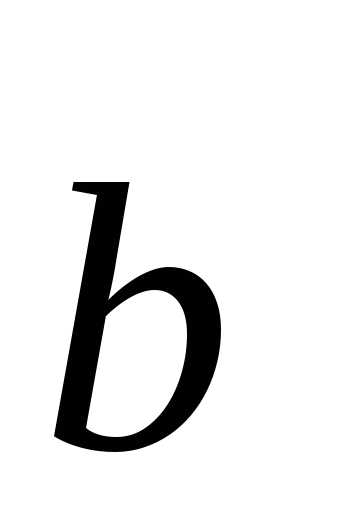 .
.
Следствие 1. Если
векторы  и
и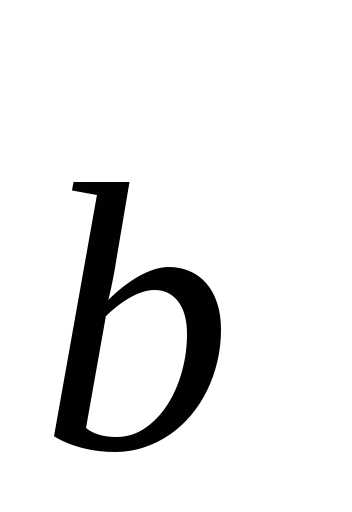 неколлинеарны, то они линейно независимы.
неколлинеарны, то они линейно независимы.
Следствие 2. Среди двух неколлинеарных векторов не может быть нулевых. (Иначе они были бы линейно зависимы).
Линейные комбинации трёх векторов
Определение: векторы называются компланарными, если они лежат в одной плоскости, либо в параллельных плоскостях.
Теорема 5. Необходимым и достаточным условием линейной зависимости трёх векторов является их компланарность.
Необходимость: пусть три вектора линейно зависимы:
.
Тогда 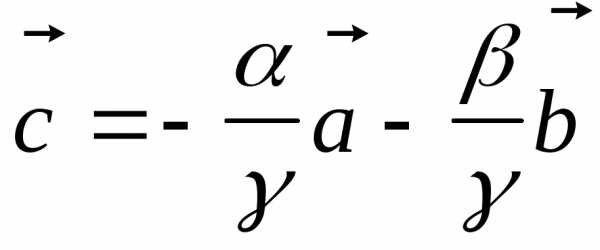 ,
или
,
или
Это равенство означает сложение двух векторов, т.е. все три вектора лежат в одной плоскости.
Достаточность:
пусть  компланарны. Исключим случай, когда
пара векторов коллинеарна и когда
какой-либо вектор равен 0. Эти случаи
тривиальны. Рассмотрим случай, когда
все неколлинеарны.
компланарны. Исключим случай, когда
пара векторов коллинеарна и когда
какой-либо вектор равен 0. Эти случаи
тривиальны. Рассмотрим случай, когда
все неколлинеарны.
Перенесём все векторы в одну плоскость. Поскольку они неколлинеарны, то существует их общая точка пересечения:
В силу теоремы 1,
найдутся такие
и,
что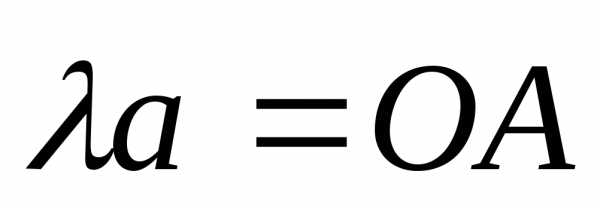

или . Теорема доказана.
Следствие:
Если векторы и
и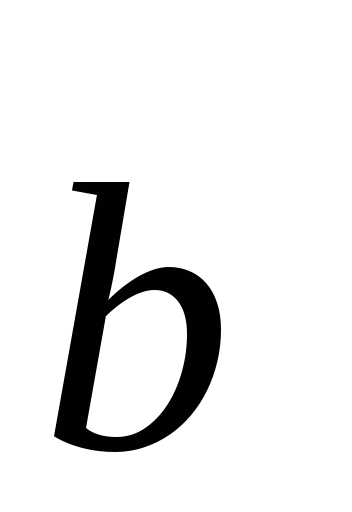 неколлинеарны,
то для любого
неколлинеарны,
то для любого ,
лежащего в одной плоскости с векторами
,
лежащего в одной плоскости с векторами и
и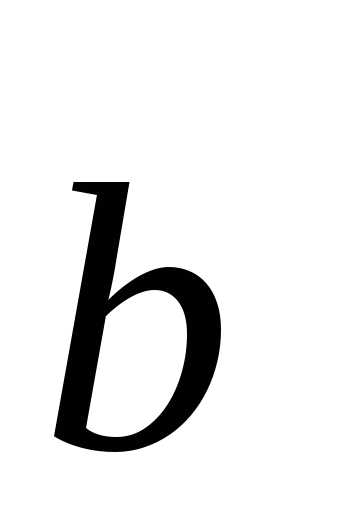 найдутся
такиеи,
что выполнится равенство:
найдутся
такиеи,
что выполнится равенство:
Наконец, линейная зависимость трёх векторов.
Теорема 6. Любые четыре вектора линейно зависимы.
Доказательство. Исключим тривиальные случаи, когда один из векторов ноль или когда какие-либо три компланарны. По предыдущим теоремам будут линейно зависимы все четыре вектора. Т.е. все векторы некомпланарны. Сведём их в одну точку и построим параллелепипед:
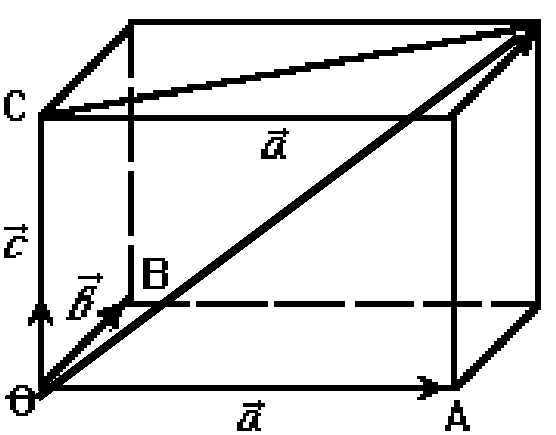
По теореме 1 найдутся такие числа, что:
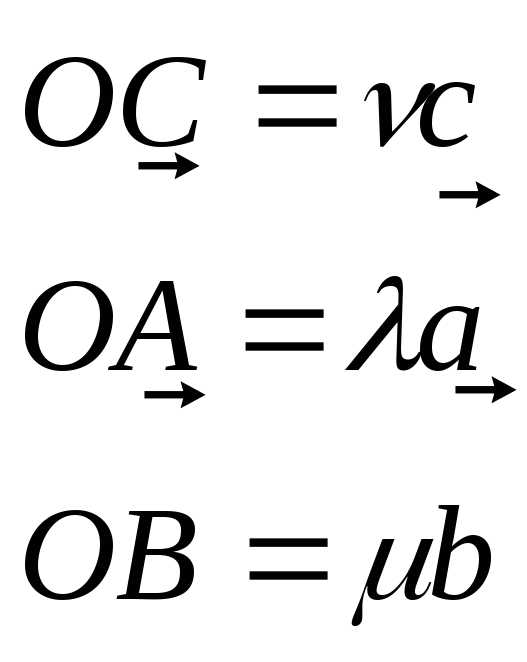
Но вектор  равенилиили.
равенилиили.
Теорема доказана.
Попутно мы доказали,
что если 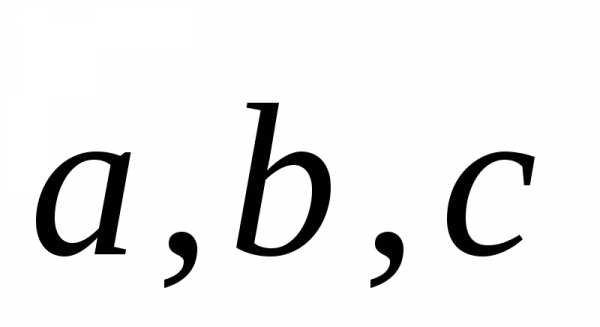 ,
какие-либо некомпланарные, т.е. линейно
независимые векторы, то для любого
вектора
,
какие-либо некомпланарные, т.е. линейно
независимые векторы, то для любого
вектора можно найти такие числа,
что
можно найти такие числа,
что
.
Понятие базиса.
Говорят, что три
линейно независимых вектора 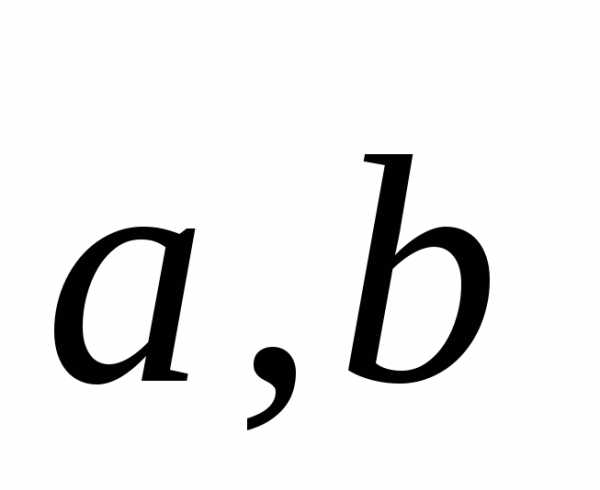 и
и образуют
в пространстве базис, если любой вектор
образуют
в пространстве базис, если любой вектор может
быть представлен в виде линейной
комбинации векторов
может
быть представлен в виде линейной
комбинации векторов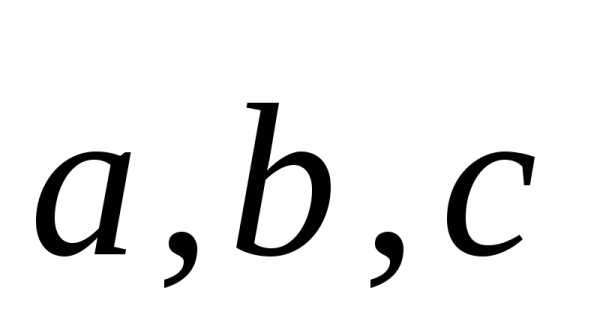
(**)
Принято называть
(**) разложением вектора d
по базису 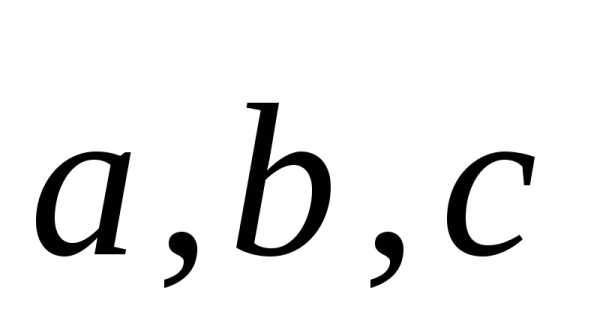 ,
а числа-координатами
вектора
,
а числа-координатами
вектора относительно
базиса
относительно
базиса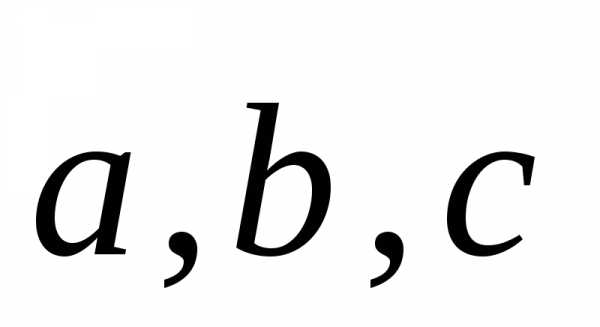 .
Причём можно доказать, что разложение
.
Причём можно доказать, что разложение по
базису
по
базису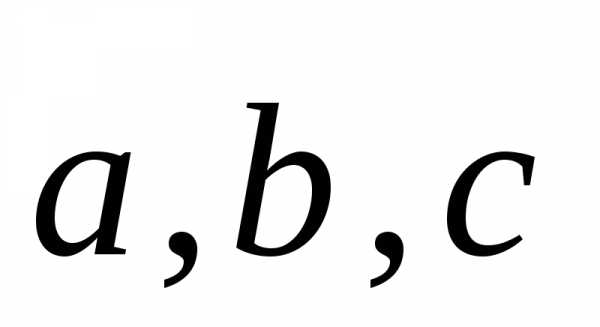 может быть единственным образом
осуществлено.
может быть единственным образом
осуществлено.
Определим так
называемые афинные
координаты.
Афинные координаты в пространстве
определяются заданием базиса 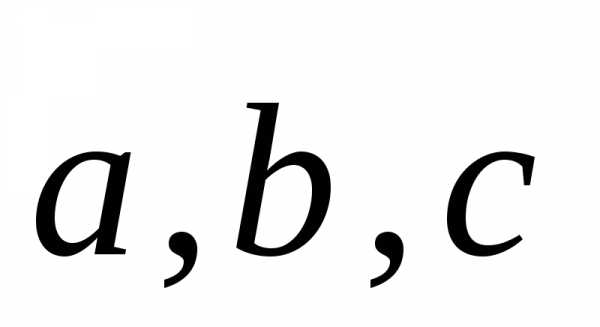 и некоторой точки О, называемой началом
координат.
и некоторой точки О, называемой началом
координат.
Частным случаем
афинных координат являются, очевидно,
прямоугольные декартовы координаты,
Здесь введём три взаимно перпендикулярных
(ортогональных) единичных векторов 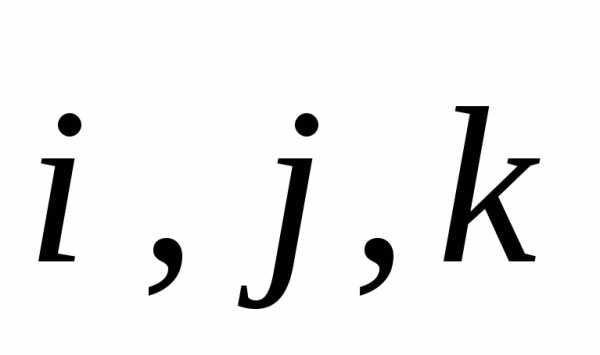 .
Для каждого вектора
.
Для каждого вектора найдётся
и при том единственная тройка чисел,
такая, что
найдётся
и при том единственная тройка чисел,
такая, что
Числа X,Y,Z называют декартовы прямоугольные координаты.
Введём определение
проекции вектора на ось v.
Дан вектор 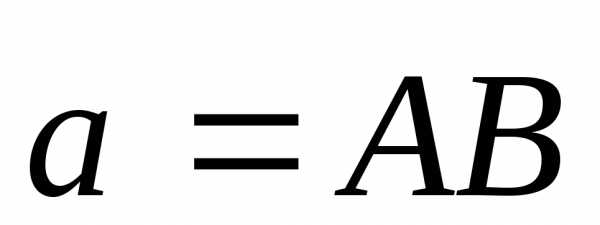 .
Опустим перпендикуляры из точек А и В
на осьv.
Основания перпендикуляров обозначим
и.
.
Опустим перпендикуляры из точек А и В
на осьv.
Основания перпендикуляров обозначим
и.
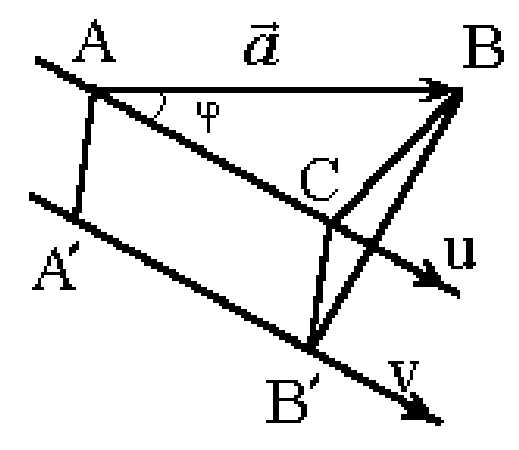
Проекцией вектора  на
осьv назовём величину направленного отрезка
на
осьv назовём величину направленного отрезка 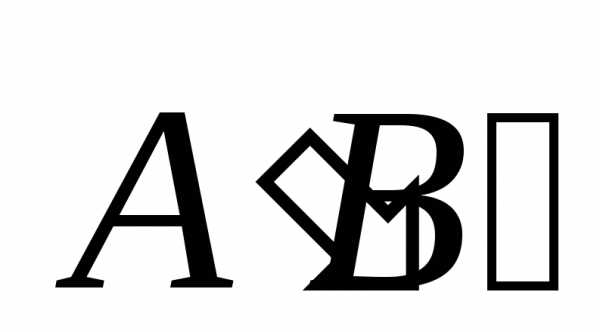 осиv.
осиv.
Углом наклона
вектора  к осиv назовём угол
между направлением вектора
к осиv назовём угол
между направлением вектора и направлением осиv.
Из рассмотрения треугольника АВС
следует, что
.
и направлением осиv.
Из рассмотрения треугольника АВС
следует, что
.
Можно доказать,
что декартовы координаты X,Y,Z вектора  являются
проекции векторана
оси соответственно ортам:
являются
проекции векторана
оси соответственно ортам:
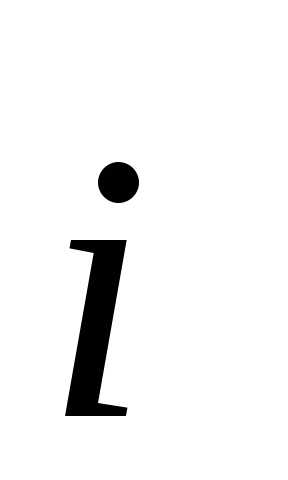 -ось
Ох,
-ось
Ох, 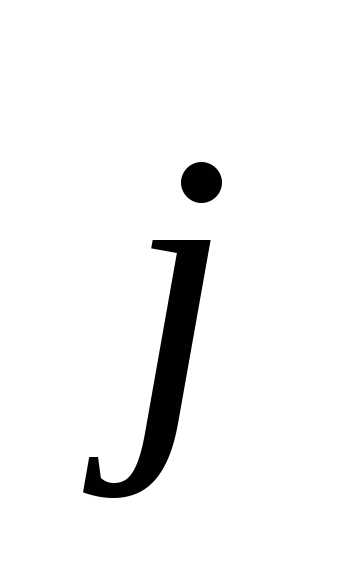 -ось
Oy ,
-ось
Oy , —
ось Oz.
—
ось Oz.
Или можно записать:
(***)
Три числа
называются направляющими косинусами
вектора .
.
Длина диагонали параллелепипеда равна
Тогда можно записать:
Возведём в квадрат и складывая, получим равенство:
.
Лекция 5.
studfiles.net
Определение вектора. Виды векторов — МегаЛекции
Математические или физические величины, которые характеризуются только числом, измеряющим их в определенных единицах меры, называют скалярными или скалярами. Скалярами являются, например масса, объем и т.п.
Кроме скалярных величин существуют величины векторные (скорость, ускорение, сила и т.п.)
Вектором называется величина, которая характеризуется числом, измеряющим ее в определенных единицах меры, и направлением в пространстве. Обозначается вектор или буквой со стрелкой , или жирной буквой a.
Число , измеряющее вектор в определенных единицах меры, называется модулем или длиной вектора. Зачастую обозначают простой буквой а.
Геометрически вектор изображают отрезком со стрелкой. Направление стрелки указывает направление вектора в пространстве, а длина отрезка изображает модуль вектора (см. рис. 1а).
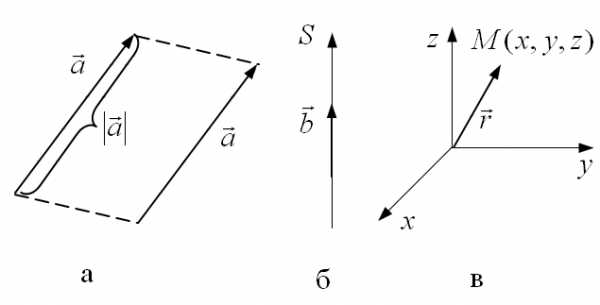
Рис. 1
Два вектора называются равными, если равны их длины и совпадают направления.
Вектор, длина которого равна нулю, называется нулевым. Его направление не определено.
Вектор, длина которого равна единице, называется единичным.
Вектор называется противоположным вектору , так как его длина равна длине вектора и он имеет обратное направление.
Единичный вектор расположенный параллельно вектору , может быть определен соотношением . Соответственно, любой вектор может быть представлен в виде .
Проекцией вектора на направление единичного вектора называется вектор , направление которого совпадает с направлением единичного вектора , а длина равна произведению длины вектора на косинус угла между векторами и (см. рис. 2):
, где
Рис.2
В зависимости от видов допускаемых инвариантных[†] преобразований векторы как математическое понятие могут быть разделены на три типа.
1. Простые векторы, которые обычно мы называем одним словом вектор. Инвариантным преобразованием для векторов является параллельный перенос в произвольном направлении (см. рис.1.а).
2. Аксиальные векторы. Эти векторы могут располагаться только вдоль определенного направления (см. рис. 1.б). Инвариантным преобразованием для аксиального вектора является его перенос вдоль этого направления.
3. Радиус – вектор соединяет начало координат с точкой, имеющей определенные координаты x, y, z. Для радиус – вектора ни параллельный перенос, ни вращение инвариантными преобразованиями не являются.
Сложение и вычитание векторов
Суммой двух векторов и называется вектор, совпадающий с замыкающей стороной треугольника, построенного на данных двух векторах (см. рис. 1.а).
Рис.4
Правило сложения векторов:
1. ,
2. .
Эти законы позволяют находить сумму любого числа векторов. На рис. 3.б приведено сложение четырех векторов.
Если многоугольник, построенный на данных векторах, окажется замкнутым так, что конец последнего слагаемого вектора совпадет с началом первого слагаемого, то сумма данных векторов будет равна нулю. И обратно, если сумма некоторых векторов равна нулю, то построенный на этих векторах многоугольник будет замкнутым.
Разностью двух векторов называется сумма вектора с вектором , противоположным вектору (см. рис. 4):
.
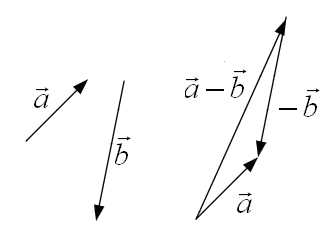
Рис.4
Умножение вектора на число
Произведением скаляра на вектор называется вектор, длина которого равна , а направление его совпадает с направлением , если , и противоположно , если . Произведение вектора на скаляр подчиняется законам умножения чисел:
.
Произведение векторов
Из двух векторов можно образовать два существенно различных произведения: скалярное и векторное.
Скалярное произведение
Скалярным произведением двух векторов и называется произведение модулей этих векторов на косинус угла между этими векторами: . Эквивалентной формой записи скалярного произведения является выражение .
Пусть — единичный вектор, , тогда , т.е. скалярное произведение любого вектора на единичный вектор определяет величину проекции вектора на направление этого единичного вектора.
Скалярное произведение векторов обладает следующими свойствами:
1. ;
2. .
Если векторы и взаимно перпендикулярны, то их скалярное произведение . И обратно, если скалярное произведение двух отличных от нуля векторов равно нулю, то эти векторы взаимно перпендикулярны.
Векторное произведение
Векторным произведением двух векторов и называется
вектор или в эквивалентной форме , который
а) направлен перпендикулярно плоскости, в которой лежат вектора и , в сторону поступательного перемещения правого винта, если его вращать от первого сомножителя ко второму в направлении наименьшего угла между векторами;
б) имеет длину, равную произведению длин векторов и на синус угла между ними (см. рис. 1): .
Векторное произведение обладает следующими свойствами:
;
;
.
Рис.5
Произведение трех векторов
Из трех произвольных векторов и и можно образовать два существенно различных произведения: смешанное и двойное векторное произведение.
Смешанное произведение трех векторов
Смешанным произведением трех векторов , и называется скалярное произведение одного из них на векторное произведение двух других:
.
Абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих трех векторах.
С помощью смешанного произведения трех векторов решается вопрос об их компланарности.
Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях. Очевидно, любые два вектора являются компланарными.
Три вектора не всегда компланарны. Для того, чтобы три вектора были компланарными необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Двойное векторное произведение
Двойным векторным произведением трех векторов называется векторное произведение одного из них на векторное произведение двух других. Вектор, получившийся в результате двойного векторного произведения , лежит в плоскости векторов и и может быть представлен выражением
.
Координатная форма представления векторов
В системе координат XYZопределим единичные векторы в направлении OX, OYи OZкак . Тогда произвольный вектор может быть представлен в виде суммы трех взаимно перпендикулярных векторов, направленных по осям координат: ,
где скаляры — проекции вектора на координатные оси OX, OYи OZсоответственно.
Векторы и взаимно перпендикулярны друг другу, поэтому для них выполняются соотношения:
;
.
Радиус – вектор, проведенный из начала координат в некоторую точку М с координатами (x;y;z), также может быть определен в координатной форме (рис.6): .

Рис.6
Правила действия над векторами, заданными в координатной форме:
,
,
.
1. Сложение и вычитание.
2. Скалярное произведение.
3. Векторное произведение.
Из формул для скалярного произведения двух векторов можно получить формулу для вычисления модуля произвольного вектора :
.
С другой стороны,
.
Поэтому .
Если — единичный вектор. Тогда его проекциями на оси координат будут косинусы углов , образованных единичным вектором с осями координат OX, OY, OZсоответственно. Из предыдущей формулы, записанной для случая единичного вектора, получим условие .
Отметим, что направляющие косинусы можно определить и для любого произвольного вектора :
.
Из формулы для скалярного произведения двух векторов можно получить также выражение, определяющее косинус угла между этими векторами:
.
Формулы дифференциального исчисления
Формулы интегрального исчисления
Соотношение между внесистемными единицами и единицами СИ
| Длина | 1 ангстрем ( ) = |
| Время | 1 сут = 86400 с, 1 год = 365,25 сут = |
| Плоский угол | |
| Объем, вместимость | |
| Масса | , |
| Сила | |
| Работа, энергия | , , |
| Мощность | |
| Давление | , , , |
| Напряжение (механическое) | |
| Частота вращения | , |
| Концентрация частиц | |
| Теплота (количество теплоты) | , |
Эффективный диаметр молекул, динамическая вязкость и теплопроводность газов при нормальных условиях
| Вещество | Эффективный диаметр , | Динамическая вязкость , | Теплопроводность , |
| Азот Аргон Водород Воздух Гелий Кислород Пары воды | 0,38 0,35 0,28 – 0,22 0,36 – | 16,6 21,5 8,66 17,2 – 19,8 8,32 | 24,3 16,2 24,1 – 24,4 15,8 |
Динамическая вязкость жидкостей при
Вода …………………..……………….…… 1,00
Глицерин ………………………………….. 1480
Масло касторовое ………………….……… 987
Масло машинное ………………………….. 100
Ртуть ……………………….…………….… 1,58
Основные физические постоянные
(округленные с точностью до трех значащих цифр)
Нормальное ускорение свободного падения ………..
Гравитационная постоянная ……………
Постоянная Авогадро ………………..………
Молярная газовая постоянная …………….
Стандартный объем *……………………….
Постоянная Больцмана ……………………….
Атомная единица массы ………………………
* Молярный объем идеального газа при нормальных условиях
[*] Бесконечно малый угол поворота , может быть представлен в виде вектора, направленного вдоль оси вращения. Это возможно, когда радиус-вектор можно считать неизменным. Определение векторного произведения двух векторов см. в приложении (стр. 103).
[†] Инвариантностью в математике называется свойство неизменности по отношению какому либо преобразованию (условию) или совокупности преобразований.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Понятие вектора [wiki.eduVdom.com]
Вектором называется направленный отрезок, имеющий определенную длину, т. е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая — за конец. Если А — начало вектора и В — его конец, то вектор обозначается символом $\overrightarrow{АВ}$ (или $\overline{АВ}$). Обычно векторы обозначают одной малой латинской буквой со стрелкой (или с чертой) либо выделяют жирным шрифтом: $\overrightarrow{a}\,,\,\ \overline{a}\,,\,\ {\bf а}$ . Вектор изображается отрезком со стрелкой на конце (рис.1).
Рис.1
Длина вектора $\overrightarrow{АВ}$ называется его абсолютной величиной или модулем и обозначается символом $|\overrightarrow{АВ}|$.
Вектор $\overrightarrow{a}$, у которого $|\overrightarrow{a}| = 1$ , называется единичным.
Вектор называется нулевым (обозначается $\overrightarrow{0}$ или ${\bf 0}$), если начало и конец его совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.
Векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Нулевой вектор коллинеарен любому вектору.
Два вектора $\overrightarrow{a}$ и $\overrightarrow{b}$ называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. В этом случае пишут $\overrightarrow{a} = \overrightarrow{b}$ . Все нулевые векторы считаются равными.
Из определения равенства векторов непосредственно следует, что, каковы бы ни были вектор $\overrightarrow{a}$ и точка Р, существует, и притом единственный, вектор $\overrightarrow{PQ}$ с началом в точке Р, равный вектору $\overrightarrow{a}$ . В самом деле, существует лишь одна прямая, проходящая через точку Р и параллельная той прямой, на которой лежит вектор $\overrightarrow{a}$ . На указанной прямой существует единственная точка Q такая, что отрезок PQ имеет длину, равную длине вектора $\overrightarrow{a}$ , и направлен в ту же сторону, что и вектор $\overrightarrow{a}$ . Таким образом, вектор можно переносить параллельно самому себе, помещая его начало в любую точку плоскости.
Пример 1. Рассмотрим квадрат ABCD (рис. 120).
На основании определения равенства векторов можно записать $\overrightarrow{AD} = \overrightarrow{ВС} \,и\, \overrightarrow{АВ} = \overrightarrow{DC} \,,но\, \overrightarrow{AB} \neq \overrightarrow{AD}\,,\, \overrightarrow{ВС} \neq \overrightarrow{DC}\,,\, хотя \overrightarrow{|АВ|} = \overrightarrow{|AD|} = \overrightarrow{|ВС|} = \overrightarrow{|DC|} $ .
Пример 2. Какой вид имеет четырехугольник ABCDy если известно, что $\overrightarrow{AD} = \overrightarrow{ВС}$ ?
Решение. Из равенства $\overrightarrow{AD} = \overrightarrow{ВС}$ следует, что стороны AD и ВС в четырехугольнике равны и параллельны и, значит (теорема 2), он параллелограмм.
Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными.
Вектор, противоположный вектору $\overrightarrow{a}$, обозначается $-\overrightarrow{a}$. Для вектора $\overrightarrow{AB}$ противоположным является вектор $\overrightarrow{BA}$ .
www.wiki.eduvdom.com
Занятие по геометрии «Понятие вектора в разных науках. Виды векторов. Действия над векторами»

Тема. Векторы в пространстве. Операции над векторами.

Цели и задачи:
- Определение вектора. Координаты вектора и его модуль. Нулевой вектор.
- Понятие вектора в разных науках.
- Виды векторов (коллинеарные, сонаправленные, противоположно направленнные, равные).
- Действия над векторами(сложение, вычитание, умножение на число, скалярное умножение).
- Условие перпендикулярности векторов.
- Угол между векторами.

«Никакой достоверности нет в науках там,
где нельзя приложить ни одной
из математических наук, и в том,
что не имеет связи с математикой».
Леонардо да Винчи .

Вектор – направленный отрезок.
Координатами вектора с началом в точке А1 (x1; y1; z1) и концом в точке
А2 (х2; y2; z2) называются числа
x2-x1, y2-y1, z2-z1 . Пример.
Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Модулем (длиной или абсолютной величиной) вектора называется длина отрезка, изображающего вектор. Формула.

Понятие вектора в науках.
Электрокардиогра́фия — методика регистрации и исследования электрических полей, образующихся при работе сердца.
На электрокардиограмме (ЭКГ) отражается усреднение всех векторов потенциалов действия, возникающих в определённый момент работы сердца.

2. В биологии.
Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

3. В микробиологии. В эпидемиологии вектор — организм, переносящий паразитов от одного организма-хозяина к другому — переносчик инфекционных заболеваний.
Например, вши переносят возбудителей сыпного тифа, крысы – чумы, а клещи являются переносчиками вируса, вызывающего энцефалит.

4. В философии:
Эмана́ция (лат. emanatio — истечение, распространение), понятие античной философии, онтологический вектор перехода от высшей сферы к низшим, менее совершенным сферам; т.е. распространение избыточной полноты абсолютного Бытия [за пределы собственно своего бытия].

5. В химии.
- Электронное строение атомов.
- Обратимые реакции.
- Знаком вектора обозначается осадок, или газ.

6. В физике
Векторы — сила , скорость , ускорение , напряженность электрического и магнитного полей . Их можно противопоставить другим величинам, таким, как масса ,площадь, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они » скалярами «.

7. В геометрии:
под векторами понимают направленные отрезки. С помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов, а так же объёмы тетраэдра и параллелепипеда.

Виды векторов.
Два ненулевых вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.
Условие коллинеарности векторов.
Два вектора коллинеарные, если их соответствующие координаты пропорциональны.
Пример.

Если векторы и коллинеарные и их лучи направлены в одну сторону, то векторы называются сонаправленными .
Обозначаются : а↑↑ b .
Если векторы и коллинеарные и их лучи направлены в разные стороны, то векторы называются противоположно направленными .
Обозначаются : a ↑↓ d .
Нулевой вектор считают сонаправленным с любым.
Два вектора называются равными , если они сонаправлены и их длины равны.
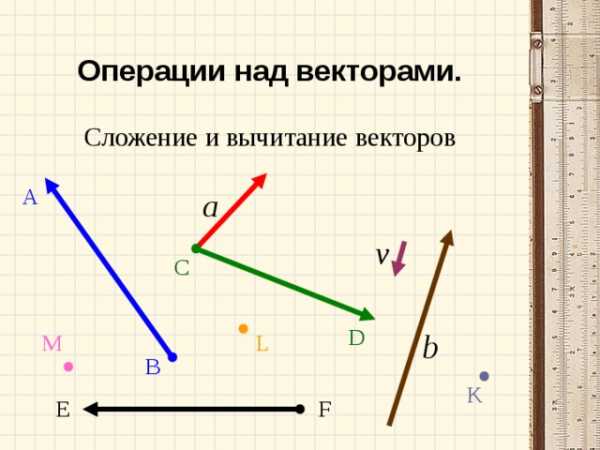
Операции над векторами.
Сложение и вычитание векторов
A
C
D
L
M
B
K
E
F

Суммой векторов a и b с координатами x1, y1 , z1 и x2 , y2 , z 2 называется вектор с координатами x1+x2, y1+y2 , z1+z2 .
Разностью векторов a и b с координатами x1, y1 , z1 и x2 , y2 , z 2 называется вектор с координатами x1 — x2, y1 — y2 , z1 — z2 .
Примеры.
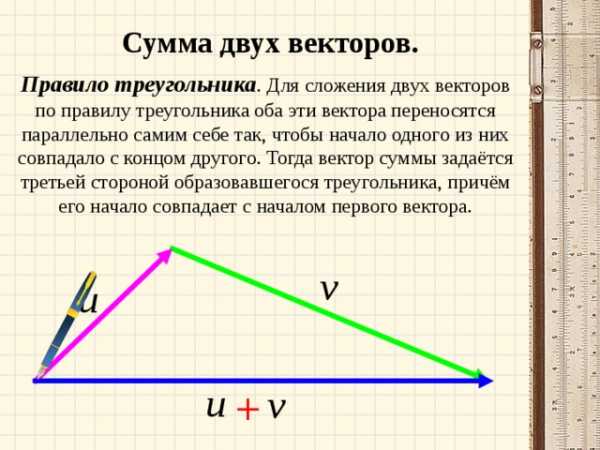
Сумма двух векторов.
Правило треугольника . Для сложения двух векторов по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
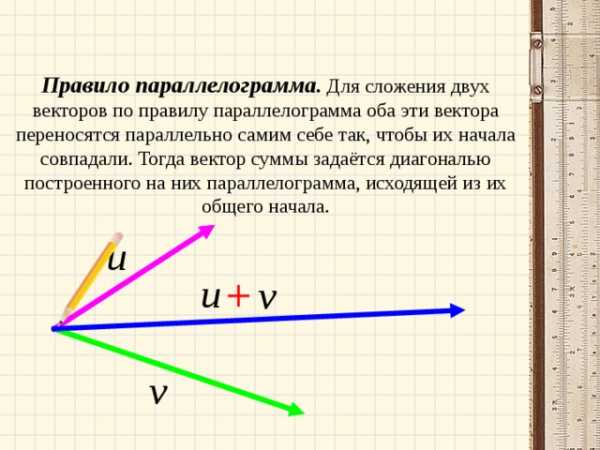
Правило параллелограмма . Для сложения двух векторов по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
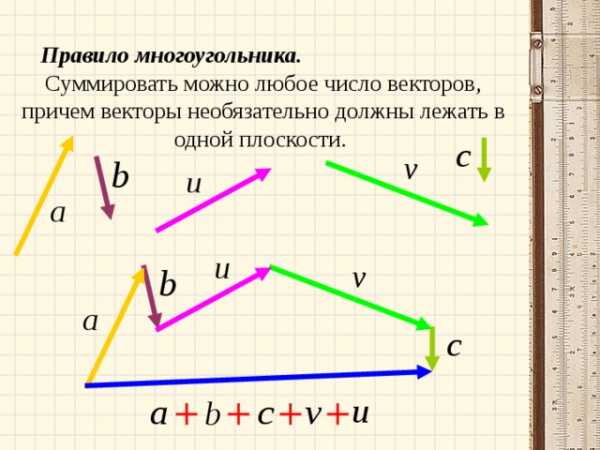
Правило многоугольника.
Суммировать можно любое число векторов, причем векторы необязательно должны лежать в одной плоскости.

4 . Правило параллелепипеда.

Разность двух векторов.
Чтобы вычесть вектор, надо прибавить коллинеарный ему вектор, направленный в противоположную сторону. Для вычитания двух векторов оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
 0 , и противоположно ему, если λ Пример. «
0 , и противоположно ему, если λ Пример. «
Произведение вектора на число.
Произведением вектора и числа λ называется вектор, обозначаемый λ , модуль которого равен , а направление совпадает с направлением вектора , если λ 0 , и противоположно ему, если λ
Пример.
 0 λ = 3 Длина вектора увеличивается в λ раз, и направление остаётся прежним. «
0 λ = 3 Длина вектора увеличивается в λ раз, и направление остаётся прежним. «
Дано :
Чертёж:
λ 0
λ = 3
Длина вектора увеличивается в λ раз, и направление остаётся прежним.

Дано :
Чертёж:
λ
λ = -3
Длина вектора увеличивается в λ раз, а направление меняется на противоположное.

Дано:
Чертёж:
λ = 0
Вектор станет нулевым, т. е. преобразуется в точку.

Скалярное произведение векторов.
Чтобы скалярно умножить два вектора, надо умножить их соответствующие координаты и сложить их. В результате получим число.
Пример.

Условие перпендикулярности векторов.
Если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны .

Угол между векторами.
Углом между двумя векторами , отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором .

- Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
- Формула вычисления угла между векторами
cos α = a·b/|a|·|b|

Спасибо за внимание!
multiurok.ru
Вектор. Что такое вектор? :: SYL.ru
Такое понятие, как вектор, рассматривается практически во всех естественных науках, причем он может иметь совершенно разное значение, поэтому дать однозначное определение вектора для всех областей невозможно. Но попробуем разобраться. Итак, вектор — что такое?
Понятие вектора в классической геометрии
Вектор в геометрии — отрезок, для которого указано, какая из его точек является началом, а какая — концом. То есть, говоря проще, вектором называется направленный отрезок.
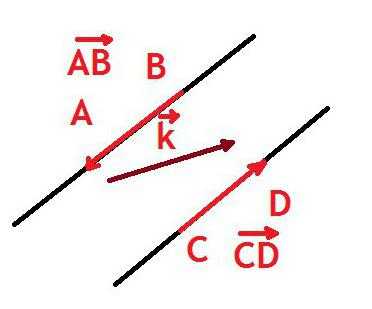
Соответственно, обозначается вектор (что такое — рассмотрели выше), как и отрезок, то есть двумя заглавными буквами латинского алфавита с добавлением сверху черты или стрелки, направленной вправо. Также его можно подписать строчной (маленькой) буквой латинского алфавита с чертой или стрелкой. Стрелка всегда направлена вправо и не меняется в зависимости от расположения вектора.
Таким образом, вектор имеет направление и длину.
В обозначении вектора содержится и его направление. Выражается это так, как на рисунке ниже.
Изменение направления меняет значение вектора на противоположное.
Длиной вектора называется длина отрезка, от которого он образован. Обозначается он как модуль от вектора. Это показано на рисунке ниже.
Соответственно, нулевым является вектор, длина которого равна нулю. Из этого следует, что нулевой вектор представляет собой точку, при чем в ней совпадают точки начала и конца.
Длина вектора — величина всегда не отрицательная. Иначе говоря, если есть отрезок, то он в обязательном порядке обладает некоторой длиной или же является точкой, тогда его длина равна нулю.
Само понятие точки является базовым и определения не имеет.
Сложение векторов
Существуют специальные формулы и правила для векторов, с помощью которых можно выполнить сложение.
Правило треугольника. Для сложения векторов по этому правилу достаточно совместить конец первого вектора и начала второго, используя при этом параллельный перенос, и соединить их. Полученный третий вектор и будет равен сложению двух других.
Правило параллелограмма. Для сложения по этому правилу необходимо провести оба вектора из одной точки, а затем провести из конца каждого из них другой вектор. То есть, из первого вектора будет проведен второй, а из второго — первый. В результате получится новая точка пересечения и образуется параллелограмм. Если совместить точку пересечения начал и концов векторов, то полученный вектор и будет результатом сложения.
Похожим образом возможно выполнять и вычитание.
Разность векторов
Аналогично сложению векторов возможно выполнить и их вычитание. Оно базируется на принципе, указанном на рисунке ниже.
То есть вычитаемый вектор достаточно представить в виде вектора, ему противоположного, и произвести расчет по принципам сложения.
Также абсолютно любой ненулевой вектор возможно умножить на какое-либо число k, это изменит его длину в k раз.
Помимо этих, существуют и другие формулы векторов (например, для выражения длины вектора через его координаты).
Расположение векторов
Наверняка многие сталкивались с таким понятием, как коллинеарный вектор. Что такое коллинеарность?
Коллинеарность векторов — эквивалент параллельности прямых. Если два вектора лежат на прямых, которые параллельны друг другу, или же на одной прямой, то такие векторы называются коллинеарными.
Направление. Относительно друг друга коллинеарные векторы могут быть сонаправленными или противоположно направленными, это определяется направлением векторов. Соответственно, если вектор сонаправлен с другим, то вектор, ему противоположный, противоположно направлен.
На первом рисунке показаны два противоположно направленных вектора и третий, который не коллинеарен им.
После введения вышеуказанных свойств возможно дать определение и равным векторам — это векторы, которые направлены в одну сторону и имеют одинаковую длину отрезков, от которых они образованы.
Во многих науках применяется еще и понятие радиус-вектора. Подобный вектор описывает положение одной точки плоскости относительно другой фиксированной точки (зачастую это начало координат).
Векторы в физике
Предположим, при решении задачи возникло условие: тело движется со скоростью 3 м/с. Это означает, что тело движется с конкретным направлением по одной прямой, поэтому данная переменная будет величиной векторной. Для решения важно знать и значение, и направление, так как в зависимости от рассмотрения скорость может равняться и 3 м/c, и -3 м/с.
В общем случае вектор в физике используется для указания направления силы, действующей на тело, и для определения равнодействующей.
При указании этих сил на рисунке их обозначают стрелками с подписью вектора над ним. Классически длина стрелки так же важна, с помощью нее указывают, какая сила действует сильнее, однако это свойство побочное, опираться на него не стоит.
Вектор в линейной алгебре и математическом анализе
Элементы линейных пространств также называются векторами, однако в данном случае они представляют собой упорядоченную систему чисел, описывающих некоторые из элементов. Поэтому направление в данном случае уже не имеет никакой важности. Определение вектора в классической геометрии и в математическом анализе сильно различаются.
Проецирование векторов
Спроецированный вектор — что такое?
Довольно часто для правильного и удобного расчета необходимо разложить вектор, находящийся в двухмерном или трехмерном пространстве, по осям координат. Данная операция необходима, например, в механике при подсчете сил, действующих на тело. Вектор в физике используется достаточно часто.
Для выполнения проекции достаточно опустить перпендикуляры из начала и конца вектора на каждую из координатных осей, полученные на них отрезки и будут называться проекцией вектора на ось.
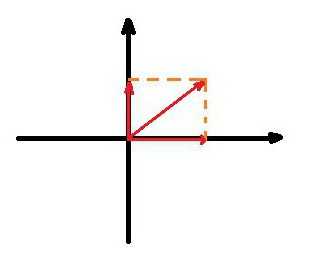
Для подсчета длины проекции достаточно умножить его изначальную длину на определенную тригонометрическую функцию, которая получается при решении мини-задачи. По сути, есть прямоугольный треугольник, в котором гипотенуза является исходным вектором, один из катетов — проекцией, а другой катет — опущенным перпендикуляром.
www.syl.ru
