Вычисление и сравнение логарифмов – Приемы и методы сравнения логарифмов

Приемы и методы сравнения логарифмов

Разделы: Математика

---

Сравнение значений логарифмов или значения логарифма с некоторым числом встречается в школьной практике решения задач не только как самостоятельная задача. Сравнивать логарифмы приходится, например, при решении уравнений и неравенств. Материалы статьи (задачи и их решения) располагаются по принципу “от простого к сложному” и могут быть использованы для подготовки и проведения урока (уроков) по данной теме, а также на факультативных занятиях. Количество рассматриваемых задач на уроке зависит от уровня класса, его профильного направления. В классах с углубленным изучением математики этот материал может быть использован для двухчасового урока-лекции.

1. (Устно.) Какие из функций являются возрастающими, а какие убывающими:

Замечание.

Это упражнение является подготовительным.

2. (Устно.) Сравните с нулем:

Замечание. При решении упражнения № 2 можно использовать как свойства логарифмической функции с привлечением графика логарифмической функции, так и следующее полезное свойство:

если положительные числа a и b лежат на числовой прямой правее 1 или левее 1 (то есть a>1 и b>1 или 0<a<1 и 0<b<1), то log_ab > 0 ;
если положительные числа a и b лежат на числовой прямой по разные стороны от 1(то есть 0<a<1<b или 0<b<1<a), то log_ab < 0 [4].

Покажем использование этого свойства при решении № 2(а).

Так как

Так как функция y = log₇t возрастает на R₊, 10 > 7, то log₇10 > log

77, то есть log₇10 > 1. Таким образом, положительные числа sin3 и log₇10 лежат по разные стороны от 1. Следовательно, log_sin3log₇10 < 0.

3. (Устно.) Найдите ошибку в рассуждениях:

. Функция y = lgt возрастает на R₊, тогда ,

Разделим обе части последнего неравенства на . Получим, что 2 > 3.

Решение.

Положительные числа и 10 (основание логарифма) лежат по разные стороны от 1. Значит, < 0. При делении обеих частей неравенства на число знак неравенства следует изменить на противоположный.

4. (Устно.) Сравните числа:

Замечание. При решении упражнений № 4(a–c) используем свойство монотонности логарифмической функции. При решении № 4(d) используем свойство:

если c > a >1, то при b>1 справедливо неравенство log_ab > log_cb.

Решение 4(d).

Так как 1 < 5 < 7 и 13 > 1, то log₅13 > log₇13.

5. Сравните числа log₂6 и 2.

Решение.

Первый способ (использование монотонности логарифмической функции).

2 = log₂4;

Функция y = log₂t возрастает на R₊, 6 > 4. Значит, log₂6 > log₂4  и log₂5 > 2.

Второй способ (составление разности).

Составим разность .

6. Сравните числа и -1.

Решение.

-1 = ;

Функция y =   убывает на R_+, 3 < 5. Значит, >  и

> -1.

7. Сравните числа и 3log₈26.

Решение.

Функция y = log₂t возрастает на R₊, 25 < 26. Значит, log₂25 < log₂26  и .

Решение.

Первый способ.

Умножим обе части неравенства на 3: 

Функция y = log ₅t возрастает на R₊ , 27 > 25. Значит,

Второй способ.

Составим разность
. Отсюда .

9. Сравните числа log₄26 и log₆17.

Решение.

Оценим логарифмы, учитывая, что функции y = log₄t и y = log₆t возрастающие на

R₊:

Решение.

Учитывая, что функции   убывающие на R₊, имеем:

. Значит,

Замечание. Предложенный метод сравнения называют методом “вставки” или методом “разделения” (мы нашли число 4, разделяющее данные два числа).

11. Сравните числа log₂3 и  log₃5.

Решение.

Заметим, что оба логарифма больше 1, но меньше 2.

Первый способ. Попробуем применить метод “разделения”. Сравним логарифмы с числом .

Второй способ (умножение на натуральное число).

Замечание 1. Суть метода “умножения на натуральное число” в том, что мы ищем натуральное число k, при умножении на которое сравниваемых чисел

a и b получают такие числа ka и kb, что между ними находится хотя бы одно целое число.

Замечание 2. Реализация вышеописанного метода бывает весьма трудоемка, если сравниваемые числа очень близки друг к другу.
В этом случае можно попробовать сравнение методом “вычитания единицы”. Покажем его на следующем примере.

12. Сравните числа log₇8 и log₆7.

Решение.

Первый способ (вычитание единицы).

Вычтем из сравниваемых чисел по 1.

В первом неравенстве мы воспользовались тем, что

если c > a > 1, то при b > 1 справедливо неравенство log_ab > log_cb.

Во втором неравенстве – монотонностью функции y = log_a

x.

Замечание. Вычитать из сравниваемых чисел можно любое натуральное число n. При этом часто бывает достаточно взять n = 1.

Второй способ (применение неравенства Коши).

13. Сравните числа log₂₄72 и log₁₂18.

Решение.

14. Сравните числа log₂₀80 и log₈₀640.

Решение.

Решение.

Пусть log₂5 = x . Заметим, что x > 0.

Получаем неравенство .

Найдем множество решений неравенства , удовлетворяющих условию x > 0.

Возведем обе части неравенства

в квадрат (при x > 0 обе части неравенства положительны). Имеем 9x² < 9x + 28.

Множеством решений последнего неравенства является промежуток .

Учитывая, что x > 0, получаем: .

Ответ: неравенство верно.

Практикум по решению задач.

1. Сравните числа:

2. Расположите в порядке возрастания числа:

3. Решите неравенство 4⁴ – 2·2⁴⁺¹ – 3 < 0. Является ли число √2 решением данного неравенства? (Ответ: (–∞; log₂3); число √2 является решением данного неравенства.)

Заключение.

Методов сравнения логарифмов много. Цель уроков по данной теме – научить ориентироваться в многообразии методов, выбирать и применять наиболее рациональный способ решения в каждой конкретной ситуации.

В классах с углубленным изучением математики материал по данной теме может быть изложен в форме лекции. Такая форма учебной деятельности предполагает, что материал лекции должен быть тщательно отобран, проработан, выстроен в определенной логической последовательности. Записи, которые делает учитель на доске, должны быть продуманными, математически точными.

Закрепление лекционного материала, отработку навыков по решению задач целесообразно проводить на уроках-практикумах. Цель практикума – не только закрепить и проверить полученные знания, но и пополнить их. Поэтому задания должны содержать задачи разного уровня, от самых простых задач до задач повышенной сложности. Учитель на таких практикумах выступает в роли консультанта.

Литература.

1. Галицкий М.Л. и др.Углубленное изучение курса алгебры и математического анализа: Метод. рекомендации и дидактические материалы: Пособие для учителя.– М.: Просвещение, 1986.
2. Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре и началам анализа для 10 класса. – СПб.: “ЧеРо-на-Неве”, 2003.
3. Литвиненко В.Н., Мордкович А. Г. Практикум по элементарной математике. Алгебра. Тригонометрия.: Учебное издание. – М.: Просвещение, 1990.
4. Рязановский А.Р. Алгебра и начала анализа:500 способов и методов решения задач по математике для школьников и поступающих в вузы. – М.: Дрофа, 2001.
5. Садовничий Ю.В. Математика. Конкурсные задачи по алгебре с решениями. Часть 4. Логарифмические уравнения, неравенства, системы. Учебное пособие.-3-е изд., стер.-М.:Издательский отдел УНЦДО, 2003.
6. Шарыгин И.Ф., Голубев В.И.Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. сред.шк.– М.: Просвещение, 1991.

15.05.2011

xn--i1abbnckbmcl9fb.xn--p1ai

Сравнение логарифмов

Ни для кого не секрет, что с помощью применения логарифмов мы упрощаем довольно много сложных алгебраических операций и не только. Логарифмы дают возможность заменять более сложные операции умножения на операции сложения, деление на вычитание. Согласитесь, ведь это намного проще. Если уже быть совсем точными, то логарифм заданного числа – это показатель степени, в которую нужно возвести другое, также заданное число, чтобы получить данное. На первый взгляд все запутано и непонятно, но это только на первый, на самом деле, все до нельзя просто. Для того, чтобы закреплять знания о логарифмах (да и не только о них), конечно же, рекомендовано после прочтения теории выполнять самостоятельные практические упражнения, это не только поможет усвоить материал, но и выявить все недочеты.

Но вернемся к логарифмам, а точнее к их сравнению. Разумеется, вам в голову может прийти вопрос: «что такое сравнение логарифмов? и как это делается?».

Зачем мы сравниваем логарифмы? Ответ достаточно прост. При решении неравенств и уравнений, довольно часто возникает вопрос, когда нужно определить принадлежность корня области допустимых значений или же сделать соотношение решений двух или более неравенств на числовой прямой, а решение, при этом, выражается иррациональным числом, которое, в свою очередь, записано с помощью логарифма. Вот тут-то нам и необходимо сравнение этих логарифмов.

Существуют несколько способов сравнения логарифмов. Какой из них использовать зависит, в первую очередь, от того, одинаковые основания у логарифмов или нет. Если первый вариант, то тут выход один – использовать монотонность логарифмических функций.

Если числа равные, но основания разные, то тут можно пойти несколькими путями:

1. Графический способ
2. Сравнение логарифмов через переход к одному основанию
3. Метод оценки
4. введение промежуточного числа
5. Алгебраические методы, которые, в свою очередь делятся еще на несколько.

Например: log[2,x]>log[4,x]

Сравнение логарифмов

Если 0   1   2 , то

log   a x   1 > log   a x   2 — знак неравенства меняется

Если a > 1 и 0   1   2 , то

log   a x   1   a x   2 — знак неравенства не меняется

Если 1 1, то log   a x > log   b x

Если 0 1, то log   a x > log   b x

mateshka.ru

Практическая работа по математике на тему «ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ ЛОГАРИФМОВ»

Математика 1 курс 234 часа

Шаповалова Н.В.

ПРАКТИЧЕСКАЯ РАБОТА

Тема работы: ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ ЛОГАРИФМОВ.

Тип занятия: практическое занятие.

Цели работы:

• Образовательная – закрепить понятие логарифма, научить применять свойства логарифмов при решении логарифмических выражений;

• Развивающая — содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать; формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;

• Воспитательная — вырабатывать самостоятельность при работе на уроке; способствовать формированию максимальной работоспособности.

Организационный момент: дежурные, отсутствующие.

Ход работы:

Основная часть урока

Повторение лекционного материала

Задачи этапа: повторить пройденный материал, необходимый для выполнения практической работы.

Рассмотрим действие обратное действию возведения в степень – нахождение логарифма

Вопрос: в какую степень надо возвести число 3, чтобы получить 243?

Ответ на этот вопрос дает действие нахождения логарифма

Говорится так: «логарифм по основанию 3 от числа 243». Тройка (маленькая и пишется чуть ниже) называется «основанием логарифма», а число 243 так и называют «числом». 

Найти логарифм – это значит найти показатель степени, в которую надо возвести основание логарифма, чтобы получить стоящее под логарифмом число.

Определения

Логарифмом числа b по основанию a называется такое число, обозначаемое , что . Т.е. .

a – основание логорифма,

Десятичный логарифм: .

Натуральный логарифм: , где e=2,71828…

Функция, заданная формулой , где , называется логарифмической

Основные логарифмические тождества.

Примеры

Закрепление нового материала:

Задачи этапа: научить применять практические приемы решения показательных уравнений

Практические задания:

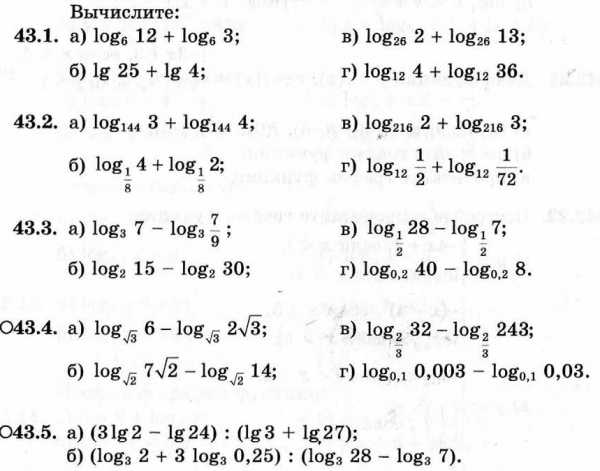
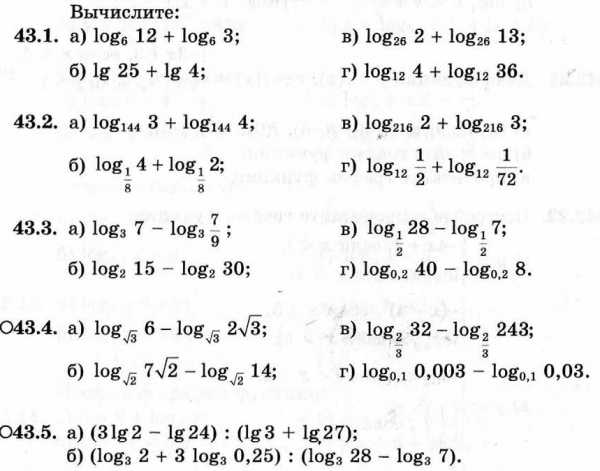
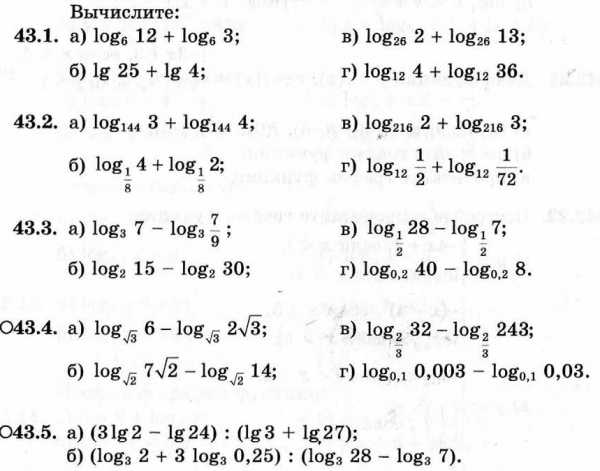
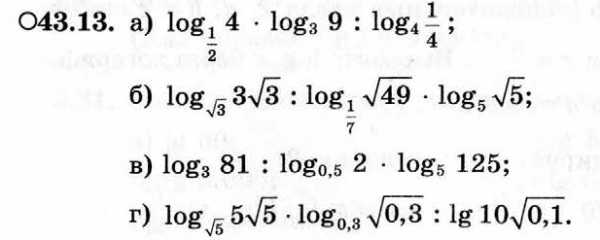
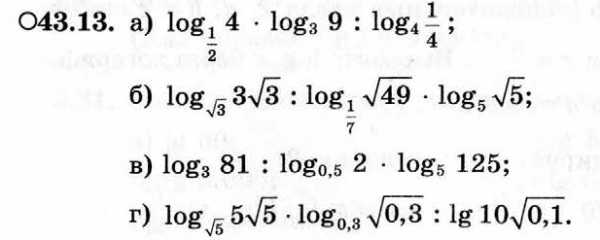
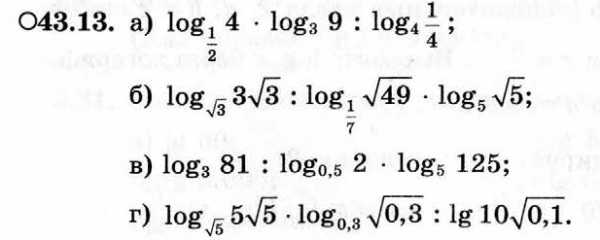
Задание на дом: невыполненные задания завершить и сдать на следующее занятие.

Вопросы:

1. Определение логарифма.

2. Виды логарифмов.

3. Что такое основание логарифма, что оно показывает?

4. Как задается логарифмическая функция?

5. Перечислите основные логарифмические свойства.

infourok.ru

§3. Логарифм числа. Свойства логарифмов. Алгебра и начала математического анализа, 10 класс: уроки, тесты, задания.

1.	Определение логарифма (основание — целое число) Сложность: лёгкое	1
2.	Определение логарифма (основание — дробь) Сложность: лёгкое	1
3.	Вычисление десятичного логарифма Сложность: лёгкое	1
4.	Вычисление логарифма, десятичные дроби Сложность: лёгкое	1
5.	Вычисление логарифма, обычные дроби Сложность: лёгкое	1
6.	Логарифм произведения Сложность: лёгкое	2
7.	Логарифм частного Сложность: лёгкое	2
8.	Формула перехода от одного основания логарифма к другому основанию Сложность: лёгкое	2
9.	Сумма логарифмов, логарифм степени Сложность: лёгкое	3
10.	Применение свойств логарифмов, сумма логарифмов Сложность: лёгкое	1
11.	Применение свойств логарифмов, разность и сумма логарифмов Сложность: лёгкое	3
12.	Формула перехода логарифма к новому основанию Сложность: лёгкое	1
13.	Числовое значение выражения (сумма) Сложность: лёгкое	3
14.	Значение выражения (целые числа) Сложность: лёгкое	3
15.	Числовое значение выражения (разность) Сложность: лёгкое	3
16.	Основное логарифмическое тождество (сложение) Сложность: среднее	3
17.	Основное логарифмическое тождество (вычитание) Сложность: среднее	3
18.	Основное логарифмическое тождество (произведение) Сложность: среднее	3
19.	Основное логарифмическое тождество (основание — дробь) Сложность: среднее	4
20.	Основное логарифмическое тождество (произведение степеней) Сложность: среднее	3
21.	Основное логарифмическое тождество (основание — натуральное число) Сложность: среднее	4
22.	Основное логарифмическое тождество (логарифм степени) Сложность: среднее	4
23.	Свойства логарифмов (степени и произведения) Сложность: среднее	4
24.	Свойства логарифмов (степени и частного) Сложность: среднее	4
25.	Логарифм степени (произведение) Сложность: среднее	3
26.	Логарифм степени (частное) Сложность: среднее	5
27.	Свойства логарифмов (степень основания, основное логарифмическое тождество) Сложность: среднее	7
28.	Основное тождество логарифмов Сложность: среднее	2
29.	Формула перехода к другому основанию, основаное логарифмическое тождество Сложность: среднее	4
30.	Логарифм произведения (сумма кубов) Сложность: среднее	3
31.	Неизвестное под знаком логарифма Сложность: среднее	2
32.	Неизвестное основание логарифма (целое число) Сложность: среднее	2
33.	Неизвестное основание логарифма (обыкновенная дробь) Сложность: среднее	3
34.	Определение логарифма (неизвестный показатель степени) Сложность: сложное	4
35.	Свойства логарифмов Сложность: сложное	7
36.	Формула перехода к новому основанию (метод подстановки) Сложность: сложное	7
37.	Логарифм произведения (тригонометрическое выражение) Сложность: сложное	7
38.	Логарифм произведения Сложность: сложное	5
39.	Логарифм произведения Сложность: сложное	5
40.	Область допустимых значений логарифма Сложность: сложное	4
41.	Определение логарифма (неизвестный показатель степени) Сложность: сложное	4
42.	Определение логарифма (неизвестное основание) Сложность: сложное	6

www.yaklass.ru

Логарифмы. Единые государственные экзамены, ЕГЭ по математике: уроки, тесты, задания.

1.	Вычисление десятичного логарифма Сложность: лёгкое	1
2.	Вычисление логарифма Сложность: лёгкое	1
3.	Вычисление логарифма Сложность: лёгкое	1
4.	Применение свойств логарифмов Сложность: лёгкое	1
5.	Применение свойств логарифмов Сложность: лёгкое	3
6.	Формула перехода логарифма к новому основанию Сложность: лёгкое	1
7.	Использование основного тождества логарифмов Сложность: среднее	2
8.	Сравнение логарифмов Сложность: лёгкое	1
9.	Нахождение области определения логарифма Сложность: среднее	1
10.	Нахождение области определения логарифма Сложность: среднее	2
11.	Определение основания логарифма Сложность: среднее	2
12.	Логарифмическое уравнение,определение логарифма Сложность: лёгкое	1
13.	Логарифмическое уравнение,определение логарифма Сложность: лёгкое	3
14.	Логарифмическое уравнение(неизвестно основание) Сложность: среднее	4
15.	Логарифмическое уравнение(произведение равно 0) Сложность: среднее	2
16.	Логарифмическое уравнение (свойства логарифмов) Сложность: среднее	4
17.	Логарифмическое уравнение (свойства логарифмов) Сложность: среднее	3
18.	Логарифмическое уравнение (логарифм в квадрате) Сложность: среднее	3
19.	Логарифмическое уравнение (новая переменная) Сложность: среднее	4
20.	Логарифмическое уравнение (новая переменная) Сложность: среднее	5
21.	Логарифмическое уравнение (разлож. на множит.) Сложность: среднее	5
22.	Логарифмическое уравнение с тригонометрией Сложность: сложное	7
23.	Логарифмическое уравнение (графический способ) Сложность: сложное	3
24.	Логарифмическое неравенство(основание меньше 1) Сложность: лёгкое	1
25.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
26.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
27.	«Ц-Уровень» Логарифмическое неравенство Сложность: сложное	1

www.yaklass.ru

Вычисление значения логарифмического выражения

В этой статье вы познакомитесь со всеми типами логарифмических выражений из Открытого банка заданий для подготовки к ЕГЭ по математике.

16 видео помогут вам понять как использовать свойства логарифмов при упрощении логарифмических выражений.

Вы можете попытаться решить каждый пример самостоятельно, и затем свериться с ответом. А можете сначала посмотреть видео с решением аналогичного задания.

Пример 1.  Найти значение выражения:

Посмотреть ответ:

показать

Ответ: 6

Видеорешение аналогичного задания:

 

Пример 2.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 30

Видеорешение аналогичного задания:

 

Пример 3.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 0,125

Видеорешение аналогичного задания:

 

Пример 4.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 1,5

Видеорешение аналогичного задания:

 

Пример 5.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 3

Видеорешение аналогичного задания:

 

Пример 6.  Найти значение выражения:

Посмотреть ответ:

показать

Ответ: 3

Видеорешение аналогичного задания:

 

Пример 7.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 0,75

Видеорешение аналогичного задания:

 

Пример 8.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 216

Видеорешение аналогичного задания:

 

Пример 9.  Найти значение выражения:
Посмотреть ответ:

показать

Ответ: 1

Видеорешение аналогичного задания:

 

Пример 10.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 0,75

Видеорешение аналогичного задания:

 

Пример 11. Найти значение выражения:Посмотреть ответ:

показать

Ответ: 1

Видеорешение аналогичного задания:

 

Пример 12.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 3

Видеорешение аналогичного задания:

 

Пример 13.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: -2

Видеорешение аналогичного задания:

 

Пример 14.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 0,5625

Видеорешение аналогичного задания:

 

Пример 15.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: -0,2

Видеорешение аналогичного задания:

 

Пример 16.  Найти значение выражения:

Посмотреть ответ:

показать

Ответ: 25

Видеорешение аналогичного задания:

 

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Логарифмы. Логарифмические формулы. Свойства логарифмов

Факт 1.
\(\bullet\) Логарифм по основанию \(a\) от \(b\) – это число \(t\), которое показывает, в какую степень нужно возвести \(a\), чтобы получить \(b\).
Ограничения: числа \(a\) и \(b\) такие, что \(a>0,\ a\ne 1,\ b>0\).
\[\Large{{\color{blue}{\log_a{b}=t\quad\Leftrightarrow\quad a^t=b }}}\]
Т.к. мы имеем право возводить в любую степень, то \(t\in \mathbb{R}\).
Таким образом, верно основное логарифмическое тождество \[{\Large{a^{\log_ab}=b}}\]
\(\bullet\) Справедливы следующие формулы: \[{\large{\begin{array}{|ll|l|} \hline \qquad \qquad \qquad \qquad {\small{\text{Формулы}}} && \qquad \qquad{\small{\text{Ограничения}}}\\ &&\\ \hline \textbf{(1)} \log_a1=0&&a>0, a\ne 1\\ &&\\ \textbf{(2)} \log_aa=1 &&a>0, a\ne 1\\ &&\\ \textbf{(3)} \log_{a}{b^m}=m\log_a|b|&(m — {\small{\text{четн.}}})&a>0, a\ne 1, b\ne 0\\ &&\\ \textbf{(4)}\log_{a}{b^m}=m\log_ab& (m — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(5)} \log_{a^n}{b}=\frac 1n\log_{|a|}b&(n — {\small{\text{четн.}}})&a\ne 0, a\ne 1, b>0\\ &&\\ \textbf{(6)}\log_{a^n}b=\frac1n\log_ab&(n — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(7)} \log_a{bc}=\log_a|b|+\log_a|c|&&a>0, a\ne 1, bc\ne 0\\ &&\\ \textbf{(8)} \log_a{\dfrac bc}=\log_a|b|-\log_a|c|&&a>0, a\ne 1,bc\ne 0 \\ &&\\ \textbf{(9)} a^{\log_ab}=b &&a>0, a\ne 1, b>0\\ &&\\ \textbf{(10)}c^{\log_ab}=b^{\log_ac}&&a>0, a\ne 1, b>0, c>0\\ &&\\ \textbf{(11)} \log_ab\cdot \log_bc=\log_ac && a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ \textbf{(11′}) \log_bc=\dfrac{\log_ac}{\log_ab}&&a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ &&\\ {\small{\text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \\ \textbf{(12)} \log_ab\cdot \log_ba=1 && a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \textbf{(12′}) \log_ab=\dfrac1{\log_ba}&&a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \hline \end{array}}}\]

Заметим, что при выполнении ограничений данные формулы верны в обе стороны!

 

shkolkovo.net