Объем тетраэдра — формулы, примеры расчета, калькулятор
Рассмотрим произвольный треугольник ABC и точку D, не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC. В результате получим треугольники ADC, CDB, ABD. Поверхность ограниченная четырьмя треугольниками ABC, ADC, CDB и ABD называется тетраэдром и обозначается DABC.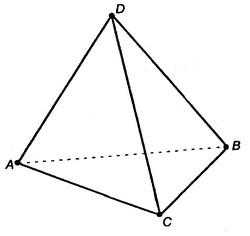 Треугольники, из которых состоит тетраэдр, называются его гранями.
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.
Таким образом, тетраэдр – это простейший многогранник, гранями которого являются четыре треугольника.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
,где
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a. DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD.
Высота BM равна BM и равна
Рассмотрим треугольник BDM, где DH, являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой
, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим
Вынесем 1/2a. Получим
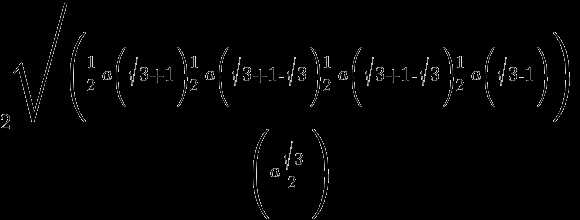
Применим формулу разность квадратов
После небольших преобразований получим
Объем любого тетраэдра можно рассчитать по формуле
,
где ,
Подставив эти значения, получим
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра
Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим
Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
2mb.ru
9 Аналитическая геометрия
Задача
1. Написать
разложение вектора 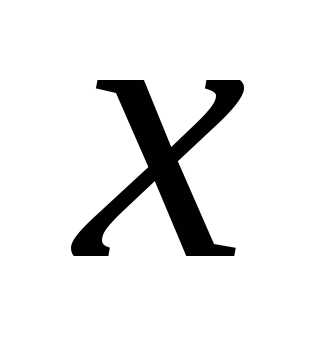 по
векторам
по
векторам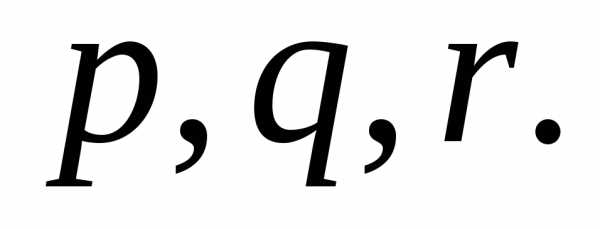
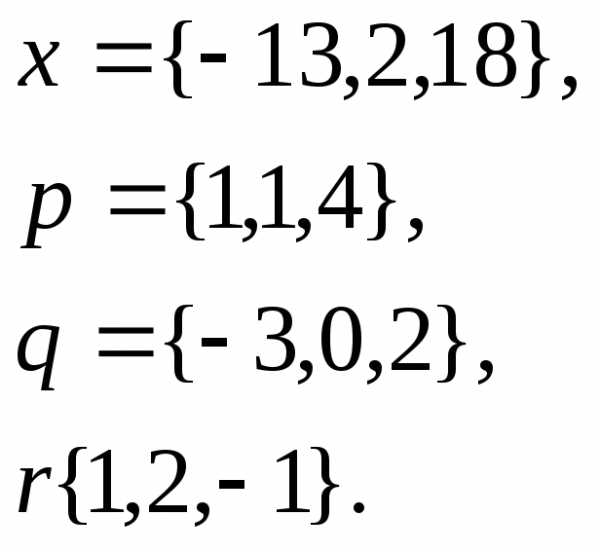
Задача 2. Коллинеарны ли векторы 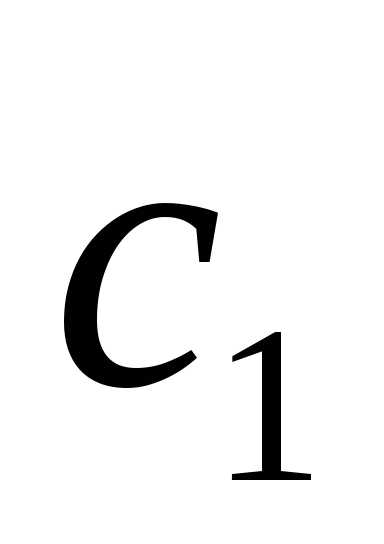 и
и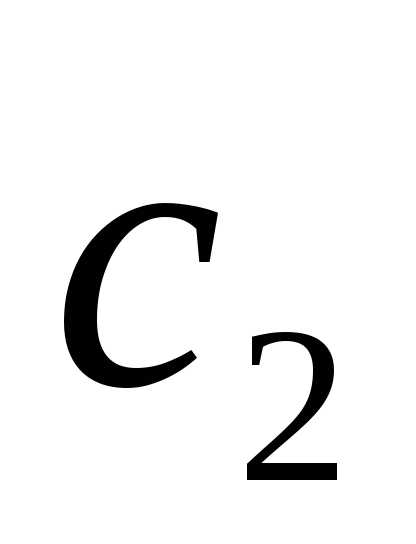 ,
построенные по векторам
,
построенные по векторам
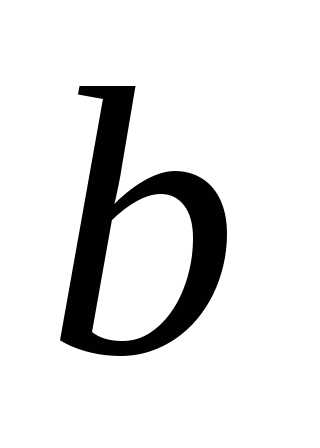 ?
? векторы 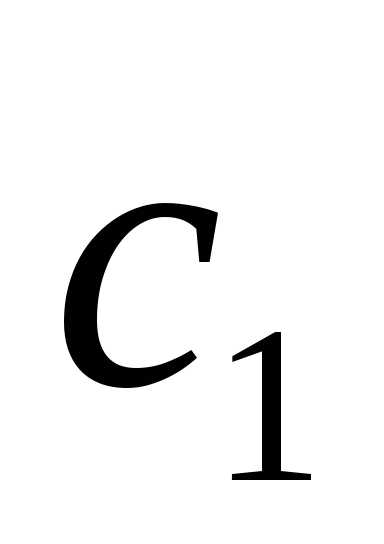 и
и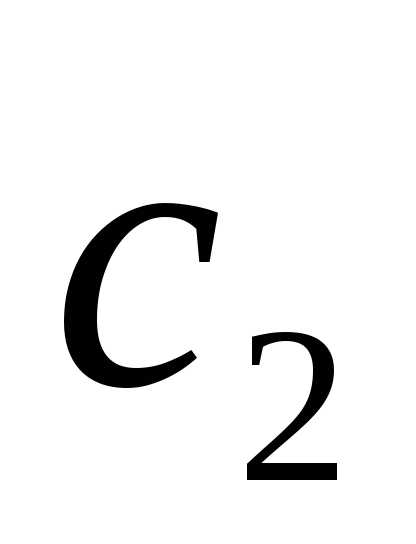 коллинеарны.
коллинеарны.
Задача 3. Найти косинус угла между векторами 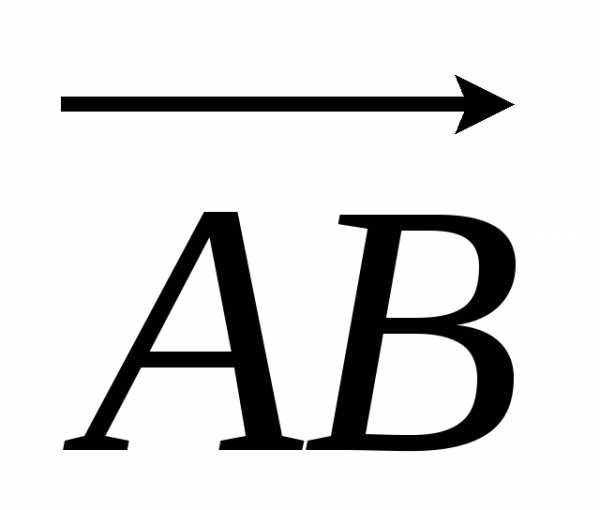 и
и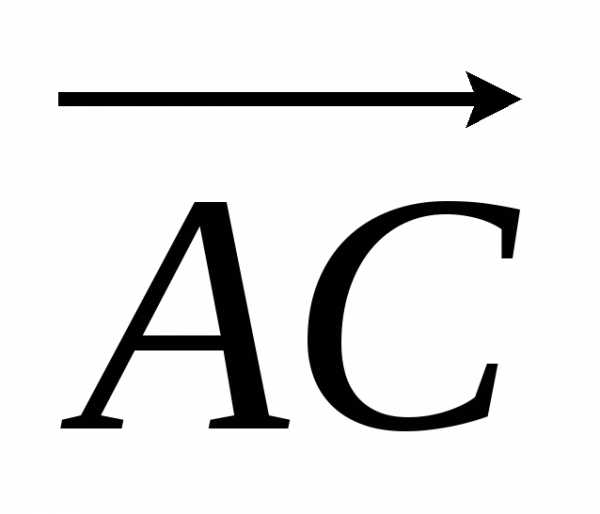 .
.

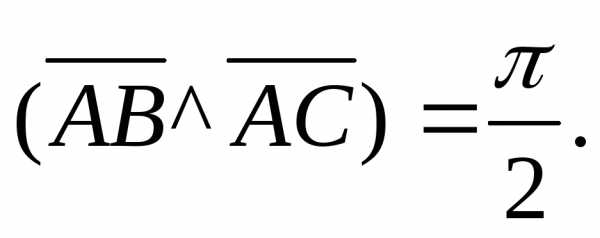
Задача 4.
Вычислить площадь параллелограмма,
построенного на векторах 
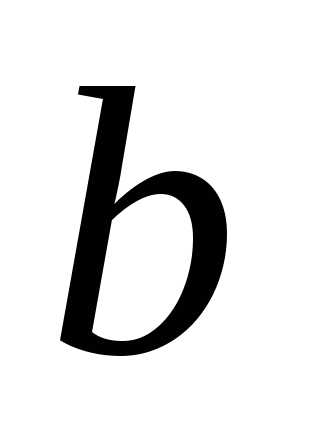 .
. 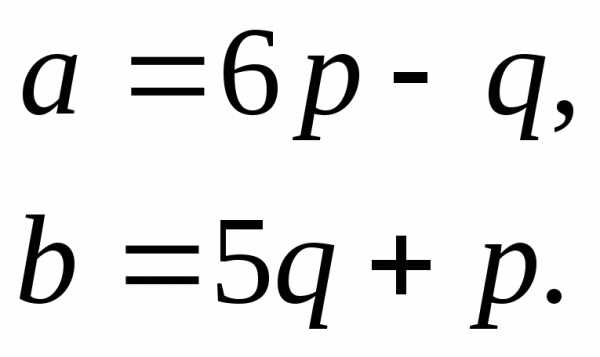
Задача 5.
Компланарны ли векторы  ,
,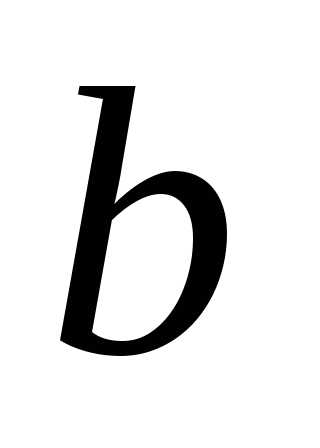 и
и .
.
векторы  ,
,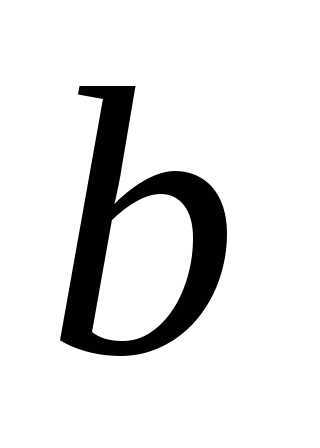 ине
компланарны.
ине
компланарны.
Задача 6.
Вычислить объем тетраэдра с вершинами
в точках
и его высоту, опущенную из вершины
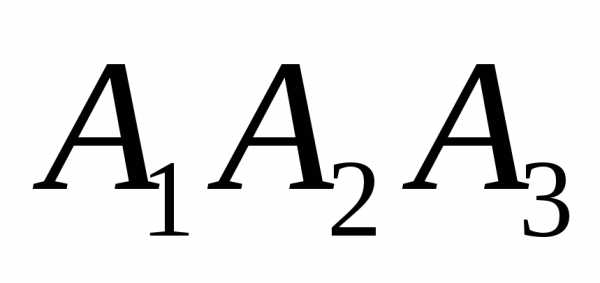 .
. 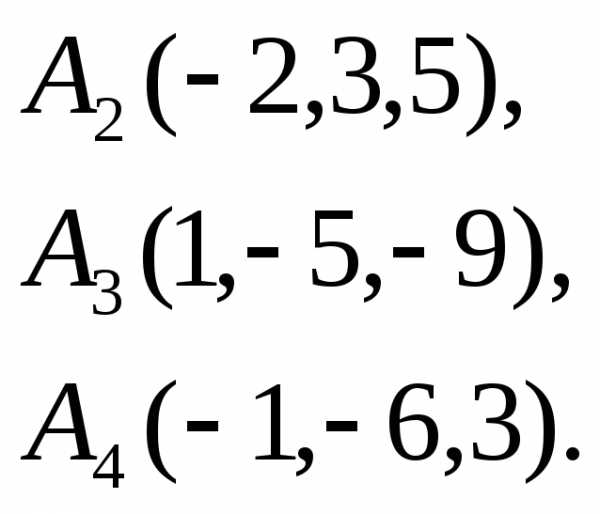
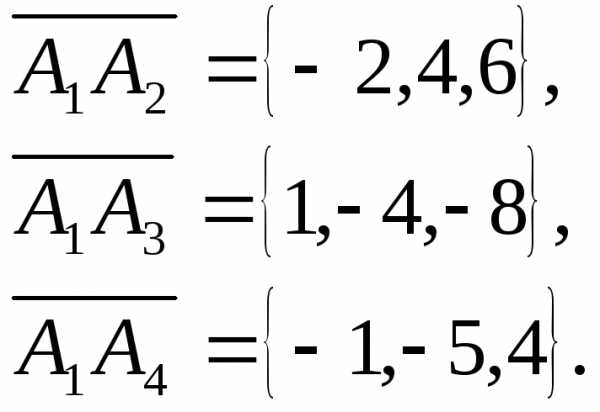
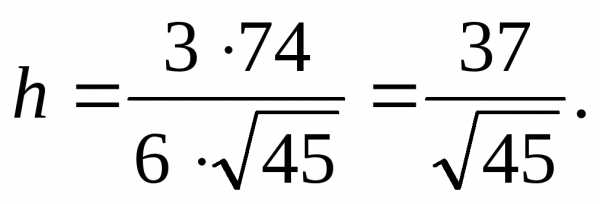
Задача 7. Найти
расстояние от точки 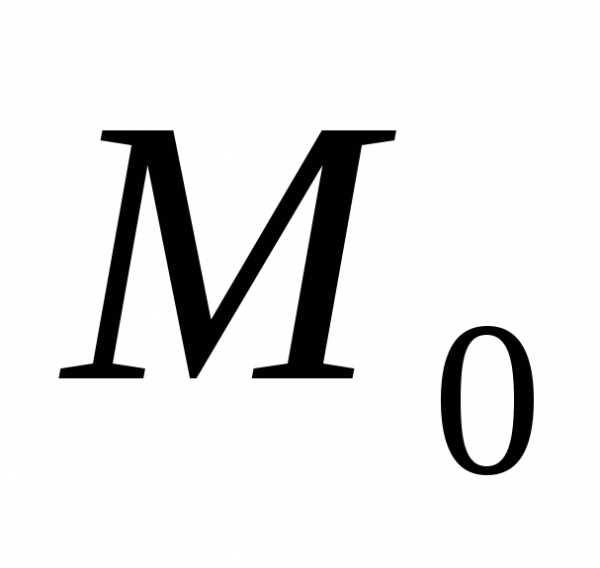 до
плоскости, проходящей через точки.
до
плоскости, проходящей через точки.
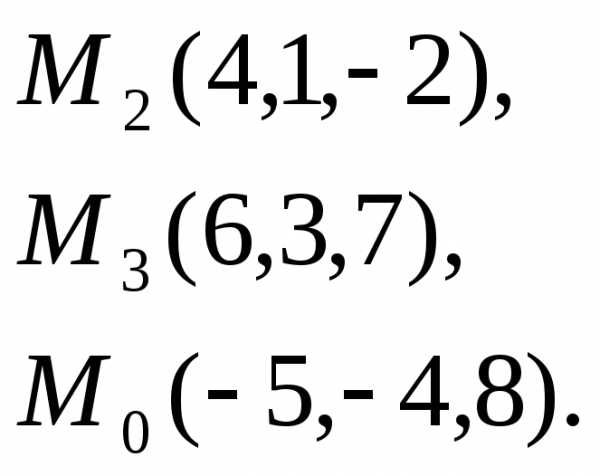
Уравнение плоскости, проходящей через 3 точки
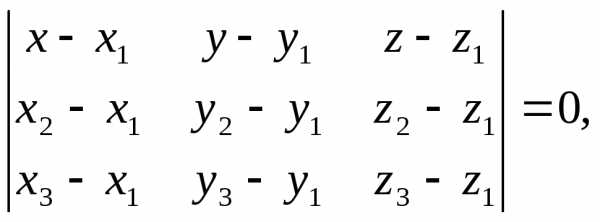
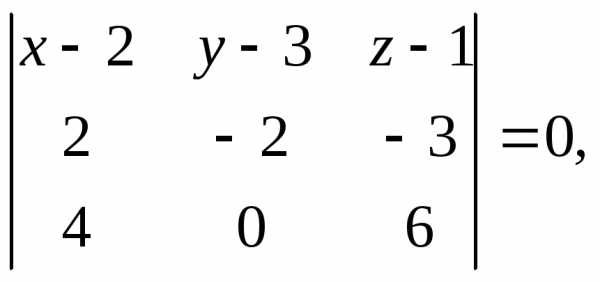
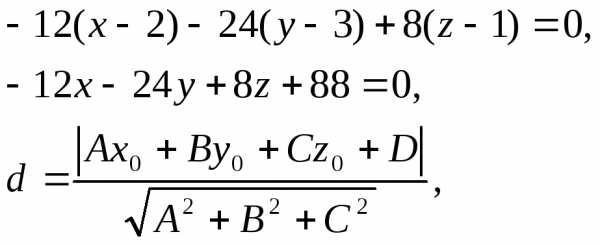
Задача 8. Написать уравнение плоскости, проходящей
через точку перпендикулярно
вектору
перпендикулярно
вектору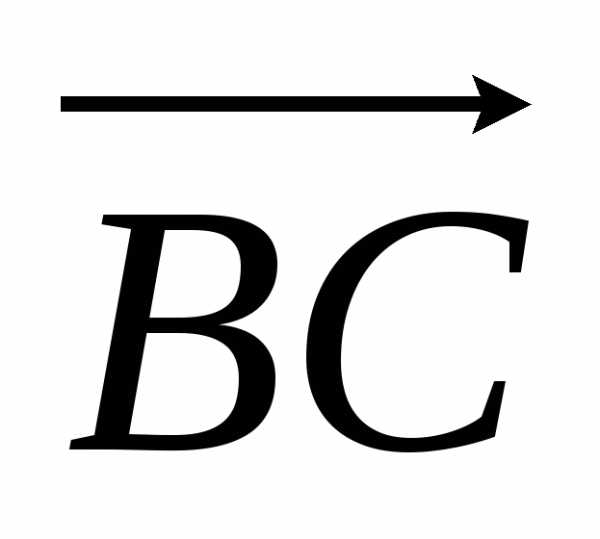 .
.

Т.к. вектор искомой плоскости, то его можно взять в качестве вектора нормали, следовательно
Задача 9. Найти угол между плоскостями.
Задача 10. Найти координаты точки 
 и
и .
. по условию
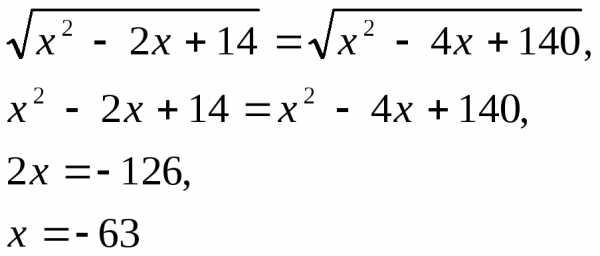
Отсюда,
Задача 11. Пусть 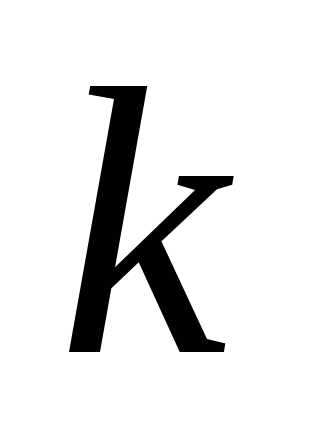 -коэффициент
гомотетии с центром в начале координат.
Верно ли, что точка
-коэффициент
гомотетии с центром в начале координат.
Верно ли, что точка принадлежит
образу плоскости
принадлежит
образу плоскости ?
?
При преобразовании
подобия с центром в начале координат
плоскость 
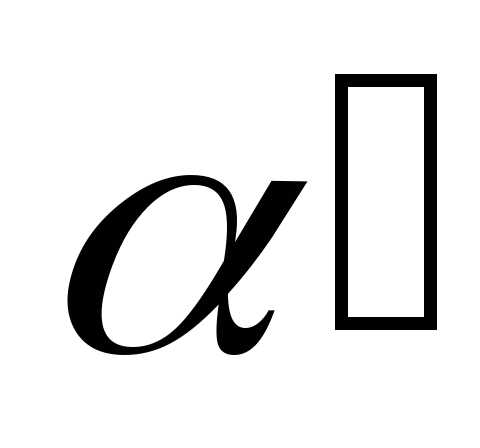 .
. 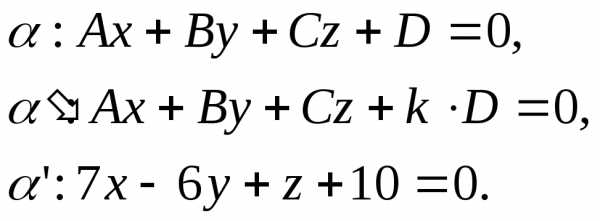
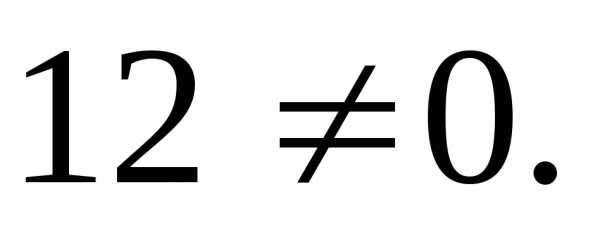
Таким образом,
точка  не
принадлежит образу плоскости
не
принадлежит образу плоскости .
.
Задача 12. Написать канонические уравнения прямой.
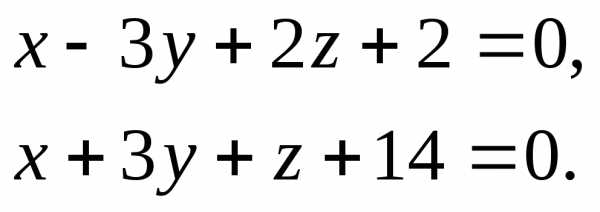
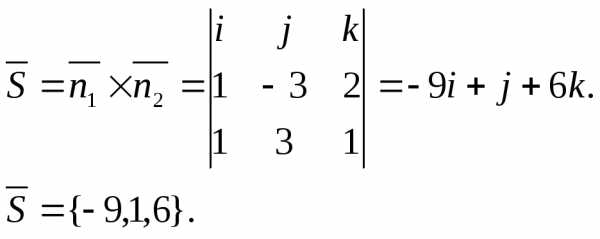
Найдем координаты одной из точек, через которые проходит прямая .
Зададим координате  значение
значение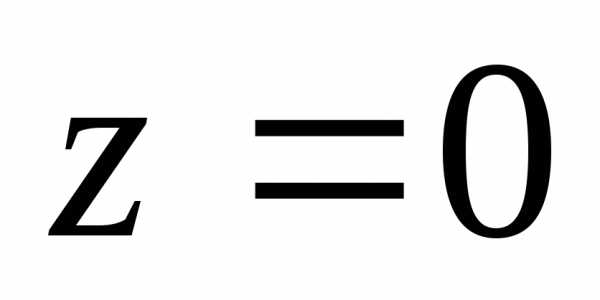 .
.
Итак, получается точка с координатами
Уравнение прямой
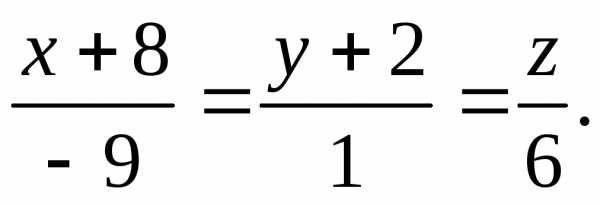
Задача 13. Найти точку пересечения прямой и плоскости.

Подставим в уравнение плоскости
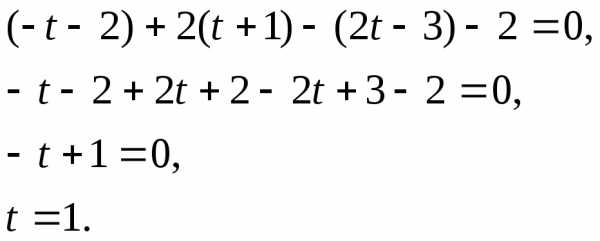
Таким образом, координаты искомой точки
Задача 14. Найти
точку 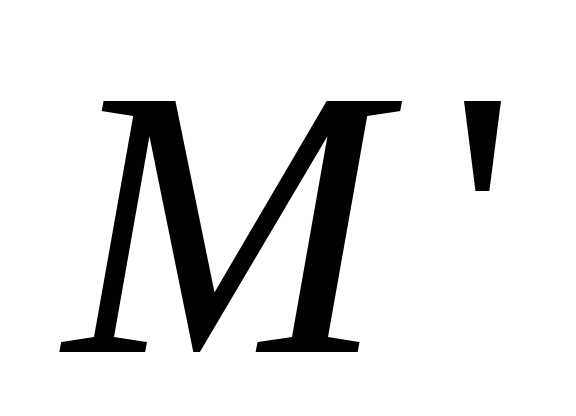 ,
симметричную точке
,
симметричную точке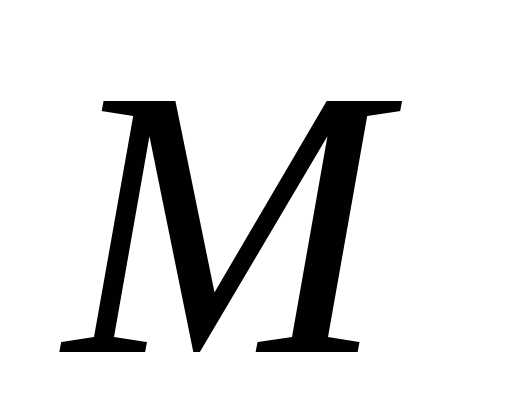 относительно
прямой.
относительно
прямой.
Найдем точку пересечения прямой и плоскости.
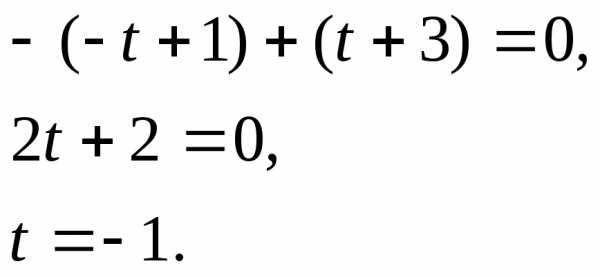
— координаты точки пересечения.
Отсюда,
Следовательно, 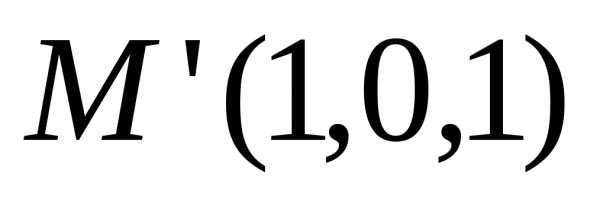 —
искомая точка.
—
искомая точка.
studfiles.net
Из основной формулы для объёма тетраэдра (1),
где S – площадь любой грани, а H – опущенная на нее высота, можно вывести еще целый ряд формул, выражающих объём через различные элементы тетраэдра. Приведем эти формулы для тетраэдра ABCD. (2) , где ∠(AD,ABC) – угол между ребром AD и плоскостью грани ABC; (3) , где ∠(ABC,ABD) – угол между гранями ABC и ABD; (4) , где |AB,CD| – расстояние между противоположными ребрами AB и CD, ∠(AB,CD) – угол между этими ребрами.
Формулы (2)–(4) можно использовать для нахождения величин углов между прямыми и плоскостями; особенно полезна формула (4), с помощью которой можно находить расстояние между скрещивающимися прямыми AB иCD. Формулы (2) и (3) аналогичны формуле S = (1/2)absin C для площади треугольника. Формуле S = rp аналогична формула (5) , где r – радиус вписанной сферы тетраэдра, Σ – его полная поверхность (сумма площадей всех граней). Имеется и красивая формула, связывающая объём тетраэдра с радиусом R его описанной сферы (формула Крелле): (6) , где Δ – площадь треугольника, стороны которого численно равны произведениям противоположных ребер (AB×CD, AC×BD,AD×BC). Из формулы (2) и теоремы косинусов для трехгранных углов (см. Сферическая тригонометрия) можно вывести формулу, аналогичную формуле Герона для треугольников: (7) , где α, β, γ – плоские углы BDC, CDA, ADB при вершине D, δ = (α+β+γ)/2 – их полусумма. Наконец, приведем векторную формулу: (8) , где внутри модуля стоит смешанное произведение векторов. С помощью этой формулы можно вычислять объём тетраэдра, зная координаты его вершин.
|
school-collection.edu.ru
