Ранг матрицы
Любая матрица A порядка m×n можно рассматривать как совокупность m векторов строк или n векторов столбцов.
Рангом матрицы A порядка m×n называется максимальное количество линейно независимых векторов столбцов или векторов строк.
Если ранг матрицы A равен r, то пишется:
rank(A)=r.
Нахождение ранга матрицы
Пусть A произвольная матрица порядка m×n. Для нахождения ранга матрицы A применим к ней метод исключения Гаусса.
Отметим, что если на каком-то этапе исключения ведущий элемент окажется равным нулю, то меняем местами данную строку со строкой, в котором ведущий элемент отличен от нуля. Если окажется, что нет такой строки, то переходим к следующему столбцу и т.д.
После прямого хода исключения Гаусса получим матрицу, элементы которой под главной диагональю равны нулю. Кроме этого могут оказаться нулевые векторы строки.
Количество ненулевых векторов строк и будет рангом матрицы
Рассмотрим все это на простых примерах.
Пример 1.
Найдем ранг следующей матрицы:
Умножив первую строку на 4 и прибавив ко второй строке и умножив первую строку на 2 и прибавив к третьей строке имеем:
Вторую строку умножим на -1 и прибавим к третьей строке:
Получили две ненулевые строки и, следовательно ранг матрицы равен 2.
Пример 2.
Найдем ранг следующей матрицы:
Умножим первую строку на -2 и прибавим ко второй строке. Аналогично обнулим элементы третьей и четвертой строки первого столбца:
Обнулим элементы третьей и четвертой строк второго столбца прибавляя соответствующие строки ко второй строке умноженной на число -1:
Наконец обнулим четвертый элемент четвертого столбца:
Получили четыре ненулевые строки. Следовательно ранг матрицы равен 4.
Онлайн нахождение ранга матрицы
Для нахождения ранга матрицы пользуйтесь матричным онлайн калькулятором . Для подробного решения используйте калькулятор для вычиления ранга матрицы.
matworld.ru
Вычисление ранга матрицы с помощью элементарных преобразований
Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,
.
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример 2 Найти ранг матрицы
А=
и привести ее к каноническому виду.
Решение. Из второй строки вычтем первую и переставим эти строки:
.
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
;
из третьей строки вычтем первую; получим матрицу
В = ,
которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
.
№19
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Система линейных алгебраических уравнений
Для того чтобы линейная система являлась совместной, необходимо и достаточно, что бы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
Доказательство (условия совместности системы)
Необходимость
Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец является линейной комбинацией столбцов матрицы . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .
Достаточность
Пусть . Возьмем в матрице какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы . Тогда, согласно теореме о базисном миноре, последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .
Следствия
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
№20
Однородная система уравнений
Предложение 15.2 Однородная система уравнений
(15.7) |
всегда является совместной.
В этом разделе мы будем использовать матричную запись системы: .
Предложение 15.3 Сумма решений однородной системы линейных уравнений является решением этой системы. Решение, умноженное на число, тоже является решением.
Доказательство. Пусть и служат решениями системы . Тогда и . Пусть . Тогда
Так как , то — решение.
Пусть — произвольное число, . Тогда
Так как , то — решение.
Следствие 15.1 Если однородная система линейных уравнений имеет ненулевое решение, то она имеет бесконечно много различных решений.
Действительно, умножая ненулевое решение на различные числа, будем получать различные решения.
Определение 15.5 Будем говорить, что решения системы образуют фундаментальную систему решений, если столбцы образуют линейно независимую систему и любое решение системы является линейной комбинацией этих столбцов.
Определение 15.6 Пусть — фундаментальная система решений однородной системы . Тогда выражение
где — произвольные числа, будем называть общим решением системы .
Из определения фундаментальной системы решений следует, что любое решение однородной системы может быть получено из общего решения при некоторых значениях . И наоборот, при любых фиксированных числовых значениях из общего решения получим решение однородной системы.
Как находить фундаментальную систему решений мы увидим позже, в разделе «Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)»
Теорема 15.3 Пусть — фундаментальная система решений однородной системы . Тогда , где — число неизвестных в системе.
Теорема (о линейном решении однородных систем). Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы.
studfiles.net
Ранг матрицы
Ранее
для квадратной матрицы 
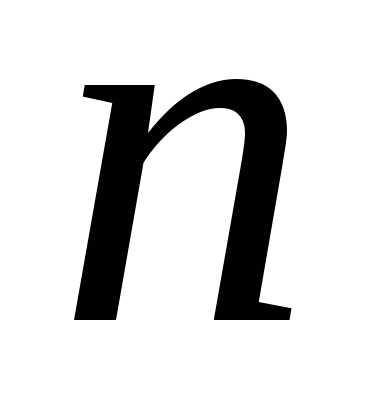 -го
порядка было введено понятие минора
-го
порядка было введено понятие минора
 .
Напомним, что так был назван определитель
порядка
.
Напомним, что так был назван определитель
порядка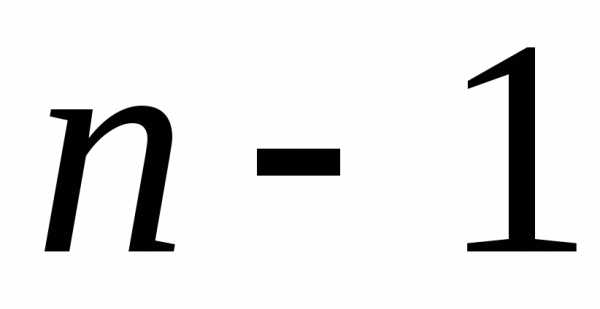 ,
полученный из определителя
,
полученный из определителя вычеркиванием
вычеркиванием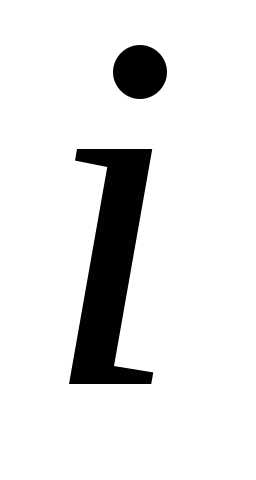 -й
строки и
-й
строки и -го
столбца.
-го
столбца. Введем
теперь общее понятие минора. Рассмотрим
некоторую, не
обязательно квадратную матрицу  .
Выберем какие-нибудь
.
Выберем какие-нибудь номеров строки
номеров строки номеров столбцов.
номеров столбцов.
Определение. Минором
порядка  матрицы
матрицы 
 ,
образованный элементами, стоящими на
пересечении выбранных строк и столбцов,
т.е. число
,
образованный элементами, стоящими на
пересечении выбранных строк и столбцов,
т.е. число 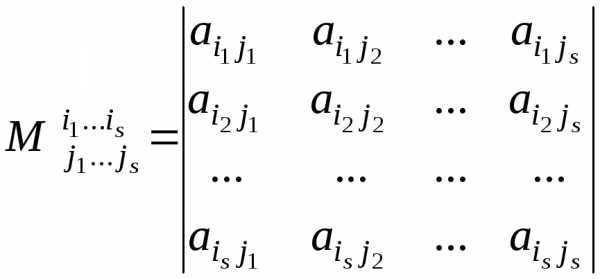 .
.
Каждая
матрица имеет столько миноров данного
порядка  ,
сколькими способами можно выбрать
номера строк
,
сколькими способами можно выбрать
номера строк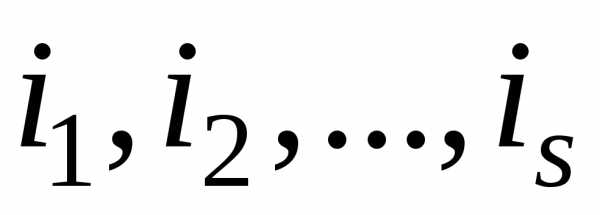 и столбцов.
и столбцов.
Определение.
В матрице  размеров
размеров минор порядка
минор порядка называетсябазисным,
если он отличен от нуля, а все миноры
порядка
называетсябазисным,
если он отличен от нуля, а все миноры
порядка 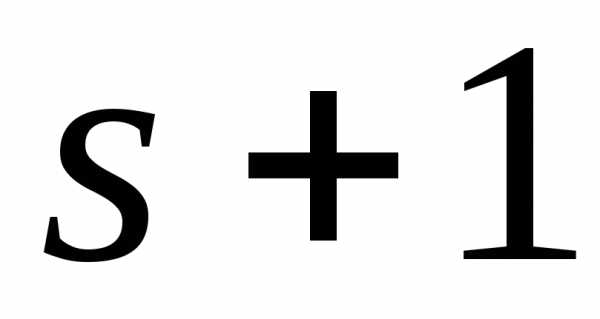 равны нулю или миноров порядка
равны нулю или миноров порядка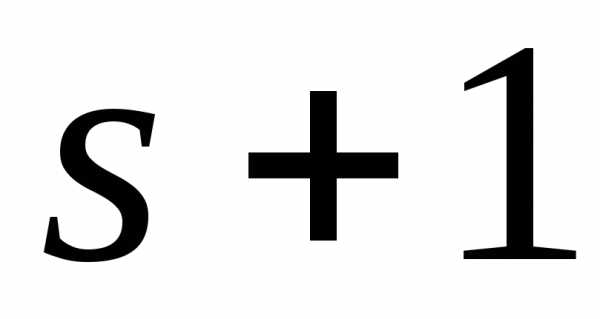 у матрицы
у матрицы вообще нет.
вообще нет.
Ясно,
что в матрице может быть несколько
разных базисных миноров, но все базисные
миноры имеют один и тот же порядок.
Действительно, если все миноры порядка 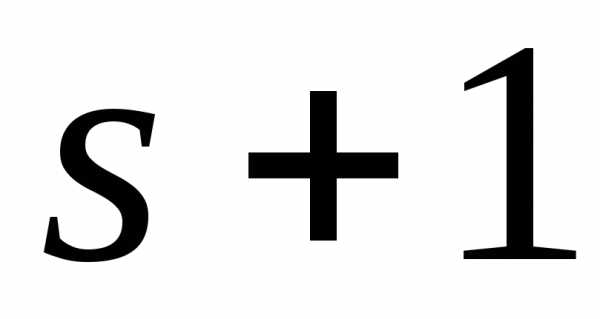 равны нулю, то равны нулю и все миноры
порядка
равны нулю, то равны нулю и все миноры
порядка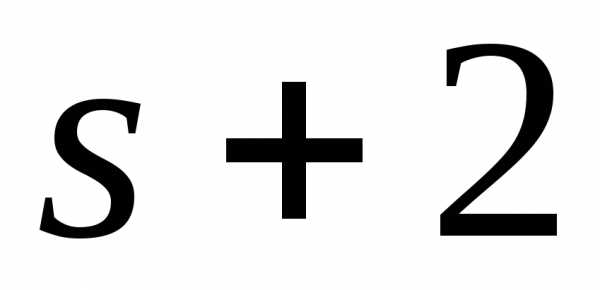 ,
а, следовательно, и всех бόльших порядков.
,
а, следовательно, и всех бόльших порядков.
Определение. Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если все элементы матрицы равны нулю, то ранг такой матрицы, по определению, считают нулем.
Ранг
матрицы  будем обозначать символом
будем обозначать символом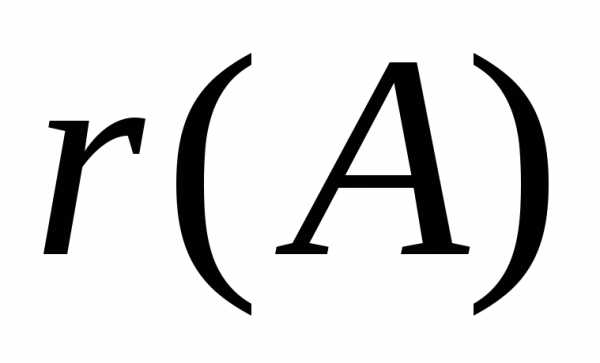 .
Из определения ранга следует, что для
матрицы
.
Из определения ранга следует, что для
матрицы размеров
размеров справедливо соотношение.
справедливо соотношение.
Два способа вычисления ранга матрицы
а) Метод окаймляющих миноров
Пусть
в матрице найден минор 
 -го
порядка, отличный от нуля. Рассмотрим
лишь те миноры
-го
порядка, отличный от нуля. Рассмотрим
лишь те миноры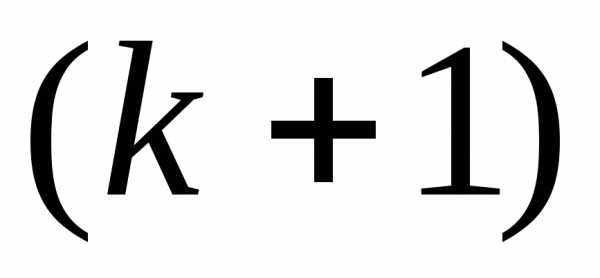 -го
порядка, которые содержат в себе
(окаймляют) минор
-го
порядка, которые содержат в себе
(окаймляют) минор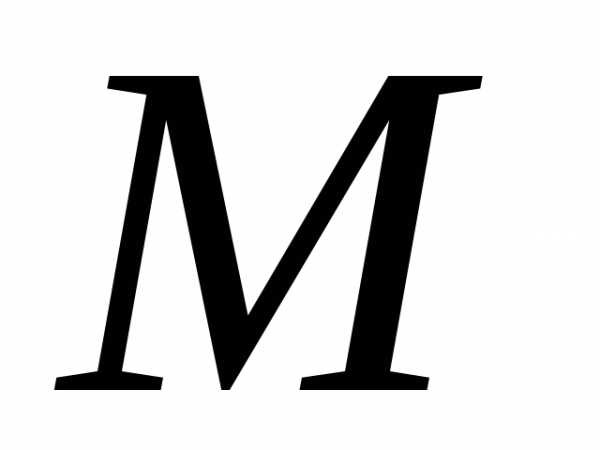 :
если все они равны нулю, то ранг матрицы
равен
:
если все они равны нулю, то ранг матрицы
равен .
В противном случае среди окаймляющих
миноров найдется ненулевой минор
.
В противном случае среди окаймляющих
миноров найдется ненулевой минор -го
порядка, и вся процедура повторяется.
-го
порядка, и вся процедура повторяется.
Пример
9. Найти
ранг матрицы  методом окаймляющих миноров.
методом окаймляющих миноров.
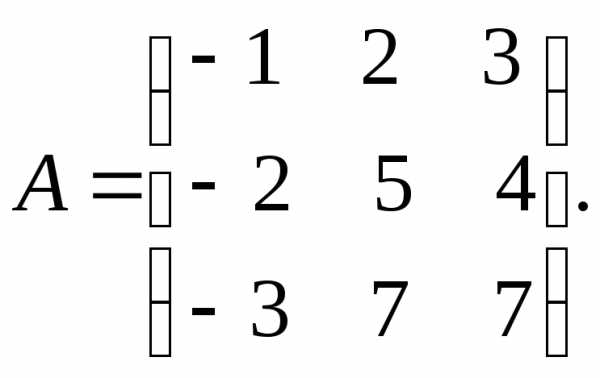
Выберем
минор второго порядка 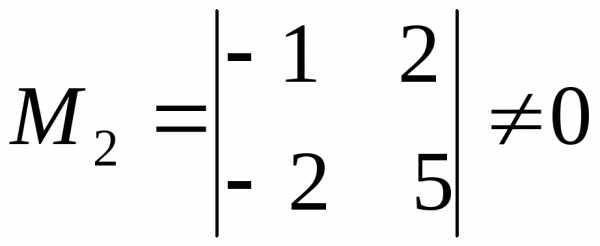 .
Существует только один минор третьего
порядка, окаймляющий выбранный минор
.
Существует только один минор третьего
порядка, окаймляющий выбранный минор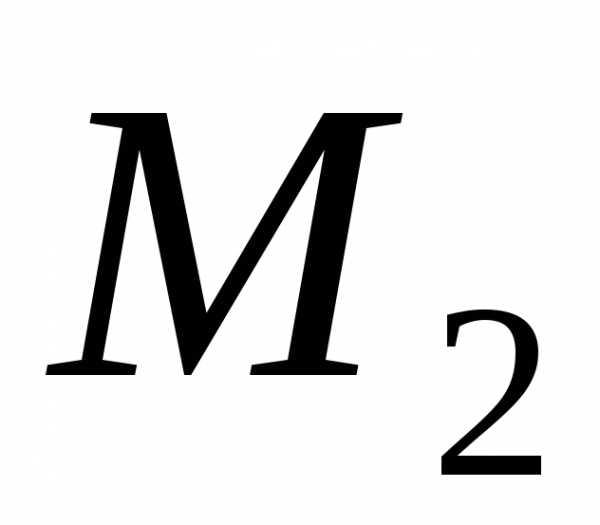 .
Вычислим его.
.
Вычислим его.
Значит, минор базисный, а ранг матрицы равен его порядку, т.е.
Ясно, что перебирать таким способом миноры в поисках базисного – задача, связанная с большими вычислениями, если размеры матрицы не очень малы. Существует, однако, более простой способ нахождения ранга матрицы – при помощи элементарных преобразований.
б) Метод элементарных преобразований
Определение. Элементарными преобразованиями матрицы называют следующие преобразования:
умножение строки на число, отличное от нуля;
прибавление к одной строке другой строки;
перестановку строк;
такие же преобразования столбцов.
Преобразования 1 и 2 выполняются поэлементно.
Комбинируя преобразования первого и второго вида, мы можем к любой строке прибавить линейную комбинацию остальных строк.
Теорема. Элементарные преобразования не меняют ранга матрицы.
(Без доказательства)
Идея практического метода вычисления ранга матрицы

заключается
в том, что с помощью элементарных
преобразований данную матрицу  приводят к виду
приводят к виду
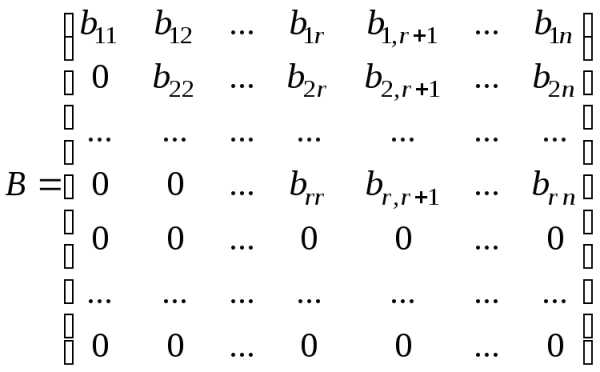 ,
(5)
,
(5)
в
котором «диагональные» элементы
отличны от нуля, а элементы, расположенные
ниже «диагональных», равны нулю. Условимся
называть матрицу такого вида треугольной (иначе, ее
называют диагональной, трапециевидной
или лестничной). После приведения матрицы
такого вида треугольной (иначе, ее
называют диагональной, трапециевидной
или лестничной). После приведения матрицы к треугольному виду можно сразу записать,
что
к треугольному виду можно сразу записать,
что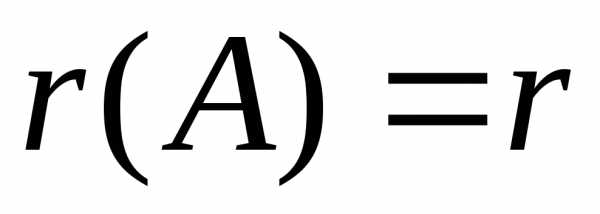 .
.
В
самом деле,
(т.к. элементарные преобразования не
меняют ранга). Но у матрицы существует отличный от нуля минор
порядка
существует отличный от нуля минор
порядка :
:
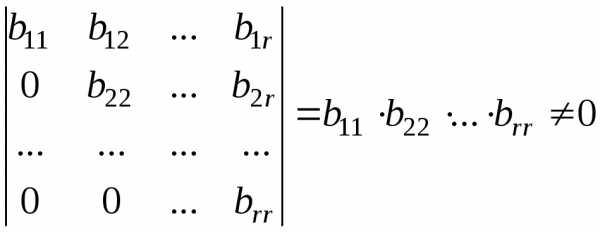 ,
,
а
любой минор порядка 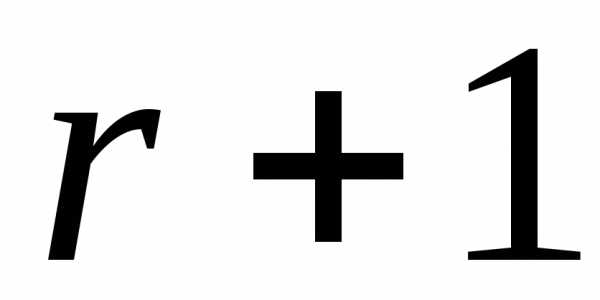 содержит нулевую строку и поэтому равен
нулю.
содержит нулевую строку и поэтому равен
нулю.
Сформулируем
теперь практическое правило
вычисления ранга матрицы  с помощью элементарных преобразований:
для нахождения ранга матрицы
с помощью элементарных преобразований:
для нахождения ранга матрицы следует с помощью элементарных
преобразований привести ее к треугольному
виду
следует с помощью элементарных
преобразований привести ее к треугольному
виду .
Тогда ранг матрицы
.
Тогда ранг матрицы будет равен числу ненулевых строк в
полученной матрице
будет равен числу ненулевых строк в
полученной матрице .
.
Пример
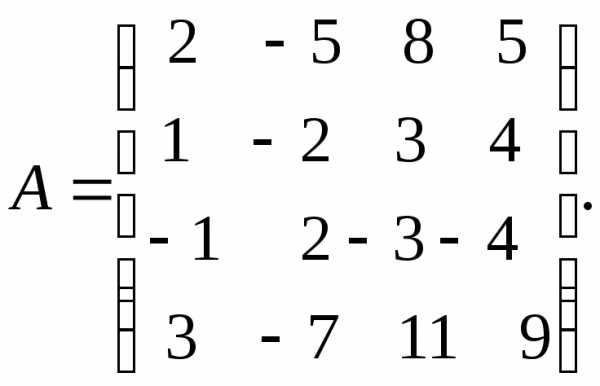
10. Найти
ранг матрицы  методом
элементарных преобразований
методом
элементарных преобразований
Решение.
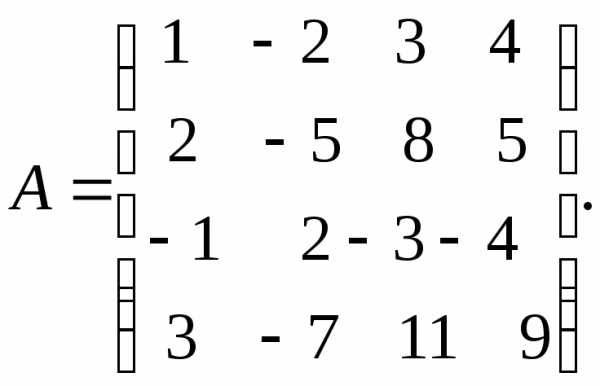
Поменяем местами первую и вторую строку (т.к. первый элемент второй строки −1 и с ней будет удобно выполнять преобразования). В результате получим матрицу, эквивалентную данной.

Обозначим 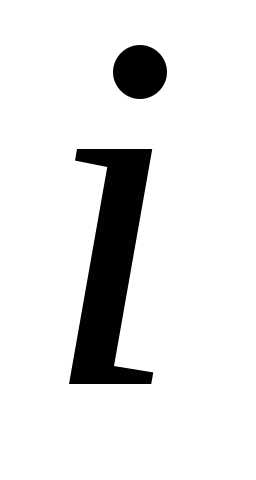 -тую
строку матрицы –
-тую
строку матрицы – .
Нам необходимо привести исходную матрицу
к треугольному виду. Первую строку будем
считать ведущей, она будет участвовать
во всех преобразованиях, но сама остается
без изменений.
.
Нам необходимо привести исходную матрицу
к треугольному виду. Первую строку будем
считать ведущей, она будет участвовать
во всех преобразованиях, но сама остается
без изменений.
На
первом этапе выполним преобразования,
позволяющие получить в первом столбце
нули, кроме первого элемента. Для этого
из второй строки вычтем первую, умноженную
на 2
,
к третьей строке прибавим первую ,
а из третьей вычтем первую, умноженную
на 3Получаем матрицу, ранг которой совпадает
с рангом данной матрицы. Обозначим ее
той же буквой
,
а из третьей вычтем первую, умноженную
на 3Получаем матрицу, ранг которой совпадает
с рангом данной матрицы. Обозначим ее
той же буквой :
:
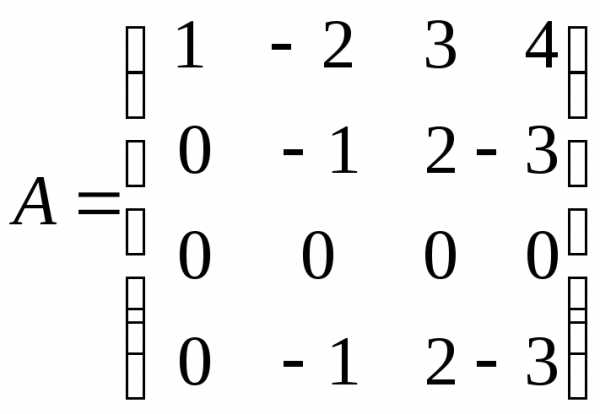 .
.
Так как нам необходимо привести матрицу к виду (5), вычтем из четвертой строки вторую. При этом имеем:
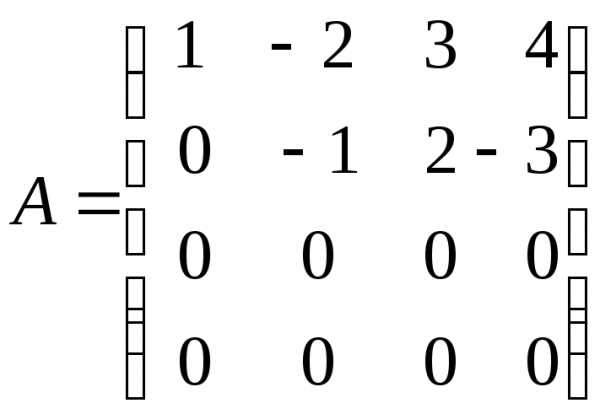 .
.
Получена
матрица треугольного вида, и можно
сделать вывод, что 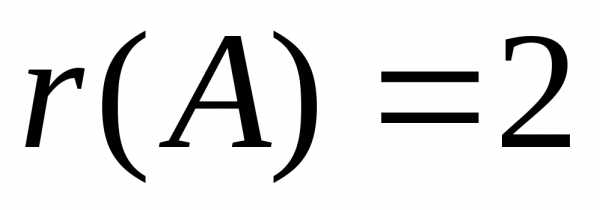 ,
т. е. числу ненулевых строк. Коротко
решение задачи можно записать следующим
образом:
,
т. е. числу ненулевых строк. Коротко
решение задачи можно записать следующим
образом:
studfiles.net
Вычисление ранга матрицы.
Метод окаймляющих миноров нахождения ранга матрицы.
Определение. Минор М матрицы А называется окаймляющим для минора М, если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы А. Т.о. порядок окаймляющего минора М на единицу больше порядка минора М.
Теорема 7. (доказательство следует из теоремы о базисном миноре). Если для некоторого минора матрицы все окаймляющие миноры равны нулю, то он является базисным.
Найти какой-нибудь минор М1 1-го порядка (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица А нулевая и r(A)=0.
Вычислять миноры 2-го порядка, содержащие М1 (окаймляющие миноры) до тех пор, пока не найдется минор М2, отличный от нуля. Если такого минора нет, то r(A)=1, если есть, то r(A)≥2.
………………
k) Вычислять (если они существуют) миноры k-го порядка, окаймляющие минор Mk-1≠0. Если таких миноров нет, то r(A)=k-1; если есть хотя бы один такой минор, то Mk≠0 r(A)≥k, и процесс продолжается.
Пример. Найдем r(A). А=. Т.к. есть ненулевые элементы, то r(A)≥1. Найдем ненулевой минор 2-го порядка. Например, М2=.
Значит, r(A)≥2. Вычислим миноры 3-го порядка, окаймляющие этот минор. ,=-30+30=0.
Все миноры 3-го порядка, окаймляющие М2 равны нулю, следовательно, r(A)<3,т.е. r(A)=2. — один из базисных миноров.
Метод элементарных преобразований нахождения ранга матрицы:
Матрицу А приводят к ступенчатому виду с помощью элементарных преобразований. Количество ненулевых строк полученной ступенчатой матрицы есть искомый ранг матрицы. Пример. Найти ранг матрицы методом элементарных преобразований.
Полученная матрица имеет 2 ненулевые строки, значит ее ранг равен 2. Следовательно, ранг исходной матрицы равен 2. Замечание. Если а11=0, то перестановкой строк или столбцов добиваемся того, чтобы а11≠0.
Системы линейных алгебраических уравнений (слау).
В общем случае система m линейных уравнений с n неизвестными (линейная система) имеет следующий вид:
(1)
Где х1,х2,…,хn-неизвестные, а11,а12,…,аmn – коэффициенты системы, b1,b2,…,bm – свободные члены.
У коэффициентов aij i-номер уравнения, j-номер неизвестного, при котором стоит этот коэффициент.
Если все свободные члены b1,b2,…,bm равны 0, то система (1) называется однородной. Если хотя бы один из b1,b2,…,bm отличен от 0, система (1) — неоднородная.
Система (1) называется квадратной, если m=n.
Решением системы (1) называется такая совокупность n чисел с1,с2,…,сn, которая при подстановке в систему вместо неизвестных х1,х2,…,хn обращает все уравнения системы в тождество.
СЛАУ можно записать в виде (i=1,2,…,m) (2)
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
СЛАУ
Пример. несовместная система.
-неопределенная (х1=с, х2=5-3с)
Две системы уравнений называются эквивалентными, или равносильными, если имеют одно и то же множество решений.
Запишем систему уравнений в матричной форме.
А=(3) , Х=(4) , В=(5)
Где А- матрица системы, Х- матрица-столбец переменных, В- матрица-столбец свободных членов.
— матрица-столбец.
Элементы этой матрицы-левые части системы (1). Т.о. систему можно записать в матричном виде: АХ=В (6)
-А* = (А|В) расширенная матрица системы (1)
Решение матричного уравнения (6) заключается в отыскании такого столбца (4), который при заданной матрице (3) и заданном столбце (5) обращает уравнение (6) в тождество.
Систему (1) можно записать и в векторной форме:
х1+х2+…+хn=
Или, обозначая столбцы соответственно a1,…,an,В
a1x1+…+anxn=В (7)
Т.о., решение СЛАУ можно трактовать как представление столбца В в виде линейной комбинации столбцов a1,…,an.
Т.о., в отношении системы (1) мы должны научиться устанавливать следующие факты:
1) является ли система (1) совместной;
2) является ли система (1) (в случае ее совместности) определенной или нет;
3) способ отыскания единственного решения совместной системы (1) (в случае ее определенности) и отыскания всех ее решений (в случае ее неопределенности).
Теорема Крόнекера-Капелли (Леопольд Кронекер (1823-1891) – немецкий математик, Альфред Капелли (1855-1910) – итальянский математик). Для того, чтобы система линейных уравнений (1) являлась совместной, необходимо и достаточно, чтобы ранг ее матрицы был равен рангу расширенной матрицы этой системы.
Доказательство. Необходимость. Пусть r=rgA rr(AВ). Поэтому достаточно показать, что ранг матрицы А не меньше ранга ее расширенной матрицы, т.е. rr(AВ). Пусть система (1) совместна.
Это означает, что столбец В=в расширенной матрице системе является линейной комбинацией остальных столбцов. Выберем какой-либо базисный минор матрицы А. Без ограничения общности, пусть он будет расположен в верхнем левом углу, т.е. Мr=.
По теореме о базисном миноре, базисные столбцы линейно независимы, в то время как j>k существуют такие числа ijR, i=1,2,…,k aj=1ja1+2ja2+…+rjar,
Где aj – j-й столбец матрицы А.
Тогда столбец b=a1x1+…+arxr+ar+1xr+1+…+anxn=
=a1x1+…+arxr+(1,r+1a1+2,r+1a2+…+r,r+1ar)xr+1+…+(1na1+2na2+…+rnar)xn
Является линейной комбинацией базисных столбцов матрицы А. Это значит, что Мr является также базисным минором расширенной матрицы (AВ), т.к.
1) он ненулевой;
2) если взять какой-либо окаймляющий минор М, то либо он будет минором матрицы А, т.е. ненулевым, либо он будет содержать столбец В и, следовательно, не может быть ненулевым, т.к. его столбцы линейно зависимы. Поэтому rg (AВ)=rg A.
Достаточность. Пусть rg (AВ)=rg A. выберем в А базисный минор М. Тогда он будет базисным и в матрице (AВ). Значит, столбец В можно представить как линейную комбинацию базисных столбцов a1,…,ar:
В=a1x1+…+arxr.
Полагая xr+1=xr+2=…=xn=0, получаем решение x1,…,xn исходной СЛАУ, т.к.
В=a1x1+…+arxr=a1x1+…+arxr+0ar+1+…+0an.
Это означает, что СЛАУ совместна. Ч.т.д.
studfiles.net
Ранг матрицы, формула и примеры
Обозначается ранг матрицы как или . Очевидно, ранг матрицы не превышает порядка самой матрицы
По определению ранг матрицы можно найти следующим образом. Если все миноры первого порядка (элементы матрицы) равны нулю, то . Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то . В случае, если есть миноры второго порядка, отличные от нуля, исследуем миноры третьего порядка. Так продолжаем до тех пор, пока, либо все миноры порядка равны нулю, либо миноров порядка не существует, тогда .
Примеры нахождения ранга матрицы
Указанный метод нахождения ранга матрицы не всегда удобен в использовании, так как связан с вычислением большого количества определителей. На практике чаще всего используют метод нахождения ранга матрицы основанный на том что, ранг матрицы не изменяется, если над матрицей выполнять элементарные преобразования, и на следующей теореме.
Теорема о ранге
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Ранг матрицы
Пусть задана некоторая матрица  :
:
 .
.
Выделим в этой матрице  произвольных строк и
произвольных строк и произвольных столбцов.
Тогда определитель
произвольных столбцов.
Тогда определитель -го
порядка, составленный из элементов
матрицы
-го
порядка, составленный из элементов
матрицы ,
расположенных на пересечении выделенных
строк и столбцов, называется минором
,
расположенных на пересечении выделенных
строк и столбцов, называется минором -го
порядка матрицы
-го
порядка матрицы .
.
Определение 1.13.Рангом матрицы называется наибольший порядок минора
этой матрицы, отличного от нуля.
называется наибольший порядок минора
этой матрицы, отличного от нуля.
Для вычисления ранга матрицы следует рассматривать все ее миноры наименьшего порядка и, если хоть один из них отличный от нуля, переходить к рассмотрению миноров старшего порядка. Такой подход к определению ранга матрицы называется методом окаймления (или методом окаймляющих миноров).
Задача 1.4.Методом окаймляющих
миноров определить ранг матрицы .
.
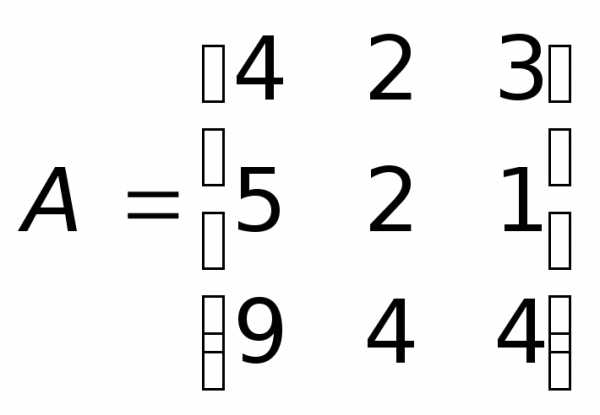 .
.
Рассмотрим окаймление первого порядка, например, . Затем перейдем к рассмотрению некоторого окаймления второго порядка.
Например, 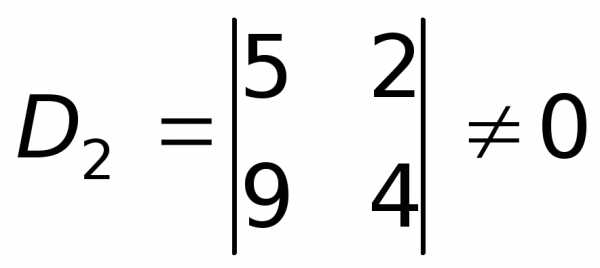 .
.
Наконец, проанализируем окаймление третьего порядка.
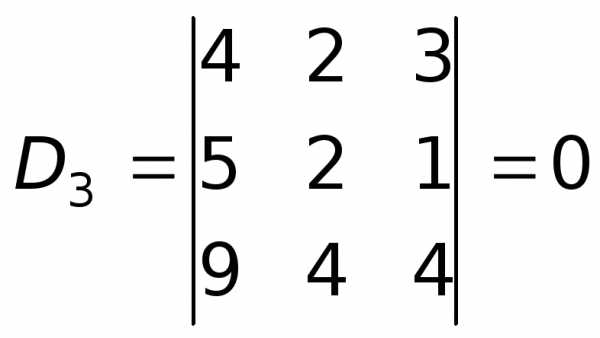 .
.
Таким образом, наивысший порядок минора,
отличного от нуля, равен 2, следовательно, 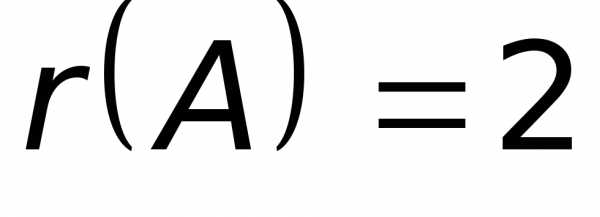 .
.
При решении задачи 1.4 можно заметить, что ряд окаймляющих миноров второго порядка отличны от нуля. В этой связи имеет место следующее понятие.
Определение 1.14.Базисным минором матрицы называется всякий, отличный от нуля минор, порядок которого равен рангу матрицы.
Теорема 1.2.(Теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы.
Заметим, что строки (столбцы) матрицы линейно зависимы тогда и только тогда, когда хотя бы одну из них можно представить как линейную комбинацию остальных.
Теорема 1.3.Число линейно независимых строк матрицы равно числу линейно независимых столбцов матрицы и равно рангу матрицы.
Теорема 1.4.(Необходимое и достаточное
условие равенства нулю определителя).
Для того, чтобы определитель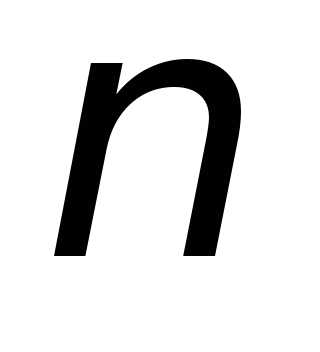 -го
порядкабыл равен нулю, необходимо и достаточно,
чтобы его строки (столбцы) были линейно
зависимы.
-го
порядкабыл равен нулю, необходимо и достаточно,
чтобы его строки (столбцы) были линейно
зависимы.
Вычисление ранга матрицы, основанное на использовании его определения, является слишком громоздкой операцией. Особенно это становится существенным для матриц высоких порядков. В этой связи на практике ранг матрицы вычисляют на основании применения теорем 10.2 — 10.4, а также использования понятий эквивалентности матриц и элементарных преобразований.
Определение 1.15.Две матрицы и
и называются эквивалентными, если их
ранги равны, т.е..
называются эквивалентными, если их
ранги равны, т.е..
Если матрицы  и
и эквивалентны, то отмечают
эквивалентны, то отмечают
 .
.
Теорема 1.5.Ранг матрицы не меняется от элементарных преобразований.
Будем называть элементарными
преобразованиями матрицы  любые из следующих действий над матрицей:
любые из следующих действий над матрицей:
— замену строк столбцами, а столбцов соответствующими строками;
— перестановку строк матрицы;
— вычеркивание строки, все элементы которой равны нулю;
— умножение какой-либо строки на число, отличное от нуля;
— прибавление к элементам одной строки
соответствующих элементов другой строки
умноженных на одно и то же число 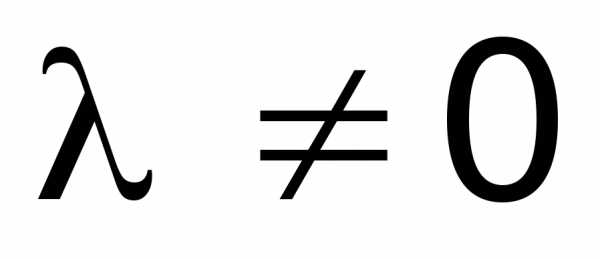 .
.
Следствие теоремы 1.5.Если матрица получена из матрицы
получена из матрицы при помощи конечного числа элементарных
преобразований, то матрицы
при помощи конечного числа элементарных
преобразований, то матрицы и
и эквивалентны.
эквивалентны.
При вычислении ранга матрицы ее следует привести при помощи конечного числа элементарных преобразований к трапециевидной форме.
Определение 1.16.Трапециевидной будем называть такую форму представления матрицы, когда в окаймляющем миноре наибольшего порядка отличного от нуля все элементы, стоящие ниже диагональных, обращаются в нуль. Например:
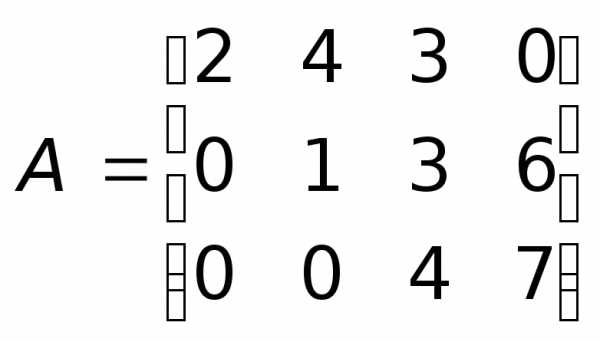 .
.
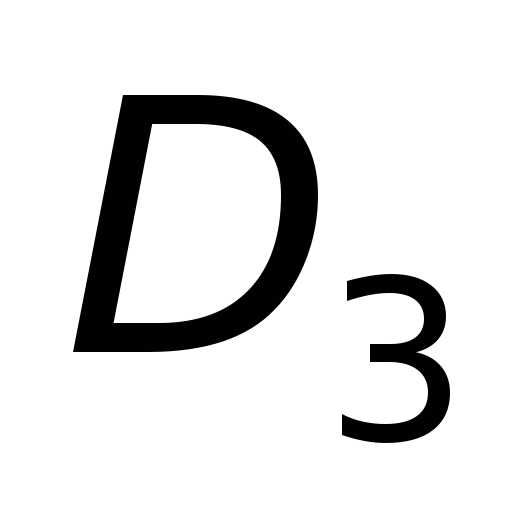
Здесь 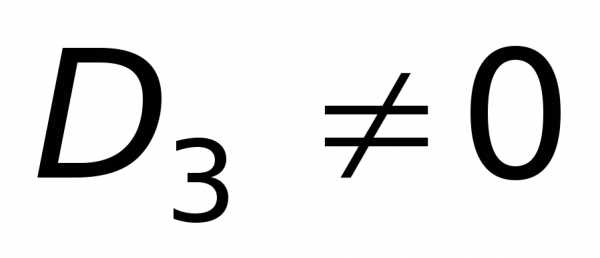 ,
элементы матрицыобращаются в нуль. Тогда форма представления
такой матрицы будет трапециевидной.
,
элементы матрицыобращаются в нуль. Тогда форма представления
такой матрицы будет трапециевидной.
Как правило, матрицы к трапециевидной
форме приводят при помощи алгоритма
Гаусса. Идея алгоритма Гаусса состоит
в том, что, умножая элементы первой
строки матрицы на соответствующие
множители, добиваются, чтобы все элементы
первого столбца, расположенные ниже
элемента 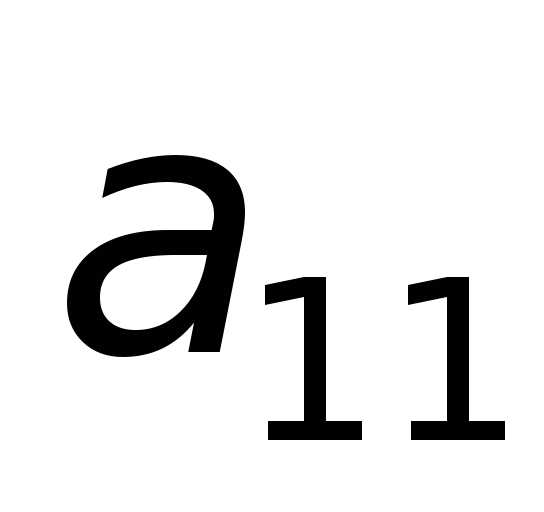 ,
превращались бы в нуль. Затем, умножая
элементы второго столбца на соответствующие
множители, добиваются, чтобы все элементы
второго столбца, расположенные ниже
элемента,
превращались бы в нуль. Далее поступают
аналогично.
,
превращались бы в нуль. Затем, умножая
элементы второго столбца на соответствующие
множители, добиваются, чтобы все элементы
второго столбца, расположенные ниже
элемента,
превращались бы в нуль. Далее поступают
аналогично.
Задача 1.5.Определить ранг матрицы путем сведения ее к трапециевидной форме.
 .
.
Для удобства применения алгоритма Гаусса можно поменять местами первую и третью строки.




 .
.
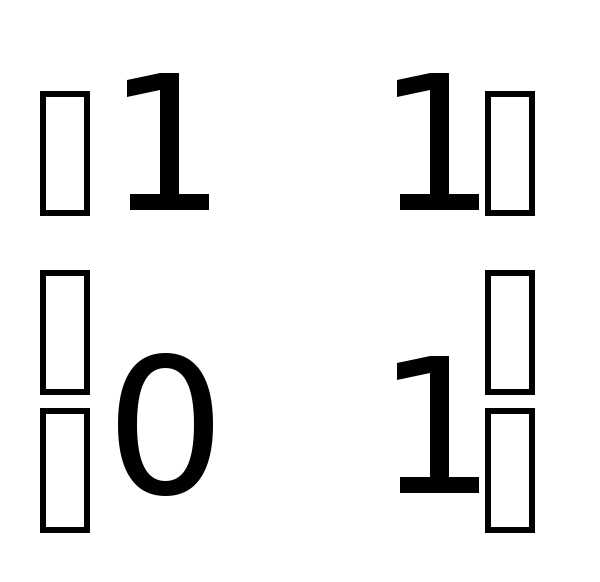
Очевидно, что здесь 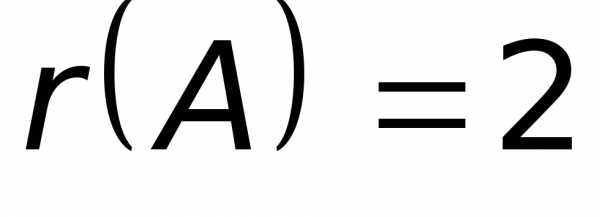 .
Однако, для приведения результата к
более изящному виду можно далее продолжить
преобразования над столбцами.
.
Однако, для приведения результата к
более изящному виду можно далее продолжить
преобразования над столбцами.
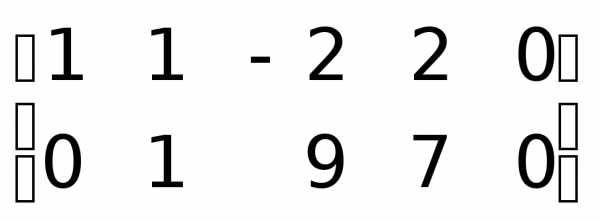
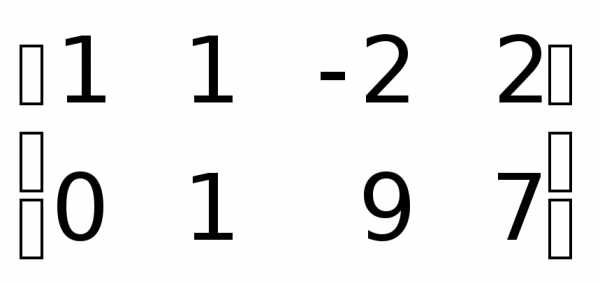
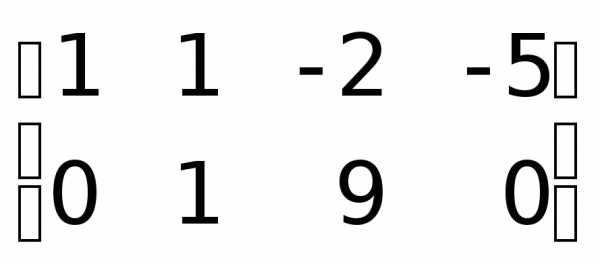

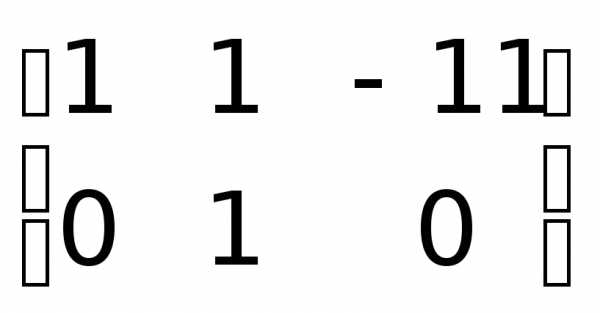

 .
.
24
studfiles.net
Ранг матрицы
Каталин Дэвид
Рангом матрицы из m строк и n столбцов называется число r, обладающее следующими свойствами:
- r меньше или равно наименьшему из чисел m и n.
- r равно наивысшему из порядков ненулевых миноров этой матрицы.
Вычисление ранга матрицы
- Выбираем ненулевой элемент матрицы.
- Перебираем миноры второго порядка, содержащие этот элемент, пока не найдем минор, отличный от нуля.
- Если все миноры второго порядка равны нулю, то ранг матрицы равен 1.
- Если существует хотя бы один ненулевой минор второго порядка, перебираем «содержащие» его миноры третьего порядка (окаймляющие миноры), пока не будет найден хотя бы один ненулевой минор.
- Если все миноры третьего порядка равны нулю, то ранг матрицы равен 2.
- Если существует хотя бы один ненулевой минор третьего порядка, перебираем окаймляющие его миноры четвертого порядка, пока не будет найден хотя бы один ненулевой минор.
- Продолжаем этот процесс, пока порядок миноров не достигнет наименьшего из чисел m и n.
Пример 42
$A=\begin{pmatrix} 1 & 2 & 4\\ 3 & 6 & 5 \end{pmatrix}$
Матрица имеет 2 строки и 3 столбца, следовательно, ее наибольший возможный ранг равен 2. Выбираем ненулевой элемент матрицы.
$\begin{pmatrix} \color{red}{1} & 2 & 4\\ 3 & 6 & 5 \end{pmatrix}$
Составляем минор второго порядка, содержащий 1.
$\begin{pmatrix} \color{red}{1} & \color{red}{2} & 4\\ \color{red}{3} & \color{red}{6} & 5 \end{pmatrix}$
Вычисляем этот минор.
$\begin{vmatrix} \color{red}{1} & \color{red}{2}\\ \color{red}{3} & \color{red}{6} \end{vmatrix}=6 — 6 = 0$
Составляем другой минор второго порядка, содержащий 1. $A=\begin{pmatrix} \color{blue}{1} & 2 & \color{blue}{4}\\ \color{blue}{3} & 6 & \color{blue}{5} \end{pmatrix}$
Вычисляем этот минор.
$\begin{vmatrix} \color{blue}{1} & \color{blue}{4}\\ \color{blue}{3} & \color{blue}{5} \end{vmatrix}= 5 — 12 = -7 \neq 0.$
Ранг равен 2.
Пример 43
$B=\begin{pmatrix} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1\\ \end{pmatrix}$
Выбираем ненулевой элемент матрицы.
$\begin{pmatrix} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & \color{red}{1} & 1 \end{pmatrix}$
Вычисляем миноры второго порядка, содержащие этот элемент. $\begin{pmatrix} 1 & 1 & 1\\ \color{red}{1} & \color{red}{1} & 1\\ \color{red}{1} & \color{red}{1} & 1 \end{pmatrix}$
$\begin{vmatrix} \color{red}{1} & \color{red}{1} \\ \color{red}{1} & \color{red}{1} \end{vmatrix}=0 $ (поскольку он имеет две одинаковых строки)
Все остальные миноры второго порядка равны нулю, так как они все идентичны. В данном случае ранг матрицы равен 1.
Пример 44
$B=\begin{pmatrix} 3 & 8 & 2\\ 2 & 1 & 1\\ 5 & 3 & 4\\ 7 & 4 & 5 \end{pmatrix}$
Матрица имеет 4 строки и 3 столбца, следовательно, ее наибольший возможный ранг равен 3.
Выбираем ненулевой элемент матрицы.
$\begin{pmatrix} 3 & 8 & 2\\ 2 & 1 & 1\\ 5 & 3 & \color{red}{4}\\ 7 & 4 & 5 \end{pmatrix}$
Вычисляем минор второго порядка, содержащий 4.
$ \begin{pmatrix} 3 & 8 & 2\\ 2 & \color{red}{1} & \color{red}{1}\\ 5 & \color{red}{3} & \color{red}{4}\\ 7 & 4 & 5 \end{pmatrix}$
$\begin{vmatrix} \color{red}{1} & \color{red}{1}\\ \color{red}{3} & \color{red}{4}\\ \end{vmatrix} = 4 — 3 = 1$
Составляем минор третьего порядка, окаймляющий предыдущий минор. $\begin{pmatrix} 3 & 8 & 2\\ \color{red}{2} & \color{red}{1} & \color{red}{1}\\ \color{red}{5} & \color{red}{3} & \color{red}{4}\\ \color{red}{7} & \color{red}{4} & \color{red}{5} \end{pmatrix}$
Вычисляем этот минор.
$\begin{pmatrix} \color{red}{2} & \color{red}{1} & \color{red}{1}\\ \color{red}{5} & \color{red}{3} & \color{red}{4}\\ \color{red}{7} & \color{red}{4} & \color{red}{5} \end{pmatrix}=0 $ because $ R_{1}+R_{2}=R_{3}$
Вычисляем другой минор третьего порядка, окаймляющий предыдущий минор.
$\begin{pmatrix} \color{blue}{3} & \color{blue}{8} & \color{blue}{2}\\ \color{blue}{2} & \color{blue}{1} & \color{blue}{1}\\ \color{blue}{5} & \color{blue}{3} & \color{blue}{4}\\ 7 & 4 & 5 \end{pmatrix}$
$\begin{vmatrix} \color{blue}{3} & \color{blue}{8} & \color{blue}{2}\\ \color{blue}{2} & \color{blue}{1} & \color{blue}{1}\\ \color{blue}{5} & \color{blue}{3} & \color{blue}{4} \end{vmatrix} =$ $12 + 12 +40 -10 -9 -64 =-19 \neq 0 $
Ранг матрицы равен 3.
Пример 45
$D=\begin{pmatrix} 1 & 5 & 1 & 6\\ 2 & 3 & 2 & 5\\ 6 & 1 & 6 & 7 \end{pmatrix}$
D — матрица из 3 строк и 4 столбцов, так что ее наибольший возможный ранг равен 3.
Выбираем ненулевой элемент матрицы.
$\begin{pmatrix} 1 & \color{red}{5} & 1 & 6\\ 2 & 3 & 2 & 5\\ 6 & 1 & 6 & 7 \end{pmatrix}$
Составляем минор второго порядка, содержащий 5.
$\begin{pmatrix} \color{red}{1} & \color{red}{5} & 1 & 6\\ \color{red}{2} & \color{red}{3} & 2 & 5\\ 6 & 1 & 6 & 7 \end{pmatrix}$
$\begin{vmatrix} 1 & 5\\ 2 & 3 \end{vmatrix}= 3 — 10 = -7 \neq 0$
Составляем минор третьего порядка, окаймляющий предыдущий минор.
$\begin{pmatrix} \color{red}{1} & \color{red}{5} & \color{red}{1} & 6\\ \color{red}{2} & \color{red}{3} & \color{red}{2} & 5\\ \color{red}{6} & \color{red}{1} & \color{red}{6} & 7 \end{pmatrix}$
$\begin{vmatrix} \color{red}{1} & \color{red}{5} & \color{red}{1}\\ \color{red}{2} & \color{red}{3} & \color{red}{2}\\ \color{red}{6} & \color{red}{1} & \color{red}{6} \end{vmatrix} = 0 $ (поскольку два столбца равны)
Тогда составляем другой минор третьего порядка, окаймляющий ненулевой минор второго порядка.
$\begin{pmatrix} \color{blue}{1} & \color{blue}{5} & 1 & \color{blue}{6}\\ \color{blue}{2} & \color{blue}{3} & 2 & \color{bl
www.math10.com
