Действия над комплексными числами
Над комплексными числами можно выполнять следующие действия:
- сложение;
- вычитание;
- умножение;
- деление;
- возведение комплексного числа в степень;
- извлечение корня $n$—й степени из комплексного числа.
Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.
Умножение, деление и возведение в степень выполняются для чисел, представленных в любой форме записи.
Извлечение корня выполняется для чисел, представленных в тригонометрической форме.
Определение 1
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ — вещественная (действительная) часть;
- $b$ — мнимая часть.
Определение 2
Запись некоторого комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.
Определение 3
Запись некоторого комплексного числа $z$ в виде $z=r\cdot e^{i\varphi } $ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.
Примечание 1
При необходимости извлечения корня из комплексного числа, записанного в показательной форме, необходимо предварительно привести его к тригонометрической форме представления.
Сумма комплексных чисел
Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством \[z_{1} +z_{2} =(a_{1} +b_{1} i)+(a_{2} +b_{2} i)=(a_{1} +a_{2} )+(b_{1} +b_{2} )\cdot i.\]
Разность комплексных чисел
Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством \[z_{1} -z_{2} =(a_{1} +b_{1} i)-(a_{2} +b_{2} i)=(a_{1} -a_{2} )+(b_{1} -b_{2} )\cdot i.\]
Пример 1
Выполнить действия: 1) $z_{1} +z_{2} $2) $z_{1} -z_{2} $ для заданных комплексных чисел $z_{1} =2+4i$ и $z_{2} =1-3i$.
Решение:
1) По определению имеем: $z_{1} +z_{2} =(a_{1} +a_{2} )+(b_{1} +b_{2} )\cdot i$
Для исходных чисел получаем:
\[z_{1} +z_{2} =(2+4i)+(1-3i)=(2+1)+(4-3)i=3+i\]
2) По определению имеем: $z_{1} -z_{2} =(a_{1} -a_{2} )+(b_{1} -b_{2} )\cdot i$
Для исходных чисел получаем:
\[z_{1} +z_{2} =(2+4i)-(1-3i)=(2-1)-(4+3)i=1-7i.\]
Произведение комплексных чисел
Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.
Произведением двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством
\[z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )].\]
Пример 2
Выполнить умножение комплексных чисел представленных в алгебраической форме:
$z_{1} =1+3i$ и $z_{2} =2-2i$.Решение:
Для исходных чисел, учитывая определение, получаем:
\[z_{1} \cdot z_{2} =(1+3i)\cdot (2-2i)=\]
\[1\cdot 2+3\cdot 2i+1\cdot (-2i)+3i\cdot (-2i)=2+6i-2i-6i^{2} =2+4i+6=8+4i\]
Пример 3
Выполнить умножение комплексных чисел представленных в тригонометрической форме:
$z_{1} =3\sqrt{3} \cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$ и $z_{2} =2\cdot (\cos \pi +i\cdot \sin \pi )$.Решение:
1) По определению имеем: $z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )]$
Для исходных чисел получаем:
\[\begin{array}{l} {z_{1} \cdot z_{2} =\left(3\sqrt{3} \cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )\right)\cdot \left(2\cdot (\cos \pi +i \cdot \sin \pi )\right)=6\cdot \sqrt{3} \cdot \left[\cos \left(\frac{\pi }{2} +\pi \right)+i\cdot \sin \left(\frac{\pi }{2} +\pi \right)\right]=} \\ {=6\sqrt{3} \cdot \left(\cos \frac{3\pi }{2} +i\cdot \sin \frac{3\pi }{2} \right)} \end{array}\]Частное комплексных чисел
Частным двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i \sin \varphi _{2} )$ является комплексное число, которое определяется равенством
\[z_{1} \div z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )].\]
Примечание 2
Чтобы выполнить операцию деления комплексных чисел, представленных в алгебраической форме, необходимо:
- представить запись операции деления в виде дроби;
- числитель и знаменатель дроби умножить на число сопряженное знаменателю;
- привести полученное выражение к алгебраической записи.
Пример 4
Выполнить деление комплексных чисел, представленных в алгебраической форме:
$z_{1} =2+i$ и $z_{2} =1-i$.Решение:
Для исходных чисел получаем:
\[\frac{z_{1} }{z_{2} } =\frac{2+i}{1-i} =\frac{(2+i)(1+i)}{(1-i)(1+i)} =\frac{2+i+2i+i^{2} }{1^{2} -i^{2} } =\frac{2+3i-1}{1+1} =\frac{1+3i}{2} = \frac{1}{2} +\frac{3}{2} i\]Пример 5
Выполнить деление комплексных чисел представленных в тригонометрической форме:
$z_{1} =3\cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)$ и $z_{2} =2\cdot (\cos 2\pi +i\cdot \sin 2\pi )$.Решение:
По определению имеем: $z_{1} \div z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )]$
Для исходных чисел получаем:
\[\begin{array}{l} {\frac{z_{1} }{z_{2} } =3\cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)\div \left(2\cdot (\cos 2\pi +i\cdot \sin 2\pi )\right)=\frac{3}{2} \cdot \left[\cos \left(\frac{2\pi }{3} -2\pi \right)+i\cdot \sin \left(\frac{2\pi }{3} -2\pi \right)\right]=} \\ {= \frac{3}{2} \cdot \left(\cos \left(-\frac{4\pi }{3} \right)+i\cdot \sin \left(-\frac{4\pi }{3} \right)\right)} \end{array}\]Степерь комплексного числа
Степенью порядка $n$ некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ).\]
Данная формула называется формулой Муавра.
Пример 6
Выполнить действие $z^{3} $, где $z=3\cdot \left(\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} \right)$.
Решение:
По формуле Муавра получим:
\[z^{3} =3^{3} \cdot \left(\cos \left(3\cdot \frac{\pi }{4} \right)+i\cdot \sin \left(3\cdot \frac{\pi }{4} \right)\right)=27\cdot \left(\cos \frac {3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right).\]Пример 7
Выполнить действие $z^{100} $, где $z=1\cdot \left(\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} \right)$.
Решение:
По формуле Муавра получим:
\[z^{100} =1^{100} \cdot \left(\cos \left(100\cdot \frac{\pi }{2} \right)+i\cdot \sin \left(100\cdot \frac{\pi }{2} \right)\right)=1\cdot \left(\cos 50\pi +i\cdot \sin 50\pi \right)=1\cdot \left(\cos 0+i\cdot \sin 0\right).\]
Корень комплексного числа
Корнем $n$-й степени некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
\[\sqrt[{n}]{z} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.\]
Пример 8
Выполнить действие $\sqrt[{3}]{z} $, где $z=4\cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi }{3} +i\cdot \sin \frac{\pi }{3} \right)$.
Для $k=1$ получаем: $w_{2} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi +2\pi }{3} +i\cdot \sin \frac{\pi +2\pi }{3} \right)=\sqrt[{3}] {4} \cdot \left(\cos \pi +i\cdot \sin \pi \right)$.
Для $k=2$ получаем: $w_{3} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi +4\pi }{3} +i\cdot \sin \frac{\pi +4\pi }{3} \right)=\sqrt[{3}] {4} \cdot \left(\cos \frac{5\pi }{3} +i\cdot \sin \frac{5\pi }{3} \right)$.
spravochnick.ru
Математический портал. Высшая математика. Математический анализ.
Комплексные числа — числа вида $x+iy,$ где $x,y\in \mathbb{R,}$ а
$\,i,$ такое число, что $ i^2=-1.$ Множество комплексных чисел
обозначается $\mathbb{C}.$
Действия над комплексными числами.
Сложение комплексных чисел:
$$(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+i(y_1+y_2).$$
Умножение двух комплексных чисел:
$$(x_1+iy_1)(x_2+iy_2)=x_1x_2-y_1y_2+(x_1y_2+x_2y_1)i.$$
Умножение комплексного числа на действительное:
$$\lambda(x+iy)=\lambda x+i\lambda y.$$
Деление комплексных чисел:
$$\frac{x_1+iy_1}{x_2+iy_2}=\frac{(x_1+iy_1)(x_2-iy_2)}{(x_2+iy_2)(x_2-iy_2)}=\frac{x_1x_2+y_1y_2+i(y_1x_2-x_1y_2)}{x_2^2+y_2^2}=$$ $$\frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+\frac{y_1x_2-x_1y_2}{x_2^2+y_2^2}i.$$
Действительные числа $x$ и $y$ комплексного числа $z=x+iy,$ называются действительной и мнимой частью числа $z$ и обозначаются, соответственно, $Re z=x$ и $Im z=y.$
Два комплексных числа $z_1=x_1+iy_1$ и $z_2=x_2+iy_2$ называются равными в том и только том случае, если $x_1=x_2,$ $y_1=y_2.$
Запись $z=x+iy$ называют алгебраической формой комплексного числа $z.$
Числа $z_1=x+iy$ и $z_2=x-iy$ называют сопряженными.
Примеры:
Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:
1.421. $(2+3i)(3-i).$
Решение:
$(2+3i)(3-i)=6-2i+9i-3i^2=6+7i+3=9+7i.$
Ответ: $9+7i.$
1.424. $(2i-i^2)^2+(1-3i)^3.$
Решение.
$(2i-i^2)^2+(1-3i)^3=(2i+1)^2+1-3(3i)^2+3(3i)-(3i)^3=$ $=4i^2+4i+1-27i^2+9i-27i^3=-4+4i+1+27-9i+27i=24+22i.$
Ответ: $24+22i.$
1.425. $\frac{2-i}{1+i}.$
Решение.
$$\frac{2-i}{1+i}=\frac{(2-i)(1-i)}{(1+i)(1-i)}=\frac{2-2i-i+i^2}{1-i^2}=\frac{2-3i-1}{1+1}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i.$$
Ответ: $\frac{1}{2}-\frac{3}{2}i.$
{jumi[*4]}
1.428. $\frac{(1+i)(3+i)}{3-i}-\frac{(1-i)(3-i)}{3+i}.$
Решение.
$$\frac{(1+i)(3+i)}{3-i}-\frac{(1-i)(3-i)}{3+i}=\frac{(1+i)(3+i)(3+i)}{(3-i)(3+i)}-$$ $$-\frac{(1-i)(3-i)(3-i)}{(3+i)(3-i)}=\frac{9+15i+7i^2+i^3}{9-i^2}-\frac{9-15i+7i^2-i^3}{9-i^2}=$$ $$=\frac{9+15i-7-i-9+15i+7-i}{10}=\frac{28}{10}i=\frac{14}{5}i.$$
Ответ: $\frac{14}{5}i.$
Найти действительные решения следующего уравнения:
1. 430. $(1+i)x+(-2+5i)y=-4+17i.$
Решение.
$(1+i)x+(-2+5i)y=-4+17i\Rightarrow$
$x+xi-2y+5yi=-4+17i\Rightarrow$
$(x-2y)+(x+5y)i=-4+17i\Rightarrow$
$$\left\{\begin{array}{lcl}x-2y=-4\\x+5y=17\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2y-4\\2y-4+5y=17\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2\\y=3\end{array}\right. .$$
Ответ: $x=2; y=3.$
Домашнее задание.
Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:
1.422. $(1+2i)^2.$
Ответ: $-3+4i.$
1.423. $(1-i)^3-(1+i)^3.$
Ответ: $-4i.$
1.426. $\frac{1}{1+4i}+\frac{1}{4-i}.$
Ответ: $\frac{5}{17}-\frac{3}{17}i.$
1.427. $\left(\frac{1-i}{1+i}\right)^3.$
Ответ: $i.$
Найти действительные решения следующего уравнения:
1.431. $12((2x+i)(1+i)+(x+y)(3-2i))=17+6i.$
Ответ: $x=1/3; y=1/4.$
Решить следующие системы линейных уравнений:
1.432. $(3-i)z_1+(4+2i)z_2=1+3i;$
$(4+2i)z_1-(2+3i)z_2=7.$
Ответ: $z_1=1; z_2=i.$
1.433. $(2+i)z_1+(2-i)z_2=6;$
$(3+2i)z_1+(3-2i)z_2=8.$
Ответ: $z_1=2+i; z_2=2-i.$
mathportal.net
Действия с комплексными числами
Время проведения –2 часа.
Цель работы:отработать навыки выполнения действий с комплексными числами; научиться решать квадратные уравнения, дискриминант которых отрицателен.
Вопросы для подготовки к работе:
1. Понятие мнимой единицы;
2. Понятие комплексного числа;
3. Понятие модуля и аргумента комплексного числа;
4. Равенство комплексных чисел;
5. Решение квадратных уравнений, дискриминант которых отрицателен;
6. Действие над комплексными числами в алгебраической форме;
7. Геометрическая интерпретация комплексного числа;
8. Тригонометрическая форма комплексного числа;
Содержание работы:
1. Решение квадратных уравнений, дискриминант которых отрицателен;
2. Выполнение действий над комплексными числами;
3. Геометрическая интерпретация комплексного числа;
4. Представление комплексного числа в тригонометрической форме.
Литература:[1, с.17-23]
Порядок выполнения задания:
При выполнении первого задания необходимо учитывать следующее: в комплексных числах можно извлечь квадратный корень из отрицательного числа, так как , где — мнимая единица. Следовательно, в поле комплексных чисел разрешимо любое квадратное уравнение, в том числе с отрицательным дискриминантом.
Пример: Решить уравнение
Решение:
Найдем дискриминант , , следовательно, уравнение имеет мнимые корни, которые находят по формуле
Ответ:
Для выполнения второго, третьего заданий необходимо уметь применять операции над комплексными числами и знать правило равенства комплексных чисел.
Отметим, что с комплексными числами, записанными в алгебраической форме, операции сложения, вычитания и умножения можно производить также, как с действительными биномами, деление выполняют путем умножения делимого и делителя на число, сопряженное делителю. Правило равенства: два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.
Пример: Найдите сумму, разность, произведение, частное двух комплексных чисел
Решение:
, где
Ответ: , , ,
Пример: Найдите действительные решения уравнения
Решение:
В соответствии с правилом равенства получаем:
Ответ:
Для выполнения четвертого, пятого заданий необходимо знать тригонометрическую форму записи комплексного числа и его геометрическую интерпретацию.
Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу ставится в соответствие точка М координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу (ось называют действительной), а коэффициент при мнимой части – ординату точки (ось называют мнимой).
Расстояние от начала системы координат до точки, соответствующей комплексному числу , называют модулем этого числа, который вычисляют по формуле: . Угол между положительной полуосью и лучом называют аргументом комплексного числа . Выражение называют тригонометрической формой комплексного числа.
Пример: Изобразить на комплексной плоскости число и записать его в тригонометрической форме.
Решение:
Комплексному числу соответствует точка плоскости
Для комплексного числа имеем: , (по чертежу).
Поэтому в тригонометрической форме комплексное число имеет вид:
Ответ:
Вариант 1
1)
2)
3)
4)
2. Выполнить действия над комплексными числами, представив результат в алгебраической форме
1)
2)
3)
4)
5)
6)
7)
3. Найти действительные решения уравнения
1)
2)
4. Изобразите на комплексной плоскости следующие комплексные числа
1)
2)
5. Записать комплексное число в тригонометрической форме
Вариант 2
1. Решить уравнение
1)
2)
3)
4)
2. Выполнить действия над комплексными числами, предствавив результат в алгебраической форме
1)
2)
3)
4)
5)
6)
7)
3. Найти действительные решения уравнения
1)
2)
4. Изобразите на комплексной плоскости следующие комплексные числа
1)
2)
5. Записать комплексное число в тригонометрической форме
Практическая работа № 8
infopedia.su
§ 2.Действия над комплексными числами
П.2.1.Сложение комплексных чисел
Суммой двух комплексных чисел z1=х1+iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством
z1+z2=(x1+x2)+i(y1+y2). (2.1)
Сложение комплексных чисел обладает переместителъным (коммутативным) и сочетательным (ассоциативным) свойствами:
z1+z2=z2+z1
(z1+z2)+z3=z1+(z2+z3).
Из определения (2.1) следует, что геометрически комплексные числа складываются как векторы (см. рис. 164).
Непосредственно из рисунка видно, что |z1+z2|≤|z1|+|z2|. Это соотношение называется неравенством треугольника.
П.2.2.Вычитание комплексных чисел
Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число zl т. е. z=z1-z2, если z+z2=z1.
Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z:
z=z1-z2=(x1-x2)+i(y1-y2). (2.2)
Из равенства (2.2) следует, что геометрически комплексные числа вычитаются как векторы (см. рис. 165).
Непосредственно из рисунка видно, что |z1-z2|≥|z1|-|z2|. Отметим, что
т. е. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости.
Поэтому, например, равенство |z-2i|=1 определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки z0=2i, т. е. окружность с центром в z0=2i и радиусом 1.
П.2.3. Умножение комплексных чисел
Произведением к омплексных чисел z1 =х1 +iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством
z=z1 z2 =(x1 x2- у1 у2)+i(x1 y2+y1x 2 ). (2.3)
Отсюда, в частности, следует важнейшее соотношение
i 2 =- 1. (2.4)
Действительно, i2=ii=(0+1 i )(0+1i )=(0-1)+i(0+0)=-1. Благодаря соотношению (2.4) формула (2.3) получается формально путем перемножения двучленов x1+ iy1 и х2+iy2:
(х1 +iy1 )(x2+iy2) =x1x 2 +x1 iy2+i у1 х2+iy1iy 2 =x1 x2 +i2y1 y2+i (x1 y2+y1 x2)=x1 x2-y1 y2+i(x1 y2+y1x 2 ).
Например,
(2-3i)(- 5+4i)=-10+8i+15i-12i2=-10+23i+12=2+23i.
Заметим, что z*z=(х+iy)(x-iy)=х2+у2 — действительное число.
Умножение комплексных чисел обладает переместительным, сочетательным и распределительным (дистрибутивным) свойствами:
z1z2=z2z1
(z1z2)z3=z1(z2z3).
z1(z2+z3)=z1z2+z1z3.
В этом легко убедиться, используя определение (2.3).
Найдем произведение комплексных чисел z1=r1(cosφ1+isinφ1) и z2=r2(cosφ2+isinφ2), заданных в тригонометрической форме:
z1z2=r1(cosφ1+isinφ1)r2(cosφ2+isinφ2)=
r1r2(cosφ1cosφ2+isinφ1cosφ2+rcosφ1siπφ2-sinφ1sinφφ2)=
=r1r2((cosφ1cosφ2-siπφ1sinφ2)+i(sinφ1cosφ2+cosφ1 sinφ2))=
=r1r2(cos(φ1+φ2)+i sin(φ1+φ2)),
т. е.
z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)).
Мы показали, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Это правило распространяется на любое конечное число множителей. В частности, если есть n множителей и все они одинаковые, то
zn=(r(cosφ+isinφ))n=rn(cosnφ+isinnφ). (2.5)
Формула (2.5) называется формулой Муавра.
studfiles.net
7 раб
Методические рекомендации к выполнению практической работы №7.
Действия над комплексными числами в алгебраической и тригонометрической форме.
Понятие комплексного числа и его геометрическая интерпретация.
Действия над комплексными числами в алгебраической форме.
Тригонометрическая форма комплексного числа.
Действия над комплексными числами в тригонометрической форме.
1. Понятие комплексного числа и его геометрическая интерпретация.
Определение 1:
Комплексными числами называются числа
вида 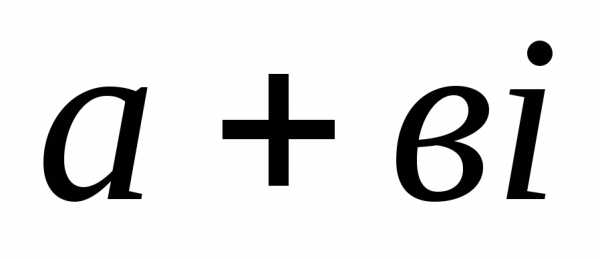 ,
где
,
где и
и — действительные числа, а число
— действительные числа, а число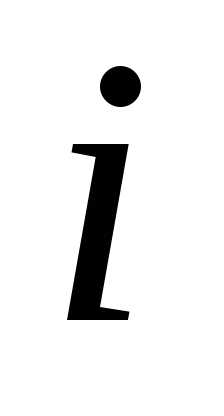 ,
определяемое равенством
,
определяемое равенством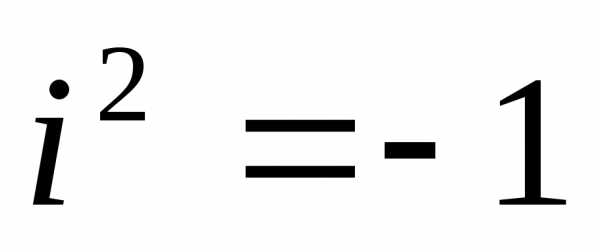 ,
называется мнимой единицей, если для
этих чисел понятия равенства и действия
сложения и умножения определены следующим
образом:
,
называется мнимой единицей, если для
этих чисел понятия равенства и действия
сложения и умножения определены следующим
образом:
1). Два комплексных
числа 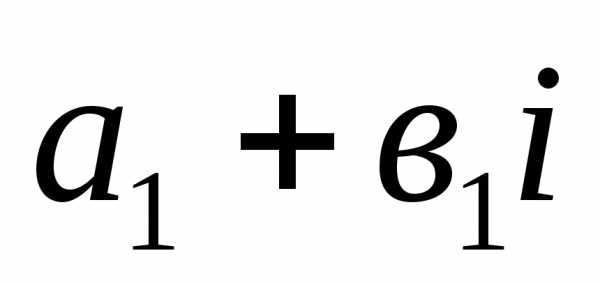 и
и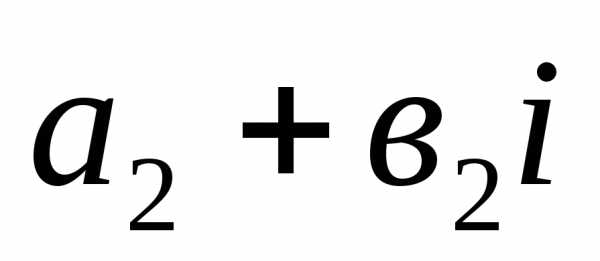 называются равными, если
называются равными, если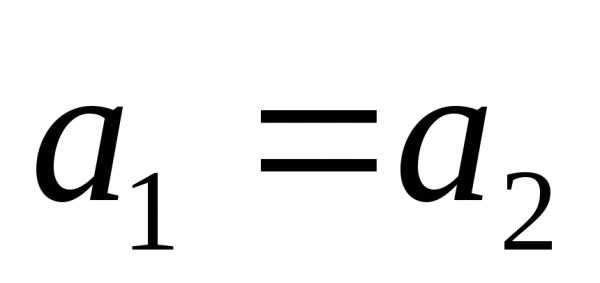 ,
,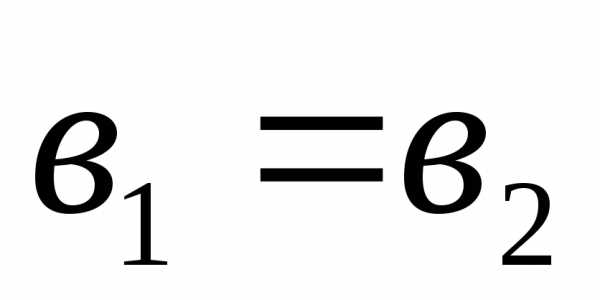 ;
;
2).
Суммой двух комплексных чисел 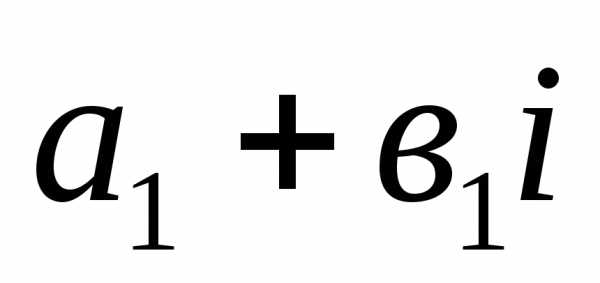 и
и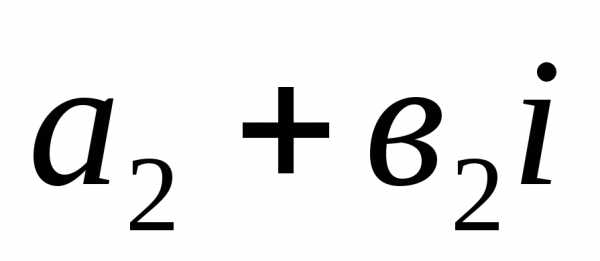 называется комплексное число;
называется комплексное число;
3).
Произведением двух комплексных чисел 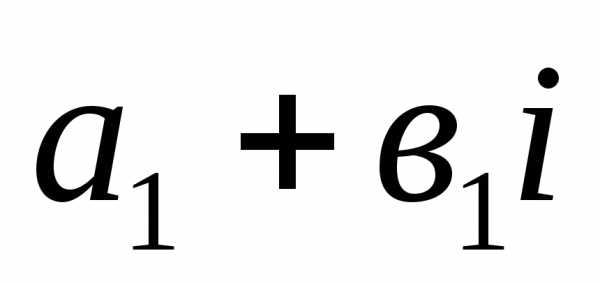 и
и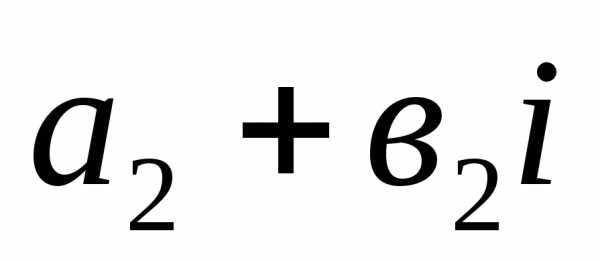 называется комплексное число;
называется комплексное число;
Запись комплексного
числа в виде называется алгебраической
формой записи комплексного числа, где  называется действительной
частью комплексного числа, а
называется действительной
частью комплексного числа, а  —мнимой
частью.
—мнимой
частью.
Пример1: 7+3i
Любое действительное
число содержится в множестве комплексных
чисел. Поэтому его можно записать так: 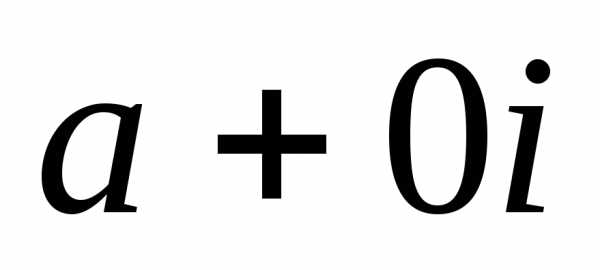 .
.
Пример: 4=4+0i
Определение 2: Комплексное число  называетсякомплексно
сопряженным
называетсякомплексно
сопряженным
с
числом 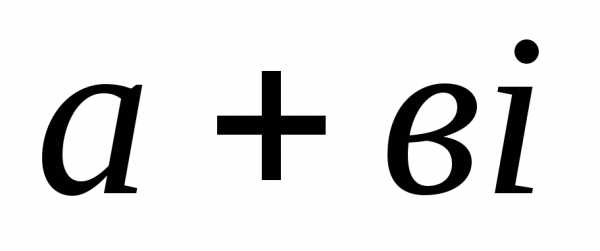 и
обозначается
и
обозначается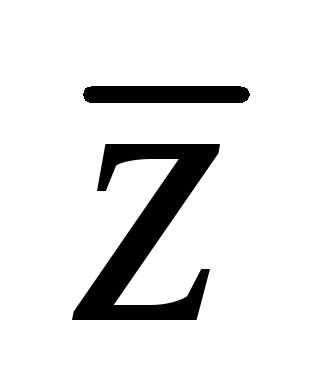 ,
то есть.
,
то есть.
Пример2: 2+5i и 2-5i
Определение 3: Модулем комплексного числа
называется число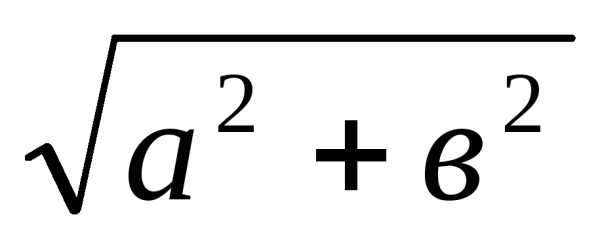 :.
Причем
:.
Причем .
.
Комплексное число можно изобразить двумя способами:
1. Точкой плоскости с координатами (а;в).
При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа- точками оси ординат, которую называют мнимой осью.
2. В виде вектора
с началом в начале координат ( )
и концом в точке М(а;в) ().
)
и концом в точке М(а;в) ().
Каждой точке
плоскости с координатами (а;в) соответствует
один и только один вектор с началом в
точке О(0;0) и концом в точке М(а;в),поэтому
комплексное число 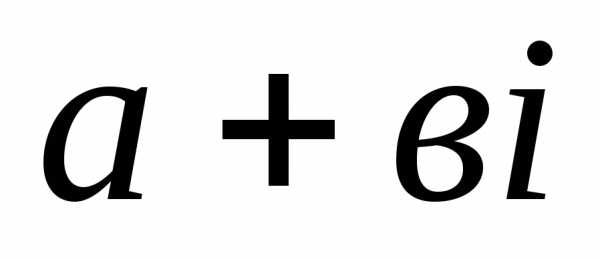 можно изобразить в виде вектора
можно изобразить в виде вектора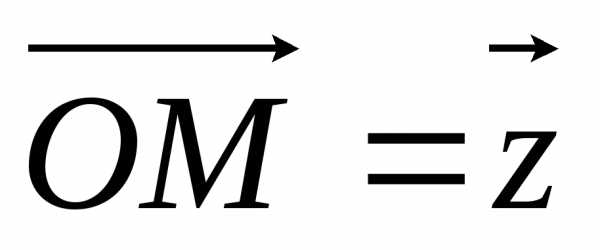 .
.
Определение 4: Угол φ
между действительной осью ОХ и вектором 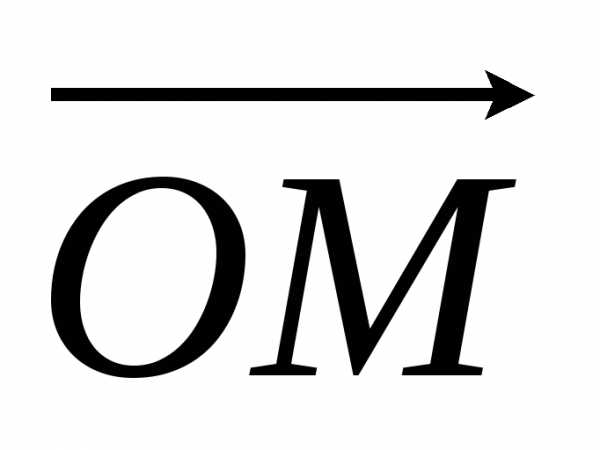 ,
отсчитываемый от положительного
направления действительной оси,
называетсяаргументом комплексного числа. Если отсчет ведется
против движения часовой стрелки, то
величина угла считается положительной,
иначе- отрицательной.
,
отсчитываемый от положительного
направления действительной оси,
называетсяаргументом комплексного числа. Если отсчет ведется
против движения часовой стрелки, то
величина угла считается положительной,
иначе- отрицательной.
Любое комплексное
число имеет бесконечное множество
аргументов, отличающихся друг от друга
на число, кратное  .
Наименьшее по абсолютной величине
значение аргумента из промежутканазываетсяглавным
значением аргумента.
.
Наименьшее по абсолютной величине
значение аргумента из промежутканазываетсяглавным
значением аргумента.
Из определения тригонометрических функций следует:
Пример3:
Изобразить геометрическую интерпретацию комплексного числа, найти модуль комплексного числа и главное значение аргумента.
а). 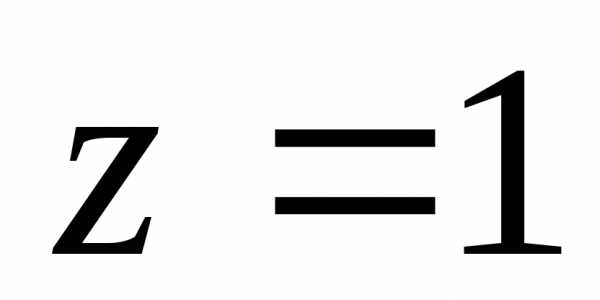 ;
б).
;
б).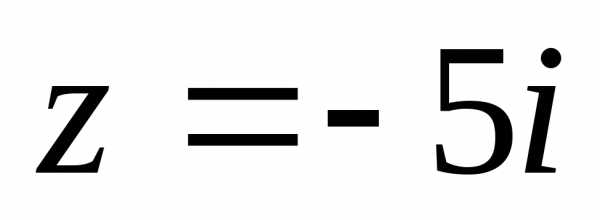 ;
в)..
;
в)..
Решение:
а). 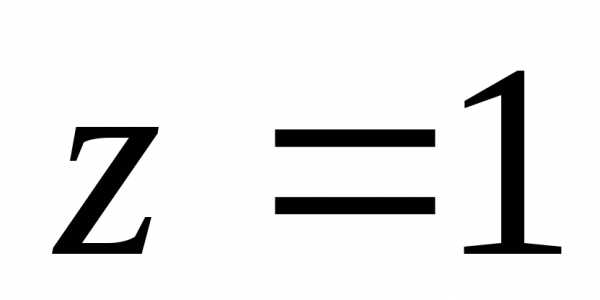
;
б). 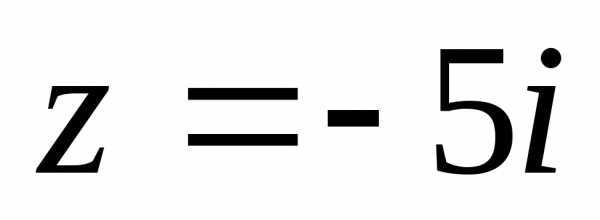
;
в).
2. Действия над комплексными числами в алгебраической форме.
Сложение и умножение комплексных чисел мы ввели в определении комплексного числа. Введем правила вычитания и деления комплексных чисел: ;
.
Но удобнее всего действия над комплексными числами производить с помощью правил соответствующих действий над многочленами и понятием мнимой единицы.
Пример4:
Выполнить действия:
а). 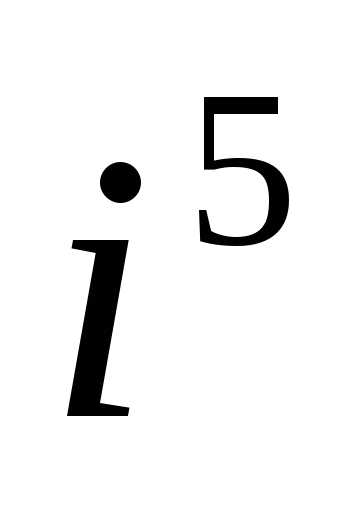 ;
б).
;
б).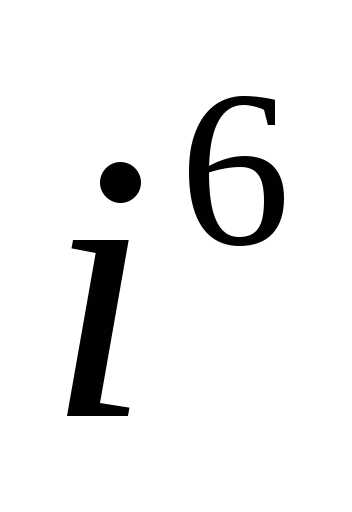 ;
в).
;
в). ;
г).;
д).;
е).;
;
г).;
д).;
е).;
ж). 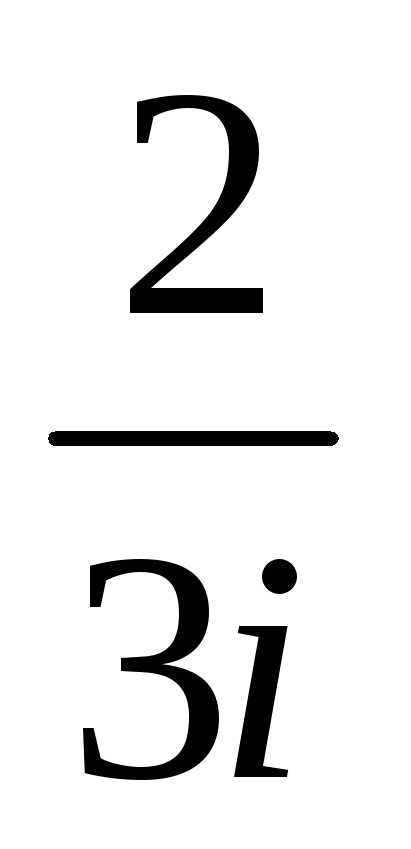 ;
з).
;
з).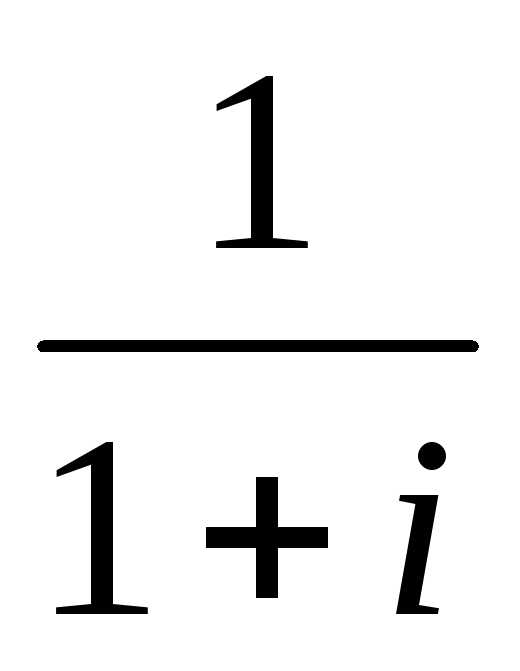 ;
и).
;
и).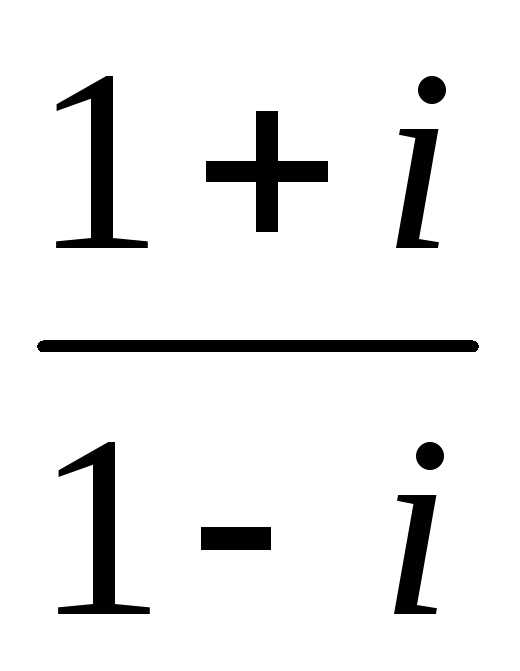 ;
к).
;
к).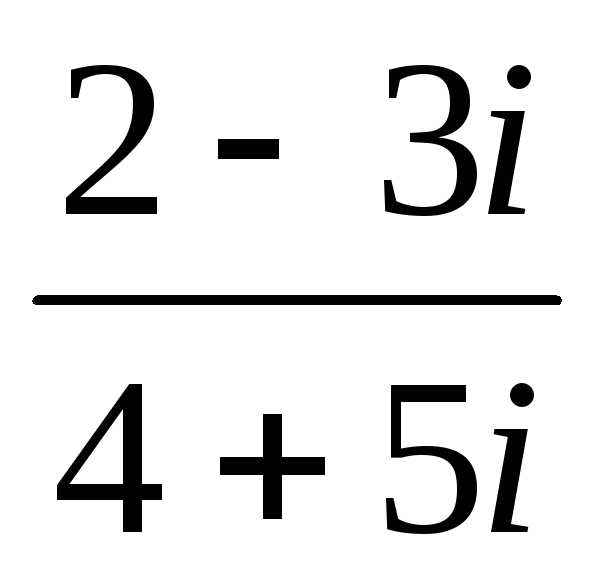 .
.
Решение:
а). ;
б). ;
в). ;
г).;
д). ;
е). ;
ж). ;
з). ;
и). ;
к). .
3. Тригонометрическая форма комплексного числа.
Изобразим комплексное число геометрически:
Обозначим модуль комплексного числа .
Аргументом комплексного числа называется угол φ, который вычисляется с помощью формул:
но , тогда
и
Подставим получившиеся формулы в , получим:
,тогда
— тригонометрическая форма комплексного числа.
Алгоритм перехода из алгебраической формы комплексного числа в тригонометрическую:
Найти: .
Изобразить геометрически число , для нахождения четверти числа φ.
Составить уравнения: и найти φ.
Записать z в тригонометрической форме .
Примеры: а).Перевести числа из алгебраической формы в тригонометрическую.
1).  .
.
1. .
2. Изобразим геометрически:
Значит φ принадлежит I четверти.
3. 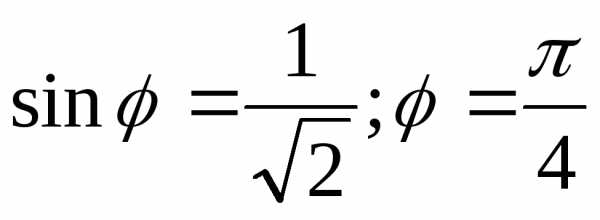 .
.
4..
2). 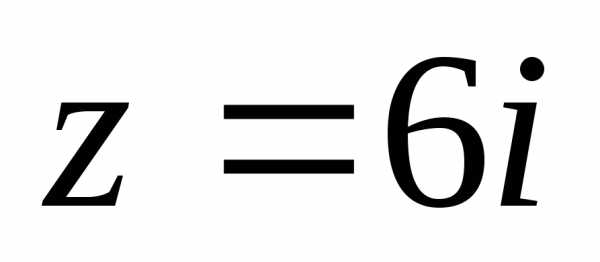 .
.
1. .
2. Изобразим геометрически:
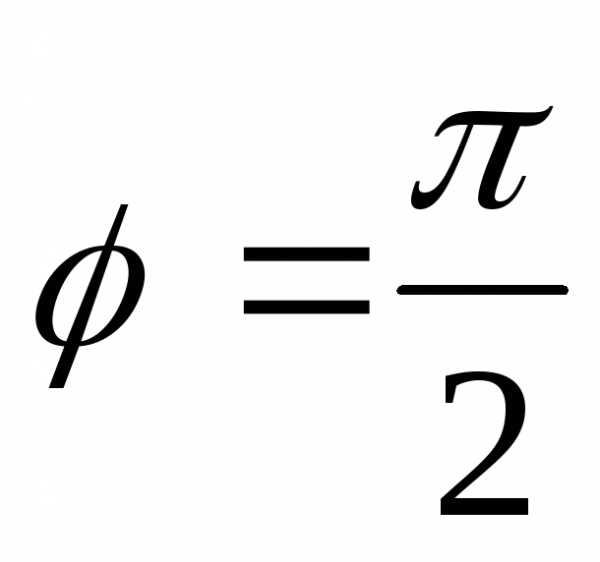 ,
так как z
принадлежит положительной полуоси ОУ.
,
так как z
принадлежит положительной полуоси ОУ.
Значит 3 пункт можно опустить.
4. .
3).
1. .
2. Изобразим геометрически:
φ принадлежит II четверти.
3. .
4.
б). перевести из тригонометрической формы в алгебраическую:
1).
Решение:
.
2).
Решение:
.
4. Действия над комплексными числами в тригонометрической форме.
Пусть даны два числа в тригонометрической форме: и.
1). При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
.
2). При делении двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются:
.
3). При возведении комплексного числа вn-ую степень используется формула:
, которая называется формулой Муавра.
4). Для извлечения корня n-ой степени из комплексного числа используется формула:
.
Примеры:
Дано: ,.
Найти: 1). 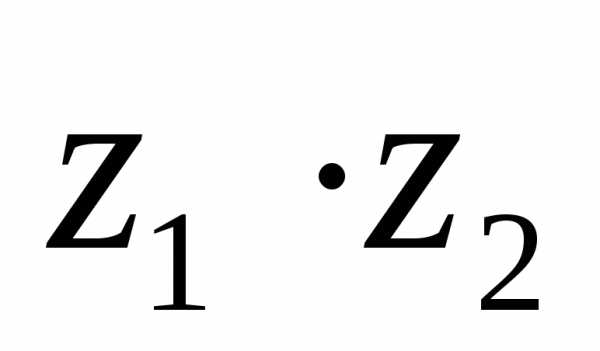 ,
2).
,
2). ,
3).
,
3).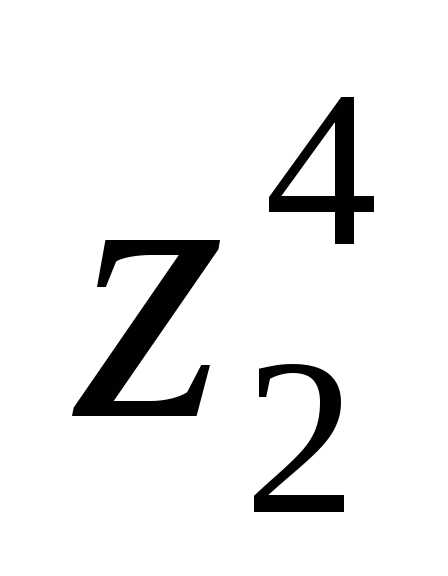 ,
4).
,
4).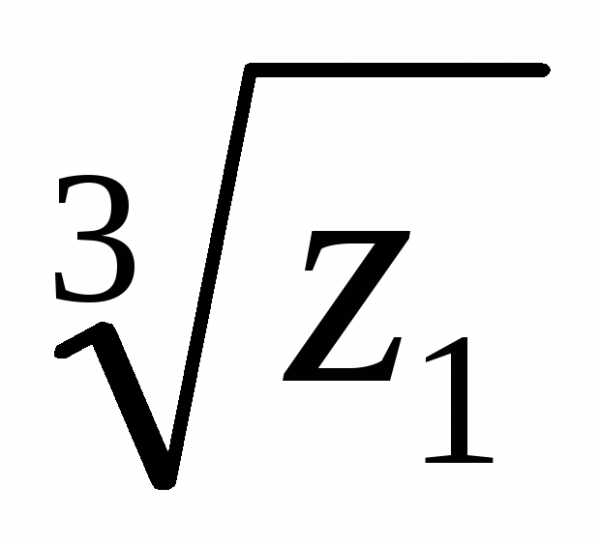 .
.
Решение: 1).
2).
3).
4).


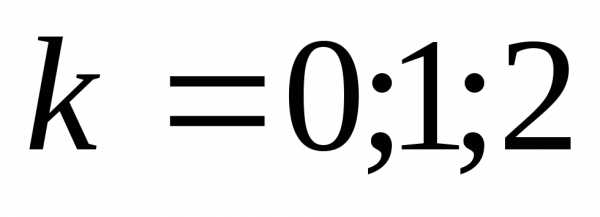
Практическая работа№7.
Тема: Действия над комплексными числами в алгебраической и тригонометрической форме.
Цель: Научить выполнять различные действия с комплексными числами; переводить комплексные числа из алгебраической формы и обратно;
Задания:
I-B II-B
1. Выполнить действия с комплексными числами в алгебраической форме:
1)., 1).,
2). 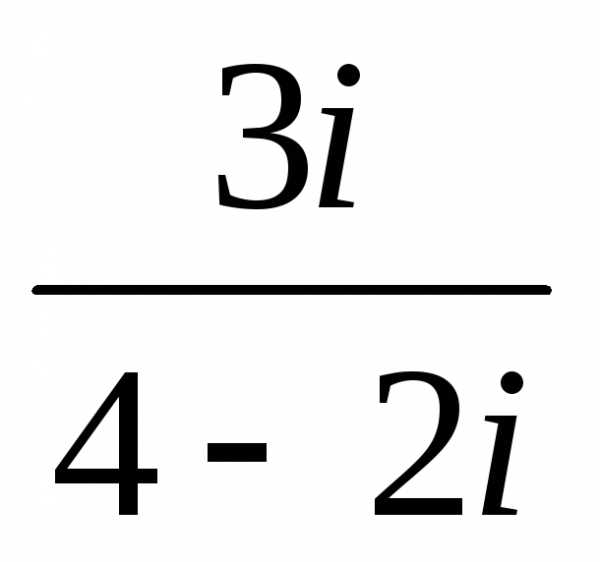 ,
3).
,
3).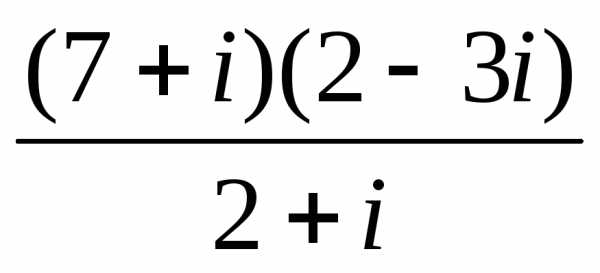 .
2).
.
2).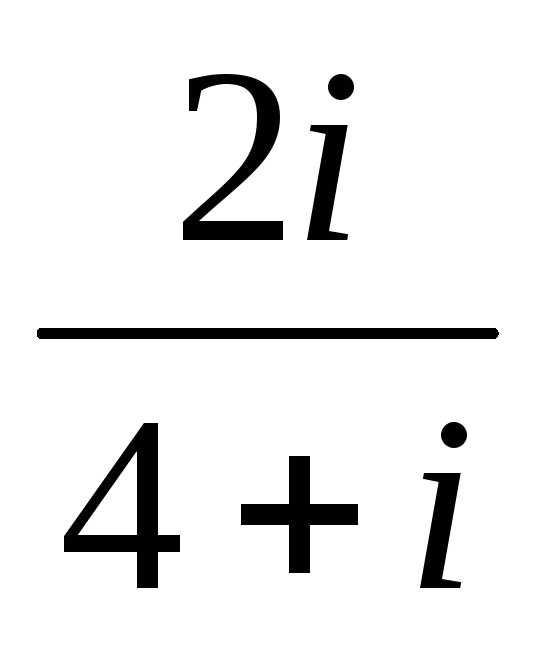 ,
3).
,
3).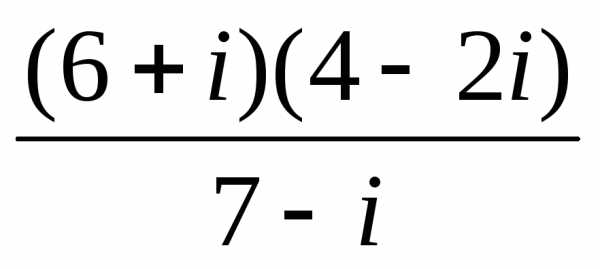 .
.
2. Записать комплексные числа в тригонометрической форме:
1). 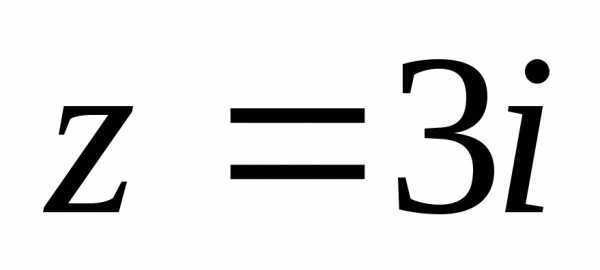 ,
2).
,
2).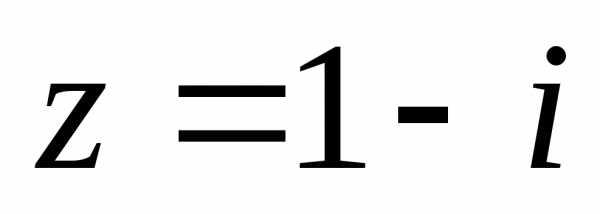 ,
3)..
1).
,
3)..
1).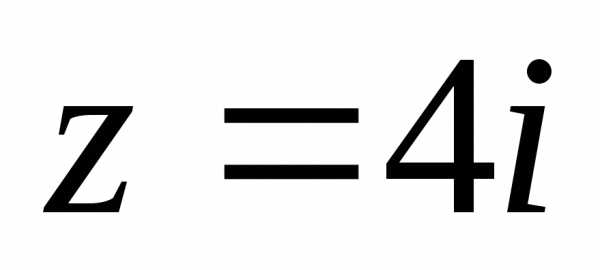 ,
2).,
3).
,
2).,
3). .
.
3. Выполнить
действия с комплексными числами в
тригонометрической форме: 1). 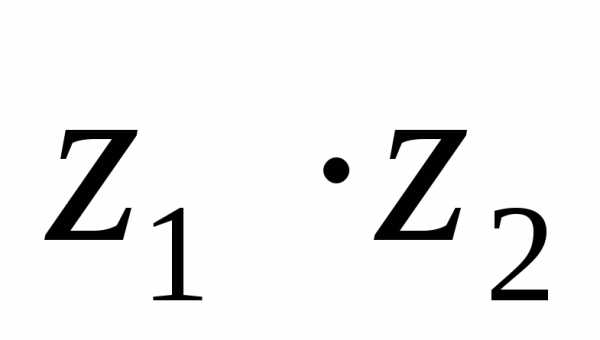 , 2).
, 2).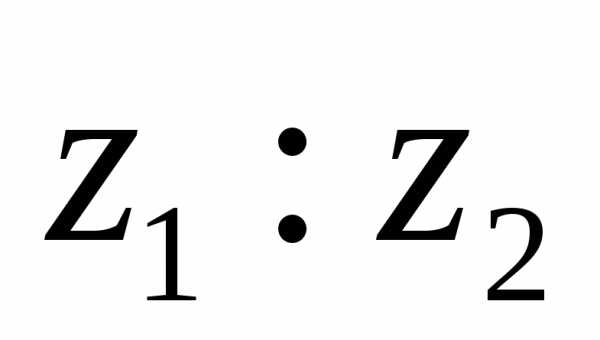 ,
если:
,
если:
, ,
. .
Ответы к практической работе № 6:
I-B. II-B.
1.
1).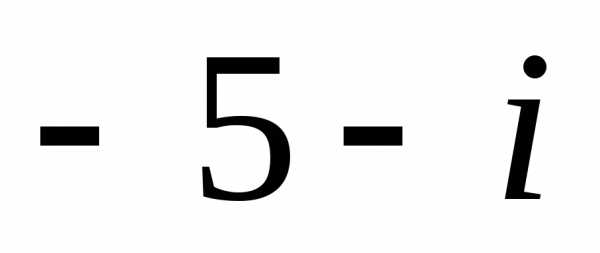 ,
1. 1).
,
1. 1).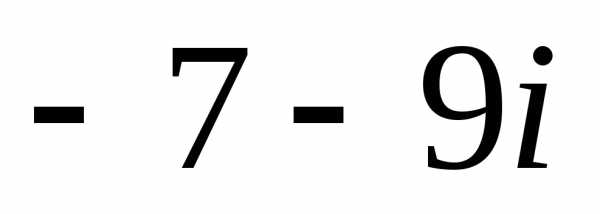
2). 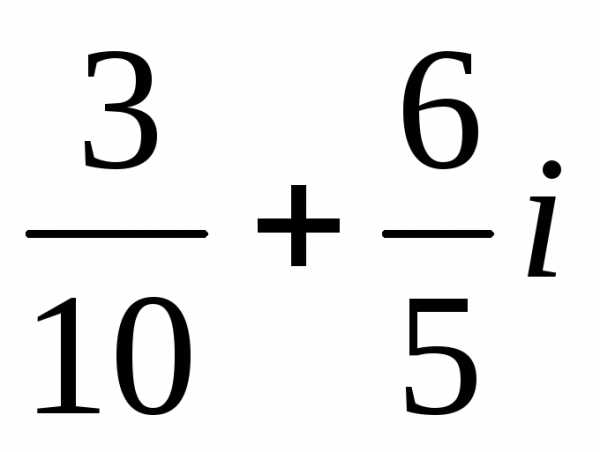 ,
2).
,
2).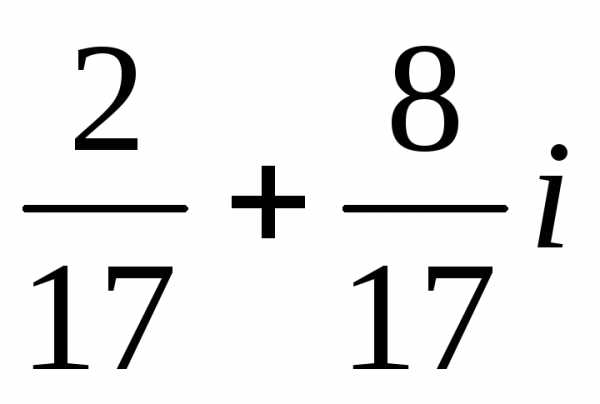 ,
,
3).
.
3). .
.
2. 1). , 2. 1).,
2). , 2).,
3). . 3)..
3. 1). 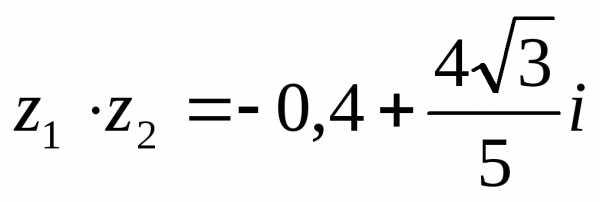 ,
3. 1).,
,
3. 1).,
2). 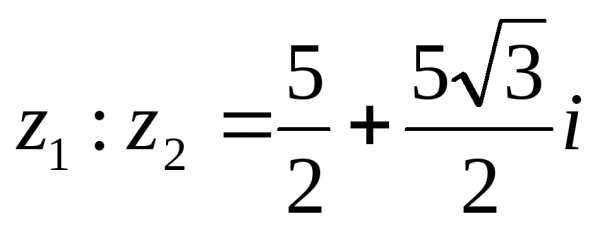 .
2)..
.
2)..
studfiles.net
Алгебраические действия над комплексными числами
1. Сложение и вычитание двух комплексных чисел:
Следствие.
Комплексные числа 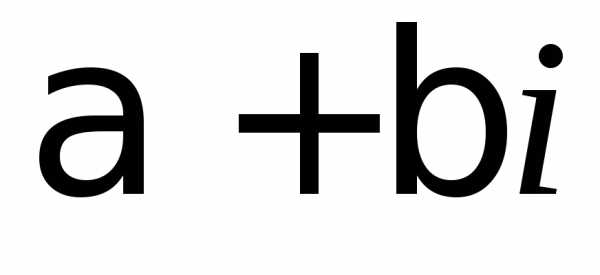 и
и называются взаимно сопряженными и
обозначаются,Следовательно,
называются взаимно сопряженными и
обозначаются,Следовательно,
для двух взаимно сопряженных чисел:
сумма – действительное число,
разность – чисто мнимое число.
2. Умножение двух комплексных чисел:
•
Произведение взаимно сопряженных чисел
–действительное число.
• Если
числа  и
и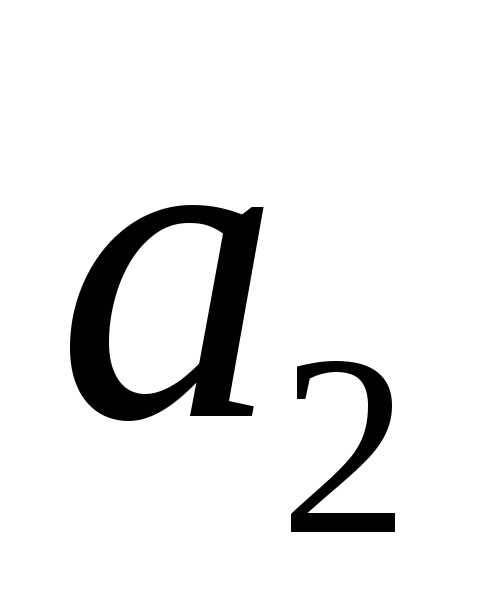 заданы в тригонометрической форме, то
заданы в тригонометрической форме, то
• Если
числа  и
и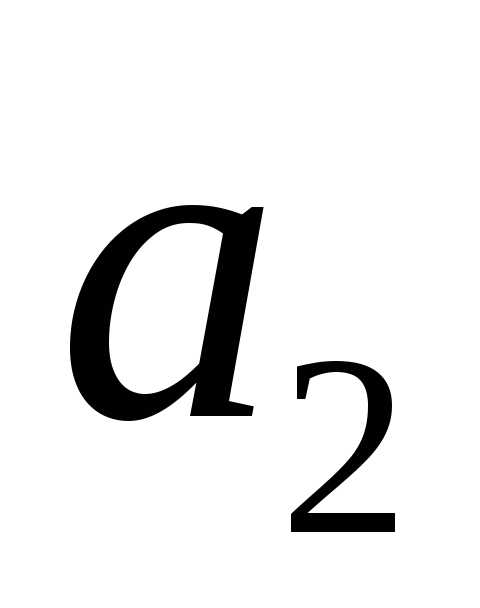 заданы в показательной форме, то
заданы в показательной форме, то
3. Деление двух комплексных чисел всегда возможно и осуществляется:
• в алгебраической форме с помощью умножения делимого и делителя на число, взаимно сопряженное делителю:
• в тригонометрической и показательной форме следующим образом:
если то
или 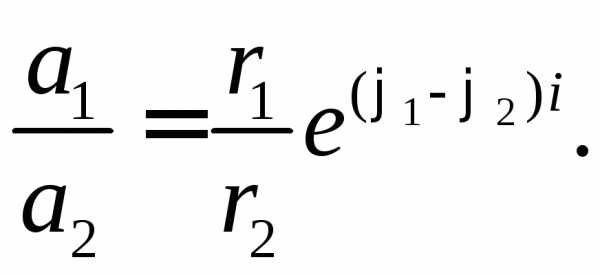
Примеры 1)
2)
3)
4)
5) 
6) Если комплексное число тообратное ему число
4. Возведение в n-ю степень комплексного числа
если  то
то
В
частности, имеем: 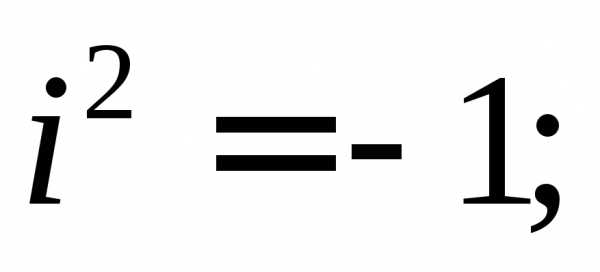
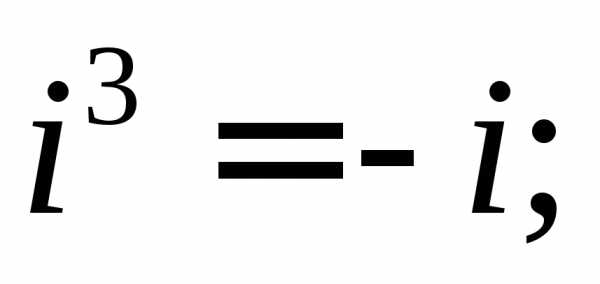
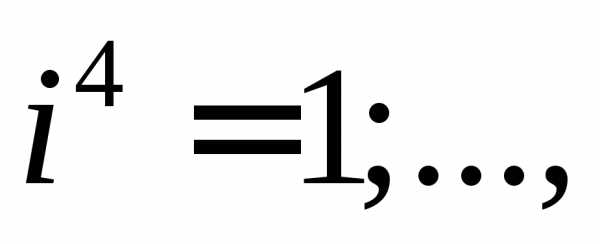
Если 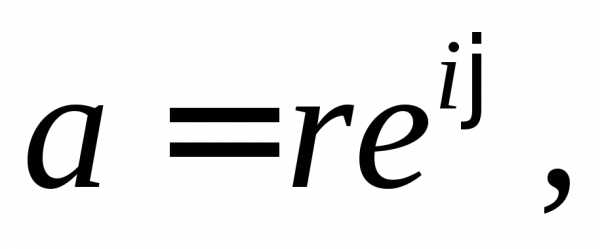 то.
то.
5. Извлечение
корня n-ой
степени как
действие, обратное возведению в степень:
если
и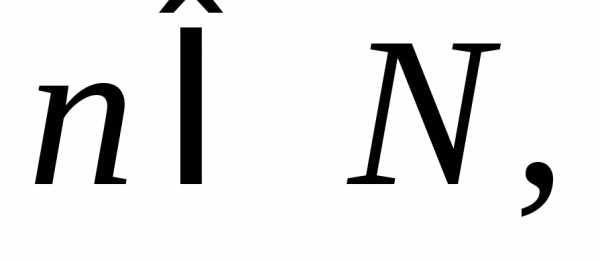 то
то
где
Если 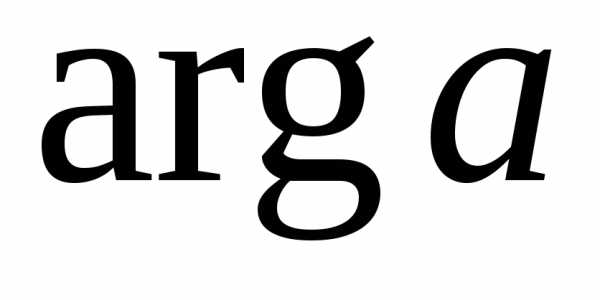 принимает значения:
принимает значения:
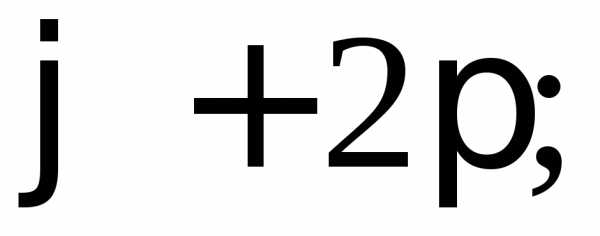
 …,то значения
…,то значения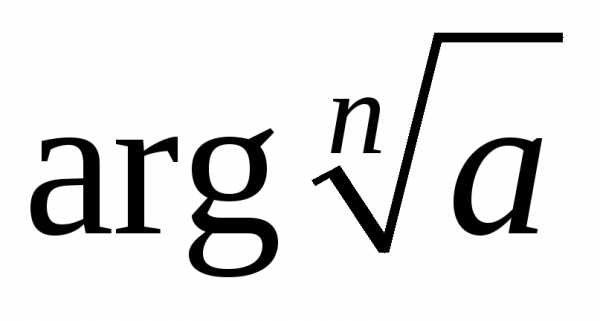 будут отличаться друг от друга на
будут отличаться друг от друга на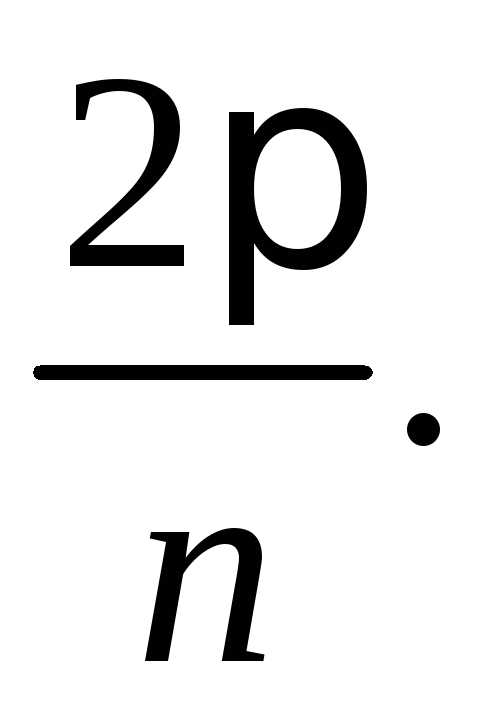 При дальнейших
При дальнейших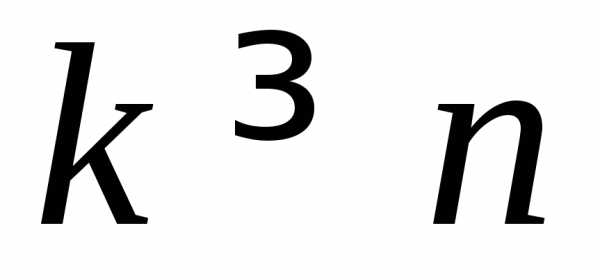 значения
значения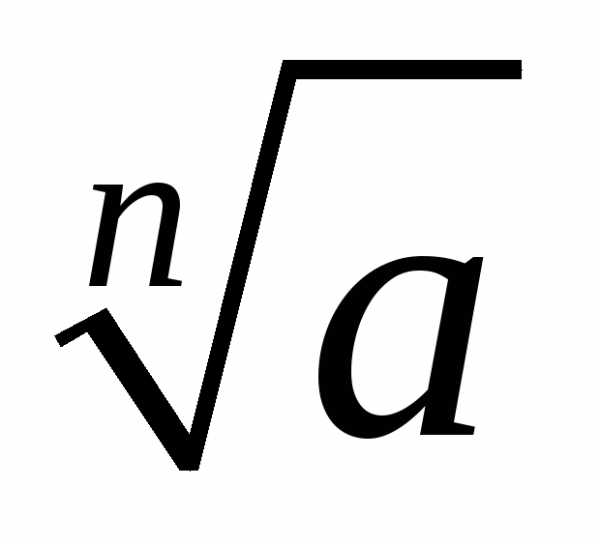 будут повторяться. В геометрической
интерпретации точки, изображающие
будут повторяться. В геометрической
интерпретации точки, изображающие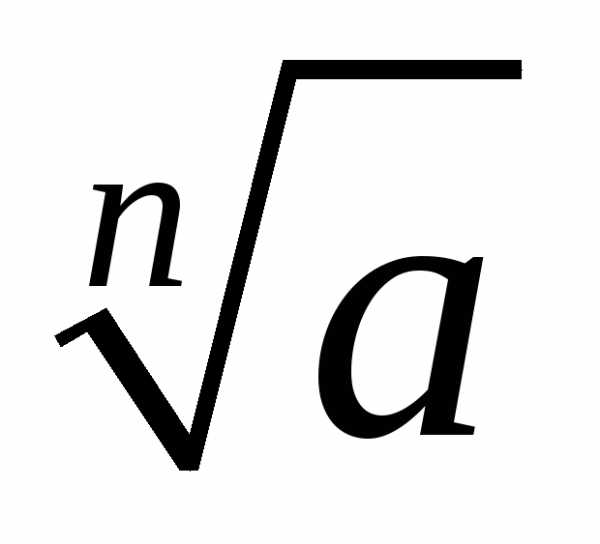 ,
являются вершинами правильногоn-угольника
с центром в начале координат. На рис. 2
изображены шесть значений
,
являются вершинами правильногоn-угольника
с центром в начале координат. На рис. 2
изображены шесть значений 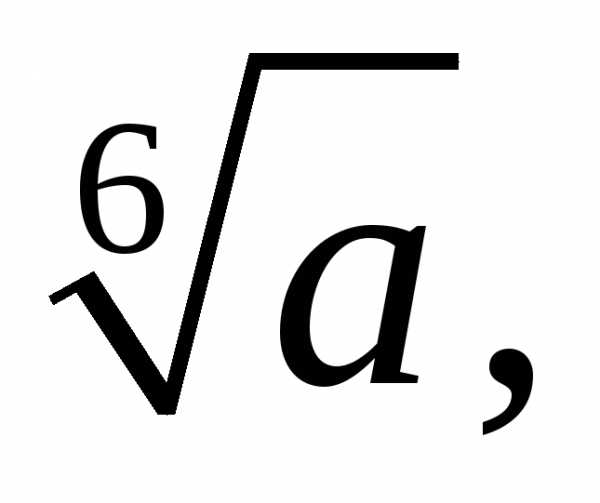 где
где
Пример 1. k = 0, 1, 2, 3.
Получаем четыре значения корня:
1) 2)
3) 4)
Пример 2. k = 0, 1.
Получаем
два значения 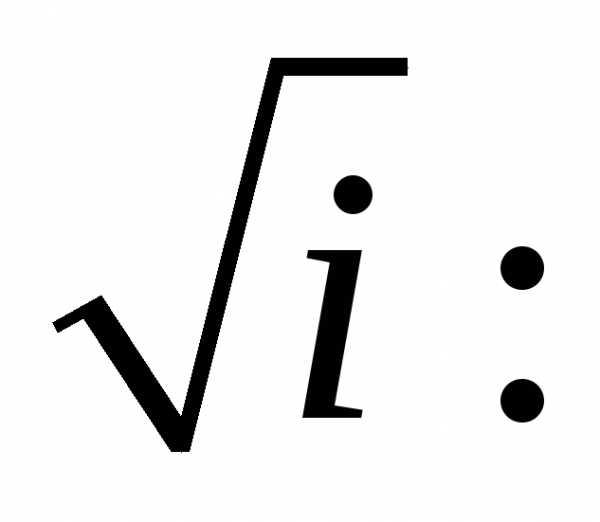 1)
1) 2)
2)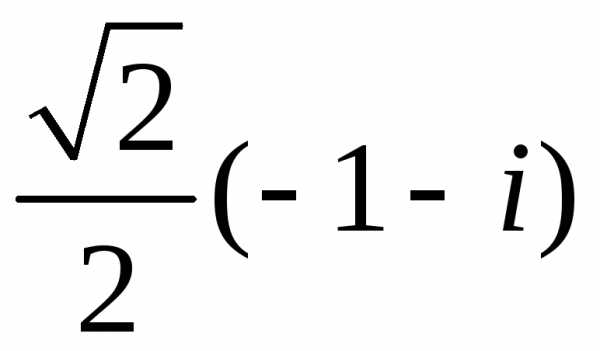 (рис. 3).
(рис. 3).
1.3. Алгебраические выражения и действия над ними
В алгебре изучаются действия с выражениями, содержащими как числовые, так и буквенные значения. При этом буквам может при необходимости придаваться конкретное численное значение.
• Одночленом называется произведение нескольких
сомножителей, являющихся числами или
буквами. Отдельные числа и буквы также
считаются одночленами. Например, 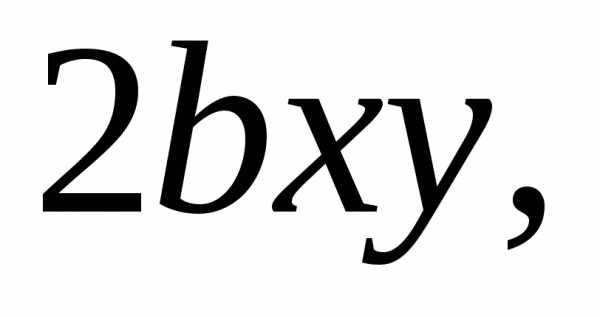
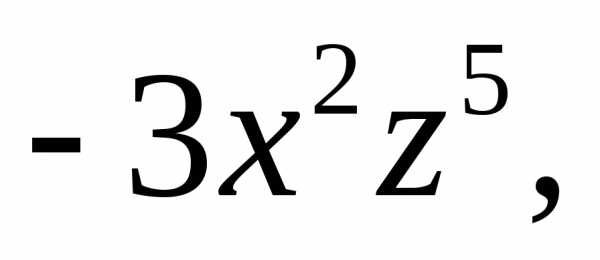 6,у – одночлены.
6,у – одночлены.
• Многочленом называется сумма одночленов. Например, – многочлены.
Основу всех алгебраических операций представляют следующие законы сложения и умножения:
Переместительный закон:
Сочетательный закон:
Распределительный закон:
При выполнении преобразований алгебраических выражений используются следующие приемы.
• Приведение подобных членов. Если несколько слагаемых имеют одинаковые буквенные части, то их числовые коэффициенты складываются, а буквенная часть сохраняется. Например,
• Вынесение множителя за скобки производится на основе распределительного закона и правил действий со степенями.
Пример 1.
Раскрытие скобок также производится с помощью распределительного закона. Необходимо помнить, что если множитель перед скобками имеет отрицательный знак, то при их раскрытии меняются знаки всех слагаемых.
Пример 2.
Пример 3.
• Деление многочленов. Для деления многочлена, зависящего от одной переменной х, на аналогичный многочлен меньшей степени используют следующую процедуру деления столбиком:
1) расположим слагаемые в многочленах в порядке убывания степени неизвестной; 2) разделим первое слагаемое делимого многочлена на первое слагаемое делителя и результат напишем в частное; 3) умножим результат на делитель и вычтем его из делимого; 4) произведем с полученным при вычитании многочленом действия аналогичные пунктам 2) и 3). Будем повторять эту операцию, пока при вычитании не получится либо ноль, либо многочлен степени меньшей, чем у делителя. Этот многочлен называется остатком.
Пример 4. Выполнить деление многочлена на многочлен
3
–
х4 – 7х3 + 12х2 – 5х + 3 х2 – 2х + 33х4 – 6х3 + 9х2 3х2 – х + 1
–х3 + 3х2 – 5х + 3– х3 + 2х2 – 3х
–
х2 – 2х + 3х2 – 2х + 3
0
Следовательно,
studfiles.net
Действия над комплексными числами — Мегаобучалка
1. При сложении двух комплексных чисел отдельно складываются их действительные части и мнимые части:
z1 + z2 = (a1 + a2) + (b1 + b2)i. (1)
2. При умножении двух комплексных чисел получается комплексное число:
z1z2 = (a1a2– b1b2) + (a1b2 + a2b1)i, (2).
3. При делении двух комплексных чисел получается комплексное число:
, (3).
@ Задача 1. Найти сумму двух комплексных чисел 2 + 3i и – 4 + 6i.
Решение: Комплексные числа суммируются по правилу (1): (2 + 3i) + (– 4 + 6i) = (2 – 4) + (3 + 6)i = – 2 + 9i.
@ Задача 2. Найти произведение двух комплексных чисел 2 + 3i и – 4 + 5i.
Решение: Комплексные числа умножаются по правилу (2):
(2 + 3i)·(– 4 + 5i) = (2·(– 4) – 3·5) + (2·5 + 3·(– 4))i = – 23 – 2i.
@ Задача 3. Найти частное двух комплексных чисел 2 + 4i и 1 + i.
Решение: Комплексные числа делятся по правилу (3):
.
Тригонометрическая форма комплексного числа
Всякое комплексное число z = a + bi можно изобразить точкой A(a,b) плоскости, такой что a = Rez, а b = Imz. Тогда a и b можно выразить через полярные координаты r и j: a = rcosj, b = rsinj, где r и j называются модулем и аргументом комплексного числа.
Таким образом, комплексное число z = a + bi можно представить в тригонометрической форме
.
Экспоненциальной формой комплексного числа называется число .
@ Задача 4. Представить в тригонометрической форме комплексное число .
Решение: Так как , то комплексное число представляется в тригонометрической форме в виде
.
Корни квадратного и биквадратного уравнений
Корни квадратного уравнения ax2 + bx + c = 0 с отрицательным дискриминантом D = b2 – 4ac < 0 являются комплексными числами и находятся по формулам .
Корни биквадратного уравнения x4 + px2 + q = 0 с отрицательным дискриминантом D = p2 – 4q < 0 являются комплексными числами и находятся по формулам:
,
.
@ Задача 5. Решить квадратное уравнение x2 – 4x + 8 = 0.
Решение: Дискриминант квадратного уравнения отрицательный: D = 42 – 4×8 = – 16 < 0 и, следовательно, корни квадратного уравнения равны .
@ Задача 6. Решить биквадратное уравнение
x4 – 4x2 + 16 = 0.
Решение: Дискриминант биквадратного уравнения отрицательный: D = 42 – 4×16 = – 48 < 0. Т.к. и , то и .
§1.7 Прямые и плоскости в аффинном пространстве. Выпуклые множества и их свойства.
В n-мерном пространстве задаётся упорядоченной системой линейно независимых векторов , выходящих из одной точки O. Аффинными координатами точки M называют такие числа xi, что
Tочку O и систему векторов называют репером или аффинным базисом; прямые, проходящие через вектора — координатными осями.
На аффинной плоскости (n = 2) координату x1 называют абсциссой, а x2 – ординатой точки M. В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.
megaobuchalka.ru
