Решение квадратных тригонометрических уравнений — МегаЛекции
Краткое изложение теоретических вопросов дифференцированного зачета
Для студентов 1 курса
Специальности 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта»
Уравнение. Корень уравнения. Что значит «решить уравнение»?
Уравнение – это равенство, содержащее переменную.
Корень уравнения — такое значение переменной, которое при подстановке его в уравнение, обращает его в верное числовое равенство.
Решить уравнение – это значит найти все его корни или доказать, что корней нет.
Система уравнений – это совокупность из двух и более уравнений с двумя и более неизвестными; причём решение одного из уравнений является одновременно и решением всех остальных.
Виды уравнений и их решение: линейное, квадратное.
Линейные уравнения – это уравнения вида: ах + b = 0, где a и b – некоторые постоянные. Если а не равно нулю, то уравнение имеет один единственный корень: х = — b : а. Если а равно нулю и b равно нулю, то корнем уравнения ах + b = 0 является любое число. Если а равно нулю, а b не равно нулю, то уравнение ах + b = 0 не имеет корней.
Способы решения линейных уравнений
1) тождественные преобразования
2) графический способ.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это число D = b2 − 4ac.
1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.
Если дискриминант D > 0, корни можно найти по формулам: Корни квадратного уравнения. Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Решение простейших тригонометрических уравнений
Общий вид решения уравнения cos x = a, где | a | ≤ 1, определяется формулой:
x = ± arccos(a) + 2πk, k ∈ Z (целые числа), при | a | > 1 уравнение cos x = a не имеет решений среди вещественных чисел.
Общий вид решения уравнения sin x = a, где | a | ≤ 1, определяется формулой:
x = (- 1)k · arcsin(a) + πk, k ∈ Z (целые числа), при | a | > 1 уравнение sin x = a не имеет решений среди вещественных чисел.
Общий вид решения уравнения tg x = a определяется формулой:
x = arctg(a) + πk, k ∈ Z (целые числа).
Общий вид решения уравнения ctg x = a определяется формулой:
x = arcctg(a) + πk, k ∈ Z (целые числа).
Решение линейных тригонометрических уравнений
Линейные тригонометрические уравнения имеют вид k*f(x) + b = 0, где f(x) – тригонометрическая функция, а k и b — действительные числа.
Для решения уравнения его приводят к простейшему виду путем тождественных преобразований
Решение линейно – комбинированных тригонометрических уравнений
Линейно — комбинированные тригонометрические уравнения имеют вид f(kx + b) = а, где f(x) – тригонометрическая функция, а, k и b — действительные числа.
Для решения уравнения его вводят новую переменную у = kx + b. Решают полученное простейшее тригонометрическое уравнение относительно у и производят обратную замену.
Решение тригонометрических уравнений с использованием формул приведения
При решении тригонометрических уравнений, не являющихся простейшими, выполняются тождественные преобразования по следующим формулам:

Решение тригонометрических уравнений с использованием тригонометрических тождеств
При решении тригонометрических уравнений, не являющихся простейшими, выполняются тождественные преобразования по следующим формулам:

Решение квадратных тригонометрических уравнений
Отличительные признаки уравнений, сводящихся к квадратным:
В уравнении присутствуют тригонометрические функции от одного аргумента или они легко сводятся к одному аргументу.
В уравнении присутствует только одна тригонометрическая функция или все функции можно свести к одной.
Алгоритм решения:
Выполняется подстановка.
Выполняется преобразование выражения.
Вводится обозначение (например, sinx = y).
Решается квадратное уравнение.
Подставляется значение обозначенной величины, и решается тригонометрическое уравнение
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Методический материал по математике на тему » Тригонометрические уравнения, сводящиеся к квадратным»
Решить уравнения:
sin 2 x + sin x – 2 = 0.
Это уравнение является квадратным относительно sin x.
Обозначим sin x = y,
тогда получим уравнение:
у 2 + у – 2 = 0.
Кони данного уравнения найдем по формуле:
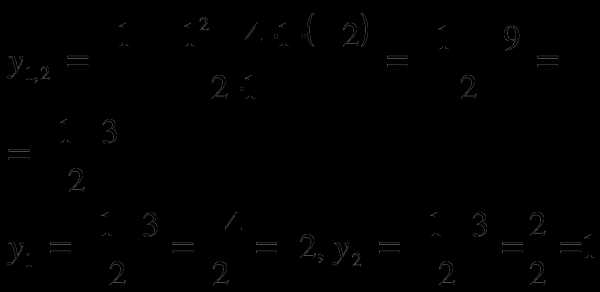
Решим простейшие уравнения:
1)sin x = 1х =  + 2π n, n
+ 2π n, n  Ζ
Ζ
2) sin x = — 2 не имеет корней
Ответ: х =  + 2π n, n
+ 2π n, n  Ζ
Ζ
2) 2 cos 2 x – 5 cos x + 2 = 0.
Это уравнение является квадратным относительно cos x.
Обозначим cos x = y,
тогда получим уравнение:
2 у 2 – 5у + 2 = 0.
Кони данного уравнения найдем по формуле:
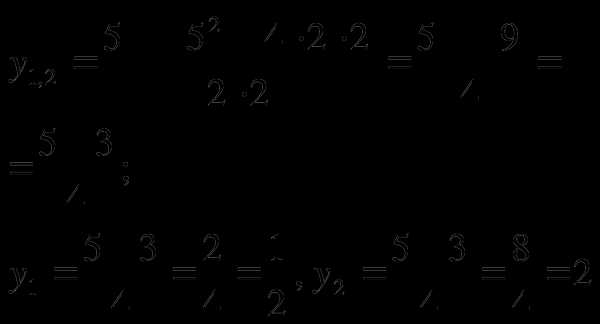
Решим простейшие уравнения:
Р.С. 1) sin 2 x + 2 sin x – 3 = 0.
2) 2 cos 2 x – 9 cos x + 4 = 0.
3) 2sin 2 x – cos x – 1 = 0.
Используя формулу sin 2 x = 1 – cos 2 x
получаем: 2 (1 – cos 2 x) – cos x – 1 = 0,
раскроем скобки
2 – 2 cos 2 x – cos x – 1 = 0,
приведем подобные
– 2 cos 2 x – cos x + 1 = 0 или 2 cos 2 x + cos x – 1 = 0.
Обозначим cos x = y,
тогда получим уравнение:
2у 2 + у – 1= 0.
Кони данного уравнения найдем по формуле:

Решим простейшие уравнения:
cos x = – 1х =
π + 2π n, n Ζ
Ζ 
Ответ: х = π + 2π n, n  Ζ
Ζ
 n
n  Ζ
Ζ
4) 2 cos 2 x – 5 sin x + 1 = 0.
Заменим соs 2 x = 1 – sin 2 x ,
тогда уравнение примет вид:
2 (1 – sin 2 x) – 5 sin x + 1 = 0,
2 – 2 sin 2 x – 5 sin x + 1 = 0,
— 2 sin 2 x – 5 sin x + 3 = 0
или 2 sin 2 x + 5 sin x – 3 = 0.
Обозначим sin x = y
тогда получим уравнение :
2у 2 + 5у – 3 = 0.
Кони данного уравнения найдем по формуле:
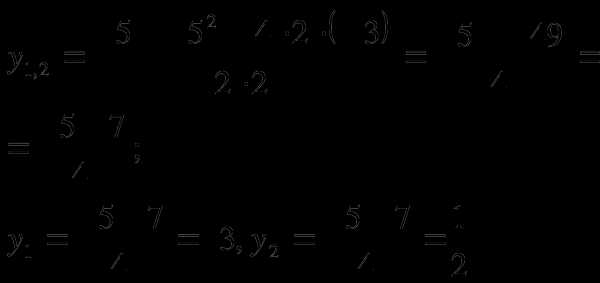
Решим простейшие уравнения:
1)sin x = — 3 не имеет корней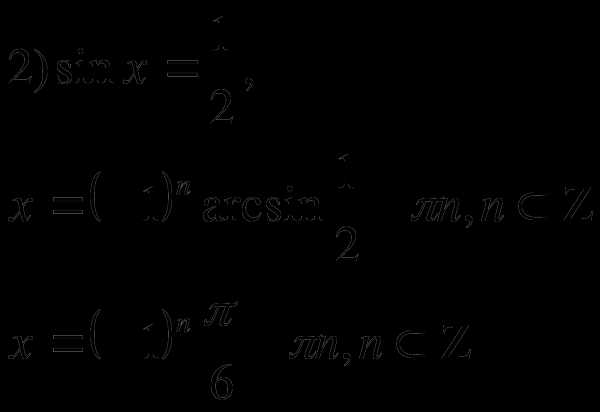
Ответ:
Р.С. 1) 4sin 2 x – 3 cos x – 3 = 0.
2) 3 cos 2 x – 2 sin x – 2 = 0.
Урок №
5) 3 tg 2 x – tg x – 2 = 0,
Обозначим tg x = y,
тогда получим уравнение:
3 у 2 – у – 2 = 0.
Корни данного уравнения найдем по формуле:
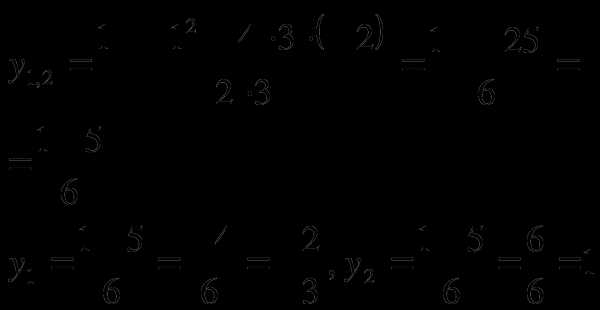
Решим простейшие уравнения:
1) tg x = 
x = arctg ( ) + π n, n
) + π n, n  Ζ
Ζ
x = – arctg  + π n, n
+ π n, n  Ζ
Ζ
tg x = 1
х =  + π n, n
+ π n, n  Ζ
Ζ
Ответ: х = 
 Ζ
Ζ x = – arctg  + π n, n
+ π n, n  Ζ
Ζ
6) tg x – 2 ctg x + 1 = 0.
Так как 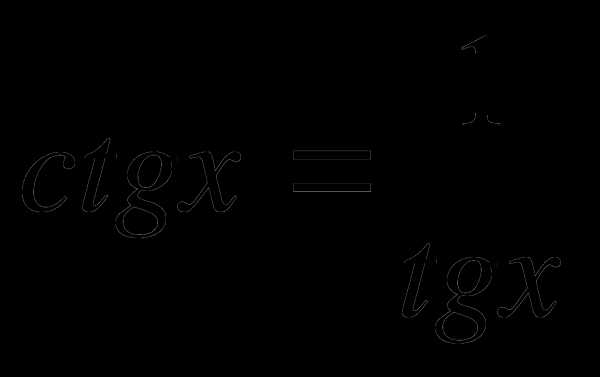 ,
,
то уравнение запишем в виде:
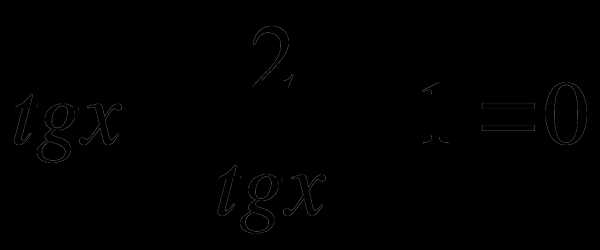
умножим обе части уравнения на tg x, получаем tg 2 x + tg x – 2 = 0,
Обозначим tg x = y,
тогда получим уравнение:
у 2 + у – 2 = 0.
Корни данного уравнения найдем по формуле:
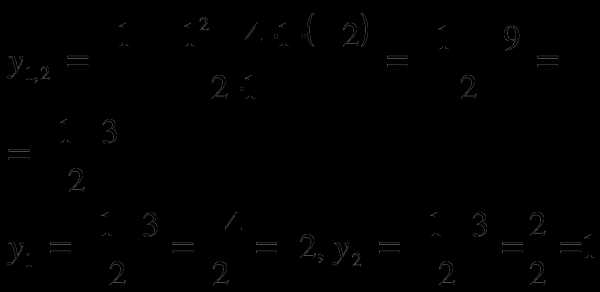
Решим простейшие уравнения:
tg x = 1
х =  + π n, n
+ π n, n  Ζ
Ζ
tg x = – 2
x = arctg (– 2 ) + π n, n  Ζ
Ζ
x = – arctg 2 + π n, n  Ζ
Ζ
Ответ: х =  + π n, n
+ π n, n  Ζ
Ζ
x = – arctg 2 + π n, n  Ζ
Ζ
Р.С. 1) 4 tg 2 x – tg x – 5 = 0,
2) tg x + 7 ctg x – 8 = 0.
infourok.ru
«Решение тригонометрических уравнений, сводящихся к квадратным». 11-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,9 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели и задачи урока.
- Образовательные:
- повторить: определение и способы решения простейших тригонометрических уравнений; определение квадратного уравнения, формулы дискриминанта и корней квадратного уравнения
- сформировать знания об отличительных признаках и способах решения тригонометрических уравнений, сводящихся к квадратным.
- уметь: выделять среди тригонометрических уравнений тригонометрические уравнения, сводящиеся к квадратным и решать их.
- Развивающие:
- развивать логическое мышление учащихся, память, внимание, речь; умения рассуждать и выделять главное; умение самостоятельно приобретать знания и применять их на практике, развивать навыки самоконтроля и взаимоконтроля.
- Воспитательные:
- воспитывать уважительное отношение к одноклассникам, самостоятельность, ответственность, эстетический вкус, аккуратность, интерес к математике.
Оборудование: мультимедийный проектор, экран, лист самооценки.
Организационные формы общения: фронтальная, групповая, индивидуальная.
Тип урока: усвоения новых знаний.
Образовательные технологии: ИКТ, проектная.
План урока.
- Организационный момент, формирование мотивации работы учащихся.
- Формулирование темы, цели урока.
- Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала.
- Этап усвоения новых знаний и способов действий.
- Этап активной релаксации и активизации.
- Этап первичной проверки понимания изученного.
- Этап рефлексии и оценивания. Подведение итогов урока.
- Этап информирования учащихся о домашнем задании, инструктаж по его выполнению.
Подготовительная работа
Учащихся класса необходимо заранее поделить на
группы. Принцип деления учащихся на группы
учитель вправе выбрать самостоятельно.
Один из вариантов – группы, в которые вошли бы
учащиеся с разным уровнем математической
подготовки: от «базового» до «продвинутого».
Каждая группа предварительно получает задание
изучить алгоритм решения одного из типов
тригонометрических уравнений (используются
предложенные учителем источники информации и
самостоятельно найденные). Результаты своей
работы члены каждой группы представляют на одном
из уроков по теме «Тригонометрические
уравнения». В зависимости от объёма
предлагаемого материала и его сложности одном
уроке могут успеть выступить 1-2 группы,
представив результаты своей работы.
Предлагаем вашему вниманию урок, на котором
рассматривается решение тригонометрических
уравнений, сводящихся к квадратным.
Из дома реальности легко забрести в лес математики, но лишь немногие способны вернуться обратно.
Х. Штейнхаус
Чем больше человек будет становиться человеком, тем меньше он согласится на что-либо иное, кроме бесконечного и неистребимого движения к новому.
Пьер Шарден
ХОД УРОКА
1. Организационный момент, формирование мотивации работы учащихся (3 мин.)
Приветствие. Фиксация отсутствующих, проверка
готовности учащихся к уроку. Далее каждому
ученику выдаётся оценочный лист. Учитель
кратко комментирует правила заполнения
оценочного листа и предлагает заполнить 1-3
строки. Приложение 1.
Организация внимания учащихся: учитель цитирует
учащимся Пьера Шардена, предлагает пояснить, как
они поняли смысл слов (можно выслушать 2-3
человека), предлагает сделать слова девизом
урока и интересуется, знают ли они, кто является
их автором. Краткая историческая справка
(Слайд 3).
*Инструкция по использованию Презентации – Приложение 2.
2. Формулирование темы, цели урока (2-3 мин.).
Учитель просит сформулировать тему
предыдущего урока (Решение простейших
тригонометрических уравнений). Интересуется у
учащихся, как они думают, существуют ли другие
типы тригонометрических уравнений? (Да. Если есть
«простейшие», то значит, есть более сложные,
иначе нет необходимости вводить термин
«простейшие», если это единственный тип
тригонометрических уравнений). Исходя из выше
сказанного, предлагает сформулировать тему
сегодняшнего урока (Решение
сложных/других/различных типов
тригонометрических уравнений).
После корректировки темы, предлагает учащимся
записать в их тетрадях: дату проведения урока,
фразу «Классная работа» и тему урока «Решение
различных типов тригонометрических уравнений:
уравнения, сводящиеся к квадратным».
На столе у каждого из учащихся находятся шаблоны
яблок и фломастеры. Предлагается написать на
«яблоках» свои ожидания от предстоящего урока,
тему которого уже сформулировали. После этого
все шаблоны яблок прикрепляются, например, с
помощью скотча на заранее приготовленный плакат
с изображением дерева. Получается «Дерево
ожиданий».
По мере достижения того или иного ожидания соответствующее яблоко можно считать созревшим и собирать в корзину. Использование этого активного метода обучения – наглядный способ отслеживания продвижения учащихся на уроке. [1]
Возможен другой вариант: учитель ставит песочные часы перед учениками класса и предлагает ответить на вопрос о том, чему они хотят научиться на уроке, тема которого уже сформулирована (достаточно 1-2 варианта).
3. Актуализация знаний и подготовка учащихся к активному и сознательному усвоению нового материала (10 мин.).
Учитель. Герберт Спенсер говорил, что если знания человека в беспорядочном состоянии, то чем больше их у него, тем сильнее расстраивается его мышление. Последуем совету этого известного британского философа (информация для общего развития личности – краткая историческая справка. (Слайд 5) Прежде чем перейти к изучению нового материала, давайте вспомним, что мы знаем из раздела «Тригонометрия».
Фронтальная работа (устно)
– Дайте определение тригонометрического
уравнения.
– Сколько корней может иметь тригонометрическое
уравнение?
– Что такое простейшие тригонометрические
уравнения?
– Что значит решить простейшее
тригонометрическое уравнение?
– Какие способы решения тригонометрических
уравнений вы знаете? (2 варианта: формулы;
единичная окружность).
а) Заполните таблицу:
б) Поставьте в соответствие уравнениям их решения, представленные на единичных окружностях (с комментарием)
Самостоятельная работа (Приложение 3)
С последующей взаимопроверкой/самопроверкой (правильность ответов проверяется с помощью презентации) на умение решать простейшие тригонометрические уравнения. Демонстрируется (Слайд 12). При необходимости решения некоторых уравнений коротко комментируются.
Заполняется пункт №4 Приложения 1.
4. Этап усвоения новых знаний и способов действий (15 мин.).
Учащиеся класса предварительно были поделены
на группы, каждая из которых самостоятельно
рассмотрела, используя материал рекомендуемый
учителем и найденный самостоятельно, один из
типов тригонометрических уравнений.
Результаты работы оформляются в виде некой
рекомендации/алгоритма/схемы решения в формате
презентации Power Point. Учитель в случае
необходимости консультирует учащихся групп и
предварительно проверяет итоговый продукт их
работы.
Для презентации результатов того или иного
способа решения на уроке выбирается один из
представителей группы, остальные на уроке
помогают отвечать на возникающие вопросы по
решению данного типа тригонометрического
уравнения. Учащиеся заранее знакомятся с
критериями оценивания своей работы в группе.
Мне приходится делить время
между политикой и уравнениями.
Однако уравнения, по-моему, гораздо важней.
Политика существует только для данного момента,
а уравнения будут существовать вечно.
Альберт Эйнштейн
Возможные варианты выполнения задания группой. (Слайды 14-18)
1 группа. Решение тригонометрических уравнений, сводящихся к квадратным.
Отличительные признаки уравнений, сводящихся к квадратным:
xn--i1abbnckbmcl9fb.xn--p1ai
Решение тригонометрических уравнений, сводящихся к квадратным. Урок 6
3. На практике часто встречаются тригонометрические уравнения, которые содержат в себе тригонометрические функции в различных степенях или различные функции одного и того же аргумента. Специального алгоритма решения тригонометрических уравнений нет. Но среди них есть такие, которые сводятся к простейшим решением квадратных уравнений относительно тригонометрических функций.
Как решаются такие уравнения?
Сегодня рассмотрим их решения.
Сообщаю тему и цель урока.
Например: cos 2x + sin x = 0
Решение.
cos2 x – sin2 x + sin x = 0
1 – sin2x – sin2x + sin x =0
2sin2x – sin x – 1 = 0
Пусть sin x = t , тогда
2t2 – t – 1 = 0
t1 = 1; t2 = –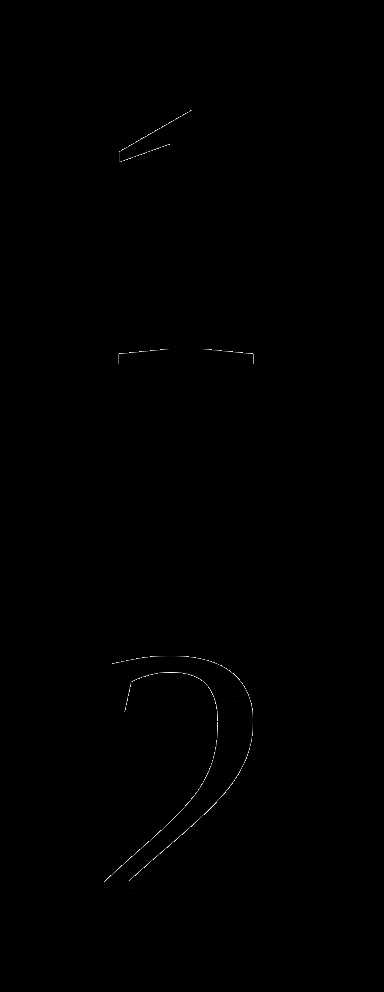 .
.
Имеем: 1) sin x = 1 ; 2) sin x = 
х = 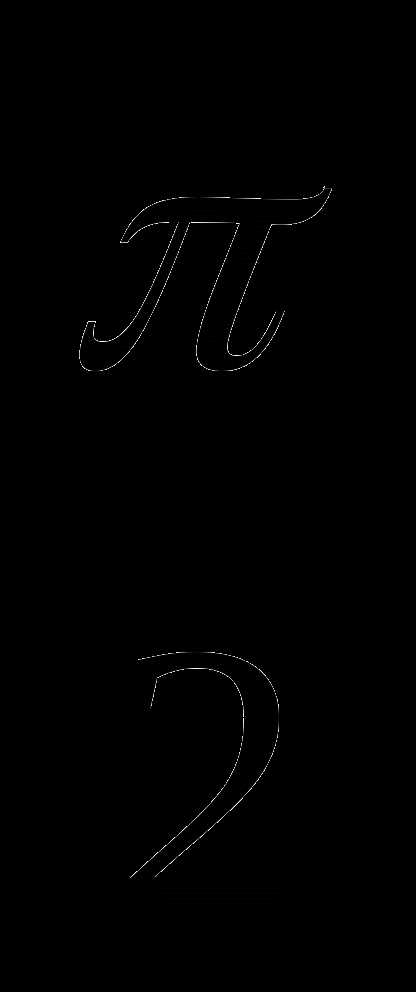 + 2pn , nÎ Z ; х = (-1)k arcsin
+ 2pn , nÎ Z ; х = (-1)k arcsin 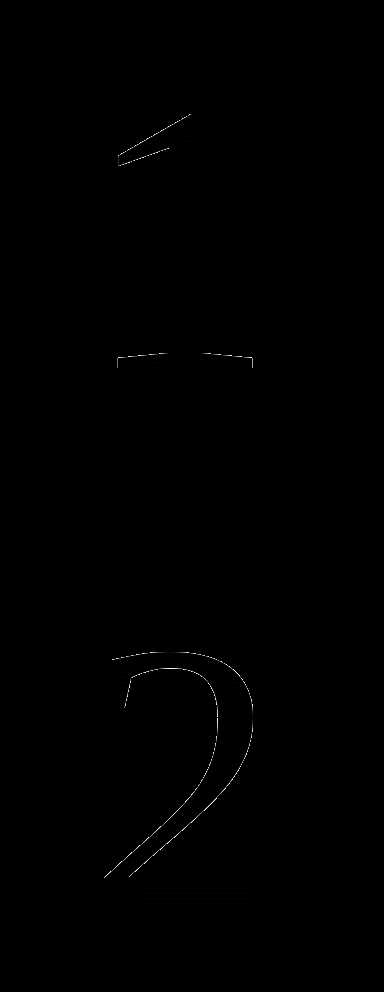 + pk , kÎ Z ;
+ pk , kÎ Z ;
х = (-1)k  + pk , kÎ Z ;
+ pk , kÎ Z ;
Ответ : 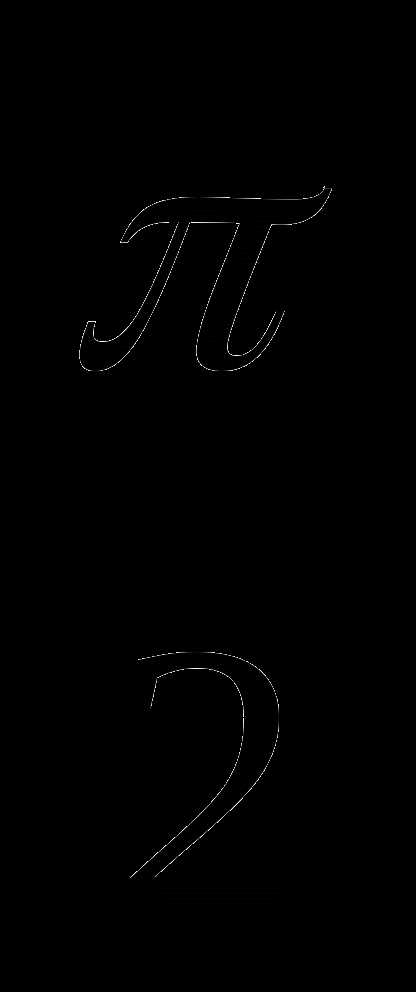 + 2pn , nÎ Z ; (-1)k
+ 2pn , nÎ Z ; (-1)k  + pk , kÎ Z .
+ pk , kÎ Z .
4.Закрепление №11.10 с объяснением у доски.
2 sin 2x + sin x – 1 = 0.
Решение.
Пусть sin x = t , тогда
2t2 + t – 1 = 0
t1 = –1 ; t2 =  .
.
Имеем: 1) sin x = – 1; 2) sin x = 
х = –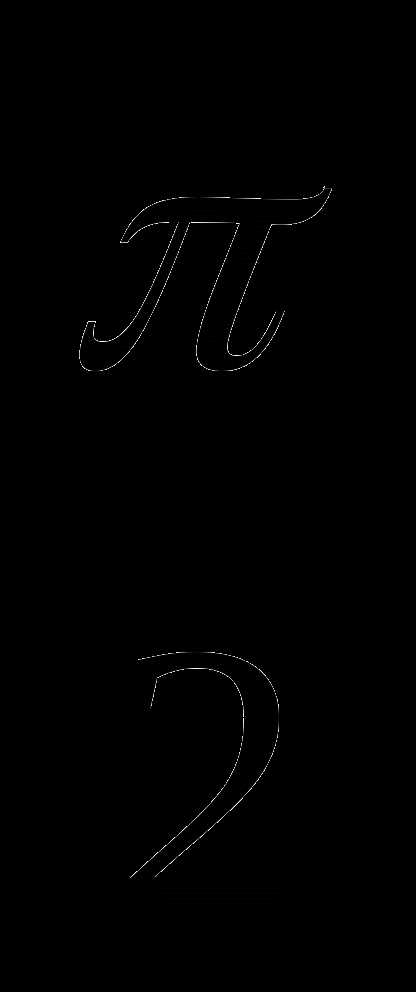 + 2pn , nÎ Z ; х = (-1)k arcsin
+ 2pn , nÎ Z ; х = (-1)k arcsin  + pk , kÎ Z ;
+ pk , kÎ Z ;
х = (-1)k  + pk , kÎ Z ;
+ pk , kÎ Z ;
Ответ: –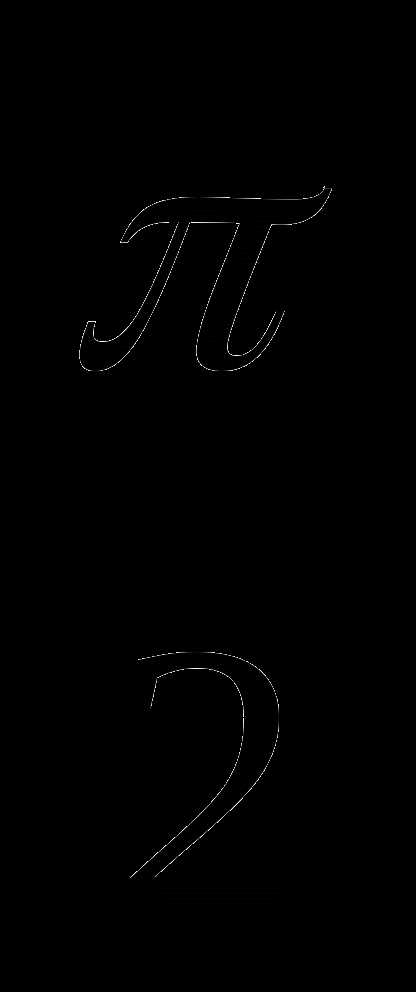 + 2pn , nÎ Z ; (-1)k
+ 2pn , nÎ Z ; (-1)k  + pk , kÎ Z .
+ pk , kÎ Z .
5.Самостоятельно по вариантам решить №11.10 (а, б)
Дома: п 11.2 №11.10(в,д,ж)
Итог урока. Какие уравнения научились решать?
Как решается квадратное уравнение?
Объявить оценки за урок.
Спасибо за работу на уроке.
infourok.ru
Урок «Тригонометрические уравнения, сводящиеся к квадратным»
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ города Москвы
«Политехнический техникум № 47 имени В.Г.Федорова»

Урок
по дисциплине Математика
«Тригонометрические уравнения, сводящиеся к квадратным»
Преподаватель
Протасевич Ольга Николаевна
ПРОФЕССИЯ: Наладчик аппаратного и программного обеспечения
ДИСЦИПЛИНА: Математика
КУРС: 1
СЕМЕСТР: 2
ГРУППА:
Тема урока:
«Тригонометрические уравнения, сводящиеся к квадратным».
Тип урока: комбинированный урок
Форма урока: коллективное обучение по методике В.К. Дьяченко
(обучение в системах малых групп)
Цели урока:
Образовательная – рассмотреть общие подходы, обобщить сведения о видах и методах решения тригонометрических уравнений, сводящихся к квадратным; формировать умения и навыки применения знаний при решении базовых уравнений и применению полученных знаний в профессиональной деятельности.
Развивающая – содействовать развитию логического мышления у обучающихся, развивать умения анализировать, рассуждать, сравнивать, делать выводы, осмысливать материал;
Воспитательная – воспитание познавательного интереса, элементов культуры общения, побуждать учащихся к преодолению трудностей в процессе умственной деятельности, формирование навыков работы в трудовом и учебном коллективе.
Задача урока:
Познакомить обучаемых с основными видами и методами решения тригонометрических уравнений, сводящихся к квадратным.
Обеспечение (ресурсы):
Аппаратное обеспечение: компьютер, мультимедийный проектор.
Программное обеспечение: Microsoft Excel.
Основные понятия:
Квадратное уравнение; простейшие тригонометрические уравнения; обратные тригонометрические функции; тригонометрические уравнения, сводящиеся к квадратным.
Литература:
Башмаков М.И. Математика: учебник для начального и среднего профессионального образования.– М.; «Академия», 2010. — 256 с.
Дьяченко В. К. Новая дидактика. — М.; «Народное образование», 2001 . — 496 с.
Методическая литература:
Башмаков М.И. Математика: книга для преподавателей. Методическое пособие.- М.; «Академия», 2013 г.- 224 с.
Электронные ресурсы:
Материалы сайта общественно-педагогического движения по созданию коллективного способа обучения: www.kco-kras.ru.
Этапы урока
Организационный момент.
Проверка домашнего задания.
Актуализация опорных знаний.
Изучение нового материала.
Закрепление и систематизация полученных знаний.
Рефлексия. Подведение итогов. Домашнее задание.
Ход урока
Организационный момент.
Преподаватель ставит перед обучаемыми цели урока:
1) Познакомить с основными видами тригонометрических уравнений, сводящихся к квадратным;
2) Познакомить с типовыми методами решения тригонометрических уравнений, сводящихся к квадратным.
3) Научить применять полученные знания и умения для решения стандартных уравнений;
4) Научить работать с информацией, представленной в различных формах, осуществлять взаимный контроль и самоконтроль, применять полученные знания в профессиональной деятельности.
II. Проверка домашнего задания.
Преподаватель включает презентацию «Домашнее задание», по которой обучаемые самостоятельно выполняют проверку домашнего задания, при необходимости вносят поправки и исправления в работу.
По просьбе обучаемых преподаватель комментирует решения уравнений, вызвавшие затруднения, после чего объявляет фамилии обучаемых, кто по окончании урока сдает на проверку тетради.
№ 1
Ответ:
№ 2
Ответ:
№ 3
Ответ:
№ 4
т.к. то уравнение корней не имеет
Ответ: корней нет
№ 5
Ответ:
№ 6
Ответ:
III. Актуализация опорных знаний.
Преподаватель формирует учебные группы/пары и предлагает на выданных бланках установить соответствие между уравнениями и ответами: «Перед вами слайд с учебным заданием. Установите соответствие между уравнениями (левая часть таблицы) и ответами (правая часть таблицы). Запишите номера верных пар высказываний в тетрадь».
Указанные задания дублируются на включённой презентации.
Установите соответствие
п/п
Уравнение
№
п/п
Ответ
,
Корней нет
По окончании работы преподаватель фронтально опрашивает представителей групп, после чего включает страницу презентации с правильными решениями.
Правильные ответы
п/п
Уравнение
№
п/п
Ответ
,
3.
8.
7.
Корней нет
1.
4.
7.
Корней нет
2.
5.
11.
13.
9.
10.
12.
IV. Изучение нового материала.
Преподаватель включает презентацию нового материала «Тригонометрические уравнения, сводящиеся к квадратным. Типы уравнений и методы их решений».
Предлагает обучаемым записывать необходимые тезисы и начинает комментировать каждый слайд, после чего включает презентацию.
Введем понятие: «Тригонометрические уравнения, которые при помощи преобразования и замены переменной приводятся к квадратным называются тригонометрическими уравнениями, сводящимися к квадратным».
Общий вид квадратного уравнения:
1 тип тригонометрических уравнений, сводящихся к квадратным – уравнения, алгебраические относительно одной из тригонометрических функций.
Преподаватель поясняет способы решения.
1. Непосредственная подстановка
Замена , тогда уравнение принимает вид
и
корней нет
Ответ:
Аналогичное решение имеют уравнения вида
Замена
Замена
2.Уравнения, требующие преобразования по формуле тригонометрической единицы
Замена , тогда уравнение принимает вид
и
Корней нет
Ответ:
Аналогичное решение имеют уравнения вида:
заменим , используя формулу тригонометрической единицы
.
Получим уравнение, содержащее только одну тригонометрическую функцию :
Замена
3.Уравнения, требующие преобразования по формуле связи tgx и сtgx
Применяем формулу:
Умножим уравнение на
Замена , тогда уравнение принимает вид
и
Ответ:
2 тип тригонометрических уравнений, сводящихся к квадратным – однородные уравнения, в которых каждое слагаемое имеет одну и туже степень.
Разделим уравнение на
Замена , тогда уравнение принимает вид
и
Ответ:
Преподаватель предлагает обобщить представленный материал и задает вопросы: «На сколько типов делятся тригонометрические уравнения, сводящихся к квадратным? Их название? Назовите способы решения тригонометрических уравнений, сводящихся к квадратным».
Преподаватель направляет действия обучаемых при составлении алгоритма решения уравнений данного типа.
Тригонометрические уравнения, сводящиеся к квадратным, делятся на два основных типа:
1 тип – уравнения, алгебраические относительно одной из тригонометрических функций:
— непосредственная подстановка — замена или ;
— уравнения, требующие преобразования по формуле тригонометрической единицы ;
— уравнения, требующие преобразования по формуле связи tgx и сtgx:
2 тип – однородные уравнения, в которых каждое слагаемое имеет одну и ту же степень: разделим уравнение на ,затем замена .
Преподаватель составляет откорректированный Алгоритм решения:
1. Определите тип уравнения. При необходимости преобразуйте уравнение так, что бы в нём присутствовала только одна тригонометрическая функция. Для этого выбери нужную формулу: или или раздели на
2. Вводится замена (например, sinx = t, cosx=t, tgx=t).
3. Решите квадратное уравнение.
4. Производится обратная замена, и решается простейшее тригонометрическое уравнение.
5. Запиши ответ.
Для закрепления полученных знаний преподаватель предлагает установить соответствие между уравнениями и возможными способами их решений: «Перед вами слайд с учебным заданием.
1. Проведите классификацию уравнений по методам решения согласно приведенной ниже таблице
(распечатанные варианты таблицы находятся у вас на столах).
2. Поставьте в соответствующей графе номер метода решения.
Заполните таблицу».
Работа выполняется в парах.
п/п
Уравнение
№
метода
Методы:
1) Введите новую переменную .
2) Введите новую переменную
3) Введите новую переменную .
4) Преобразуйте уравнение, применив формулу , введите новую переменную .
5) Преобразуйте уравнение, применив формулу , введите новую переменную .
6) Разделите каждый член уравнения на , введите новую переменную .
7) Преобразуйте уравнение применив формулу , умножьте члены уравнения на , введите новую переменную .
Проверка задания осуществляется в форме фронтальной беседы.
Преподаватель: «Перед вами слайд с правильными ответами к учебному заданию. Выполните проверку, сверяясь с правильными ответами к учебному заданию. Выполните работу над ошибками в тетради».
Бланки с заданиями собираются в конце урока.
п/п
Уравнение
№
метода
2
4
2
1
7
1
3
5
6
3
6
2
6
VI. Закрепление и систематизация полученных знаний.
Преподаватель предлагает обучаемым продолжить работу в группах.
Преподаватель: «Решите уравнения. Выполните проверку результата в редакторе Microsoft Excel. По окончании решения представитель группы выходит к учебной доске и представляет решение уравнения, выполненное группой». Преподаватель проверяет решение, оценивает работу группы и при необходимости указывает на ошибки».
Преподаватель:
1) Обсудите способы решения в группе.
2) Запишите решение и полученный ответ в тетрадь.
3) Выполнить проверку результата в редакторе Microsoft Excel.
4) Сообщите о готовности преподавателю.
5) Объясните свое решение, записав его на доске, членам других групп.
6) Вдумчиво выслушайте выступления товарищей, при необходимости задавайте вопросы.
Учебным группам, выполнившим задания в полном объеме, предлагается выполнить задание других групп. Состав успешных групп поощряется повышением итогового балла на одну единицу.
Первая группа:
Применяем формулу:
Замена , тогда уравнение принимает вид
и
Корней нет
т.к.
Ответ:
Вторая группа:
Применяем формулу:
Замена , тогда уравнение принимает вид
и
Ответ: ;
Третья группа:
Применяем формулу :
Умножим уравнение на
Замена , тогда уравнение принимает вид
и
Ответ:
Четвертая группа:
Разделим уравнение на
Замена , тогда уравнение принимает вид
и
Ответ:
Пятая группа:
Замена , тогда уравнение принимает вид
и
Ответ:; .
VII. Рефлексия. Подведение итогов. Домашнее задание.
Преподаватель: Подведем итоги вашей работы, соотнося результаты вашей деятельности с поставленной целью.
Повторим понятия:
«Тригонометрические уравнения, которые при помощи преобразования и замены переменной приводятся к квадратным называются тригонометрическими уравнениями, сводящимися к квадратным».
— непосредственная подстановка — замена или ;
— уравнения, требующие преобразования по формуле тригонометрической единицы ;
— уравнения, требующие преобразования по формуле связи tgx и сtgx:
2 тип – однородные уравнения, в которых каждое слагаемое имеет одну и туже степень: разделим уравнение на ,затем замена .
Алгоритм решения:
1. Определите тип уравнения. При необходимости преобразуйте уравнение так, что бы в нём присутствовала только одна тригонометрическая функция.
Для этого выбери нужную формулу:
или или раздели на
2. Вводится замена (например, sinx = t, cosx=t, tgx=t).
3. Решите квадратное уравнение.
4. Производится обратная замена, и решается простейшее тригонометрическое уравнение.
5. Запиши ответ.
Преподаватель проводит оценивание работы обучаемых, учебных групп и объявляет оценки.
Преподаватель: «Запишите домашнее задание: Башмаков М.И. Математика: учебник для начального и среднего проф. образования.– М.; «Академия», 2010. Стр. 114-115. В номере 10 решить уравнения № 4,5,7,9. стр. 118. Выполните проверку результата в редакторе Microsoft Excel».
infourok.ru
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, СВОДЯЩИХСЯ К КВАДРАТНЫМ
ТЕМА: РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, СВОДЯЩИХСЯ К КВАДРАТНЫМ.
Цели:
Расширить и углубить знания и умения учащихся при решении нового вида тригонометрических уравнений – уравнений, сводящихся к квадратным.
Содействовать развитию математического мышления учащихся.
Побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей деятельности, вызывать у них потребность к обоснованию своих высказываний.
Этапы урока:
I.Постановка цели и мотивация учебной деятельности учащихся. (2 мин.)
II. Восстановление опорных знаний – актуализация. (11 мин.)
III.Формирование знаний, умений, навыков. (7 мин)
IV.Формирование способов умственных и практических действий с новыми знаниями. (10 мин.)
V.Самостоятельная работа. (8 мин.)
VI.Подведение итогов урока. (2 мин.)
Оборудование: учебник «Алгебра и начала анализа», копировальная бумага, листы для самостоятельной работы, карточки с тригонометрическими уравнениями.
ХОД УРОКА.
На прошлом уроке мы учились решать простейшие тригонометрические уравнения, однако существует более широкий круг разных видов тригонометрических уравнений. сегодня мы будем учиться решать уравнения, сводящиеся к квадратным.
Но сначала повторим то, что нужно будет для изучения новой темы.
1.Найди ошибку (записано на обратной стороне доски слева)
arcsin = ; arcsin(-) =; arccos0=; arccos(-)=-; arctg=; arctg(-)=-.
2. Решите простейшие тригонометрические уравнения под копировальную бумагу. (Работа проводится по карточкам, на которых записаны 10 простейших тригонометрических уравнений. после отведённого времени листы сдаются, копии остаются у учащихся. Учитель открывает заранее записанные на закрытой доске справа правильные решения и критерии оценок. Проводится самопроверка. Для оценки работы надо поставит «+» напротив верного ответа и знак «-» напротив неправильного. Критерии оценок: «5» — за 10 плюсов, «4» — 8-9 плюсов, «3» — 5-7 плюсов, «2» — менее 5 плюсов.
3. В то время, пока учащиеся решают тест, одного ученика вызвать к доске решать уравнение на открытой доске слева 2х2-х-1=0. После анализа теста рассмотреть решение и повторить способы решения квадратного уравнения в зависимости от дискриминанта.
4. Подвести итог II этапа.
III. Мы научились решать простейшие тригонометрические уравнения вида sin x=a, cos x=a, tg x=a. Но есть более сложные уравнения. Для их решения требуется применение различных формул и преобразование тригонометрических выражений. Сегодня будем учиться решать уравнения, которые сводятся к квадратным. ( Записать тему урока)
Рассмотрим на конкретном примере, как решаются данные уравнения.
2sin2x+sinx-1=0.
Обозначим sinx=y.
Совершим замену и получим квадратное уравнение 2у2+у-1=0.
D=9>0, то уравнение имеет 2 различных корня.
у1=-1; у2=.
Совершим обратную замену:
Sinx=-1 sinx=
Х=-+2n, nZ; х=(-1)n+, nZ.
Ответ:-+2n, nZ; (-1)n+, nZ.
Итак, чтобы решить уравнение такого вида, нужно
Ввести новую переменную у.
Совершить замену простейшего тригонометрического уравнения на у.
Решить получившееся квадратное уравнение.
Совершить обратную замену.
Решить простейшие тригонометрические уравнения.
Записать ответ.
IV.Решить в тетрадях уравнения, два ученика решают на доске:
6cos2x+cosx-1=0 и 3tg2x+2tgx-1=0.
(ученики сверяют свои решения с решениями на доске)
V.Самостоятельно решить на листочках:
I вариант: 2sin2x-sinx-1=0
II вариант: 4cos2x-8cosx+3=0.
VI.подвести итог урока.
Домашнее задание: решить уравнения 2tg2x+3tgx-2=0 и 2cos23x-5cos3x-3=0.
Решение второго уравнения проверим на следующем уроке.
infourok.ru
урок по теме «Решение тригонометрических уравнений»
УРОК
«РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ»
Цель урока:
Образовательная: 1. Закрепить навык решения простейших тригонометрических
уравнений;
2. Рассмотреть различные виды тригонометрических
уравнений;
3. Способствовать развитию навыков самостоятельного
применения знаний при решении тригонометрических
уравнений.
Развивающая: 1. Работать над развитием понятийного аппарата;
2. Развивать навыки самоконтроля.
Воспитательная: 1. Воспитывать ответственное отношение к труду;
2. Воспитывать волю и настойчивость для достижения
конечных результатов.
Тип урока: применение знаний.
ПЛАН УРОКА:
Организационный момент.
Объяснение цели урока.
Устная работа.
Работа по технологическим картам (с проверкой ответов и решений)
Объяснение других способов решения тригонометрических уравнений.
Дифференцированная самостоятельная работа (с самопроверкой).
Подведение итогов урока, выставление оценок.
Получение домашнего задания.
Рефлексия.
ХОД УРОКА:
Организационный момент.
Объяснение цели урока.
Устный счет.
В следующих формулах найти ошибки –
1. sin2x + cos2x = 1
2. tg x = 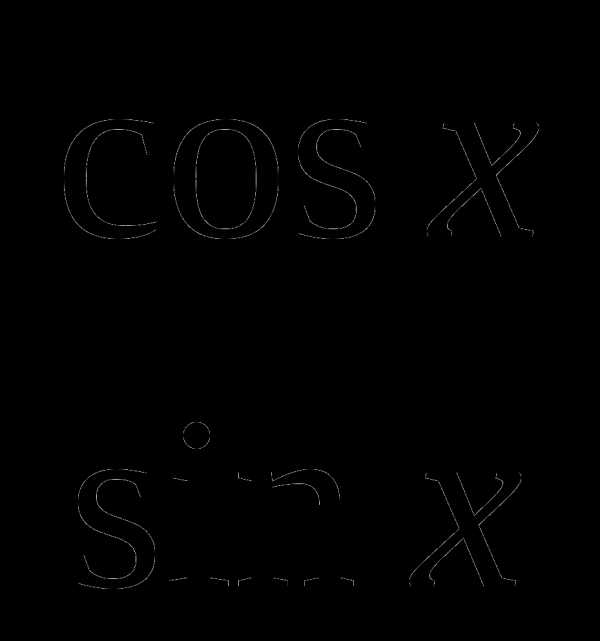 [
[ 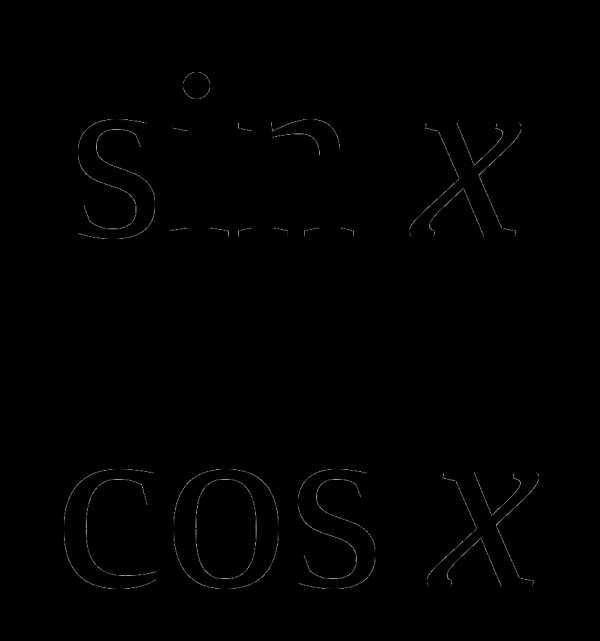 ]
]
3. sin 2x = sin x cos x [ 2sin x cos x]
4. cos 2x = cos2 x + sin2 x [cos2 x — sin2 x ]
5. sin x = a , a = (-1)n arcsin a +  n [x = (-1)n arcsin a +
n [x = (-1)n arcsin a +  n ]
n ]
6. cos x = a, x =  arccos a +
arccos a +  n, [x =
n, [x =  arccos a + 2
arccos a + 2 n ]
n ]
7. tg x = a, a = arctg a + 2 n, [ x = arctg a +
n, [ x = arctg a +  n ]
n ]
Работа по технологическим картам.
Прочитать текст, разобрать приведенный пример, записать в тетрадь. Выполнить первое задание своего варианта. Второе задание варианта выполняют только после того, как будет выполнено первое задание из каждого пункта.
ТЕХНОЛОГИЧЕСКАЯ КАРТА
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ.
1) Заметим, что если тригонометрическое уравнение целого вида содержит только синусы или косинусы (синусы и косинусы), то область допустимых значений переменной – множество действительных чисел, так как эти функции определены для любого действительного значения. Область допустимых значений для уравнений вида
a sin2f(x) + b sin f(x) + c = 0 или a cos2f(x) + b sin f(x) + c = 0 не устанавливается.
2) Справедливы соотношения:
а) sin 2  = 1 – cos2
= 1 – cos2  (1)
(1)
б) cos2  = 1 – sin2
= 1 – sin2  (2)
(2)
3) Формулы корней уравнений:
а) sin x = a, x = (-1)n arcsin a +  n, n
n, n  (3)
(3)
б) cos x = a, x =  arcos a + 2
arcos a + 2 n, n
n, n  (4)
(4)
в) ax2 + bx + c = 0, x =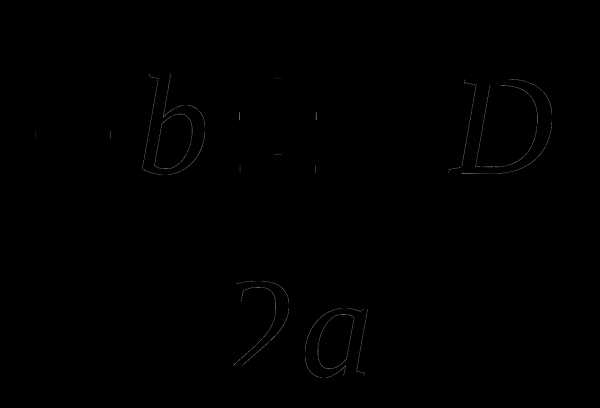 (5)
(5)
ОБРАЗЕЦ РЕШЕНИЯ УРАВНЕНИЯ:
8 sin2x – 6 sin x – 5 = 0
Обозначим sin x = у, тогда данное уравнение можно записать в виде
8 у2 – 6у – 5 = 0
D = b2 – 4ac= (-6)2 – 4 8
8 (-5)= 36 + 160 = 196
(-5)= 36 + 160 = 196
у1 =
у2 =  .
.
Значит sin x = — или sin x =
или sin x =  — уравнение не
— уравнение не
имеет корней, так как sin х
x= (-1)n+1 +
+  n, n
n, n  не может быть больше единицы.
не может быть больше единицы.
Ответ: x= (-1)n+1 +
+  n, n
n, n 
РЕШИТЬ УРАВНЕНИЯ:
1 вариант: 1) sin2x – 2 sin x – 3 = 0
2) 2 cos2x + 3 sin2 x + 2 cosx = 0
2 вариант: 1) cos2x — 2 cos x – 3 = 0
2) 2 sin2 x + 3 cos2x + 2sin x = 0
П. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ:
1) Справедливы соотношения:
a) tg ctg
ctg =1; б) tg
=1; б) tg  =
=  ; в) ctg
; в) ctg  =
=  ;
;
г) 1 + tg2 =
= 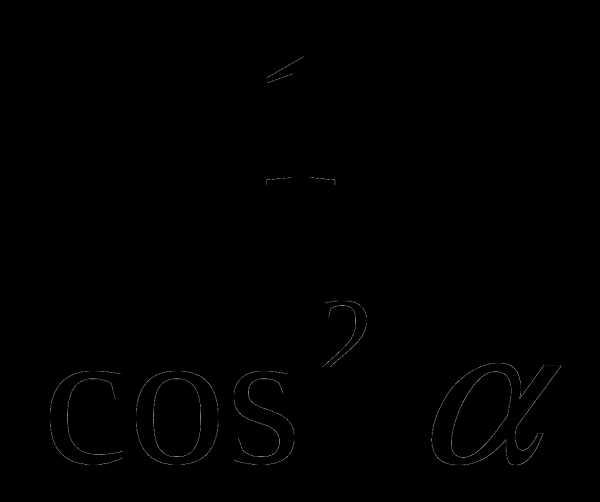 ; д) 1 + ctg2
; д) 1 + ctg2 =
= 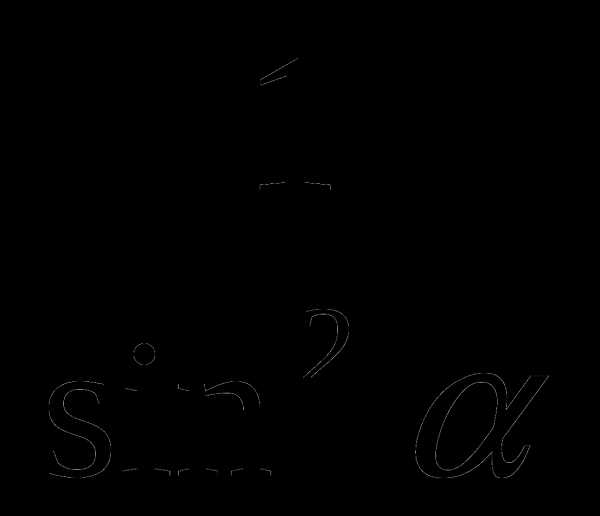
2) Уравнение вида a tg x + b ctg x + c = 0 приводится к квадратному уравнению одной
тригонометрической функции путем замены ctg x =  .
.
Уравнение вида a sin x + b cos x = 0 (a
 0, b
0, b  0) называется однородным первой степени
0) называется однородным первой степени
относительно sin x и cos x. Оно решается делением обеих частей на cos x 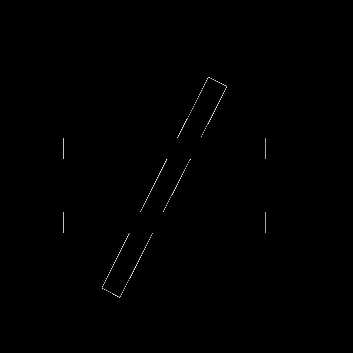 0. В результате
0. В результате
получается уравнение вида a tg x + b = 0.
4) Уравнение вида a sin2f(x) + b sin f(x) cos f(x) + k cos2f(x) = 0 называется однородным
Уравнением второй степени относительно sin f(x) и cos f(x), если все три
коэффициента а, b, k или какие-либо два из них  0.
0.
Разделим обе части уравнения на cos2f(x)  0. Получим
0. Получим
а tg2f(x) + b tg f(x) + k = 0, которое решается заменой переменной.
ОБРАЗЕЦ РЕШЕНИЯ УРАВНЕНИЯ:
sin x +  cos x = 0.
cos x = 0.
Разделим каждое слагаемое на cos x.

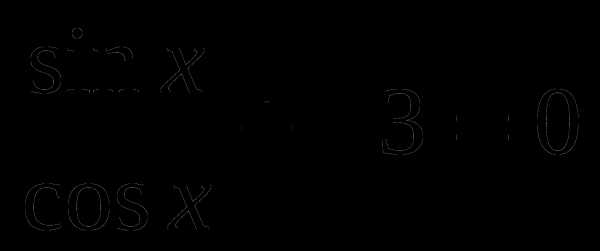
 tg x +
tg x +  = 0
= 0
tg x = — 
x = — +
+  n, n
n, n  .
.
Ответ: x = — +
+  n, n
n, n  .
.
РЕШИТЬ УРАВНЕНИЯ:
1 ВАРИАНТ 1) 2sin x – 3 cos x = 0
2) sin x —  cos x = 0
cos x = 0
2 ВАРИАНТ 1)  sin x + cos x = 0
sin x + cos x = 0
2) 2 cos2 x + 2 sin x = 2.5
Ш. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ РАЗЛОЖЕНИЯ НА
МНОЖИТЕЛИ.
ОБРАЗЕЦ РЕШЕНИЯ УРАВНЕНИЯ:
 cos x = sinx cos x
cos x = sinx cos x
 cos x — sinx cos x = 0
cos x — sinx cos x = 0
Вынесем за скобки cos x
cos x ( — sinx) = 0
— sinx) = 0
cos x = 0 или  — sin x = 0
— sin x = 0
х =  +
+  n, n
n, n  sinx =
sinx =  ,
, 
 1,7
1,7
решений нет
Ответ: х =  +
+  n, n
n, n  .
.
РЕШИТЬ УРАВНЕНИЯ:
1 ВАРИАНТ 1)  sin x = cos x sin x
sin x = cos x sin x
2) sin 2x =  cos x
cos x
2 ВАРИАНТ 1) sin 2x =  sin x
sin x
2) sin 2x – cos x = 0
Результаты работы по технологическим картам учащиеся записывают на листочках, которые сдают учителю. Проверку производят по тетрадям, выполняя некоторые, где было сделано много ошибок на доске. Оценки ставят себе сами (выполнено 6 заданий – «5», выполнено 4 -5 заданий – «4», выполнено 3 задания «3»).
1. Рассмотрим однородные тригонометрические уравнения:
3 sin2x – 4 sin x cos x + cos2x = 0
Разделим обе части уравнения на cos2x.
3 tg2x – 4 tg x + 1 = 0
Мы получили тригонометрическое уравнения, приводимое к квадратному.
Заменим tg x = y
3y2 – 4 y + 1 = 0 tg x = 1, x = 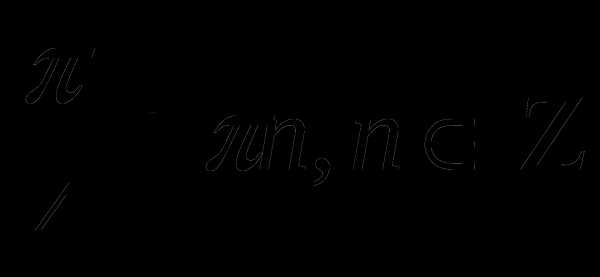
D = 4, y1 = 1, y2 = 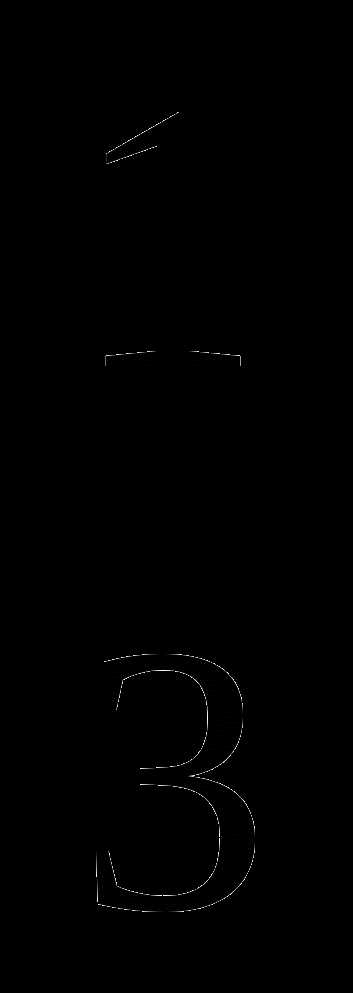 tg x =
tg x =  , x = arctg
, x = arctg  +
+
ответ: x = 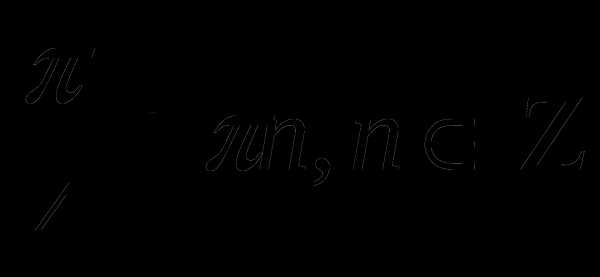 , x = arctg
, x = arctg  +
+
2.Решим уравнение, применяя универсальную подстановку:
Sin 2x + 2 cos 2x = 1
Делаем замену: sin 2x = 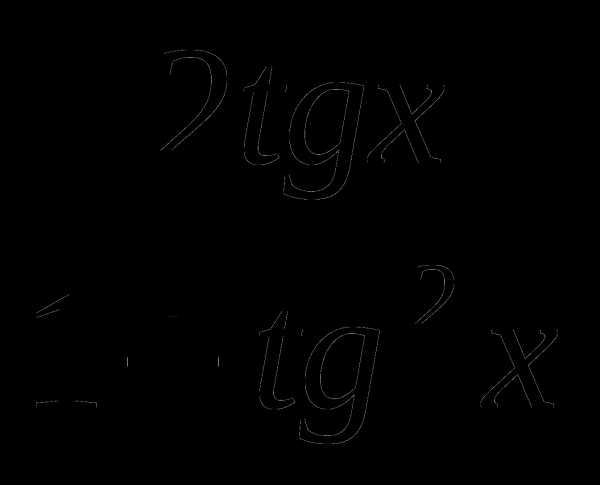 , cos 2x =
, cos 2x = 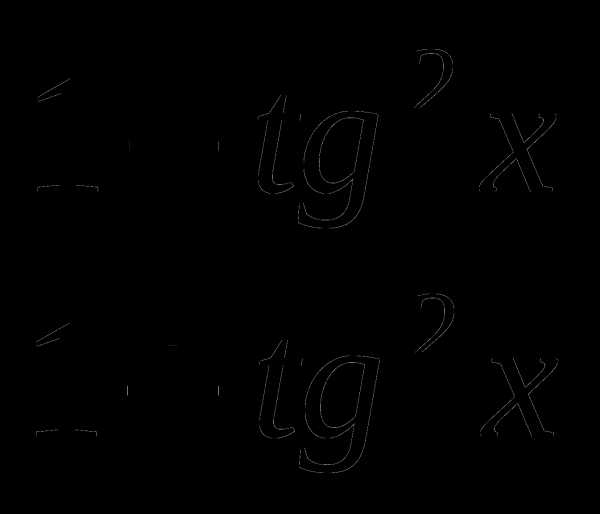
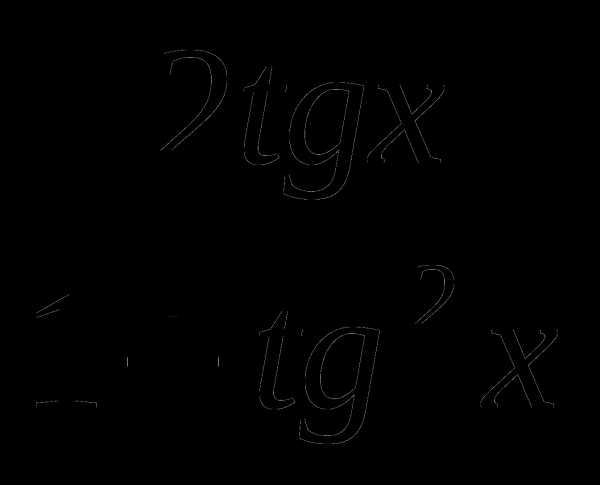 + 2
+ 2 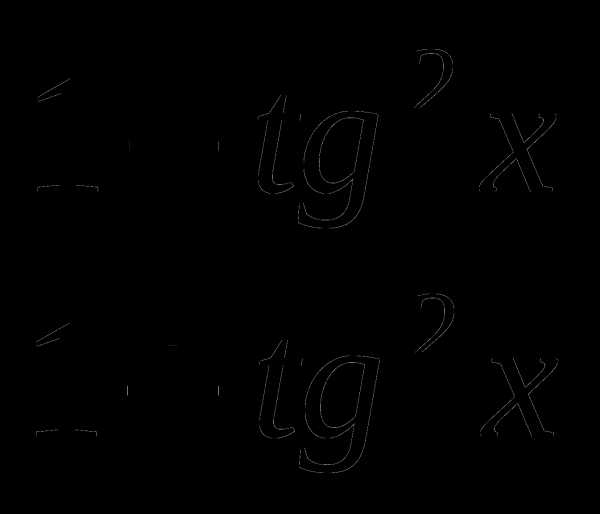 = 1. Pазделим обе части на 1 + tg2x
= 1. Pазделим обе части на 1 + tg2x
2 tg x + 2 – 2 tg2x = 1 + tg2x
3 tg2 x – 2 tg x – 1 = 0, tg x = y tg x = 1, x = 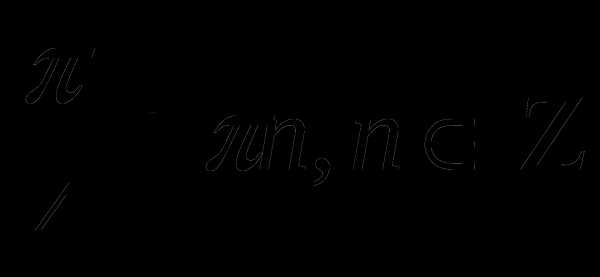
3y2 – 2y – 1 = 0 tg x = —  , x = — arctg
, x = — arctg  +
+
D = 16, y1 = 1, y2 = —  Ответ: x =
Ответ: x = 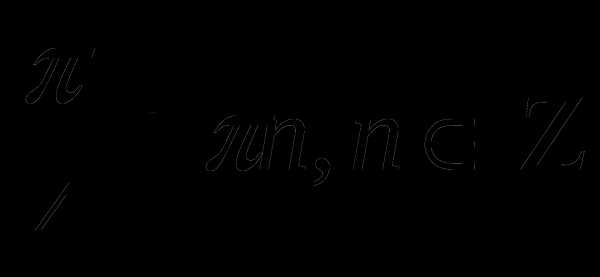 , x = — arctg
, x = — arctg  +
+
3.Решение тригонометрических уравнений с помощью формул сложения, формул суммы и разности синусов (косинусов):
2 sin 11x +  sin 5x + cos 5x = 0.
sin 5x + cos 5x = 0.
Разделим левую и правую части этого уравнения на 2, получим
sin 11x + 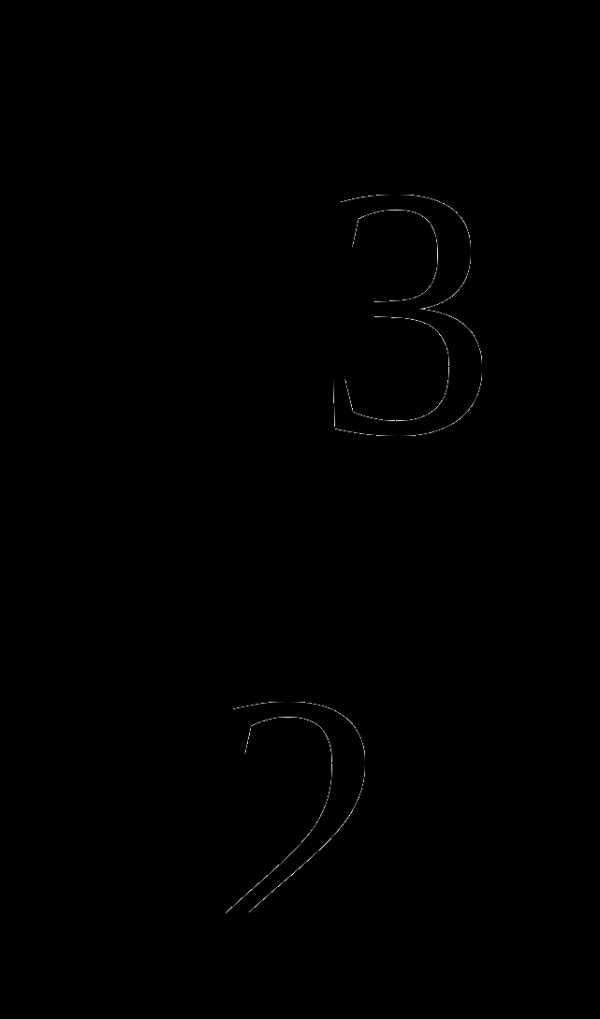 sin 5x +
sin 5x +  cos 5x = 0
cos 5x = 0
так как 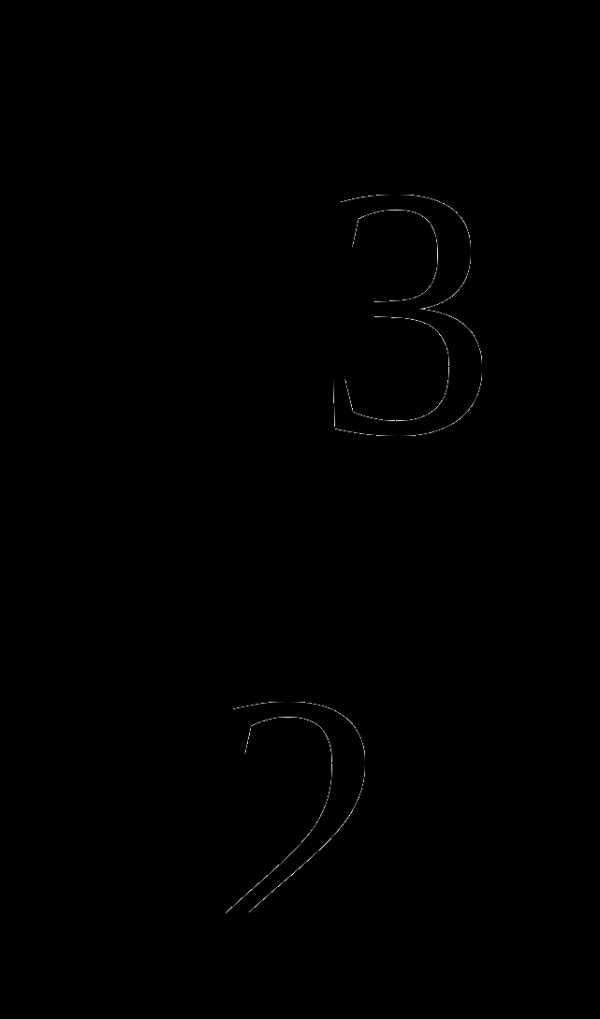 = cos
= cos  , a
, a  = sin
= sin  , то это уравнение имеет вид:
, то это уравнение имеет вид:
sin 11x + cos  sin 5x + sin
sin 5x + sin  cos 5x = 0
cos 5x = 0
sin 11x + sin (5x +  ) = 0; 2 sin = 0
) = 0; 2 sin = 0
sin  = 0,
= 0,  =
=  n, 16x +
n, 16x +  = 2
= 2 n, x = —
n, x = —  +
+ 
cos 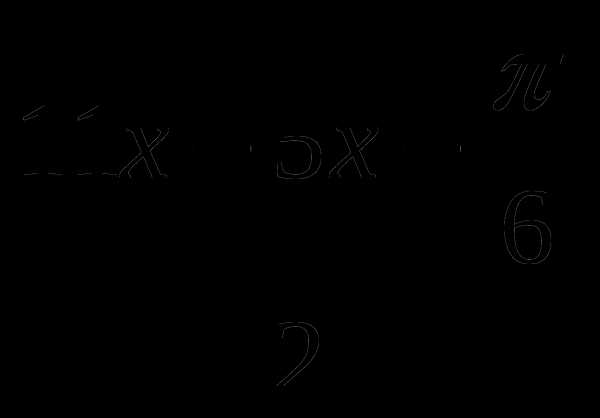 = 0,
= 0, 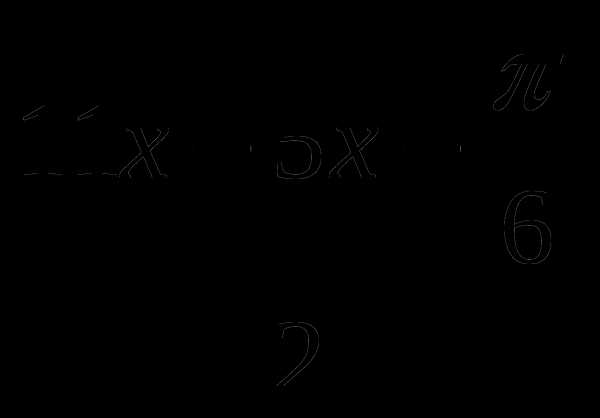 =
=  +
+  n, 6x —
n, 6x —  =
=  + 2
+ 2 n, x =
n, x = 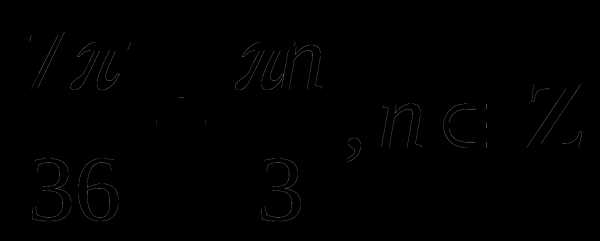
Ответ: x = —  +
+  , x =
, x = 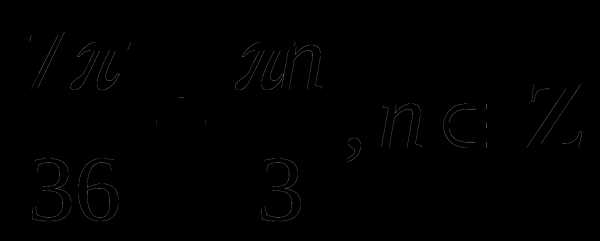
САМОСТОЯТЕЛЬНАЯ РАБОТА
ВАРИАНТ 1
Решить уравнения:
2cos2x + 3 sin x = 0
sin x + cos x = 0
2 sin x cos x + sin x = 0
ВАРИАНТ 1
Решить уравнения:
2cos2 x + 3 sin x = 0
sin x + cos x = 0
2 sin x cos x + sin x = 0
ВАРИАНТ 2
Решить уравнения:
2 cos2 x = 3 sin x
3 sin x + 4 sin (
 + x ) = 0
+ x ) = 0 cos x + sin 2x = 0
cos x + sin 2x = 0
ВАРИАНТ 2
Решить уравнения:
2 cos2 x = 3 sin x
3 sin x + 4 sin (
 + x ) = 0
+ x ) = 0 cos x + sin 2x = 0
cos x + sin 2x = 0
ВАРИАНТ 3
Решить уравнения:
2 sin2 x – 5 = — 5 cos x
2. 7 sin2 x = 8 sin x cos x – cos2 x
3. 2 sin x cos x = cos x
ВАРИАНТ 3
Решить уравнения:
2 sin2 x – 5 = — 5 cos x
7 sin2 x = 8 sin x cos x – cos2 x
2 sin x cos x = cos x
Самостоятельную работу выполняют на листочках, в листах ответов записывают результат.
Проверка самостоятельной работы (по плакату).
РЕФЛЕКСИЯ:
Среди уравнений, данных на плакате выбрать те, которые решаются
а) приведением к квадратному (ответ: № 3, 4, 8)
б) как однородные (ответ: № 1, 5, 9)
в) с помощью формул суммы и разности (ответ: № 6, 7)
г) вынесением множителя за скобки (2, 10)
д) с помощью универсальной подстановки (ответ: № 11)
2 sin2 x + cos2 x = 5 sin x cos x
Sin 2x – cos x = 0
Sin2 x —
 sin 2x = cos2 x
sin 2x = cos2 xSin2 x – 2 sin x – 3 = 0
 cos x – sin x = 0
cos x – sin x = 0Sin x + sin 3x = sin 5x – sin x
Sin x – sin 2x + sin 3x – sin 4x = 0
2 cos2 x + 3 sin2 x + 2 cos x = 0
Cos2 x + 3 sin2 x + 2
 sin x cos x = 3
sin x cos x = 3
10)  sin x = cos x sin x
sin x = cos x sin x
11) sin x + cos x = 1
Ф.И.
вариант
1.
1)
2)
П.
1)
2)
Ш.
1)
2)
ЛИСТ ОТВЕТОВ
Ф.И.
Вариант
1.
2.
3.
Разработала учитель математики средней школы № 6 г.Павлодара
Смагулова Шолпан Жазкеновна
infourok.ru

 sin 2x = cos2 x
sin 2x = cos2 x