Задачи на дроби с решением 6 класс – Урок по теме «Решение задач на дроби». 6-й класс

Задачи на дроби для 6 класса

Просмотр содержимого документа
«Задачи на дроби для 6 класса»

В столовую

На рынок

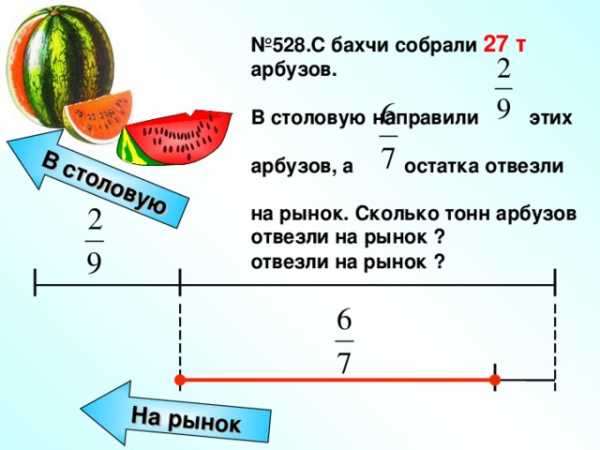
№ 528.С бахчи собрали 27 т арбузов.

В столовую направили этих

арбузов, а остатка отвезли

на рынок. Сколько тонн арбузов

отвезли на рынок ?

отвезли на рынок ?

Математика 6 класс. Н.Я.Виленкин. № 512.

РЕШЕНИЕ:

ВЕРНОЕ РЕШЕНИЕ:

За три дня на элеватор доставили 651 т зерна.

В первый день было доставлено

всего зерна .

Во второй 0,9 того, что было доставлено в первый день.

№ 514 . Математика 6 класс. Н.Я.Виленкин.

?

Сколько тонн зерна было доставлено на элеватор в третий день?

РЕШЕНИЕ:

ВЕРНОЕ РЕШЕНИЕ:

ЗАДАЧА

ДРОБЬ

УМНОЖЕНИЕ

ЧИСЛО

• ЗАДАЧА
• ДРОБЬ
• ЧИСЛО
• УМНОЖЕНИЕ

ЦЕЛЬ УРОКА:

• упражняться в нахождении числа от дроби, умножении и сокращении дробей

Куплено 15 кг яблок на приготовление варенья

израсходовали купленных яблок.

Сколько килограммов яблок было израсходовано на

варенье?

Сколько килограммов яблок осталось?

Математика 6 класс. Н.Я.Виленкин. № 543.

В баке автомобиля 60 л бензина. За день

было израсходовано 25 % этого бензина.

Сколько бензина израсходовали?

Сколько бензина осталось в баке?

Математика 6 класс. Н.Я.Виленкин. № 544.

60л

18

Сварили уху

поджарили

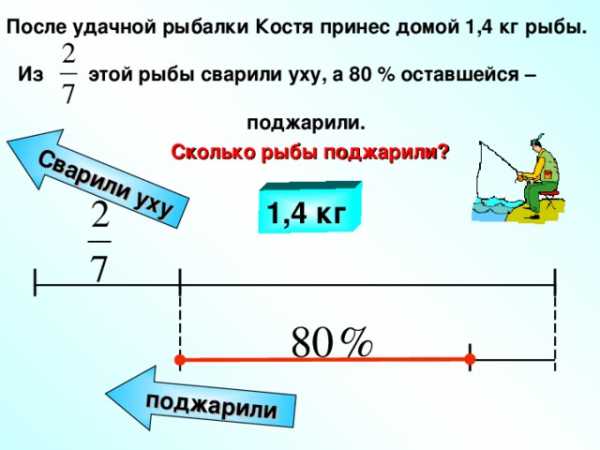
После удачной рыбалки Костя принес домой 1,4 кг рыбы.

Из этой рыбы сварили уху, а 80 % оставшейся –

поджарили.

Сколько рыбы поджарили?

1,4 кг

Математика 6 класс. Н.Я.Виленкин. № 557.

18

ФИЗКУЛЬТМИНУТКА

Съели в 1 раз

Съели на обед

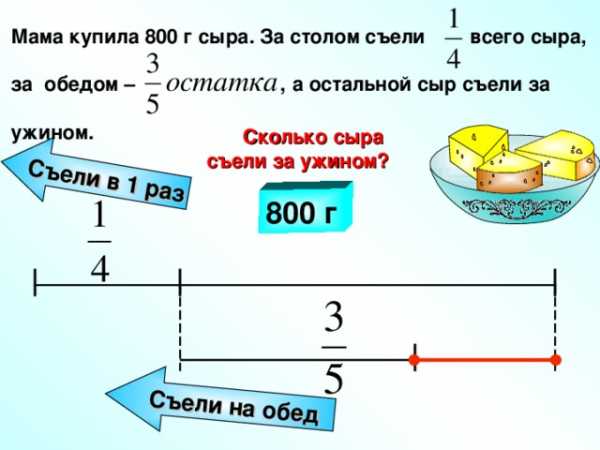
Мама купила 800 г сыра. За столом съели всего сыра,

за обедом – , а остальной сыр съели за

ужином.

Сколько сыра

съели за ужином?

800 г

Математика 5 класс (часть 2). Г.В. Дорофеев, Л.Г. Петерсон. № 677.

21

multiurok.ru

Репетитор по математике о задачах на дроби в 5-6 классе

Задачи на части (на дроби) в 5 — 6 классе, безусловно, тяжелейшая тема для преподавания. Возможно даже самая тяжелая за весь школьный курс. Как может построить свою работу с ней репетитор по математике? Рассмотрим некоторые приемы обучения решению таких задач, опишем связанные с темой проблемы и поговорим о ее дидактике.

Причиной большинства обращений к репетитору в 5 классе является повальное непонимание законов разделения на части. Это естественно, ибо задачи, на которых формируется представление о долях, предъявляют достаточно высокие (для этого возраста) требования к уровню развития ученика, часто связанные с его физиологией. Этот обстоятельство часто не позволяет репетитору математики действовать стандартно, опираясь на традиционые объяснения.

Несмотря на влияние физиогогии родители ребенка обычно стараются повлиять на ситуацию как можно быстрее. Большинству из них нужен репетитор по математике для скорейшего исправления текущей отметки. Иногда это мешает планомерно и неспешно объяснять математические законы и выстраивать темы в логически правильном порядке.

Долгое время я не решался написать об этих задачах. И дело не только в сложности восприятия материала школьниками. В изучении темы выделяется несколько этапов с различными ограничениями в использовании чисел. Не случайно дроби проходят не один год. Программа 5 класса переплетается с программой 6-го класса (а по Петерсону еще и с четвертым). Поэтому даже при одном и том же характере работы преподавателя с дробями разница в индивидуальных особенностях учеников и программах не позволяют описать методы работы репетитора по математике с темой точно и коротко. Более того, в разных учебниках «доли» изучаются в разное время, по-разному «обкладываются» задачами и по-разному интегрируются в дидактику смежных тем. Поэтому очень сложно охватить все проблемы. Надеюсь, что

репетиторы по математике со стажем меня понимают.

Много раз я сталкивался с проблемами задач на дроби и уяснил для себя главное: тема требуют постепенного и долгого изучения. Ее нельзя проработать за один-два урока. Поэтому первое, что я делаю, — объясняю родителям ситуацию и прошу предоставить дополнительные часы для занятий. Не менее двух раз в неделю. Для репетитора по математике это стандартный график, позволяющий в большинстве случаев полноценно заниматься пробелами.

Репетитор по математике о своей методике

Формально мой подход не отличается от того, что предлагают другие репетиторы, а именно — решение задач в большом количестве. Однако к ним еще нужно поготовить ученика, предложить ему некий план или даже алгоритм подбора пути решения. К сожалению, его точность и прозрачность не всегда соответствует желаемому. Репетитор по математике должен понимать, какие задачи и с каким учеником следует разбирать, в каком порядке и в каком количестве. Подходы разных преподавателей могут отличаться порядком разбора задач, пояснениями, терминологией, сопровождениями в рисунках, схемах и даже их полным отсутствием. Я использую собственную базу типовых примеров и наводящих вопросов, систему записей, оформлений и обозначений (немного схожую с Петерсоновской). Оптимизирую краткие записи к задачам, делаю их удобными, информативными и ориентированными на поиск решения.

Попробую изложить …

Разбор элементарных задач

Первый этап работы репетитора — знакомство ученика с базовыми задачами, обучение составлению для них кратких записей. Очень важно вложить в ученика мысль о том, что сложная задача на дроби состоит из нескольких упакованных в нее простых, с определенной последовательных элементарных операций. Их выделением и проработкой репетитор по математике занимается на первом уроке.

Выделяется 3 типа простейших задач на дроби:
1) Целая величина известна
2) Целая величина неизвестна
3) Неизвестна дробь

Для каждой из них подбирается реальная ситуация, которую удобно моделировать рисунком. Распространены примеры деления яблока или плошади. Например: Яблоко имеет массу 160 грамм, найдите вес яблока. Пример стандартный, но подходит не всех ученикам, ибо для проверки правильности демонстрируемых репетитором ариметических действий приходится делить то, что нельзя взять в руки, именно вес. При низком интеллектуальном уровене развития ученика репетитор по математике оказывается бессильным что-либо ему объяснить, ибо проблемы уходят далеко от темы «дроби». Если такое происходит, я использую пример с полом:

Пол выложен одинаковыми плитками как показано на рисунке. На каждую плитку положили по шарику. Сколько шариков лежит на пола?
Преимущество этого примера в том, что ребенок может не только выделить (закрасить) 5/8 пола, но и

пересчитать количество шариков непосредственно. При этом репетитор по математике указывает на возможность ответить на вопрос через простые арифметические действия (на рядах и колонках).

Наводящие вопросы репетитора по математике

Cлабого ребенку можно еще и полдвести к выполнению действий. Для этого репетитор по математике задает ему систему наводящих вопросов, например:

Репетитор: сколько колонок на рисунке?
Ученик: 8 колонок
Репетитор: сколько шариков расположено в одной колонке?
Ученик: 4 шарика
Репетитор: Каким действием это можно найти?
Ученик: 32:8=4
Репетитор: сколько колонок в 5/8 пола?
Ученик: 5 колонок
Рептитор: Если в одной колонке 32:8=4 шарика, то в пяти колонках шаров будет …
Ученик: шариков.
Привильно !!!!!

Главное преимущество задачи на плитки и шарики состоит в использовании арифметических действий, каждое из которых удается проверить простым пересчетом. После того, как репетитор по математике убедился в понимании действий, он диктует ученику проверенное правило: «делим на знаменатель и умножаем на числитель».

Несмотря на то, что можно пересчитывать количество не шариков, а самих плиток, я намеренно оставляю шары в сюжете задачи. Почему? На их примере изучается ситуация, когда какой-нибудь целый объект удерживает внутри себя (или на себе) мелкие объекты (в нашем случае пол удерживает шарики). Это широко распространено в дидактике математики 5-6 класса. Часто что-то куда-то засыпается, заливается, вкладывается и равномерно распределяется по объекту. В мешки засыпают сахар, в бидоны заливают молоко и т.д. Репетитор по математике на примере шариков помогает ребенку быстрее разобраться в числовых особеннностях этих ситуаций и понять законы измерения частей объектов.

Далее … На том же рисунке с шариками нужно поставить обратную задачу: Допустим, мы знаем, что на 5/8 пола лежит 20 шаров. Как найти их общее количество? И здесь репетитору по математике тоже помогает рисунок, на котором можно просто пересчитать кружочки. Легко подбирать и комментировать выполняемые действия: . Все ясно и прозрачно. Наводящие вопросы (если они нужны) аналогичны первому случаю.

Репетитору по математике важно остановиться на терминологии и оформлении краткой записи.От того, насколько как она будет зависит идентификация правил. Ученик должен усвоить, что целый объект — это такая же величина, как и его часть, измеряемая двумя единицами: привычной (метрами, сантиметрами, килограммами, литрами, страницами, деревьями, шариками и т.д.) и «особой». В роли последней выступает целая величина. Рядом с ней в кратких записях можно поставить 1ед. Все участники элементарной задачи получают названия. То, от чего ищется часть называется целой величиной, сама дробь так и остается дробью, а часть, которую находят от целого репетитор по математике называет «частью» или «значением» дроби». Я предпочитаю второй вариант.

Как правило, к репетитору обращаются в момент, когда тема набрала обороты и в классе решают в перемешку задачи на разные базовые правила. Поэтому, их приходится включать в один урок. Если ребенок не самый слабый, то вместо плиток я применяю яблоко, причем с одним и тем же набором значений величин для всех типов задач. Выписываю из образцы в отведенную для этого теоретическую тетрадь (или на форзац рабочей тетради). Каждую запись отдельно комментирую и специальным образом оформляю:
Задача 1-го типа: целая величина известна.
(г) -вес части яблока.
Чтобы найти значение дроби нужно целую величину разделить на знаменатель и умножить на числитель.

Задача 2-го типа: целая величина неизвестна.
(г) — вес яблока.
Чтобы найти целую величину нужно значение дроби разделеить на числитель и умножить на знаменатель.

Задача 3-го типа: неизвестна дробь.
(яблока) -вес его части

В третьей задаче для 5 класса репетитором по математике должны быть выбраны другие числа, ибо сократить дробь пятиклашки еще не могут. Обратите внимание на то, что обыгрывается один и тот же комплект чисел. В первой задаче репетитор по математике находит целого яблока, а во второй выполняет обратные действия: по той же дроби и найденному ранее значению 100 восстановливает число 160 (его даже можно в определенный помент стереть ластиком). Прием обратных действий полезен для работы с невнимательными школьниками. Он позволяет быстро сконцентрироваться на правилах, а не на изучении нового условия новой задачи. Более того, при заранее изветном ответе ребенок убеждается в правильности выбора этих действий. Действительно, как можно в них усомниться, если репетитор по математике получает в ответе то, что и должно получиться?

Под каждой краткой записью оформляется решение и записывается правило:

1) чтобы найти значение дроби, нужно целую величину разделить на знаменатель и умножить на числитель.
2) Чтобы найти целую величну нужно разделить на числитель и умножить на знаменатель.
3) Чтобы найти дробь нужно разделить ее значение на целую величину.

Как репетитор математики работает с комбинированными задачами

Чаще всего они встречаются в 6 классе, хотя в учебнике Петерсона сочетания двух и даже трех типов задач предлагаются уже в 5 классе. Прежде всего ученик должен знать с чего начинать исследование задачи. Важно отработать каждый его этап в отдельности.

Краткая запись

Краткая запись к задаче — важнейший и незаменимый элемент методики любого хорошего репетитора по математике. Она является одновременно и опорой и средством заставить ученика перечитывать условие как минимум — два три раза. Правильно составленная краткая запись в сочетании с четкими правилами «трех типов» позволяют разложить комбинированную задачу на несколько элементарных. Поэтому репетитору чрезвычайно важно научить правильно ее составлять.

Как репетитор по математике работает с текстами?
Главной проблемой составления краткой записи является проблема анализа текста задачи. Практика показывает, что дети крайне невнимательно и низкоэффективно с ним работают. Не умеют выделять ценную информацию о величинах и сами величины, сортировать главное и второстепенное. Для борьбы с такими проблемами репетитор математики может взять на вооружение метод слежения. Что такое краткая запись? — всего лишь короткий текст условия, из которого выброшены лишние слова, а названия величин и их значения записаны отдельными строками. Что мешает репетитору по математике выделять эти слова в тексте? Особенно важно научить поиску целых величин, на которые в краткой записи будут указывать стрелки. Репетитор должен обратить внимание ученика на то, что слово или фраза, написанная сразу после дроби, указывает на единицу измерения дроби, то есть на ее целую величину. Репетитору по математике никто не запрещает выделить ее в тексте (подчеркнуть или записать другим цветом) и поставить к ней стрелочку. Пример оформления:

Если внимание ребенка ослаблено, на первых порах ему лучше предлагать уже размеченные тексты, с выделенными целыми величинами и стрелочками.

Для того, чтобы не пропустить ни одну из участвующих величин репетитору по математике нужно задать вопрос: Что в задаче можно измерить? Пок ученик думато, репетитор подчеркивает в тексте соответствующие им слова. В нашем случае это показано синим цветом.

Важно отработать поиск и применение типовых задач внутри комбинированной. Дети часто путают когда им делить на знаменатель, а когда на числитель. В 6 классе путают умножать ли на дробь или делить на нее. Проблема усугубляется когда в задачу встревает еще и сумма (разность) величин. Ребенок пытается запомнить эти ситуации, но от их многообразия пухнет голова. Чем может помочь ему репетитор по математике? Самое эффективное запоминание — зрительное. При многократном зрительрном анализе ребенок «фотографирует» расположение известных и неизвестных компонент выделенных репетитором строк (связанных «дробной стрелкой») и распознает эту же комбинацию величин в другой задаче. по нему в другой задаче что именно надо лелать. Для увеличения числа обращений к правилам типовых задач я рекоментдую репетиторам по математике использовать визуальные образы задач (без текстов). Репетитор подает ученику задачу ее краткой записью с полной информацией о всех известных взаимосвязях между величинами . Сложности возникают с суммами нескольких величин. В таком случае репетитору по математике приходится искать дополнительные обозначения для суммы. Я решил это пробьлему так: поле суммы закрашивается, а поля ее слагаемых обводятся тем же цветом по периметру. Очень удобно. Если какое-то из слагаемых тоже равно сумме других, более мелких величин, то его внутренняя частсь закрашивается другим цветом, а поля слагаемых этим же цветом обводятся по контуру. И таких вложений может быть сколько угодно.

Например, краткая запись к задаче про вишню может быть следующей:

Попрбуйте составить краткую запись к олимпиадной задачке: мама испекла булочки. Аня съеха 2/3 всех булочек и еще 2. Петр съел 2/3 остатка и еще 2 булочки, а Денис съел 2/3 последнего остатки и последние 2 булочки. Сколько булочек испекла мама?

Александр Николаевич, репетитор по математике Москва (м.Щукинская, Строгино)

Метки: Работа репетитора, Репетиторам по математике

ankolpakov.ru

Задачи на дроби 6 класс с решением и ответами сложные

Задача №1557. Найдите с помощью микрокалькулятора объём прямоугольного параллелепипеда по формуле V = abc, если а = 2,81 дм; b = 1,76 дм; с = 4,9 дм; ответ округлите до сотых. Решение задачи №1557: а) Если а=987,25 см; b=68,76 см; с=4 ,14 см V=abc=987,25•68,76•4,14=281036,9034 см³ ?281037.

Задачи на дроби

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на дроби.

Прежде чем решать задачи на дроби, необходимо досконально изучить все темы, касающиеся дробей. Ниже приведен список уроков, которые можно повторить.

Каждая задача, приведенная в данном уроке, относится к категории элементарных. Если какая-то задача непонятна, это указывает на то, что предыдущий материал усвоен недостаточно хорошо.

Задачи на дроби

24 : 6 × 1 = 4 × 1 = 4 (отличника)

24 : 6 × 3 = 4 × 3 = 12 (хорошистов)

24 : 6 × 2 = 4 × 2 = 8 (троечников)

4 + 12 + 8 = 24 (школьника)

16 : 4 × 1 = 4 × 1 = 4 (отличника)

16 : 16 × 12 = 1 × 12 = 12 (хорошистов)

16 : 8 × 1 = 2 × 1 = 2 (отличника)

16 : 16 × 10 = 1 × 10 = 10 (хорошистов)

16 : 4 = 4 (троечника)

Теперь найдем массу кормовых отходов. Для этого вычтем из 500 ц массу полтавской крупы:

Значит из 500 центнеров зерен пшеницы можно получить 320 центнеров полтавской крупы и 180 центнеров кормовых отходов.

44 × 1 = 44 рубля

22 × 1 = 22 рубля

В одном килограмме фиников содержится 720 грамм сахара. Чтобы узнать сколько грамм сахара содержится в четырех килограммах, нужно 720 умножить на 4

В одном килограмме фиников содержится 15 грамм минеральных солей. Чтобы узнать сколько грамм минеральных солей содержится в четырех килограммах, нужно 15 умножить на 4

Значит в 4 кг фиников содержится 2880 грамм сахара и 60 грамм минеральных солей.

Решение для данной задачи можно записать значительно короче, двумя выражениями:

А поскольку весь путь состоит из семи частей, то расстояние всего пути можно найти, умножив 210 на 7:

210 × 7 = 1470 км.

Теперь ответим на второй вопрос задачи — какое расстояние осталось пройти поезду? Если длина пути 1470 км, а пройдено 840, то оставшийся путь равен 1470−840, то есть 630

45 : 9 × 140 = 5 × 140 = 700

Узнаем сколько составляют учебники по математике:

900 : 25 × 8 = 288 (книг по математике)

Узнаем сколько учебников по русскому языку:

900 : 100 × 33 = 297 (книг по русскому языку)

Узнаем сколько учебников по литературе. Для этого из общего числа книг вычтем учебники по математике и по русскому:

900 – (288+297) = 900 – 585 = 315

288 + 297 + 315 = 900

180 : 9 × 5 = 100 (страниц)

Во второй день Вера прочитала на меньше, чем в первый. Найдем от 180 страниц, и вычтем полученный результат из 100 листов, прочитанных в первый день

180 : 6 × 1 = 30 × 1 = 30 (страниц)

100 − 30 = 70 (страниц во второй день)

180 : 18 × 7 = 10 × 7 = 70 (страниц)

Теперь ответим на второй вопрос задачи — успела ли Вера прочитать все 180 страниц за два дня. Ответ — не успела, поскольку за два дня она прочла только 170 страниц

100 + 70 = 170 (страниц)

180 : 18 × 1 = 10 × 1 = 10 (страниц)

1000 : 2 × 1 = 500 × 1 = 500 г

1000 : 5 × 1 = 200 × 1 = 200 г

Во втором пакете на 200 граммов меньше, поэтому чтобы определить массу второго пакета, нужно из 500 г вычесть 200 г

500 − 200 = 300 г

Ну и напоследок сложить массы обоих пакетов:

500 + 300 = 800 г

24 : 4 × 7 = 6 × 7 = 42 км

42 : 7 × 3 = 6 × 3 = 18 км

Зная, что пути составляют 42 километра, мы можем найти длину всего пути:

42 : 3 × 4 = 56 км

Значит длина пути от турбазы до озера составляет 56 километров. Сделаем проверку. Для этого сложим все пути, пройденные туристами в каждый из четырех дней.

Сначала найдем путь пройденный в первый день:

56 : 4 × 1 = 14 (в первый день)

14 + 18 + 12 + 12 = 56

Задача из арифметики известного среднеазиатского математика Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.)

«Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10»

Изобразим число, которое мы хотим найти, в виде отрезка, разделенного на три части. В первой части отрезка отметим треть, во второй — четверть, оставшаяся третья часть будет изображать число 10.

Сложим треть и четверть:

Зная, что пять двенадцатых числа составляют число 10, мы можем найти всё число:

10 : 5 × 12 = 2 × 12 = 24

Мы нашли всё число — оно равно 24.

Эту задачу можно решить не приводя рисунков. Для этого, сначала нужно сложить треть и четверть. Затем из единицы, которая играет роль неизвестного числа, вычесть результат сложения трети и четверти. Затем по полученной дроби определить всё число:

80 : 40 × 7 = 14 (тыс. на еду)

80 : 20 × 1 = 4 × 1 = 4 (тыс. на коммунальные услуги)

80 : 20 × 1 = 4 × 1 = 4 (тыс. на Интернет и ТВ)

80 : 20 × 3 = 4 × 3 = 12 (тыс. на лечение и походы по врачам)

80 : 10 × 1 = 8 × 1 = 8 (тыс. на пожертвование в детский дом)

80 : 20 × 3 = 4 × 3 = 12 (тыс. на проживание в съемной квартире)

80 : 40 × 13 = 2 × 13 = 26 (тыс. в копилку)

14 + 4 + 4 + 12 + 8 + 12 + 26 = 80

Определим длину пути, пройденного туристами за второй час. Для этого к 3 км 700 м нужно прибавить 1 км 200 м

3 км 700 м + 1 км 200 м = 3700м + 1200м = 4900м = 4 км 900 м

Определим длину пути, пройденного туристами за два часа:

3 км 700 м + 4 км 900 = 3700м + 4900м = 8600м = 8 км 600 м

Значит за два часа туристы прошли 8 километров и еще 600 метров. Решим эту задачу с помощью дробей. Так её можно значительно укоротить

Сложим части пути, пройденные в первый и во второй день:

28 : 4 × 9 = 7 × 9 = 63 км

63 : 9 × 5 = 7 × 5 = 35

63 : 9 × 4 = 7 × 4 = 28

Задача 20. Для приготовления крема использовали сливки, сметану и сахарную пудру. Сметану и сливки составляют 844,76 кг, а сахарная пудра и сливки 739,1 кг. Сколько в отдельности сливок, сметаны и сахарной пудры содержится в 1020,85 кг крема?

Сметана и сливки — 844,76 кг

Сахарная пудра и сливки — 739,1 кг

Вытащим из 1020,85 кг крема сметану и сливки (844,76 кг). Так мы найдем массу сахарной пудры:

1020,85 кг — 844,76 кг = 176,09 (кг сахарной пудры)

Вытащим из сахарной пудры и сливок сахарную пудру (176,09 кг). Так мы найдем массу сливок:

739,1 кг

poiskvstavropole.ru

Задачи на дроби для 6 класса

Просмотр содержимого документа
«Задачи на дроби для 6 класса»

В столовую

На рынок

№ 528.С бахчи собрали 27 т арбузов.

В столовую направили этих

арбузов, а остатка отвезли

на рынок. Сколько тонн арбузов

отвезли на рынок ?

отвезли на рынок ?

Математика 6 класс. Н.Я.Виленкин. № 512.

РЕШЕНИЕ:

ВЕРНОЕ РЕШЕНИЕ:

За три дня на элеватор доставили 651 т зерна.

В первый день было доставлено

всего зерна .

Во второй 0,9 того, что было доставлено в первый день.

№ 514 . Математика 6 класс. Н.Я.Виленкин.

?

Сколько тонн зерна было доставлено на элеватор в третий день?

РЕШЕНИЕ:

ВЕРНОЕ РЕШЕНИЕ:

ЗАДАЧА

ДРОБЬ

УМНОЖЕНИЕ

ЧИСЛО

• ЗАДАЧА
• ДРОБЬ
• ЧИСЛО
• УМНОЖЕНИЕ

ЦЕЛЬ УРОКА:

• упражняться в нахождении числа от дроби, умножении и сокращении дробей

Куплено 15 кг яблок на приготовление варенья

израсходовали купленных яблок.

Сколько килограммов яблок было израсходовано на

варенье?

Сколько килограммов яблок осталось?

Математика 6 класс. Н.Я.Виленкин. № 543.

В баке автомобиля 60 л бензина. За день

было израсходовано 25 % этого бензина.

Сколько бензина израсходовали?

Сколько бензина осталось в баке?

Математика 6 класс. Н.Я.Виленкин. № 544.

60л

18

Сварили уху

поджарили

После удачной рыбалки Костя принес домой 1,4 кг рыбы.

Из этой рыбы сварили уху, а 80 % оставшейся –

поджарили.

Сколько рыбы поджарили?

1,4 кг

Математика 6 класс. Н.Я.Виленкин. № 557.

18

ФИЗКУЛЬТМИНУТКА

Съели в 1 раз

Съели на обед

Мама купила 800 г сыра. За столом съели всего сыра,

за обедом – , а остальной сыр съели за

ужином.

Сколько сыра

съели за ужином?

800 г

Математика 5 класс (часть 2). Г.В. Дорофеев, Л.Г. Петерсон. № 677.

21

multiurok.ru

Урок по математике на тему «Основные задачи на дроби» (6 класс)

Этапы урока

Организации

Актуализации знаний и умений

Личностные. Прогнозирование и саморегуляция на основе ложной аналогии. Коммуникативные. работа в парах. Совместное решение.

Целеполагания

Регулятивные, личностные. Работа с определениями, с контрпримерами. Работа с гипотезами.

Анализ речевых конструкций

Использование нового алгоритма и приведение аргументов

Познавательные. Работа с учебниками. Формирование регуляторного опыта: прогнозирование, оценивание.

Наблюдение, сравнительный анализ.

Коммуникативные.Выполнять практическую работу с использованием нового теоретического факта.

Целеполагания

Познавательные, метапредметные и регулятивные. с определениями, с контрпримерами. Работа с гипотезами.

Анализ речевых конструкций

Использование нового алгоритма и приведение аргументов

Формирование регуляторного опыта: прогнозирование, оценивание.

Наблюдение, сравнительный анализ.

Выполнять практическую работу с использованием нового теоретического факта.

Целеполагания

Личностные. Работа с определениями, с контрпримерами. Работа с гипотезами.

Анализ речевых конструкций

Использование нового алгоритма и приведение аргументов

Формирование регуляторного опыта: прогнозирование, оценивание.

Наблюдение, сравнительный анализ.

Выполнять практическую работу с использованием нового теоретического факта.

Информирования о домашней работе

Познавательные и регулятивные. Развитие навыков нахождения закономерностей.

Знакомство с табличными способами систематизации.

Планирование и прогнозирование, самоопределение через выбор

Приобщение к заботливому отношению к близким. Эстетическое восприятие геометрических форм.

Работа с инструкцией.

Применение знаний в решении практической задачи.

Рефлексия

Коммуникативные. Давать оценку проделанной работе, оценивать, целесообразность, объяснять причины успехов и неудач.

Этапы урока

Задачи этапа

Визуальный ряд

Деятельность учителя

Деятельность учащихся

Организации

Определить цель занятия

На доске дата и название темы: «Основные задачи на дроби»

На столах учащихся открыт учебник с. 16-17. «Вы узнаете» (учитель просит вначале урока открыть)

— Ребята, мы уже с вами знаем что такое дроби. Приведите примеры дробей.

Приводят примеры дробей

Какие действия с дробями мы можем выполнять?

— сокращать дроби;

— приводить дроби к новому знаменателю;

-складывать и вычитать дроби.

— Слева на странице учебника 16 обозначена цель сегодняшнего занятия – давайте узнаем, что мы еще можем сделать с помощью дробей?

Читают рубрику.

Отвечают:

-находить часть от числа;

-находить число по его части;

-как узнать, какую часть одно число составляет от другого.

Актуализации знаний и умений

Продемонстрировать необходимость знания точного определения

Презентация на ИД

Давайте вспомним и посчитаем устно примеры с дробями

Выполняют устные упражнения и сразу проверяют правильность своих действий

Целеполагания

Объяснение материала

Презентация на ИД

Рассмотрим пример: квадрат разделен на 4 равные части. Одна часть заштрихована.Какая часть квадрата заштрихована?

А если площадь этого квадрата – 16см², найдите площадь заштрихованной части.

16:4*1=4см²

Площадь прямоугольника 12 см². прямоугольника заштрихованы. Какова площадь заштрихованной части?

12: 3 *2 = 8 см²

Работа с учебником

Решим задачу 1 из учебника.

Читают условие задачи самостоятельно.

— Сколько всего жителей в городе?

80 тыс. человек.

— Какая часть всех жителей города борются против загрязнения окружающей среды?

— Сколько жителей участвуют в движении «Гринпис»?

Находят ответ, используя понятие дроби.

(80 000 : 5) * 2 = 32 000(чел)

Эту задачу можно решить другим способом, по правилу нахождения части от числа. Прочитаем это правило.

Дети читают правило нахождения части от числа.

Решим задачу, используя правило.

80000*

Использование нового алгоритма и приведение аргументов

Закрепление и отработка алгоритма.

Работа с учебником

Решим , используя полученные знания

№35 (а – в),

№ 37 (а)

В тетрадях решают задания, по окончании решения проверяем, называя ответы, если есть необходимость, уточняя решение.

Целеполагания

Объяснение материала

Рассмотрим другой пример: квадрат разделен на 4 равные части. Одна часть заштрихована и её площадь равна 5 см² Какова площадь всего квадрата?

5*4=20см²

Ещё один пример.

Прямоугольник разделен на 3 равные части. Заштрихованы 2 части, и их площадь 8 см². Найти площадь прямоугольника.

8 : 2 * 3 = 12см²

Работа с учебником.

Рассмотрим задачу 2 из учебника.

Читают условие задачи самостоятельно.

— Сколько жителей города присоединились к движению «Гринпис»?

32 тыс. жителей

-Какую часть они составляют от всех жителей города?

Эту задачу можно решить другим способом, по правилу нахождения числа по его части. Прочитаем это правило.

Дети читают правило нахождения числа по его части.

Решим задачу, используя правило.

Использование нового алгоритма и приведение аргументов

Закрепление и отработка алгоритма.

Работа с учебником

Решим , используя полученные знания

№41 (а – в),

№ 42 (а)

В тетрадях решают задания, по окончании решения проверяем, называя ответы, если есть необходимость, уточняя решение.

Целеполагания

Объяснение материала

Решим устно задачи:

1 В классе 26 учащихся, из них 13 посещают кружок математики. Какую часть класса составляют учащиеся, которые посещают кружок?

13 : 26 =

2 В парке «Победы» ветераны ВОВ посадили к празднику 35 саженцев деревьев, 14 из них берёзы. Какую часть саженцев составляют берёзы?

14 : 35 =

Работа с учебником

Мы познакомились ещё с одним видом задач на дроби – нахождение части одного числа от другого.

Читаем правило.

Дети читают правило нахождения части одного числа от другого.

Работа с учебником

Рассмотрим задачу 3.

Читают условие задачи самостоятельно.

— Сколько человек проживает в городе Синегорске?

80 000 человек

— Сколько из них присоединились к движению «Гринпис»?

32 000 человек

-Определите какая часть жителей присоединились к движению «Гринпис»?

Один человек — это

Тогда 32000 чел.-

Использование нового алгоритма и приведение аргументов

Закрепление и отработка алгоритма.

Работа с учебником

Решим , используя полученные знания

№45 (а, б, в),

№ 46 (б)

В тетрадях решают задания, по окончании решения проверяем, называя ответы, если есть необходимость, уточняя решение.

Рефлексии

Показать способ аргументирования ссылкой на верный факт

Работа с учебником

№ 34 из учебника.

Привести учащихся к выводу.

По ходу чтения упражнения, учащиеся рассуждают и приходят к выводам:

Чтобы найти половину некоторого числа, нужно его разделить на 2 или умножить на .

Чтобы найти четверть некоторого числа, нужно его разделить на 4 или умножить на .

Информирования о домашней работе

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.

Работа с учебником

Работа с тетрадью — тренажёром

№ 36, № 38, — обязательное задание

№ 39 для увлекающихся

№ 42 (б), № 47 — обязательное задание

№ 44, № 48 для увлекающихся

Записывают задание

На партах открыты стр. 16-17 учебника, на экране тоже -рубрика «Вопросы и задания»

— На какой из вопросов «Вы узнаете» вы получили ответ сегодня на уроке, а на какие вопросы раздела «Вопросы и задания» вы можете теперь ответить.

Указывают, читают и отвечают на вопросы

рубрики

— Из рубрики «Вы узнаете»: как найти часть от числа

Чтобы найти часть от числа, нужно это число умножить на данную дробь

Как найти число по его части?

Чтобы найти число по его части, нужно эту часть разделить на дробь ей соответствующую

Как найти какую часть составляет одно число от другого?

Чтобы узнать какую часть одно число составляет от другого, надо первое число разделить на второе.

Из рубрики «Вопросы и задания»:

а) найдите от числа 600

б) найти число, если этого числа составляют 28

в) найти какую часть число 24 составляет от числа 54?

а) 1000;

б) 49;

в) ;

infourok.ru

Урок по математике на тему » Решение задач на дроби» 6 класс

Комитет по образованию Администрации г. Улан- Удэ

МАОУ « Средняя общеобразовательная школа № 42»

План – конспект урока в 6 классе по теме:

« Решение текстовых задач на дроби.»

Составлен: Береговой Татьяной Михайловной,

учителем математики МАОУ СОШ № 42

г.Улан — Удэ 2014 г.

Урок систематизации и обобщения знаний в 6 классе по теме:

« Решение текстовых задач на дроби».

Основные цели:

1. обобщение, систематизация и коррекция знаний по решению основных трех видов задач на дроби;

2. развитие логического мышления, умения анализировать условие задачи для выбора верного, рационального способа решения;

3. воспитание у учащихся аккуратности, трудолюбия, упорства в достижении цели, взаимопонимания;

4. развитие коммуникативных навыков: уметь слушать друг друга, аргументировать и отстаивать свою точку зрения, работать в группах, осуществлять взаимопомощь.

Оборудование на уроке:

индивидуальные доски учащихся для устного счета, папки с заданиями , инструкции, альбомные листы и клей – карандаш для каждой из групп.

План урока:

1. Организационный момент (3 мин)

2. Этап подготовки учащихся к активному усвоению знаний (7 мин)

Устный счет + фронтальная работа.

3. Этап обобщения и систематизации изученного (30 мин)

Групповая работа « Построй свой дом».

4. Итог урока и информация о домашнем задании ( 5 мин ).

Ход урока.

1. Организационный момент:

« Здравствуйте, ребята! Сегодня на уроке мы с вами будем строителями, мы будем строить свои дома. Каждая группа это строительная бригада. Чтобы построить дом, вам надо вспомнить способы решения задач на дроби, выбрать нужный способ решения задачи и решить ее. Кто будет самой дружной, трудолюбивой бригадой мы узнаем в конце урока! Начнем урок с подготовки к стройке.

2. Устный счет. Работа с индивидуальными досками.

а/ Учащиеся решают примеры из № 605, записывая на досках только ответы. Все номера взяты из учебника « Математика 6» ( см. список литературы). Ответы показываются учителю. Очень хорошая обратная связь, видно кто затрудняется при вычислении, где делают ошибки. Учащиеся и сами могут себя проверить, после указания правильных ответов.

№ 605

а) 184 -112

:8

+45

:3

?

б) 700 : 14

+90

:18

?

в ) 0,64 : 0,8

+ 2,8

: 100

?

г ) 3,6

: 0,6

+ 3,6

: 1,4

?

д ) 1 – 0,44

: 0,7

0,5

— 0,12

?

Ответы:

а ) 72

9

54

18

б) 50

450

540

30

в ) 0,8

7,2

10

0,1

г ) 0,36

0,6

4,2

3

д ) 0,56

0,8

0,4

0,28

б/ Найти 7/9 от 36 (28 ) , найти 0,5 от 6 ( 3 ), найти 20% от 4 ( 0,8 ).

К какому виду задач на дроби относится задание? Как решить?

( Нахождение дроби от числа. Выполняем умножение числа на дробь.)

Найдите число, если 2/5 его равны 16 (40 ), найдите число , если 0,4 равны 44 (110), найдите число, если 10% его равны 6 ( 60 ).

К какому виду задач на дроби относится задание? Как решить?

(Нахождение числа по его дроби. Выполняем деление. )

Какую часть составляет 20 минут от часа? ( 1/3 )

Какую часть составляет 3 суток от недели ? ( 3/7 )

Какую часть составляет 13 см от метра ? ( 13/100 )

Какую часть составляет 57 м от километра ? ( 57/1000 )

К какому виду задач на дроби относится задание? Как решить?

( Задача на отношения. Составляем отношение двух чисел. )

3. Групповая работа: « Построй свой дом.»

В папке группы находятся нарезанные из цветной бумаги части дома. На обратной стороне элементов дома указаны номера задач и количество баллов.

Учащиеся разбиты на дифференцированные группы по уровню своих способностей. Основное задание — 3 задачи даются по уровню сложности А,В,С.

Дополнительные задачи также различного уровня сложности, но выбирают их учащиеся сами по своим возможностям и желанию. Решив задачу группа должна проверить решение у учителя или консультанта . Только после этого она имеет право наклеить элемент дома на альбомный лист, зафиксировать баллы, отметить автора идеи, предложившего способ решения или решившего задачу. Решение задач оформляется в рабочей тетради учащегося.

Группы разбиты по 4 – 5 человек в зависимости от количества в классе. Обычно это 5 -6 групп. Способ работы в группе учащиеся выбирают сами или решают каждую задачу вместе, или каждый берет по задаче решает и затем обсуждают решение. Необходимо, чтобы учащиеся помогали друг другу. Учитель контролирует работу учащихся, проверяет правильность решения, помогает найти верное решение в случае затруднения, так как эта работа объемная, то желательно выбрать 2 консультантов из числа сильных учащихся закрепив за ними группы с которыми они будут работать. Заранее дать им возможность прорешать задачи, обсудить возможные способы решения, чтобы на уроке они имели право проверять и оценивать группы. Обязательно оценив их работу в конце урока.

Обязательное задание для групп:

Группы А Крыша — № 648 (30 б ), дом — № 548 ( 30 б), окно — №721 ( 30 б).

Группы В Крыша — № 714 ( 20 б ), дом — № 543 ( 20 б ), окно — № 696 ( 20 б).

Группы С Крыша — № 692 ( 10 б ), дом — № 545 (10 б), окно — № 713 ( 10 б).

Дополнительные задачи:

Солнце — № 486 ( 30 б)

Дерево — № 488 ( 30 б)

Дерево — № 645 ( 30 б)

Труба — № 557 (2 0 б)

Бабочка — № 644 (20 б)

Забор — № 712 ( 10 б)

Забор — № 695 ( 10 б)

Забор — № 507 ( 10 б)

Забор — № 479 ( 10 б)

Петров С.

Иванова Л.

Орлов АА.

Смирнов А.

Инструкция для учащихся:

1. Распределите задания по мере своих сил.

2. Решение задач оформляйте в рабочей тетради.

3. Решив задачу и обсудив ее в группе, проверьте ваше решение у учителя или консультанта.

4. Если решение верно, элементы дома наклейте на альбомный лист. Укажите автора решения.

5. Отметьте в тетради количество набранных вами баллов.

6. Оцените себя по данным критериям:

Оценка «5»- от 90 баллов -…

Оценка «4» — от 60 — 89 баллов.

Оценка «3» — от 30 – 59 баллов.

4. Итог урока и информация о домашнем задании:

Подведем итог нашей работе. Кто же оказался самой лучшей бригадой и построил самый красивый дом? ( Учащиеся показывают свои работы. Наглядно видно, кто прорешал задач больше.) Молодцы! Оцените себя по критериям в данных вам инструкциях. Окончательные результаты я объявлю на следующем уроке после просмотра ваших работ.( Необходимо проверить объективность оценки, бывает, что некоторые учащиеся или занижают оценки , или завышают.) Дома прошу вас придумать свои три задачи , по одной на каждый вид задач на дроби. Буду оценивать оригинальность, сложность и правильность решения. Спасибо всем за урок !

Список используемой литературы на уроках в 6 классе:

1. Н.Я.Виленкин, В.И.Жохов, А.С. Чесноков, С.И. Шварцбурд « Математика 6» ,

изд-во « Мнемозина», Москва 2002г.

2. Е.Е Тульчинская «Математика. Тесты 5-6».

infourok.ru

Разработка урока математики в 6 классе по теме «Две основные задачи на дроби» с презентацией.

Класс: 6б

Предмет:  Математика

Тема и номер урока в теме «Нахождение числа по его дроби и дроби от числа» (второй урок в теме из четырех)

Цель урока: 

Научиться решать задачи на нахождение дроби от числа и числа по его дроби.

Задачи:

(формирование предметных и познавательных УУД)

— выражают структуру задачи разными средствами. Выбирают, сопоставляют и обосновывают способы решения задачи;

— формировать навыки составления обратных задач;

(формирование коммуникативных и личностных УУД)

— формирование интереса к способам решения новых учебных задач, положительной оценки и самооценки результатов учебной деятельности;

— оформление мысли в устной и письменной речи с учетом речевых ситуаций

(формирование регулятивных УУД )

— определение цели учебной деятельности, осуществление поиска средств ее достижения.

Тип урока: 

Поисково-исследовательский

Используемые учебники и учебные пособия: 

Математика. 6 класс: учеб. для общеобразоват. учреждений / Н. Я. Виленкин, В. И.  Жохов, А. С. Чесноков, С. И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2012.

Используемая методическая литература: 

Поурочные разработки по математике: 5 класс. / Л. П. Попова – М.: ВАКО, 2012. – 496 с. – (В помощь школьному учителю).

Используемое оборудование: 

мультимедиапроектор, компьютер, презентация к уроку.

 

 

Краткое описание: 

 Урок математики 6 класс тема » Нахождение числа по его дроби и дроби от числа » второй урок по теме , включает в себя повторение правил нахождения дроби от числа и числа по его дроби, групповую работу по решению текстовых задач на нахождение части от целого и целого по его части, составление и решение обратных задач.

Ход урока

 1.Организационный момент. Распределение на группы, выбор командира, оформление тетрадей.

2.Вывод темы урока Слайд 1

Анализ условия двух задач, ответы на вопросы

Формулирование темы урока.

Какие вопросы у вас возникли после определения данной темы

3. Фронтальная работа по теме урока. Слайд 2

Решение задач на нахождение дроби от числа и числа по его дроби.

Памятка с вопросами, помогающими определить тип задачи.

4. Работа в группах: Решение задач различного типа, составление и решение обратных задач.

Ответы к задачам: 614. 24 км, 615 – 477 р, 616 – 132 бабочки, 618 – 192 мальчика.

Составление обратных задач.

Отчет групп по составленным задачам.

Оценивание в группе.

5. Физкультминутка.

6 Индивидуальная работа

Командиры выдают индивидуальные задания каждому в группе. Работа выполняется на отдельном листке.

 №1. Велосипедист проехал 15 км, что составило всего пути. Каков весь путь?

№ 2.  Мама посадила 6 грядок, что составило всех грядок. Сколько всего грядок посадила мама?

№ 3. В саду посадили 16 деревьев. всех деревьев – яблони. Сколько яблонь в саду?

№ 4. Туристы планировали пройти за 2 дня 24 километра. В первый день они прошли пути.

Сколько километров прошли туристы в первый день?

№ 5. В первый день Лиза прочитала книги, что составило 24 страницы. Сколько страниц в книге?

 

    7. Подведение итогов урока Слайд №

1. Какие основные задачи на дроби вы знаете?

2. Какие вопросы вы должны задать себе, чтобы определить тип задачи и способ ее решения?

3. Как решить задачу на нахождение дроби от целого?

4. Как решить задачу на нахождение числа по его дроби?

 .     Домашнее задание: №680, составить и решить обратную задачу.

№678(а,б).

   8. Рефлексия

Притча. Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?» и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»

• Ребята! Давайте мы попробуем каждый с вами оценить свою работу за урок.

• Кто работал так, как первый человек? (поднимите одну руку)

• Кто работал добросовестно? (поднимите две руки)

• Кто принимал участие в строительстве храма? (встаньте)

 

infourok.ru