Решение задач по комбинаторике
специальность 35.02.12 «Садово-парковое и ландшафтное строительство»
группа СП-17
курс 1
Технологическая карта учебного занятия
Занятие № 26
по дисциплине Математика: алгебра и начала математического анализа; геометрия
Количество часов 2
Цель занятия: выработать у обучающихся умения решения комбинаторных задач.
Задачи:
Образовательные:
— обобщить и систематизировать знания обучающихся по теме «Основные понятия комбинаторики»;
— совершенствовать навыки решения комбинаторных задач
Развивающая:
— развивать аналитические способности, логическое мышление,
— формирование умения анализировать, выделять главное, обобщать и делать выводы.
Воспитательная:
— формирование у обучающихся ответственного отношения к обучению, культуры общения.
Тип занятия: комбинированное
Вид занятия: практикум
Форма обучения: фронтальная, индивидуальная
Метод обучения: репродуктивный, словесный, наглядный
Методы контроля: устный, письменный
Ход занятия
I. Организация и мотивация (5 мин)
Проверка готовности обучающихся и кабинета к занятию, проверка отсутствующих. Сообщение темы, целей урока.
II. Актуализация опорных знаний (10 мин)
Блиц – опрос
Какой раздел математики называется комбинаторикой.
Какова главная задача комбинаторики.
Какие виды соединений или выборок вам известны?
Какие методы решения комбинаторных задач мы рассматривали, в чем их суть?
Решить устно:
1. Сократить дроби: 1) , 2) , 3) , 4) , 5)
2. Вычислите:
1) , 2) .
2. Сколькими способами можно разместить 5 человек на скамейке
II. Практикум по решению комбинаторных задач (60 мин)
Задача 1. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбрать решение?
Решение. Соберем все варианты в таблице:
Задача 2. Сколько четных двузначных чисел можно записать с помощью цифр 0, 1, 2, 4, 5, 9? (составить таблицу)1. Сколько различных трехзначных чисел можно записать при помощи цифр 1, 2, 3, 4, если цифры в числе не могут повторяться?
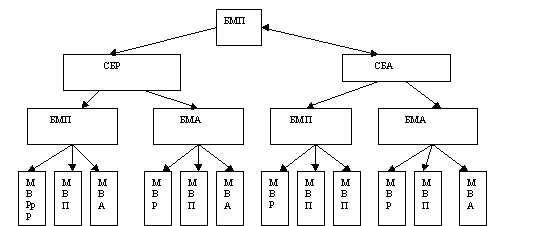
3. В коридоре висит 3 лампочки. Сколько имеется различных способов освещения коридора?
Задача 4. У Лены есть 8 разных красок. Она хочет написать ими слова «Новый Год». Сколькими способами она может это сделать, если каждая буква может быть раскрашена одним цветом и все 8 букв должны быть разные по цвету.
Решение.
Число возможных вариантов равно
40320
Ответ: 40320
Задача 5. С понедельника по пятницу Оля посещает дополнительные занятия по физике, математике, химии, русскому и английскому языках (по одному предмету в день). Сколько у Оли способов составить расписание дополнительных занятий на неделю?
Задача 6. Семеро терпеливых стоят в очереди в кассу. Сколькими способами можно составить очередь?
Задача 7. Сколькими способами можно расставить на полке 6 различных книг?
Задача 8. В классе 30 учеников. Необходимо избрать старосту, культорга и редактора стенгазеты. Сколькими способами это можно сделать, если одно лицо может занимать только один пост.
Решение. В данном случае нам важен порядок выбора каждого ученика, поэтому можно использовать формулу для количества размещений. При этом, n = 30, m = 3.
.
Ответ: 24360 способов.
Задача 9. Тренер отбирает 5 спортсменов из 12. Сколькими способами он может составить команду?
Решение. Порядок выбора спортсменов в данном случае не важен. Используем формулу для количества сочетаний, учитывая, что n = 12, m = 5.
.
Ответ: 792 способа.
Задача 10. На складе имеются 5 одинаковых деталей. Мастеру необходимо выбрать 4 детали. Сколькими способами он может это сделать? Ответ обоснуйте.
Задача 11. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
Задача 12. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики?
Задача 13. В подразделении 60 солдат 5 офицеров. Сколькими способами можно выделить караул, состоящий из 3 солдат и одного офицера?
Задача 14. В рекламного агентстве имеется 19 агентов и четыре менеджера. Сколькими способами можно составить бригаду, состоящую из трех агентов и одного менеджера?
Задача 15. Возвести в степень двучлены:
, 2) .
III. Подведение итогов (5 мин)
Ответить на вопросы, отметить активность, выставить оценки.
VII. Домашнее задание
Повторить весь материал по теме «Основные понятия комбинаторики» с целью подготовки к контрольной работе.
VII. Литература, необходимая для подготовки к занятию.
Башмаков М.И. Математика: учебник для СПО, — М. 2014
Интернет-ресурсы
преподаватель Чертенкова Е.И.
infourok.ru
4.2 Простейшие комбинаторные задачи
Знакомство с новыми понятиями начнем с двух простых задач.
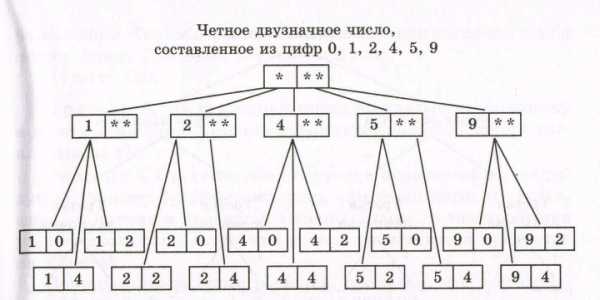
Пример 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 9?
Решение. Составим таблицу: слева от первого столбца поместим первые цифры искомых чисел, а выше первой строки – вторые цифры этих чисел. Так как в двузначном числе на первом месте может стоять любая цифра, кроме 0, то строки будут отмечены цифрами 1, 2, 4, 5, 9. Значит, в нашей таблице будет пять строк. На втором месте в искомом числе должна стоять четная цифра, значит, столбцы будут отмечены цифрами 0, 2, 4. Всего в таблице будет три столбца.
0 | 2 | 4 | |
1 | 10 | 12 | 14 |
2 | 20 | 22 | 24 |
4 | 40 | 42 | 44 |
5 | 50 | 52 | 54 |
9 | 90 | 92 | 94 |
Клетки таблицы заполняются следующим образом: первая цифра числа равна метке строки, а вторая цифра – метке столбца, поэтому каждое из интересующих нас чисел попадет в определенную клетку таблицы. По строкам и столбцам мы перечислили все возможные варианты, значит, искомых чисел будет столько же, сколько клеток в таблице, т. е. 5 • 3 = 15.
Ответ: 15.
Здесь был осуществлен полный перебор всех возможных вариантов или, как обычно говорят в таких случаях, всех возможных комбинаций. Поэтому подобные задачи называют комбинаторными.
Пример 2. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?
Решение. Соберем все варианты в такой таблице: в ней три строки и четыре столбца, они образуют 12 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоять один из возможных вариантов завтрака и, наоборот, любой вариант завтрака будет записан в одной из клеток. Значит, всего вариантов столько же, сколько клеток в таблице.
-
Плюшка
Бутерброд
Пряник
Кекс
Кофе
Кофе, плюшка
Кофе, бутерброд
Кофе, пряник
Кофе, кекс
Сок
Сок, плюшка
Сок, бутерброд
Сок, пряник
Сок, кекс
Кефир, плюшка
Кефир, бутерброд
Кефир, пряник
Кефир, пряник
Ответ: 12.
Мы видим, что, хотя примеры 1 и 2 очень разные, их решения совершенно одинаковые. Основаны они на общем правиле умножения.
4.3 Правила умножения и сложения
Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Правило умножения для двух независимых испытаний удобно объяснять, используя прямоугольники, разбитые на квадратики, или прямоугольные таблицы. Но если проводятся три испытания, то для иллюстрации надо использовать и длину, и ширину, и высоту, и на картинке получится прямоугольный параллелепипед, разбитый на кубики. Здесь уже рисунок и объяснения становятся сложнее, поскольку, например, будут невидимые кубики. Еще хуже дело обстоит с четырьмя испытаниями. В этом случае для рисунка нам просто не хватит измерений, ведь окружающее нас пространство всего лишь трехмерно.
Оказывается, правило умножения для трех, четырех и т. д. испытаний можно объяснить, не выходя за рамки плоскости, с помощью геометрической модели, которую называют деревом возможных вариантов. Она, во-первых, наглядна как всякая картинка, и, во-вторых, позволяет все учесть, ничего не пропустив.
Пример
3. Несколько
стран в качестве символа своего
государства решили использовать флаг
в виде трех горизонтальных полос
одинаковых по ширине, но разных по цвету:
белый, синий, красный. Сколько стран
могут использовать такую символику при
условии, что у каждой страны свой,
отличный от других, флаг?
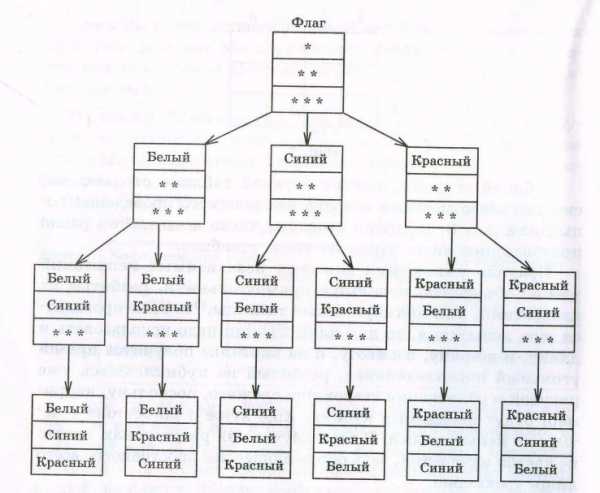
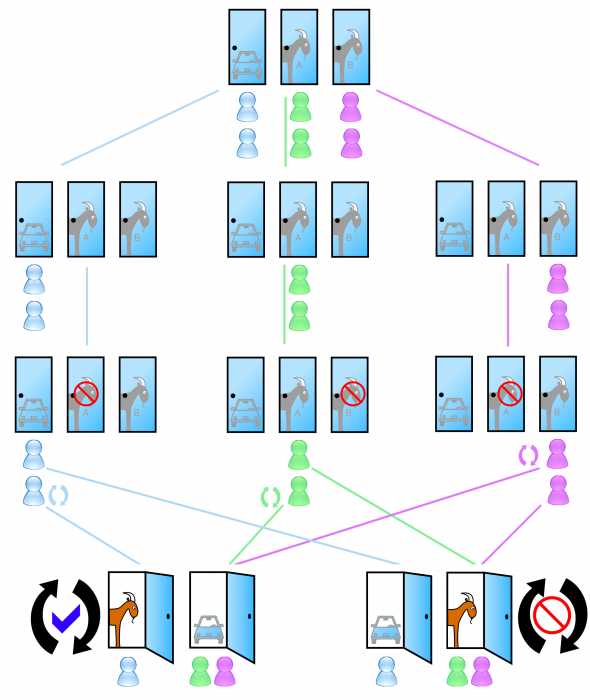
Решение. Будем искать решение с помощью дерева возможных вариантов (рис. 4.1). Посмотрим на его левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя.
Пусть теперь верхняя полоса – синего цвета, это вторая «веточка».
Рисунок 4.1
Тогда средняя полоса может быть белой или красной, а нижняя – соответственно, красной или белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая.
Аналогично рассматривается случай для верхней полосы красного цвета. Получится еще два варианта: красная, белая, синяя и красная, синяя, белая полосы флагов. Всего 6 комбинаций.
Ответ: 6.
Построенная схема действительно напоминает дерево, только перевернутое. Видимо, поэтому ее и называют деревом возможных вариантов.
Вот как, например, выглядит дерево возможных вариантов для примера 1 (рисунок 4.2):
Для
следующего примера мы приведем три
различных способа решения: с помощью
простого перебора, с помощью дерева
вариантов и по правилу умножения.
Рисунок 4.2
Пример 4. В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?
Решение.
Первый способ. Пронумеруем лампочки и будем писать «+» или «-» в зависимости от того, горит или не горит очередная лампочка. Тогда все способы освещения можно просто перечислить: + + +, + + -, + — +, — + +, + — -, — + -, — — +,
Всего 8 способов.
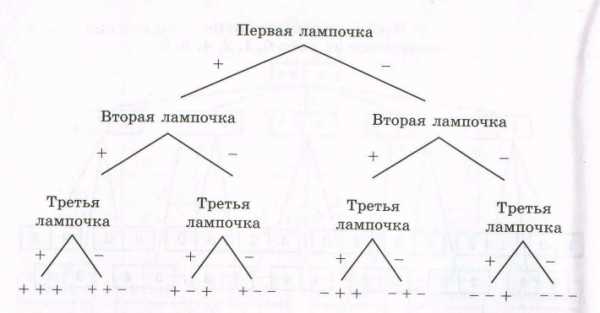Второй
способ.
Дерево возможных
вариантов представлено на рисунке 4.3.
С его помощью находим, что осветить
коридор можно 8 способами.
Третий способ. Первая лампочка может или гореть, или не гореть, т.е. имеется два возможных исхода. То же самое относится и ко второй, и к третьей лампочкам. Мы предполагаем, что лампочки горят или нет независимо друг от друга. По
Рисунок 4.3 правилу умножения получаем, что число всех способов освещения равно 2 • 2 • 2 = 8.
Ответ: 8.
У каждого из этих трех способов решения в каждом конкретном случае есть свои преимущества и свои недостатки. Выбор способа решения – за вами! Отметим все же, что правило умножения позволяет в один шаг решать самые разнообразные задачи. Например, оно приводит к крайне важному в математике понятию факториала. Рассмотрим сначала примеры.
Пример 5. В семье – 6 человек, и за столом в кухне стоят 6 стульев. В семье решили каждый вечер, ужиная, рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?
Решение. Ответ оказывается неожиданно большим: почти два года! Объясним его. Для удобства рассуждений будем считать, что семья (бабушка, дедушка, мама, папа, дочь, сын) будет рассаживаться на стулья поочередно. Нас интересует, сколько всего существует различных способов их размещения на стульях.
Предположим, что первой усаживается бабушка. У нее имеется 6 вариантов выбора стула. Вторым садится дедушка и независимо выбирает стул из 5 оставшихся. Мама делает свой выбор третьей и выбор у нее будет из 4 стульев. У папы будет уже 3 варианта, у дочки – 2, ну а сын сядет на единственный незанятый стул. По правилу умножения получаем, что всего имеется 6·5·4·3·2·1 = 720 различных способов размещения. Таким образом, в «игру с рассаживаниями» семья может играть 720 дней, т. е. почти 2 года.
Ответ: 720.
Пример 6. Десять разных писем раскладывают по одному в десять конвертов. Сколько существует способов такого раскладывания?
Решение. Предложенная ситуация отличается от предыдущей (пример 5). Действительно, там были люди и стулья, здесь – письма и конверты. Однако и здесь, и там требуется узнать, сколькими способами можно разместить п предметов на п местах.
Повторяя предыдущее решение, получаем, что всего имеется 10·9·8·7·6·5·4·3·2·1=3 628 800 способов раскладывания писем по конвертам. Более 3,5 миллионов!
Ответ: 3628800.
Как мы видим, условия задач – разные, а решения, да и полученные ответы, по сути дела, одинаковы. Удобно поэтому ввести и одинаковые обозначения для таких ответов.
Определение. Произведение первых подряд идущих п натуральных чисел обозначают п!
п! = 1·2·3·…·(п-2)·(п-1)·п
Знак п! читается как «эн факториал», что в дословном переводе с английского языка означает «состоящий из п множителей». Приведем несколько первых значений для п:
1! = 1
2! = 1·2 = 2
3! = 1·2·3 = 6
4! = 1·2·3·4 = 24
5! = 1·2·3·4·5 = 120
6! = 1·2·3·4·5·6 = 720 и т.д.
Рассмотрим еще несколько примеров:
Пример
7. Вычислить:
а) 3!; б) 7!5!;
в) 
.
Решение. а) 3!=1∙2∙3=6.
б) т.к. 7!= 1∙2∙3∙4∙5∙6∙7 и 5!= 1∙2∙3∙4∙5, то 5! можно вынести за скобки, тогда получим 5!(6∙71)= 1∙2∙3∙4∙5∙41=4920.
в) .
Пример
8. Упростить
выражение: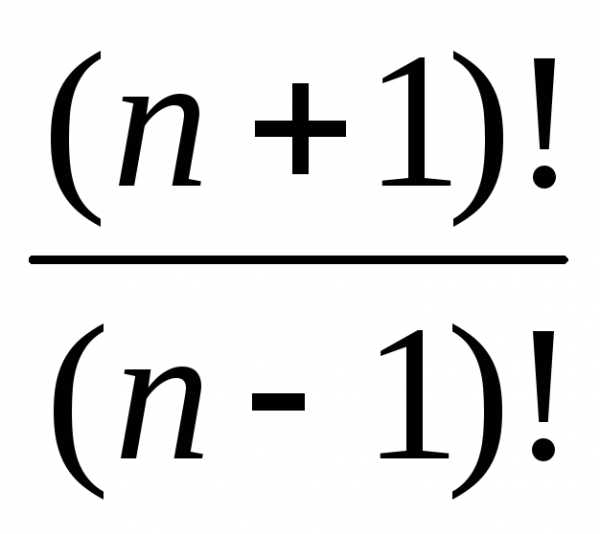 
.
Решение.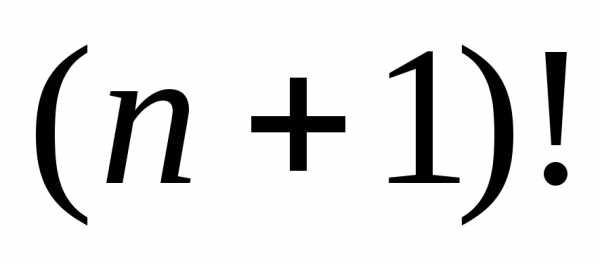 
=1∙2∙3∙…∙(п 1)∙п∙(п+1), а 
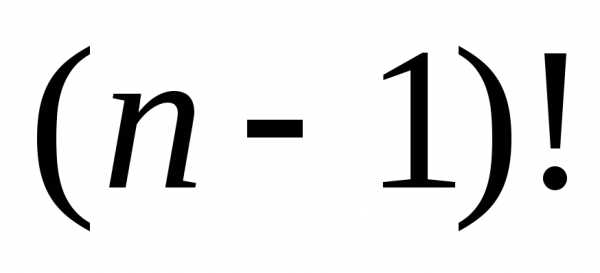=1∙2∙3∙…∙(п1), после
сокращения получим п∙(п+1).
Как же сформулировать общее утверждение, частными случаями которого являются решения примеров 3, 5 и 6? Вот один из возможных вариантов.
ТЕОРЕМА: п различным элементам можно присвоить номера от 1 до п ровно п! различными способами.
Каждый способ нумерации от 1 до п, о котором идет речь в теореме, часто называют перестановкой данного п-элементного множества. Действительно, можно считать, что каждая такая нумерация просто расставляет или переставляет все элементы множества в некотором порядке.
Перестановками из п элементов называют комбинации, которые отличаются друг от друга только порядком элементов.
Число перестановок множества из п элементов обозначают Рп. Значит, приведенную теорему можно записать в виде формулы:
Рп = п!
Кроме правила умножения в комбинаторике иногда используется еще правило сложения: Для того чтобы найти число всех возможных исходов независимого проведения одного из двух испытаний А или В, следует сложить число всех исходов испытания А и число всех исходов испытания В.
Пример 9. На столе в стаканчике стоит 5 карандашей и 3 ручки. Для того, чтобы написать записку (записать телефонный номер и т.п.), мы можем взять 1 из 5 карандашей или 1 из 3 ручек, то есть у нас имеется 5 возможностей выбора одного карандаша и 3 возможности выбора одной ручки. Так как мы выбираем только 1 предмет, карандаш или ручку, то число всех возможностей выбора равно: 5 + 3 = 8.
Правила умножения и сложения применимы для любого количества независимых испытаний.
Подведем итоги нашего знакомства с простейшими комбинаторными задачами. Мы получили основное правило – правило умножения, рассмотрели его геометрическую модель – дерево возможных вариантов, ввели новое понятие – факториал, сформулировали теорему о перестановках, в которой это понятие используется.
studfiles.net
Задачи по комбинаторики для 11 класса
Задачи по комбинаторики
Задача 1: Сколькими способами можно составить список из 5 учеников?
Ответ: перестановки, 5! = 120.
Задача 2: В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Ответ: размещения из 11 по 2, А211= 110.
Задача 3: Расписание на день содержит 5 уроков. Определить количество возможных расписаний при выборе из 14 предметов, при условии, что ни один предмет не стоит дважды.
Ответ: размещения из 14 по 5, 1320.
Задача 4: Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета?
Ответ: перестановки, 6 способов.
Задача 5: В классе 24 ученика. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
Ответ: сочетания из 24 по 4,
Задача 6: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?
Ответ: перестановки, 6 способов.
Задача 7: Сколькими различными способами можно избрать из 15 человек делегацию в составе 3 человек?
Ответ: сочетания, 455 способами.
Задача 8: Из ящика, где находится 15 шаров, нумерованных последовательно от 1 до 15, требуется вынуть 3 шара. Определить число возможных комбинаций при этом?
Ответ: размещения, 2830 способами.
Задача 9: Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?
Ответ: перестановки, 4! – 3! =18.
Задача 10: Сколькими способами можно разместить 6 пассажиров в четырехместной каюте?
Ответ: размещения из 6 элементов по 4, 360 способами.
Задача 11: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
Ответ: сочетания из 10 элементов по 2, 45 способами.
Задача 12: Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек?
Ответ: сочетания из 13 по 4, 715 бригад.
Задача 13: При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Ответ: сочетания из 16 по 2, 120 рукопожатий.
Задача 14: Группа учащихся в 30 человек пожелала обменяться своими фотокарточками. Сколько всего фотокарточек потребовалось для этого?
Ответ: сочетание из 30 по 2, 435 фотокарточек.
Задача 15: Сколько различных плоскостей можно провести через 10 точек, если никакие три из них не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости?
Ответ: сочетание из 10 по 3; 120 точек
Задача 16: Сколько существует различных семизначных телефонных номеров?
Ответ: 107.
Задача 17: Сколько существует различных семизначных телефонных номеров, если в каждом номере нет повторяющихся цифр?
Ответ: размещение из 10 по 7.
Задача 18: Сколько существует таких перестановок 7 учеников, при которых 3 определенных ученика находятся рядом друг с другом? Ответ: 720 = 3! · 5!
Задача 19: На книжной полке стоит собрание сочинений в 30 томах. Сколькими различными способами их можно переставить, чтобы: а) тома 1 и 2 стояли рядом; б) тома 3 и 4 рядом не стояли?
Ответ: а)2∙29!; б)28∙29!
Задача 20: Сколько существует трёхзначных чисел, все цифры которых нечётные и различные?
Ответ: размещение из 5 по 3, 60.
Задача 21: У одного мальчика имеется 10 марок для обмена, а у другого – 8. Сколькими способами они могут обменять 2 марки одного на 2 марки другого?
Ответ: сочетания, С210·С28 = 1260.
multiurok.ru
Примеры решений задач по комбинаторике
Примеры решений задач по комбинаторикеБольшинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения.
Выбор правила | Выбор правила |
Правило суммы | Правило произведения |
Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор объекта либо А, либо В можно осуществить m + n способами. | Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары А и В можно осуществить m · n способами. |
Задача 1. В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?
Решение.
Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).
Ответ: 24.
Задача 2. При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 6 друзей?
O формуле для числа сочетаний.
Как известно, деление может быть обозначено разными символами: __, /, :
Косую черту и двоеточие удобно использовать для записи формулы в одну строку, что здесь и сделано для экономии места в таблице. Горизонтальную черту используют для записи дроби. Если формулу для числа сочетаний записать дробью, то хорошо видно, как она сокращается.
Решение:
В одном рукопожатии равноправно участвуют два человека. 6 друзей объединялись в группы по 2 без учёта порядка следования. Такие группировки (выборки) называются сочетаниями. Число сочетаний определяем по формуле
С62 = 6!/2!/(6 — 2)! = 6!/2!/4! = 5·6/2 = 15.
Ответ: 15.
Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема:
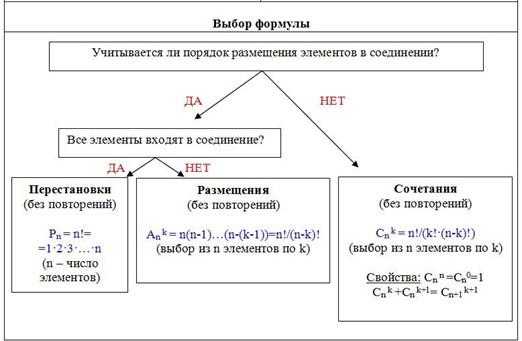
Рассмотрим решение нескольких задач на разные виды соединений без повторений.
Задача 3. Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.
Решение.
Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A73 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.
Ответ: 210.
Задача 4. Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?
Решение.
На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:
A107 – A96 = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.
Ответ: 544 320.
Задача 5. Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?
Решение.
Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р8. Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р8 · Р5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.
Ответ: 8! · 5!
Задача 6. В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?
Решение.
Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:
С164 · С123 = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.
Ответ: 400 400.
Задача 7. Сколькими способами 10 футбольных команд могут разыграть между собой золотые, бронзовые и серебряные медали?
Решение.
На пьедестале почёта находятся 3 команды из 10, и для них очень существенно, кто какое место занял, т.е. порядок следования. Составление групп с учетом порядка следования — размещения. Число размещений определяем по формуле
А103 = 10!/(10 — 3)! = 10!/7! = 8·9·10 = 720.
Другой способ решения с использованием И-правила, как в задаче 2б. Однако, чем больше выборка, тем удобнее сразу применять готовую формулу.
Ответ: 720.
Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.
multiurok.ru
Задачи по комбинаторике. Часть 1
В этой статье использован материал из лекций Шарича Владимира Златковича и Максимова Дмитрия Васильевича на КПК foxford.
Очень рекомендую абитуриентам курсы foxford для подготовки к ЕГЭ и олимпиадам.
1. Сколько четырехзначных чисел содержит ровно одну семерку?
Решение.
Четырехзначное число имеет вид . Если четырехзначное число содержит ровно одну семерку, то она может стоять
1) на первом месте, и тогда на остальных трех местах могут стоять любые цифры от 0 до 9, кроме цифры 7, и по правилу произведения мы получаем четырехзначных чисел, у которых семерка стоит на первом месте.
2) на любом месте, кроме первого, и тогда по правилу произведения мы получаем . У нас три возможности расположения цифры 7, на первом месте может стоять 8 цифр (все цифры, кроме нуля и 7), на тех местах, где не стоит цифра 7 — 9 цифр.
Сложим полученные варианты, и получим четырехзначных чисел, содержащих ровно одну семерку.
2. Сколько пятизначных чисел содержит ровно две семерки?
Решение.
Так же как в предыдущей задаче у нас две возможности:
1) Одна из семерок стоит на первом месте, а вторая на любом из оставшихся четырех мест. На трех местах, не занятых цифрой 7 может стоять любая из 9 цифр (все, кроме цифры 7). В этом случае мы получаем чисел.
2) Ни одна из семерок не стоит на первом месте. В этом случае мы имеем возможностей расставить 2 семерки на оставшихся 4-х местах. У нас осталось 3 места, не занятых цифрой 7, одно из которых первое, и таким образом мы получаем чисел.
Сложим полученные варианты, и получим пятизначных чисел, содержащих ровно две семерки.
3. Сколько существует пятизначных чисел, цифры которых различны и расположены в порядке возрастания?
Так как первой цифрой не может быть 0, рассмотрим последовательность цифр 1-9, расположенных в порядке возрастания.
1, 2, 3, 4, 5, 6, 7, 8, 9
Если мы выберем из этой последовательности 5 произвольных цифр, например так:
1, 2, 3, 4, 5, 6, 7, 8, 9
то получим пятизначное число, цифры которого различны и расположены в порядке возрастания.
Осталось посчитать, сколькими способами мы можем выбрать из 9 цифр 5:
Итак существует 126 пятизначных чисел, цифры которых различны и расположены в порядке возрастания.
Треугольник Паскаля и число сочетаний.
4. Задача о хромом короле. Пусть есть доска размером . Король находится в левом верхнем углу доски и может перемещаться по доске, двигаясь только вправо и вниз. Сколькими способами король может добраться до левого нижнего угла доски?
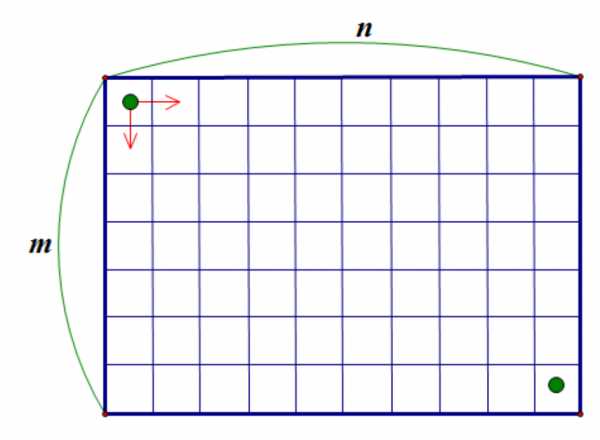
Решение.
Посчитаем, для каждой клетки, сколькими способами король может до нее добраться.
Так как король может двигаться только вправо и вниз, до любой клетки первого столбца и первой строки он может добраться единственным способом: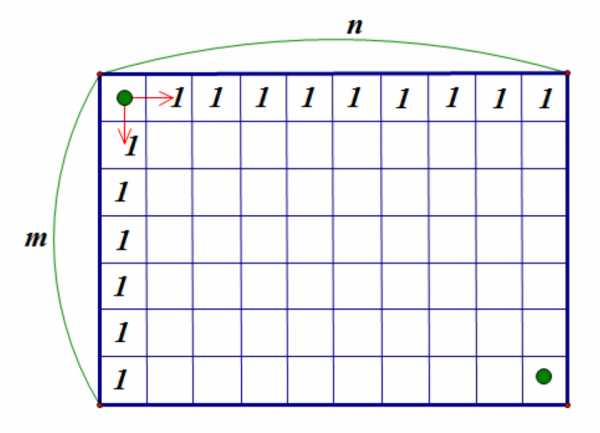
Рассмотрим произвольную клетку доски. Если в клетку, стоящую над ней можно добраться способами, а в клетку, стоящую слева от нее способами, то в саму клетку можно добраться способами (это следует из того, что король может двигаться только вправо и вниз, то есть не может дважды зайти на одну клетку):
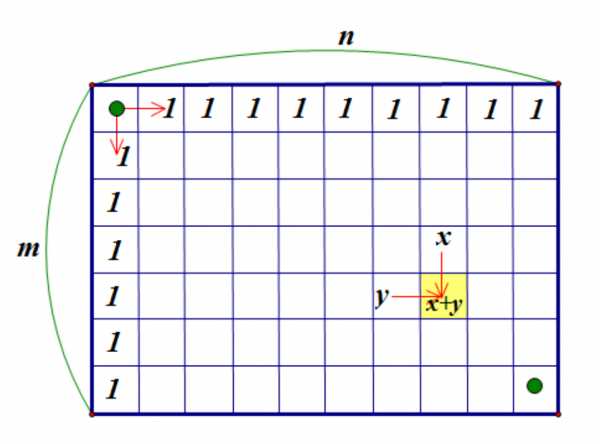
Заполним начальные клетки, пользуясь этим правилом:
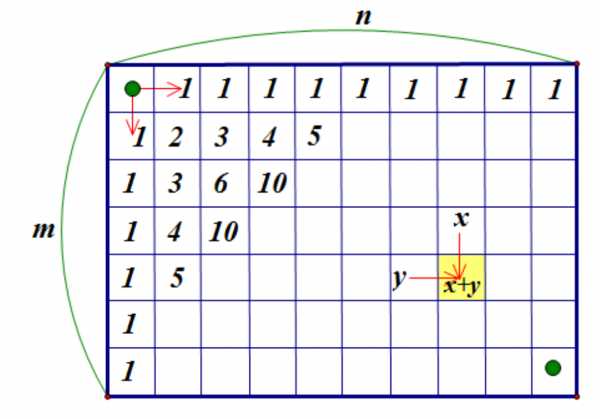
Мы видим, что при заполнении клеток у нас получается треугольник Паскаля, только повернутый на бок.
Число в каждой клетке показывает, сколькими способами король может попасть в эту клетку из левой верхней.
Например, чтобы попасть в клетку (4;3) — четвертая строка, третий столбец, король должен сделать 4-1=3 шага вправо, и 3-1=2 шага вниз. То есть всего 3+2=5 шагов. Нам нужно найти число возможных последовательностей этих шагов:
То есть найти, скольким способами мы можем расположить 2 вертикальные (или 3 горизонтальные) стрелки на 5-ти местах. Число способов равно:
— то есть ровно то число, которое стоит в этой клетке.
Для того, чтобы попасть в последнюю клетку, король должен сделать всего шага, из которых по вертикали. Таким образом, он может попасть в последнюю клетку
способами.
Можно получить рекуррентное соотношение для числа сочетаний:
Смысл этого соотношения следующий. Путь у нас есть множество, состоящее из n элементов. И нам нужно выбрать из этого множества l элементов. Все способы, которыми мы можем это сделать делятся на две группы, которые не пересекаются. Мы можем:
а) зафиксировать один элемент, и из оставшихся n-1-го элемента выбрать l-1 элемент. Это можно сделать способами.
б) выбрать из оставшихся n-1-го элемента все l элементов. Это можно сделать способами.
Всего получаем
способов.
Также можно получить соотношение:
Действительно, левая часть этого равенства показывает число способов выбрать какое-то подмножество из множества, содержащего n элементов. (Подмножество, содержащее 0 элементов, 1 элемент и так далее.) Если мы пронумеруем n элементов, то получим цепочку из n нулей и единиц, в которой 0 означает, что данные элемент не выбран, а 1 — что выбран. Всего таких комбинаций, состоящих из нулей и единиц .
Кроме того, число подмножеств с четным числом элементов равно числу подмножеств с нечетным числом элементов:
Докажем это соотношение. Для этого докажем, что между подмножествами с четным числом элементов и подмножествами с нечетным числом элементов существует взаимно однозначное соответствие.
Зафиксируем один элемент множества:
Теперь возьмем произвольное подмножество, и если оно не содержит этот элемент, то поставим ему в соответствие подмножество, состоящее из тех же элементов, что и выбранное, плюс этот элемент. А если выбранное подмножество уже содержит это элемент, то поставим ему в соответствие подмножество, состоящее из тех же элементов, что и выбранное, минус этот элемент. Очевидно, что из этих пар подмножеств одно содержит четное число элементов, а другое — нечетное.
5. Рассмотрим выражение
1. Сколько слагаемых имеет этот многочлен?
а) до приведения подобных членов
б) после приведения подобных членов.
2. Найти коэффициент при произведении
Решение. показать
При возведении суммы слагаемых в степень , мы должны эту сумму умножить на себя раз. Мы получаем сумму одночленов, степень каждого из которых равна m. Число всевозможных произведений, состоящих из переменных из множества с учетом порядка и возможностью повторения равно числу размещений с повторениями из k по m:
Когда мы приводим подобные члены, мы считаем одинаковыми произведения, содержащие равное число множителей каждого вида. В этом случае, чтобы найти число слагаемых многочлена после приведения подобных членов, мы должны найти число сочетаний с повторениями из k по m:
Найдем коэффициент при произведении .
Выражение представляет собой произведение m элементов из множества , причем элемент взят раз, элемент взят раз, и так далее, и, наконец, элемент взят раз. Коэффициент при произведении равен числу возможных произведений:
Рассмотрим частный случай: — Бином Ньютона. И получим формулу для биномиальных коэффициентов.
Произвольный член многочлена, полученного возведением двучлена в степень имеет вид , где А — биномиальный коэффициент, . Как мы уже получили,
Таким образом,
Тогда если мы положим х=1 и y=1, то получим, что
6. Задача про кузнечика.
Есть n клеточек, расположенных последовательно. Кузнечик должен попасть из крайней левой клеточки в крайнюю правую, прыгая вправо на произвольное число клеток.
а) Сколькими способами он может это сделать?
Решение. показать
Изобразим условие задачи:
Кузнечик может попасть в крайнюю правую клетку, побывав, или не побывав в любой внутренней клетке. Присвоим клетке значение 1, если кузнечик в ней побывал, и 0, если нет, например, так:
Тогда у нас есть n-2 клеточек, каждая из которых может принимать значение 0 или 1. Задача сводится к нахождению числа последовательностей, состоящих из n-2 нулей и единиц. Таких последовательностей .
б) сколькими способами кузнечик может добраться в n-ю клетку, сделав k шагов?
Решение. показать
Чтобы попасть в n-ю клетку, сделав k шагов, кузнечик должен попасть ровно в k—1 клетку между первой и последней. Так как последний шаг он делает всегда в последнюю клетку. То есть стоит вопрос, сколькими способами можно выбрать k—1 клетку из n-2 клеток?
Ответ: .
в) сколькими способами кузнечик может добраться в n-ю клетку, двигаясь на одну или на две клетки вправо?
Решение.
Распишем, сколькими способами можно попасть в каждую клетку.
В первую и вторую клетки можно попасть единственным способом: в первую — никуда из нее не уходя, и во вторую из первой:
В третью можно попасть из первой или второй, то есть двумя способами:
В четвертую — из второй или третьей, то есть 1+2=3 способами:
В пятую — из третьей или четвертой, то есть 2+3=5 способами: Можно заметить закономерность: чтобы найти число способов, которыми кузнечик может попасть в клетку с номером k нужно сложить число способов, которыми кузнечик может попасть в две предыдущие клетки:
Мы получили интересную последовательность чисел — числа Фибоначчи — это линейная рекуррентная последовательность натуральных чисел, где первое и второе равно единице, а каждое последующее — сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…
ege-ok.ru
|
Поиск Лекций
ЗАДАЧИ 1. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе — мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье — чай и компот. Сколько различных обедов можно составить из указанных блюд? 1 способ. Перечислим возможные варианты
18 вариантов. 3 способ. Используя правило умножения, получаем: 3х3х2=1 2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу? 1 способ. Обозначим мячи — М1, М2, игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5. М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5, Ответ: 40 вариантов. 3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9? 1 способ. 2 способ. Дерево возможностей. 3 способ. Используя правило умножения, получаем: 5х3=15 . 4. Мисс Марпл, расследуя убийство, заметила отъезжающее от дома мистера Дэвидсона такси. Она запомнила первую цифру “2”. В городке номера машин были трехзначные и состояли из цифр 1,2,3,4 и 5. Скольких водителей, в худшем случае, ей придется опросить, чтобы найти настоящего убийцу? 1 способ. Перечислим возможные варианты номеров такси: Ответ: 25 человек. 2 способ. Используя правило умножения, получаем: 5х5=25 5. Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения? 1 способ. Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно: №1 — Саша — есть возможность выбрать из 5 вариантов (стульев) Используя правило умножения, получаем: 5х4х3х2х1=120 2 способ. Решаем, используя понятие факториала: 5!=120 6. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)? 1 способ. Перечислим возможные варианты состава пары: 11А-11Б, 11А-11В, 11А-11Г, 11А-11Д, Ответ: 10 пар. 2 способ. Из пяти классов нужно выбрать 2 дежурных. 7. В 8 “а” классе лучше всех математику знают 5 учеников: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами учительница может эту пару выбрать? 1 способ. Обозначим имена детей первыми заглавными буквами. Ответ: 6 пар. 2 способ. Мальчиков 3, из них 1 можно выбрать , девочек 2, из них можно 1 выбрать , используя правило умножения, получаем: 8. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы. Сколькими способами могут распределится места по окончании соревнований? 2 способ. Используя понятие факториала, получаем: 6!=720 9. В 9 “б” классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Департамент образования премировал лучших учащихся путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора учеников на отдых? Обозначим первыми заглавными буквами имен учащихся. 2 способ. Из 6 человек нужно выбрать 4, число элементарных событий равно = 15 10. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого? Вычислим, сколько четверок из 7 дисков можно составить у Пети: 11. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых? Из 5 офицеров выбрать 2 можно с помощью числа сочетаний =10 способами, из 8 сержантов 4 — =70, из 70 рядовых 15 — . По правилу умножения находим число выбора отряда: 12. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет? Из 6 изумрудов 3 он может выбрать =20 способами, из 9 алмазов 5 — =126, из 7 сапфиров 2 — =21. По правилу умножения находим число вариантов 20х126х21=52920 13. На выборах победили 9 человек — Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать? Здесь речь идет о размещениях 14. В районе построили новую школу. Из пришедших 25 человек нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими способами это можно сделать? На должность директора выбираем из 25 человек, на завуча начальной — из 24, завуча среднего звена — из 23, завуча по воспитательной работе — 22. По правилу умножения получаем: 15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)? Для Пети набор можно набрать 6х8х10=480 способами, для Васи — 5х7х9=315, для Коли — 4х6х8=192. По правилу умножения получаем 16. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся? В русском языке 9 гласных букв — а, е, е, и, о, у, э, ю, я. Выбрать из них 2 можно =36 способами. Из 10 цифр выбрать 3 можно =120 способами. Применяя правило умножения, получаем: 17. Сколькими способами можно составить трехцветный флаг из полос разной ширины, если имеются материи из 8 тканей? Другой способ решения. 18. В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различные? Из 15 предметов 5 любых можно выбрать 19. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета? 1 способ. Обозначим белые — Б1, Б2, Б3, алые — А1,А2, чайные — Ч1, Ч2, Ч3,Ч4 Ответ: 24 варианта. 2способ. Дерево возможностей 3 способ. Используя правило умножения, получаем: 2х3х4=24 20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка-Быковка-Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М- пешком или на автобусе, из М вВ — по реке, пешком или автобусе. Сколько вариантов похода есть у щкольников? 1 способ. Обозначим СБ — путь из Сосновки в Бытовку, ВГ — путь из Быковки в Масловку, МВ — путь из Масловки в Видово. 2 способ. Дерево возможностей
Задачи по комбинаторике. Примеры решений
На данном уроке мы коснёмся элементов комбинаторики, которые потребуются для дальнейшего изучения теории вероятностей. Следует отметить, что комбинаторика является самостоятельным разделом высшей математики (а не частью тервера) и по данной дисциплине написаны увесистые учебники, содержание которых, порой, ничуть не легче абстрактной алгебры. Однако нам будет достаточно небольшой доли теоретических знаний, и в данной статье я постараюсь в доступной форме разобрать основы темы с типовыми комбинаторными задачами. А многие из вас мне помогут 😉 Чем будем заниматься? В узком смысле комбинаторика – это подсчёт различных комбинаций, которые можно составить из некоторого множества дискретных объектов. Под объектами понимаются какие-либо обособленные предметы или живые существа – люди, звери, грибы, растения, насекомые и т.д. При этом комбинаторику совершенно не волнует, что множество состоит из тарелки манной каши, паяльника и болотной лягушки. Принципиально важно, что эти объекты поддаются перечислению – их три (дискретность)и существенно то, что среди них нет одинаковых. С множеством разобрались, теперь о комбинациях. Самыми распространёнными видами комбинаций являются перестановки объектов, их выборка из множества (сочетание) и распределение (размещение). Давайте прямо сейчас посмотрим, как это происходит:
Рекомендуемые страницы: Поиск по сайту |
|
poisk-ru.ru
Как решать задачи по комбинаторике 🚩 перестановка без повторений 🚩 Математика
Автор КакПросто!
Решение задач на нахождение различных комбинаций представляет неподдельный интерес, а комбинаторика применяется во многих областях науки, например, в биологии для расшифровки кода ДНК или на спортивных соревнованиях для расчета количества игр между участниками.
Статьи по теме:
Вам понадобится
Инструкция
Перестановки без повторений – это такие комбинации из n-го количества различных элементов, в которых количество элементов остается равным n, а порядок их меняется различными способами. P(n )= 1*2*3*…*n=n!ПримерСколько перестановок можно составить из цифр 5,8,9? Из условия задачи n = 3 (три цифры 5,8,9). Воспользуемся формулой для расчета возможного количества перестановок без повторений: P_(n )= n!
Подставив в формулу n = 3, получим P= 3! = 1*2*3 = 6 Перестановки с повторениями – это такие комбинации из n-го количества элементов (в том числе и повторяющихся), в которых количество элементов остается равным n, а порядок их меняется различными способами.Рn = n!/n1!* n2!*…*nk!
где n – общее количество элементов, n1, n2…nk – количество повторяющихся элементов
Сочетания без повторений – это все возможные комбинации (группы) из n различных элементов по m в каждой группе (m?n), которые отличаются друг от друга только составом элементов (группы отличаются друг от друга хотя бы одним элементом).
С = n!/m!(n — m)!
Сочетания с повторениями – это все возможные комбинации (группы) из n различных элементов по m каждой группе (m – любое), причем допускается повторение одного элемента несколько раз (группы отличаются друг от друга хотя бы одним элементом)
С = (n + m – 1)!/m!(n-1)!
Размещения без повторений – это все возможные комбинации (группы) из n различных элементов по m в каждой группе (m?n), которые различаются между собой как составом элементов, входящих в группы, так и их порядком.
А = n!/(n – m)!
Размещения c повторениями – это все возможные комбинации (группы) из n различных элементов по m каждой группе (m – любое), которые различаются между собой как составом элементов, входящих в группы, так и их порядком, в которых также допускается повторение элементов.
А = n^m
Данный вопрос можно рассмотреть как с точки зрения стандартных методов и подходов комбинаторики, так и с применением теории вероятности. Это позволяет несколько расширить кругозор, а также взглянуть на поставленную задачу с нестандартной точки зрения.
Инструкция
Как известно, вероятность простых событий определяется по классической формуле Р(А)=m/n, в которой число событий (исходов) конечно и равновозможно. При этом n — общее число исходов, а m – число благоприятных исходов (условию задачи). Теперь, необходимо рассмотреть три наиболее распространенные формулы комбинаторики: перестановки, сочетания и размещения. ПерестановкиПредставьте себе, что на столе лежат пять карточек, на невидимой стороне которых написаны цифры: 1, 2, 3, 4 и 5. Произвольным образом, по одной, они вынимаются, переворачиваются и укладываются по очереди. Какова вероятность того, что извлеченная комбинация будет числом 12345?Количество благоприятных исходов m очевидно – m=1. В то время как всего вариантов n=5!=120, где «!» — знак факториала будет целых 120, а искомая вероятность данного события Р= 1/120, соответственно. В данном примере общее число исходов искали как число всевозможных перестановок пяти элементов по пяти позициям. Поэтому и в произвольном случае n элементов это число называют числом перестановок и обозначают Pn (Pn=n!) СочетанияСледует рассмотреть следующий пример. В корзине находится некоторое количество шаров двух цветов, равное n. В такой постановке задачи, число сочетаний из n элементов по m называют множество способов, отличающихся друг от друга количеством шаров разного цвета в каждой комбинации. При этом n – общее число шаров (элементов), m – число элементов в извлеченной комбинации. Комбинации различны, если они отличаются хотя бы одним элементом. Обозначение числа сочетаний и формула для вычисления приведены на рисунке 1.Предположительно, необходимо вычислить вероятность выигрыша в спортлото 6 из 49, где «угадано» 4 из 6-ти. Очевидно, что при этом используется формула для сочетания.Общее число исходов С (из 49 по 6)=49!/43!6! Благоприятное число исходов можно найти из следующих соображений. Имеется 6 «хороших» из общего количества 49 номеров. По вопросу задачи достаточно 4-х совпадений. Из 6-ти «хороших» 4 можно выбрать С (из 6 по 4) способами. При этом из оставшихся 43 «плохих» выбираются 2 для дополнения выбранной комбинации до шести элементов С (из 43 по2) способами. Звучит это следующим образом.
Число благоприятных ситуаций собирается как С (из 6 по 4) и С (из 37 по 2) (ситуация логического умножения). Значит m=С(из 6 по 4)∙С(из 43 по 2). Таким образом, вероятность даже самого «мизерного» выигрыша Р=m/n=С(из 6 по 4)∙С(из 43 по 2)/С(из 49 по 6)=(6!/2!4!)(43!/2!41!)/(49!/6!43!)=15*21*43/66*92*47*49=9*43/92*47*154=0,000347.
РазмещенияЕсли в задаче о сочетаниях учесть порядок следования элементов в выбранной комбинации из m элементов, то появится задача о размещениях. Вопрос, на основании которого принимается решением о применении формулы числа сочетаний должен добавочно (по сравнению с сочетаниями) содержать данные о необходимости учета порядка расположения элементов в выбираемых комбинациях. Если выбрано m элементов, то вычисляя число размещений необходимо число сочетаний умножить на число перестановок Pm=m!. Обозначение числа размещений и формулы для его вычисления даны на рис. 2.
Видео по теме
www.kakprosto.ru