Эффективные методы решения определенных и несобственных интегралов
Данный раздел содержит дополнительные материалы по методам решения определенных и несобственных интегралов. Предполагается, что читатель владеет средними или высокими навыками интегрирования. Если это не так, пожалуйста, начните с азов: Неопределенный интеграл, примеры решений.
Где неопределенный интеграл – там неподалёку и Определенный интеграл, с формулой Ньютона-Лейбница вы тоже должны быть знакомы не понаслышке. Кроме того, уметь решать простейшие задачи на вычисление площади плоской фигуры (см. 7.2.3.) и на вычисление объёма тела вращения (см. 7.2.4.).
Урок предназначен для тех, кто хочет научиться быстрее и эффективнее решать определенные и несобственные интегралы. Сначала рассмотрим особенности интегрирования четной и нечетной функции по симметричному относительно нуля интервалу. Затем мы разберем задачу о нахождении площади круга с помощью определенного интеграла. Эта задача важна еще и тем, что знакомит вас с распространенным приемом интегрирования определенного интеграла –
Аналогично, рассмотрим несобственные интегралы от четных и нечетных функций по симметричному интервалу. В том числе, более редкие типы несобственных интегралов, которые не вошли в основной материал предыдущих разделов: когда нижний предел стремится к «минус бесконечности», когда оба предела стремятся к бесконечности, когда в обоих концах отрезка интегрирования функция терпит бесконечный разрыв (это уже интеграл второго рода). И совсем редкий несобственный интеграл – с точкой разрыва на отрезке интегрирования.
Метод решения определенного интеграла от четной функции по симметричному относительно нуля отрезку
Рассмотрим определенный интеграл вида
.Легко заметить, что отрезок интегрирования [-c; c] симметричен относительно нуля.
Если подынтегральная функция f(x) является чётной, то интеграл
можно вычислить по половине отрезка, а результат – удвоить:
.
Многие догадались, почему это так, но рассмотрим конкретный пример с чертежом:
Пример 1
Вычислить определенный интеграл
.
О чётности функции много говорилось в методическом материале Графики и свойства элементарных функций. Повторим ещё раз: функция является чётной, если для неё выполняется равенство f(-x) = f(x).
Как проверить функцию на чётность? Нужно вместоx подставить —x.
В данном случае: и .
Значит, данная функция является чётной.
Согласно правилу, на симметричном относительно нуля отрезке [-2; 2] наш интеграл от чётной функции можно вычислить следующим образом:
А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу….
Любая чётная функция, в частности , симметрична относительно оси OY:

Определенный интеграл
численно равен площади плоской фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а, значит, и симметричности её графика относительно оси OY, достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые половинки есть геометрическое выражение свойства четности. Именно поэтому справедливо действие
.
Аналогичная история происходит с любой чётной функцией f(x) по симметричному относительно нуля отрезку:
.
Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим:
Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Заметим, что это еще был простой демонстрационный пример, на практике всё бывает хуже.
Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает.
Короткий пример для самостоятельного решения:
Пример 2
Вычислить определенный интеграл
.
Полное решение и ответ в конце урока.
Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Рисунок к Примеру 1 дан только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка:
Пример 3
3.1. Вычислить определенный интеграл
.
3.2. Вычислить площадь плоской фигуры, ограниченной линиями
, и осью OX на интервале .
Это две разные задачи!Сначала разберемся с первым пунктом:
1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:
.
Определенный интеграл получился отрицательным и так бывает!
Теперь найдем площадь плоской фигуры. Вот здесь без чертежа обойтись трудно:
На отрезке график функции расположен ниже оси OX, поэтому:
Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (см. также Пример 3 из раздела 7.2.3.).
Заметьте, что чётность косинуса никто не отменял, поэтому мы опять разделили отрезок и удвоили интеграл.
infopedia.su
Определенный интеграл
Определенный интеграл
Содержание
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
2. Геометрический смысл определенного интеграла
3. Основные свойства определенного интеграла
4. Формула Ньютона–Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям
Лекция 2. Применение определенных интегралов. несобственные интегралы
1. Площадь криволинейной трапеции
2. Объем тела вращения
3. Длина дуги плоской кривой
4. Несобственные интегралы с бесконечными пределами интегрирования
5. Несобственные интегралы от неограниченных функций
Литература
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
Пусть функция
определена на отрезке , . Выполним следующие операции:1) разобьем отрезок
точками на n частичных отрезков ;2) в каждом из частичных отрезков
, выберем произвольную точку и вычислим значение функции в этой точке: ;3) найдем произведения
, где – длина частичного отрезка , ;4) составим сумму
, (1)которая называется интегральной суммой функции y = f ( x ) на отрезке [ а, b ]. С геометрической точки зрения интегральная сумма
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки , а высоты равны соответственно (рис. 1). Обозначим через длину наибольшего частичного отрезка ; 5) найдем предел интегральной суммы, когда.Рис. 1
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка
на частичные отрезки, ни от выбора точек в них, то этот предел называется определенным интегралом от функции на отрезке и обозначается .Таким образом,
.В этом случае функция
называется интегрируемой на . Числа а и b называются соответственно нижним и верхним пределами интегрирования, – подынтегральной функцией, – подынтегральным выражением, – переменной интегрирования; отрезок называется промежутком интегрирования.Теорема 1. Если функция
непрерывна на отрезке , то она интегрируема на этом отрезке.2. Геометрический смысл определенного интеграла
Пусть на отрезке
задана непрерывная неотрицательная функция .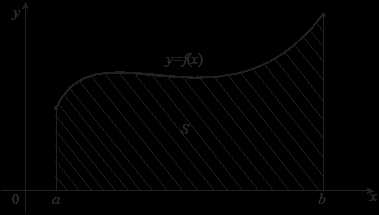
Рис. 2
Определенный интеграл
от неотрицательной функции с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа – отрезками прямых и , снизу – отрезком оси Ох.3. Основные свойства определенного интеграла
1. Значение определенного интеграла не зависит от обозначения переменной интегрирования:
.2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
3. Если
, то, по определению, полагаем4. Постоянный множитель можно выносить за знак определенного интеграла:
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
.6. Если функция
интегрируема на и , то .7. ( теорема о среднем ). Если функция
непрерывна на отрезке , то на этом отрезке существует точка , такая, что .4. Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема 2. Если функция
непрерывна на отрезке и – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:, (2)
которая называется формулой Ньютона–Лейбница. Разность
принято записывать следующим образом: ,где символ
называется знаком двойной подстановки.Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную
для подынтегральной функции ; на втором – находится разность значений этой первообразной на концах отрезка .mirznanii.com
Эффективные методы решения определенных и несобственных интегралов
Данный раздел содержит дополнительные материалы по методам решения определенных и несобственных интегралов. Предполагается, что читатель владеет средними или высокими навыками интегрирования. Если это не так, пожалуйста, начните с азов: Неопределенный интеграл, примеры решений.
Где неопределенный интеграл – там неподалёку и Определенный интеграл, с формулой Ньютона-Лейбница вы тоже должны быть знакомы не понаслышке. Кроме того, уметь решать простейшие задачи на вычисление площади плоской фигуры (см. 7.2.3.) и на вычисление объёма тела вращения (см. 7.2.4.).
Урок предназначен для тех, кто хочет научиться быстрее и эффективнее решать определенные и несобственные интегралы. Сначала рассмотрим особенности интегрирования четной и нечетной функции по симметричному относительно нуля интервалу. Затем мы разберем задачу о нахождении площади круга с помощью определенного интеграла. Эта задача важна еще и тем, что знакомит вас с распространенным приемом интегрирования определенного интеграла – тригонометрической подстановкой. Она еще нигде не рассматривалась – новый материал!
Аналогично, рассмотрим несобственные интегралы от четных и нечетных функций по симметричному интервалу. В том числе, более редкие типы несобственных интегралов, которые не вошли в основной материал предыдущих разделов: когда нижний предел стремится к «минус бесконечности», когда оба предела стремятся к бесконечности, когда в обоих концах отрезка интегрирования функция терпит бесконечный разрыв (это уже интеграл второго рода). И совсем редкий несобственный интеграл – с точкой разрыва на отрезке интегрирования.
Метод решения определенного интеграла от четной функции по симметричному относительно нуля отрезку
Рассмотрим определенный интеграл вида
.
Легко заметить, что отрезок интегрирования [-c; c] симметричен относительно нуля.
Если подынтегральная функция f(x) является чётной, то интеграл
можно вычислить по половине отрезка, а результат – удвоить:
.
Многие догадались, почему это так, но рассмотрим конкретный пример с чертежом:
Пример 1
Вычислить определенный интеграл
.
О чётности функции много говорилось в методическом материале Графики и свойства элементарных функций. Повторим ещё раз: функция является чётной, если для неё выполняется равенство f(-x) = f(x).
Как проверить функцию на чётность? Нужно вместоx подставить —x.
В данном случае: и .
Значит, данная функция является чётной.
Согласно правилу, на симметричном относительно нуля отрезке [-2; 2] наш интеграл от чётной функции можно вычислить следующим образом:
А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу….
Любая чётная функция, в частности , симметрична относительно оси OY:
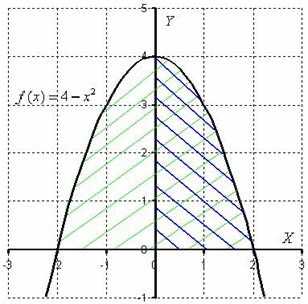
Определенный интеграл
численно равен площади плоской фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а, значит, и симметричности её графика относительно оси OY, достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые половинки есть геометрическое выражение свойства четности. Именно поэтому справедливо действие
.
Аналогичная история происходит с любой чётной функцией f(x) по симметричному относительно нуля отрезку:
.
Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим:
Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Заметим, что это еще был простой демонстрационный пример, на практике всё бывает хуже.
Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает.
Короткий пример для самостоятельного решения:
Пример 2
Вычислить определенный интеграл
.
Полное решение и ответ в конце урока.
Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Рисунок к Примеру 1 дан только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка:
Пример 3
3.1. Вычислить определенный интеграл
.
3.2. Вычислить площадь плоской фигуры, ограниченной линиями
, и осью OX на интервале .
Это две разные задачи!Сначала разберемся с первым пунктом:
1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:
.
Определенный интеграл получился отрицательным и так бывает!
Теперь найдем площадь плоской фигуры. Вот здесь без чертежа обойтись трудно:
На отрезке график функции расположен ниже оси OX, поэтому:
Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (см. также Пример 3 из раздела 7.2.3.).
Заметьте, что чётность косинуса никто не отменял, поэтому мы опять разделили отрезок и удвоили интеграл.
megaobuchalka.ru
