Смежные и вертикальные углы. Определения и свойства.
Смежные и вертикальные углы.
Напомним, что угол – это геометрическая фигура, состоящая из двух лучей, имеющих общее начало. По своему взаимному расположению углы объединяются в группы. Две такие группы мы изучим сегодня.
Смежные углы.
Изобразим прямую , отметим на ней точку . Получили развёрнутый угол . Проведём произвольный луч с началом в точке .
Луч разделил развёрнутый угол на два угла: и . Эти два угла и являются смежными.
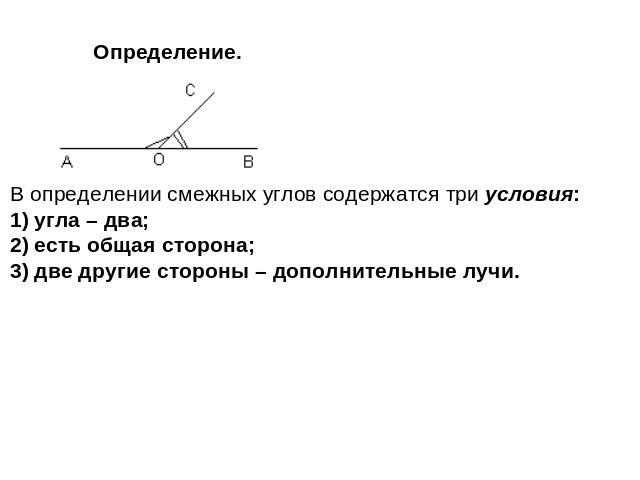
Определение. Смежными называются два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.
На рисунке сверху – общая сторона, и – дополнительные полупрямые. (Напомним, что дополнительные
полупрямые – это две полупрямые, лежащие на одной прямой, имеющие общее начало
и направленные в разные стороны).
Поскольку смежные углы вместе составляют развёрнутый угол, то они обладают следующим свойством:
ТЕОРЕМА: Сумма смежных улов равна .
Дано: и – смежные
Доказать:
Доказательство.
По определению смежных углов, луч является общей стороной углов и , значит, он проходит между сторонами угла . По аксиоме V (градусная мера угла равна сумме градусных мер углов, на которые он разбивается каким-нибудь лучом, проходящим между его сторонами) можем записать равенство:
Опять-таки, по определению смежных углов, лучи и – дополнительные, значит, образуют развёрнутый угол
. А развёрнутый угол имеет градусную меру, равную . Значит,ч.т.д.
Из этой теоремы выходят три следствия, которые
предлагаются для самостоятельного доказательства.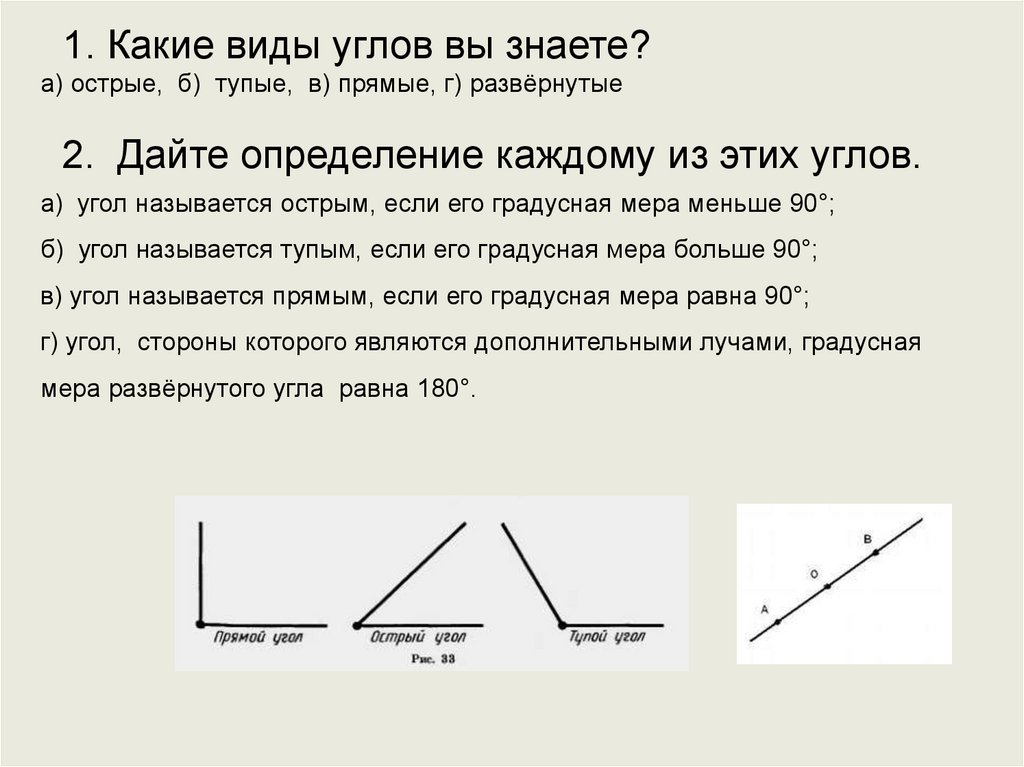
Следствие 1. Если два угла равны, то смежные с ними углы тоже равны.
Следствие 2. Угол, смежный с прямым углом, есть прямой угол.
Следствие 3. Угол, смежный с острым углом, — тупой; угол, смежный с тупым углом, — острый.
Вертикальные углы.
Проведём две прямые
Определение. Вертикальными называются два угла, у которых
стороны одного угла являются дополнительными полупрямыми к сторонам другого
угла.
На рисунке луч является дополнительным к лучу , а луч – дополнительным к лучу . Значит, и – вертикальные. Аналогично, и – тоже вертикальные. Т.е., при пересечении двух прямых получается две пары вертикальных углов. Визуально вы, наверное, заметили, что вертикальные углы равны. А теперь мы это докажем.
ТЕОРЕМА: Вертикальные углы равны.
Дано: и – вертикальные,
и – вертикальные
Доказать: и
Доказательство.
1. – развёрнутый, значит, . Луч проходит между его сторонами, т.е.
2. – развёрнутый, значит, . Луч проходит между его сторонами, т.е.
3. Рассмотрим последние равенства из пункта 1 и пункта 2:
Здесь
мы использовали логическую связку: «Если в двух равенствах правые части равны,
значит, равны и левые части».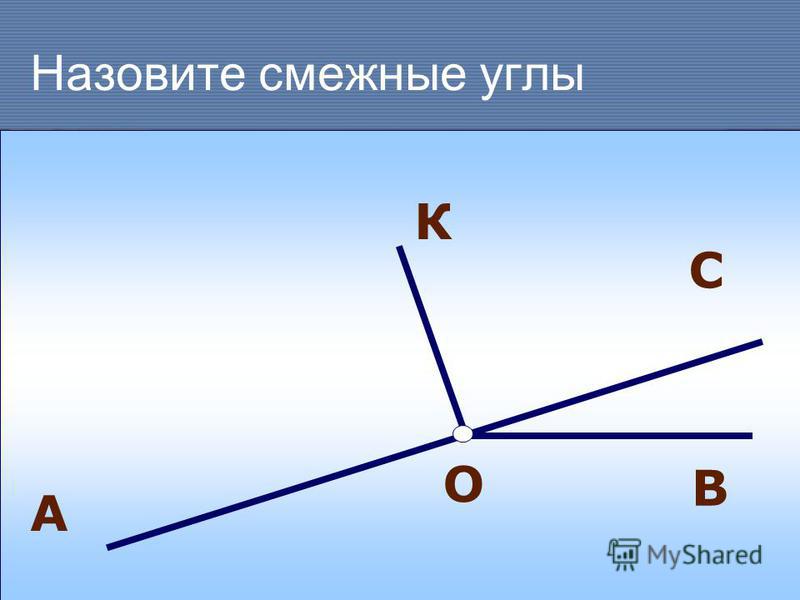
Аналогично доказывается равенство углов . Предлагаю это доказательство провести самостоятельно.
Теорема доказана.
1. Укажите, на каком рисунке изображены смежные углы.
2.
На прямой отмечена точка , из которой проведены два луча и . Назовите пары смежных углов, которые вы видите на этом рисунке.
3. Угол смежный с углом , равен . Найдите угол .
4.
Поставьте
нужные обозначения и выпишите углы, смежные с углом, изображённым на рисунке.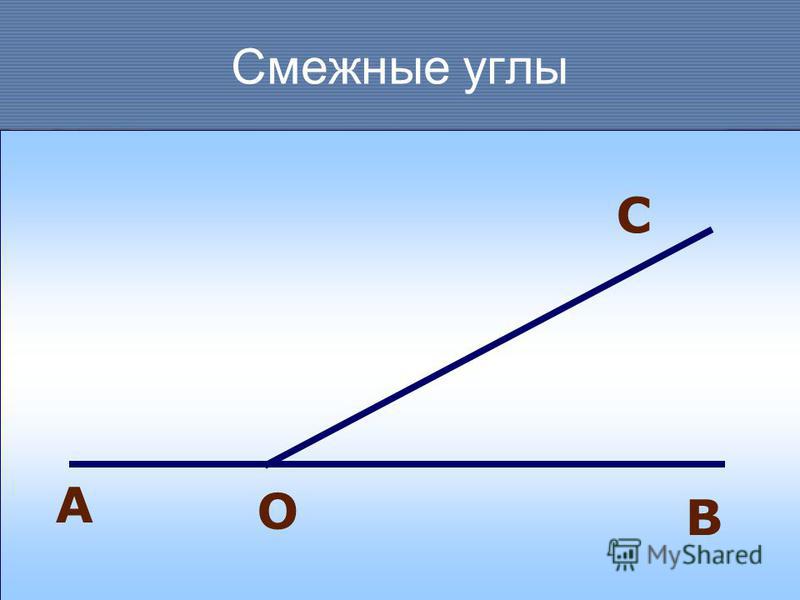
5. Углы и – смежные. Угол больше угла в 4 раза. Найдите угол .
6. Из четырёх углов, образованных при пересечении двух прямых, меньший угол равен . Найдите остальные углы.
7. Нарисуйте угол. Постройте смежный с ним угол. Сколько таких углов можно построить?
8. Нарисуйте луч . Нарисуйте ещё два луча так, чтобы вместе с данным они образовали смежные углы.
9. Найдите угол, смежный с углами: .
10. Нарисуйте два смежных угла. Какая фигура является их пересечением? объединением?
11. Найдите смежные углы, если:
а) один из них на больше другого;
б) их разность равна ;
в) один в 5 раз меньше другого;
г) они равны.
12. Найдите смежные углы, если их градусные меры относятся как:
а)
б)
в)
г) .
13. Чему равен угол, если два смежных с ним угла составляют в сумме ?
14. На рисунке . Найдите .
15.
Из
двух смежных углов один больше другого на . Найдите больший их этих углов.
16. На рисунке . Найдите .
17. Углы и являются смежными. Угол равен . Найдите угол .
18. Из четырёх углов, образованных при пересечении двух прямых, больший угол равен . Найдите остальные углы.
19. Три прямые пересекаются в точке . Найдите сумму углов 1, 2 и 3.
20. На рисунке . Найдите .
21. Укажите, на каком рисунке изображены вертикальные углы.
22. Углы и – смежные, при этом угол меньше угла на . Найдите угол .
23. Сколько различных углов образуется при пересечении двух прямых? Какими свойствами они обладают?
24.
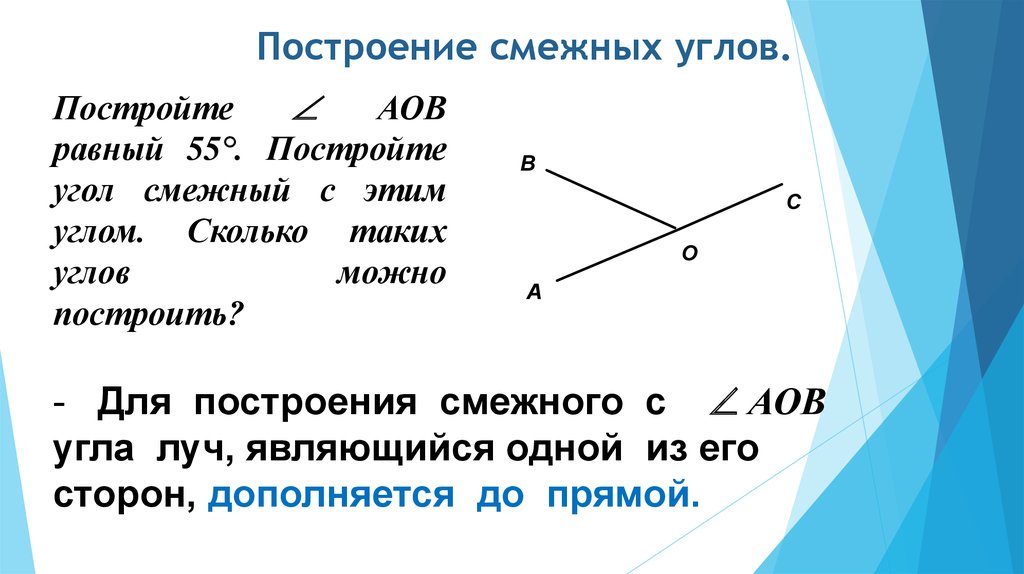
Сколько пар вертикальных углов и сколько пар смежных углов изображено на рисунке? Назовите их.
25. Один из углов, которые получаются при пересечении двух прямых, равен . Чему равны остальные углы?
26. Докажите, что если один из четырёх углов, образованных двумя пересекающимися прямыми, имеет величину , то величины трёх остальных углов также равны .
27. Сумма величин двух вертикальных углов равна . Найдите величину каждого из них.
28. Из двух смежных углов один больше другого на . Найдите меньший их этих углов.
29. На рисунке . Найдите .
30. Один из смежных углов равен . Чему равен второй угол?
31.
На
рисунке изображены три прямые, проходящие через одну точку . Соотношения величин трёх из шести
образовавшихся углов указаны на рисунке.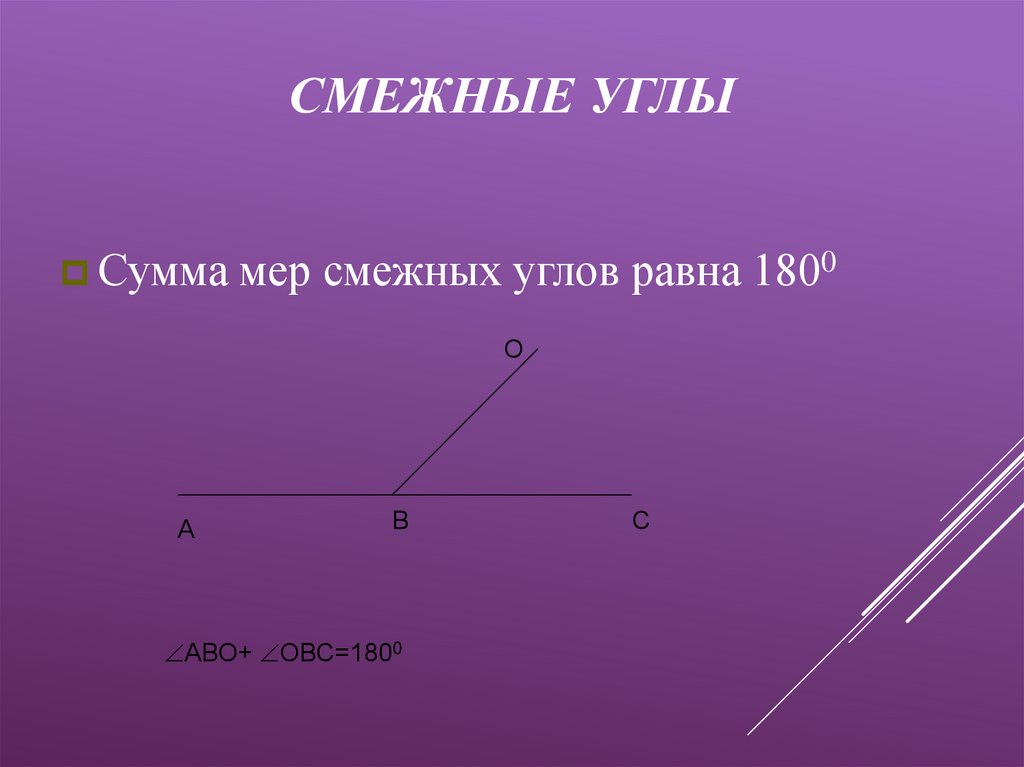
Найдите их градусные меры. Чему равен
наименьший из них?
32.
Нарисуйте два угла и , имеющие общую сторону и общую вершину так, чтобы они были а) смежными; б) не смежными.
33. Найдите , если:
а) на меньше, чем
б) в 3 раза меньше, чем
в) величины углов и относятся, как т.е.
34. Даны пары смежных углов: , причём, луч – биссектриса . Известно, что . Сделайте чертёж и найдите градусную меру .
35. Даны углы и . Какой может быть величина угла ? Сделайте чертёж.
36. Один из двух вертикальных углов равен . Найдите второй угол.
37.
На
рисунке изображены три прямые, проходящие через одну точку .
Соотношения величин трёх из шести
образовавшихся углов указаны на рисунке. Найдите их градусные меры. Чему равен
наибольший из них?
38. Нарисуйте два угла, имеющие общую вершину так, чтобы сторона одного из этих углов являлась бы дополнительной прямой к стороне другого угла, и так, чтобы они были: а) вертикальными; б) не вертикальными.
39. Найдите , если:
а) на меньше, чем
б) в 2 раза меньше
в)
величины углов и относятся как т.е.
40. Даны две пары смежных углов: , причём, луч – биссектриса , а луч – биссектриса . Сделайте чертёж и найдите градусную меру .
41. Даны углы и . Какой может быть величина угла ?
42.
На
рисунке изображены три прямые, проходящие через одну точку .
Соотношения величин трёх из шести образовавшихся
углов указаны на рисунке. Найдите их градусные меры. Чему равен наибольший из
них?
43. Нарисуйте два угла и , имеющие общую сторону и общую вершину так, чтобы они были: а) смежными; б) не смежными.
44. Найдите , если:
а) на меньше, чем
б) в 2 раза меньше
в)
величины углов и относятся как т.е.
45. Даны две пары смежных углов: , причём, луч – биссектриса . Известно, что . Сделайте чертёж и найдите градусную меру .
46. Даны углы и . Какой может быть величина угла ? Сделайте чертёж.
47.
На
рисунке показаны величины двух углов. Найдите величины углов и .
29. При пересечении двух прямых образовалось четыре угла, один из которых в 4 раза меньше суммы остальных трёх углов. Найдите все эти четыре угла.
30.
На рисунке показаны величины двух углов. Найдите величины углов и .
31. При пересечении двух прямых образовалось четыре угла, один из которых относится к сумме трёх других как . Найдите эти четыре угла.
32.
На рисунке показаны величины двух углов. Найдите величины углов и .
33. При пересечении двух прямых образовалось четыре угла, один из которых в 2 раза больше суммы двух других углов. Найдите все эти четыре угла.
34. Смежные углы относятся, как . Найдите эти углы.
35. Один из смежных
углов больше другого на .
Найдите эти углы.
36. При пересечении двух прямых образовалось четыре угла меньше развёрнутого. Найдите эти углы, зная, что один из них на больше половины другого.
37. При пересечении двух прямых образовалось четыре угла меньше развёрнутого. Найдите эти углы, зная, что градусные меры двух из них относятся как .
38. Прямые и пересекаются в точке . Внутри угла взята точка , а внутри угла – точка . .
а) Найдите углы и .
б) Являются ли углы и вертикальными? Ответ объясните.
39. Развёрнутый угол делит плоскость на две полуплоскости. Точка лежит в одной полуплоскости, а точка – в другой; .
а) Равны ли углы и ? Ответ объясните.
б) Являются ли углы и вертикальными? Ответ объясните.
40. Найдите величины углов, образованных при пересечении двух прямых, если один из них равен .
41. Найдите величины углов, образованных при пересечении двух прямых, если:
а) один из них на больше другого;
б) один из них составляет половину другого;
в) сумма величин двух
из них равна .
42. Один из углов, которые образуются при пересечении двух прямых, на меньше другого. Найдите эти углы.
43. Найдите углы, которые образуются при пересечении двух прямых, если сумма трёх углов равна .
44. Дан угол со сторонами и . Проведите полупрямую , дополнительную к . Чему равен угол со сторонами и ? Какими являются углы со сторонами и ?
45.
На рисунке изображены три прямые, пересекающиеся в точке . Найдите сумму углов .
46.
На рисунке . Найдите углы .
47. Сумма вертикальных углов в два раза больше угла, смежного с обоими. Найдите эти углы.
48.
На
плоскости расположены четыре прямые.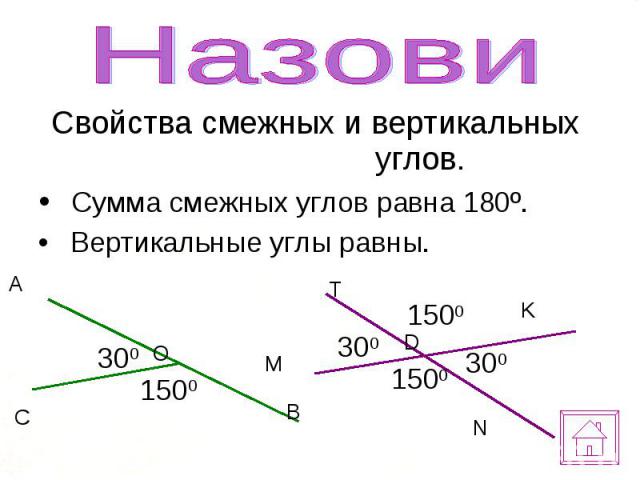
Известны углы между некоторыми из них: . Найдите углы между
остальными парами прямых.
49. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если разность двух из них равна .
50. Точка лежит на биссектрисе угла , а точка лежит внутри угла, смежного с углом . Найдите угол , если .
51. Найдите смежные углы, если их градусные меры относятся как .
52. Точка лежит на биссектрисе угла , а точка лежит внутри угла, вертикального по отношению к углу . Найдите угол , если .
53. Сумма градусных мер двух вертикальных углов равна . Найдите градусную меру каждого из этих углов.
54. Сумма градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
55. Разность градусных мер двух вертикальных углов равна . Найдите градусную меру каждого из этих углов.
56. Разность градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
57. Градусная мера
одного из смежных углов в три раза больше другого.
Найдите градусную меру
большего из смежных углов.
58. Прямые и пересекаются в точке . Сумма градусных мер углов и равна . Найдите градусную меру угла .
59. Прямые и пересекаются в точке . Сумма градусных мер углов и равна . Найдите градусную меру угла .
60. Сумма градусных мер вертикальных углов равна . Найдите градусные меры каждого из этих углов.
61. Сумма градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
62. Разность градусных мер двух вертикальных углов равна . Найдите градусную меру каждого из этих углов.
63. Разность градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
64. Градусная мера одного из смежных углов в семь раз больше другого. Найдите градусную меру большего из смежных углов.
65. Прямые и пересекаются в точке . Сумма градусных мер углов и равна . Найдите градусную меру угла .
66. Прямые и пересекаются в точке . Сумма градусных мер
углов и равн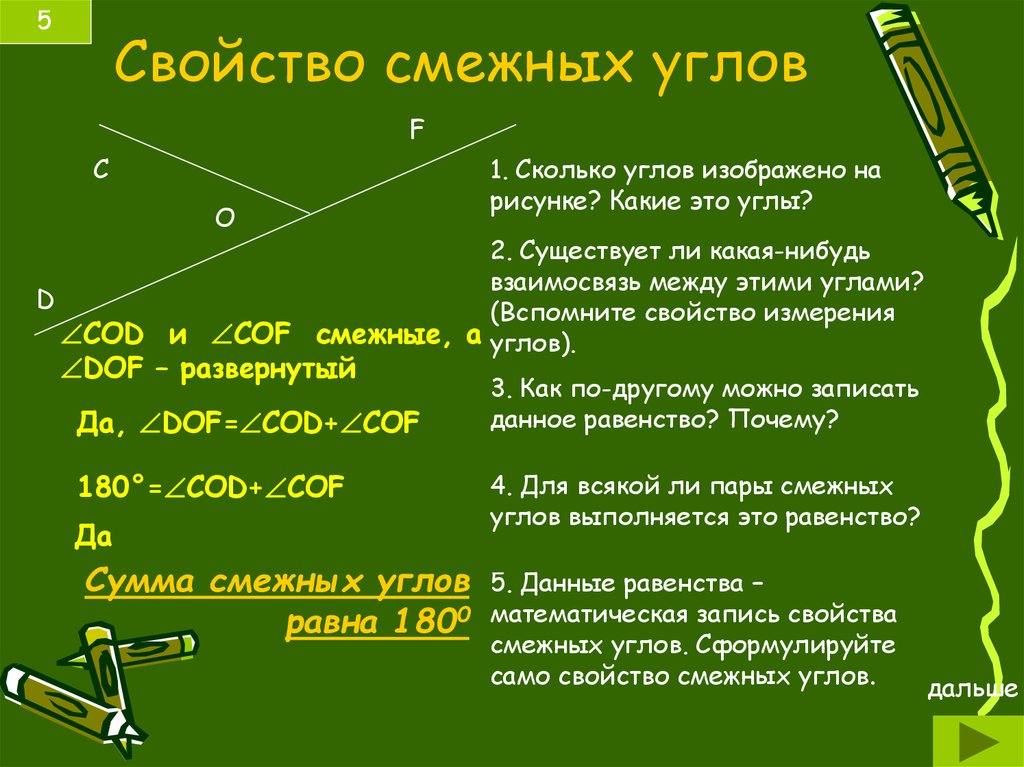а .
Найдите градусную меру
угла .
67. Один из смежных углов на меньше другого. Найдите эти смежные углы.
68. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна .
69. Один из смежных углов в 11 раз больше другого. Найдите эти смежные углы.
70. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна .
71. С помощью транспортира начертите угол, равный , и проведите биссектрису смежного с ним угла.
72. С помощью транспортира начертите угол, равный , и проведите биссектрису смежного с ним угла.
73.
На плоскости проведены четыре попарно пересекающиеся прямые. Укажите пары смежных углов.
74. Углы и – смежные. Угол на больше угла . Найдите угол . Сделайте чертёж.
75. Из точки выходят четыре луча и .
Каждый из углов и является смежным с углом
. Найдите угол , если угол равен . Сделайте рисунок.
76. Углы и – смежные, луч – биссектриса угла . Найдите угол , если . Сделайте рисунок.
77.
На рисунке и . Найдите угол 1.
78. Найдите угол, если сумма двух смежных с ним углов равна .
79.
На плоскости проведены четыре попарно пересекающиеся прямые. Укажите пары смежных углов.
80. Углы и – смежные. Угол в 3 раза больше угла . Найдите угол . Сделайте чертёж.
81. Из точки выходят четыре луча и . Лучи и лежат на одной прямой, а углы и – смежные. Найдите угол , если угол равен . Сделайте рисунок.
82. При пересечении
прямых и образовались четыре
угла.
Углы и – вертикальные, луч – биссектриса угла . Найдите угол , если . Сделайте чертёж.
83.
На рисунке и . Найдите угол 4.
84. Один из смежных углов в пять раз больше другого. Найдите эти углы.
что это такое в геометрии, формула с формулировкой, как найти, чему равна сумма
Содержание:
- Свойства и виды смежных углов в геометрии
- Как найти, чему равна сумма
- Примеры решения задач
Содержание
- Свойства и виды смежных углов в геометрии
- Как найти, чему равна сумма
- Примеры решения задач
Определение
Смежные углы — это два угла, у которых есть общая вершина и одна сторона, а две другие стороны являются продолжением друг друга и лежат на одной прямой.
\circ.\)
Примечание
В паре, если один угол тупой, то по правилу другой обязательно острый.
Если один из углов является прямым, то второй тоже прямой.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).
\circ.\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Что такое смежные углы? | Определение и примеры
Смежные углы — важное понятие для понимания в математике. Они являются ключевым понятием в геометрии и обычно вводятся в математике 4-го класса. Несмотря на то, что дети изучают углы на математических курсах на протяжении всего обучения в школе, часто бывает трудно понять эту концепцию. Если вашему ребенку трудно понять не только углы, но и любые другие понятия в математике, вы можете подумать о курсах репетиторства.
Чтобы помочь вам или вашему ребенку в вашем путешествии к пониманию углов, мы составили это небольшое руководство, которое проведет вас по ключевым понятиям, определениям и часто задаваемым вопросам, касающимся смежных углов.
Воспользуйтесь помощью наставника
Смежные углы Определение
Смежные углы — это два угла, которые имеют общую сторону и общую вершину (угловую точку), но никоим образом не перекрываются. Когда вы разбиваете фразу на смежные углы, становится легко визуализировать, что это такое; это два угла, которые находятся рядом друг с другом.
Как определить смежные углы?
Способность идентифицировать общую сторону и общую вершину — самый простой способ идентифицировать смежный угол. Если два угла имеют одну сторону и оба исходят из одной точки угла (вершины), то они являются смежными углами.
Важно помнить, что смежных угла должны иметь ОБЕ общую сторону и общую вершину . Следовательно, если вы видите два угла, которые выходят из одного угла, но есть другой угол посередине, это означает, что у них нет общих сторон. Это означает, что они не являются смежными углами, поскольку у них нет общих сторон и вершин.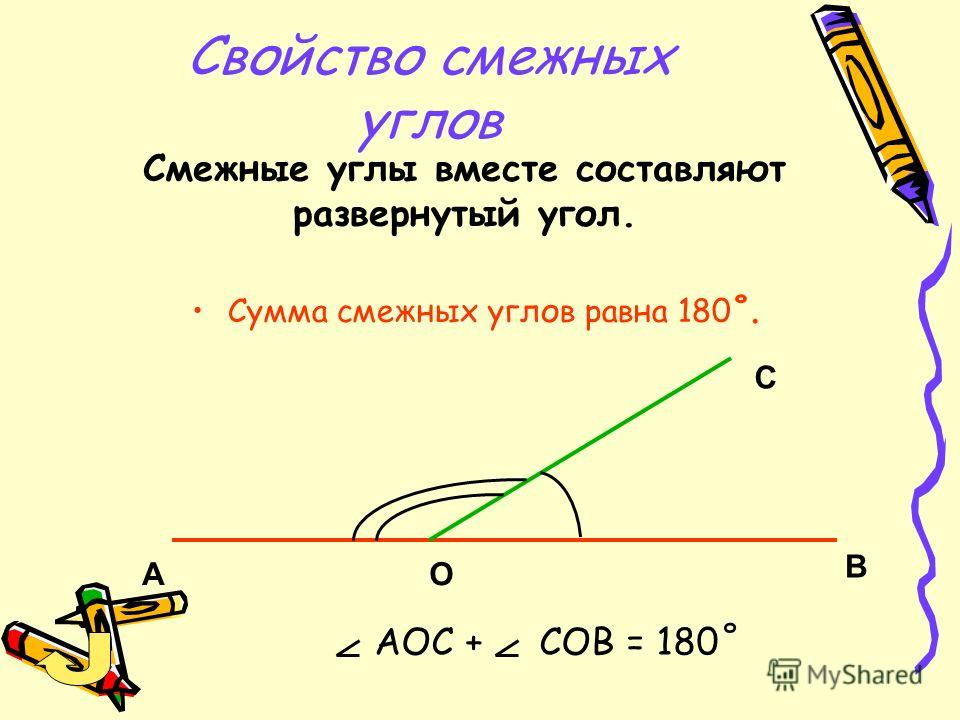
С практикой становится легче определять смежные углы, а примеры помогут вам понять, что вы ищете.
В чем разница между вертикальным и смежным углами?
Определение разницы между соседними углами и вертикальными углами является важным навыком в геометрии. Лучший способ визуализировать разницу между этими двумя типами углов — представить две прямые линии, пересекающиеся друг с другом, образуя крест.
При формировании креста образуются четыре угла. Мы знаем, как определить смежные углы, потому что они имеют общую сторону и общую вершину. Но как определить вертикальный угол? Определить вертикальный угол так же просто, как найти смежный угол. Подобно соседним углам, набор вертикальных углов будет иметь общую точку вершины. Однако им не обязательно иметь общую сторону.
Когда думаешь о кресте, вертикальные углы — это углы, которые составляют против друг друга. Вот почему их иногда называют вертикально противоположными углами .
Какими свойствами обладают смежные углы?
Чтобы еще больше помочь вам визуализировать, как выглядят смежные углы, вот краткий список их свойств:
- У них общая сторона
- Они имеют общую вершину
- Углы не перекрываются
- Хотя они имеют общую сторону в центре, другая сторона не является общей
- У них нет общей внутренней точки
- Они могут быть дополнительными или дополнительными
Примеры смежных углов?
Линейная пара
Чтобы понять, как выглядит линейная пара, вы должны представить себе крест. При пересечении двух прямых образуются четыре угла.
Если вы посмотрите на картинку справа, то увидите, что есть четыре угла, обозначенных цифрами 1, 2, 3 и 4. На этом изображении линейные углы равны 1 и 3, 3 и 2, 2 и 4, 4 и 1.
Вы можете трижды проверить, что два угла являются линейной парой, посмотрев, составляют ли они в сумме 180 градусов.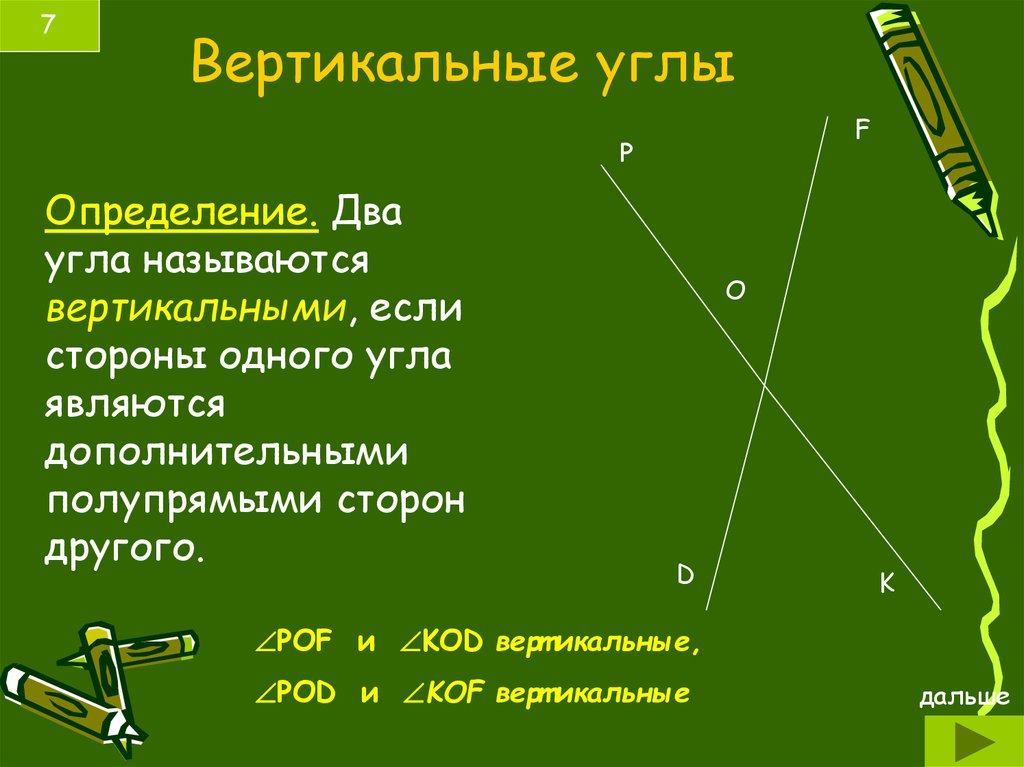
Все линейные пары углов являются дополнительными, поэтому сумма всегда дает 180 градусов . Если углы смежные и в сумме дают 180 градусов, можно с уверенностью утверждать, что они представляют собой линейную пару смежных углов.
Вертикально противоположные углы
Вертикально противоположные углы технически не являются соседними углами, но там, где вы найдете смежные углы, вы, вероятно, также найдете некоторые вертикально противоположные углы.
Вертикальные углы уже были изучены, но для уточнения: вертикальные углы имеют одну и ту же вершину, но разные стороны. Если мы возьмем приведенную выше картинку, 3 и 4 и 1 и 2 считаются вертикально противоположными углами.
Ключевое свойство вертикально противоположных углов состоит в том, что они измеряют точно так же, как . Например, если угол 1 равен 30 градусам, угол 2 также будет равен 30 градусам.
Часто задаваемые вопросы
1.
Что такое смежные углы?Проще говоря, смежные углы — это углы, имеющие общую сторону и общую вершину (угловую точку).
2. Смежные углы равны 180?
В некоторых случаях это ПРАВДА! Дополнительные смежные углы всегда дают в сумме 180. Это потому, что два угла расположены рядом друг с другом на прямой, а все углы на прямой в сумме дают 180.
Однако, если соседние углы не являются линейными парами и другой угол находится в смеси, два соседних угла не дадут в сумме 180.
3. Могут ли вертикальные углы быть смежными?
Поскольку вертикальные и смежные углы часто могут существовать вместе на небольшой площади, многие люди считают, что вертикальные углы также могут быть смежными углами. Это ЛОЖЬ. Вертикальные углы не имеют одной и той же стороны, то есть они не могут быть смежными.
4. Могут ли смежные углы быть линейными парами?
ДА! Смежные углы могут быть линейными парами. Поскольку линейные пары имеют общую сторону и общую вершину, их можно считать смежными углами.
Однако не все смежные углы являются линейными парами.
Это был краткий обзор смежных углов, чтобы помочь вам разобраться с этой неотъемлемой частью программы по геометрии. Тем не менее, вы всегда можете сделать больше, чтобы получить желаемую оценку.
Домашнее репетиторство
Нужна помощь с домашним заданием?
Запросить частного репетитора
Смежные углы — определение, свойства и примеры
Смежные углы — это углы, которые имеют общую вершину и общую сторону, но не пересекаются. Напомним, что вершина — это точка, в которой встречаются два сегмента или две стороны угла, а стороны — это просто сегменты линии, содержащие угол. Типичным примером смежных углов являются внутренние углы многоугольника. Любая пара внутренних углов, имеющих одну общую сторону в многоугольнике, называется смежными внутренними углами.
Здесь мы рассмотрим более подробное определение этих типов углов вместе с диаграммами, иллюстрирующими эти концепции.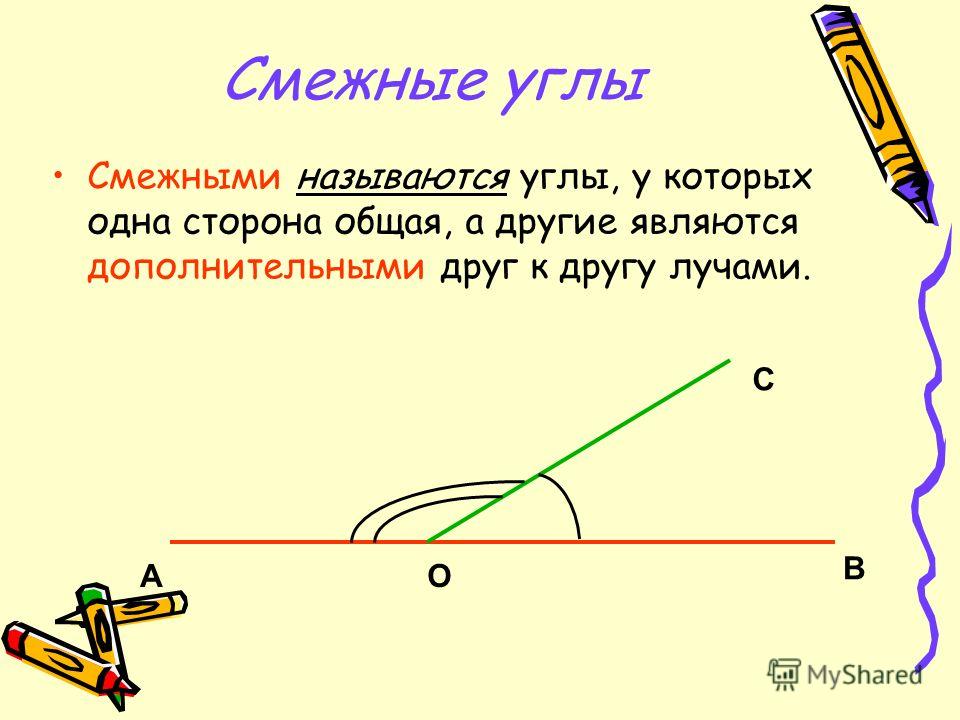
Также мы узнаем о наиболее важных свойствах смежных углов и рассмотрим несколько примеров.
ГЕОМЕТРИЯ
Актуально для …
Изучение смежных углов на примерах.
См. характеристики
Содержание
ГЕОМЕТРИЯ
Актуально для …
Изучение смежных углов на примерах.
См. свойства
Что такое смежные углы?
Смежные углы — это углы, имеющие общую вершину и общую сторону. Точка, где встречаются две стороны и находится угол, называется вершиной. Смежные углы могут быть дополнительными или дополнительными, если эти углы имеют общую вершину и сторону.
Рассмотрим следующие углы. Зеленый угол образован сегментами OA и OC и представлен как ∠AOC. Розовый угол образован сегментами OC и OB и представлен как ∠COB. Эта пара углов расположена близко друг к другу и считается смежной.
Эти углы являются смежными, так как имеют общую вершину, вершину О.
Кроме того, углы также имеют общую сторону, сторону ОС.
Свойства смежных углов
Ниже приведены некоторые важные свойства смежных углов:
- Смежные углы имеют общую вершину.
- Эти углы имеют общую сторону.
- Углы не перекрываются.
- Эти углы не имеют общей внутренней точки.
- Смежные углы могут быть комплементарными или дополняющими.
- Эти углы имеют необщую сторону с обеих сторон общей стороны.
Смежные дополнительные углы
Мы знаем, что смежные углы имеют общую вершину и одну сторону. Напомним, что если сумма двух углов равна 90°, то такие углы называются дополнительными. Следовательно, смежные дополнительные углы — это углы, которые имеют общую вершину и сторону и в сумме дают 90°.
На следующей диаграмме показан пример смежных дополнительных углов.
Смежные дополнительные углы
Эти виды углов одновременно удовлетворяют условиям дополнительных углов и смежных углов.