Формулы по геометрии площади всех фигур: Как найти площадь фигуры, формула

Все формулы по геометрии. Задача в3: площади фигур

Больше половины всех задач В3 из вариантов ЕГЭ — это задачи, в которых надо посчитать площадь фигуры. Чтобы решить их, надо знать формулы по геометрии — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

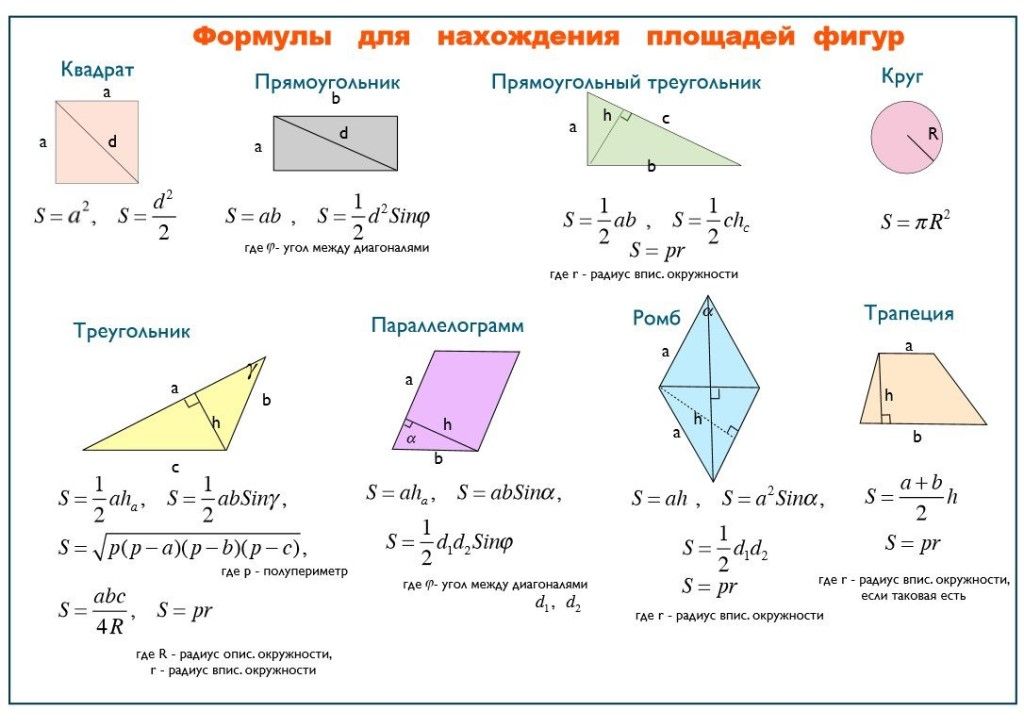
Для начала стоит выучить формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

Конечно же, не все формулы по геометрии есть в нашей таблице. Например, для решения задачи С4 применяются и другие формулы площади треугольника. О них мы обязательно расскажем.

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:

S = 5 + 7,5 = 12,5.

Ответ: 12,5.

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:

S = 25 – 5 – 5 – 4,5 = 10,5.

Ответ: 10,5.

3. Иногда в задании В3 надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.

Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.

На этом рисунке мы видим часть круга. Площадь всего круга равна πR² = π, так как R=1. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна 2πR = 2π (так как R=1), а длина дуги данного сектора равна 2, следовательно, длина дуги в π раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в π раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в π раз меньше, чем площадь всего круга.

Ответ: 1.

И ещё примерно половина прототипов задачи В3 — это простые задачи на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по Х) и что такое ордината (координата по Y). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами. Все прототипы задачи В3 можно найти на сайте

mathege.ru.

Геометрия на ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.

Геометрия на ЕГЭ — это четыре задачи в части и В (две по планиметрии и две по стереометрии), а также задача С2 и для многих недосягаемая С4. Как же научиться их решать?

Начнем с планиметрии. Прежде всего, вам нужно выучить основные формулы геометрии.

На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части В.

Для решения задачи С4 нужна более серьезная подготовка. Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.

Программа по геометрии.

1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).

2. Построение треугольника: практические задания. а) Три стороны треугольника АВС равны 4, 6 и 8 сантиметров соответственно. Постройте треугольник АВС с помощью циркуля и линейки. б) В треугольнике АВС угол В равен 48 градусов, сторона АВ равна двум, ВС равна 9. Постройте треугольник АВС. в) В треугольнике АВС сторона ВС равна 5, угол В равен 26°, угол С равен 58°. Постройте треугольник АВС.

3. Три признака равенства треугольников. Неравенство треугольника.

4. Постройте с помощью циркуля и линейки: а) серединный перпендикуляр к отрезку; б) биссектрису угла.

5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.

6. Теорема о сумме углов треугольника.

7. Внешний угол треугольника.

8. Постройте в одном и том же треугольнике а) три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника. б) три биссектрисы. в) три медианы.

9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.

10. Средняя линия треугольника и ее свойства.

11. Прямоугольный треугольник. Теорема Пифагора.

12. Определения синуса, косинуса и тангенса — для острого угла прямоугольного треугольника — для произвольного угла.

13. Четырехугольники. Сумма углов четырехугольника.

14. Параллелограмм. Определение и свойства. Площадь параллелограмма.

15. Виды параллелограммов и их свойства. (ромб, прямоугольник, квадрат).

16. Трапеция. Средняя линия трапеции. Площадь трапеции.

17. Подобные треугольники. Три признака подобия треугольников.

18. Площадь треугольника. Формулы    и  .

19. Теоремы синусов и косинусов.

20. Чему равно отношение площадей подобных фигур.

21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)

22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)

23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.

24. Теорема о радиусе, проведенном в точку касания.

25. Центральный и вписанный углы. Связь между ними.

26. Теоремы о вписанных углах.

27. Теорема о пересекающихся хордах.

28. Теорема об отрезках длин касательных, проведенных из одной точки.

29. Теорема о секущей и касательной.

30. Дан треугольник АВС. Постройте а) окружность, вписанную в данный треугольник б) окружность, описанную вокруг данного треугольника. Где находятся центры этих окружностей?

31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).

32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?

(Программа по стереометрии будет размещена в ближайшее время.)

Отдельно — тема «Векторы». Напомним, что на ЕГЭ по математике векторы встречаются в задаче В3. Они также пригодятся вам в решении задачи С2.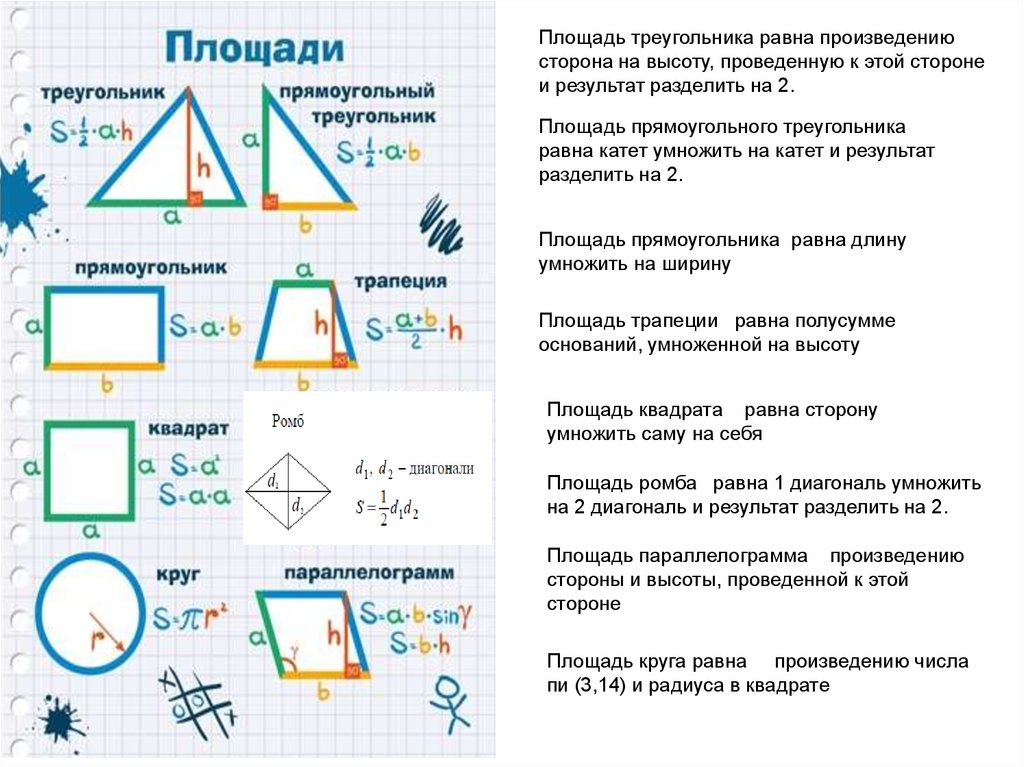

Освоив теорию, можно приступать к решению сложных задач по геометрии, входящих в часть С ЕГЭ. Мы рекомендуем вам сборники: Р. К. Гордин «

ЕГЭ 2012. Математика. Задача С4. Геометрия. Планиметрия» и А. Г. Корянов и А. А. Прокофьев «Пособие по решению заданий типа С4». Можно найти на сайте alexlarin.net.

Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части В, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные С4.

Решая на ЕГЭ задачи С4 по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:

«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника.

Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90º. Другими словами, половина развернутого угла.

Острый угол — меньший 90º.

Тупой угол — больший 90º. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается С. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла А, обозначается а.

Угол А обозначается соответствующей греческой буквой α.

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет а, лежащий напротив угла α, называется

противолежащим (по отношению к углу α). Другой катет b, который лежит на одной из сторон угла α, называется прилежащим.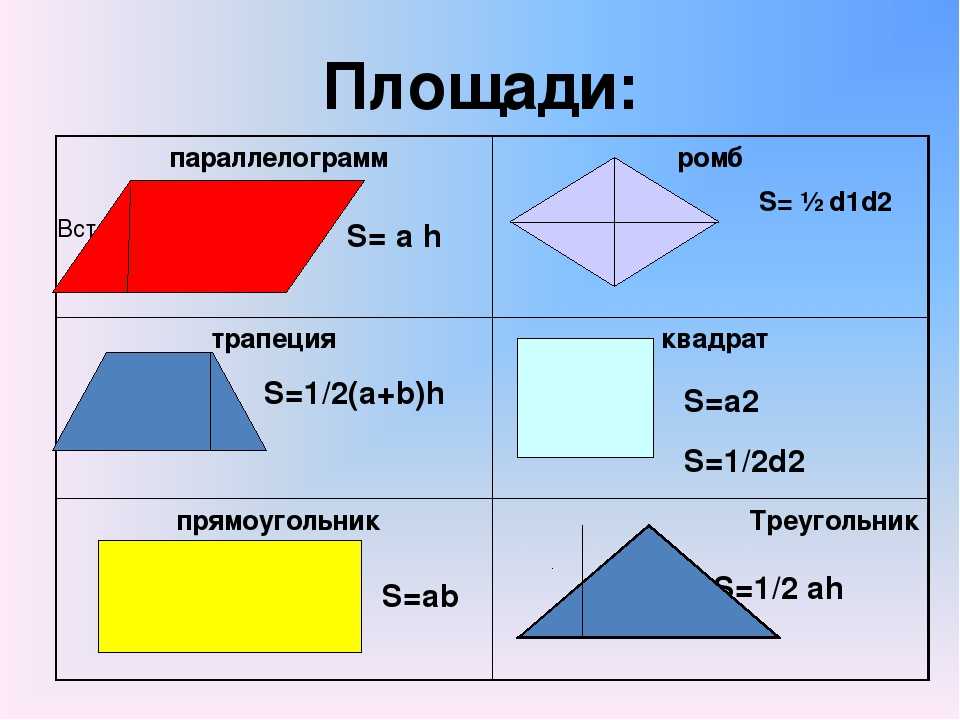

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна 180º. Значит, сумма двух острых углов прямоугольного треугольника равнa 90º.

2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла β катет а будет прилежащим.

Получаем, что cos β = sin A. Иными словами, cos (90º — А) = sin A.

3. Возьмем теорему Пифагора: a² + b² = c².

Поделим обе части на cos² A:

Мы получили основное тригонометрическое тождество:

4. Поделив обе части основного тригонометрического тождества на cos² A, получим:

Это значит, что если нам дан тангенс острого угла α, то мы сразу можем найти его косинус.

Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна 180°.

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: a² + b² = с².

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от 0 до 90°.

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике ABC угол C равен 90°, sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку А+В = 90°, sin A = cos B = 0,1.

2. В треугольнике ABC угол C равен 90°, АВ = 5, . Найдите AC.

Имеем:

Отсюда

Найдем АС по теореме Пифагора.

Задача решена.

Часто в задачах встречаются треугольники с углами 90°, 30° и 60° или с углами 90°, 45° и 45°. Основные соотношения для них запоминайте наизусть!

Для треугольника с углами 90°, 30° и 60° катет, лежащий напротив угла в 30°, равен половине гипотенузы.

Треугольник с углами 90°, 45° и 45° — равнобедренный. В нем гипотенуза в раз больше катета.

Научно-исследовательская работа «Вычисление площади фигур по формуле Пика» • Наука и образование ONLINE

Главная Работы на конкурс Предметное образование Физико-математические дисциплины Научно-исследовательская работа «Вычисление площади фигур по формуле Пика»

Автор: Кобелева Дарья Александровна

Место работы/учебы (аффилиация): МБОУ СОШ №4, 6 класс

Научный руководитель: Гусейнова Раият Аразовна

Всегда было интересно, почему тетрадь по математике – именно в клеточку? Наверное, чтобы удобнее было записывать числа, а еще, чтобы легче было выполнять построения. Клетки на бумаге позволяют выполнять разные чертежи с помощью линейки. Но нужно помнить свойства геометрических фигур, ведь именно они позволяют использовать клетки в полной мере.

Однажды на уроке математики учитель предложил найти нам площадь фигуры по клетчатой бумаге. Все сразу начали делить эту фигуру на составные, и это заняло у нас много времени. И тут я задалась вопросом, какие еще есть способы нахождения площадей фигур по клетчатой бумаге. В поисках рационального способа нахождения площади многоугольника по клетчатой бумаге в интернете, я наткнулась на формулу Пика. Мне сразу же стало интересно, как она работает.

Актуальность работы заключается в том, что задачи по клетчатой бумаге рассматриваются в контрольно-измерительных материалах ОГЭ и ЕГЭ. Существуют разные способы выполнения таких заданий: способ сложения, способ вычитания и др. Формула Пика не изучается в школьной программе курса геометрии. Поэтому, считаю изучение этого материала полезным для применения его не только в дальнейшем учебном процессе, но и для решения нестандартных олимпиадных задач.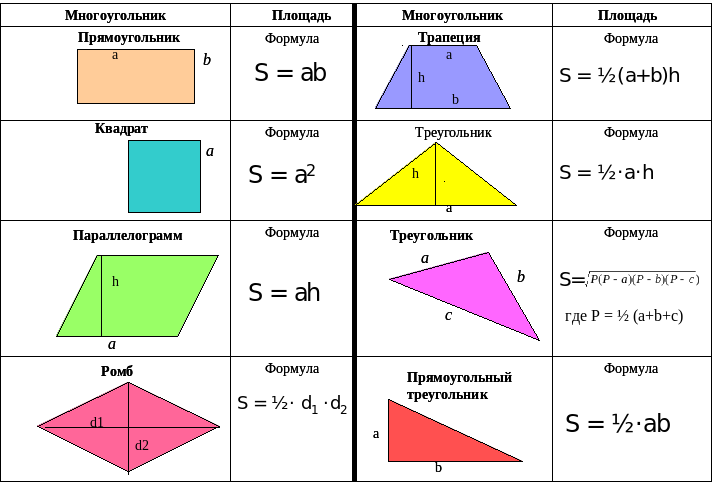

Новизна работы заключается в применении формулы Пика в школьной программе.

Гипотеза: вычисление площади фигуры по формуле Пика обеспечит правильное и быстрое решение задач по сравнению с вычислением площади фигур по формулам планиметрии.

Объект исследования: формула Пика.

Предмет исследования: применение формулы Пика при решении задач на нахождение площади фигур, изображенных на клетчатой бумаге.

Цель исследования: изучение формулы Пика и ее применение для вычисления площади многоугольников по клетчатой бумаге.

Задачи:

1. Изучить литературу по теме исследования.
2. Отобрать материал для исследования, выбрать главную, интересную, понятную информацию.
3. Проанализировать и систематизировать полученную информацию.
4. Провести эксперимент, направленный на выявление эффективного способа вычисления площадей фигур по клетчатой бумаге.
5. Сделать выводы по результатам работы.
6. Подобрать наиболее интересные, наглядные примеры.
7. Разработать рекомендации по использованию формулы Пика в школьной программе.

Методы исследования:

• Моделирование.
• Анализ и классификация информации.
• Синтез.
• Сравнение, обобщение.

Исследовательский проект «Математика в архитектуре»

Доступна к просмотру полнотекстовая версия работы

Математика – наука, изучающая пространственные формы  и количественные отношения. Меня заинтересовал вопрос о том, где применяются законы математики, я начала углубляться в эту тему и поняла, что  многие математические теории нередко кажутся искусств…

Посмотреть работу

Урок геометрии в 9 классе «Умножение вектора на число»

Доступна к просмотру полнотекстовая версия работы

В ходе данного урока был реализован системно-деятельностный подход: наличие мотивации на каждом этапе урока; система вопросов учителя, способствующих созданию ситуации успеха, дающих возможность учащимся самостоятельно сформулировать тему, цели урока…

Посмотреть работу

4″>Исследовательская работа «Лента Мёбиуса — простая и невероятная»

Доступна к просмотру полнотекстовая версия работы

Изучение различных необычных фигур, их свойств и их неожиданных и нестандартных применений является достаточно актуальным явлением. В настоящее время в математическую жизнь вошла компьютерная геометрия, позволяющая представить сложные математические…

Посмотреть работу

Презентация «Неевклидовы геометрии»

Доступна к просмотру полнотекстовая версия работы

Изучая геометрию, ученики развивают свое мышление и расширяют горизонты своего познания. Школьный курс геометрии предполагает изучение евклидовой геометрии. Учащиеся, широко интересующиеся наукой математика и историей её развития, пытаются узнать о «…

Посмотреть работу

Мероприятие завершено

Основные формулы геометрии — GeeksforGeeks

В математике геометрия выступает как дисциплина изучения и предмет для анализа форм и структур вместе с их свойствами.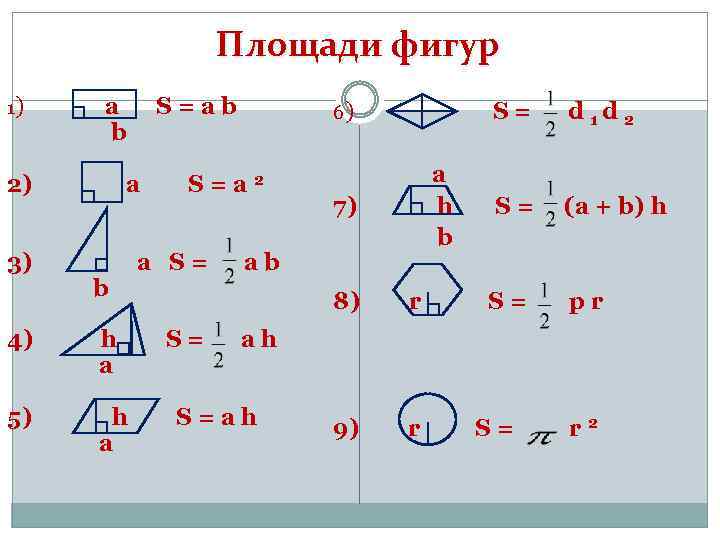 Приведенная ниже статья иллюстрирует стандартные фиксированные или производные формулы геометрии для расчета различных параметров конкретной формы. Эти формулы используются для определения неизвестных сторон, углов или других его величин.

Формула базовой геометрии

Формула представляет собой математическое правило, которое формируется путем вывода взаимосвязи между двумя или более физическими величинами или математическими отношениями. формулы обычно представляются в символической форме с помощью математических символов. Эти символические представления формул состоят из переменных, констант, операционных знаков и терминов.

Геометрические формулы являются стандартными производными формулами для расчета параметров фигур. Этими параметрами являются площадь, объем, периметр, окружность, общая площадь поверхности, площадь боковой поверхности и т. Д. Каждая форма, изучаемая в геометрии, имеет для них свою собственную формулу. Эти формулы перечислены ниже.

Квадрат

• Периметр Квадрата = 4a
• Площадь Квадрата = a ²

Где «a» — длина стороны квадрата

Прямоугольник

• Периметр прямоугольника = 2(l + b)
• Площадь прямоугольника = l2 9009 × b 90 ‘l’ — это длина, а ‘b’ — это ширина

Треугольник

• Площадь треугольника = A = 1/2 × b × h

Где ‘b  – основание треугольника 903.

и «h» высота треугольника

Трапеция

• Площадь трапеции = A =1/2 × (b1 + b2) × h

Где b1 и b2 — высота основания трапеции 9, h0030 90 of the Trapezoid

Circle

• Area of ​​Circle = A = π × r2
• Circumference of Circle = A = 2πr

Where ‘r’ is the radius of a Circle

Куб

• Площадь поверхности куба = 6A ²

, где ‘A’ — длина сторон куба

Цилиндер

.
• Общая площадь поверхности цилиндра = 2πr(r + h)
• Объем цилиндра = V = πr2h

Цилиндр

Конус

• Площадь криволинейной поверхности конуса = πrl
• Общая площадь поверхности конуса = πr(r + l) = πr[r + √(h 90 2 ^{2 900) )]}
• Объем конуса = V =1/2× πr ² h

Здесь ‘r’ — радиус основания конуса

, а h — высота конуса

Сфера

• Площадь поверхности сферы = 4πr ²
• Объем сферы = 4/3 × πr ³

Где r – радиус сферы

Примеры задач

Задача 1. Если радиус окружности равен 14 см. Найдите площадь данного круга.

Решение:

Дано

Радиус окружности равен 14см.

Имеем,

Площадь круга (A)=πr ²

=>22/7 x 14 x 14

=>616см ²

Задача 2. Найдите площадь треугольника с основанием 12см и высотой 8см.

Решение:

Дано

Основание треугольника равно 12см.

Высота треугольника 8см.

Имеем,

Площадь треугольника(А)=1/2 x b x h

=>1/2 x 12 x 8

=>48 см ²

Задача 3. Найти периметр заданного треугольника. прямоугольник длиной 10 см и шириной 4 см.

Решение:

Дано

Длина прямоугольника 10см.

Ширина прямоугольника 4см.

Имеем,

Периметр прямоугольника(P)= 2(l+b)

=>2(10+4)

=>2 x 14

=>28см

Задача 4. Найти периметр квадрата, длина которого 5 см.

Решение:

Дано

Длина квадрата 5см.

Имеем,

Периметр квадрата(P)= 4l

=> 4 x 5

=>20см

Задача 5. Найдите объем сферы, имеющей радиус 9см.

Решение:

Дано

Радиус сферы равен 9см.

У нас есть

Объем сферы (V)=4/3 πr ³

=>4/3 x 22/7 x (9) ³

=>3054,805см

2 3

Задача 6. Вычислите площадь трапеции с основаниями 8см и 10см и высотой 12см.

Решение:

Дано

Пусть основания трапеции равны b1 и b2 со значениями 8см и 10см соответственно.

Высота трапеции 12см.

У нас есть,

Площадь трапеции = A =1/2 × (b1 + b2) × h

=>1/2 x (8 +10) x 12

=>1/2 x 18 x 12

=> 216/2

=>108см ²

Задача 7. Найти объем данного конуса радиусом 6см и высотой 12см.

Решение:

Дано

Радиус конуса равен 6см.

Высота данного конуса 12см

Имеем,

Объем конуса = V =1/2× πr ² h

=>1/2 x 22/7 x (6) ² x 12

=>9504/14

=>678,85 см ³

Задача 8. Вычислить площадь криволинейной поверхности цилиндра радиусом 4см и высотой 8см.

Решение:

Дано

Радиус цилиндра равен 4см.

Высота цилиндра 8см.

Имеем,

Площадь криволинейной поверхности = 2πrh

=>2 x 22/7 x 4 x 8

=>201,14 см ²

Задача 9. Вычислите площадь куба. сторона 3 см.

Решение:

Дано

Длина стороны 3см.

У нас есть,

Площадь куба(A)= 6a ²

=> 6 x 3 x3

=> 54 см ²

Основы геометрии никоим образом не является «сексуальным» предметом; на самом деле, как правило, вычисление

углов, объемов и площадей редко считается заманчивым или забавным.

Возможно ли обратное?

За последние 10 лет мы видели, как математика проникла в фильмов и телешоу ; Теория большого взрыва — яркий тому пример. Конечно, уравнения не занимают центральное место в сюжете, и, честно говоря, только первые несколько шоу были насыщены математикой. После этого алгебраическая работа всплывала лишь изредка.

Тем не менее, приятно видеть, как сложные расчеты разыгрываются на популярной арене, а еще лучше, что в 9 участвуют как мужские, так и женские персонажи.0011 корректировка уравнений ; всего 20 лет назад кинематографическими математиками могли быть только мужчины!

Теперь ваша очередь освоить уравнения базовой геометрии , и вам нужен самый эффективный способ сделать это. Или, может быть, вы поклонник Декарта и хотите поднять декартовскую геометрию на новый уровень, но для начала вам нужен прочный фундамент.

Ваш Superprof поможет вам разобраться в основных геометрических формулах; хватайте свои угольники и циркуль… мы пошли!

Найдите рядом со мной репетитора по математике на Superprof.

Лучшие репетиторы по математике

Поехали

Основные фигуры

Ищите здесь репетитора по математике из Юты.

Сколько геометрических фигур вы можете найти в этом узоре? Изображение от monicore с Pixabay

У вас может возникнуть соблазн подумать «круг», «треугольник» или «квадрат», и вы будете абсолютно правы.

Каждая из этих геометрических фигур относится к одной из следующих четырех основных категорий:

• Треугольники имеют три стороны; стороны могут быть одинаковой длины (равносторонний треугольник) или все разной длины (разносторонний треугольник).
• Четырехугольник — это любой четырехугольник. Это могут быть прямоугольники, квадраты, ромбы, ромбы…
  • параллелограмм , фигура с двумя парами равных сторон, которая также является четырехугольником
• Многоугольники: буквально «много сторон». Эти формы могут быть треугольниками, шестиугольниками, пятиугольниками… все эти «угольники» являются многоугольниками. По сути, все, что имеет прямые стороны, называется многоугольником.
• Окружности являются классом сами по себе, потому что они не имеют прямых линий

Их уникальные характеристики включают:

• Квадраты имеют четыре равные стороны и четыре прямых угла
• Прямоугольники имеют две пары равных сторон
• Трапеция имеет только одна пара параллельных сторон
  • Трапеция не имеет сторон одинаковой длины
• Ромбы: противоположные стороны и противоположные углы равны
• Равнобедренный треугольник имеет две равные стороны
• Прямоугольные треугольники имеют один угол в 90 градусов, противоположный гипотенузе

У каждой из этих фигур есть собственная формула для вычисления периметра, площади и углов. С некоторыми вы, возможно, знакомы, например, с теоремой Пифагора , в то время как другие, возможно, менее запоминающиеся.

Давайте посмотрим на них сейчас.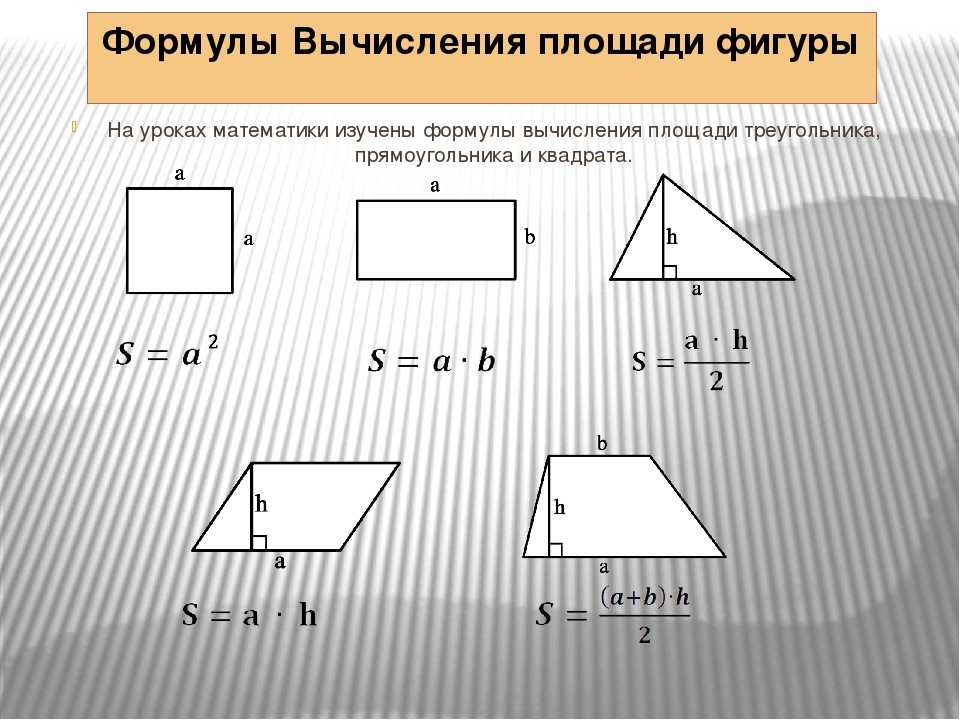

Вам нужна помощь в изучении геометрии? Возможно, вы могли бы найти репетитора по геометрии…

Вычисление треугольников

Начиная с форм с наименьшим количеством сторон (но иногда и с самыми сложными формулами), мы беремся за геометрические формулы!

Простейшая формула для периметра любого треугольника: a+b+c, , где каждая буква обозначает сторону. Он прекрасен в своей простоте и с ним легко работать, если вы знаете длину каждой стороны.

Допустим, ваш треугольник имеет следующие размеры: a = 3 дюйма, b = 4 дюйма и c = 5 дюймов

Тогда его периметр будет 3+4+5=12 дюймов.

Ясно, что этот треугольник не является ни равносторонним, ни равнобедренным; и не прямоугольный треугольник. Как бы мы вычислили периметр, если даны только два значения, нижняя и одна сторона?

В таком случае мы должны опираться на теорему Пифагора : a ² +b ² =c ² .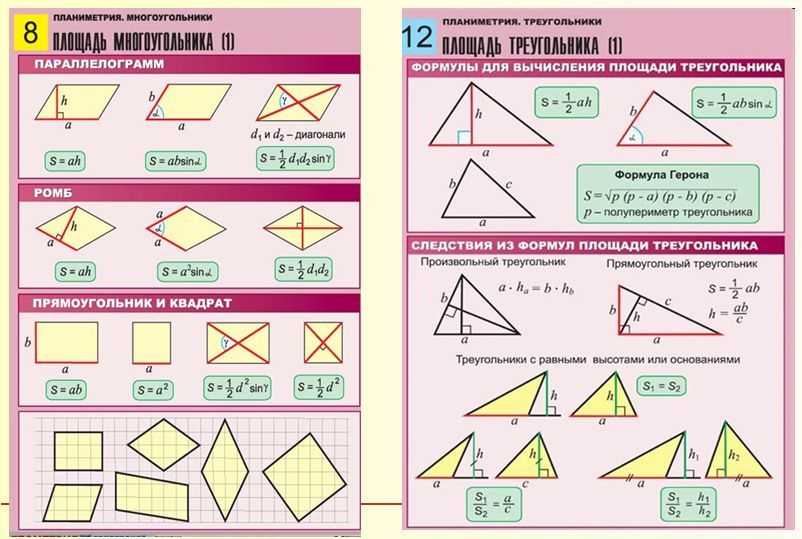 Ты помнишь тот, да?

Сначала проведите линию от вершины треугольника прямо к его основанию. Эта линия, h, должна быть перпендикулярной к основанию, тем самым образуя две Уголки 90 градусов – по одному с каждой стороны линии.

Теперь у вас есть два прямоугольных треугольника, один из которых имеет измерения как для a, так и для b. Отсюда очень просто подставить известные значения в теорему (не забудьте возвести их в квадрат!) и найти недостающее значение.

Попробуем его с вымышленным треугольником:

A = неизвестный B = 5 C = 7

A ² * 5 ² = 7 ²

A ² * 25 = 49. значение должно стоять отдельно на одной стороне уравнения

a ² = 49 – 25 переместите 25 в другую сторону от знака равенства, вычтя его из заданного значения c

a ² = 24

Теперь вам нужно вычислить квадратный корень из 24, чтобы найти значение ‘a’ , которое равно 4,898. После того, как вы вычислили периметр одного прямоугольного треугольника, вы должны вычислить второй, чтобы получить размеры исходного треугольника.

Поздравляем! Теперь вы знаете, как вычислить периметр любого треугольника!

Выполните поиск здесь, чтобы найти некоторые из лучших эффективных онлайн-курсов по математике на суперпрофессионале.

Этот и подобные знаки в виде треугольников используются, чтобы призвать к осторожности на дорогах Изображение Герда Альтманна с Pixabay , вычисление площади треугольника немного сложнее.

Если значения даны для всех трех сторон, вы можете применить Формулу Герона :

площадь = квадратный корень из [s(s-a)(s-b)(s-c)], где s равно полупериметр, то есть (a+b+c)/2

Это только кажется сложным; помните, что при работе с формулой вам нужно только подставить известные значения, чтобы найти неизвестное. Если подумать таким образом, Hero’s Formula , как ее еще называют, довольно проста!

Теперь об уравнениях «площади треугольников», где одно или несколько значений неизвестны.

Если вы знаете только значение основания треугольника и его высоты , вы можете применить: площадь = (½) * b * h

Если известны только длина двух сторон и степень угла, соединяющего их, вы должны использовать тригонометрию , чтобы найти пропущенные значения. Основная формула:

Площадь = (½) * a * b * sin C

Имейте в виду, что строчные буквы обозначают линейные размеры, а прописные буквы обозначают углы.

Если бы вы знали только значения сторон a и c, вы бы подставили их и вычислили sin B . Точно так же, если вы знаете b и c, вы бы использовали sin A , чтобы получить площадь вашего треугольника.

Почему бы не попрактиковаться в них, прежде чем двигаться дальше…

Лучшие репетиторы по математике

Поехали

Вычисление четырехугольников

Возможно, вы сможете вычислить периметр квадрата или прямоугольника в своем спать. Эти формулы таковы: P=4a (a представляет стороны квадрата) и P=2l + 2w соответственно.

Эти расчеты площадей также должны прийти к вам довольно легко. Для квадратов это A=a ² , а для прямоугольников это A=l * w . Просто, верно?

Все становится сложнее, когда мы переходим к параллелограммам и трапециям; чтобы решить оба этих уравнения, вам нужно знать высоту фигуры (h) и длину основания (b) — линия внизу.

Зная эти значения, выберите соответствующую формулу для фигуры:

b * h = площадь параллелограмма (½)(a+b) * h = площадь трапеций, где «a» представляет собой сторону, противоположную «b».

Четырехугольники могут быть самыми простыми фигурами для работы. Если вам нужна дополнительная практика, в Интернете есть множество ресурсов, где вы можете найти рабочие листы по геометрии и уравнения для решения.

Вычисление многоугольников

Столкнулись ли вы с апейрогеном (многоугольник с бесконечным числом сторон) или с более знакомым шестиугольником, вам нужно знать, как вычислить его периметр и площадь.

К счастью, апейрогоны существуют только гипотетически; представьте, что у вас есть такая фигура, для которой можно вычислить площадь!

Если все стороны вашего многоугольника имеют одинаковую длину, вы можете применить P=n * v , где « n » — количество сторон, а « v » — значение каждой стороны.

Если стороны указанного многоугольника не имеют одинаковой длины, вам придется сложить эти значения , чтобы получить его периметр.

Знак «Стоп», пожалуй, самый известный правильный многоугольник. Изображение Walter Knerr с Pixabay

Вычисление площадей многоугольников

Существует несколько способов определения значения площади любого многоугольника, некоторые из которых включают вычисления для треугольников.

Сначала мы займемся уравнениями правильного многоугольника; такой, у которого все стороны одинаковой длины. Прежде чем мы сможем начать любое шифрование, мы должны определить радиус многоугольника .

Это включает в себя рисование круга внутри многоугольника таким образом, чтобы периметр круга касался периметра многоугольника. это называется вписанный круг . Как только мы узнаем значение этого радиуса, мы можем применить эту формулу:

A = ½ * p * r

Формулы становятся более сложными, чем больше сторон у многоугольника.

Допустим, количество сторон представлено ‘n’ , а количество сторон — s . Радиус, также называемый апофемой , обозначается как « a ». Конечно, «A» представляет собой «площадь», что дает формулу, которая выглядит так:

A = ns/4 √ 4-s ²

Отсюда формулы становятся еще более сложными. Они заставляют вас бороться с основами геометрии? Вы можете обратиться к нашему полному руководству!

Вычисление окружностей

Окружности не содержат ни углов, ни прямых, а их периметры называются «окружностями». Однако для их вычислений требуется по крайней мере отрезок прямой, который необходим для любой формулы для окружностей.

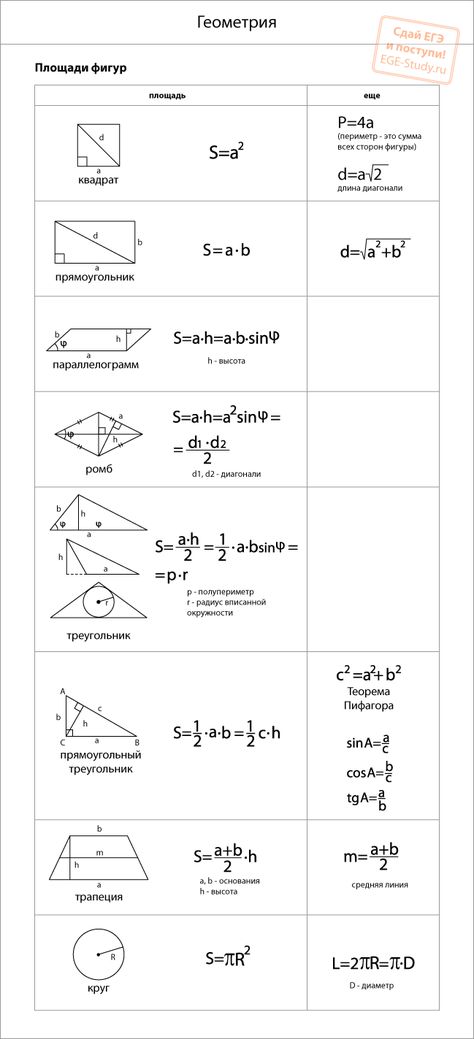
Как ни странно, формула для вычисления площадей кругов известна больше, чем, возможно, для любой другой геометрической фигуры: πr ² , или pi * r2

Наверняка вы знаете/помните, что число pi (π) равно 3,1415…

Менее известная формула для вычисления окружностей. равно: 2 * π * r

Имейте в виду, что это формулы для вычисления площади и периметра двумерных фигур ; как только они приобретают дополнительное измерение – они становятся трехмерными формами и заслуживают расчета объема, а также площади и периметра.