Какой угол считается острым: Острые и тупые углы — урок. Математика, 2 класс.

Содержание

Виды углов. Измерение углов

На каждом из рисунков 82, a − г изображены два луча. На каком из рисунков пара лучей образует угол, сторонами которого являются эти лучи?

Поскольку на рисунках 82, а − в начала лучей не совпадают, то они не могут служить сторонами угла. Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.

Угол, стороны которого образуют прямую, нахывают развернутым.

Углы, как и отрезки, можно измерять. Напомним, что для измерения отрезков мы использовали единичный отрезок (1 мм, 1 см и т.п.).

Однако для измерения углов мы пока не имеем такого единичного угла.

Создать его можно, например, так. Разделим развернутый угол на 180 равных углов (рис. 83). Угол, образованный двумя соседними лучами, выбирают за единицу измерения. Его величину называют градусом (от лат. gradus − «шаг», «ступенька») и записывают 1°.

Измерить угол − значит подсчитать, сколько единичных углов в нем помещается.

Тогда величина или, как еще принято говорить, градусная мера развернутого угла равна 180°.

Для измерения углов используют специальный прибор − транспортир (рис. 84). Он состоит, как правило, из полукольца, соединенного с линейкой. Его шкала содержит 180 делений.

Чтобы измерить угол, совместим его вершину с центром транспортира таким образом, чтобы одна из сторон угла прошла по линейке (рис. 85).

Тогда штрих на шкале, через который пройдет вторая сторона, укажет градусная (величину) этого угла.

Так, на рисунке 85 градусная мера угла AOB равна 55°. Пишут: ∠AOB = 55°. На рисунке 86 имеем: ∠MON = 134°.

Равные углы имеют равные градусные меры. Из двух неравных углов бОльшим будем считать тот, градусная мера которого больше. Например, из трех углов, изображенных на рисунке 87, ∠MON − наибольший. В этом легко убедиться, измерив углы транспортиром.

Величина угла обладает следующим свойством.

Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (рис. 88), т.е.

∠ABC = ∠ABD + ∠DBC.

Угол, градусная мера которого меньше 90°, называют острым (рис. 89, a).

Угол, градусная мера которого равна 90°, называют прямым (рис. 89, б).

На рисунке прямой угол обозначает так: ∟.

Угол, градусная мера которого больше 90°, но меньше 180° называют тупым (рис. 89, в).

Отметим, что биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90°. Следовательно, биссектриса развернутого угла делит его на два прямых угла (рис. 90).

Пример 1. Дан луч OA. Постройте угол BOA, равный 72°.

Решение.

Совместим центр транспортира с точкой O так, чтобы луч OA прошел по линейке. Выберем на кольце транспортира штрих, который соответствует 72°. Возле этого штриха отметим точку B (рис. 91). Проведем луч OB. Угол BOA − искомый.

Если дан луч OA и построен угол BOA, то говорят, что от луча OA отложен угол BOA.

Пример 2. Из вершины угла ABC проведены два луча BK и BM так, что ∠ABK = 48°, ∠CBM = 72° (рис. 92).

Вычислите величину угла ABC, если ∠MBK = 16°.

Решение.

Имеем: ∠ABM = ∠ABK − ∠MBK, ∠ABM = 48° − 16° = 32°;

∠ABC = ∠ABM + ∠СBM, ∠ABC = 32° + 72° = 104°.

Ответ: 104°.

Измерение углов | 7 класс | Геометрия

Содержание

На прошлом уроке выяснилось, что единицей измерения углов и дуг является градус, равный $\frac{1}{360}$ окружности. Измерение углов, следовательно, представляет из себя «процесс нахождения», сколько частей окружности ($\frac{x}{360}$) заключено между сторонами угла.

Это отвечает на большую часть вопросов, что мы задавали ранее, однако не на все.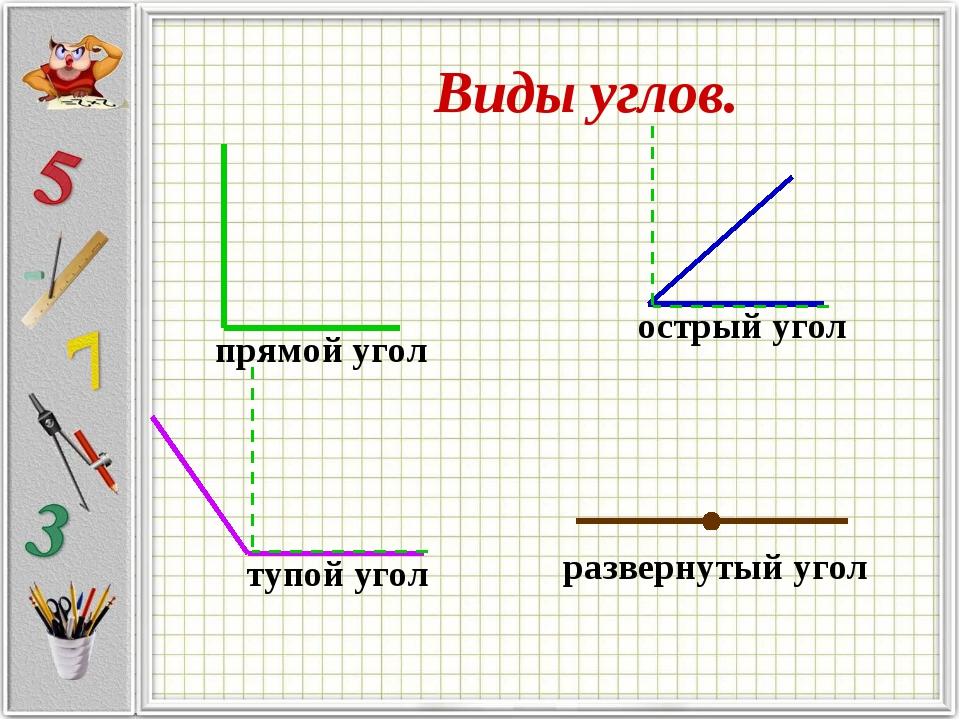 \\circ$$»]}]}

Измерение углов транспортиром

Измерительным инструментом углов является транспортир. Он представляет из себя пластину, выполненную в форме круга или полукруга, основанием которого иногда бывает линейка. Разметка полукругового транспортира состоит из 180 градусов, кругового — из 360. По своей сути транспортир — это конечный результат идеи о делении окружности на 360 ровных частей и нанесении на окружность соответствующей разметки.

Полукруговой транспортир

Круговой транспортир

Как пользоваться транспортиром для измерени

Измерение углов в школьном курсе геометрии вполне обходится упрощенной версией транспортира — полукруговой. На самом деле, транспортир используется не только для измерения, но и для построения углов. Вначале мы разберем, как проводить измерение углов транспортиром.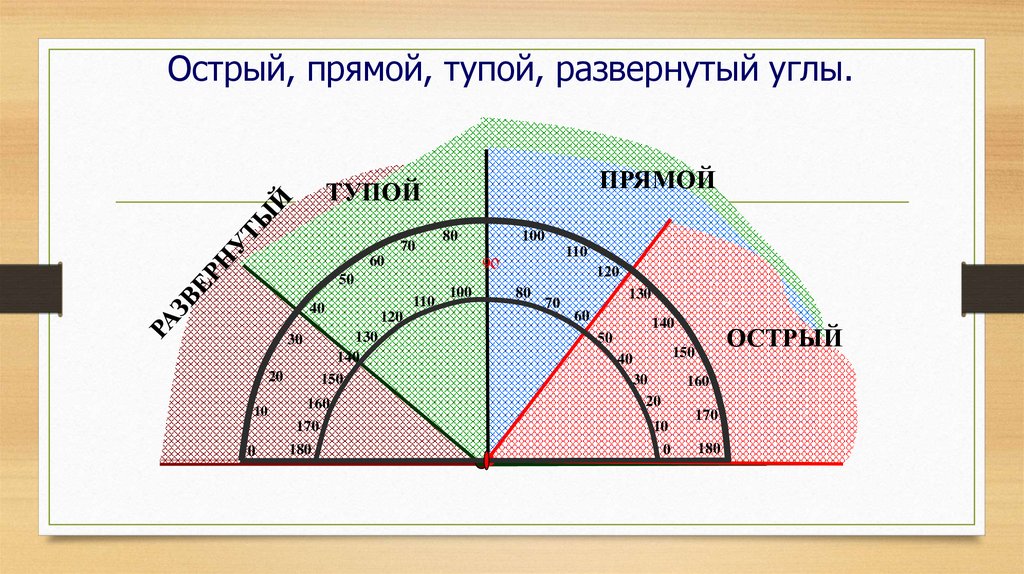 \circ$ небольшой вспомогательной точкой. Теперь проведем через эту вспомогательную точку и точку $A$ луч.

Нюанс!

Обратите внимание, что углы принято откладывать против часовой стрелки. Альтернативная разметка ниже основной — по часовой стрелке — предлагается на транспортире, чтобы было удобно проводить измерение углов. Ориентация углов на плоскости разная, и не всегда бывает хорошо иметь под рукой разметку, нанесенную только против часовой стрелки.

Построения линейкой

Руководствуясь условием поставленной задачи, отметим точку $C$ на основании таким образом, чтобы расстояние между точками $A$ и $C$ составляло $4~см$. Применим для этого линейку. Проделаем ту же самую последовательность действий с точкой $B$ с поправкой на $AB=3~см$.

Немного самостоятельной практики!

Возьмите карандаш, транспортир и лист бумаги. Отложите от стороны на основании транспортира два произвольных угла в границе $0^\circ<x<180^\circ$.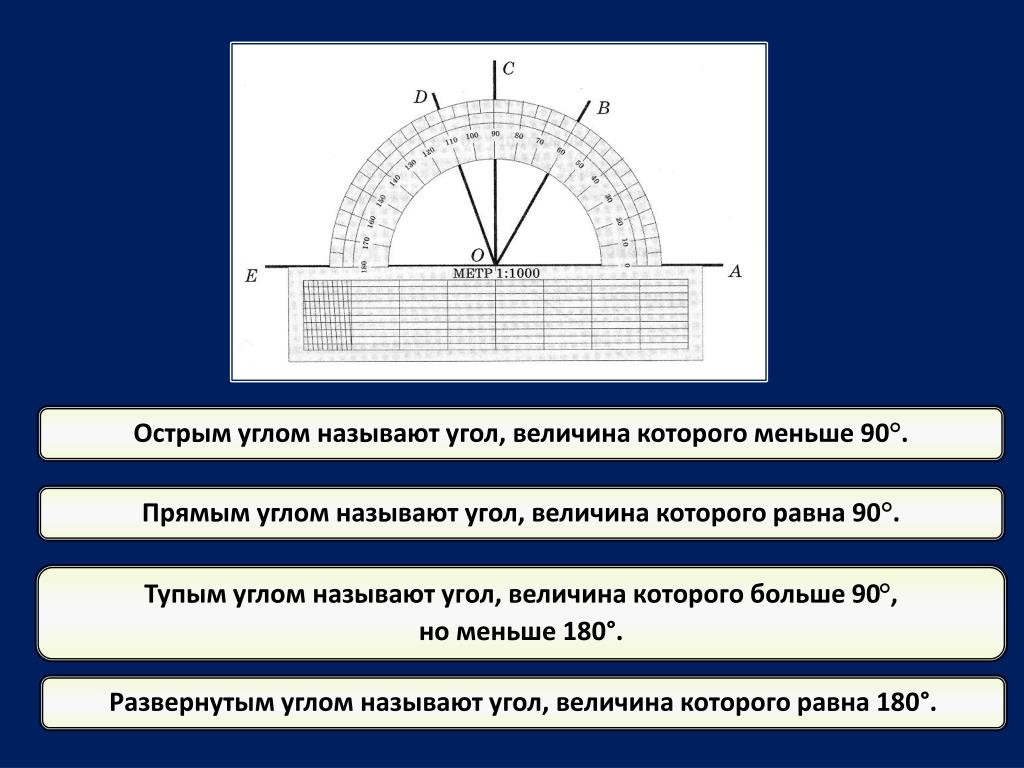 \\circ$.

Распределите углы согласно подходящим типам по градусам. [[grouper-1]]»,»widgets»:{«grouper-1»:{«type»:»grouper»,»labels»:[«Полный угол»,»Прямой угол»,»Тупые углы»,»Острые углы»,»Развернутый угол»,»Выпуклые углы»],»items»:[[«$\\angle{A_1}$»],[«$\\angle{A}$»],[«$\\angle{A_2}$»,»$\\angle{F}$»],[«$\\angle{С}$»,»$\\angle{\\alpha}$»],[«$\\angle{B_1}$»],[«$\\angle{B}$»,»$\\angle{D}$»]]}}}]}

Острый угол – Определение с примерами

Содержание

Последнее изменение: 6 сентября 2022 г.

Что такое острый угол

Острый угол определяется как угол, величина которого больше 0° и меньше 90°.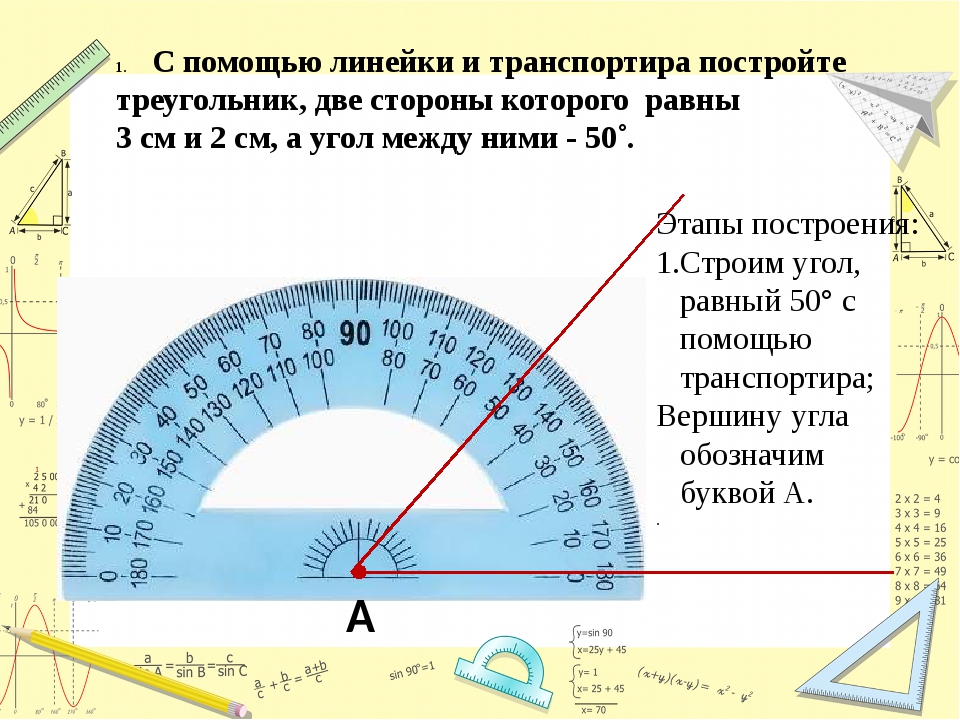 Другими словами, любой угол, меньший прямого угла, является острым углом.

Два или более острых угла могут образовывать прямой угол (равный 90°) или тупой угол (более 90°). Когда два острых угла образуют прямой угол по 45° каждый, они называются конгруэнтными острыми углами.

Ниже приведены еще несколько примеров острого угла:

Острые углы в реальной жизни

Все углы в остроугольном треугольнике, по два угла в тупоугольном и прямоугольном треугольнике
Алфавиты A, K, M, N, V, W, X, Y и Z
Предметы повседневного обихода, такие как воронка, вешалка для одежды, стрелки настенных часов, показывающие 10 часов, частично открытая дверца шкафа и кухонные щипцы
Учебные материалы, такие как острие карандаша, открытая книга, разделитель , циркуль и квадраты
Геометрические фигуры, такие как наконечник стрелки, знаки «<» и «>»
Ломтик арбуза
Ветки дерева
Спицы велосипеда
Открытая пасть крокодила
Открытый клюв птицы поворот’

Выберите из предложенных вариантов острые углы.

Решение:

Как известно,
Острые углы — это углы меньше 90°,
Следовательно, варианты (а), (б) и (в) — острые углы.

Какой из следующих вариантов, заданных в часах, дает острый угол?

Решение:

Как известно,
Острые углы — это углы меньше 90°,
Следовательно, варианты (б) и (г) — острые углы.

Найдите x в данном треугольнике и укажите, является ли он остроугольным0055 Таким образом,
In △ABC,
∠ABC + ∠BCA + ∠CAB = 180°, здесь ∠ABC = 60°, ∠CAB = 60°
60° + ∠BCA + 60° = 180°
∠BCA = 180 ° – (60° + 60°)
∠BCA = (x°) = 60°
Поскольку все три угла ∠ABC, ∠BCA, ∠CAB меньше 90°, △ABC является остроугольным треугольником

Найдите острые углы в данном многоугольнике ABCDE.

Решение:

Как известно,
Сумма внутренних углов пятиугольника = 540°
Теперь
∠ABC +∠BCD + ∠CDE + ∠DEA +∠EAB = 540°
80° + 158° + ∠CDE + 94° + 132° = 540°
∠CDE = 540° – 464°
∠CDE = (x°) = 76°
Таким образом, ∠ABC и ∠CDE меньше 90 ° и — острые углы.

Часто задаваемые вопросы

Q1. Сколько острых углов в остроугольном треугольнике?

Ответ . В остроугольном треугольнике три острых угла.

Q2. Сколько острых углов у прямоугольного треугольника?

Ответ . В прямоугольном треугольнике два острых угла.

Q3. Сколько острых углов в тупоугольном треугольнике?
Ответ . В тупоугольном треугольнике два острых угла.
Q4. Сколько острых углов у ромба?
Ответ . Два из четырех углов ромба острые.
Последнее изменение: 6 сентября 2022 г.
Тупой, прямой, прямой и острый угол
Что такое угол? Прямой, тупой, прямой, острый угол… что это такое и какое отношение они имеют к углам? Если их можно измерить… как мы можем их измерить? Для чего они используются? .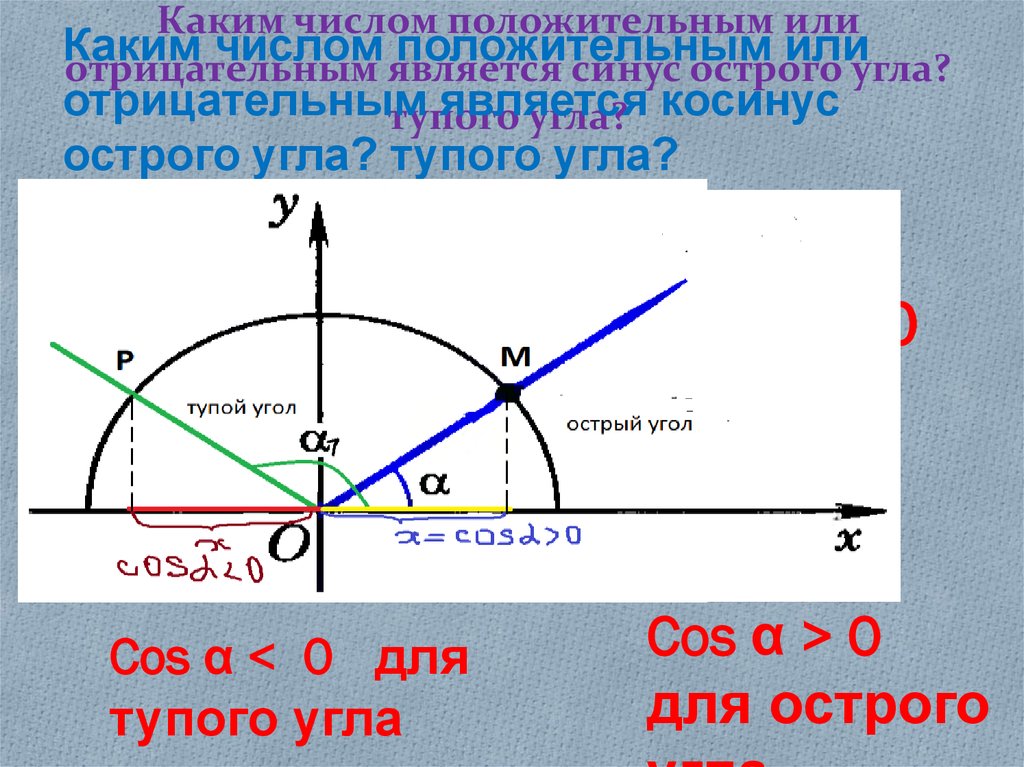 .. Вот некоторые из вопросов, на которые мы собираемся ответить в этом посте. Итак… давайте сделаем это!
Углы: область, отмеченная двумя отрезками с одинаковым началом.
Это математическое определение, но давайте рассмотрим его поближе. В углах нет ничего нового, мы окружены ими; мы можем найти их в нашей повседневной жизни: дома, в парке или на школьной площадке, в горах или на пляже, в городе… даже на животных, растениях и на себе!
Теперь, когда мы выяснили, что такое углы, помимо знания того, как их идентифицировать, нам нужно определить их элементы, потому что это позволяет нам анализировать и воспроизводить их. Как вы можете видеть на картинке выше, они состоят из следующих элементов:
a: Сторона один или, другими словами, один из отрезков, образующих угол. Вместе с другой стороной он отмечает амплитуду угла.

b: вторая сторона; он имеет то же начало, что и другая сторона (а), завершает угол и отмечает его амплитуду.
C: Вершина. Это общее начало обоих отрезков.
α: Амплитуда вогнутого угла, образованного отрезками.
β: Амплитуда выпуклого угла, образованного отрезками прямой.
Стороны являются отрезками и, таким образом, имеют бесконечную длину. Однако, когда мы их рисуем, нам нужно нарисовать конечную точку, чтобы они могли поместиться на бумаге. Вершина всегда имеет одинаковые размеры, потому что это точка, начало отрезков прямой, единственная изменчивость которых зависит от координат на сетке. Итак, амплитуда — единственный элемент угла, который изменяется и, таким образом, определяет его характеристики; Вот почему так важно знать, как его измерить.

Мы классифицируем различные углы в соответствии с их амплитудами.
Таким образом, мы можем найти прямых углов, тех, которые измеряют точные 90º, прямых углов , которые являются углами, которые измеряют ровно 180º, и, помимо этих двух, мы можем классифицировать другие:
Острый угол : углы меньше 90º.
Тупой угол : углов больше 90º.
Угол вогнутости: углы больше 180º
Выпуклый угол: углы меньше 180º
Для измерения амплитуд мы используем инструмент, называемый «компас», но есть много других способов, которые мы можем использовать для измерения и рисования различных видов углов:
Окружность с известным центром позволяет нам рисовать прямые углы , как это делали египтяне, когда таких инструментов не существовало.

Все прямые углы определяют прямой угол.
Все треугольники (линейки) имеют следующие угловые измерения и, комбинируя их по-разному, могут образовывать другие углы. Треугольник имеет прямой угол, угол 60 градусов и угол 30 градусов. Другой вид имеет прямой угол и два угла по 45º.
Вот так мы открыли углы. Они являются частью повседневной жизни, и мы узнали, что можем делать больше, чем просто наблюдать за ними. Мы можем измерить их и воспроизвести точно так, как они есть на самом деле.
No related posts.