Надежный метод разложения на множители простых квадратичных чисел
Жесткий случай («Коробка») «Твердые» примеры Странный случай
Purplemath
+ c», где «a», «b» и «c» — просто числа (и любой из b и c, но никогда a, может быть равен нулю).
Для простого случая факторизации квадратичных многочленов нам нужно будет найти два числа, которые при умножении равны постоянному члену c, а также дают в сумме равный b, коэффициент при линейной х — термин посередине. Почему?
Квадратичные числа — это многочлены второй степени. Когда вы учились умножать многочлены вместе, они, вероятно, начинали с умножения двух двучленов вместе (и они, вероятно, называли этот процесс «фольгированием»).
Содержание продолжается ниже
MathHelp.com
Факторирование квадратичных уравнений: трехчлены
Чтобы получить квадратное уравнение со старшим коэффициентом 1 (и без дробей), каждый из исходных двучленов также должен был иметь старший коэффициент 1.
Глядя на два общих бинома (используя переменную x и общие числа p и q), мы можем перемножить биномы следующим образом: x 2 + p x + q x + pq
x 2 + (p + q) x + pq
90, pq = c из » x 2 + b x + c». Это умножение и упрощение объясняет, почему, чтобы разложить квадратное число, нам нужно начать с нахождения двух чисел (являющихся p и q выше), которые в сумме равны b, где эти числа также умножаются на c. Этого требует логика разложения на множители (а разложение на множители является «отменой» исходного биномиального умножения). (Кстати, я называю эту тему «разложением на множители квадратичных чисел», хотя в вашем учебнике эта тема может упоминаться как «разложение на множители трехчленов». является полиномом второй степени. И не все квадратичные уравнения имеют три члена. Так что название раздела или главы книги в лучшем случае немного не соответствует цели.
Не беспокойтесь о разнице, однако, название книги означает то же самое, что объясняется в этом уроке.)
Какой пример разложения на множители простого квадратичного числа?
Коэффициент
x 2 + 5 x + 6
Старший коэффициент этого квадратичного числа равен 1, так что это простой случай разложения на множители. Для начала мне нужно найти множители c = +6, которые в сумме дают b = +5. У меня есть два варианта, потому что 6 делят как произведение 2 и 3 или как произведение 1 и 6.
Теперь, потому что я умножаю на положительное шесть, то мои множители должны иметь тот же знак; они оба должны быть положительными, иначе они оба должны быть отрицательными, потому что так работают отрицания. Поскольку я прибавляю к положительной пятерке, то оба фактора должны быть положительными.
Я проверю суммы пар потенциальных множителей, чтобы увидеть, какие из них работают:
1 + 6 = 7
2 + 3 = 5
будем использовать факторы +2 и +3.
Когда я научился перемножать многочлены, я знаю, что они получили этот квадрат, перемножив два двучлена. Поскольку старший коэффициент равен всего 1, я знаю, что старший коэффициент каждого из этих биномов также должен быть равен 1. Это означает, что произведение вначале выглядело примерно так:
( x )( x )
На концах каждой скобки ставятся числа, которые умножаются на +6 и прибавляются к +5. Это означает, что я могу закончить факторинг, подставив эти числа в скобки в любом порядке:
( x + 2)( x + 3)
Почему «в любом порядке»? Поскольку передние концы двух скобок были одинаковыми, я бы в любом случае получил одинаковую факторизацию. Помните: порядок не имеет значения при умножении.
Вот как будут работать все «простые» квадраты: мы находим множители постоянного члена, которые в сумме составляют средний член, а затем мы используем эти множители, чтобы заполнить наши скобки.
Кстати, мы всегда можем проверить нашу работу, снова перемножив наши множители, и убедиться, что мы вернулись к исходному ответу.
Чтобы проверить приведенную выше факторизацию, умножение выглядит следующим образом:
Ваш текст или учитель могут ссылаться на факторизацию «по группировке», которая рассматривается здесь, на Purplemath, в уроке по простой факторизации. В «простом» случае факторинга использование метода «группировки» просто дает вам дополнительную работу. Например, в приведенной выше задаче, в дополнение к нахождению множителей +6, которые складываются в +5, вам пришлось бы выполнить следующие дополнительные шаги:
x 2 + 5 x + 6
x 2 + 3 x + 2 x + 6
( x 2 + 3
x ( x + 3) + 2( x + 3)
( x + 3)( 090 + 20007 x 9000 получить тот же ответ, что и я, но (я думаю) проще сразу перейти к заполнению скобок.
Коэффициент
x 2 + 7 x + 6
Старший член равен всего 1, так что это простой случай факторинга.
Постоянный член равен 6, что можно записать как произведение 2 и 3 или 1 и 6, как и в предыдущем упражнении. Но коэффициент на средний срок на этот раз другой. Вместо +5 у меня +7.
Знак постоянного члена тот же, что и раньше (а именно, «плюс»), поэтому мне все равно нужно «плюсовать» множители. Но сумма (т. е. среднесрочный коэффициент) другая; теперь это 7. В то время как 2 + 3 = 5 работало для предыдущего квадратного числа, +2 и +3 не являются числами, которые мне нужны в этом случае. С другой стороны, 1 + 6 = +7, поэтому я буду использовать +1 и +6 для факторизации. И я также перейду сразу от этого вывода к записи моего окончательного ответа:
( x + 1)( x + 6)
Опять же, помните, что порядок умножения не имеет значения, поэтому приведенный выше ответ можно было бы также правильно записать как «( x + 6) ( x + 1)».
Коэффициент
x 2 − 5 x + 6
Постоянный член (созданный умножением) равен +6, поэтому мои множители будут либо оба «плюс», либо оба «минус».
А вот средний коэффициент на этот раз «минус». Поскольку я прибавляю к «минусу» (а именно к −5), то оба множителя должны быть «минусовыми».
Когда средний коэффициент был «плюс» пять, я использовал коэффициенты +2 и +3. Теперь, когда коэффициент моего среднего члена равен «минус», я буду использовать -2 и -3: какие пары факторов использовать, как я показал в предыдущих упражнениях. Формально правила выглядят так:
Правила нахождения множителей квадратного уравнения
- Если c равно «плюс», то множители будут либо оба «плюс», либо оба «минус».
- Если b «плюс», то оба множителя «плюсовые».
- Если b «минус», то оба множителя «минусовые».
- В любом случае ищите множители, которые добавляют к b.
- Если b равно «плюс», то больший из двух множителей есть «плюс».
- Если b равно «минус», то больший из двух множителей равен «минус».
- В любом случае ищите множители, которые вычитают из b; то есть факторы, которые составляют b единиц друг от друга .
Коэффициент
x 2 − 7 x + 6
Старший коэффициент равен 1, так что это простой квадратичный фактор. Я умножаю на «плюс» шесть, поэтому множители будут либо оба «плюс», либо оба «минус». Глядя на средний член, я вижу, что добавляю к «минус» семь, поэтому оба моих множителя будут «минусовыми».
(Отрицательные) множители +6, которые в сумме дают 7, равны -1 и -6, поэтому я буду использовать -1 и -6 для факторизации:
( x — 1)( x — 6 )
До сих пор c (постоянный член) всегда был плюсом. Что, если c — это «минус»?
Коэффициент
x 2 + x − 6
Поскольку я умножаю на «минус» шесть, мне нужны множители с противоположными знаками; то есть один фактор будет «плюс», а другой будет «минус».
Пары множителей для числа 6 — это 1 и 6, а также 2 и 3. Значения во второй паре отличаются на одну единицу, поэтому я знаю, что буду использовать 2 и 3.
Поскольку мне нужно получить «плюс » ответьте на сумму двух множителей, мне нужно большее из двух чисел, чтобы получить знак «плюс»; а именно, 3 получит знак «плюс» (таким образом, 2 получит знак «минус»). Тогда моя факторизация:
( x — 2)( x + 3)
Коэффициент
x 2 − x − 6
Это похоже на предыдущее квадратичное, за исключением того, что теперь средний член равен «минус».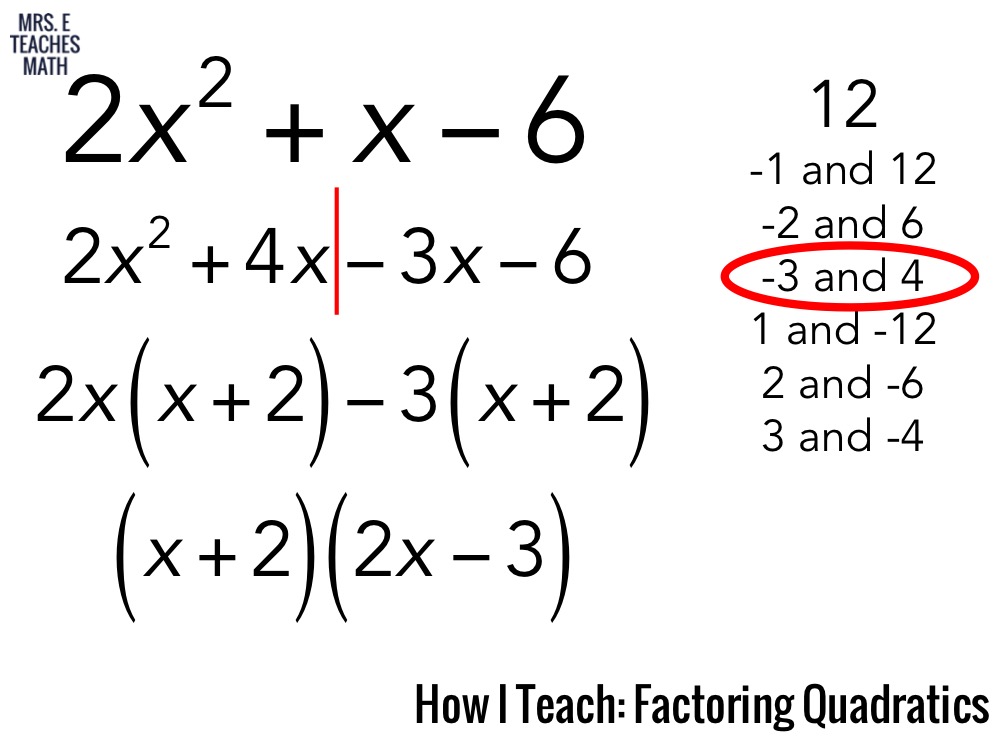
Постоянный член по-прежнему «минус», поэтому мне все еще нужны множители с противоположными знаками. И коэффициент среднего члена (кроме его знака) по-прежнему равен 1, поэтому мне по-прежнему нужны факторы, отстоящие на одну единицу. Но на этот раз больший множитель получит знак «минус».
Все остальные соображения остаются прежними. Я по-прежнему хочу, чтобы множители 6 были разделены на одну единицу, поэтому я по-прежнему буду использовать 2 и 3. Но на этот раз знак 3 будет «минус»:
( х — 3)( х + 2)
Коэффициент
x 2 − 5 x − 6
В этом квадратном выражении постоянный член равен «минус», поэтому мне нужны множители противоположных знаков.
Однако на этот раз коэффициент среднего члена (кроме его знака) равен 5, а не 1, поэтому теперь я хочу, чтобы два моих множителя находились на расстоянии пяти единиц друг от друга.
И поскольку коэффициент среднего члена равен «минус», больший из двух моих коэффициентов получит знак «минус».
Пары множителей для числа шесть: 1 и 6, а также 2 и 3. Числа в первой паре множителей отличаются друг от друга на пять, поэтому я буду использовать числа 1 и 6. Я прибавляю к «минус» , поэтому я поставлю большему из моих множителей знак «минус»; то есть я буду использовать +1 и −6 для этой факторизации:
( x − 6)( x + 1)
Между прочим, есть один особый случай для факторизации квадратичных чисел. Когда вы разлагали на множители простые старые числа, были некоторые числа, которые не разлагались, например 5 или 13. Вспомните, что эти неразлагаемые числа называются «простыми» числами. Вы всегда можете умножить два целых числа, чтобы получить другое целое число, но некоторые целые числа нельзя разделить, чтобы получить два (нетривиальных) целых числа.
Точно так же существуют квадратичные числа, которые не учитываются. Вы можете умножить два двучлена (без дробей), чтобы получить квадратное число (без дробей), но не все квадратные числа можно разложить на множители, чтобы получить два (нетривиальных) двучлена.
Терминология для таких квадратичных чисел (или любого нефакторизуемого многочлена) также является «простым».
Что является примером попытки разложить на множители простое квадратное число?
Коэффициент
x 2 + 7 x − 6
Старший коэффициент равен 1, так что это случай простого факторинга. Поскольку постоянным членом является «минус», мне понадобятся «плюс» и «минус», чтобы, когда я их перемножил, я получил -6, а когда я их сложил, я получил +7. Другими словами, мне понадобятся два множителя, отстоящих друг от друга на семь единиц, причем больший множитель получит знак «плюс».
Пары множителей для числа 6 — это 1 и 6, а также 2 и 3. На первый взгляд я могу предположить, что мне следует использовать 1 и 6, но —
Один из множителей должен быть «минус», чтобы при умножении получилось «минус» шесть! Попробовав первую пару множителей 1 и 6, сумма будет одной из следующих:
(−1) + 6 = 5
1 + (−6) = −5
Хорошо; ни один способ не работал.
Так что, может быть, мне следует использовать другую пару факторов…? Проверяя сложение с этими числами, я получаю:
(−2) + 3 = 1
2 + (−3) = −1
Кто-то может подумать: «Ну, может быть, мне следует делать знаки по-другому». Но единственный способ получить множители из шести, равные семи, — это присвоить этим множителям один и тот же знак. Но если я это сделаю, то множители не будут умножаться на «минус» шесть.
Другими словами, не существует пары множителей -6, которая дает +7. А если что-то неразложимо, то оно простое. Таким образом, x 2 + 7 x − 6 является простым квадратичным полиномом. С технической точки зрения, это «неразложимая над целыми числами», так называемая, потому что я не мог найти пару целых чисел, которые бы работали. Тогда мой ответ:
Prime
URL: https://www.purplemath.com/modules/factquad.htm
Page 2Page 3Page 4
Уроки факторинга полностью — Уроки Византа
Введение
Предыдущие уроки факторинга были посвящены разложению многочлена на множители с использованием одного шаблона, такого как
Наибольший общий множитель
Пример: 3x 2 + 9x 3 + 12x 4 разложить на 3x 2 (1 + 2×0 0 9×0 + 0 4)
Разница между двумя квадратами
Пример: y 2 – 9 размножить на (y + 3)(y – 3)
Трехчленный
Пример: x 2 – 2x – 3 разложить на (x + 1)(x – 3)
Уроки, связанные выше, дают систематические методы факторизации определенных типов многочленов.
На практике решение уравнений с помощью факторинга часто требует использования более сложного процесса, который называется «Полный факторинг». В этом уроке объясняется, как полностью разложить число
на множители, комбинируя три основных метода, перечисленных выше.
Во-первых, давайте подробнее рассмотрим, зачем нам нужен процесс факторинга полностью. Изучите выражение ниже:
(х 2 + 1)(х + 1)(х – 1)
Если упростить это выражение, то получим:
(х 2 + 1)(х 2 + х – х — 1)
(x
2 + 1) (x 2 — 1)
(x
4 + x 2 — x 2 — 1)
x
4 — 1
Теперь вы должны распознать это выражение как разницу между двумя квадратами. Используя технику, представленную в уроке
Разница между двумя квадратами, мы можем учесть это в
(x 2 + 1)(x 2 – 1)
Но обратите внимание, что это выражение отличается от факторизованного выражения, с которого мы начали.
Нам нужен еще один шаг, чтобы учесть это в выражении, с которого мы начали. Вот где факторинг полностью приходит.
Процесс
Полный факторинг состоит из трех шагов:
- Факторизируйте GCF из выражения, если это возможно.
- Разложите трехчлен на множители, если это возможно.
- Учитывайте разницу между двумя квадратами как можно больше раз.
Первый пример
Давайте посмотрим, как это применимо к нашему исходному примеру:
(x 4 – 1)
Шаг 1
Первый шаг – факторизация GCF. Поскольку GCF x 4 и 1 равен 1, мы пропускаем этот шаг.
Шаг 2
Поскольку выражение содержит только два члена, мы не можем разложить трехчлен на множители.
Шаг 3
Разложение (x 4 – 1) на разность двух квадратов приводит к
(х 2 + 1)(х 2 – 1).
Теперь обязательно запомните ключевую фразу «как можно больше раз».
Теперь мы должны посмотреть, есть ли где-нибудь еще мы можем факторизовать другую разницу между двумя квадратами. В (x 2 + 1) оба члена положительны, поэтому это нельзя учитывать. Однако
дюймов (x 2 – 1), второй член отрицателен, и в противном случае оба члена являются полными квадратами. Таким образом, (x 2 – 1) делится на (x + 1)(x – 1). В результате наше примерное выражение, наконец, учитывается в
(x 2 + 1)(x + 1)(x – 1)
, которое полностью учитывается.
Чем это отличалось от нашей первой (и неудачной) попытки разложить пример на множители? При факторинге полностью мы использовали метод «Разница между двумя квадратами» более одного раза.
Второй пример
Давайте попробуем другой пример, который требует факторизации в шагах 1 и 2:
5x 3 – 10x 2 – 15x
Опять же, три шага в факторинге полностью:
- Фактор GCF из выражения, если это возможно.
- Разложите трехчлен на множители, если это возможно.
- Умножьте разницу между двумя квадратами как можно больше раз.
Шаг 1
Мы видим, что члены в нашем примере имеют наибольший общий делитель 5x. В соответствии с инструкциями мы вынесем этот GCF за скобки:
5x(x 2 – 2x – 3)
Шаг 2
Мы видим, что (x 2 – 2x – 3) является факторизуемым трехчленом, поэтому факторизуем его:
5x(x + 1)(x – 3)
Переходя к шагу 3, мы можем просмотреть наше выражение и увидеть, что ни 5x, ни (x + 1), ни (x – 3) нельзя разложить на множители. разница между двумя квадратами. Мы полностью умножили 5x
3 — 10x 2 — 15x.
Заключительный пример
В нашем последнем примере мы будем использовать все три шага факторизации полностью.
12x 4 – 3x 2 – 54
Шаг 1
Выносим за скобки наибольший общий делитель 3,
3 (4x 4 — x 2 — 18)
Шаг 2
3 (4x 2 — 9) (x 2 + 2)
Шаг 3
Наконец, мы идентифицируем 4x 2 – 9) в виде бинома, который можно разложить на (2x + 3)(2x – 3).