Понятие треугольника — Геометрия — Математика
Математика->Треугольники->основные понятия, равенство треугольников->
Тестирование онлайн
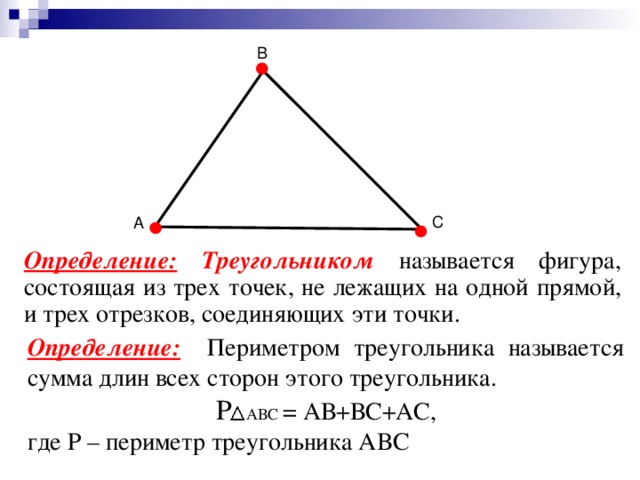
Основные понятия треугольника
Понятие треугольника
Если три точки, не лежащие на одной прямой, соединить отрезками, получим треугольник. Одну из сторон треугольника часто называют его основанием.
Теорема. Сумма углов треугольника равна 1800
Если все три угла треугольника острые, то треугольник называется остроугольным.
Если один из углов треугольника тупой, то треугольник называется тупоугольным.
Если один из углов треугольника прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами.
В любом треугольнике против большей стороны лежит больший угол; против равных сторон — равные углы, и обратно. Любая сторона треугольника меньше суммы двух других сторон, а также больше разности двух других сторон.
Продолжив одну из сторон треугольника, получим внешний угол. Угол АВD — внешний.
Признаки равенства треугольников
Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
Теорема. Два треугольника равны, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого.
Теорема. Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим углам другого.
Теорема. Два треугольника равны, если три стороны одного треугольника соответственно равны трем сторонам другого.
Медиана, биссектриса и высота треугольника
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой.
Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Замечательные точки треугольника. 1) Биссектрисы треугольника пересекаются в одной точке.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
3) Высоты треугольника (или их продолжения) пересекаются в одной точке.
4) Медианы треугольника пересекаются в одной точке.
Равнобедренный треугольник
Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
Треугольник, у которого все стороны равны, называется равносторонним.
Теорема. В равнобедренном треугольнике углы при основании равны.
Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Треугольник, все про треугольники
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Определение треугольника
В любом треугольнике три угла и три стороны.
Против большего угла треугольника лежит большая сторона.
Виды треугольников
Треугольники бывают
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется
- равнобедренным, если две его стороны равны.
- равносторонним, если все три стороны равны,
- разносторонним, если все его стороны разные.
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
I признак (по двум сторонам и углу между ними).
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Подробнее про признаки равенства треугольников читайте по ссылке.
Признаки подобия треугольников
Треугольники называются подобными, если их стороны пропорциональны.
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Подробнее про признаки подобия треугольников читайте по ссылке.
Теоремы треугольников
Для любого треугольника справедливы следующие теоремы.
Подробнее про теорему косинусов читайте по ссылке.
Подробнее про теорему синусов читайте по ссылке.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Геометрия: введение в треугольники
Геометрия: введение в треугольники https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 ШколаРепетиторская Академия ШколаРепетиторская Академия https://secure.gravatar.com/avatar/983a20e95a059722e4981790f518b20b?s=96&d=mm&r=g
Треугольник — это замкнутая кривая, состоящая из трех отрезков. Отрезки, из которых образован треугольник, называются сторонами треугольника. Точки пересечения сторон треугольника называются вершинами треугольника. Углы, образованные при вершинах, называются углами треугольника.
Итак, в треугольнике 3 стороны, 3 вершины и 3 угла.
Здесь мы будем называть этот треугольник как ΔABC, где,
Стороны: AB, BC, CA
Vertices: A, B, C
угло БЦА.
Части треугольника:
Существует некоторая терминология, связанная с треугольниками.
Основание: Это нижняя сторона треугольника.
Углы основания: Два угла, которые касаются основания.
Вершина треугольника: Угол, противолежащий основанию
Ноги: Две стороны, не являющиеся основаниями.
Типы треугольников:
Треугольники классифицируются по сторонам и углам.
В зависимости от сторон треугольники классифицируются следующим образом.
а) Равносторонний треугольник:
Треугольник, в котором все три стороны (углы) равны.
б) Равнобедренный треугольник:
Треугольник, в котором любые две стороны (углы) равны.
c) Разносторонний треугольник:
Треугольник, у которого нет двух равных сторон (углов).
В зависимости от углов треугольники классифицируются следующим образом.
a) Остроугольный треугольник:
Любой треугольник, в котором все углы меньше 90 0 .
b) Тупоугольный треугольник:
Любой треугольник, один из углов которого больше 90 0 .
c) Прямоугольный треугольник:
Треугольник, в котором один из углов равен 90 0 .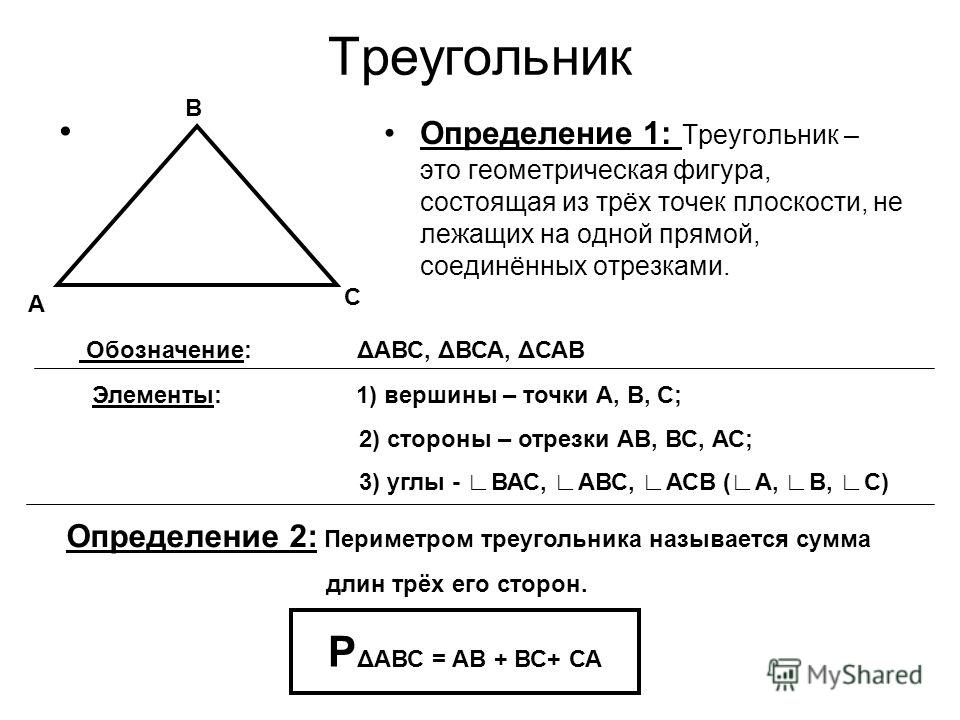
Вам также нужна помощь в обучении? Взгляните на наши услуги репетиторства Study Skills.
SchoolTutoring Academy — это ведущая компания, предоставляющая образовательные услуги для учащихся K-12 и колледжей. Мы предлагаем программы репетиторства для учащихся K-12, классов AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и учащимся на острове Принца-Эдварда, посетите: Репетиторство на острове Принца-Эдварда.
Треугольники | Математика ∞ Блог
Треугольники — это двумерные фигуры, состоящие из трех сторон и трех углов. Хотя не все они одинаковы, все они должны иметь эти два элемента на месте, чтобы быть треугольником. Вы столкнетесь с несколькими различными типами, каждый из которых определяется своими сторонами и/или углами.
- Острый: В остроугольном треугольнике все три угла меньше 90 градусов.
- Тупоугольные: Тупоугольные треугольники имеют один угол больше 90 градусов.
- Право: В прямоугольном треугольнике один угол равен 90 градусов.
- Равносторонний: Равносторонний треугольник имеет три равные стороны и три равных угла.
- Разносторонний: В разностороннем треугольнике у вас не будет равных сторон или углов.
- Равнобедренные: Равнобедренные треугольники имеют две равные стороны и два равных угла.
В любом треугольнике, независимо от его типа, сумма всех трех углов составляет 180 градусов. Вы можете использовать этот факт, чтобы найти измерение недостающих углов. Например:
В этом треугольнике один угол равен 85 градусам, а другой 65. Сумма трех углов должна равняться 180 градусам, поэтому:
85 + 65 + x = 180
150 + x = 180
150 – 150 + x = 180 – 150
X = 30
Геометрия также дает нам правила для нахождения площади треугольника. Ваша формула для нахождения площади — это ½ основания, умноженное на высоту, или ½ x b x h = A.
Основание — это нижний край треугольника, а высота — это вертикальная линия, идущая от основания к противоположному углу в 90 градусов.
Предположим, что основание (b) треугольника в этом примере равно 72, а высота (h) равна 50. Когда вы подставите эти числа в уравнение площади (A), оно будет выглядеть так:
½ x 72 x 50 = A
Затем, если вы продолжите решать задачу, чтобы найти площадь, вы выполните следующие шаги:
½ x 3600 = A
A = 3600 x 1/2
A = 1800
Помните, всегда сначала умножайте основание на высоту. Затем умножьте это число на ½. Вы также можете думать об этом как о делении b x h на два.
Конгруэнтность
Два треугольника считаются конгруэнтными, если их стороны и углы равны. Неважно, перевернуты ли они боком, вверх ногами или являются зеркальными отражениями друг друга: они все равно будут иметь одинаковые размеры. Пять теорем о конгруэнтных треугольниках были созданы на протяжении веков, и вы можете использовать их, чтобы выяснить, идентичны ли два треугольника, или нарисовать треугольник, конгруэнтный тому, который у вас уже есть на бумаге.
- Бок-бок-бок (SSS): Если все три стороны двух разных треугольников одинаковы, то и их углы будут одинаковыми, значит, они конгруэнтны.
- Side-Angle-Side (SAS): Если две стороны треугольника и угол, образованный при их пересечении, идентичны углам другого треугольника, то треугольники конгруэнтны.
- Угол-Сторона-Угол (ASA): Если два угла и сторона, соединяющая их, равны в двух отдельных треугольниках, они конгруэнтны.
- Угол-Угол-Сторона (AAS): Если два угла одного треугольника равны двум углам другого и одна сторона каждого из этих треугольников имеет одинаковую меру, вы можете поспорить, что они конгруэнтны.
- Катет гипотенузы (HL): Эта теорема применима только к прямоугольным треугольникам или треугольникам с одним углом 90 градусов. Когда гипотенуза, или самая длинная сторона, и другая сторона двух треугольников имеют одинаковую длину, треугольники конгруэнтны.
