Какие бывают треугольники в геометрии: Виды треугольников по углам и сторонам

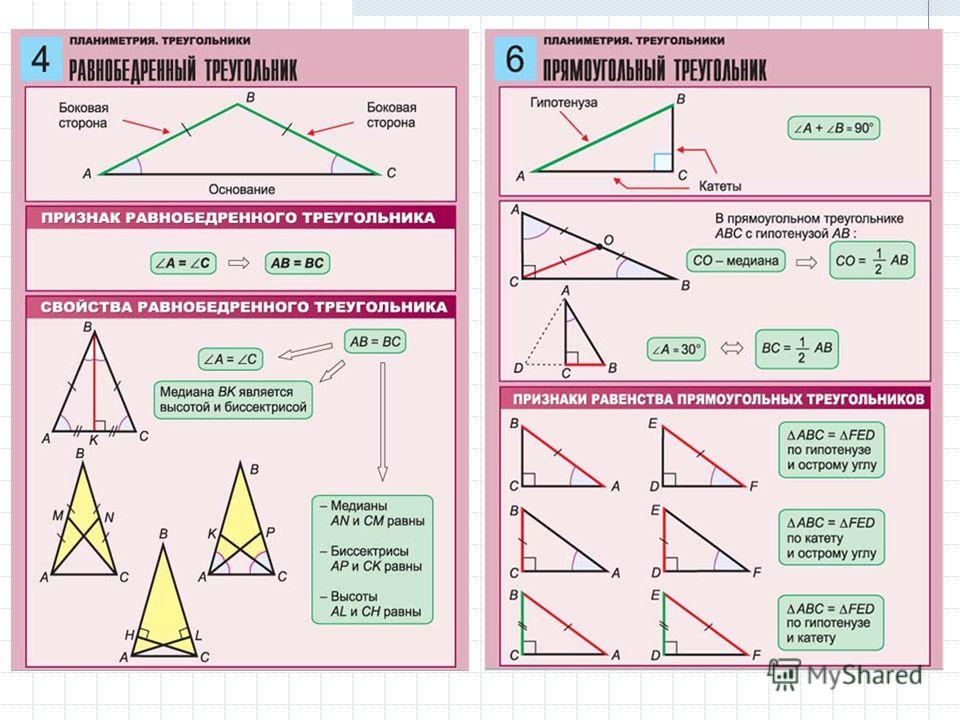
Виды треугольников — Геометрия — Уроки

Треугольники

Цель урока: Формировать знания, умения и навыки по теме «треугольники. Равенство треугольников. Виды треугольников»

Задачи урока:

• Образовательные: 

  • ввести определение треугольника и его элементов, периметра треугольника, понятие равных треугольников.

• Развивающие:

  • расширение кругозора учащихся;

  • развивать умение видеть математические понятия в окружающем нас мире;

  • развивать устную и письменную математическую речь.

• Воспитательные:

  • воспитывать умение работать в группе, воспитывать устойчивый интерес к предмету.

План урока:

1. Организационный момент.

2. Сообщение темы и целей урока.

3. Изучение нового материала.

4. Применение полученных знаний при закреплении и углублении знаний по теме.

5. Подведение итогов урока, оценка знаний.

6. Работа над ошибками.

7. Домашнее задание.

Ход урока

1. Организационный момент

2. Сообщение темы и целей урока

Определение темы урока через разгадывание кроссворда, используя ранее изученный материал.

Определение задач урока:

• узнать какая геометрическая фигура называется треугольником;

• элементы треугольника;

• какие бывают треугольники;

• научиться решать задачи и правильно их оформлять;

• развивать математическую речь

Таким образом, изучив эту тему

Вы должны знать: определение треугольника и его элементов, определение равных треугольников, что такое периметр.

Вы должны уметь: решать задачи на нахождение периметра треугольника по записи равных треугольников находить пары равных элементов  этих треугольников.

1. Изучение нового материала поисково-исследовательский этап урока

Замечательный русский ученый-геометр Иван Федорович Шарыгин сказал: ”Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и вселенная”. И наш первый урок главы 2 посвящен этой геометрической фигуре. А по-скольку,

«Лучший способ изучить что-либо – это открыть самому»

Д. Пойа,

то давайте проведем сегодня с вами маленькое исследование. Согласно теме урока

объектом исследования становится: ТРЕУГОЛЬНИК.

Предметом исследования:

• Понятие … треугольника.

• Виды … треугольников.

• Равные …треугольники и их свойства.

Цель исследования: расширить представления о треугольниках и их видах.

Задачи исследования:

• Изучение исторических сведений о треугольниках;

• Изучение сведений о нахождении треугольников в окружающем мире;

• Исследование свойств треугольников и их применения их в практической жизни.

Новизна исследования: актуализация изучения треугольников, как одних из интереснейших геометрических фигур в разряде многоугольников.

Знает даже и дошкольник, что такое треугольник.

Так как понятие «треугольник» уже знакомо учащимся, то целесообразно организовать изучение нового материала в виде поисковой работы. 
Попробуйте сформулировать определение треугольника. 
Ученики высказывают разные предложения, и учитель быстро изображает на доске высказанное предположение: 
1) Из трёх прямых: 

Вывод: цели не достигли, треугольник не построили. 
2) Из трёх отрезков: 

Вывод: цели не достигли, треугольник не построили 
3) Из трёх углов: 

Вывод: цели не достигли, треугольник не построили. 
4) из трех отрезков и трех точек 
Учитель: Какие условия должны выполняться для того, чтобы можно было построить треугольник? 
Учащиеся сами предлагают условия для расположения точек и отрезков (три точки не должны лежать на одной прямой и отрезки попарно соединяют эти точки).  
И доходят до предположения: из трёх точек и трёх отрезков, не лежащих на одной прямой, соединяющих эти точки.

Попробуйте сформулировать определение треугольника, сделав его чертеж. 

Ученики: треугольник это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой и трёх отрезков, попарно соединяющих эти точки. 

• указывает, что отрезки называются в треугольнике сторонами, а точки вершинами;

• дает задание учащимся записать в тетради данное определение, построить произвольный треугольник, записать его вершины, стороны, углы

1. Исследовательская деятельность (работа в группах)

Первая группа «Жесткость треугольника»

Нам надо было доказать, что треугольник жесткая фигура. Жесткая фигура — это фигура, не подверженная деформации.

И действительно:

Вырезанные из картона 4 полоски мы попробовали соединить между собой булавками или декоративными кнопками в четырехугольник, а затем попробовали изменить форму четырехугольника (просто взявшись руками за две противоположные стороны и покачать вверх-вниз). Получаем, что можно изменять градусную меру углов четырехугольника, не меняя длины его сторон. Можно менять величины углов у пятиугольников, шестиугольников и многоугольников с большим количеством сторон.

С треугольником так поступить не удалось. Из 3-х полосок сложим треугольник и соединим кнопками или булавками и попробуем изменить форму треугольника.

Стороны треугольника определяют его углы однозначно.

Треугольник не подвержен деформации. В нём нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному.

Поэтому треугольник — жесткая фигура. Из всех многоугольников только треугольник является жесткой фигурой.

Вывод: Треугольник — фигура жёсткая. Если заданы три его стороны, то форма треугольника уже не может измениться.

?? Что в жизни вы встречали в форме треугольника?

Ответ: крыши домов; подставка для подтягивания; музыкальные инструменты; сыр; украшения; линейка; дорожный знак; окна и т. п.

Вторая группа «Равные треугольники и их свойства»

Нам надо было доказать, что среди треугольников встречаются равные.

Мы воспользовались определением равных отрезков (два отрезка равны, если их можно совместить наложением). И совмещали все предложенные нам треугольники. И, действительно, среди предложенных треугольников такие нашлись. Значит, треугольники называются равными, если их можно совместить наложением.

Наша группа пришла к выводу, что против равных сторон лежат равные углы, а против равных углов – равные стороны.

Вывод:

Определение. Треугольники называются равными, если их можно совместить наложением.

Свойства равных треугольников. Против равных сторон лежат равные углы, а против равных углов – равные стороны

Третья группа «Классификация (виды) треугольников»

Нам надо было распределить по группам предложенные треугольники.

Мы заметили, что треугольники различаются углами и длиной сторон.

Например, были предложены треугольники, у которых все углы острые, у которых есть по одному прямому и тупому углу.

С другой стороны, у треугольников были стороны с равными и разными длинами.

Результаты наших исследований мы занесли в таблицу:

по сторонам по углам	равносторонние	равнобедренные	разносторонние
остроугольные
прямоугольные
тупоугольные

Вывод:

Определения.

Треугольник, у которого все стороны равны, называется равносторонним.

Треугольник, у которого две стороны равны, называется равнобедренным.

Треугольник, у которого все углы острые, называется остроугольным.

Треугольник, у которого есть прямой угол, называется прямоугольным.

Треугольник, у которого есть тупой угол, называется тупоугольным.

Периметр треугольника – сумма длин его сторон.

1. Рефлексия работы в группах

И, так, давайте подведем итоги нашей исследовательской деятельности.

Что называется треугольником?

Тест 1 (с.52)

Знает даже и дошкольник,
Что такое треугольник.
А уж вам-то как не знать!
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И по краю, и внутри

Сколько всего треугольников можно назвать на рисунке?

1 группа. «Жесткость».

Это свойство треугольника используется, в частности, при создании железных ажурных конструкций. Мосты, башни, подъемные краны, каркасы зданий, опоры для высоковольтных линий электропередач изготавливают таким образом, чтобы они содержали как можно больше треугольных элементов.

2 группа. Равные треугольники и их свойства»

Тест 2 (с.53)

Какие треугольники, по-вашему, мнению можно совместить наложением?

3 группа. «Классификация треугольников»

Тест 3 (с.54)

1. Применение полученных знаний при закреплении и углублении знаний по теме

№ 53.

Пусть в равнобедренном Δ АВС АВ = ВС = 14 дм, АС = 8 дм, то

Р_АВС = 2 · 14 + 8 = 36 (дм), но

Р_АВС = Р _DEF, то каждая сторона

равностороннего Δ DEF

Р _DEF = 36 : 3 = 12 (дм)

Ответ: 12 дм.

1. Рефлексия

Простая это фигура треугольник: три вершины, три стороны, три угла. А задумаешься…, нет, вовсе не простая, мы ещё многое о ней не знаем. Не умеем вычислять площади треугольников, не знаем о признаках равенства и подобии треугольников, о признаках равенства прямоугольных треугольников, не знаем и не умеем применять теоремы косинусов, синусов, и многое ещё осталось загадочным для вас.

1. Подведение итогов урока, оценка знаний

Оцените свою работу в группе, заполнив таблицу

1. Постановка домашнего задания

§ 1, гл.2, №№ 51, 55

Подготовить сообщения по темам:

• Место треугольника в истории.

• Треугольник и его роль в жизни народов.

• Треугольник в строительстве.

• Треугольник и творчество

1. Работа над ошибками

Математический диктант (с последующей проверкой)

Отметьте знаком «+»правильные утверждения и знаком « – » – ошибочные.
Треугольник является объемной фигурой.
Треугольник является плоской фигурой.
Треугольником называется геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и соединенных попарно отрезками.
В треугольнике АВС стороны, прилежащие к углу ВАС – это АВ и АС.
Периметром треугольника называется сумма длин всех сторон этого треугольника.
Если два треугольника равны, то их соответственные элементы могут быть не равны.
Если два треугольника равны, то их периметры всегда равны.
В равных треугольниках против соответственно равных сторон лежат равные углы.
В равных треугольниках АВС и МKD соответственными являются элементы: АС и МD, ВС и КD, АВ и МК;  А и М, В и К, С и  D.

правильный ответ – +–+++–+++

Решение задач

Ребята находят решение в группах, помогая друг другу. Результаты обсуждаются в классе.

№1

Известно, что треугольник МРК равен треугольнику СОЕ. \\circ$. Второй — по величине в два раза больше первого. Чему равен третий угол?»}}}]}

Сумма углов треугольника: комментарий к доказательству

Совершенно нормальный вопрос при изучении геометрии: «Почему именно такой нестандартный чертеж?! Боковой стороной?»

Располагать треугольник на чертеже боковой стороной — нетипичная практика. Обычно мы рисуем эту фигуру по принципу его геометрического значка — $\bigtriangleup$. Однако допустите мысль, что теоремы об углах при параллельных таки навели вас на мысли, чему может равняться сумма углов треугольника. Что бы вы сделали первым делом при чертеже к доказательству?

Расположили бы треугольник таким образом, чтобы его стороны «играли роль» потенциальных секущих, а третья сторона —  «роль» одной из возможных параллельных прямых.

Так что подобный чертеж — попытка сразу «подогнать» ситуацию к удобному графическому использованию уже ранее доказанных теорем. Это — геометрическая сноровка. \circ$.  

Задача для самостоятельного решения

Образавр предупреждает: задача может показаться непростой. Это только кажется.

В треугольнике $\bigtriangleup{ABC}$ медиана $BD$ равна половине стороны $AC$. Чему равняется $\angle{B}$ треугольника?

Показать решение

Скрыть решение

Дано:

$\bigtriangleup{ABC}$
$AD=DC=DB$

Найти:

$\angle{B}$ — ?

Решение. При правильно выполненном чертеже видно, что $\bigtriangleup{ABC}$ прямоугольный. Однако это нужно доказать. Для этого рассмотрим $\bigtriangleup{ABD}$ и $\bigtriangleup{BCD}$.

В треугольнике $\bigtriangleup{ABD}$ стороны $AD$ и $BD$ равны. Значит, треугольник равнобедренный. Из этого следует равенство углов $\angle{A}$ и $\angle{ABD}$. В треугольнике $\bigtriangleup{BCD}$ стороны $DB$ и $DC$ равны. Этот треугольник также равнобедренный. Откуда следует, что $\angle{C}=\angle{DBC}$.

По теореме о сумме углов треугольника $\angle{A}+\angle{B}+\angle{C}=180^\circ$. \circ$.

Все, что вы должны знать о треугольниках

Все, что вы должны знать о треугольниках https://schooltutoring.com/help/wp-content/uploads/sites/2/2012/09/triangles1.jpg 233 216 Репетиторство в школе Репетиторство в школе https://secure.gravatar.com/avatar/78d03a5c650efdb2b2c5c83686f0c95a?s=96&d=mm&r=g 12 октября 2012 г. 2 декабря 2014 г.

Треугольник — это геометрическая фигура, состоящая из трех сторон и трех углов.

Треугольники имеют три специальных названия, которые говорят вам, сколько сторон и углов равны друг другу.

В треугольнике может быть 3, 2 или не быть равных сторон и углов.

 

Три типа треугольников:

1. Равносторонние треугольники , у которых три равные стороны и три равных угла всегда равны 60 градусам.

2. Равнобедренные треугольники , у которых две равные стороны и два равных угла.

3. Разносторонние треугольники , у которых нет равных сторон и нет равных углов.

 

Треугольники могут также иметь имена, которые описывают тип угла, который они содержат:

1. У остроугольного треугольника все три угла будут меньше 90 градусов.

2. Прямоугольный треугольник будет иметь один прямой угол, который составляет угол 90 градусов.

3. У тупоугольного треугольника один угол больше 90 градусов.

 

Когда мы называем треугольник, мы можем комбинировать эти имена, чтобы дать как можно больше информации о треугольнике.

Например: Рассмотрим прямоугольный равнобедренный треугольник.

Слово right в названии говорит нам о том, что в этом треугольнике будет один угол в 90 градусов.

Слово isosceles в названии говорит нам о том, что две стороны треугольника равны и два угла треугольника равны.

Из этой информации мы знаем, как должен выглядеть треугольник.

В прямоугольном равнобедренном треугольнике один угол равен 90 градусов, а два других угла равны 45 градусам.

 Нахождение периметра треугольника

Периметр — это расстояние вокруг сторон треугольника. Чтобы найти периметр треугольника, нам нужно сложить длины трех сторон треугольника.

Пример:                     C

A  B

Если сторона AC = 4 см, сторона CB = 5 см и сторона AB = 7 см, то периметр этого треугольника равен:

периметр = 4 см + 5 см + 7 см = 16 см

 Нахождение площади треугольника

Площадь треугольника равна половине произведения основания на высоту.

Вот формула, которую всегда можно использовать при нахождении площади треугольника:

A = ½ (b)(h)

В этой формуле «b» — это расстояние вдоль основания, а «h» — это высота треугольника, измеренная под прямым углом к ​​основанию.

Пример:

Если мы знаем, что высота треугольника равна 5 см, а основание треугольника равно 12 см, то мы можем применить формулу площади, чтобы найти площадь треугольника.

A = ½ (b) (h) = ½ (5 см) (12 см) = 30 см в квадрате

  Свойства треугольников

1. Внутренние углы (внутренние углы) в сумме составляют 180 градусов.

2. Теорема о неравенстве треугольника. Эта теорема утверждает, что сумма длин любых двух сторон треугольника должна быть больше, чем длина третьей стороны.

3. Соотношение между измерениями сторон и углов в треугольнике: наибольший внутренний угол и сторона противоположны друг другу. То же правило применяется к углу и стороне наименьшего размера, а также к углу и стороне среднего размера.

Хотите подготовиться к SAT? Мы можем помочь с подготовкой к SAT

Эта статья была написана для вас Миа , одним из преподавателей Академии подготовки к экзаменам.

Геометрические фигуры с примерами — Smartick

Сегодня вы узнаете о геометрические фигуры . Мы научим вас характеристикам основных геометрических фигур, а чтобы помочь вам лучше понять, объясним на примерах.

Что такое геометрические фигуры?

Древние греки определяли прямые и изогнутые линии, глядя на окружающую среду. Думаете, они остановились на этом? Конечно, нет! Это потому, что прямые линии являются основой для нахождения некоторых фигур, которые мы часто встречаем в реальном мире: геометрических фигур.

Под геометрическими фигурами понимаются плоские поверхности, ограниченные линиями, которые могут быть изогнутыми или прямыми. Чтобы помочь вам лучше понять, мы собираемся объяснить на примере.

Начнем с простого: две прямые .

Можно ли составить фигуру из двух прямых?

Ну конечно можно! При этом мы не называем эту фигуру геометрической фигурой. Для этого он должен быть закрыт. Это означает, что если мы поместим шарик внутрь фигуры, он не сможет убежать. На сделанном нами рисунке мяч мог улететь!

Если вы попытаетесь переместить две прямые линии, то увидите, что замкнуть их невозможно.

Трехсторонние геометрические фигуры: треугольники

Теперь попробуем три прямые линии .

Вот и все! Теперь мы можем создать фигуру, которая не позволит мячу убежать.

Каждая из использованных нами линий, которые теперь составляют часть фигуры, называется сторонами фигуры . У этой фигуры три стороны, и мы называем ее треугольником. Когда мы говорим «треугольник», мы можем иметь в виду либо форму трех линий, либо пространство, которое они заключают.

Можете ли вы назвать места, где мы можем найти треугольники вокруг нас? Я нашел кое-что в Smartick! Посмотрим, узнаете ли вы их.

Классификация треугольников

Существуют различные способы классификации треугольников по сторонам и углам.

В соответствии с их углами

• Прямоугольный треугольник : имеет прямой угол, другими словами, он измеряет 90º.
• Остроугольный треугольник : имеет три острых угла и имеет размеры менее 90º.
• Тупоугольный треугольник : имеет тупой угол и имеет размеры более 90º.

По сторонам

1. Равносторонний : имеет 3 равные стороны.
2. Равнобедренный : две стороны равны, а другая нет.
3. Scalene : все стороны имеют разную длину.

Четырехсторонние геометрические фигуры: четырехугольники

Теперь попробуем четыре прямые линии .

Например, мы могли бы расположить их так:

Мы называем эти фигуры четырехугольниками . Есть несколько особых четырехугольников, стороны которых параллельны две на две; другими словами, две стороны, которые параллельны друг другу, а затем две другие, которые также параллельны. Кроме того, параллельные стороны также равны. Как мы могли сделать эту форму? Берем две стороны и располагаем их так, чтобы они были параллельны:

Как расположить две другие стороны так, чтобы они тоже были параллельны? Вот и все!

Когда линии параллельны и правильны, у нас есть три возможности.

Ромб

Если четыре стороны равны, то получается ромб.

Прямоугольник

Если четыре угла на рисунке прямые, то они образуют прямоугольник .

Квадрат

Если оба предыдущих пункта верны, то у нас есть квадрат с равными сторонами и четырьмя прямыми углами.

Видео для ознакомления с классификацией четырехугольников

Четырехугольники — геометрические фигуры с квадратными сторонами. Эти многоугольники подразделяются на параллелограммы и непараллелограммы. Для лучшего понимания предлагаю вам посмотреть следующее видео от Smartick, метод обучения математике для детей от 4 до 14 лет.

Это интерактивный учебник, преобразованный в видео, но если вы хотите решить его самостоятельно, зарегистрируйтесь в Smartick бесплатно и получите доступ ко всем нашим интерактивным учебникам.

 

Правильные геометрические фигуры с числом сторон более 4

Мы можем продолжить добавлять все равные линии, которые мы хотим создать, чтобы создать различных геометрических фигур с разными сторонами.

Пятиугольник

Имеет 5 равных сторон.

Шестиугольник

Имеет 6 равных сторон.

Мы можем найти их в сотах!

Откуда пчелы умеют создавать такие идеальные геометрические формы?

Обзор геометрических фигур с примерами из реальной жизни

Даже не осознавая этого, геометрические фигуры стали частью нашей жизни в большей степени, чем мы думаем. Посмотрите внимательно на следующее изображение и посмотрите, сколько геометрических фигур вы сможете найти.

Мы рассмотрим некоторые из них.

Окружность

Окружность — это геометрическая фигура, построенная путем построения кривой, которая всегда находится на одном и том же расстоянии от точки, которую мы называем центр . Линия, которая ограничивает круг, называется окружностью .

Мы получаем окружность, когда делаем кривую, сохраняющую расстояние от определенной точки. Например, с помощью циркуля мы выбираем точку с помощью стрелки, а затем, держа ее открытой, обводим карандашом окружность. Вы можете найти круги вокруг себя, например, на колесах автомобиля или теннисном мяче.

Треугольник

Треугольник — это многоугольник, полученный в результате соединения 3 точек прямыми линиями. Точки пересечения — это вершины, а отрезки — стороны.

В данном случае в школе Смартика мы нашли равнобедренный треугольник. У равнобедренных треугольников две стороны одинаковой длины и одна разной длины.

Квадрат

Квадрат представляет собой четырехсторонний многоугольник, все его стороны равны, а четыре угла равны 90 градусов каждый.

Прямоугольник

Прямоугольник представляет собой фигуру, состоящую из 4 прямых линий, называемых сторонами. Характеристики прямоугольников заключаются в том, что их противоположные стороны параллельны, а их 4 угла равны 9.0º.

Трапеция

Трапеция представляет собой четырехсторонний многоугольник, ни одна из сторон которого не параллельна другой. Трапеции могут быть симметричными или асимметричными, в зависимости от их характеристик.

В данном случае воздушный змей представляет собой симметричную трапецию . Это трапеции, у которых две пары равных сторон, причем одна из этих пар сторон меньше другой.

Восьмиугольник

Восьмиугольник — восьмиугольник. Правильный восьмиугольник — это многоугольник, у которого восемь равных сторон и восемь равных углов.