Sh x ch x: Открытая Математика. Функции и Графики. Гиперболические функции

2x = 1$

Содержание

Отрицателени аргументи

sh(-x) = -sh x

ch(-x) = -ch x

th(-x) = -th x

csch(-x) = -csch x

sech(-x) = -sech x

cth(-x) = -cth x

Формули за сбор

sh (x ± y) = sh x ch y ± ch x sh y

ch (x ± y) = ch x ch y ± sh x sh y

th(x ± y) = (th x ± th y)/(1 ± th x.th y)

cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)

Формули за двоен ъгъл

sh 2x = 2 sh x ch x

ch 2x = ch²x + sh²x = 2 ch²x — 1 = 1 + 2 sh²x

th 2x = (2th x)/(1 + th²x)

Формули за половин ъгъл

$\text{sh} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{2}}$ [+ ако x > 0, — ако x

$\text{ch} \frac{x}{2} = \sqrt{\frac{\text{ch} x + 1}{2}}$

$\text{th} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{\text{ch} x + 1}}$ [+ ако x > 0, — ако x

$=\frac{sh x}{ch x — 1} = \frac{ch x + 1}{sh x}$

Формули за 3 и 4 пъти ъгъл

sh 3x = 3 sh x + 4 sh³ x

ch 3x = 4 ch³ x — 3 ch x

th 3x = (3 th x + th³ x)/(1 + 3 th²x)

sh 4x = 8 sh³ x ch x + 4 sh x ch x

ch 4x = 8 ch⁴ x — 8 ch² x + 1

th 4x = (4 th x + 4 th³ x)/(1 + 6 th² x + th⁴ x)

Формули за сваляне на степента на хиперболичните функции

sh²x = ½ch 2x — ½

ch² x = ½ch 2x + ½

sh³x = ¼sh 3x — ¾sh x

ch³ x = ¼ch 3x + ¾ch x

sh⁴x = 3/8 — ½ch 2x + 1/8ch 4x

ch⁴ x = 3/8 + ½ch 2x + 1/8ch 4x

Формули за сума, разлика и произведение на хиперболични функции

sh x + sh y = 2 sh ½(x + y) ch ½(x — y)

sh x — sh y = 2 ch ½(x + y) sh ½(x — y)

ch x + ch y = 2 ch ½(x + y) ch ½(x — y)

ch x — ch y = 2 sh ½(x + y) sh ½(x — y)

sh x sh y = ½(ch (x + y) —

ch (x — y))

ch x ch y = ½(ch (x + y) + ch (x — y))

sh x ch y = ½(sh (x + y) + sh (x — y))

Изразяване на хиперболичните функции чрез хиперболични функции

При x > 0(При x < 0 използваме формулите за отрицателен ъгъл) имаме:

~	$sh x = u$	$ch x = u$	$th x = u$	$cth x = u$	$sech x = u$	$esch x = u$
$sh x$	$u$	$\sqrt{u^2 — 1}$	$\frac{u}{\sqrt{1 — u^2}}$	$\frac{1}{\sqrt{u^2 — 1}}$	$\frac{\sqrt{1 — u^2}}{u}$	$\frac{1}{u}$
$ch x$	$\sqrt{1 + u^2}$	$u$	$\frac{1}{\sqrt{1 — u^2}}$	$\frac{u}{\sqrt{u^2 — 1}}$	$\frac{1}{u}$	$\frac{\sqrt{1 + u^2}}{u}$
$th x$	$\frac{u}{\sqrt{1 + u^2}}$	$\frac{\sqrt{u^2 — 1}}{u}$	$u$	$\frac{1}{u}$	$\sqrt{1 — u^2}$	$\frac{1}{\sqrt{1 + u^2}}$
$cth x$	$\frac{\sqrt{1 + u^2}}{u}$	$\frac{u}{\sqrt{u^2 — 1}}$	$\frac{1}{u}$	$u$	$\frac{1}{\sqrt{1 — u^2}}$	$\sqrt{1 + u^2}$
$sech x$	$\frac{1}{\sqrt{1 + u^2}}$	$\frac{1}{u}$	$\sqrt{1 — u^2}$	$\frac{\sqrt{u^2 — 1}}{u}$	$u$	$\frac{u}{\sqrt{1 + u^2}}$
$esch x$	$\frac{1}{u}$	$\frac{1}{\sqrt{u^2 — 1}}$	$\frac{\sqrt{1 — u^2}}{u}$	$\sqrt{u^2 — 1}$	$\frac{u}{\sqrt{1 — u^2}}$	$u$

Графики на хиперболичните функции

y = sh x

y = ch x

y = th x

y = cth x

y = sech x

y = csch x

Обратни хиперболични функции

Ако x = sh y, то y = sh^-1 се нарича обратен хиперболичен синус от x. 2} + 1})$ $x \neq 0$

Зависимости на обратните хиперболични функции

csch^-1 x = sh^-1 (1/x)

sech^-1 x = ch^-1 (1/x)

cth^-1 x = th^-1 (1/x)

sh^-1(-x) = -sh^-1x

th^-1(-x) = -th^-1x

cth^-1 (-x) = -cth^-1x

csch^-1 (-x) = -csch^-1x

Графики на обратните хиперболични функции

y = sh^-1x

y = ch^-1x

y = th^-1x

y = cth^-1x

y = sech^-1x

y = csch^-1x

Връзка между тригонометричните и хиперболичните функции
sin(ix) = i sh x cos(ix) = ch x tg(ix) = i th x
csc(ix) = -i csch x sec(ix) = sech x cotg(ix) = -i cth x
sh(ix) = i sin x ch(ix) = cos x th(ix) = i tg x
csch(ix) = -i csc x sech(ix) = sec x cth(ix) = -i cotg x
Период на хиперболичните функции
Във формулите k е произволно цяло число.
sh (x + 2kπi) = sh x     csch (x + 2kπi) = csch x
ch (x + 2kπi) = ch x     sech (x + 2kπi) = sech x
th (x + kπi) = th x     cth (x + kπi) = cth x
Връзка между обратните хиперболични и обратните тригонометрични функции

sin^-1 (ix) = ish^-1x sh^-1(ix) = i sin^-1x
cos^-1 x = ±i ch^-1 x ch^-1x = ±i cos^-1x
tg^-1(ix) = i th^-1x th^-1(ix) = i tg^-1x
cotg^-1(ix) = -i cth^-1x cth^-1 (ix) = -i cotg^-1x
sec^-1 x = ±i sech^-1x sech^-1 x = ±i sec^-1x
csc^-1(ix) = -i csch^-1x csch^-1(ix) = -i csc^-1x
Хиперболични функции във форума
Форум за висша математика
заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
написание лабораторных, рефератов и курсовых
выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

Форум, где посетители обмениваются идеями и помогают друг другу
Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
Аукцион, где цена за товар или услугу определяется в результате торгов
Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.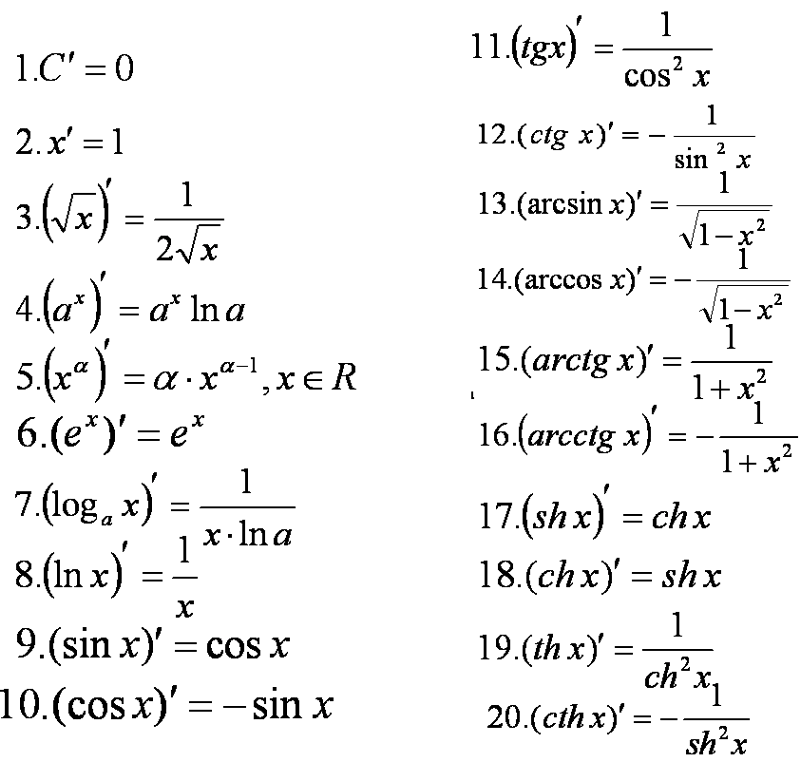
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

Выбрать платежную систему.
Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Добавляя -es к существительным, оканчивающимся на -ch, -s, -sh, -ss, -x и -z
Добавляя -s к существительным, оканчивающимся на -o.

Единственное число Множественное число Единственное число Множественное число
адрес адреса рыба рыбы
партия партии дюйм дюйма
пляж пляжи зуд чешется
босс боссы поцелуй поцелуи
коробка коробки объектив линзы
филиал отделения обед обеды
кисть щетки соответствует соответствует
автобус автобусы минус минус
гудок гудки патч патчи
улов ловит персик персики
церковь церкви плюс плюс
класс классы префикс префиксы
сцепление сцепления проспект проспекты
междугородний автобус вагоны викторина викторины
комплекс комплексы шесть шестерки
крест кресты косая черта косая черта
блюдо посуда речь выступления
платье платья суффикс суффиксы
ресница ресницы налог налоги
мигание мигает дрозд дрозды
лиса лисы вирус вирусы
газ газы часы часы
стекло очки желание пожелания

Добавляя –s к существительным, оканчивающимся на -o.
Калькулятор — sh(x) — Solumaths
Ш, расчет онлайн
Резюме:
Функция sh позволяет в режиме онлайн вычислить гиперболический синус числа.
sh онлайн
Описание :
Калькулятор позволяет использовать большинство гиперболические функции , можно вычислить гиперболический косинус (отмечено гл. или кош), гиперболический синус (отмеченный ш или грех ), гиперболический тангенс (отмеченный й или танх ), и гиперболический котангенс (отмеченный ткань или котан ).
Функция гиперболического синуса записывается ш, она определяется следующим формула :
`ш(х)=(ехр(х)-ехр(-х))/2`
эксп это обозначение экспоненциальный функция.
Расчет гиперболического синуса
Калькулятор гиперболического синуса позволяет через функцию sh вычислить онлайн гиперболический синус числа.
Чтобы вычислить гиперболический синус числа, просто введите число и примените функция ш . Для расчет гиперболический синус следующего числа 0, введите sh(`0`) или напрямую 0, если кнопка sh уже появляется, возвращается результат 0.
Производная гиперболического синуса
Производная гиперболического синуса равна ch(x).
Первообразная гиперболического синуса
Первообразная гиперболического синуса равна ch(x).
Пределы гиперболического синуса
Пределы гиперболического синуса существуют при `-oo` и `+oo`:
Функция гиперболического синуса имеет предел в `-oo`, который равен `-oo`.
`lim_(x->-oo)sh(x)=-oo`
Функция гиперболического синуса имеет предел в `+oo`, который равен `+oo`.
`lim_(x->+oo)sh(x)=+oo`
Синтаксис:
sh(x), x — число.
Иногда используются другие обозначения: sinh
Примеры:
sh(`2`), возвращает 3,62686040785
Производный гиперболический синус:
можно использовать калькулятор производной, который позволяет вычислить производную функции гиперболического синуса
Производная функции sh(x) является производной(`sh(x)`)=`ch(x)`
Гиперболический синус.
Первопроизводная функции sh(x) является первообразной(`sh(x)`)=`ch(x)`
Предельный гиперболический синус :
Калькулятор пределов позволяет вычислить пределы функции гиперболического синуса .
Предел sh(x) is limit(`sh(x)`)
Графический гиперболический синус :
Графический калькулятор может отображать функцию гиперболического синуса в заданном интервале.
Свойство функции гиперболического синуса:
Гиперболический синус является нечетной функцией.
Расчет онлайн с помощью sh (гиперболический синус)
См. также
Список связанных калькуляторов:
Экспоненциальный : exp. Функция exp вычисляет в режиме онлайн экспоненту числа.
Гиперболический косинус: гл. Функция ch вычисляет в режиме онлайн гиперболический косинус числа.
Гиперболический котангенс : coth. Функция coth вычисляет в режиме онлайн гиперболический котангенс числа.
Гиперболический синус: ш. Функция sh позволяет вычислить в режиме онлайн гиперболический синус числа.
Гиперболический тангенс: th. Функция th позволяет в режиме онлайн вычислить гиперболический тангенс числа.
Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
Синус : грех.
No related posts.