Формула интегралов умножение: интеграл умножения формула

Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница / Хабр

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

К сожалению, так сложилось, что многим (и мне) она, порой кажется, слишком сложной, недоступной, наукой для избранных. Между тем, так только кажется ! Безусловно, она требует интеллектуального напряжения, памяти, воображения и много чего ещё, как и многие другие интеллектуальные занятия.

Отличительными особенностями её являются:

1. использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),

2. логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),

3. последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),

4. высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

1. Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин

2. Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы

3. Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т.д.)

4. Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук

5. Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными

6. Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее

7. Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т.д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Во введении к книге «Развитие понятия интеграла» известный историк математики профессор Фёдор Андреевич Медведев так охарактеризовал сущность интегрирования и процесс его развития в науке «… Интегрирование представляет собой абстрактное выражение разнообразнейших способов измерения величин, и по мере вовлечения в человеческое познание всё новых и новых объектов реальной действительности математики создают всё более и более общие схемы интеграционных процессов с тем, чтобы охватить всё расширяющийся круг объектов, подлежащих измерению» [1].

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

2. Геометрический и аналитико-алгебраический смысл интегрирования

Естественным образом, возникает два вида задач, которые отражают два смысла интегрирования: — геометрический и аналитико-алгебраический. Первый — отыскание площади плоской фигуры под произвольной кривой (квадратура) и отыскание объёма (кубатура). Второй — подсчёт суммарного значения некой переменной величины [2], которая изменяется, принимает различные значения сообразно единицам времени, длины и т. д.

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

• В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].

• В случае с вещественными числами.

  • Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.

  • Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.

  • В случае с отрицательными числами (-2,3 × 4,3), умножение — сумма произведений и разворот числовой оси или иными словами отражение суммарного значения произведения — в данном случае числа 9,89 относительно начала отсчёта, то есть числа ноль, в результате получаем -9,89.

• В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

• Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».

• Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где а .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

3. Интуитивные способы отыскания значения интеграла

Итак, каким же образом вычислить интегральную сумму ? Можно попробовать несколько способов:

1. Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

• Функция является числовой, то есть область определения и область значений являются числовыми — принимают числовые значения (более точно — вещественные значения).

• Функция непрерывна и принимает значения в каждой точке с соответствующим значением переменной (к примеру, в точкесуществует значение функции , а в точке значение

• Функция может иметь любое выражение. Мы можем иметь набор значений функции в соответствующих точках в виде таблицы (функция задана таблично). Или функция может быть явно задана в виде аналитического выражения (к примеру, в случае с функцией от одной вещественной переменной — , и т.д.).

• Функция может описывать зависимость величины любой природы — физической, биологической, экономической и т.д.

Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

[1]. Медведев Ф.А. Развитие понятия интеграла. — М.: Наука, 1974. С. 4

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для и одно и тоже. Далее, мы покажем, что производная , то есть можно записать или .

[7]. То есть . К примеру, пусть функция задана выражением . Тогда, при , , а значение . Если. Тогда, при , , а значение .

[8]. Пусть имеется точка, число 7 и 10, чтобы найти величину промежутка между этими значениями надо найти разность то есть 10 — 7 = 3.

В помощь слепым — 2 (добавил) — Современные математики

В статье Попытка скрестить ужа с ежом как основа математической лженауки. Синтез и анализ я показал две математические формулы артикулирующие, что такое ПАРАМЕТРИЧЕСКИЙ и АНАЛИТИЧЕСКИЙ интегралы.

ПАРАМЕТРИЧЕСКИЙ ИНТЕГРАЛ — это есть результат умножения двух НЕЗАВИСМЫХ ДРУГ ОТ ДРУГА величин. То есть, это умножение производится в двух вариантах:

— либо одна из двух величин принимается за исследуемую переменную, а вторая, в этом случае, считается параметром;
— либо другая из этих двух величин считается переменной, а параметром считается та, которая в первом случае принималась за переменную исследуемую величину.

В чем здесь смысл, в отличие от алгебры? В том, что в алгебре ПОРЯДОК не имеет значения, а имеет значение только МЕРА.
А в матанализе основным объектом изучения является именно ПОРЯДОК! Мера второстепенна.

Поэтому, если Вы не уясните разделение чисел на порядок и меру, то не поймете дальнейшее развитие РЕАЛЬНОЙ математической науки. На Декартовой плоскости МЕРА — длина отрезков относительно длины единичного отрезка. ПОРЯДОК — расположение точек относительно точки начала отсчета. Современная версия математической шизофрении указывает на точку числовой оси как на число, хотя имеет ввиду количество единичных отрезков от точки отсчета до этой точки.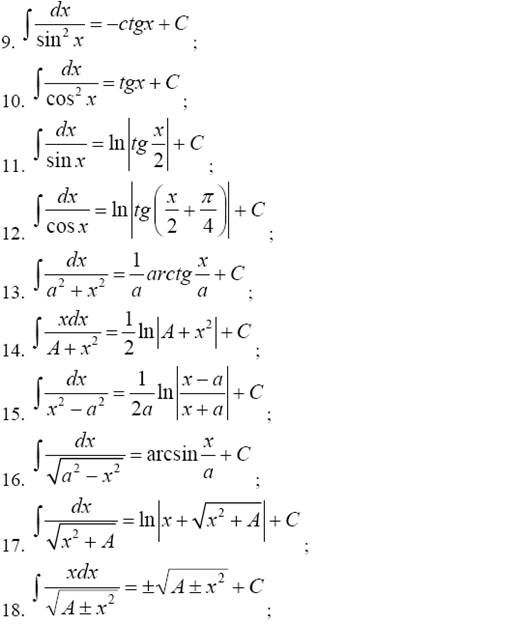 Обыкновенная шизофрения… )))

На самой же Декартовой плоскости числа действительно находятся в точках. Потому, что на этой плоскости используются не геометрические точки, а топологические. Но современная версия математической шизофрении этого различия не «видит», хотя Рене Декарт даже показывал рисунками этот момент в «Правилах для руководства ума».

Итак, ПАРАМЕТРИЧЕСКИЙ ИНТЕГРАЛ ВСЕГДА ОДИН. Почему? Потому, что второй интеграл, согласно формуле интегрирования по частям, РАВЕН НУЛЮ. Почему? Потому, что дифференциал параметра — величины не изменяющей своего значения при изменении значения исследуемой переменной — равен нулю. Поэтому интеграл по дифференциалу параметра «исчезает».

АНАЛИТИЧЕСКИЙ ИНТЕГРАЛ — это есть ОДИН ИЗ ДВУХ смежных интегралов. Оба этих интеграла есть результат умножения двух ЗАВИСИМЫХ ДРУГ ОТ ДРУГА величин. Поэтому, согласно формуле интегрирования по частям, этих интегралов всегда два, так как при умножении двух зависимых величин их произведение есть сумма интеграла первой величины по дифференциалам второй величины и интеграла второй величины по дифференциалам первой величины.

А, теперь, самое главное. И параметрический, и аналитический интегралы описываются соответствующим вариантом формулы интегрирования по частям. Согласно этой формулы ИНТЕГРАЛ — ЕСТЬ СОСТАВНАЯ ЧАСТЬ ПРОИЗВЕДЕНИЯ. То есть, интеграл — это не самостоятельный математический объект, а результат математического действия умножения ПРИ УЧЕТЕ РАЗЛИЧНОГО ПОРЯДКА между сомножителями ЭТОГО ДЕЙСТВИЯ!!!

«Интегралы» РИМАНА и ЛЕБЕГА не имеют интегральных формул, потому, что они не являются результатом действия умножения. Они — суммы.

Для подставной легитимации их существования произведена манипуляция визуального мошеннического обмана с использованием подмены действия умножения действием сложения. ВАС Н@ЕБАЛИ! Интеграл не может быть результатом действия сложения именно потому, что он есть результат действия умножения. Дифференцирование — деление. Обратное ему интегрирование — умножение.

Интеграция формулы ультрафиолета — Что такое интеграция формулы ультрафиолета? Примеры

Интегрирование формулы uv является удобным средством нахождения интегрирования произведения двух функций u и v. Кроме того, две функции, используемые в этом интегрировании формулы uv, могут быть алгебраическими выражениями, тригонометрическими отношениями или логарифмическими функциями. Разложим дифференциал произведения функций и выразим данный интеграл через известный интеграл. Таким образом, интегрирование формулы uv также известно как интегрирование по частям или правило интегрирования произведения. Давайте изучим интеграцию формулы uv и ее приложений.

Что такое интегрирование формулы УФ?

Интегрирование формулы uv – это специальное правило интегрирования по частям. Здесь мы интегрируем произведение двух функций. Если u(x) и v(x) являются двумя функциями и имеют форму ∫u dv, то формула интегрирования uv задается как:

• ∫ uv dx = u ∫ v dx — ∫ (u’ ∫ в дх) дх
• ∫ u дв = uv — ∫ v дю

где,

• u = функция u(x)
• дв = переменная дв
• v = функция v(x)
• du = переменная du

Интегрирование формулы UV

Чтобы найти интеграл от произведения двух функций, выполните следующие простые быстрые шаги:

• Определите функцию u(x) и v(x). Выберите u(x), используя правило LIATE: в зависимости от того, что придет первым в этом порядке: логарифмическая, обратная, алгебраическая, тригонометрическая или экспоненциальная функция.
• Найдите производную от u: du/dx
• Интегрировать v: ∫v dx
• Введите значения в формулу ∫u.v dx = u. ∫v.dx- ∫( ∫v.dx.u’). дх
• Упрости и реши.

Вывод интегрирования формулы UV

Мы выведем интегрирование формулы uv, используя правило дифференцирования произведения. Рассмотрим две функции u и v, такие что y = uv. Применив правило дифференцирования произведения, мы получим

d/dx (uv) = u (dv/dx) + v (du/dx) 9Мы имеем dx) (dx) = ∫ d/dx (uv) dx — ∫ v (du/dx) dx

⇒ ∫u dv = uv — ∫v du

Отсюда выводится формула интегрирования uv.

Давайте попробуем несколько примеров, чтобы лучше понять, как применять интегрирование формулы uv.

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами

Закажите бесплатный пробный урок

Решенные примеры с использованием интегрирования формулы UV

Пример 1: Найдите интеграл x.Sinx.

Решение:

Здесь u = x и dv = sin x dx

du = dx и v = ∫sinx dx= — cos x dx

Используя формулу uv ∫u.dv = ув- ∫v du получаем

∫x sinx dx = x. (-cos x) — ∫(-cos x dx)

= -x cos x — (-sin x) + C

= -x cos x + sin x + C

Ответ: ∫x.sinx.dx = sin x — x cos x + C

Пример 2: Найдите интеграл от x ² .logx

Решение:

Здесь u = logx и dv = x ² dx 900 03

du = 1/x dx и v = x ³ /3 + C

Интегрируя формулу uv ∫u.dv = uv- ∫v du, получаем

∫x ² log x dx= log x. (х ³ /3) — ∫(x ³ /3)(1/x)dx

= log x.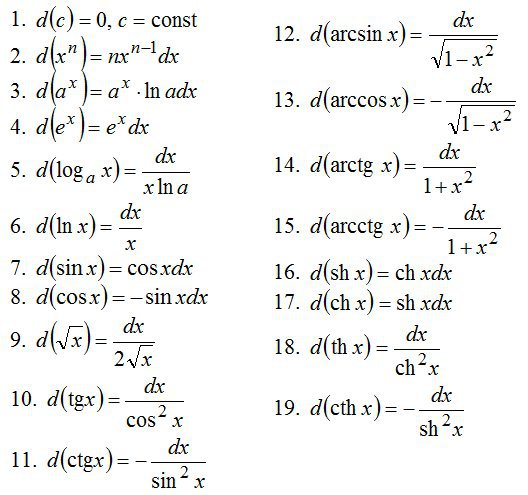 (x ³ /3) -(1/3) ∫(x ³ )(1/x)dx

= log x. (x ³ /3) -(1/3) ∫x ² dx

= (x ³ /3)log x — (1/3) (x ³ /3)+C

=(x ³ /3) log x- (x ³ /9)+ C

Ответ: ∫x ² logx = (x ³ /3 ) лог х- (х ³ /9)+ C

Пример 3: Найти интеграл от xe ^х дх.

Решение:

Здесь u = x ^{и dv = e x dx.}

du = dx и v = e ^x

Интегрируя формулу uv ∫u.dv = uv- ∫v du, получаем

∫xe ^x dx = x e ^{x 901 03 — ∫ е x dx}

= xe ^x — e ^x + C

Ответ: Таким образом, интеграл от xe ^x dx = ^{xe x — e 9 0102 х} +С

Часто задаваемые вопросы по формуле интеграции УФ

Что такое формула интеграции УФ?

Формула интегрирования uv: ∫u. v = u. ∫v.dx- ∫( ∫v.dx.u’). дх. Формула интегрирования uv помогает нам вычислить интегралы от произведения двух функций.

Как использовать формулу интегрирования УФ?

Определите интеграл формы ∫u.vdx. Выберите u(x), используя правило LIATE, и продифференцируйте его. Выберите v(x) и интегрируйте dv. Затем подставьте все полученные значения в формулу ∫u.v = u. ∫v.dx- ∫( ∫v.dx.u’). dx и вычислить интеграл.

Что означает DV в формуле интеграции ультрафиолета?

Когда интеграл имеет вид ∫u.vdx, нам нужно применить формулу интегрирования uv. Используйте правило LIATE и определите функцию u(x). Другая функция v(x) имеет форму dv. Интегрируем dv, чтобы получить v.

Что подразумевается под интеграцией по частям?

Интегрирование по частям — это метод, используемый в качестве формулы интегрирования uv для интегрирования определенного или неопределенного интеграла, являющегося произведением двух функций. Разложим дифференциал произведения функций и выразим исходный интеграл через известный интеграл как ∫u. v = u. ∫v.dx- ∫( ∫v.dx.u’). дх

Интегрирование по частям — формула, вывод, приложения, примеры

Идея интегрирования по частям в исчислении была предложена в 1715 году Бруком Тейлором, который также предложил знаменитую теорему Тейлора. Обычно интегралы вычисляются для функций, для которых существуют формулы дифференцирования. Здесь интегрирование по частям является дополнительным методом, используемым для нахождения интегрирования произведения функций, и его также называют частичным интегрированием. Он изменяет интегрирование произведения функций в интегралы, для которых можно легко вычислить решение.

Некоторые обратные тригонометрические функции и логарифмические функции не имеют целочисленных формул, и здесь мы можем использовать формулу интегрирования по частям, также известную как формула интегрирования uv. Здесь мы проверим вывод, графическое представление, приложения и примеры интегрирования по частям.

1.	Что такое интеграция по частям?
2.	Интегрирование по частям Формула
3.	Интегрирование по формуле частей
4.	Визуализация интеграции по частям
5.	Применение интеграции по частям
6.	Формулы, связанные с интегрированием по частям
7.	Часто задаваемые вопросы об интеграции по частям

Что такое интеграция по частям?

Интегрирование по частям используется для интегрирования произведения двух или более функций. Две интегрируемые функции f(x) и g(x) имеют вид ∫f(x)·g(x). Таким образом, его можно назвать продуктовым правилом интегрирования. Среди двух функций первая функция f(x) выбирается такой, что формула ее производной существует, а вторая функция g(x) выбирается такой, что интеграл от такой функции существует.

∫ f(x)·g(x)·dx = f(x) ∫ g(x)·dx — ∫ [(f'(x) ∫ g(x)·dx)·dx] + C

Интегрирование (первая функция x вторая функция) = (первая функция) x (интегрирование второй функции) — интегрирование (дифференциация первой функции x интегрирование второй функции).

При интегрировании по частям формула разбивается на две части и мы можем наблюдать производную первой функции f(x) во второй части, и интеграл второй функции g(x) в обеих частях . Для простоты эти функции часто обозначаются как «u» и «dv» соответственно. Формула интегрирования uv с использованием обозначений «u» и «dv»:

∫ u dv = uv — ∫ v ду.

Интеграция по формуле частей

Формула интегрирования по частям используется для нахождения интеграла от произведения двух различных типов функций, таких как логарифмическая, обратная тригонометрическая, алгебраическая, тригонометрическая и экспоненциальная функции. Формула интегрирования по частям используется для нахождения интеграла произведения.

В правиле дифференцирования произведения, где мы дифференцируем произведение uv, u(x) и v(x) можно выбирать в любом порядке. Но при использовании формулы интегрирования по частям для выбора первой функции u(x) мы должны посмотреть, какая из следующих функций идет первой в следующем порядке, и затем принять ее за u.

• Логарифмический (L)
• Обратный тригонометрический (I)
• Алгебраический (А)
• Тригонометрический (Т)
• Экспоненциальная (E)

Это можно запомнить с помощью правила LIATE . Обратите внимание, что этот заказ также может быть формулой

ILATE . Например, если нам нужно найти ∫ x ln x dx (где x — алгебраическая функция, а ln — логарифмическая функция), мы выберем ln x как u(x), как в LIATE, логарифмическая функция стоит перед алгебраической функцией. функция. Формула интегрирования по частям определяется двумя способами. Мы можем использовать любой из них для интегрирования произведения двух функций.

Вывод формулы интегрирования по частям

Доказательство интегрирования по частям можно получить из формулы производной произведения двух функций. Таким образом, формула интегрирования по частям также известна как правило интегрирования произведения.

Выведем формулу интегрирования по частям, используя правило дифференцирования произведения. Рассмотрим две функции u и v. Пусть их произведение равно y. т. е. у = ув. Применяя правило дифференцирования произведения, получаем

d/dx (uv) = u (dv/dx) + v (du/dx)

Это можно записать как:

u (dv/dx) = d/dx (uv) — v (du/ dx)

Интегрируя в обе стороны по x,

∫ u (dv/dx) (dx) = ∫ d/dx (uv) dx — ∫ v (du/dx) dx

Сокращая члены,

∫ u dv = uv — ∫ v du

Отсюда выводится формула интегрирования по частям.

Визуализация интеграции по частям

Рассмотрим параметрическую кривую (x, y) = (f(θ), g(θ)). Будем считать эту кривую интегрируемой и взаимно однозначной функцией. Интегрирование по частям представляет площадь синей области на приведенной ниже кривой. Сначала рассмотрим области синей и желтой областей отдельно.

Рассмотрим кривую вдоль оси y, у нас есть функция x(y) и через пределы [y ₁ , y ₂ ]. Также мы можем рассматривать кривую вдоль оси x и иметь функцию y(x) в пределах [x ₁ , x ₂ ].

Площадь желтой области = ∫ ^{y ₂}

_y1 x(y)·dy

Площадь синей области = ∫ x 2 9 0356 х1 у(х)·дх

Общая площадь этих двух областей равна площади большего прямоугольника минус площадь меньшего прямоугольника.

∫ y 2 y1 x(y)·dy + ∫ x 2 x1 y(x)·dx = [x· у(х)] х 2 x1

Без определенных интегралов можно записать как.

∫ y·dx+ ∫ x·dy = xy

∫x·dy = xy — ∫ y·dx

Далее, это можно изменить, чтобы получить формулу интегрирования по частям.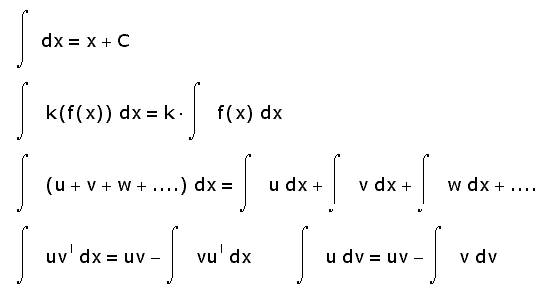

∫f(x)·g(x)·dx = f(x)·∫ g(x)·dx — ∫(f'(x) · ∫ g(x)·dx) ·dx

Приложения интеграции по частям

Эта формула интегрирования по частям применяется к функциям или выражениям, для которых не существует формул интегрирования. Здесь мы пытаемся включить эту формулу интегрирования по частям и пытаемся вывести интеграл. Для логарифмических функций и для обратных тригонометрических функций интегральных формул не существует. Попробуем решить и найти интегрирование log x и tan

-1 x.

Интегрирование логарифмической функции

∫ log x·dx = ∫ log x,1·dx

= лог х. ∫1·dx — ∫ ((log x)’.∫ 1·dx)·dx

= log x·x -∫ (1/x ·x)·dx

= x log x — ∫ 1·dx

= x log x — x + C

Интегрирование обратной тригонометрической функции

∫ tan ^-1 x·dx = ∫tan ^-1 x.1·dx

= tan ^{-1 90 103 х·∫ 1·dx — ∫((tan -1 x)’.∫ 1·dx)·dx}

= tan ^-1 x· x — ∫(1/(1 + x ² )·x) ·dx

= x· tan ^-1 x — ∫ 2x/(2(1 + x ² ))·dx

= x· tan ^-1 x — ½. log(1 + x ² ) + C

Следующие формулы были получены из формулы интегрирования по частям и полезны в процессе интегрирования различных алгебраических вычислений. выражения.

• ∫ e ^x (f(x) + f'(x))·dx = e ^x f(x) + C
• ∫√(x ² + a ² )·dx = ½ . x·√(x ² + a ² )+ a ² /2· log|x + √(x ² + a ² )| С
• ∫√(x ² — a ² )·dx =½ x·√(x ² — a ² ) — a ² /2 · log|x +√(x 9 0102 2 — а ² ) | С
• ∫√(a ² — x ² )·dx = ½ x·√(a ² — x ² ) + a ² /2· sin ^-1 х/а + С

☛ Статьи по теме:

• Исчисление
• Формулы дифференцирования и интегрирования
• Дифференциальные уравнения
• Формулы интегрирования

Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Решенные примеры интегрирования по частям

1. Пример 1: Найдите интеграл от x ² e ^x , используя формулу интегрирования по частям.

   Решение:

   Используя LIATE, u = x ² и dv = e ^x dx.

   Тогда du = 2x dx, v = ∫ e ^x dx = e ^x .

   Используя одну из формул интегрирования по частям,

   ∫ u dv = uv — ∫ v du

   ∫ x ² e ^x dx = x ² e ^x — ∫ e ^x (2x) dx

   = x ² e ^x — 2 ∫ x e ^x dx

   900 02 Повторное применение формулы интегрирования по частям для оценки ∫ x e ^x dx . = х ² е ^х — 2 х е ^х + 2 е ^х + С

   = е ^х (х ² — 2 х + 2) + С

   Ответ: ∫ x ² e ^x dx = = e ^x (x ² — 2 x + 2)+ C

2. Пример 2: Найдите интеграл от x sin 2x, используя формулу интегрирования по частям.

   Решение:

   Для интегрирования данного выражения используем формулу интегрирования по частям: Здесь u = x и v = sin 2x

   ∫x sin 2x dx

   = x ∫sin 2x dx — ∫d/dx (x) ∫ sin 2x dx dx

   = x (-(cos 2x)/2) — ∫(1.-(cos 2x) /2). dx

   = — x (cos 2x) /2. dx + 1/2 ∫cos2x dx

   = -x/2 cos 2x + (1/4) sin 2x + C

   Ответ: Таким образом, ∫x sin 2x dx = -x/2 cos 2x + (1/ 4) грех 2х + С

3. Пример 3: Вычислите интеграл ∫ x ln x dx, используя интегрирование по частям.

   Решение:

   Первый метод:

   Используя LIATE, u = ln x и v = x.

   С помощью одной из формул интегрирования по частям x) (∫ x dx) dx

   = ln x (x ² /2) — ∫ (1/x) (x ² /2) dx

   = (x ² ln x)/2 — (1/2) ∫ x dx

   = (x ² ln x) / 2 — (1/2) (x ² /2) + C

   = (x ² ln x) / 2 — (х ² /4) + С

   = (x ² /4)(2 ln x -1) + C

   Второй метод:

   Используя LIATE, u = ln x и dv = x dx.

   Тогда du = (1 /x) dx и v = ∫ x dx = x ² /2

   , используя одну из формул интеграции по частям,

   ∫ U DV = UV — ∫ V Du

   ∫ x ln x dx = ln x (x ² /2) — ∫ (x ² /2) (1/x) dx

   = (x ² ln x)/2 — (1/2) ∫ x dx

   = (x ² ln x) / 2 — (1/2) (x ² /2) + C

   = (x ² ln x) /2 — (x ² / 4) + C

   = (x ² /4)(2 ln x -1) + C

   Ответ: По обоим методам ∫ x ln x dx = (x ² /4)(2 ln x -1) + C

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по интеграции по частям

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об интеграции по частям

Что такое интегрирование вычислений по частям?

Интеграция по частям — это интеграция произведения двух функций. Эти две функции обычно представляются как f(x) и g(x). Среди двух функций первая функция f(x) выбирается так, что существует формула ее производной, а вторая функция g(x) выбирается так, что существует интегральная формула этой функции.

∫ f(x)·g(x)·dx = f(x) ∫ g(x)·dx — ∫(f'(x) ∫g(x)·dx)·dx + C

Что такое Интеграция по формуле частей?

Формула интегрирования по частям — это формула, используемая для нахождения интеграла от произведения двух различных типов функций. Эта формула также известна как формула частичного интегрирования и гласит:

∫ u dv = uv — ∫ v du

Здесь первая функция ‘u’ должна быть выбрана в соответствии с формулой LIATE (или) ILATE. (логарифмический (L), обратный тригонометрический (I), алгебраический (A), тригонометрический (T), экспоненциальный (E)).

Почему мы используем формулу интегрирования по частям?

Формула интегрирования частей используется, когда нормальная форма интегрирования невозможна. Интегрирование, как правило, возможно для функций, для которых доступна формула производной. Такие выражения, как логарифмические функции, обратные тригонометрические функции, не могут быть легко интегрированы, поэтому интегралы находятся с использованием формулы интегрирования по частям.

Как получить формулу интегрирования по частям?

Использование правила дифференцирования произведения,

d/dx (uv) = u (dv/dx) + v (du/dx)

u (dv/dx) = d/dx (uv) — v (du/dx)

Применение интеграла к обоим стороны,

∫ u (dv/dx) (dx) = ∫ d/dx (uv) dx — ∫ v(du/dx) dx

Это дает,

∫ u dv = uv — ∫ v du

Таким образом, получается формула интегрирования по частям.

Какие существуют другие методы интеграции помимо интеграции по частям?

Для интеграции используются три различных метода.

(a) Интеграция путем замены
(b) Интегрирование неполными дробями
(c) Интеграция по частям

Как узнать, когда использовать интеграцию по частям?

Интеграция по частям используется, когда простой процесс интеграции невозможен. Если есть две функции и произведение между ними, мы можем взять формулу интегрирования между частями. Также для одной функции мы можем взять 1 в качестве других функций и найти интегралы, используя интегрирование по частям. Например, мы можем интегрировать sin ^-1 x, log x, x cos x, используя эту формулу.

Какая из функций должна быть выполнена в виде буквы «U» при интегрировании по частям?

Формула интегрирования по частям: ∫ uv·dx = u∫ v·dx — ∫( u’∫ v·dx)·dx. Здесь функция «u» выбрана так, чтобы можно было вычислить формулу производной этой функции. Эта формула также известна как формула интегрирования УФ.

В чем разница между интеграцией по частям и заменой?

Интегрирование частей можно использовать для нахождения интегралов от произведения двух функций f(x)·g(x). Интегрирование путем замены может быть рассчитано для функций, имеющих подфункции, f (g (x)). Интегрирование по частям можно использовать для таких функций, как x cos x, e ^x загар x, x e ^x . А интегрирование подстановкой можно использовать для таких функций, как sin(log x). √tan x, cosec ² (5 ^x ).

Как применять ограничения при интегрировании по частям?

Пределы интегрирования по частям могут применяться аналогично определенным интегралам. Применяя нижний предел «a» и верхний предел «b» к интегрированию по частям, мы имеем ∫ ^b _a uv·dx = [ u∫ ^b _a v·dx — ∫( u’ ∫ v·dx)·dx] ^b _a

Как узнать, когда использовать формулу интегрирования по частям?

Когда мы встречаем интеграл от произведения двух функций, то мы должны применить формулу интегрирования.