Полезные факты для решения задач по геометрии
Анна Малкова
Полезные факты для решения задач ЕГЭ по геометрии (ЕГЭ по математике, Часть 2, профильный уровень).
Как научиться решать задачи ЕГЭ по геометрии (задача 16, Профильный уровень)?
Школьные учебники геометрии (Л. С. Атанасян, А. Г. Мерзляк…) неплохие. Даже лучше, чем по алгебре. Однако в них нет задач из вариантов ЕГЭ. Непонятно, как по ним готовиться к ЕГЭ, на что обращать внимание. Да и нет времени в 11-м классе заново читать учебник и решать все задачи подряд.
В освоении планиметрии важен правильный подход. Многие начинают с реальных задач ЕГЭ, а когда не получается, чувствуют разочарование. Не стоит так делать.
Первый этап: выучите теорию. Определения, теоремы, признаки. Основные формулы. Например, для площади треугольника нам нужны 5 формул. Помните их? Все они применяются в решении задач. Теоремы синусов и косинусов. Свойства высот, медиан и биссектрис. И многое другое.
В этом вам поможет Полный справочник Анны Малковой для подготовки к ЕГЭ по математике. Именно то, что нужно для решения задач ЕГЭ. Ничего лишнего. А цветные картинки запоминаются сами собой.
И конечно, практика! Решаем задачи ЕГЭ. Сначала – Часть 1, задачи 3 и 6. Не меньше 50 задач первой части ЕГЭ по теме «Планиметрия» надо решить, чтобы выучить и уметь применять теоремы и формулы планиметрии.
Изучить планиметрию и потренироваться в решении задач можно на нашем Онлайн-курсе.
Задачи, решения, видеоразбор.
Отлично, освоили задачи по планиметрии 1 части Профильного ЕГЭ по математике. Пора переходить ко второй! К задаче 16. Но не будем спешить. Пункт (а) задачи 16 Профильного ЕГЭ по математике – доказательство. А вы знаете, что пункт (а) нужен не только для того, чтобы вы получили один из трех баллов за эту задачу? Что во многих задачах ЕГЭ №16 пункт (а) содержит идеи для решения пункта (б). Намеки на то, как решить задачу полностью. Надо научиться доказывать всевозможные утверждения планиметрии.
Мы публикуем для вас новый и ценный материал — доказательство полезных фактов. Это и повторение всего курса (7-9 класс), и «заготовки» для многих задач ЕГЭ.
Приведем список из 32 полезных фактов. Докажите их самостоятельно и проверьте решения по ссылкам.
Для большинства этих полезных фактов приведены примеры решения задач и первой, и второй части Профильного ЕГЭ по математике.
Углы, треугольники, четырехугольники
1. Биссектрисы смежных углов перпендикулярны.
2. Свойство медианы прямоугольного треугольника.
3. Сумма квадратов диагоналей параллелограмма.
4. Площадь выпуклого четырехугольника
5. Свойства трапеции: отрезок, соединяющий середины диагоналей
6. Свойства равнобедренной трапеции
7. Замечательное свойство трапеции.
8. Свойство серединных перпендикуляров к сторонам треугольника.
9. Свойства биссектрис треугольника.
10. Свойства медиан треугольника
11. Свойство высот треугольника.
Окружности
12. Диаметр, перпендикулярный хорде, делит ее пополам.
13. Теорема о пересекающихся хордах.
14. Теорема о серединном перпендикуляре к хорде.
15. Равные хорды удалены от центра окружности на равные расстояния.
16. Дуги окружности, заключенные между параллельными хордами, равны.
17. Угол между касательной и хордой.
18. Теорема о секущей и касательной.
19. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
20. Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружности.
21. Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен .
22. Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
23. Если расстояние между центрами окружностей радиусами R и r равно а и , то отрезки общих внешних и общих внутренних касательных, заключенные между точками касания, равны соответственно и
24.
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусов.
25. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
26. Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии.
27. Если М – точка касания со стороной АС окружности, вписанной в треугольник АВС, то АМ = р – ВС, где р – полупериметр треугольника АВС.
28. Если окружность касается стороны ВС треугольника АВС и продолжений сторон АВ и АС, то расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру треугольника АВС.
29. Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен , то угол KLM .
30. Если прямые, проходящие через точку А, касаются окружности S в точках В и С, то центр вписанной окружности треугольника АВС лежит на окружности S.
31. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна .
32. Свойство биссектрисы треугольника. Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.
*При составлении списка полезных фактов использованы учебные пособия Р. К. Гордина.
Геометрические задачи на доказательство
Теоремы или задачи на доказательство имеют определенную структуру.
Рассмотрим классическую структуру теоремы.
Наиболее привычной является следующая формулировка: из условия 1, условия 2, … , условия n следует справедливость заключения. Другими словами, из выполнения всех условий теоремы, причем одновременного, вытекает истинность заключения.
Рассмотрим конкретные примеры.
Если ABCD – параллелограмм и его диагонали равны (AC = BD), то ABCD – прямоугольник.
В этой теореме два условия (эти условия еще называют посылками):
А = «ABCD – параллелограмм»,
В = «AC = BD».
И заключение: С = «ABCD – прямоугольник».
Условие задачи может быть представлено в виде схемы: «из А и В следует С».
Для доказательства теоремы, сформулированной по данной схеме, нужно построить цепочку рассуждений Т
Подробно разберем, по каким правилам выбираются или придумываются рассуждения Т1, …, Тk.
Первое правило. В качестве таких утверждений можно брать любое условие теоремы.
Второе правило. Можно взять любую известную теорему или формулу и применить ее к условиям задачи.
Итак, механизм этой операции следующий: подставляем в формулировку теоремы или в формулу те данные, которые содержатся в условиях.
Такую операцию можно назвать «правилом подстановки».
Рассмотрим примеры применения этого правила.
Пример 1 (алгебра).
Решить квадратное уравнение х2 – 10х + 24 = 0.
Решение.
Используем известную формулу для решения полных квадратных уравнений:
D = b2 – 4ac; x₁,₂ = (-b ± √D)/2a;
и подставим в нее данные из задачи a = 1, b = -10, c = 24.
Получим результат подстановки:
D = 100 – 4 · 24 = 4, откуда x1,2 = (10 ± √4)/2 или x1 = 4, x2 = 6.
Пример 2 (геометрия).
Рассмотрим четырехугольник A1A2B1B2, вписанный в окружность.
Известна следующая теорема: у вписанного в окружность четырехугольника суммы противоположных углов равны.
Сделаем подстановку в теорему конкретных условий задачи. В результате получим рассуждение:
В рассматриваемом четырехугольнике A1A2B1B2 сумма углов A1A2B1 и B1B2 A1 равна 180°.
Вернемся теперь к правилам, по которым строятся рассуждения в доказательстве.
Третий способ получения утверждений в цепочке доказательства состоит в следующем: на основе истинности уже полученных рассуждений (то есть каких либо из предыдущих Т1, …, Тk) делается заключение об истинности следующего рассуждения Тk+1.
Обычно применяется следующая схема: «из верности рассуждения А и верности рассуждения «из А следует В» следует верность рассуждения В».
Это правило получило название «правило заключения».
Рассмотрим пример применения правила заключения.
Пример 3.
А = «Данный четырехугольник ABCD – прямоугольный (AC и BD – его диагонали)» – условие.
В = «Если четырехугольник прямоугольный, то его диагонали равны» – известная теорема.
По правилу заключения получаем:
С = «У данного четырехугольника ABCD : AC = BD».
В математике существует еще ряд правил, позволяющих получать новые правила из известных рассуждений.
Эти правила получили название «правила естественного вывода» или «производные правила вывода».
Подведем некоторые итоги.
Доказательство теоремы – это цепочка рассуждений Т1, …, Тk. Последнее рассуждение – это суть заключение теоремы (т.е. это то, что требуется доказать). Рассуждения Тi в цепочке – это либо условия теоремы, либо известные аксиомы, теоремы, формулы, либо те данные, которые были получены из предыдущих рассуждений поправилам вывода (правило подстановки, правило заключения и др.).
Рассмотрим теперь другие виды формулировок теорем.
Кроме классической формулировки, рассмотренной выше, существует еще ряд распространенных формулировок теорем. Рассмотрим примеры таких формулировок.
«Утверждение А выполняется тогда и только тогда, когда выполняется утверждение В». «Утверждения А
Смысл этих формулировок очень схож. В них говорится о том, что утверждения А и В (А1, А2, …, Аn) одновременно истинны или одновременно ложны.
Фактически, в первой формулировке объединены две теоремы: «Из утверждения А следует утверждение В» (прямая теорема) и «Из утверждения В следует утверждение А» (обратная теорема).
Вторая формулировка также распадается на несколько классически сформулированных теорем.
Пример 4.
Теорема. «Четырехугольник ABCD вписывается в окружность тогда и только тогда, когда суммы его противоположных углов равны 180°».
Эта теорема распадается на две:
Прямая теорема. Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°.
Обратная теорема. Если суммы противоположных углов четырехугольника равны 180°, то он вписывается в окружность.
Существует еще один, вид теорем, для доказательства которых часто применяется особый метод – метод математической индукции.
Примерами таких задач могут быть:
Доказать, что квадраты всех нечетных чисел при делении на 4 дают остаток 1.
Или задача: если сумма цифр целого числа делится на 9, то и само число делится на 9.
Общая схема решения таких задач такова: «Доказать, что все объекты множества М обладают общим свойствома».
Два способа доказательства теорем.
На страницах учебника математики встречается в основном классический способ доказательства теорем. В нем идет последовательный переход от одного рассуждения к другому, пока не получится утверждение теоремы.
Также в математике весьма эффективен способ доказательства
Как правило, условия теоремы содержат несколько рассуждений А1, А2, … , Аn. Если в ходе доказательства появляется рассуждение «Неверно, что выполняется Аi», то возникает так называемое противоречие.
Сам же метод доказательства «от противного» состоит в следующем:
а) Предполагается, что вместо нужного заключения теоремы (утверждение В), выполняется противоположное утверждение «неверно, что В».
б) Из утверждения «неверно, что В» и утверждений, содержащихся в условии теоремы выводится утверждение «неверно, что Аi» (где Аi – одна из посылок теоремы).
Таким образом, и получается противоречие: одновременно должны выполняться условия Аi и «неверно, что Аi».
в) Делается вывод: предположение о неверности заключения В привело к противоречию, поэтому заключение В вытекает из условий теоремы.
Рассмотрим пример.
Пример 5.
Доказать, что если биссектрисы треугольника разбивают его на шесть равных по площади треугольников, то данный треугольник – правильный.
Доказательство.
1) Очевидно, что треугольник правильный, если его биссектрисы одновременно являются и его медианами.
2) Биссектриса, проходящая через точку пересечения медиан, является и медианой треугольника.
Вывод: надо доказать, что если три прямых, проходящих через вершины треугольника, пересекаются в одной его внутренней точке М и разбивают треугольник на шесть равных по площади, то М – точка пересечения медиан.
Рассмотрим треугольник ABC (рис.
1), где АА1, ВВ1, СС1 – медианы, а М0 – точка их пересечения.
Теперь используем метод «от противного».
Пусть точка М не совпадает с точкой М0. Рассмотрим треугольники АВМ, АСМ и ВСМ. Из условия вытекает, что площади этих треугольников равны (площадь каждого равна 1/3 площади DАВС). Точка М должна попасть внутрь или на сторону одного из треугольников АВМ0, АСМ0 или ВСМ0 (предположим, что внутрь треугольника АВМ0).
Очевидно, что SDАВМ < SDАВМ0 = 1/3 · SDАВС.
Итак, получено противоречие, т.к. с одной стороны, SDАВМ = 1/3 · SDАВС, а с другой – она меньше.
Из этого следует, что предположение о том, что М не совпадает с М0 ошибочно, поэтому имеем, что М0
= М.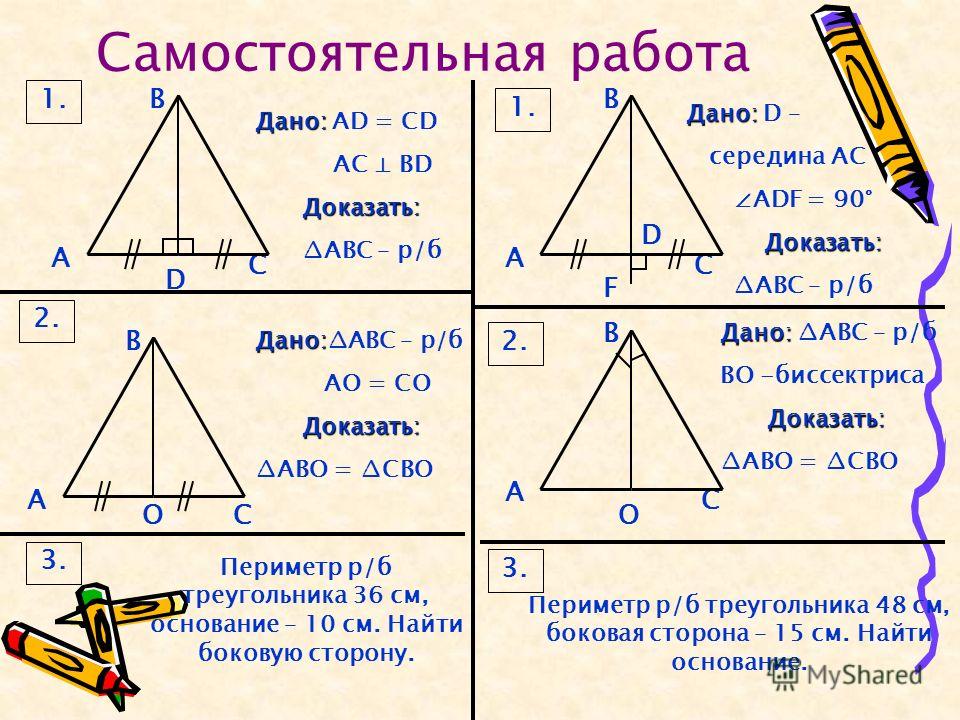
Таким образом, доказано, что биссектрисы проходят через точку пересечения медиан, то есть биссектрисы являются медианами, а это верно только для правильных треугольников.
Остались вопросы? Не знаете, как решать задачи на доказательство?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Справка по геометрии — Бесплатная справка по математике
Нужна помощь по геометрии? У нас есть более тридцати отличных уроков геометрии, разбитых на общие темы. Обязательно просмотрите все темы, чтобы найти то, что вам нужно, или выполните поиск по ключевому слову.
Линии графика
- Асимптоты
- Домен и диапазон
- Нахождение горизонтальных асимптот
- Форма уклона точки
- Форма пересечения склонов
- Наклон линии
- Ось X-Y
- Построение параболы
Формы
- Треугольники
- 30-60-90 Прямоугольный треугольник
- Параллелограммы
- Трапеции
- Специальные параллелограммы
- Конгруэнтные треугольники
- Равнобедренные треугольники
- полигонов
Углы, линии и точки
- Формула расстояний
- Мир углов
- Специальные уголки
- Параллельные линии
- Длина сегмента линии
- Сумма углов треугольника
- Внешние углы треугольника
- Внутренние углы многоугольника
- Неравенства треугольников
- Формула средней точки
Другие уроки
- Заполнение уравнений квадрата в круге
- Среднее геометрическое
- Геометрические термины
- Словарь по геометрии
Формулы
- Формулы площади
- Формулы периметра
- Площадь поверхности
- Объемные формулы
Другое
- Важный словарь по геометрии
- Вертикальные углы
Уроки с других сайтов:
- Площади, объемы, площади поверхности
- Длина окружности
- Классификация углов
- Конические сечения/круги
- Внутренние углы правильных многоугольников
- Основы многоугольника
- Теорема Пифагора
- Трехмерные фигуры
Последние вопросы по геометрии
Доказательство, сколько и что имеет значение? Среда, 21 декабря 2022 г.
Логика теории чисел Среда, 21 декабря 2022 г.
Вычислите определитель этой матрицы Tuesday December 20, 2022
Rational Zeros Theorem Tuesday December 20, 2022
Looking for a gif of orderly vs disorderly 2D shapes or information about it Tuesday December 20, 2022
Избранный урок
Прочтите о свойствах прямоугольных треугольников 30-60-90.
Ресурсы для репетиторов
Онлайн-уроки по математике и ссылки могут быть действительно полезными, если у вас есть конкретный вопрос или вы ищете освежение знаний по определенной теме. Но если вам нужна дополнительная помощь, вам может понадобиться репетитор по геометрии. Будь то друг или учитель в школе, местный репетитор или онлайн-репетитор, реальный человек может быстрее ответить на вопросы и объяснить то, чего вы не понимаете, лучше, чем любой урок или доска объявлений.
Изучайте геометрию с помощью онлайн-курсов, классов и уроков
Что такое геометрия?
Геометрия – это область математики, изучающая перпендикулярные прямые, дополнительные углы, координатные плоскости, смежные углы, прямые углы, внешние углы, геометрические фигуры, расстояния и отношения между ними. Примеры включают вычисление углов треугольника, длины кривой или площади поверхности сферы.
Изучите основы геометрии с помощью курсов и уроков для начинающих
Пройдите фундаментальные курсы на edX, чтобы изучить основы геометрии. В курсе SchoolYourself’s Introduction to Geometry вы узнаете, как измерять углы и правила определения конгруэнтности углов, доказывать и применять свойства треугольников, четырехугольников и других многоугольников, вычислять площади многоугольников, кругов, эллипсов и других сложных форм и т. д.
Онлайн-курсы и программы по геометрии
Пройдите бесплатные онлайн-курсы геометрии, чтобы освоить новые навыки и повысить эффективность обучения в классе.
14-недельный базовый курс геометрии от School Yourself можно пройти вместе с курсом старшей школы, и он может служить углубленным учебным пособием по геометрии для дополнительной практики и мастерства. Изучите все основы геометрии, в том числе, как вычислять площади сложных фигур, как измерять углы, как доказывать и применять теорему Пифагора, как применять свойства треугольников и четырехугольников и как применять геометрические формулы. Курс является самостоятельным, поэтому студенты могут переходить к любому разделу по мере необходимости.
Готовы к чему-то более продвинутому? Вычислительная геометрия — это бесплатный онлайн-курс Университета Цинхуа, который может помочь вам подготовиться к углубленному изучению робототехники, автоматизированного проектирования (CAM и CID) и географических информационных систем (ГИС). Изучите геометрические алгоритмы и структуры, а также основные стратегии решения геометрических задач.
В каких работах используется геометрия?
Геометрия сегодня используется во многих областях и профессиях.
Вы можете быть удивлены количеством рабочих мест и профессий, которые требуют практических знаний геометрии для выполнения повседневных задач. Ниже приведены несколько примеров профессий, требующих понимания геометрии для выполнения повседневных задач.
Дизайнеры компьютерной графики должны знать и понимать геометрию, чтобы создавать реалистичные трехмерные космические изображения. Некоторые примеры графических дизайнеров включают создателей видеоигр и аниматоров. Понимание того, как использовать фигуры и манипулировать ими, упрощает компьютерные вычисления, поэтому геометрия необходима графическому дизайнеру для выполнения повседневных задач.
Инженерам-робототехникам необходимо понимать геометрию для выполнения сложных задач в своей сфере деятельности. Понимание того, какие углы использовать для диапазона движения робота, является обычной задачей для этих профессионалов. Возможность управлять этими роботами вплоть до малейшего движения заранее определяется дугами и углами.
Некоторые роботы созданы с диапазоном зрения для обнаружения объектов, поэтому измерение углов и восприятие являются повседневными задачами в этой профессии.
Медицинские работники используют геометрию для создания трехмерных моделей медицинских проблем, таких как опухоли у пациентов. Получение результатов компьютерной томографии и правильное масштабирование 3D-модели этой опухоли может дать врачам и хирургам информацию, необходимую им для решения этой проблемы непосредственно у их пациентов. Медицинская визуализация с помощью гарнитур виртуальной реальности, таких как Microsoft HoloLens, позволит врачам в будущем реконструировать органы, кости и все остальное в человеческом теле, используя геометрию для точного соединения всех частей воедино.
Модельеры ежедневно используют геометрию, чтобы создавать идеальные образы для своих клиентов. Измерение одежды на основе типа тела и углов может создать или разрушить определенный внешний вид для кого-то. Как модельер, вы должны знать, как создавать трехмерные формы и модели для своих клиентов.
Зачем изучать геометрию онлайн?
Геометрия является общим навыком для многих профессионалов в своей сфере деятельности. Записавшись на онлайн-курсы геометрии, вы сможете выбрать правильный курс, который наилучшим образом соответствует вашим потребностям. Возможно, вы хотите пройти базовый курс геометрии, чтобы освежить свои навыки, если прошло много времени с момента вашего последнего занятия. Возможно, вы ищете более продвинутые курсы, если хотите стать архитектором и вам нужно практиковать передовые методы геометрии. Независимо от того, где вы находитесь, edX предлагает широкий спектр онлайн-курсов по геометрии, разработанных с учетом вашего плотного графика.
Некоторые из наших курсов охватывают понимание параллельных прямых, теоремы Пифагора, прямоугольных треугольников, конических сечений, касательных окружностей, правильных многоугольников, формулы Герона, конгруэнтных углов, геометрических кривых, длин дуг, геометрических понятий, дополнительных углов, измерения ромба.