Метод наименьших квадратов онлайн калькулятор: Метод наименьших квадратов онлайн

alexxlab / / Разное

Содержание

Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями

Данный калькулятор использует метод наименьших квадратов (МНК) для аппроксимации функции одной переменной, аналогично калькулятору Аппроксимация функции одной переменной. Но, в отличии от указанного калькулятора, данный калькулятор поддерживает аппроксимацию функции с использованием ограничений на ее значения. То есть, можно задать условия равенства аппроксимирующей функции определенным значениям в определенных точках. Формулы аппроксимации будут выведены с учетом этих условий.

Используемый метод (метод множителей Лагранжа) накладывает ограничения на набор аппроксимирующих функций, так что этот калькулятор не поддерживает экспоненциальную аппроксимацию, аппроксимацию степенной функцией и показательную аппроксимацию. Одним словом поддерживается только линейная регрессия. Зато в него были добавлены аппроксимация полиномами 4-ой и 5-ой степени. Формулы и немного теории можно найти под калькулятором.

Если не ввести значения x, калькулятор будет считать, что значение x меняется начиная с 0 с шагом 1.

Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями

83 71 64 69 69 64 68 59 81 91 57 65 58 62

Значения x, через пробел

183 168 171 178 176 172 165 158 183 182 163 175 164 175

Значения y, через пробел

Ограничения на значения аппроксимирующей функции в точках
xy
Записей:

51020501001000

Ограничения на значения аппроксимирующей функции в точках

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50. 5;-50.5

Загрузить данные из csv файла

Аппроксимирующие функции

Линейная аппроксимация

Квадратичная аппроксимация

Кубическая аппроксимация

Аппроксимация полиномом 4-ой степени

Аппроксимация полиномом 5-ой степени

Аппроксимация полиномом 6-ой степени

Аппроксимация полиномом 7-ой степени

Аппроксимация полиномом 8-ой степени

Логарифмическая аппроксимация

Гиперболическая аппроксимация

Точность вычисления

Знаков после запятой: 4

Квадратичная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Кубическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Полином 4-ой степени

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Полином 5-ой степени

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Линейная регрессия

 

Коэффициент линейной парной корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Логарифмическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Гиперболическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Полином 6-ой степени

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Полином 7-ой степени

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Полином 8-ой степени

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Результат

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

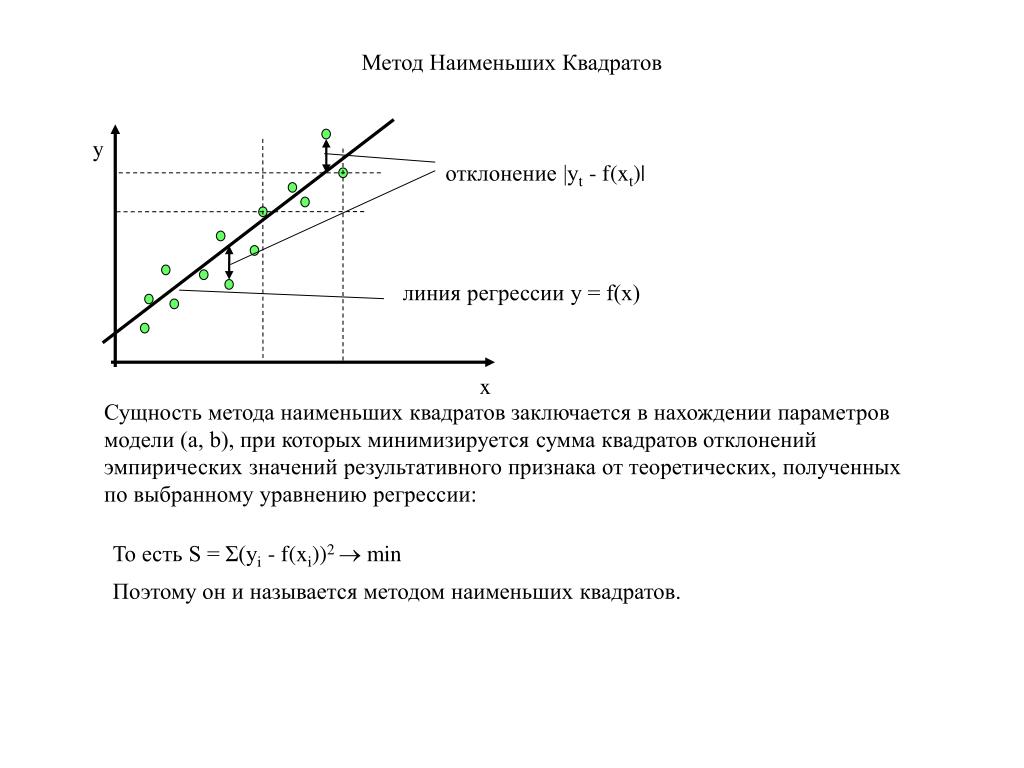
Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Использованием этого метода для вывода формул аппроксимации для различных аппроксимирующих функций можно посмотреть в теоретической части статьи Аппроксимация функции одной переменной.

Подход, описанный по ссылке, можно обобщить для случая линейной комбинации параметров (для построения линейной регрессии).

Если аппроксимирующая функция является линейной комбинацией параметров, которые нужно определить, например
, то набор значений аппроксимирующей функции в заданных точках можно описать следующим образом

При использовании метода наименьших квадратов нам надо найти набор параметров, минимизирующих функцию

Значение этой функции есть расстояние от вектора y до вектора Xa. Для минимизации этого значения Xa должно быть проекцией на пространство столбцов матрицы

X и вектор Xa-y должен быть ортогонален этому пространству (подробнее можно посмотреть здесь).

где v — произвольный вектор в пространстве столбцов. Так как этот вектор может быть любым, очевидно что равенство выполняется только в случае

Последняя формула и используется калькулятором выше для построения линейной регрессии без дополнительных ограничений.

Теперь разберемся с построением линейной регрессии при наличии ограничений. Такими ограничениями могут быть ограничения на значение функции в заданных точках. Например, нам известно, что функция, которую мы аппроксимируем ДОЛЖНА проходить через ноль (точку с координатами 0;0). Также могут существовать ограничения на значения производной функции в некоторых точках (наклона кривой функции). Наличие дополнительных ограничений говорит о том, что нам надо искать условный экстремум, то есть экстремум (в нашем случае минимум) функции, достигнутый при условии что переменные функции удовлетворяют

уравнению связи.

Для решения такой задачи используется метод множителей Лагранжа. В методе множителей Лагранжа осуществляют переход от функции к функции Лагранжа через добавление множителей Лагранжа

Далее ищется экстремум данной функции. После всех вычислений, которые я здесь не привожу (их мало где приводят, да и я тоже мог бы написать что-нибудь вроде «очевидно, что» 🙂 ), получается следующая формула для нахождения параметров, при которых функция достигает условного экстремума

Именно эту формулу использует калькулятор выше для построения линейной регрессии в случае накладывания дополнительных условий на аппроксимирующую функцию.

Калькулятор расчета по методу наименьших квадратов

Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.

Калькулятор расчета элементов прямой по методу наименьших квадратов

Онлайн калькулятор нахождения углового коэффициента, точки пересечение  и уравнения прямой линии по методу наименьших квадратов

Формула метода наименьших квадратов:

где,

  • b = Наклон линии регрессии
  • a = Точка пересечения оси Y и линии регрессии.
  • X̄ = Среднее значений х
  • Ȳ = Среднее значений y
  • SDx = Стандартное отклонение x
  • SDy = Стандартное отклонение y
  • r = (NΣxy — ΣxΣy) / корень ((NΣx2 — (Σx)2) x (NΣy)2 — (Σy)2)

Пример

Найти регрессию методом наименьших квадратов

Значение XЗначение Y
56
23
16
79

Получаем,

Значение XЗначение Y
56
23
16
79

Найдем,

Уравнение линии регрессии методом наименьших квадратов

Решение:

Шаг 1 :

Количество значений x.

N = 4

Шаг 2 :

Найдем XY, X2 для полученных значений. Смотрите таблицу ниже

Значение XЗначение YX*YX*X
603.160 * 3.1 = 18660 * 60 = 3600
613.661 * 3.6 = 219.661 * 61 = 3721
623.862 * 3.8 = 235.662 * 62 = 3844
63463 * 4 = 25263 * 63 = 3969
65
4.1		65 * 4.1 = 266.565 * 65 = 4225

Шаг 3 :

Найдем ΣX, ΣY, ΣXY;, ΣX2 для значений

  • ΣX = 311
  • ΣY = 18.6
  • ΣXY = 1159.7
  • ΣX2 = 19359
Шаг 4 :

Подставим значения в приведенную выше формулу.

Наклон(b) = (NΣXY — (ΣX)(ΣY)) / (NΣX2 — (ΣX)2)

  • = ((5)*(1159. 7)-(311)*(18.6))/((5)*(19359)-(311)2)
  • = (5798.5 — 5784.6)/(96795 — 96721)
  • = 13.9/74
  • = 0.19
Шаг 5 :

Подставив значения в формулу

Пересечение (a) = (ΣY — b(ΣX)) / N

  • = (18.6 — 0.19(311))/5
  • = (18.6 — 59.09)/5
  • = -40.49/5
  • = -8.098
Шаг 6 :

Подставим значения в уравнение прямой

Уравнение прямой(y) = a + bx

= -8.098 + 0.19x

Предположим, если мы хотим, узнать приблизительное

у значение переменной x = 64, необходимо подставить значение в формулу

Уравнение прямой(y) = a + bx

  • = -8.098 + 0.19(64)
  • = -8.098 + 12.16
  • = 4.06

Синонимы: Least-Squares method, МНК

людей нашли эту статью полезной. А Вы?

Калькулятор наименьших квадратов — Cuemath

Калькулятор наименьших квадратов , который помогает найти линию наилучшего соответствия формы

Что такое калькулятор наименьших квадратов?

Метод наименьших квадратов — это метод статистического регрессионного анализа, используемый для нахождения линии наилучшего соответствия формы ‘ y = mx + b’  для заданного набора данных. «Калькулятор наименьших квадратов» – это бесплатный онлайн-инструмент, который за несколько секунд находит линию, наиболее подходящую для заданного набора данных.

Калькулятор наименьших квадратов

Как пользоваться калькулятором наименьших квадратов?

Выполните указанные ниже действия, чтобы найти наиболее подходящую линию.

  • Шаг 1 — Введите точки данных в соответствующее поле ввода.
  • Шаг 2 — Нажмите « Вычислить «, чтобы найти линию наименьших квадратов для заданных данных.
  • Шаг 3  — Нажмите « Сбросить «, чтобы очистить поля и ввести новый набор значений.

Как вычислить метод наименьших квадратов?

Метод наименьших квадратов используется для нахождения линейной прямой формы y = mx + b. Здесь «y» и «x» — переменные, «m» — наклон линии, а «b» — точка пересечения с осью y.

Здесь значение уклона m определяется по формуле m = (n ∑ (XY) — ∑ Y ∑ X) / (n ∑ (X 2 ) — (∑ X) 2 ) , а b рассчитывается по формуле  b = (∑ Y — m∑ X) / n

Давайте рассмотрим пример того, как найти линию наименьших квадратов для заданного набора данных.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Решенные примеры на калькуляторе наименьших квадратов

Пример 1:

Найдите линию наименьших квадратов для данных, показанных ниже, и проверьте ее с помощью калькулятора наименьших квадратов.

Х 1 2 3 4 5
Д 2 5 3 8 7

Решение:  

X Д XY Х 2
1 2 2 1
2 5 10 4
3 3 9 9
4 8 32 16
5 7 35 25
∑ Х = 15  ∑ Y = 25 ∑ XY = 88 ∑ X
2 = 55

Найдите значение m.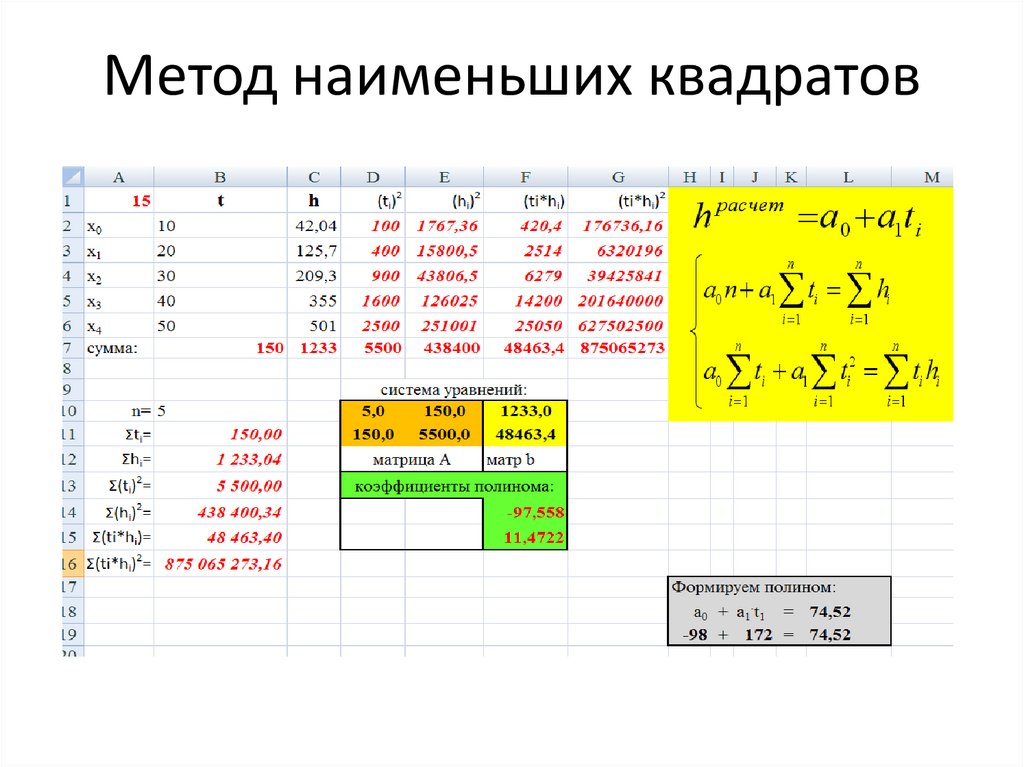

m = (n ∑ (XY) — ∑ Y ∑ X) / (n ∑ (X 2 ) — (∑ X) 2 )

= ( 5(88) — (15 × 25) ) / ( 5(55) — (15) 2 )

= 13/10

= 1,3

Найдите значение b.

b = (∑ Y — m∑ X) / n

= (25 — (1,3 × 15)) / 5

= 11/10

= 1,1

Итак, требуемое уравнение наименьших квадратов: y = (1,3)x + 1,1

Теперь воспользуйтесь нашим онлайн Калькулятор наименьших квадратов и найдите линию наименьших квадратов для заданных точек данных

X 1,7 2,3 3.1 4,5 5,9
Д 12 45 29 65 45

☛ Статьи по теме:
  • Метод наименьших квадратов
  • Вероятность и статистика

☛ Математические калькуляторы:

Рабочие листы по математике и визуальные учебные программы

Калькулятор линии регрессии методом наименьших квадратов

Создано Войцехом Сас, доктором философии

Рецензировано Богна Шик

Последнее обновление: 10 октября 2022 г.

Содержание:
  • Как найти наиболее подходящую строку?
  • Уравнение линии регрессии методом наименьших квадратов
  • Метод наименьших квадратов
  • Как найти линию регрессии методом наименьших квадратов?
  • Ограничения приближения методом наименьших квадратов

Это калькулятор линии регрессии методом наименьших квадратов — удобный инструмент, который отвечает на вопрос «Как найти линию наилучшего соответствия?» . Если вам интересно, как найти среднюю скорость изменения для автомобиля, который увеличивает свою скорость, то вы находитесь в правильном месте!

В этой статье вы также можете найти полезную информацию о методе наименьших квадратов, о том, как найти линию регрессии наименьших квадратов и на что обратить особое внимание при выполнении подбора методом наименьших квадратов.

Вы также можете попробовать наш калькулятор линейной регрессии, который вычисляет линейной регрессии с помощью проекционной матрицы .

Как найти наиболее подходящую линию?

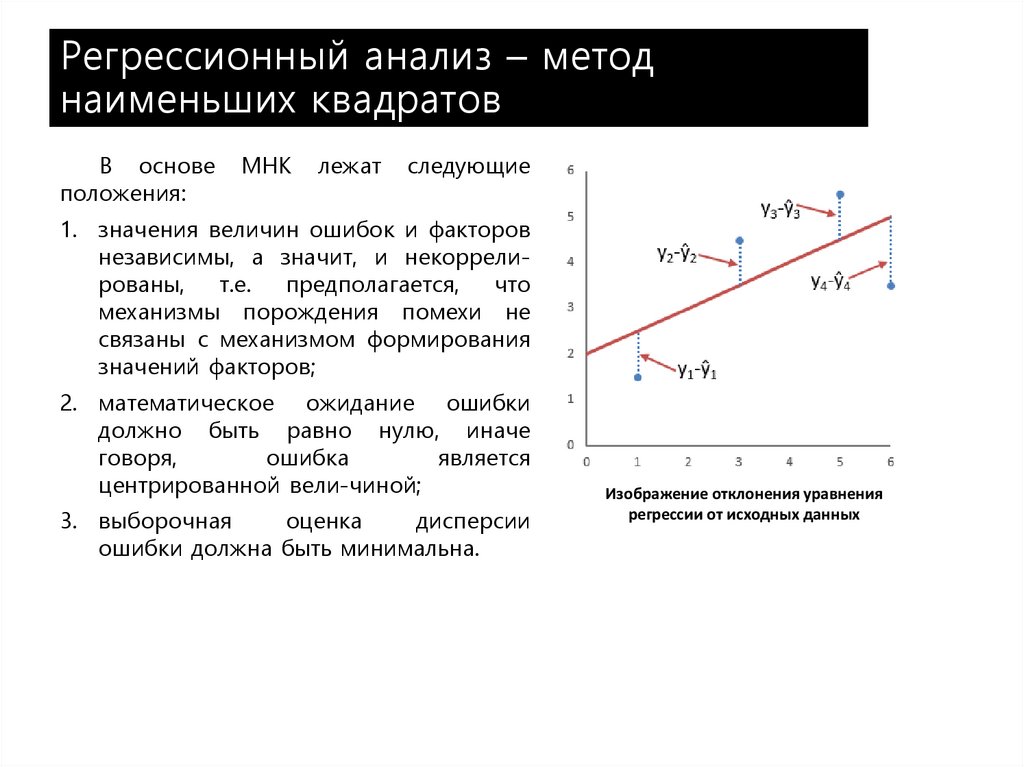
Интуитивно можно попытаться нарисовать линию, которая проходит как можно ближе ко всем точкам. Иногда это может быть прямая линия , что означает, что мы будем выполнять линейную регрессию . Существует несколько методов решения этой задачи, наиболее популярным и широко используемым из которых является оценка методом наименьших квадратов . Вот несколько примеров из реальной жизни:

Чем быстрее вы едете, тем больше сгорания в двигателе вашего автомобиля. Может быть, зимой холодно, а летом изнуряюще жарко, поэтому вам нужно купить больше электроэнергии, чтобы использовать ее для обогрева кондиционера. Можно представить еще много подобных ситуаций, когда увеличение A вызывает рост (или распад) B .

Почему мы его используем? Что ж, имея всего несколько точек данных, , мы можем примерно предсказать результат будущего события . Вот почему полезно знать, как найти линию наилучшего соответствия. В случае только двух точек, калькулятор наклона является отличным выбором. Это поможет вам найти соотношение B и A в определенный момент времени.

В отличие от стандартного коэффициента, который может работать только с одной парой чисел одновременно, этот калькулятор линии регрессии методом наименьших квадратов показывает вам как найти линию регрессии методом наименьших квадратов для нескольких точек данных .

Уравнение линии регрессии методом наименьших квадратов

Чтобы все было как можно понятнее, найдем прямую с наклоном a и точкой пересечения b . Тогда формула для линии наилучшего соответствия с оценкой методом наименьших квадратов будет следующей:

y = a · x + b .

Как видите, уравнение линии регрессии методом наименьших квадратов ничем не отличается от стандартного выражения линейной зависимости. Магия заключается в способе определения параметров а и б .

💡 Если вы хотите найти точку пересечения по оси x, попробуйте наш калькулятор формы точки пересечения!

Отлично! Так что же на самом деле означает наименьших квадратов ? Перейдите к следующему разделу, чтобы узнать!

Метод наименьших квадратов

Вам интересно, как найти линию наилучшего соответствия, используя метод наименьших квадратов? Идея проста:

  1. Проведите прямую линию: f(x) = a·x + b .
  2. Оценить все вертикальные расстояния, dᵢ , между точками и вашей линией: dᵢ = |yᵢ - f(xᵢ)| .
  3. Square им: dᵢ² .
  4. Сложите их вместе, Z = ∑dᵢ² = d₁² + d₂² + d₃² + … .
  5. Найдите такую ​​строку, чтобы значение Z стало как можно меньше .
  6. Наслаждайтесь знанием происхождения названия метода наименьших квадратов.

На первый взгляд это может показаться немного расплывчатым, поэтому, чтобы прояснить ситуацию, давайте взглянем на несколько изображений. Для одних и тех же точек данных установлены три разные линии (1,2), (2,6), (3,4), (4,7):

Как видите, Z в каждом случае имеет разные значения. Это минимально для третьего сюжета, но можем ли мы сделать еще лучше? Используйте наш калькулятор линии регрессии наименьших квадратов, чтобы узнать, является ли это наиболее оптимальным решением!

Как найти линию регрессии методом наименьших квадратов?

Или, другими словами, как работает наш калькулятор линии регрессии методом наименьших квадратов ? Мы хотим оценить параметры линии регрессии a и b . В стандартном методе наименьших квадратов мы можем вычислить несколько вспомогательных значений, которые упростят окончательную формулу:

  • S x = ∑xᵢ = x₁ + x₂ + x₃ + … ;
  • S y = ∑yᵢ = y₁ + y₂ + y₃ + … ;
  • S xx = ∑xᵢ² = x₁² + x₂² + x₃² + … ;
  • S yy = ∑yᵢ² = y₁² + y₂² + y₃² + … ;
  • S xy = ∑xᵢyᵢ = x₁y₁ + x₂y₂ + x₃y₃ + … ;
  • Δ = n·S xx — S x ² .

, где n — общее количество баллов. Подгонка методом наименьших квадратов получается из этих коэффициентов:

  • а = (n·S xy — S x ·S y ) / Δ ;
  • b = (S xx · S y — S x · S xy ) / Δ .

Решая эти формулы, вы получаете числовые значения. Но есть ли способ решить, сколько значащих цифр мы должны включить? Будет удобно оценить погрешность этих параметров (в данном случае стандартных отклонений): {расколоть} \sigma_a &= \sqrt{\frac{n}{n\!-\!2}\frac{(S_\text{yy} — a\!\cdot\!S_\text{xy} — b\!\ cdot\!S_\text{y})}{Δ}} \\ \sigma_b &= \sqrt{\frac{S_\text{xx}}{n}} \cdot \sigma_a \end{split}σa​σb​=n−2n​Δ(Syy​−a⋅Sxy​−b⋅Sy​)​

​=nSxx​

​⋅σa​

Теперь посмотрите на две значащие цифры стандартных отклонений и округлите параметры до соответствующих десятичных чисел. 2)}}r=(n ⋅Sxx​−Sx2​)(n⋅Syy​−Sy2​)

​n⋅Sxy​−Sx​⋅Sy​​

Абсолютное значение r может находиться в диапазоне от 0 до 1. Чем ближе оно к единице (1), тем лучше подходит метод наименьших квадратов . Если значение приближается к 0, наши точки данных не показывают никакой линейной зависимости. Проверьте калькулятор корреляции Пирсона Omni для получения многочисленных наглядных примеров с интерпретациями графиков с различными значениями r .

Небольшое замечание: мы предполагаем, что существует нормальное распределение значений y вокруг реальной зависимости, которое мы пытаемся воспроизвести с помощью нашей линии регрессии.

Ограничения методом наименьших квадратов

Хотя метод наименьших квадратов распространен и широко используется, мы должны помнить, что в некоторых случаях он может быть несовершенным и вводить в заблуждение. Вот наиболее распространенные факторы, влияющие на качество оценки методом наименьших квадратов:

  • Как правило, чем больше точек в ваших данных, тем выше точность метода наименьших квадратов.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *