Что такое вектор в геометрии 9 класс – Векторы — урок. Геометрия, 9 класс.

alexxlab / / Геометрия

Содержание

Векторы ( геометрия 9 класс)

Просмотр содержимого документа
«Векторы ( геометрия 9 класс)»

Муниципальное бюджетное общеобразовательное учреждение

«средняя общеобразовательная школа №4»

Презентации к урокам математики

Заслуженный учитель РФ

Кулиашвили Елена Николаевна

Историческая справка

  • Термин вектор (от лат. Vector – “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем.

Что такое вектор ?

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением: например, скорость, сила, давление. Такие величины называются векторными величинами или векторами .

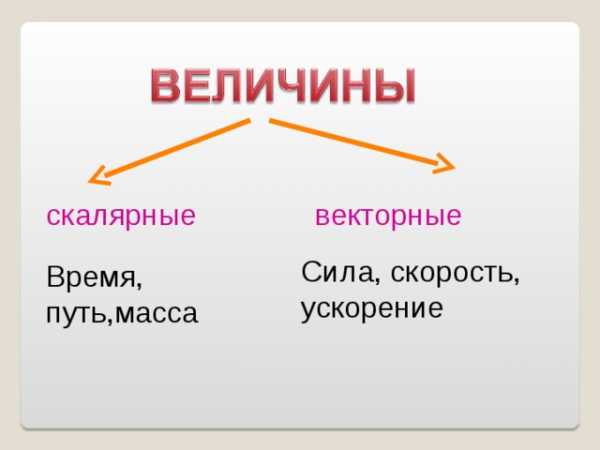
скалярные

векторные

Сила, скорость, ускорение

Время, путь,масса

ВЕКТОР или направленный отрезок – отрезок, у которого указано, какая из его граничных точек считается началом, а какая — концом

В

А

Конец вектора

Начало вектора

Вектор АВ

  • векторы обозначают двумя заглавными латинскими буквами со стрелкой над ними или одной строчной латинской буквой со стрелкой над ней
  • любая точка плоскости является нулевым вектором
  • длиной или модулем ненулевого вектора АВ называется длина отрезка АВ

Длина вектора

  • Расстояние между началом и концом вектора называется длиной или модулем вектора. Длина вектора обозначается |а| или |АВ|.
  • Длина нулевого вектора считается равной нулю.

A

B

|AB| = 6 |CD| = 5

|a| = 5 |NN| = 0

(каждая клетка на рисунке имеет сторону, равную единице измерения отрезков)

C

a

D

N

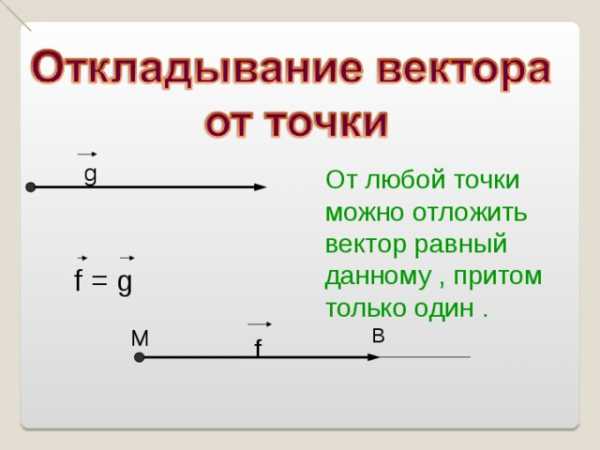
g

От любой точки можно отложить вектор равный данному , притом только один .

f = g

M

B

f

  • ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых
  • коллинеарные векторы могут быть направлены одинаково и называются сонаправленными или противоположно направлены и называются противоположно направленными

Коллинеарные векторы

  • Ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых.
  • Нулевой вектор считается коллинеарным любому вектору.

O

b

CD, KF, O, a, b – коллинеарные

O, a – коллинеарные

O, NP – коллинеарные

NP, m – не коллинеарные

N

D

a

K

P

F

C

m

a

f

f = a

Векторы называются равными , если они сонаправлены и их длины равны .

h

n

n = h

Задача

  • Какие из векторов, изображенных на рисунке:
  • коллинеарны;
  • сонаправлены;
  • противоположно направлены;
  • имеют равные длины?

Отложите эти векторы от одной точки.

d

c

a

b

Задача

  • На рисунке изображена равнобедренная трапеция KLMN.

а) Укажите сонаправленные, противоположно направленные, равные вектора.

б) Укажите векторы, длины которых равны. Равны ли при этом сами векторы?

L

M

K

N

Задачи

  • Даны вектор BC и точка D(1;-2). Отложите от точки D вектор, равный вектору BC.
  • Как должен быть расположен ненулевой вектор a относительно прямой k , чтобы нашлись лежащие на этой прямой векторы, равные a ? Сколько таких векторов найдется? Отметьте на чертеже три из них.
  • Векторы AB и DC равны. Докажите, что если точки A, B, C и D не лежат на одной прямой, то четырехугольник ABCD ― параллелограмм.
  • На рисунке изображен параллелограмм ABCD.Укажите векторы, длины которых равны. Равны ли при этом сами векторы?
  • В ромбе ABCD l AC l = 12см, l BD l = 16см. От вершины A отложен вектор AE, равный вектору BD. Найдите длину вектора EC.

B

C

A

D

Для любых чисел k , l и любых векторов a , b справедливы равенства :

Для любых чисел k , l и любых векторов a , b справедливы равенства :

  • (kl )a = k (la ) ( сочетательный закон )
  • (k+l) a = ka + la ( первый распределительный закон )
  • K ( a+b ) = ka + kb (второй распределительный закон ) .
  • (kl )a = k (la ) ( сочетательный закон )
  • (k+l) a = ka + la ( первый распределительный закон )
  • K ( a+b ) = ka + kb (второй распределительный закон ) .

а

2а

3а

multiurok.ru

Векторы. Геометрия, 9 класс: уроки, тесты, задания.

Вход на портал
Вход на портал Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Подписка Я+ Новости Переменка Отправить отзыв
  • Предметы
  • Геометрия
  • 9 класс

  1. Понятие вектора

  2. Сложение и вычитание векторов

  3. Умножение векторов на число

  4. Применение векторов к решению задач

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2019 ООО ЯКласс Контакты Пользовательское соглашение

www.yaklass.ru

Геометрия, 9 класс: уроки, тесты, задания

  • Векторы

    1. Понятие вектора
    2. Сложение и вычитание векторов
    3. Умножение векторов на число
    4. Применение векторов к решению задач

  • Метод координат

    1. Координаты вектора
    2. Простейшие задачи в координатах
    3. Уравнение окружности. Уравнение прямой

  • Соотношение между сторонами и углами треугольника. Скалярное произведение векторов

    1. Синус, косинус, тангенс угла
    2. Соотношения между сторонами и углами треугольника
    3. Скалярное произведение векторов

  • Длина окружности и площадь круга

    1. Правильные многоугольники
    2. Длина окружности и площадь круга

  • Движение

    1. Понятие движения. Симметрия
    2. Параллельный перенос и поворот

  • Начальные сведения о стереометрии

    1. Многогранники
    2. Тела и поверхности вращения

    • www.yaklass.ru

    геометрия 9 класс тема»векторы» | Социальная сеть работников образования

    Слайд 1

    Выполнил ученик 9 «Б» класса МОАУ «Гимназия № 7» Бабин Сергей Учитель Негодяева Елена Владимировна Векторы

    Слайд 2

    Оглавление Понятие вектора Коллинеарные вектора Сонаправленные вектора Противоположно направленные вектора Равные вектора Противоположные вектора Сложение векторов Правило треугольника Правило параллелограмма Сложение нескольких векторов Вычитание векторов Вычитание векторов II случай Произведение вектора на число

    Слайд 3

    Понятие вектора Многие физические величины характеризуются не только числовым значением, но и направлением в пространстве. Такие физические величины называют векторными величинами.

    Слайд 4

    Понятие вектора Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется направленным отрезком или вектором AB Конец вектора Начало вектора — вектор B A

    Слайд 5

    Нулевой вектор считается коллинеарным любому вектору Коллинеарные вектора Коллинеарные вектора – это вектора которые лежат на одной прямой или на параллельных прямых. c a b a||b, b||c, a||c

    Слайд 6

    Сонаправленные вектора Сонаправленные вектора – это вектора, которые коллинеарны и имеют одинаковые направления. c b a d a b, b d, a d

    Слайд 7

    Противоположно направленные вектора Противоположно направленные вектора – это вектора, которые коллинеарны и имеют разное направление. c b a d a c, b c, d c

    Слайд 8

    Равные вектора Равные вектора – это сонаправленные вектора, имеющие одинаковые длины. a b a=b : 1) a b 2) |a|=|b|

    Слайд 9

    Противоположные вектора Противоположные вектора – противоположно направленные вектора, имеющие одинаковые длины. a b a = — b : 1) a b 2) |a| = |b|

    Слайд 10

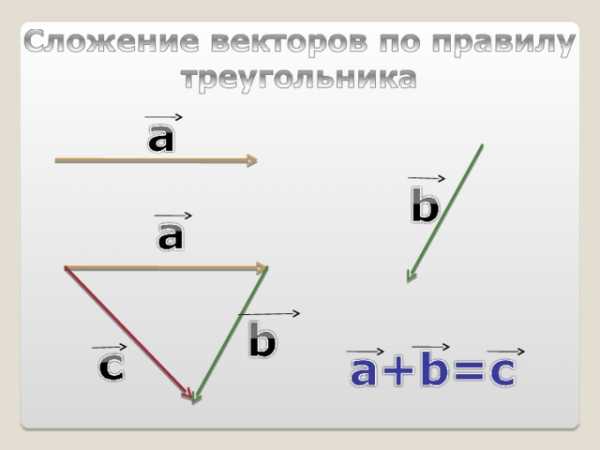
    Сложение векторов Правило треугольника Дано: a, b Построить: c = a + b Построение: a b b a a + b = c c Вектор суммы – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (при условии, если конец первого вектора совпадает с началом второго).

    Слайд 11

    Сложение векторов Правило параллелограмма a + b = c Дано: a, b Построить: c = a + b Построение: a b a b c b

    Слайд 12

    Сумма нескольких векторов a + b + c + d + e + f = k a b c d e f Построение: Дано: a, b , с , d, e, f k Построить: a + b + c + d + e + f = k a b c d e f

    Слайд 13

    Вычитание векторов a — b = c Построение: Дано: a, b Построить: c = a — b b a a b c Вектор разности – вектор, начало которого совпадает с концом второго вектора, а конец – с концом первого (при условии, если начало первого вектора совпадает с началом второго).

    Слайд 14

    Вычитание векторов II случай Дано: a, b Построить: c = a — b a b Построение: a — b c a + (- b ) = c = > a — b = c

    Слайд 15

    Произведение вектора a на число k k· a = b если k> 0, то a ↑↑ b если k

    Слайд 16

    СПАСИБО ЗА ВНИМАНИЕ!!!

    nsportal.ru

    Вектор в системе координат — урок. Геометрия, 9 класс.

    Вспомним, что при умножении вектора на число k≠0 мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если k>0, или противоположно направлены, если k<0. Длины векторов различаются \(k\) раз.

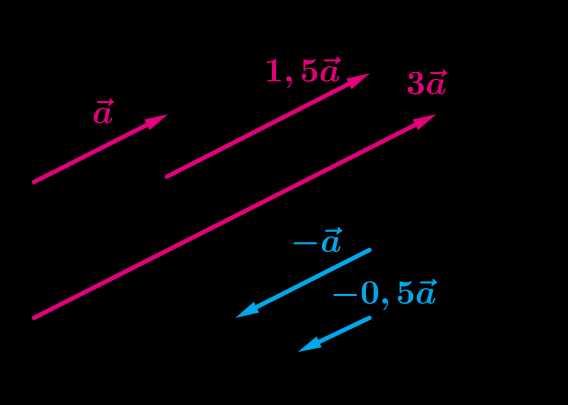
    Справедливо и обратное суждение.

    Если ненулевые векторы коллинеарны, то обязательно можно найти число k≠0 так, что b→=k⋅a→.

    Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде c→=k⋅a→+m⋅b→. Говорят, что вектор c→ разложен по векторам a→ и b→, а числа \(k\) и \(m\) называют коэффициентами разложения.

    Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.

    Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают i→ и j→.

     

     

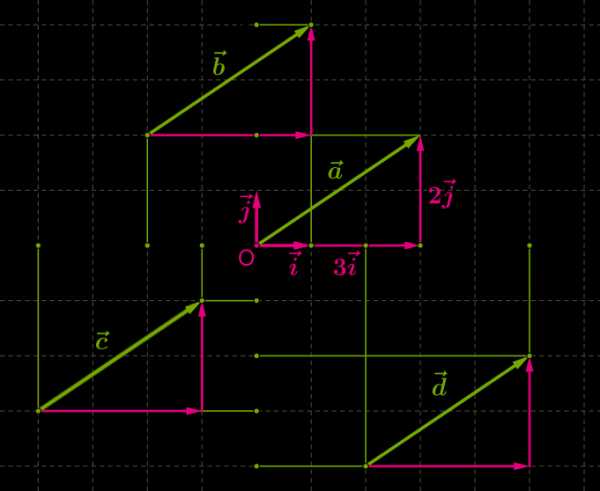
    Если от начала координат отложить вектор a→, то его можно разложить по векторам i→ и j→ следующим образом: a→=3⋅i→&plus;2⋅j→.

    В этом разложении коэффициенты координатных векторов называют координатами вектора a→.

    Это записывают как a→3;2.

     

    Любой вектор, который равен с вектором a→, можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.

    Равные векторы имеют равные координаты.

    Но в то же время в координатной системе можно переместить векторы i→ и j→, таким образом определить координаты векторов независимо от их места расположения в координатной системе.

     

    Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.

     

    Связь между координатами противоположных векторов следует из того, что, если умножить вектор на \(-1\), результатом будет противоположный вектор.

    У противоположных векторов противоположные координаты.

    Важно понять ещё несколько интересных связей между координатами векторов одинаковой длины.

     

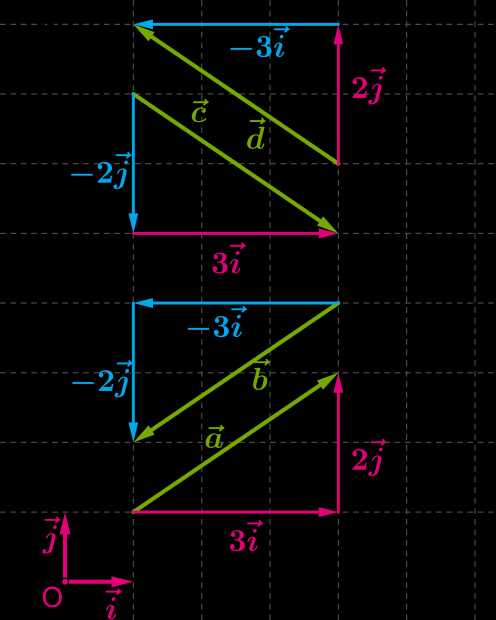
    www.yaklass.ru

    Координаты вектора. Геометрия, 9 класс: уроки, тесты, задания.

    1. Координаты вектора

    Сложность: лёгкое

    		3
    2. Сложение и вычитание векторов с координатами

    Сложность: лёгкое

    		2
    3. Определение координат вектора по координатам его начала и конца

    Сложность: лёгкое

    		6
    4. Координаты вектора

    Сложность: среднее

    		3
    5. Математические операции с координатами векторов

    Сложность: среднее

    		2
    6. Сумма, разность и произведение вектора на число

    Сложность: среднее

    		3
    7. Равенство разложений по координатными векторами

    Сложность: среднее

    		6
    8. Действия с векторами в координатной форме

    Сложность: среднее

    		2
    9. Одинаково и противоположно направленные векторы

    Сложность: среднее

    		2
    10. Разложение вектора по данным векторам

    Сложность: среднее

    		2
    11. Разложение векторов по данным координатным векторам

    Сложность: сложное

    		4,5
    12. Определение координат вектора по данным координатным векторам

    Сложность: сложное

    		5

    www.yaklass.ru

    Векторы — 9 класс

    Векторы — 9 класс:

    Векторы — это направленные отрезки прямой, у которых обозначено направление, т.е. имеется начало и конец.

    Векторы всегда изображены в виде отрезка со стрелочкой.

    На письме обозначаются так:  — 1-я буква — начало, вторая — конец.

    Векторы (или векторные величины) широко используются в геометрии и физике. С помощью векторов легко показать какие-либо изменения в пространстве, например, скорость, силу и др.

    По сути, любая точка на плоскости — это тоже вектор, который может быть направлен в другую сторону. Такой вектор называют нулевым и обозначают так: 

    Если вектор ненулевой, то он имеет определенную длину и эта длина записывается так: 

    Векторы могут лежать на одной прямой, в таком случае они называются коллинеарными.

    Нулевой вектор будет коллинеарным любому другому вектору.

    Если векторы коллинеарные и вдобавок направлены в одну сторону, то они сонаправленные (обозначаются так: ↑↑). Если же в разные стороны, то противоположно направленные (обозначаются так: ↑↓).

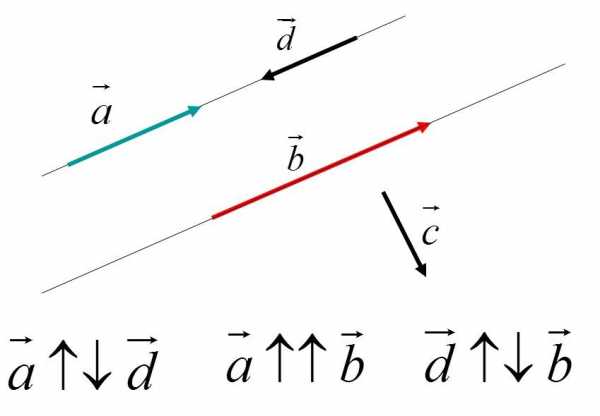
    Равные векторы всегда сонаправлены и равны по длине (часто их обозначают одинаковыми буквами).

    Если векторы неколлинеарны, то между ними есть угол, который обозначается так:  = 35°, если угол прямой, то это перпендикулярные векторы и их можно обозначить так: ​​​​​​​

    Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно

    Добавить новость и получить деньги

    Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

    uchilegko.info

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *