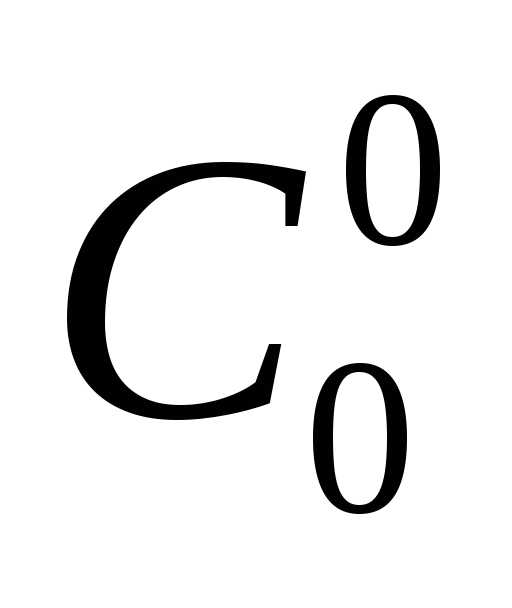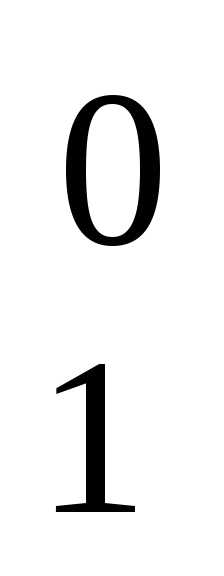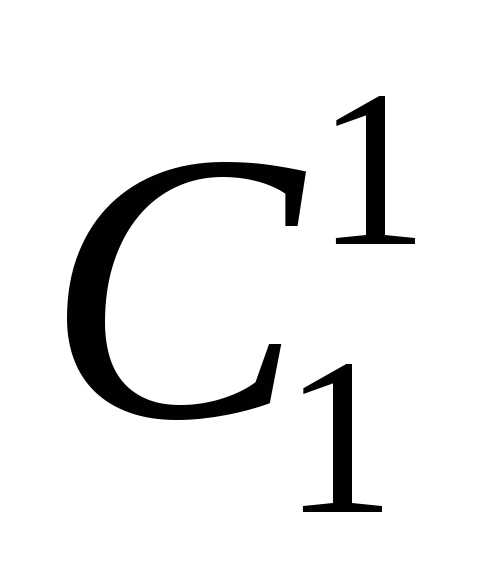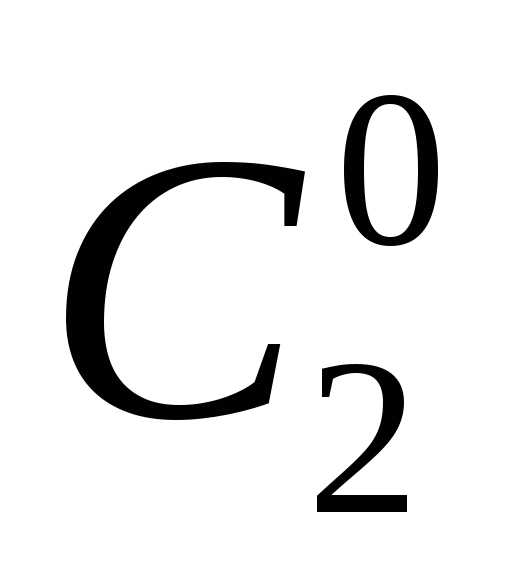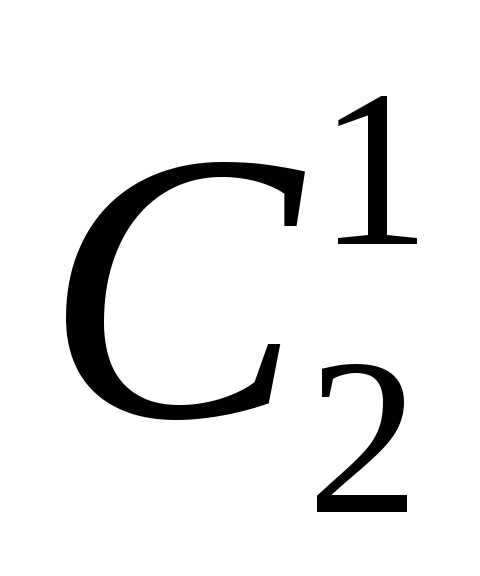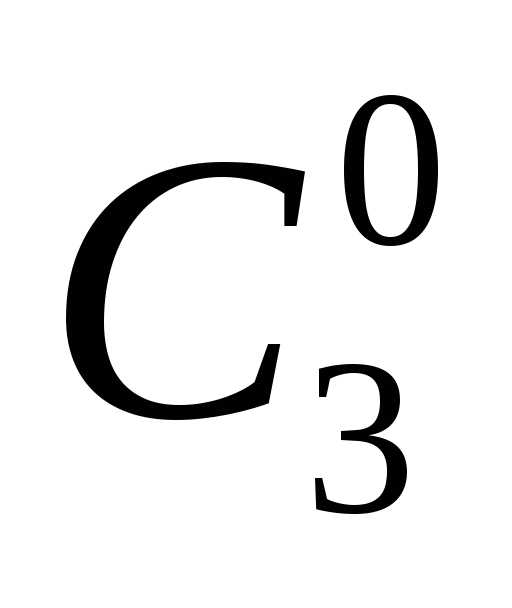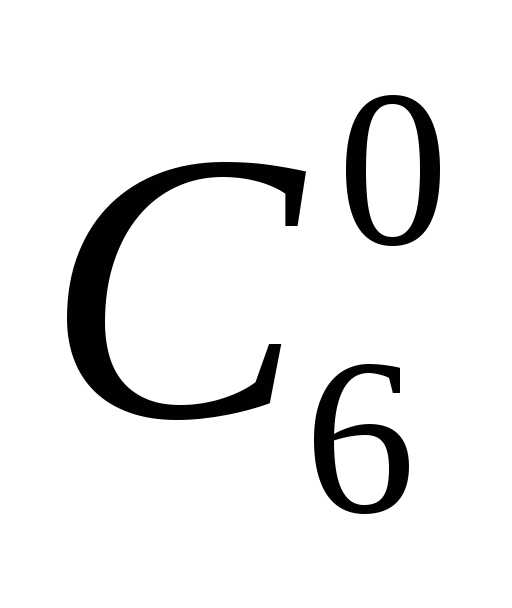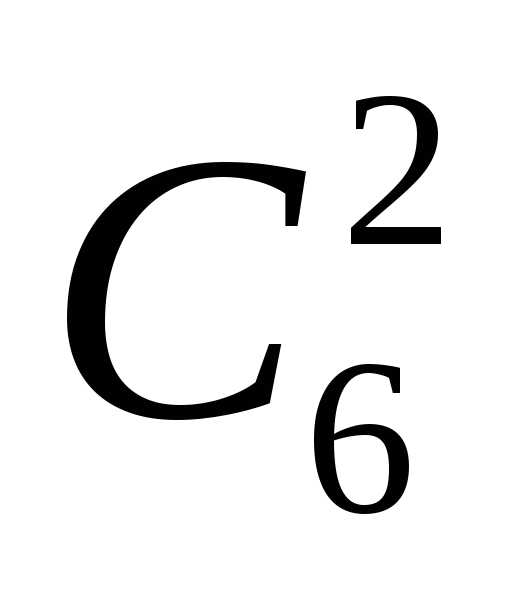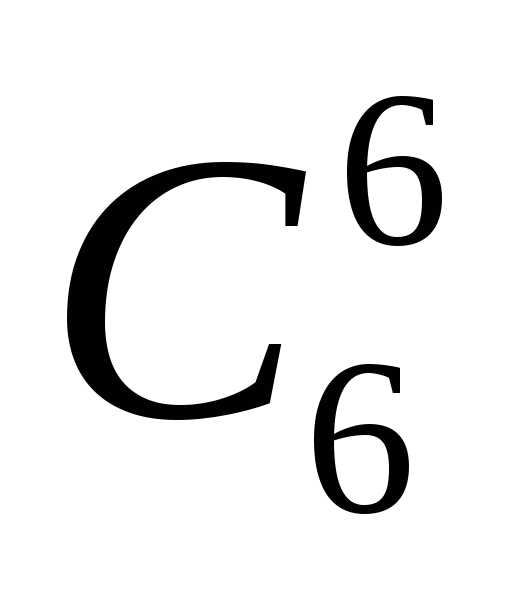Бином ньютона пирамида – , .

Лекция на тему «Бином Ньютона. Биномиальные коэффициенты и треугольник Паскаля»

Лекция № 6 (3 ч.)

Раздел 1. Комбинаторика.

Тема: Бином Ньютона. Биномиальные коэффициенты и треугольник Паскаля.

Цели занятия:

• дать понятие «Бином Ньютона»;

• вывести формулу бинома Ньютона, рассмотреть свойства его разложения;

• ввести общую формулу вычисления биномиальных коэффициентов, проследить закономерность их появления в треугольнике Паскаля.

Литература:

1. Халамайзер А.Я. Комбинаторика и бином Ньютона. — М: Просвещение. 1980

2. Прикладная комбинаторная математика

3. Энциклопедический словарь юного математика/Сост. А.П. Савин. – М.: Педагогика, 1985г.

План:

1. Бином Ньютона.

2. Биномиальные коэффициенты.

3. Треугольник Паскаля.

1. Бином Ньютона — название формулы, выра­жающей степень двучлена в виде суммы одночленов.

Формулу для квадрата двучлена

(а + b)² = = а² + 2ab + b²

знали, еще ма­тематики Древнего Вавилона, а древнегрече­ские математики знали ее геометрическое ис­толкование.

Если умножить обе части этой формулы на (а + b) и раскрыть скобки, то получим:

(а + b)³ = (а² + 2ab + b²)(

а + b) = а³ + a²b + 2a²b + 2ab² + ab² + b³,

т. е. (а + b)³ = a³ + 3a²b + 3ab² + b³.

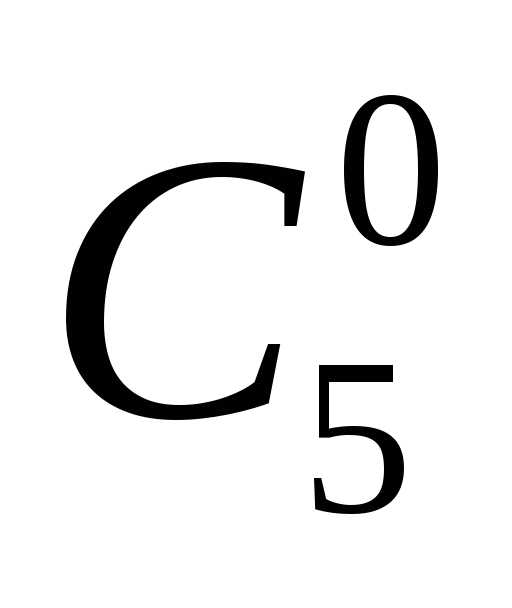
Аналогичный шаг может привести к следующей формуле:

(а + b)⁴ = а⁴ + 4а³b + 6

a²b² + 4ab³ + b⁴ .

Легко заметить закон образования коэффи­циентов: коэффициент 4 при a³b есть сумма коэффициентов 3 и 1 при a²b и а³. Аналогич­но, коэффициент 6 при a²b² является суммой (3 + 3) коэффициентов при ab² и a²b. По то­му же закону получаем и коэффициент 4 при ab³.

Таким образом, коэффициент С ^k_n при а^n—k b^k

в разложении (а + b)ⁿ равен сумме коэффи­циентов C^k-1 _n-1 и C^k _n-1 при а^n—k b^k-1 и при а^n—k-1 b^k разложении

(а + b)^n-1, а коэффи­циенты при аⁿ и при bⁿ равны единице.

Отсюда следует, что коэффициенты С ^k_n в равенстве:

(а + b

)ⁿ = аⁿ + С¹_n а^n-1b + … + С^k_n а^n-kb^k + … + bⁿ (1)

являются членами (n+1)-й строки треуголь­ника Паскаля.

Это утверждение было известно задолго до Па­скаля — его знал живший в XI-XII вв. средне­азиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло).

2. Биномиальные коэффициенты.

Первое дошедшее до нас описание формулы бинома Ньютона содержится в по­явившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел С

k_n (биномиальных коэффициентов) до п = 12 включительно.

Европейские ученые познакомились с фор­мулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов про­вел французский математик и философ Блез Па­скаль в 1654 г. Еще до этого было известно, что числа

являются в то же время числами «сочетаний без повторений» из n элементов по k.

В 1664-1665 гг. И. Ньютон установил, что формула (1) обобщается на случай про­извольных (дробных и отрицательных) пока­зателей, но при этом получается сумма из бе­сконечного множества слагаемых. Именно он показал, что при | х | < 1

(2)

При п = — 1 формула (2) превращается в из­вестную формулу для суммы бесконечной гео­метрической прогрессии:

4. Треугольник Паскаля.

На рис. 1 изображено несколько первых строк числового треугольника, образованного по следующему правилу: по краям каждой строки стоят единицы, а каждое из остальных чисел равно сумме двух стоящих над ним чи­сел предыдущей строки.

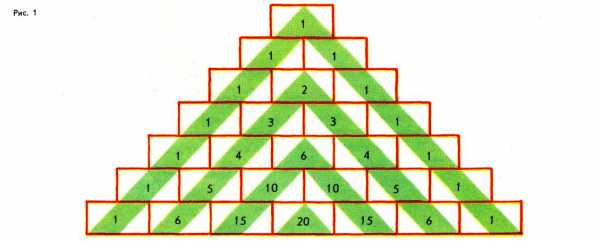По этому правилу легко выписывать одну за другой новые стро­ки этого треугольника. Именно в такой фор­ме он приведен в «Трактате об арифметиче­ском треугольнике» французского математика Б. Паскаля (1623-1662), опубликованном в 1665 г., уже после смерти автора.

Популярность чисел, составляющих треу­гольник Паскаля, не удивительна: они возни­кают в самых естественных задачах алгебры, комбинаторики, теории вероятностей, матема­тического анализа, теории чисел.

Сколько различных k-элементных множеств (сочетаний) можно образовать из данных п элементов?

Каковы коэффициенты многочлена (1 +х)ⁿ?

Сколько существует строчек из п единиц и нулей, в которых ровно k единиц?

Сколькими разными путями можно спу­ститься из верхней точки А на рис 2. в k-й перекресток n-го ряда?

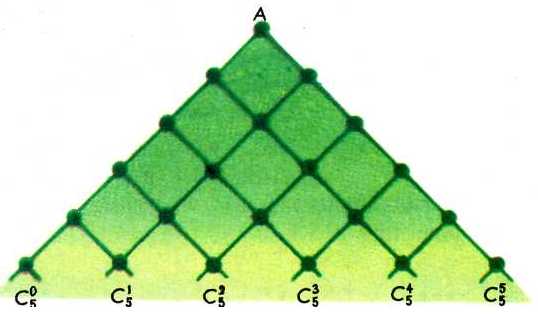
Рис 2

На все эти вопросы ответ дают числа С^k_n , треугольника Паскаля. Обозначение С^k_n пред­полагает, что верхняя строка треугольника Паскаля состоит из одного числа С

0₀ = 1, сле­дующая (первая)-из двух чисел С ⁰₁ = С¹₁ =1, и вообще п-я строка состоит из п+1 чисел:

Числа С ^k_n называют обычно числами соче­таний из п элементов по k, или биноми­альными коэффициентами в некоторых книгах для них используют обозначение 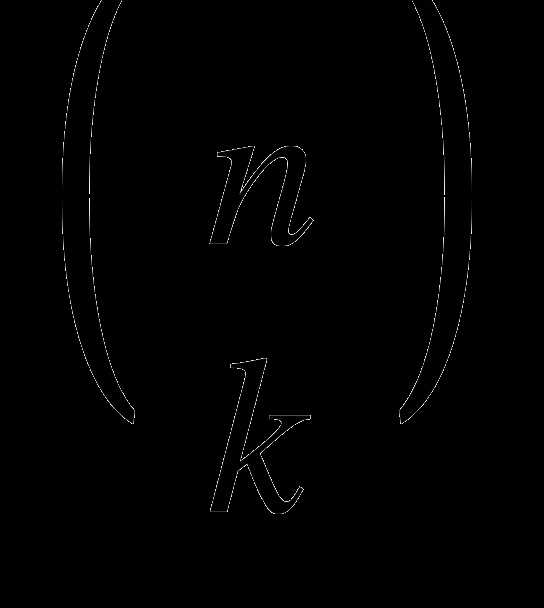. Оно удобно для запоминания простой формулы, позволяющей по заданным номерам n и k сразу вычислить, какое число стоит на к-м месте в n-й строке тре­угольника Паскаля:

Используя обозначение факториала т! = = 1 • 2 •… • m, эту формулу можно записать еще короче:

В «равнобедренной» форме треугольника Паскаля на рис. 1 очевидно

свойство симмет­рии каждой строки С ^k_n = С ^n—k_n ; при этом посе­редине строки стоит самое большое число 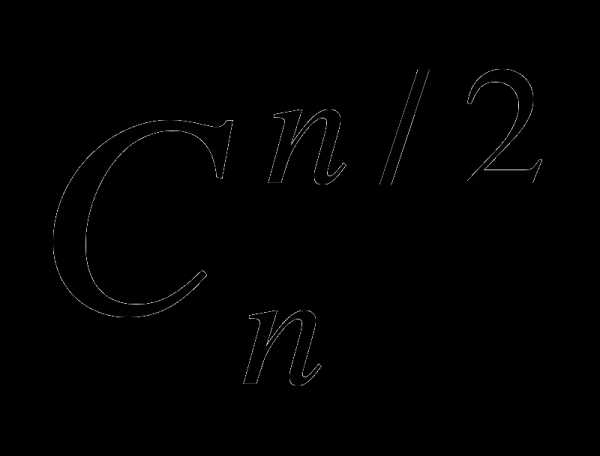(если п четно) или два самых больших числа (если п нечетно), а к краям числа монотонно убывают.

Если записать тот же треугольник в «пря­моугольной» форме (рис.3), то целый ряд свойств треугольника Паскаля, связанный с суммами его чисел, будет удобнее наблю­дать. В частности, сумма нескольких первых чисел каждого столбца равна идущему за ни­ми числу следующего столбца:

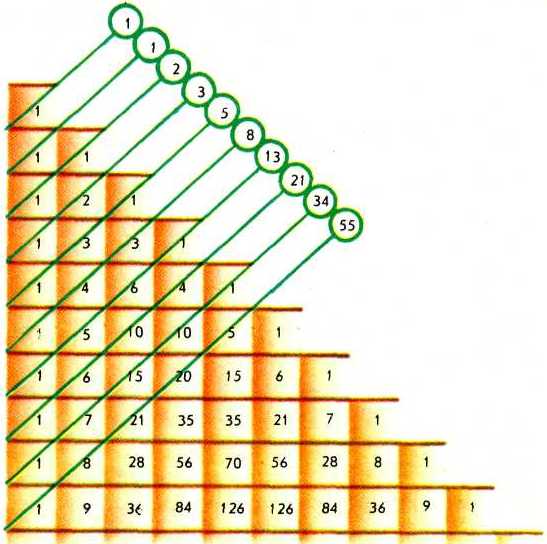
Рис.3

Числа называются треу­гольными числами

, а числа
— пирамидальными;

а при т> к,

Суммы чисел по «восходящим» (зеленым) диагоналям на рисунке 3 равны последова­тельным числам Фибоначчи.

Для применений в теории вероятностей особенно важны асимптотические формулы для чисел треугольника Паскаля, т.е. прибли­женные оценки этих чисел при больших п.

infourok.ru

2 часа лекции, 2 часа семинарское занятие Свойства Сочетаний (биномиальных коэффициентов)

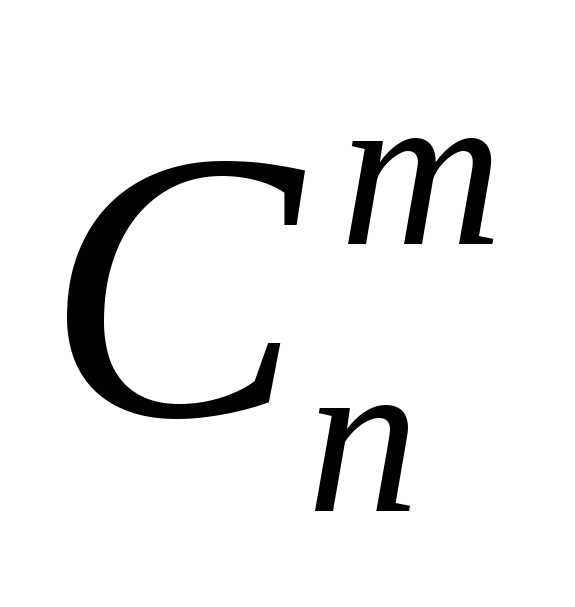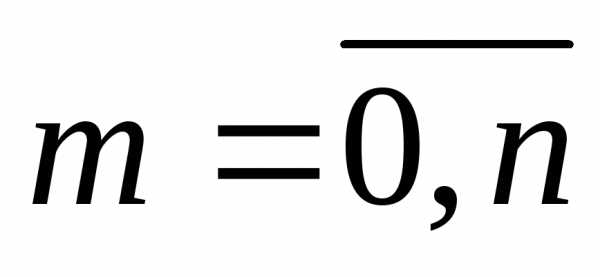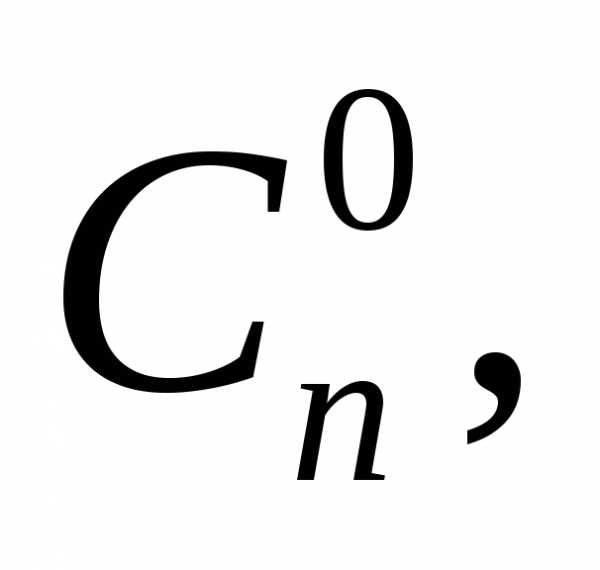
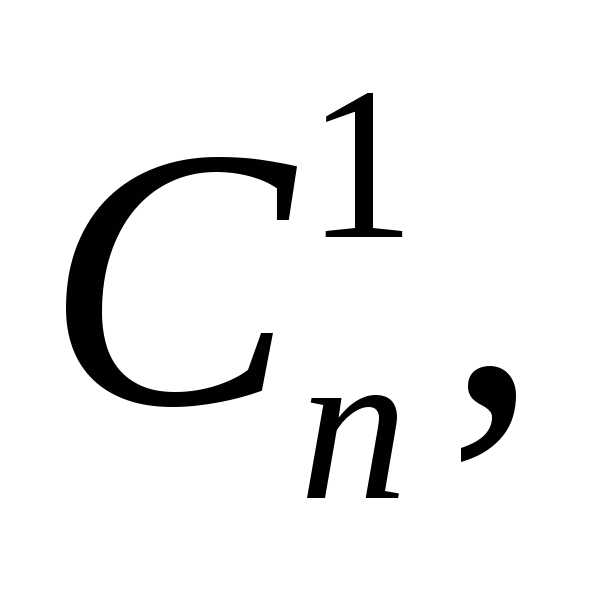
Сочетания — при, т.е. числа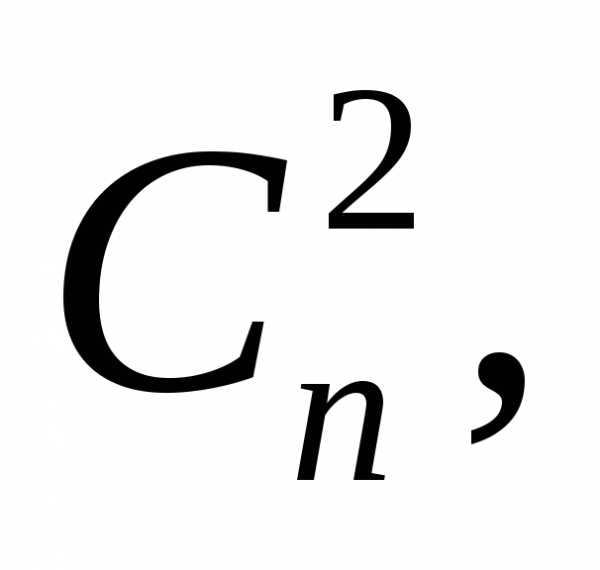…,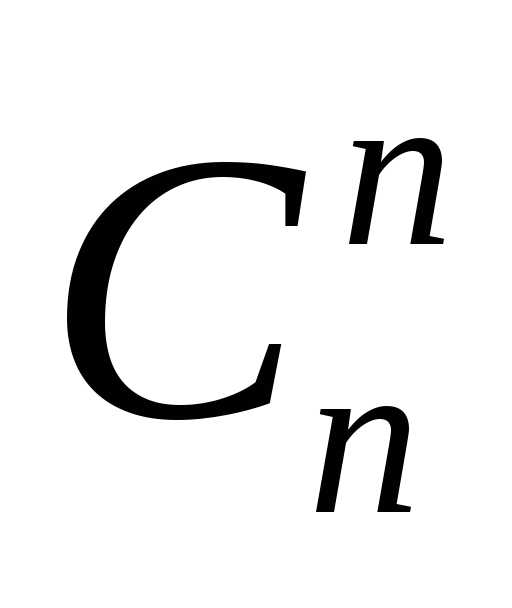используются в формуле бинома Ньютона. Их достаточно часто называют биномиальными коэффициентами, поскольку они являются коэффициентами в разложении бинома Ньютона. В школе каждый заучивал формулы квадрата, куба и других степеней суммы двух чисел:

(a + b)² = a² + 2ab + b²,

(a + b)³ = a³ + 3a²b + 3ab² + b³.

Определение. Формула для произвольной степени суммы двух слагаемых выглядит так:

Эту формулу обычно называют формулой бинома Ньютона. Слово «бином» означает «двучлен», а коэффициенты в разложении называются, как мы уже знаем, биномиальными коэффициентами.

Треугольник Паскаля

Для чисел 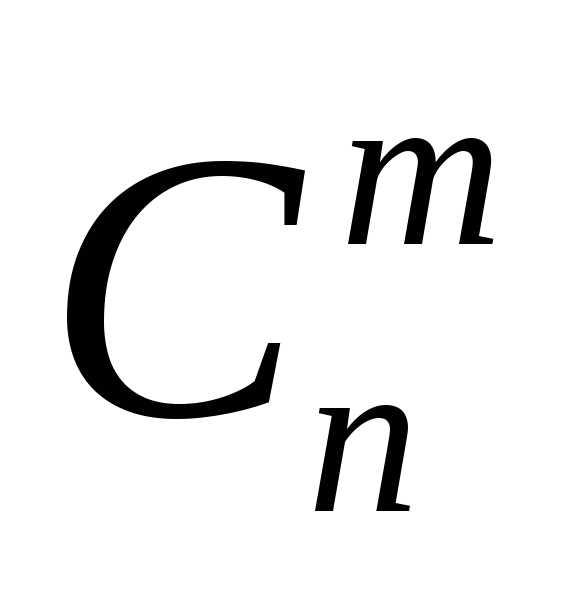имеется красивый и удобный способ из записи в виде треугольной таблицы. Эту таблицу называюттреугольником Паскаля.

С

…

…

…

…

…

…

Получается бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается как сумма двух предшествующих чисел.

1

				1		1
			1		2		1
		1		3		3		1
	1		4		6		4		1
1		5		10		10		5		1
…	…	…	…	…	…	…	…	…	…	…

Биномиальные коэффициенты обладают многими замечательными свойствами.

1). Все они целые положительные числа.

2). Крайние коэффициенты равны единице.

3). Коэффициенты возрастают от краев к середине.

4). Сумма всех коэффициентов равна 2ⁿ. Это следует из формулы бинома, если в ней положить, что a = b = 1.

5). Сумма биномиальных коэффициентов на четных местах равна сумме коэффициентов на нечетных местах.

6). Если a заменить на -a, то знаки перед биномиальными коэффициентами будут чередоваться.

7). В разложении бинома содержится на один член больше, чем его степень.

8). Разложение есть однородный многочлен, то есть все члены имеют одну и ту же степень относительно a и b;

9). Правило симметрии: для всех m = 0, 1, …, n (записывается: )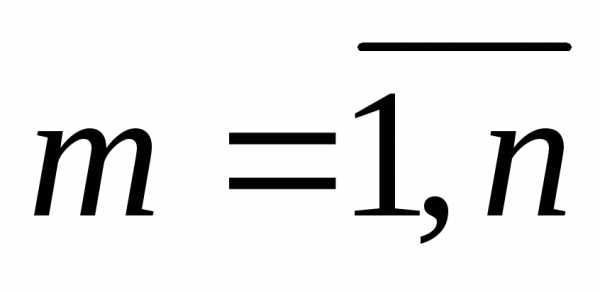

Правило симметрии удобно использовать в расчетах количества сочетаний 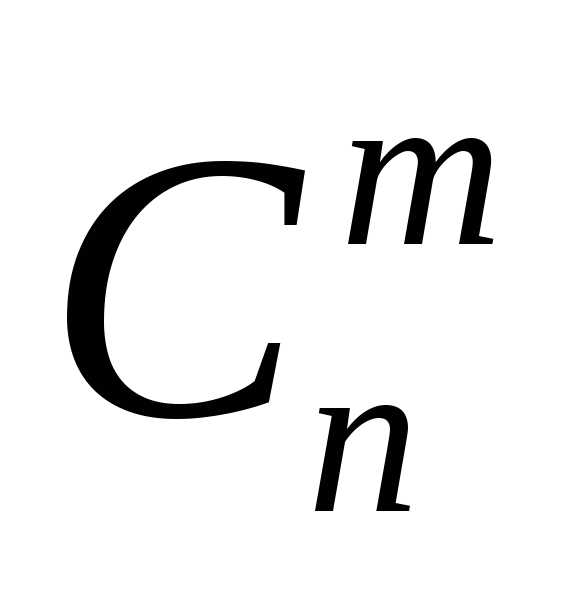, еслиm превышает половину объема исходного множества, т.е. m >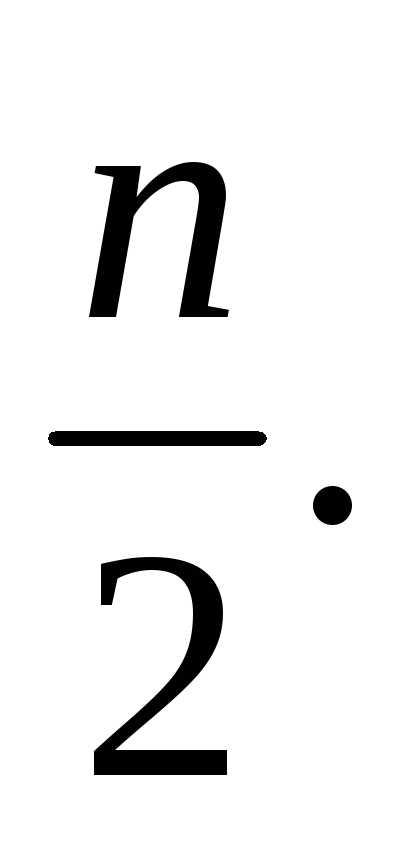

10). Из свойств (7) и (9) следует, что если показатель бинома четный, то в разложении средний член имеет наибольший коэффициент, а если показатель бинома нечетный, то в разложении имеется два средних члена с одинаковым наибольшим коэффициентом.

Особенно важное значение имеет следующее свойство.

11). Правило Паскаля или рекуррентное свойство числа сочетаний:

Основная закономерность образования строк состоит в следующем: каждое число в треугольнике Паскаля равно сумме двух чисел, стоящих над ним в предыдущей строке (5 = 1 + 4; 10 = 4 + 6; 6 = 3 = 3 и т.д.). Или то же в строгой формулировке: сумма двух соседних коэффициентов в разложении (а + b)ⁿ равна определённому коэффициенту в разложении

(а + b)ⁿ⁺¹.

studfiles.net

Доклад на тему «Бином Ньютона и треугольник Паскаля»

Бином Ньютона — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

где — биноминальные коэффициенты, — неотрицательное целое число.

Это формула, представляющая выражение ( a + b ) ⁿ при положительном целом n в виде многочлена:

          

Заметим, что сумма показателей степеней для a и b постоянна и равна n.

Числа   называются биномиальными коэффициентами.

Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1;  вторая — для n = 2;  третья — для   n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:

( a + b )⁷ ,

мы можем получить результат моментально, используя таблицу:

Свойства биномиальных коэффициентов.                                                                                               

1. Сумма коэффициентов разложения ( a + b ) ⁿ равна  2 ⁿ .

Для доказательства достаточно положить  a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения:

3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна

Для доказательства воспользуемся биномом: Здесь чётные члены имеют знак  « + » , а нечётные — « — ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна: что и требовалось доказать.

3a1ka.livejournal.com

Биномиальные коэффициенты — это… Что такое Биномиальные коэффициенты?

Биномиальные коэффициенты — коэффициенты в разложении (1 + x)ⁿ по степеням x (т. н. бином Ньютона):

Иначе говоря, (1 + x)ⁿ является производящей функцией для биномиальных коэффициентов.

Значение биномиального коэффициента определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:

для ;

для k < 0 или ;

для ,

где n! и k! — факториалы чисел n и k.

Биномиальный коэффициент является обобщением числа сочетаний , которое определено только для неотрицательных целых чисел n, k.

Биномиальные коэффициенты часто возникают в комбинаторных задачах и теории вероятностей.

Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.

Треугольник Паскаля

Тождество

позволяет расположить биномиальные коэффициенты для неотрицательных n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:

Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).

Свойства

Интересно, что если рассмотреть ряды в треугольнике Паскаля, состоящие из биномиальных коэффициентов, то в пределе получим функцию нормального распределения — распределение Гаусса.

Из теоремы Люка следует, что:

• нечётен в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули,
• некратен простому p в p-ичной записи числа k все разряды не превосходят соотв. разрядов числа n,
• В ряду биномиальных коэффициентов :
  • все числа не кратны заданному простому p n = mp^k − 1, где натуральное m < p,
  • все числа, кроме первого и последнего, кратны заданному простому p n = p^k, где натуральное m < p,
  • количество нечётных чисел равно степени двойки,
  • не может быть поровну чётных и нечётных чисел,
  • количество не кратных простому p чисел равно , где числа — разряды p-ичной записи числа n; а число m = [log_pn] + 1

Тождества

Асимптотика и оценки

Алгоритмы вычисления биномиальных коэффициентов

Биномиальные коэффициенты могут быть вычислены с помощью формулы , если на каждом шаге хранить значения при . Этот алгоритм особенно эффективен, если нужно получить все значения при фиксированном n. Алгоритм требует O(n) памяти (O(n²) при вычислении всей таблицы биномиальных коэффициентов) и O(n²) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).

Второй способ основан на тождестве . Он позволяет вычислить значения при фиксированном k. Алгоритм требует O(1) памяти (O(l) если нужно посчитать l последовательных коэффициентов с фиксированным k) и O(k) времени.

См. также

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru

6.1.2 Формулы числа сочетаний и перестановок. Бином Ньютона

Видеоурок 1: Сочетания

Видеоурок 2: Перестановки

Видеоурок 3: Бином Ньютона

Лекция: Формулы числа сочетаний и перестановок. Бином Ньютона

Формулы числа сочетаний и перестановок

Существует основные формулы для сочетаний и перестановок:

В данной таблице важно внимательно смотреть на условие задачи: по горизонтали происходит разделение формул в зависимости от возможности повторения элементов. По вертикали сверху описаны случаи задач, в которых важен или не важен порядок элементов. А снизу Вы можете наблюдать задания, которые следует выполнить над элементами.

Бином Ньютона

С частным случаем Бинома Ньютона мы уже сталкивались при использовании формул сокращенного умножения, а именно при возведении суммы или разности чисел во вторую и в третью степень. Сейчас же мы рассмотрим формулу, которая позволит возвести сумму некоторых двух чисел в любую степень.

Формула Бинома Ньютона:

Чтобы найти коэффициенты, следует воспользоваться сочетательным законом комбинаторики без повторений:

Давайте для начала рассмотрим знакомую нам формулу и как она получилась:

Коэффициенты Бинома Ньютона

Для более простого подсчета коэффициентов Бинома Ньютона для невысоких степеней удобно пользоваться треугольником Паскаля:

Данный треугольник несложно вычислить и самостоятельно. По бокам в каждой строчке имеется коэффициент, равный единице. Все средние коэффициенты считаются, как сумма верхних, которые находятся над ними.

Существует очень важное свойство коэффициентов для Бинома Ньютона, которое позволит проверить правильность их расставления. Для этого необходимо сложить все коэффициенты на четных местах, затем сложить коэффициенты на нечетных местах, после чего сравнить полученные значения. Они должны получиться равными.

cknow.ru

Бином Ньютона — ПриМат

Бином Ньютона — формула, представляющая выражение при  в виде:

,

где — число сочетаний из элементов по элементов.

.

Докажем верность данного утверждения:

Доказательство методом математической индукции.

Для :

Для  утверждение выполняется.

Предположим, что утверждение выполняется для .

Докажем верность формулы для .

Докажем, что .

Вынесем слагаемое при из первой суммы:

Вынесем слагаемое при из последней суммы:

Прибавим данные суммы:

Также с помощью бинома Ньютона строится треугольник Паскаля, в котором числа в строке обозначают коэффициенты при соответствующих степенях:

Примеры:

       

Список литературы:

Тест «Бином Ньютона»

Лимит времени: 0

Информация

Тестовые вопросы по вышеизложенной теме.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 3

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

Ваш результат был записан в таблицу лидеров

1. С ответом
2. С отметкой о просмотре

Таблица лучших: Тест «Бином Ньютона»

максимум из 3 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

 

Поделиться ссылкой:

Похожее

ib.mazurok.com

Урок на тему: «Бином Ньютона»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«НИЖЕГОРОДСКИЙ ЭКОНОМИКО-ПРАВОВОЙ КОЛЛЕДЖ ИМ. ГЕРОЯ СОВЕТСКОГО СОЮЗА БОРИСА ПАВЛОВИЧА ТРИФОНОВА»

МАТЕМАТИКА

Методическая разработка

На тему «Бином Ньютона и треугольник Паскаля»

на примере открытого урока

2014

Рассмотрено на заседании

методической комиссии

естественнонаучных и

математических дисциплин

Протокол №______от_____

Председатель МК

__________________Н.Н. Борышнева

Автор: Боброва Н.П., преподаватель ГБОУ СПО «НЭПК»

Рецензент: Кордюкова Н.П., преподаватель «ГБОУ СПО НЭПК»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Данное учебно­-методическое пособие составлено в соответствии с рабочей программой и относится к разделу «Комбинаторика», занятие № 95. Оно предназначено для подготовки студентов первого курса дневного отделения.

Учебный материал пособия состоит из методических указаний и упражнений, которые необходимы для усвоения и закрепления изученного материала.

В результате изучения студент должен:

иметь представление о:

знать:

уметь:

Урок изучения и первичного закрепления новых знаний

Тема: « Бином Ньютона. Треугольник Паскаля»

“Тысячи неразгаданных тайн таит в себе наука,

и без вас, без вашей молодости, смелости, энтузиазма,

они не будут разгаданы. Наука ждёт вас, друзья».

Академик А.С. Несмеянов.

Цели урока – изучение и первичное осознание нового учебного материала, осмысление связей и отношений в объектах изучения.  Познакомиться с биномом Ньютона, показать его связь с треугольником Паскаля.

Познавательные задачи — сформировать навыки в применении бинома

Ньютона.

Развивающие задачи

• Расширять кругозор учащихся.

• Развивать познавательную активность, интерес к математике и истории.

• Развивать индивидуальные способности учащихся, потребность к самообразованию.

• Учить анализировать и строить аналогии.

Воспитательные задачи

• Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

• Воспитание внимательности, аккуратности.

• Прививать интерес к предмету.

Оборудование занятия: мультимедиа, презентация, учебник, приложение.

№

п/п

Этап и содержание урока

Методические замечания

1

Организационный момент

— Здравствуйте, ребята. Садитесь. Отметим отсутствующих и проверим готовность аудитории к занятию.

Проверка готовности

группы к занятию

2

Сообщение темы, целей и задач урока

Тема нашего урока “Бином Ньютона. Треугольник Паскаля”.

Сегодня на уроке мы должны обобщить и повторить пройденный материал. Полученные знания и навыки в применении биноминальных формул, закрепим на решении математических задач. В течение урока работать будем по группам, затем подведём итог урока, и вы получите домашнее задание.

На экране слайд

3

Актуализация знаний: проверка домашнего задания,

устная работа

Группа №1 и №2 представляют свою работу у доски.

1. Разгадайте кроссворд.

1. Свойство умножения, используемое при умножении одночлена на многочлен. 2. Способ разложения многочлена на множители. 3. Значение переменной, при котором уравнение обращается в верное равенство. 4.Равенство, верное при любых значениях переменных. 5. Выражение, представляющее собой сумму одночленов. 6. Слагаемые, имеющие одну и ту же буквенную часть. 7. Числовой множитель у одночленов.

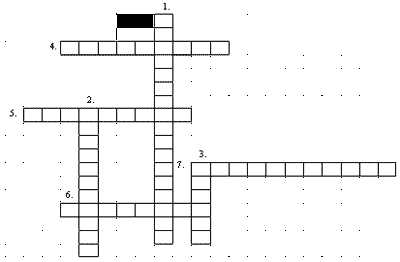
Ответы:

1. Распределительное

2. Группировки

3. Корень

4. Тождество

5. Многочлен

6. Подобные

7. Коэффициент

2.

— Какими формулами вы пользовались в данном задании?

Давайте назовём их и сформулируем.

1. Формулы квадрата суммы и разности двух выражений 

2. Формула разности квадратов 

3. Формулы суммы и разности кубов 

4. Свойство степени.

Презентации с домашними заданиями по группам

Листы с заданиями на столах, работа №1 и №2 в группах

3

Объяснение нового материала

Формулы сокращённого умножения являются частным случаем бинома Ньютона. Сегодня на уроке мы обобщим полученные знания и познакомимся с данными формулами.

Формула бинома Ньютона. Как возвести в степень n сумму двух слагаемых?

Исаак Ньютон был поистине Великим физиком своего времени, а может быть и величайшим физиком всех времен и народов. Но мы не будем судить об этом. Однако следует заметить, что Ньютон был еще и прекрасным математиком. Кстати формула бинома Ньютона была выгравирована на надгробии его могилы, как самое великое открытие современности того времени! 

Кроме формулы бинома Ньютона, со школьной скамьи всем известна формула Ньютона-Лейбница. Таким образом, великий Ньютон вместе с Лейбницем заложили основы дифференциального и интегрального исчисления. Основы теории пределов и строгий подход в математическом анализе был начат и развивался в трудах таких гениев как Огюстен Коши, Георг Кантор, Карл Вейерштрасс. Нельзя, конечно, обойти стороной имя Леонарда Эйлера.

Но мы отвлеклись здесь от основной линии рассуждений. Ведь Формула бинома Ньютона относится к алгебре, а также к ветви математики, называемой комбинаторикой! 
Вы спросите: а почему, собственно, формула бинома, и что такое бином вообще. Здесь употребляется алгебраическая терминология: в алгебре есть понятие многочлена. Многочлен это Полином — другими словами — сумма произвольного числа слагаемых называется полином. 
Например — это полином! 
А сумма двух слагаемых называется Бином! То есть — это бином, или например x+y — тоже бином. Здесь x и y предполагаются неизвестными переменными величинами! Но формула бинома Ньютона на самом деле это не просто формула бинома (иначе, что это за формула такая, которая состоит из суммы двух произвольных слагаемых?). Ничего, собственно, примечательного и ничего содержательного! Ньютон был гораздо умнее, чем изобретатель простой суммы двух слагаемых! Что же он тогда изобрел?

Ньютон изобрел формулу, которая позволяет возвести сумму двух слагаемых в степень с любым показателем, а не только с показателем равным 2! Невозможно переоценить значение формулы бинома Ньютона при решении пределов функций. Поэтому правильно формула, о которой идет здесь речь, называется Формулой Ньютона для степени бинома. Мы не будем сразу писать эту формулу в общем виде, а вначале обратимся к школьной алгебре!
Вспомним из школьного курса что:

Это и есть формула квадрата суммы или формула квадрата двучлена, или формула второй степени бинома! А теперь возведем в третью степень сумму двух слагаемых или раскроем бином третьей степени.

Скобки раскрываем аналогично, как всегда использую распределительный или дистрибутивный закон алгебры:

Здесь мы имеем уже шесть слагаемых, а если быть точным, не шесть, а 8=2³ слагаемых, поскольку два слагаемых имеют коэффициенты 2.

Мы доказали формулу суммы кубов. Она должна быть вам хорошо известна из школьного курса алгебры.
Однако не будем останавливаться на достигнутом, и пойдем дальше, возведем бином в четвертую степень! Но возводить мы будем по — хитрому! Не с нуля, а воспользовавшись предыдущей формулой для третьей степени бинома:

Здесь мы не стали делать подробных раскрытий скобок, а сразу записали результат раскрытия, поскольку вычисления аналогичны тому, как мы это уже проделали дважды.
Хорошо, мы уже добрались до четвертой степени бинома! Но не будем на этом останавливаться и снова возведем в бином, но уже в пятую степень! Что нам стоит дом построить – нарисуем, будем жить! 
Ведь сложного то ничего нет, ведь всего лишь для возведения бинома в пятую степень надо умножить результат возведения бинома в четвертую степень на известный нам бином! Вот в чем заключалась гениальная идея Ньютона!

То есть вместо четвертой степени бинома мы подставляем уже вычисленное ранее его выражение и снова раскрываем скобки, опуская подробные вычисления, поскольку они уже не однократно выполнялись выше при вычислении третьей и второй степени бинома.

 

Вы спросите: а сколько же можно так продолжать увеличивать порядок степени возведения бинома? Ответ: до бесконечности можно! Точно также, например при n=100 умножим результат возведения в степень 99 на x+y, тогда получим результат возведения в степень 100.

Но мы не будем расписывать все это выражение, поскольку после приведения подобных членов оно имеет 101 слагаемое и не уместится в одну строчку, а в десять строчек прочтение будет очень затруднительно!
Но гениальность Ньютона в том и заключалось, что он смог записать эту формулу в общем виде в одну строчку для любого n, то есть формулу для

Здесь мы делаем простой и гениальный вывод: чтобы получить формулу для n, надо знать эту формулу для (n-1). Чтобы знать формулу для (n-1) надо получить ее (n-1) раз так, как мы это делали для 2,3,4, и 5-й степени, то есть умножали уже известный результат для степени на единицу меньшей заданной степени на степень равную единице!

А теперь напрашивается второй гениальный вывод! А что если все эти действия, которые приводят к формуле бинома для степени n-1 можно записать одним махом?! Тогда можно будет не переписывать (n-1) раз фактически одни и те же вычисления для 2, 3, 4, 5, 6,…,n-1 степени бинома, а записать их одной формулой, умножить эту формулу еще раз на первую степень бинома и полностью доказать искомую формулу! Вот вам и алгоритм рассуждений Ньютона!

Здесь мы выделили последние предложения жирным шрифтом, поскольку они являются основой доказательства формулы бинома Ньютона и наиболее серьезным и сложным шагом во всех наших рассуждениях. Кстати этот шаг, называется индуктивным, а метод, основанный на индуктивном шаге — методом математической индукции. Таким образом, мы здесь познакомились с одним из наиболее фундаментальных и важных методов математики. Но теперь возникает следующая трудность: как же записать общую формулу для степени бинома, равной n-1? В этом нам помогут уже доказанные формулы степени бинома, равные 3,4,и 5.

Очевидно, что коэффициенты крайних слогаемых равны 1, показатели степени — наивысшие (n). Показатели степени переменных изменяются в обратной зависимости, а вот определить коэффициенты достаточно сложно. Имеет смысл вернуться к определению сочетания из n элементов по m, где

n – степень бинома, а m является номером слогаемого, начиная с 0. Тогда для 3 степени бинома мы получим следующие коэффициенты:

Можно, конечно, привести вывод формулы бинома, но это достаточно сложно и не входит в нашу программу, так что запишем эту формулу и начнем ею пользоваться:

где — сигма, знак суммы слогаемых от 0 до n.

Если мы имеем бином (х — у) ⁿ, то знаки слогаемых чередуются.

Согласитесь, что возводя в степень бином, вычислять коэффициенты через сочетания достаточно трудоемко. Чтобы облегчить эти вычисления, используют:

№

Треугольник Паскаля

0

1

1

1     1

2

1     2     1

3

1     3     3     1

4

1     4     6     4     1

5

1     5     10     10     5     1

6

1     6     15     20     15     6     1

…

…

№

Треугольник Паскаля

0

1

2

3

4

5

6

…

…

 

    Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:

Слайды презентации на экране

4

Первичное закрепление

Продолжите формулу, используя бином Ньютона и треугольник Паскаля.

1. (1/3а+2/5в)³ =(1/3а)³+3(1/3a)²∙2/5b+3(1/3a)(2/5b)²+(2/5b)³=

1/27a³+1/3a²∙2/5b+a∙4/25b²+8/125b³

Ответ: 1/27a³+2a²b/15+4ab²/25+8b³/125

2. (0.2а-0,3b)⁴ =0,0016a⁴— 4∙(0,2a)³∙0,3b+6(0,2a)²(0,3b)²-4∙0,2a(0,3b)³+(0,3b)⁴= 0,0016(a⁴)-0,032a∙³∙0,3b+0,24a²∙0,09b²-

0,8a∙0,027b³+0,0081b⁴

Ответ: 0,0016а⁴-0,0096а³b+0,0216a²b²-0,0216ab³+0,0081b⁴

3. (1/2a-3/4b)³=(1/2a)³-3(1/2a)²∙3/4b+3(1/2a)(3/4b)²-(3/4b)³=

=a³/8-3/8a²∙3/4b+3/2a∙9/16b²-27/64b³= a³/8-9a²b/32+27ab²/32-27b³/64

Ответ: a³/8-9a²b/32+27ab²/32-27b³/64

Решается у доски преподавателем с помощью студентов.

5

Самостоятельная работа в группах

1 группа

1. Найти значение:

а) 1!

б) 7!

в)

г) 9!/6!

2. Вычислить значение бинома:

1)

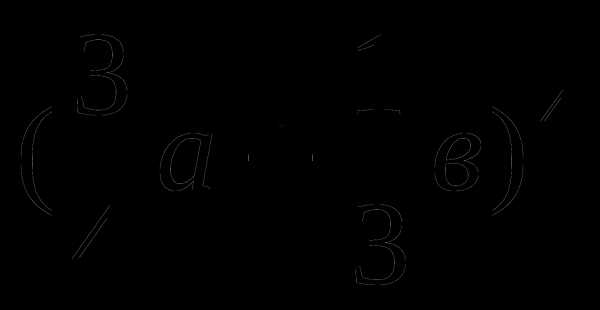
2)

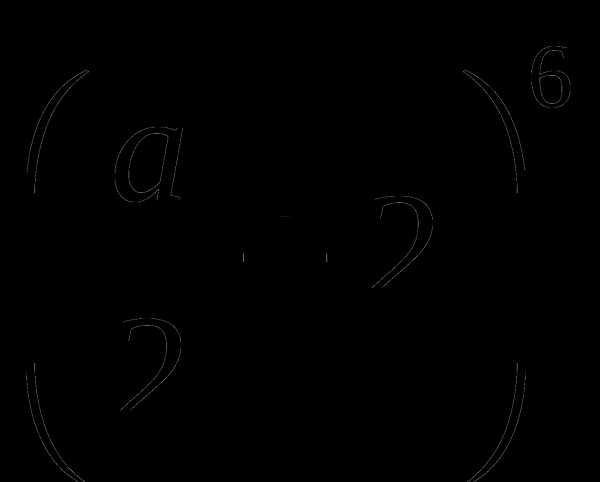
3)

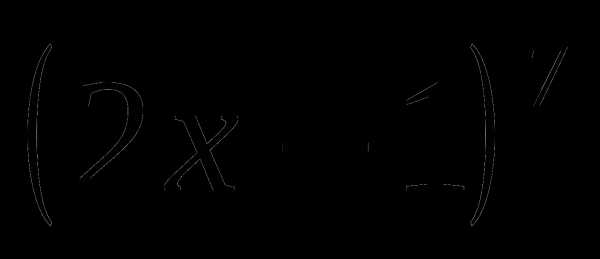
4)

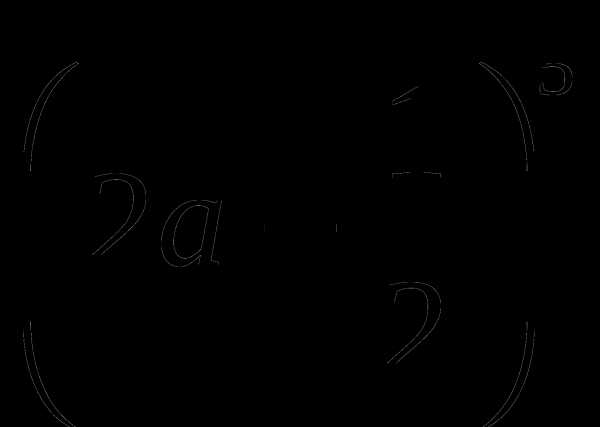
3. Как иначе называется многочлен __

4. Как располагаются биноминальные коэффициенты (монотонность)__

2 группа

1. Найти значение:

а) 0!

б) 6!

в)

г) 10!/5!

2. Вычислить значение бинома:

1)

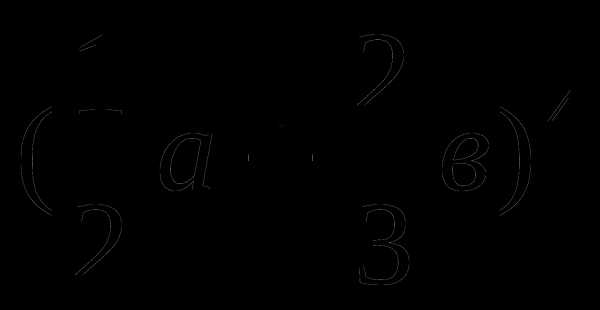
2)

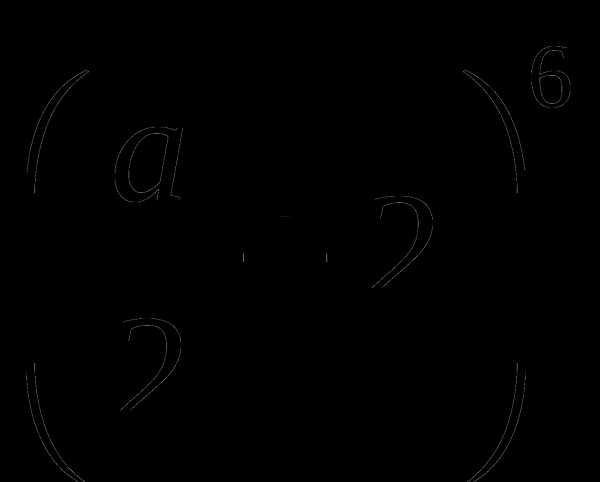
3)

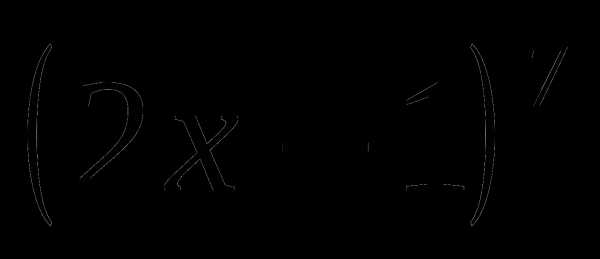
4)

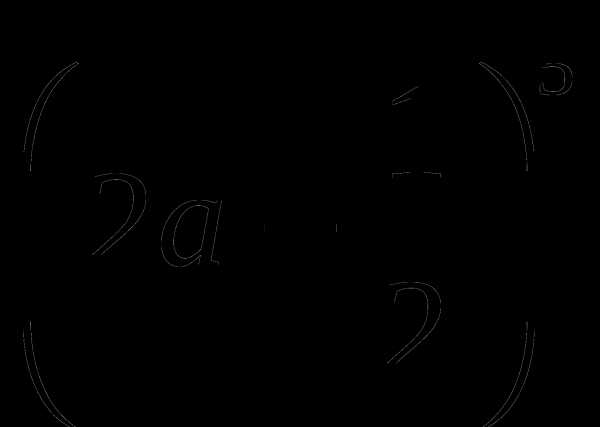
3. Как иначе называется двучлен__

4. Как располагаются знаки биноминальных коэффициентов (а-в)ⁿ __

3 группа

1. Найти значение:

а) 8!

б) 5! – 3!

в)

г) 12!/7!

2. Вычислить значение бинома:

1)

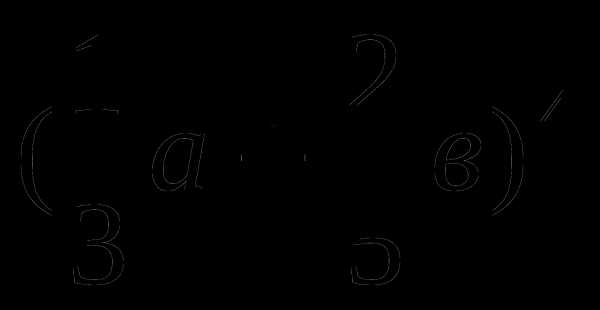
2)

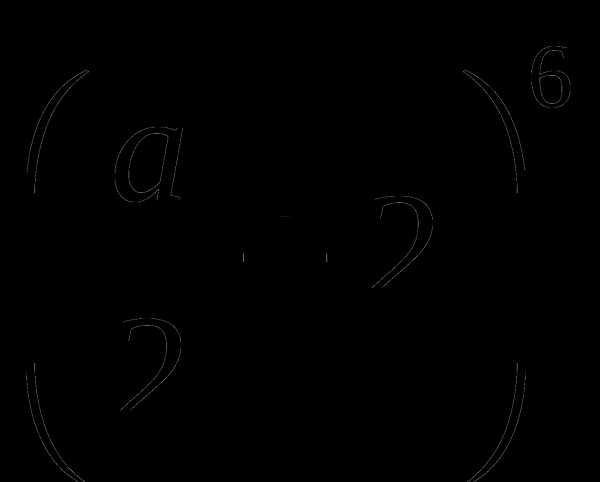
3)

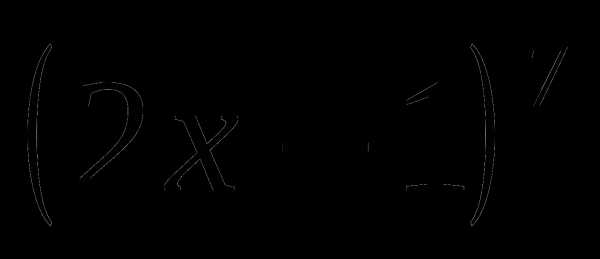
4)

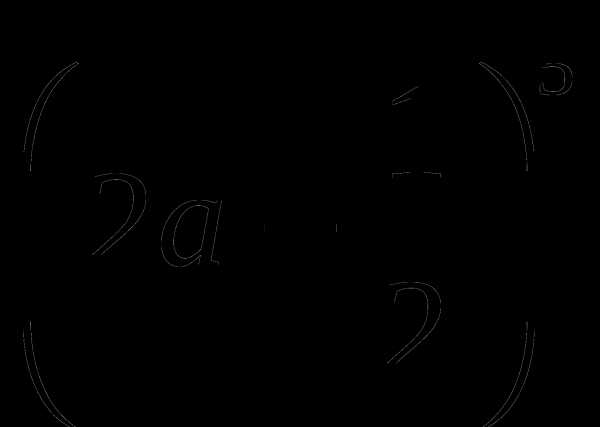
3. Как составляется строка в треугольнике Паскаля относительно предыдущей строки__

4. Сколько экзаменационных комиссий, состоящих из 3 человек, можно образовать из 10 преподавателей__

4 группа

1. Найти значение:

а) 7!

б) 9! – 5!

в)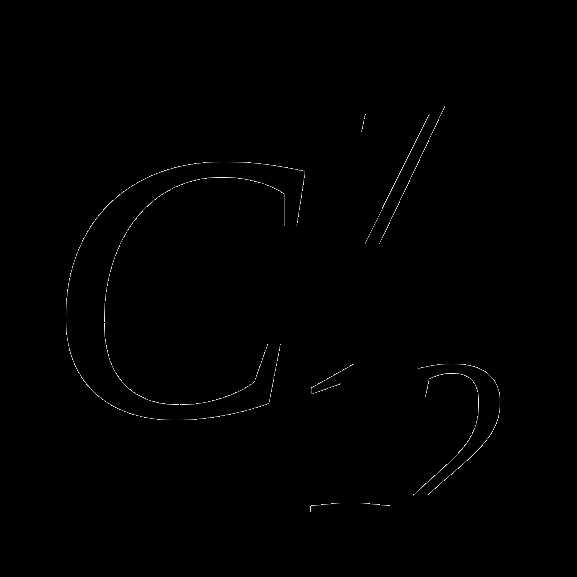

г) 15!/11!

2. Вычислить значение бинома:

1)

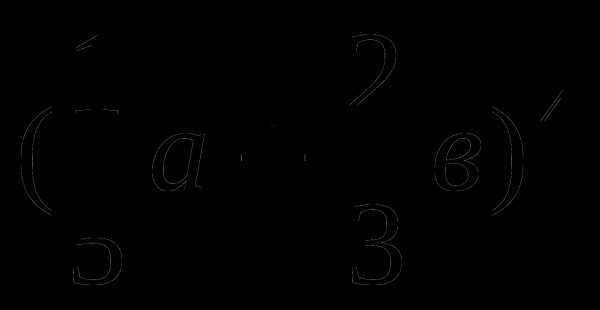
2)

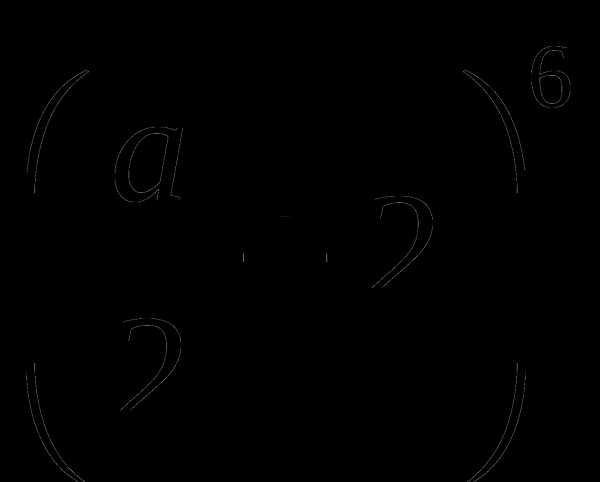
3)

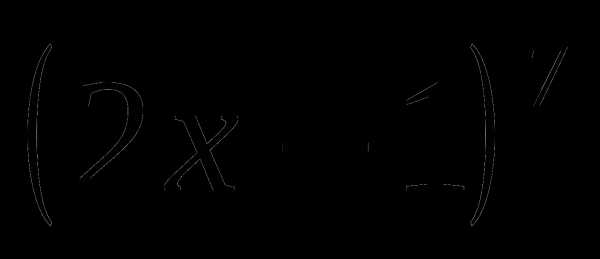
4)

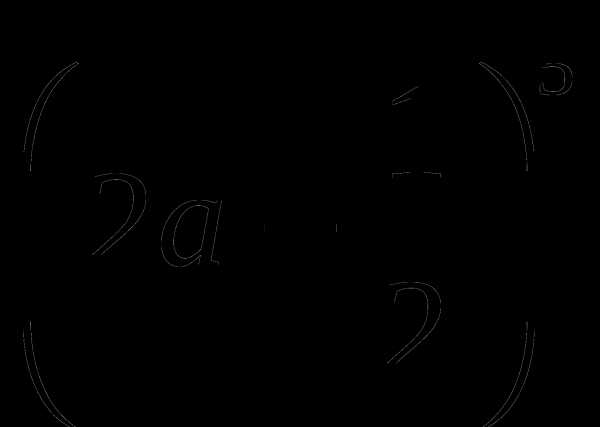
3. Сколько строк можно составить в треугольнике Паскаля

4. Студенту дали на лето задание – прочитать 10 книг. Сколькими способами он может выбрать их них 6 книг__

Критерии оценивания работы:

1. (а — г) – 1 балл, всего 4 балла

2. – по 4 балла, всего 16 баллов

3. — 1 балл

4. — 1 балл Ʃ = 22 балла

Баллы снижаются:

1) плохая дисциплина (шум, некорректность в поведении)

2) небрежность в оформлении работы

За проверку работы соседней группы и анализ ее выполнения 6 баллов.

max Ʃ = 28 баллов

ОТВЕТЫ НА РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ:

1)

2)

3) 4)

Работа в 4-х группах.

Каждая группа имеет задания:

а) теория (тестовые вопросы разные для каждой группы)

б) практика (решение примеров)- задания общие

Затем группы попарно обмениваются своими заданиями и проверяют их, тем самым команды проверяют работы друг друга и дают им свою оценку по определенным критериям.

В первую очередь оценивается взаимодействие и слаженность работы, дисциплина в команде. Качество работы (скорость и точность).

6, 7

Подведение итогов, рефлексия

По итогам работы: группа №1 – «5»

группа №2 – «3»

группа №3 – «5»

группа №4 – «4»

Используем метод незаконченных предложений.

• Сегодня на уроке я узнал(а) …

• Мне оказались непонятны следующие моменты …

• Мне понравилось на уроке …

• Я понял(а), что надо еще раз посмотреть тему …

• Покажите на графике свое эмоциональное состояние на занятии

Группы обмениваются выполненными заданиями и проверяют работы друг друга.

Оценивают работы по критериям:

«5» — 24-28 б.

«4» — 18-23 б.

«3» — 12-17 б.

8

Домашнее задание

• Составить 2 задачи на сочетания и 2 примера на Бином Ньютона с решением. Весьма желательно подготовить образец выполнения в печатном варианте.

• Автор Ю.М. Колягин. Учебник 11 класса. Стр. 138 §31 — теоретический материал знать.

• Вычислите степени бинома:

Заключение

Наш урок мне хочется закончить словами известного мудреца.

Когда-то давно жил выдающийся арабский поэт – математик Омар Хайям:

…Мне мудрость не чужда была земная,

Разгадки тайн ища, не ведал сна я

За 70 перевалило мне,

Что ж я узнал! –

Что ничего не знаю.

Как вы думаете, что он этим хотел сказать?

Спасибо за урок.

Заключение.

Современный специалист, независимо от профессиональной области должен владеть суммой знаний как гуманитарных, так и естественнонаучных дисциплин.

Чтобы быть конкурентоспособным специалистом, прежде всего, необходимо владеть навыками самостоятельной работы и работы в команде.

Целью учебно-методического пособия является ознакомление и получение навыков в разложении бинома, возведения в любую степень двучлена.

В пособии предложен теоретический и практический материал. В теоретической части даны достаточно подробные сведения, необходимые для получения основных сведений об изучаемой теме, в практической части – задания, в которых приведены подробные инструкции по их выполнению.

Методика, которая положена в основу пособия, позволя­ет существенно ускорить процесс закрепления знаний, полученных при изучении дисциплины, освоить новый материал, необходимый для осуществления профессиональной деятельности, а также приобрести опыт работы в команде.

Пособие может быть рекомендовано в помощь преподавателям естественнонаучных дисциплин.

• Цель урока достигнута, учащиеся справились с заданием и затруднений не возникло.

• Структура урока соответствует его типу и цели. Материал дан последовательно, этапы урока взаимосвязаны:

— проверка домашнего задания;

— устные упражнения;

— объяснение нового материала;

— закрепление;

— самостоятельная групповая работа;

— рефлексия и т.д.

• Использование мультимедиа оправдано. План урока в основном выполнен.

• Студенты группы 11Б имеют достаточно высокий уровень школьной подготовки. Они показали самый высокий балл при входном тестировании и по результатам 1 семестра. Ребята активные, любознательные и подвижные. В подавляющем большинстве имеют высокую мотивацию к учебе. Вследствие этого не возникло проблем в усвоении нового материала.

04.03.14г. Н.П. Боброва/_________________

infourok.ru