О взаимосвязи простых и иррациональных чисел / Хабр
После некоторых моих исследований простых чисел, я обнаружил интересную связь с иррациональными числами. Эта связь дает ответ на вопрос, почему простые числа расположены столь «хаотично» и почему они так сложно устроены. Под катом объяснение этой связи и вариант улучшенного алгоритма RSA.
Введение
Рассмотрим множество . Теперь попробуем его упорядочить. То есть найти способ найти следующую пару чисел n и m, зная предыдущую. Очевидно, что: 2 + 2 + 2 = 3 + 3 и 2 + 2 > 3, 2 < 3. Таким образом, пары чисел распределены следующим образом:
(1,0), (0,1), (2,0), (1,1), (3,0), (2,1), (4,0), (3,1), (5,0)…
Заметим, что четко прослеживается порядок и, соответственно, способ получения следующей пары чисел. Здесь нет никаких проблем и задача тривиальна.
Теперь рассмотрим множество . К сожалению или к счастью, но это множество не получится упорядочить в том смысле, как предыдущее:
(1,0), (0,1), (2,0), (1,1), (3,0), (0,2), (2,1), (4,0), (3,1), (0,3)…
Если вы решили, что нашли точный порядок, то достройте эти пары дальше и увидите, что он нарушается. «Хаос» этих пар чисел напрямую связан с иррациональностью числа , доказанная Иоганном Ламбертом в 1761 году. Действительно, чтобы выстроить пары в ряд, мы вначале пытаемся уложить отрезок длиной 2 в отрезок длиной . Полученный остаток мы пытаемся уложить в отрезок длиной 2. Он вместится только один раз. Это означает, что наш остаток «сыграет» свою роль уже на отрезке длиной , где вместится уже не два отрезка длинной 2, а три. Проделывая такую операцию и далее, становится понятно, что как только у нас складывается впечатление, что мы нашли порядок, он сломается через какое-то число шагов. Так как последний, еще не используемый, остаток рано или поздно «сыграет» свою роль и порядок поменяется. Стало быть, вопрос о нахождении «хорошего» алгоритма для этой задачи остается открытым.
«Хаос» этих пар чисел напрямую связан с иррациональностью числа , доказанная Иоганном Ламбертом в 1761 году. Действительно, чтобы выстроить пары в ряд, мы вначале пытаемся уложить отрезок длиной 2 в отрезок длиной . Полученный остаток мы пытаемся уложить в отрезок длиной 2. Он вместится только один раз. Это означает, что наш остаток «сыграет» свою роль уже на отрезке длиной , где вместится уже не два отрезка длинной 2, а три. Проделывая такую операцию и далее, становится понятно, что как только у нас складывается впечатление, что мы нашли порядок, он сломается через какое-то число шагов. Так как последний, еще не используемый, остаток рано или поздно «сыграет» свою роль и порядок поменяется. Стало быть, вопрос о нахождении «хорошего» алгоритма для этой задачи остается открытым.
Немного определений
Пусть , где — изоморфизм такой, что:
И, соответственно, для — обратной к :
.
Теперь определим интересующее нас множество:
И пусть .
И — образ множества для отображения .
И, наконец, — множество простых чисел для операции .
Теперь легко пояснить эти определения на привычном нам примере. Для операции умножения, . А множество — это . Тут стоит остановиться и объяснить, почему это важно.
Сама связь
На самом деле, мы, используя изоморфизм, получили, что сложность всех задач про простые числа эквивалента задачам про суммы логарифмов, которые являются иррациональными. То есть, как мы убедились на примере с множеством из чисел и 2, именно иррациональность вносит хаос. Так же и тут, иррациональность логарифмов распределяет простые числа на числовой прямой практически хаотичным способом. Возникает сложность в упорядочивании пар n и m во множестве, например, . Другими словами, простота какого-нибудь числа напрямую зависит от, например, какого-то знака после запятой в числе . Но мы определили простые числа не только для умножения, а вообще для произвольной бинарной операции.
RSA
Для бинарной операции x + xy + y:
.
Хаотичность данного множества характеризуется иррациональными значениями изоморфизма на натуральных числах. К тому же, изоморфизм, по-видимому, не выражается через элементарные функции. Здесь мы по операции построили другие простые числа, распределение которых очевидным образом не зависит от распределения обычных простых чисел. Это дает нам возможность построения RSA на произвольной бинарной операции такой, чтобы изоморфизм был иррационален. Ведь функция логарифма слишком «хорошая» для криптоаналитиков. А здесь она ведет себя абсолютно непредсказуемым образом. Можно же и наоборот, построить изоморфизм, по которому будет определена коммутативная бинарная операция.
Взяв за основу произвольные простые числа, мы меняем задачу разложения составного числа на множители на задачу разложения практически произвольного иррационального числа на сумму двух других из заданного множества. Что-то мне подсказывает, что это задача должна относиться к классу NP.
Что-то мне подсказывает, что это задача должна относиться к классу NP.
В заключение
Человечество еще не решило много задач про простые числа, как математика подкидывает еще бесконечное число подобных задач. Естественно будет задаться вопросом, что с этим делать? Мое предложение заключается в том, чтобы рассматривать все теоремы из Теории чисел не для сложения и умножения, а для сложения и произвольной коммутативной бинарной операции, замкнутой на натуральных числах. Тогда каждое утверждение про простые числа, было бы лишь следствием определенных свойств операции. Например, бесконечность простых чисел была бы следствием монотонности операции и достаточно быстрым ее ростом. Но это уже тема для отдельной статьи. Спасибо за внимание.
Иррациональное число в дискретной математике
следующий → ← предыдущая Иррациональные числа можно описать как действительные числа. Мы не можем представить эти типы действительных чисел как отношение целых чисел. Определение иррациональных чиселМножество действительных чисел содержится в иррациональном числе , и эти типы чисел никогда не будут выражены как дробь , такая как p/q. Здесь p используется для отображения числителя, q используется для обозначения знаменателя, и оба являются целыми числами. Здесь q не должно быть равно 0, т. е. q ≠ 0. Примерами иррациональных чисел являются √ 7 и √ 5 и т. д. Если есть десятичное разложение иррациональных чисел, то оно не будет ни повторяющимся, ни конечным. Принимая во внимание, что если какое-либо число выражено в виде x/y, а y ≠ 0, а x и y оба являются целыми числами, то эти числа будут называться рациональные числа . Представление иррационального числа Можно описать как действительные числа, что нельзя выразить в виде простой дроби . Если попробовать вычисления на основе иррациональных чисел, то будет немного сложновато. Значение иррационального иррациональное означает отсутствие отношения . Это означает, что иррациональное число не может иметь отношения. Мы можем использовать корни только для обозначения иррационального числа и не можем выразить его никак иначе. Символ иррационального числаСлово «P» используется для обозначения символа иррационального числа . Иррациональное число и рациональное число содержатся в действительных числах. Так как мы определили иррациональное число отрицательно. Таким образом, иррациональное число можно определить как набор действительных чисел (R), который не может быть рациональным числом (Q). Из-за ассоциации рационального числа и действительного числа, поскольку ассоциация содержит буквенную последовательность P, Q, R, поэтому мы использовали символ P для обозначения иррационального числа. Но чаще всего мы представляем иррациональное число с помощью разницы между набором действительных чисел (R) и набором рациональных чисел (Q). Таким образом, мы можем использовать следующий способ записи иррациональных чисел следующим образом: R — Q или R\Q. Следовательно, символ P показывает иррациональное число. Распространенные примеры иррациональных чиселЕсть несколько специфических типов иррациональных чисел, которые мы в основном использовали при нахождении иррациональных чисел, которые описываются следующим образом: Pi(π):π известно как иррациональное число. Значение числа пи равно 3,14159265. Значение decimal не может быть остановлено в любое время. Так как значение π и дробь 22/7 подобны друг другу. Таким образом, мы также можем принять значение π равным 3,14 или 22/7. Примечание. Число 22/7 известно как рациональное число.√2: Квадратный корень из 2 или √2 известен как иррациональное число. Пусть имеется прямоугольный равнобедренный треугольник, у которого две стороны АВ и ВС равны друг другу, а длина этих сторон равна 1 единице. С помощью теоремы Пифагора мы знаем, что гипотенуза AC будет равна √2 = 1⋅414213…. Число Эйлера: Число Эйлера обозначается буквой e, что равно числу 2,718281… Золотое сечение: Золотое сечение обозначается φ, что равно числу 1,61803398874989…. Свойства иррациональных чиселЕсть много свойств, связанных с иррациональными числами, которые будут полезны, чтобы найти иррациональные числа из заданного множества действительных чисел. Некоторые свойства иррациональных чисел описываются следующим образом:
Набор иррациональных чиселМы можем получить множество иррациональных чисел, записав некоторые иррациональные числа в скобках. Есть некоторые свойства, которые помогут определить множество иррациональных чисел, которые описываются следующим образом:
Список иррациональных чисел описан в следующей таблице:
Рациональные числа VS Иррациональные числа Рациональное число может быть определено теми типами чисел, которые могут быть указаны как дробь p/q или отношение.
Разница между иррациональными числами и рациональными числами описывается следующим образом:
Интересные факты об иррациональных числахИррациональное число используется для того, чтобы содержать в себе много классных и интересных фактов, которые описываются следующим образом: 1. Случайное изобретение √2: √2, или квадратный корень из 2, известен как иррациональное число. Первое придуманное иррациональное число на момент обработки расчета длины равнобедренного треугольника – это квадратный корень из 2 или √2. Для его расчета используется знаменитая формула Пифагора, которая описывается следующим образом: а 2 = б 2 + в 2 АС 2 = АВ 2 + ВС 2 ? AC 2 = 1 2 + 1 2 ? АС = √2 Поскольку мы знаем, что значение √2 равно 1,41421…. Это потому, что √2 лежит между 1 и 2 числами. Таким образом, он показал, что мы не можем выразить длину AC в виде целых чисел или дробей. 2. Значение π Когда мы вычисляем значение π , мы нашли примерно 22 триллиона цифр , у которых нет конца. Чтобы вычислить значение π , компьютеру с 24 жесткими дисками обычно требуется около 15 дней. 3. Изобретения числа Эйлера e: Швейцарский математик Леонард Эйлер ввел понятие числа Эйлера в 1731 году. Мы также можем называть «е» числом Непера. Мы можем использовать это число «е» в области логарифмирования и тригонометрии. Сложение и умножение двух иррациональных чиселЗдесь мы узнаем о сложении и умножении двух иррациональных чисел. Сначала мы обсудим умножение двух иррациональных чисел, а затем изучим сумму двух иррациональных чисел. Произведение двух иррациональных чисел Утверждение: Если мы выполним операцию умножения над двумя иррациональными числами, то в результате будут получены либо рациональные, либо иррациональные числа. Например: Предположим, что существует иррациональное число √2, и если мы умножим √2 на √2, то в результате получим 2. Где 2 — рациональное число. Итак, √2 * √2 = 2 Предположим, что имеется иррациональное число Π, и если мы умножим Π на Π, то получим Π 2 в результате, что является иррациональным числом. Итак, П * П = П 2 Итак, мы пришли к выводу, что при умножении двух иррациональных чисел в результате мы можем получить либо иррациональное число, либо рациональное число. Сложение двух иррациональных чисел Утверждение: Если мы выполним операцию сложения над двумя иррациональными числами, то в результате получится рациональное или иррациональное число. Точно так же, как умножение двух указанных выше иррациональных чисел, сложение двух иррациональных чисел также приводит к тому же результату в виде рациональных чисел или иррациональных чисел. Например: Предположим, что есть два иррациональных числа, 3√2+ 4√3, и если мы сложим эти числа, то их сложение будет иррациональным числом. Но предположим, что есть два иррациональных числа, +4√2 и -4√2, и если мы сложим эти числа, то в результате получим 3, что является рациональным числом. Итак, если мы умножаем или складываем два иррациональных числа, нам нужно соблюдать осторожность, потому что результатом этих операций может быть рациональное число или иррациональное число. Теорема и доказательство иррационального числаМы можем доказать приведенные выше утверждения, касающиеся сложения и умножения, с помощью следующей теоремы: Теорема: Предположим, что существует простое число p и 2 делится на p, тогда можно сделать вывод, что p также делит a. Доказательство: С помощью основной теоремы арифметики мы можем выразить положительные целые числа с помощью произведений их простых чисел, которые описываются следующим образом: а = р1 * р2 * р3 * р4 …. Здесь p1, p2, p3, p4 …., pn используются для обозначения всех простых множителей a. Теперь возведем в квадрат обе части вышеприведенного уравнения (1) следующим образом: a 2 = (p1 * p2 * p3 * p4 …. * pn) (p1 * p2 * p3 * p4 …. * pn) ? a 2 = (p1) 2 * (p2) 2 * (p3) 2 * (p4) 2 …. * (номер) 2 На основании Фундаментальной теоремы арифметики мы знаем, что существует уникальная простая факторизация натуральных чисел, за исключением порядка ее множителей. p1, p2, p3, p4 …., pn используются для хранения только простого множителя числа 2 . Если существует простое число p и множитель a 2 , в этом случае p будет одним из p1, p2, p3, p4…., pn. Таким образом, p также является фактором a. Отсюда следует, что если p делит a 2 , то p также будет делить a. С помощью этой теоремы мы также можем доказать, что √2 иррационально. Нахождение иррационального числа:Здесь мы должны определить иррациональное число между 2 и 3. Как мы знаем, 2 — это квадратный корень из 4, т. е. √ 4 = 2, а 3 — квадратный корень из 9, т. е. √ 9 = 3. Поэтому √5, √6, √7 и √8 называются числами иррациональных чисел. Эти числа являются иррациональными числами, потому что они не могут быть дополнительно упрощены, а также не содержат полных квадратов. Точно так же, если мы хотим определить иррациональное число между любыми другими двумя числами с полным квадратом, мы также можем это сделать. Другой ящик: Предположим, есть случай √2. Теперь нам нужно определить, является ли данное число √2 иррациональным числом или нет. Теперь будем считать, что √2 — рациональное число. Тогда мы можем записать это число следующим образом с помощью определения рациональных чисел следующим образом: √2 = p/q ….. (1) Здесь p и q используются для обозначения взаимно простых целых чисел, а q не должно быть равно 0, т. Теперь возведем в квадрат обе части уравнения (1) следующим образом: 2 = р 2 /q 2 ? р 2 = 2q 2 ….. (2) С помощью приведенной выше теоремы мы знаем, что если 2 является простым множителем p 2 , в этом случае 2 также будет простым множителем p. На основе начального предположения мы знаем, что p и q взаимно просты, но мы получаем, что вывод выше противоречит этому предположению, поскольку p и q не содержат 1 в качестве общего простого множителя, но оно содержит 2. Только из-за неверного предположения, что √2 рационально, возникло это противоречие общего простого множителя как 2. Итак, корень 2 (√2) иррационален. Таким же образом можно доказать и утверждение, которое мы обсуждали в начале, что если существует простое число p, то √p также будет иррациональным числом. Примеры иррациональных чиселПример 1: В этом примере у нас есть 5 чисел, и мы должны определить, какие числа являются иррациональными, а какие рациональными.
Решение: -2, 6.5, оба числа содержат завершающие десятичные знаки. Вот почему эти числа являются рациональными числами. -.45678…, √2, √3 содержат неповторяющееся или не завершающееся десятичное расширение. Вот почему эти числа являются иррациональными числами. Пример 2: В этом примере у нас есть 4 числа, и мы должны определить, какие числа являются иррациональными, а какие рациональными.
Решение: 2, 5/11, -5,12, 0,31, все числа содержат завершающее десятичное расширение. Важные моменты
Следующая темаЛинейный граф в дискретной математике ← предыдущая следующий → |
Что такое иррациональные числа? (с картинками)
`;
Наука
Факт проверен
Иррациональные числа — это числа, которые нельзя выразить в виде дроби, а также невозможно записать в виде полного десятичного числа. Люди работали с иррациональными числами со времен греков и римлян, а некоторые числа были определены математиками на протяжении веков. Существует ряд интересных приложений и способов использования иррациональных чисел, начиная от разочаровывания студентов-математиков и заканчивая выполнением сложных уравнений.
Все так называемые рациональные числа могут быть записаны в десятичной форме или в виде дроби. ¾, например, является рациональным числом, которое также может быть выражено как 0,75. Когда число иррациональное, его нельзя записать в виде дроби с целыми числами, и число будет невозможно записать в десятичной форме. Пи — известный пример иррационального числа; хотя его часто упрощают до 3,14 для грубых вычислений, на самом деле пи нельзя полностью записать в десятичной форме, потому что десятичная дробь бесконечна.
¾, например, является рациональным числом, которое также может быть выражено как 0,75. Когда число иррациональное, его нельзя записать в виде дроби с целыми числами, и число будет невозможно записать в десятичной форме. Пи — известный пример иррационального числа; хотя его часто упрощают до 3,14 для грубых вычислений, на самом деле пи нельзя полностью записать в десятичной форме, потому что десятичная дробь бесконечна.
Некоторые другие примеры включают квадратный корень из двух, число Эйлера и золотое сечение. Для простоты некоторые из этих чисел записываются в виде символов, как в случае «е» для числа Эйлера, а иногда они будут представлены в частично десятичной форме. Когда иррациональное число представлено в десятичной форме, многоточие обычно используется после последнего числа в десятичной дроби, чтобы указать, что оно продолжается, как в 3.14… для пи.
Когда иррациональное число представлено в десятичной форме, многоточие обычно используется после последнего числа в десятичной дроби, чтобы указать, что оно продолжается, как в 3.14… для пи.
Люди часто начинают работать с этими числами в юном возрасте, хотя они могут быть ознакомлены с понятиями рациональных и иррациональных чисел только позже. Пи — одно из первых иррациональных чисел, которое изучают многие люди, потому что оно используется в уравнениях для нахождения площади и длины окружности, и эти уравнения часто служат прекрасным введением в более продвинутую математику для маленьких детей. Люди также знакомятся с этой концепцией во многих науках, когда они начинают узнавать об уравнениях, которые обычно используются.
Люди также знакомятся с этой концепцией во многих науках, когда они начинают узнавать об уравнениях, которые обычно используются.
С этими необычными числами может быть трудно работать на обычном калькуляторе из-за его ограничений. Обычно необходимо иметь продвинутый научный или графический калькулятор, который был запрограммирован с этими числами и их значениями.
Некоторые математики делают изучение этих чисел делом своей жизни.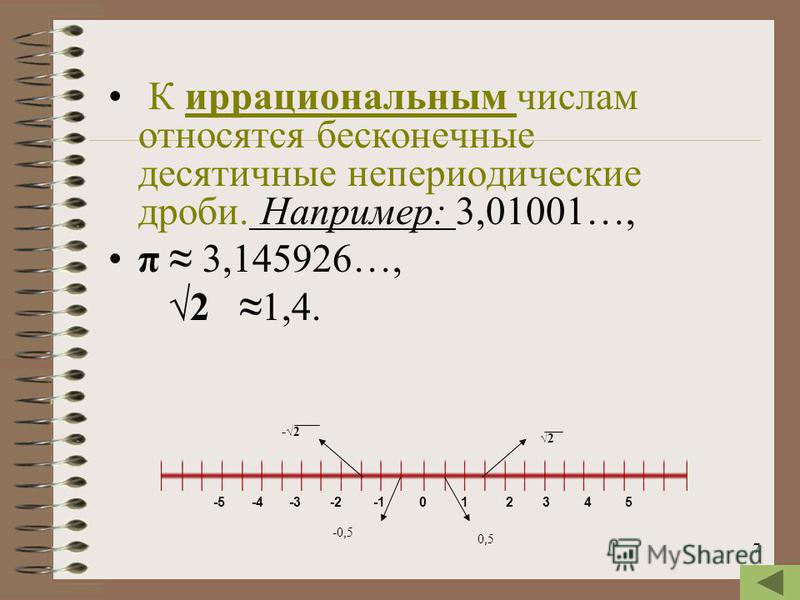 Эти числа часто имеют ряд интригующих свойств, которые интересно исследовать людям, любящим математику, и математик также может найти новое применение для иррационального числа.
Эти числа часто имеют ряд интригующих свойств, которые интересно исследовать людям, любящим математику, и математик также может найти новое применение для иррационального числа.
С тех пор как несколько лет назад Мэри начала работать над сайтом, она приняла захватывающая задача быть исследователем и писателем AllTheScience. Мэри имеет степень по гуманитарным наукам в Годдард-колледже и проводит свободное время за чтением, приготовлением пищи и прогулками на свежем воздухе.
Мэри МакМахон С тех пор как несколько лет назад Мэри начала работать над сайтом, она приняла
захватывающая задача быть исследователем и писателем AllTheScience.

 Другими словами, иррациональные числа также могут быть описаны как те действительные числа, которые не являются рациональными. Например: √ 5 — иррациональное число.
Другими словами, иррациональные числа также могут быть описаны как те действительные числа, которые не являются рациональными. Например: √ 5 — иррациональное число.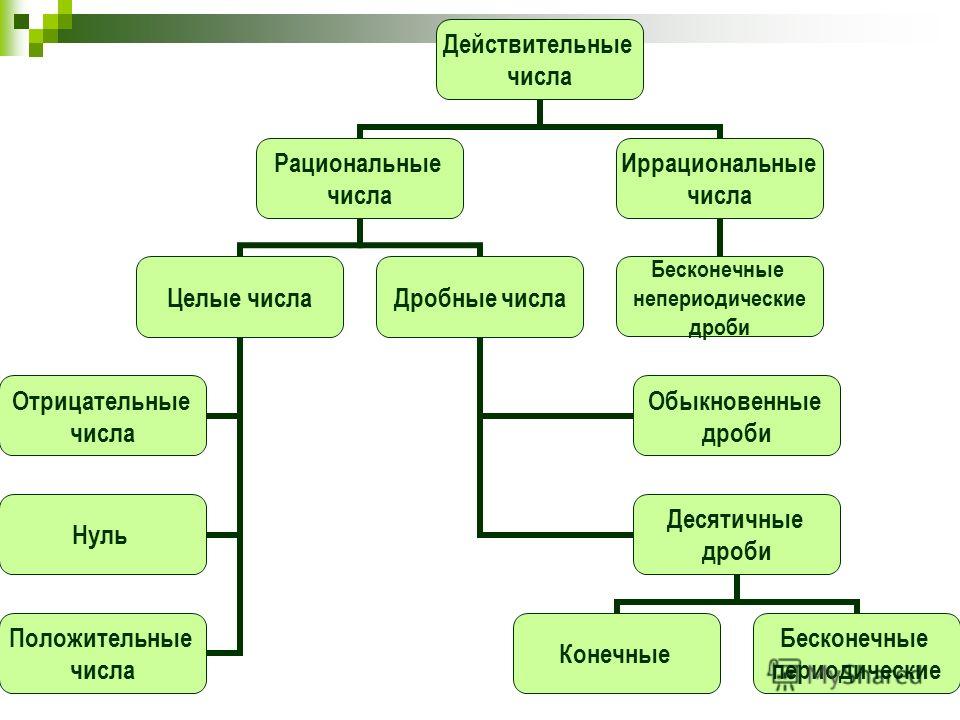 С помощью символа «\» можно указать иррациональных чисел , т. е. R\Q . Здесь \ называется символом обратной косой черты, который используется для обозначения «установить минус». Мы также можем указать его как R-Q , что в основном описывает разницу между набором действительных чисел и набором рациональных чисел.
С помощью символа «\» можно указать иррациональных чисел , т. е. R\Q . Здесь \ называется символом обратной косой черты, который используется для обозначения «установить минус». Мы также можем указать его как R-Q , что в основном описывает разницу между набором действительных чисел и набором рациональных чисел.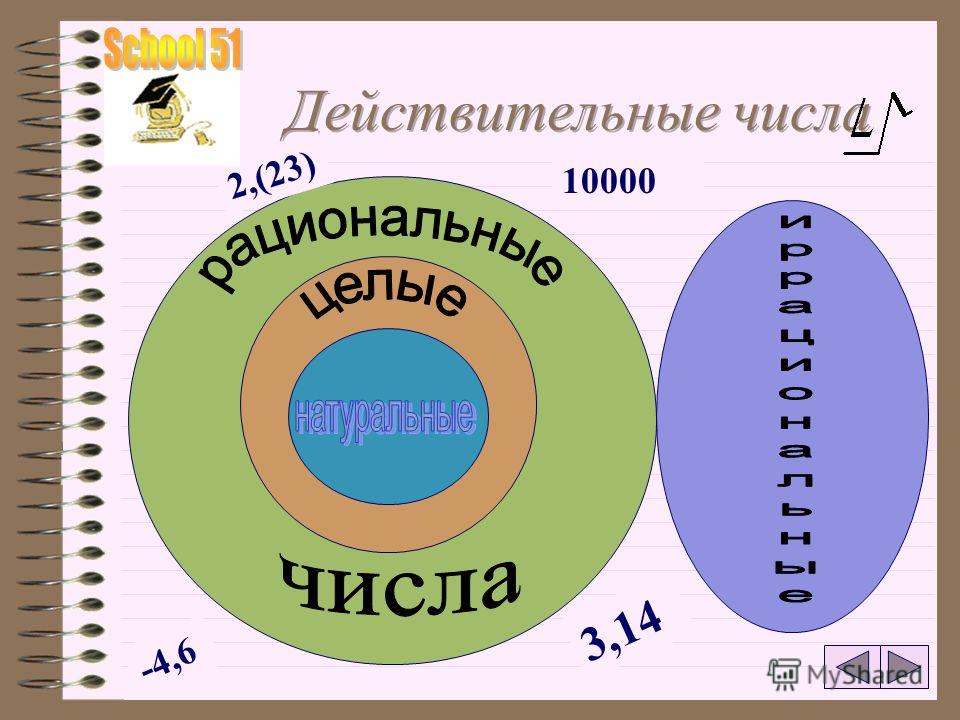 Мы также не можем выразить эти типы чисел как отношение двух целых чисел.
Мы также не можем выразить эти типы чисел как отношение двух целых чисел.

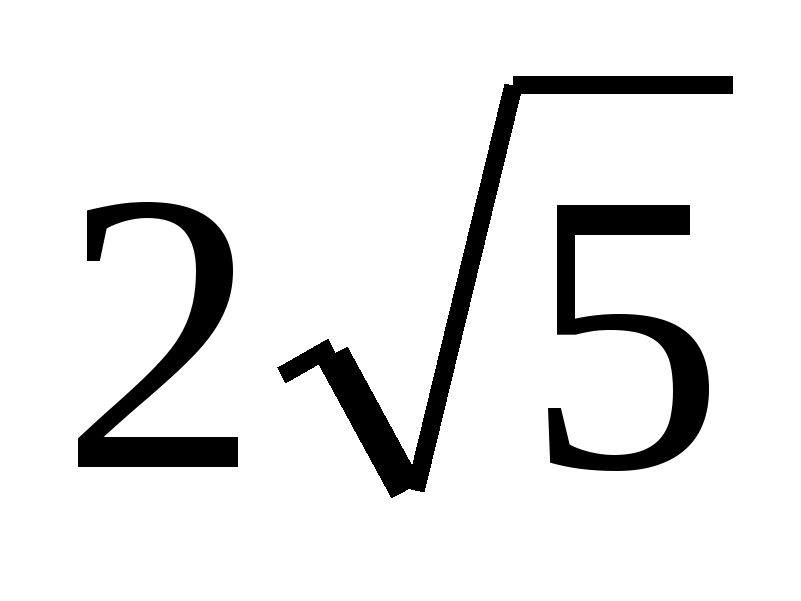
 Например: √2, √3, √5, √8.
Например: √2, √3, √5, √8. Рациональное число может содержать целые числа или целые числа. В рациональном числе p — числитель, q — знаменатель, где p не должно быть равно нулю.
Рациональное число может содержать целые числа или целые числа. В рациональном числе p — числитель, q — знаменатель, где p не должно быть равно нулю. д.
д.


 * номер ……(1)
* номер ……(1)
 е. q ≠ 0. (Данное число будет взаимно простым числом, если общий делитель данных чисел равен 1 ).
е. q ≠ 0. (Данное число будет взаимно простым числом, если общий делитель данных чисел равен 1 ).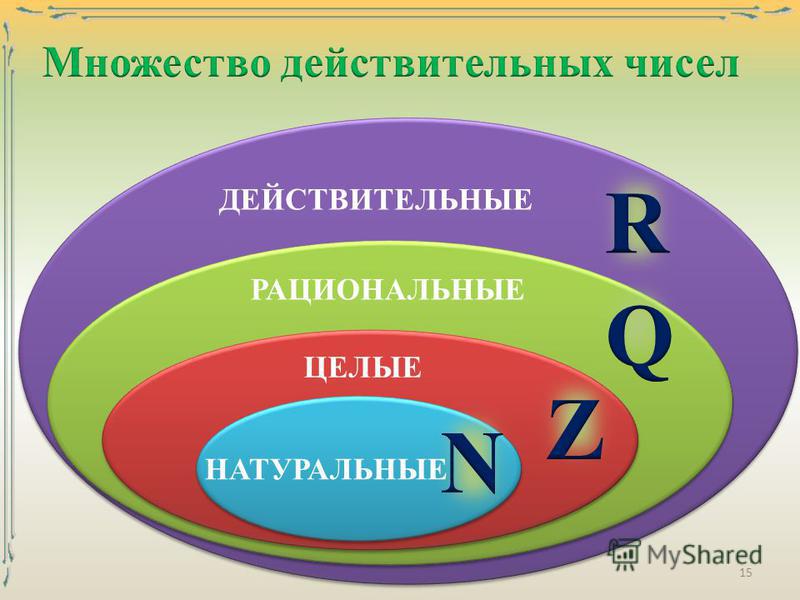 Точно так же мы можем доказать, что √p иррационально для любого простого числа p.
Точно так же мы можем доказать, что √p иррационально для любого простого числа p. Вот почему эти числа являются рациональными числами.
Вот почему эти числа являются рациональными числами.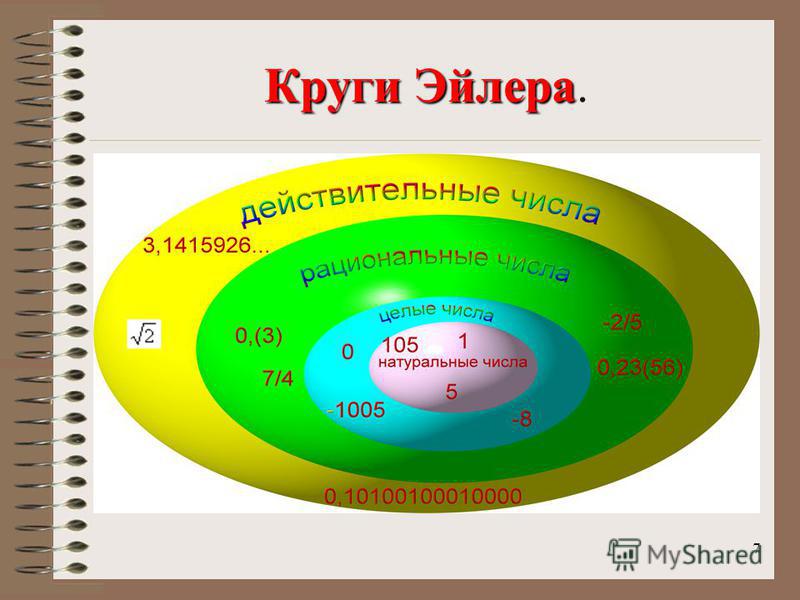 е. 2,9.0089
е. 2,9.0089