Равенство равнобедренных треугольников: Признак равенства равнобедренных треугольников — ответ на Uchi.ru

Равенство равнобедренных треугольников. Задача 134 § 2 II глава Геометрия 7-9 класс Атанасян Л.С. – Рамблер/класс

Равенство равнобедренных треугольников. Задача 134 § 2 II глава Геометрия 7-9 класс Атанасян Л.С. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Можете дать пример доказательства?
Докажите, что равнобедренные треугольники равны, если основание и прилежащий к нему угол одного треугольника соответственно равны основанию и прилежащему к нему углу другого треугольника.

ответы

Дано: АВ=ВС
А1В1=В1С1
АC=А1С1 
Доказать: АВC=А1B1C1
Доказательство.
Из  — равнобедренные, следует что 
  

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.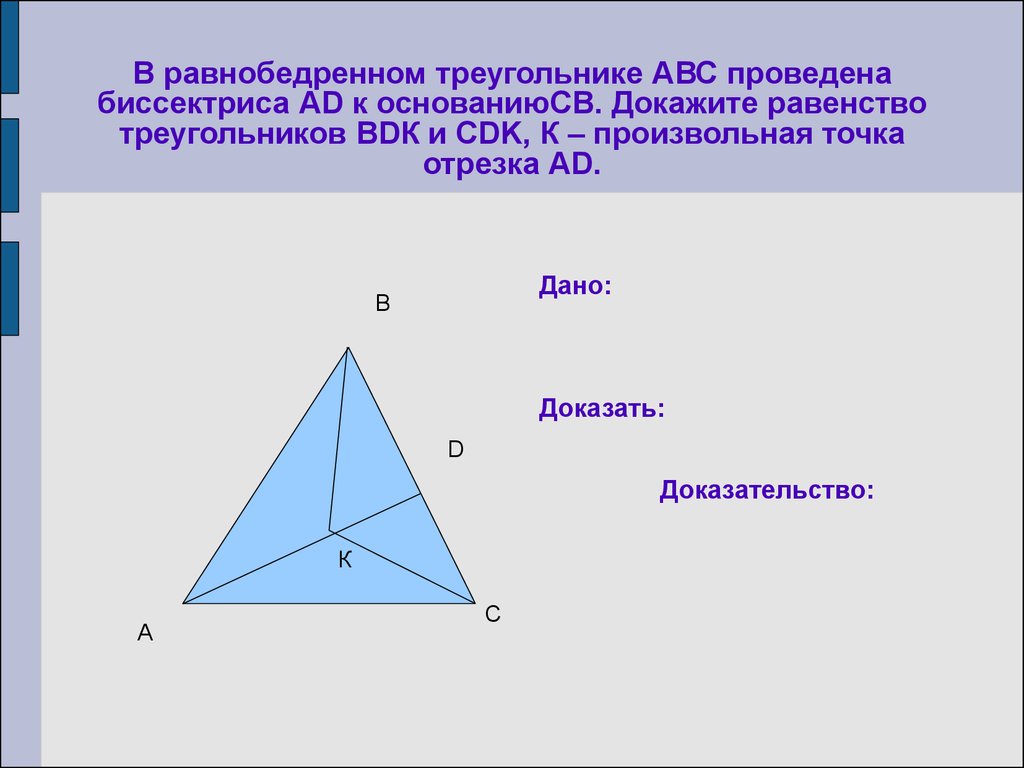
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Это правда, что будут сокращать иностранные языки в школах?

 Хочется узнать, когда собираются сократить иностранные языки в школе? Какой в итоге оставят? (Подробнее…)

ШколаНовостиИностранные языки

Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 9 ОГЭ Русский язык 9 класс Однородные обособленные приложения

    Среди предложений 27-32: 
 
   (27) Нет-нет да и набирала Анюта, когда была дома одна и было грустно, Митрошин номер, и (Подробнее…)

ГДЗРусский языкОГЭ9 классВасильевых И.П.

7 класс.

Геометрия. Треугольники, признаки равенства треугольников. — Равнобедренный треугольник и его свойства.

Комментарии преподавателя

Опре­де­ле­ние: Рав­но­бед­рен­ным на­зы­ва­ет­ся тре­уголь­ник, у ко­то­ро­го равны две сто­ро­ны.

Рис. 1. Рав­но­бед­рен­ный тре­уголь­ник

АВ = АС – бо­ко­вые сто­ро­ны. ВС – ос­но­ва­ние.

Пло­щадь рав­но­бед­рен­но­го тре­уголь­ни­ка равна по­ло­вине про­из­ве­де­ния его ос­но­ва­ния на вы­со­ту.

Опре­де­ле­ние: Рав­но­сто­рон­ним на­зы­ва­ет­ся тре­уголь­ник, у ко­то­ро­го все три сто­ро­ны равны.

Рис. 2. Рав­но­сто­рон­ний тре­уголь­ник

АВ = ВС = СА.

Пло­щадь рав­но­сто­рон­не­го тре­уголь­ни­ка равна 

Тео­ре­ма 1: В рав­но­бед­рен­ном тре­уголь­ни­ке углы при ос­но­ва­нии равны.

Дано: АВ = АС.

До­ка­зать: ∠В =∠С.

Рис. 3. Чер­теж к тео­ре­ме

До­ка­за­тель­ство: тре­уголь­ник АВС = тре­уголь­ни­ку АСВ по пер­во­му при­зна­ку (по двум рав­ным сто­ро­нам и углу между ними). Из ра­вен­ства тре­уголь­ни­ков сле­ду­ет ра­вен­ство всех со­от­вет­ству­ю­щих эле­мен­тов. Зна­чит, ∠В = ∠С, что и тре­бо­ва­лось до­ка­зать.

Тео­ре­ма 2: В рав­но­бед­рен­ном тре­уголь­ни­ке бис­сек­три­са, про­ве­ден­ная к ос­но­ва­нию, яв­ля­ет­ся ме­ди­а­ной и вы­со­той.

Дано: АВ = АС, ∠1 = ∠2.

До­ка­зать: ВD = DC, AD пер­пен­ди­ку­ляр­но BC.

 

Рис. 4. Чер­теж к тео­ре­ме 2

До­ка­за­тель­ство: тре­уголь­ник ADB = тре­уголь­ни­ку ADC по пер­во­му при­зна­ку (AD – общая, АВ = АС по усло­вию, ∠BAD = ∠DAC). Из ра­вен­ства тре­уголь­ни­ков сле­ду­ет ра­вен­ство всех со­от­вет­ству­ю­щих эле­мен­тов. BD = DC, так как они лежат про­тив рав­ных углов. Зна­чит, AD яв­ля­ет­ся ме­ди­а­ной. Также ∠3 = ∠4, по­сколь­ку они лежат про­тив рав­ных сто­рон. Но, к тому же, они в сумме рав­ня­ют­ся . Сле­до­ва­тель­но, ∠3 = ∠4 = . Зна­чит, AD яв­ля­ет­ся вы­со­той тре­уголь­ни­ка, что и тре­бо­ва­лось до­ка­зать.

В един­ствен­ном слу­чае a = b = . В этом слу­чае пря­мые АС и ВD на­зы­ва­ют­ся пер­пен­ди­ку­ляр­ны­ми.

По­сколь­ку бис­сек­три­сой, вы­со­той и ме­ди­а­ной яв­ля­ет­ся один и тот же от­ре­зок, то спра­вед­ли­вы и сле­ду­ю­щие утвер­жде­ния:

— Вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка, про­ве­ден­ная к ос­но­ва­нию, яв­ля­ет­ся ме­ди­а­ной и бис­сек­три­сой.

— Ме­ди­а­на рав­но­бед­рен­но­го тре­уголь­ни­ка, про­ве­ден­ная к ос­но­ва­нию, яв­ля­ет­ся вы­со­той и бис­сек­три­сой.

При­мер 1: В рав­но­бед­рен­ном тре­уголь­ни­ке ос­но­ва­ние в два раза мень­ше бо­ко­вой сто­ро­ны, а пе­ри­метр равен 50 см. Най­ди­те сто­ро­ны тре­уголь­ни­ка.

Дано: АВ = АС, ВС = AC. Р = 50 см.

Найти: ВС, АС, АВ.

Ре­ше­ние:

Рис. 5. Чер­теж к при­ме­ру 1

Обо­зна­чим ос­но­ва­ние ВС как а, тогда АВ = АС = 2а.

2а + 2а + а = 50.

5а = 50, а = 10.

Ответ: ВС = 10 см, АС = АВ = 20 см.

При­мер 2: До­ка­жи­те, что в рав­но­сто­рон­нем тре­уголь­ни­ке все углы равны.

Дано: АВ = ВС = СА.

До­ка­зать: ∠А = ∠В = ∠С.

До­ка­за­тель­ство:

Рис. 6. Чер­теж к при­ме­ру       

∠В = ∠С, так как АВ=АС, а ∠А = ∠В, так как АС = ВС.                           

Сле­до­ва­тель­но, ∠А = ∠В = ∠С, что и тре­бо­ва­лось до­ка­зать.

Ответ: До­ка­за­но.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/7-klass/treugolnikib/ravnobedrennyy-treugolnik-i-ego-svoystva

http://www.youtube.com/watch?v=i45BFcjW_hs

http://school-assistant.ru/?predmet=geometr&theme=ravnobedrennij_treugolnik

http://nsportal. ru/sites/default/files/2014/11/24/7.rar

 

Isocles Triangle Теорема — Доказательство, Converse и примеры

Написано

Malcolm McKinsey

11 января 2023

. что означает слово «равнобедренный»). Ура им, но что мы знаем об их углах основания? Откуда мы знаем, что тоже равны? Мы беремся за инструменты нашего геометра и достаем теорему о равнобедренном треугольнике. Его не нужно подключать или перезаряжать батареи — он прямо у вас в голове!

Здесь мы демонстрируем величественный равнобедренный треугольник  △DUK . Вы можете нарисовать его сами, взяв за образец △DUK .

Равнобедренный треугольник со свойствами

Решётка показывает стороны  ∠DU ≅ ∠DK , что указывает на то, что у вас равнобедренный треугольник. Если  эти две стороны, называемые катетами , равны, тогда  это равнобедренный треугольник. Что еще у тебя есть?

Свойства равнобедренного треугольника

Let’s use  △DUK  to explore the parts:

• Like any triangle,  △DUK  has three interior angles:  ∠D ,  ∠U , and  ∠K

• All три внутренних угла острые.

• Как и любой треугольник, △ Duk имеет три стороны: DU , UK и DK

• Ϫdu ∠dk , так что мы обращаемся на ноги.

• Третья сторона называется основанием (даже если треугольник не лежит на этой стороне).

• Два угла, образованные между основанием и ножками, ∠DUK и ∠DKU или ∠D и ∠K для краткости, называются углами с основанием 90,21.

Теорема о равнобедренном треугольнике

Зная части треугольника, вот задача: как мы докажем , что углы при основании равны? Это сердце Теорема о равнобедренном треугольнике , которая строится как условное (если, то)  утверждение:

Чтобы математически доказать это, нам нужно ввести срединную линию, линию, построенную от внутреннего угла до середины противоположной стороны . Находим Точку C на базе UK и строим отрезок DC :

Равнобедренный Треугольник Теорема Пример

Вот! Это просто УТКА ! Посмотрите на два треугольника, образованных медианой. Нам дано:

Мы только что показали, что три стороны △DUC конгруэнтны △DCK , что означает, что у вас есть Постулат Стороны Стороны Стороны , который дает конгруэнтность. Таким образом, если два треугольника конгруэнтны, то соответствующие части конгруэнтных треугольников конгруэнтны (CPCTC), что означает: условное утверждение делается путем замены гипотезы (если…)  с выводом (тогда…) . Возможно, вам придется повозиться с ним, чтобы убедиться, что он имеет смысл. Итак, здесь снова теорема о равнобедренном треугольнике:

Если   две стороны треугольника конгруэнтны, , то углов, противоположных этим сторонам, конгруэнтны.

Чтобы сделать обратное, мы могли бы  в точности поменять местами части, получив небольшую мешанину:

Если углов, противоположных этим сторонам, равны, , затем две стороны треугольника равны.

Это неудобно, так что приведите в порядок формулировку:

Обратное из теоремы о равнобедренном треугольнике

Теперь это понятно, но так ли это? Не каждое обратное утверждение условного утверждения истинно.

Если  исходное условное утверждение ложно, , то  обратное также будет ложно. Если  посылка верна, тогда  обратное может быть истинным или ложным:

• Если  я увижу медведя, тогда  я лягу и буду неподвижен.

• Если  лежать и оставаться неподвижным, то  я увижу медведя.

Чтобы это обратное утверждение было правдой, сон в вашей постели стал бы странным опытом.

Или вот этот:

• Если  у меня есть мед, , то  я привлечу медведей.

• Если  медведей притягиваю,  , затем  мой мед.

Если только медведи не принесут вам приманки, обратное вряд ли когда-нибудь произойдет. А медведи известны своей эгоистичностью.

Доказательство обратного утверждения

Чтобы доказать обратное, построим еще один равнобедренный треугольник,  △BER .

Учитывая, что ∠BER ≅ ∠BRE , мы должны доказать, что BE ≅ BR .

Добавьте биссектрису угла от ∠EBR до основания ER . Там, где биссектриса угла пересекает основание ER , обозначьте его Point A .

Теперь у нас есть два маленьких прямоугольных треугольника вместо одного большого равнобедренного треугольника:

△BEA и △BAR . Поскольку отрезок BA  является биссектрисой угла, получается ∠EBA ≅ ∠RBA .

Поскольку отрезок BA используется в обоих меньших прямоугольных треугольниках, он конгруэнтен сам себе. Что у нас есть?

Доказательство теоремы о равнобедренном треугольнике

Посмотрим… это угол, другой угол и сторона. Это будет Теорема об угле-угле-стороне (AAS).

Теорема «Угол-Угол-Сторона» утверждает, что Если  два угла и не включенная в них сторона одного треугольника конгруэнтны соответствующим частям другого треугольника, , то  треугольники конгруэнтны. Поскольку сами треугольники оказались конгруэнтными, их соответствующие части конгруэнтны (CPCTC), что делает BE ≅ BR . Обратная теорема о равнобедренном треугольнике верна!

Итоги урока

Выполняя эти упражнения, вы теперь в состоянии распознавать и рисовать равнобедренный треугольник, математически доказывать конгруэнтность равнобедренных треугольников с помощью  теоремы о равнобедренных треугольниках , а также математически доказывать обратную теорему о равнобедренных треугольниках.

Теперь вы также должны увидеть связь между теоремой о равнобедренном треугольнике, постулатом о стороне, стороне и теореме об угле, стороне, стороне.

Теорема о равнобедренном треугольнике. Обратное, доказательство, примеры

LearnPracticeDownload

Треугольник, две стороны которого имеют одинаковую меру, а третья сторона имеет другую меру, называется равнобедренным треугольником. Теорема о равнобедренном треугольнике в математике гласит, что в равнобедренном треугольнике углы, противоположные равным сторонам, также равны по измерению. В этой статье мы узнаем о теореме о равнобедренном треугольнике и ее обратной стороне.

1.	Что такое теорема о равнобедренном треугольнике?
2.	Теорема, обратная теореме о равнобедренном треугольнике
3.	Часто задаваемые вопросы по теоремам о равнобедренном треугольнике

Что такое теорема о равнобедренном треугольнике?

Теорема о равнобедренном треугольнике утверждает, что если две стороны треугольника конгруэнтны, то и углы, противоположные конгруэнтным сторонам, также конгруэнтны. Чтобы понять теорему о равнобедренном треугольнике, мы будем использовать свойства равнобедренного треугольника для доказательства, как описано ниже.

Доказательство теоремы о равнобедренном треугольнике

Нарисуем равнобедренный треугольник с двумя равными сторонами, как показано на рисунке ниже.

Дано: ∆ABC равнобедренный треугольник с AB = AC.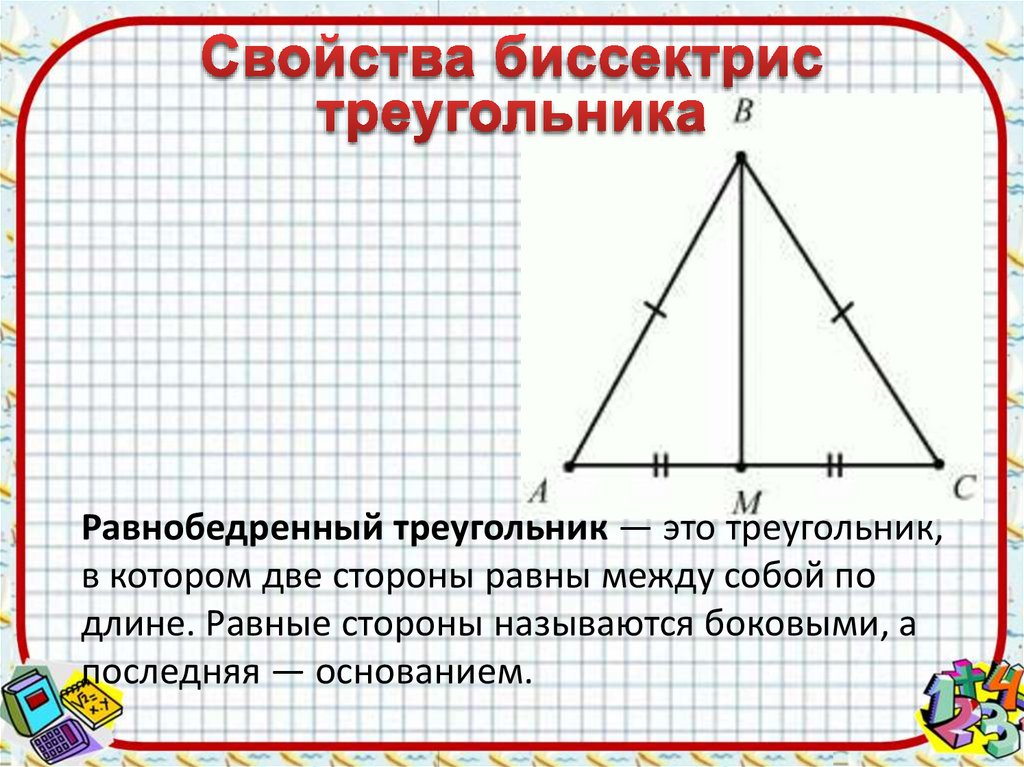
Построение: Высота AD от вершины A до стороны BC.
Доказать: ∠B = ∠C.

Доказательство: Мы знаем, что высота равнобедренного треугольника от вершины равна серединному перпендикуляру третьей стороны. Таким образом, мы можем сделать вывод, что
∠ADB = ∠ADC = 90º ———— (1)
BD = постоянный ток ———- (2)
Рассмотрим ∆ADB и ∆ADC
. АВ = АС [Дано]

AD = AD [общая сторона]
BD = DC [Из уравнения (2)]
Таким образом, по конгруэнтности SSS мы можем сказать, что
∆АДБ ≅ ∆АДК
По CPCT ∠B = ∠C.

Таким образом, мы доказали, что если две стороны треугольника равны, то углы, лежащие против равных сторон, равны.

Обратное утверждение теоремы о равнобедренном треугольнике

Теорема, обратная теореме о равнобедренном треугольнике, утверждает, что если два угла треугольника равны, то стороны, противоположные конгруэнтным углам, равны. Это прямо противоположно теореме, которую мы обсуждали выше. Мы будем использовать свойства равнобедренного треугольника, чтобы доказать обратное, как обсуждается ниже.

Теорема, обратная равнобедренному треугольнику Доказательство

Давайте нарисуем треугольник с двумя конгруэнтными углами, как показано на рисунке ниже, с отмеченными метками.

Дано: ∆ABC с ∠B = ∠C.

Построение: Высота AD от вершины A до стороны BC.
Доказать: AB = AC

Доказательство: Мы знаем, что высота треугольника всегда находится под прямым углом к ​​стороне, на которую он брошен.
Следовательно, ∠ADB = ∠ADC = 90º ———— (1)
Рассмотрим ∆ADB и ∆ADC,
∠B = ∠C [Дано]
AD = AD [общая сторона]
∠ADB = ∠ADC = 90º [Из уравнения (1)]
Таким образом, по AAS-конгруэнтности мы можем сказать, что
∆АДБ ≅ ∆АДК
Согласно CPCT, AB = AC

Таким образом, мы доказали, что если два угла треугольника равны, то стороны, противоположные равным углам, равны.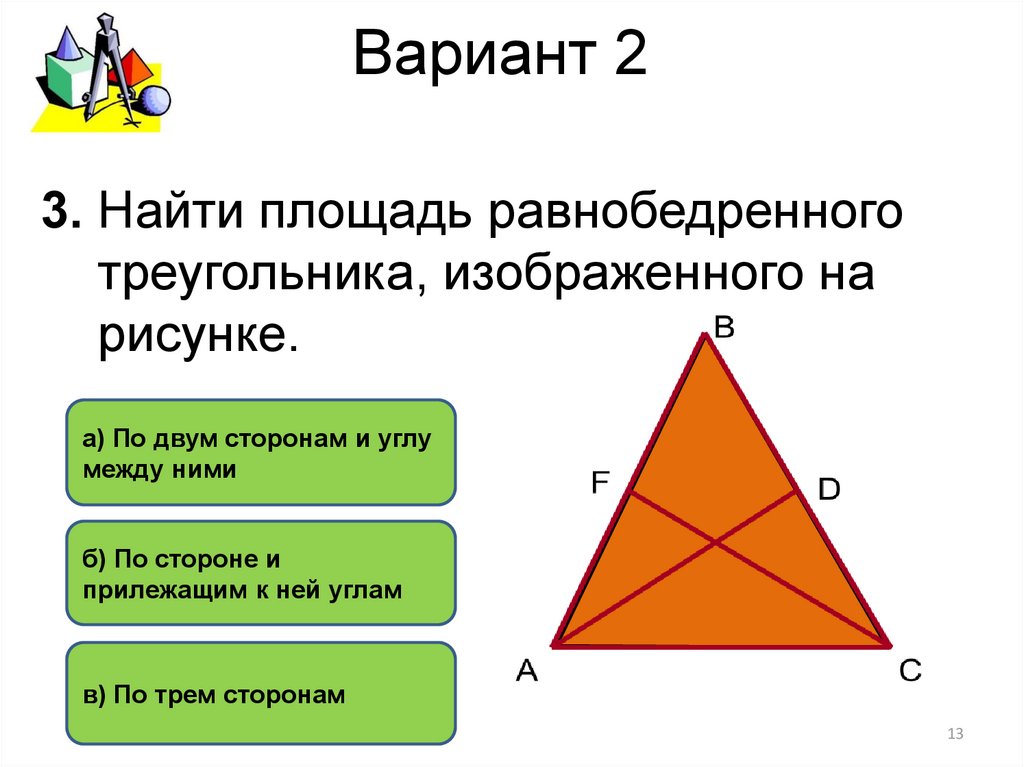

Статьи по теме

Проверьте эти статьи, связанные с концепцией теоремы о равнобедренном треугольнике.

• Равнобедренный треугольник
• Биссектриса
• Конгруэнтность в треугольниках

 

Примеры теоремы о равнобедренном треугольнике

1. Пример 1: На приведенном ниже рисунке найдите значение x, используя теорему о равнобедренном треугольнике.

   Решение: Согласно данному рисунку,

   Из ∆XYZ мы видим, что XY = XZ = 12 см

   Согласно теореме о равнобедренном треугольнике, если две стороны треугольника равны, то углы, противолежащие прилежащим сторонам, равны.

   Таким образом, ∠Y = ∠Z [Поскольку XY = XZ]

   ∠Y = 35º, ∠Z = x

   Таким образом, ∠Y = ∠Z = 35º.

   Следовательно, значение x равно 35º.

2. Пример 2: Если ∠P и ∠Q для ∆PQR равны 70º и QR = 7,5 см, найдите значение PR.

   Решение: Нарисуем фигуру в соответствии с данным вопросом,

   Учитывая, что в ∆PQR ∠P = ∠Q = 70º.

   Согласно обратной теореме о равнобедренном треугольнике, если два угла треугольника равны, то стороны, противоположные конгруэнтным углам, равны.

   Таким образом, PR = QR [Поскольку ∠P = ∠Q]

   Но, QR = 7,5 см

   Следовательно, значение PR = 7,5 см.

перейти к слайдуперейти к слайду

Хотите создать прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

Практические вопросы по теореме о равнобедренном треугольнике

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по теореме о равнобедренном треугольнике

Что такое теорема о равнобедренном треугольнике?

Теорема о равнобедренном треугольнике гласит, что если две стороны равнобедренного треугольника равны, то углы, противоположные равным сторонам, также будут иметь одинаковую величину.

Как доказать теорему о равнобедренном треугольнике?

Теорему о равнобедренном треугольнике можно доказать, используя свойства конгруэнтности и свойства равнобедренного треугольника. Можно нарисовать равнобедренный треугольник, а затем построить его высоту. Два треугольника, образованные теперь с высотой в качестве общей стороны, могут быть доказаны конгруэнтными с помощью конгруэнтности SSS с последующим доказательством равенства углов, противоположных равным сторонам, с помощью CPCT.

Что такое теорема, обратная теореме о равнобедренном треугольнике?

Обратная теорема о равнобедренном треугольнике утверждает, что если два угла треугольника равны, то стороны, противоположные равным углам треугольника, имеют одинаковую меру.

Как доказать обратную теорему о равнобедренном треугольнике?

Обратное утверждение теоремы о равнобедренном треугольнике можно доказать, используя свойства конгруэнтности и свойства равнобедренного треугольника.