Приведение к треугольному виду онлайн: Треугольный вид матрицы онлайн с подробным решением

Вычислительные методы для инженеров

Вычислительные методы для инженеров

Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. — М.: Высш. шк., 1994. — 544 с. В книге рассматриваются вычислительные методы, наиболее часто используемые в практике инженерных и научно-технических расчетов: методы решения задач линейной алгебры и нелинейных уравнений, проблема собственных значений, методы теории приближения функций, численное дифференцирование и интегрирование, поиск экстремумов функций, решение обыкновенных дифференциальных уравнений. Значительное внимание уделяется особенностям реализации вычислительных алгоритмов на ЭВМ и оценке достоверности полученных результатов. Имеется большое количество примеров и геометрических иллюстраций. Для студентов и аспирантов технических вузов, а также для инженеров и научных работников, применяющих вычислительные методы. Оглавление ПРЕДИСЛОВИЕ Глава 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И РЕШЕНИЕ ИНЖЕНЕРНЫХ ЗАДАЧ С ПРИМЕНЕНИЕМ ЭВМ § 1.2. Основные этапы решения инженерной задачи с применением ЭВМ § 1.3. Вычислительный эксперимент § 1.4. Дополнительные замечания Глава 2. ВВЕДЕНИЕ В ЭЛЕМЕНТАРНУЮ ТЕОРИЮ ПОГРЕШНОСТЕЙ § 2.1. Источники и классификация погрешностей результата численного решения задачи § 2.2. Приближенные числа. Абсолютная и относительная погрешности 2. Правила записи приближенных чисел. 3. Округление. § 2.3. Погрешности арифметических операций над приближенными числами § 2.4. Погрешность функции § 2.5. Особенности машинной арифметики 2. Представление целых чисел. 3. Представление вещественных чисел. 4. Арифметические операции над числами с плавающей точкой. 5. Удвоенная точность. 6. Вычисление машинного эпсилон. § 2.6. Дополнительные замечания Глава 3. ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ И АЛГОРИТМЫ. ОСНОВНЫЕ ПОНЯТИЯ § 3.2. Обусловленность вычислительной задачи 2. Примеры плохо обусловленных задач. 3. Обусловленность задачи вычисления значения функции одной переменной. 4. Обусловленность задачи вычисления интеграла … 5. Обусловленность задачи вычисления суммы ряда. § 3.3. Вычислительные методы § 3.4. Корректность вычислительных алгоритмов § 3.5. Чувствительность вычислительных алгоритмов к ошибкам округления § 3.6. Различные подходы к анализу ошибок § 3.7. Требования, предъявляемые к вычислительным алгоритмам § 3.8. Дополнительные замечания Глава 4. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ § 4.2. Обусловленность задачи вычисления корня § 4.3. Метод бисекции § 4.4. Метод простой итерации § 4.5. Обусловленность метода простой итерации § 4.6. Метод Ньютона § 4. 7. Модификации метода Ньютона § 4.8. Дополнительные замечания Глава 5. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ § 5.2. Нормы вектора и матрицы § 5.3. Типы используемых матриц § 5.4. Обусловленность задачи решения системы линейных алгебраических уравнений § 5.5 Метод Гаусса § 5.6. Метод Гаусса и решение систем уравнений с несколькими правыми частями, обращение матриц, вычисление определителей § 5.7. Метод Гаусса и разложение матрицы на множители. LU-разложение § 5.8. Метод Холецкого (метод квадратных корней) § 5.9. Метод прогонки § 5.10. QR-разложение матрицы. Методы вращений и отражений § 5.11. Итерационное уточнение § 5.12. Дополнительные замечания Глава 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ § 6.1. Метод простой итерации § 6.2. Метод Зейделя § 6.3. Метод релаксации § 6.4. Дополнительные замечания Глава 7. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ § 7. 2. Метод простой итерации § 7.3. Метод Ньютона для решения систем нелинейных уравнений 7.4. Модификации метода Ньютона § 7.5. О некоторых подходах к решению задач локализации и отыскания решений систем нелинейных уравнений § 7.6. Дополнительные замечания Глава 8. МЕТОДЫ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ § 8.2. Степенной метод § 8.3. Метод обратных итераций § 8.4. QR-алгоритм § 8.5. Дополнительные замечания Глава 9. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ § 9.2. Обусловленность задачи минимизации § 9.3. Методы прямого поиска. Оптимальный пассивный поиск. Метод деления отрезка пополам. Методы Фибоначчи и золотого сечения § 9.4. Метод Ньютона и другие методы минимизация гладких функций § 9.5. Дополнительные замечания Глава 10. МЕТОДЫ МНОГОМЕРНОЙ МИНИМИЗАЦИИ § 10.1. Задача безусловной минимизации функции многих переменных § 10.2. Понятие о методах спуска. Покоординатный спуск § 10.3. Градиентный метод § 10.4. Метод Ньютона § 10. 5. Метод сопряженных градиентов § 10.6. Метода минимизации без вычисления производных § 10.7. Дополнительные замечания Глава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ И СМЕЖНЫЕ ВОПРОСЫ § 11.2. Интерполяция обобщенными многочленами § 11.3. Полиномиальная интерполяция. Многочлен Лагранжа § 11.4. Погрешность интерполяции § 11.5. Интерполяция с кратными узлами § 11.6. Минимизация оценки погрешности интерполяции. Многочлены Чебышева § 11.7. Конечные разности § 11.8. Разделенные разности § 11.9. Интерполяционный многочлен Ньютона. Схема Эйткена § 11.10. Обсуждение глобальной полиномиальной интерполяции. Понятие о кусочно-полиномиальной интерполяции § 11.11. Интерполяция сплайнами § 11.12. Понятие о дискретном преобразовании Фурье и тригонометрической интерполяции § 11.13. Метод наименьших квадратов § 11.14. Равномерное приближение функций § 11.15. Дробно-рациональные аппроксимации и вычисление элементарных функций § 11.16. Дополнительные замечания Глава 12. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ § 12.1. Простейшие формулы численного дифференцирования § 12.2. О выводе формул численного дифференцирования § 12.3. Обусловленность формул численного дифференцирования § 12.4. Дополнительные замечания Глава 13. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 13.2. Квадратурные формулы интерполяционного типа § 13.3. Квадратурные формулы Гаусса § 13.4. Апостериорные оценки погрешности. Понятие об адаптивных процедурах численного интегрирования § 13.5. Вычисление интегралов в нерегулярных случаях § 13.6. Дополнительные замечания Глава 14. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 14.1. Задача Коши для дифференциального уравнения первого порядка § 14.2. Численные методы решения задачи Коши. Основные понятия и определения § 14.3. Использование формулы Тейлора § 14.4. Метод Эйлера § 14.5. Модификации метода Эйлера второго порядка точности § 14.6. Методы Рунге-Кутты § 14.7. Линейные многошаговые методы. Методы Адамса § 14.8. Устойчивость численных методов решения задачи Коши § 14.9. Неявный метод Эйлера § 14.10. Решение задачи Коши для систем обыкновенных дифференциальных уравнений и дифференциальных уравнений m-го порядка § 14.11. Жесткие задачи § 14.12. Дополнительные замечания Глава 15. РЕШЕНИЕ ДВУХТОЧЕЧНЫХ КРАЕВЫХ ЗАДАЧ § 15.1. Краевые задачи для одномерного стационарного уравнения теплопроводности § 15.2. Метод конечных разностей: основные понятия § 15.3. Метод конечных разностей: аппроксимации специального вида § 15.4. Понятие о проекционных и проекционно-разностных методах. Методы Ритца и Гадеркина. Метод конечных элементов § 15.5. Метод пристрелки § 15.6. Дополнительные замечания

Public Science Framework-Journals — Paper

Сначала рассмотрим случай, когда количество матриц d = 2.

    (1)

Имеются две квадратные матрицы B _{1 и B2 2 над полем комплексных чисел. Требуется найти преобразование подобия (1), приводящее обе матрицы к равному блочно-треугольному виду. Вот блок матрицы B n , расположенный в i -я колонка и j -я строка этой секционированной матрицы. Диагональные блоки должны быть квадратными подматрицами.}

Необходимо, чтобы количество l диагональных блоков было максимально возможным.

Идея метода опубликована в авторской монографии [1]. Соответствующие вычислительные алгоритмы и результаты расчетов по решению прикладных задач представлены в работах [2,3]. В данной работе дается подробное теоретическое обоснование разработанных методов.

Существует решение для случая только одной матрицы. Одна матрица может быть приведена к жордановой форме. Есть известная нерешенная проблема — создать каноническую форму для пары матриц. Эта задача и эквивалентные задачи называются дикими задачами [4].

2. Общая схема расчета

Используем «метод коммутативной матрицы» и «метод инвариантного подпространства». Первый позволяет найти преобразование подобия, приводящее обе матрицы к блочно-диагональному виду с двумя (не менее) блоками на главной диагонали, либо определить, что такое приведение для этих матриц невозможно. Другой метод предназначен для приведения таких двух матриц, не приводящихся к блочно-диагональному виду, к блочно-треугольному виду, либо для определения того, что они не могут быть также приведены к «строгому» блочно-треугольному виду. Также используется метод преодоления частного случая (см. раздел 6).

Этот подход последовательно применяется сначала к исходной паре матриц, затем к парам блоков, которые появляются на главной диагонали. Процесс продолжается до тех пор, пока не будут получены пары блоков, неприводимых к одной и той же блочно-треугольной форме. Из теоремы единственности следует, что такой подход дает решение задачи.

3. Метод коммутативной матрицы

Возможность применения коммутативной матрицы для разделения системы уравнений описана в учебниках по квантовой механике (например, см. книгу Ферми [5]). Сам метод коммутативной матрицы был предложен одновременно А.К. Лопатин [6] и Е.Д. Якубович [7].

Рассмотрим множество всех матриц, коммутативных с матрицами B ₁ , B ₂ . Это множество представляет собой алгебру над полем комплексных чисел. называется централизатором матриц { B _n }.

Теорема 1. LET MATRICES A и x Будь коммутативно:

Aх = хa,

Матрица x имеет блок-диагональную форму, где спектр взаимно непересекающиеся. Тогда матрица А также имеет блочно-диагональную форму

А = диаг .

Эта теорема приведена в [8] — гл. VIII, теорема 3. См. также [1; § 2.5].

Следствие. Пусть существует матрица, имеющая не менее двух различных собственных значений. Пусть столбец матрицы S будет векторами канонического базиса матрицы X . Затем преобразование подобия приводит обе матрицы к блочно-диагональному виду с двумя (как минимум) блоками на главной диагонали.

Доказательство . Свойство коммутативности матриц сохраняется при преобразовании подобия. Действительно:

,

, где S — невырожденная матрица.

Пусть матрица X имеет не менее двух различных собственных значений и коммутирует с матрицами B ₁ , B ₂ и пусть столбцы матрицы S являются векторами канонических базисов матрица X . В этом случае преобразование уменьшает матрицу X в его форму Джордана. Следовательно, , где X ₁ — клетка Жордана, соответствующая первому собственному значению матрицы X , а X ₂ — второму и последующим (если они есть) собственным значениям. Оба блока непусты и не имеют общих собственных значений. Матрицы коммутируют с матрицей. Из теоремы 1 следует, что они имеют блочно-диагональную форму.

Теорема 2. Если матрицы B _n приведены к блочно-диагональному виду с двумя (не менее) блоками на главной диагонали с помощью преобразования подобия, то существует матрица  как минимум с двумя различными собственными значениями.

Доказательство. Лет. Составим матрицу, где E ₁ и E ₂ — единичные матрицы. Матрица коммутирует с B _n и имеет два различных собственных значения l ₁ = 1, l ₂ = 2,

Итак, для одновременного приведения двух матриц к блочно-диагональному виду необходимо и достаточно, чтобы централизатор матрицы содержал матрицу X с разными собственными значениями.

Чтобы найти централизатор (точнее — его базис), можно объявить все элементы матрицы X неизвестными числами и составить систему линейных однородных алгебраических уравнений, соответствующих матричным уравнениям

B ₁ Х = ХВ ₁ ,    Б ₂ Х = ХВ 1 21 21 (2)

Имеем 2 n ² уравнений с n ² неизвестными. Если n мало, то общее решение этой системы уравнений можно произвести известными методами. Вычислительный метод преодоления больших n приведен в [9].

Пусть Вт ₁ , W ₂ ,…, W _r матрицы составляют основу централизатора Λ( B _{n422 ). Если ранг r централизатора равен 1, то весь централизатор состоит только из матриц, кратных единичной матрице. В этом случае приведение матриц B n к блочно-диагональному виду невозможно. Если r > 1, то среди матриц W k мы выбираем матрицу X , которая имеет по крайней мере два различных собственных значения.}

Составим матрицу преобразования подобия векторов-столбцов канонического базиса матрицы X .

Частный случай, когда r > 1, но все матрицы базиса не имеют различных собственных значений, обсуждается ниже (см. раздел 6).

4. Метод инвариантного подпространства

Идея метода предложена в [1] (глава 7).

Рассмотрим матрицы B _n ( n = 1, 2), не приводящиеся одновременно к блочно-диагональному виду. В противном случае мы бы уже сделали это методом коммутативной матрицы. Мы хотим выяснить, можно ли их привести к блочно-треугольному виду.

4.1. Построение алгебры

Первым шагом метода является построение алгебры с единицей, порожденной исходными матрицами. Можно поступить следующим образом [2]: сначала выберем линейно независимые элементы матрицы { E , B ₁ , B ₂ } и назовем их «предполагаемый базис». Затем мы рассматриваем все возможные произведения этих матриц. Если следующий продукт не принадлежит линейному отрезку «предполагаемого базиса», мы добавляем его в это множество и считаем произведениями элементов нового «предполагаемого базиса». Продолжаем этот процесс до тех пор, пока ни одно из произведений не выйдет за пределы линейного размаха. Признаком того, что элемент не принадлежит линейной области «предполагаемой базы», ​​является то, что добавление нового элемента дает линейно независимый набор элементов. Проверка линейной независимости возможна с помощью программы SLAU5 [1].

Возможность приведения матриц к блочно-треугольному виду эквивалентна сводимости алгебры. Критерий сводимости алгебры: ранг алгебры j( Â _n ) меньше, чем n ² , где n — порядок матриц. Это следует из теоремы Бернсайда [10] (см. также [6, теорема 1′).

4.2. Вычисление алгебраического радикального идеала

Теорема 3. Если ранг r алгебры j(В _n ) меньше, чем n ² и если централизатор Λ( B _n ) не содержит матрицы X с другими собственными значениями Â _n ) неполупрост.

Доказательство. Условие r < n ² означает, что алгебра j( Â _n ) приводима [10,11]. Приводимая алгебра может быть полупростой или неполупростой. Алгебра не является полупростой, поскольку матрицы (включая { B _n }) не приводятся к блочно-диагональному виду (если бы они были приводимы, мы могли бы сделать это методом коммутативной матрицы). Поэтому алгебра неполупроста.

Неполупростая алгебра имеет нетривиальный радикальный идеал. Для его нахождения существуют формулы [11]: координаты a = [a ₁ , a ₂ , …, a _r ] ^х любого радикального идеального элемента в основном множестве алгебры удовлетворяют уравнение

D a = 0, D = { D _IJ }, (3)

, где D _IJ = SP ( W _I W _{J 12} ). , Sp(.) — след матрицы. { W _i } — базовый набор алгебры.

Общее решение уравнения (3) может быть получено известными методами. Можно, например, использовать программу SLAU5 [1]. Следовательно, можно получить базис радикального идеала.

4.3. Нахождение инвариантного подпространства

Пусть Z-множество есть пересечение всех ядер радикальных идеальных элементов алгебры j( Â _n ). Мы можем найти Z -множество (его базис) как общее решение соответствующей системы алгебраических уравнений.

Теорема 4. Z-множество является подпространством пространства .

Доказательство. Этот набор можно найти только с элементами основы. Расчет соответствует нахождению решения системы линейных однородных алгебраических уравнений. Общее решение этой системы, как известно, есть подпространство.

Теорема 5. Если алгебра неполупроста, то Z-множество является нетривиальным подпространством.

Доказательство. В этом случае ненулевым радикальным идеалом является набор матриц , где t — вектор параметров. Радикальный идеал является нильпотентной подалгеброй, так как все его элементы нильпотентны (см. [11, § 7, теорема 2]). Следовательно, , . Пусть   – ненулевая матрица множества ,         — его ненулевой столбец. Затем, поскольку. Итак, уравнение имеет нетривиальные решения.

Теорема 6. Подпространство Z-множество является инвариантом относительно матриц {B _ }.

Доказательство. Радикальный идеал алгебры j( Â _ ) является ее идеалом. Матрицы являются элементами алгебры j( Â _ ). Отсюда получаем где , т.е. Z -множество инвариантно относительно множества матриц { B _i }.

Таким образом, для случая, когда матрицы не приводятся к блочно-диагональному виду, ранг алгебры j( Â _n ) меньше n ² , мы имеем метод построения нетривиального подпространства, инвариантный относительно этих матриц.

4.4. Построение матрицы преобразования

Теорема 7. Одновременное приведение пары матриц к блочно-треугольному виду возможно тогда и только тогда, когда существует нетривиальный инвариант относительно обоих подпространств матриц .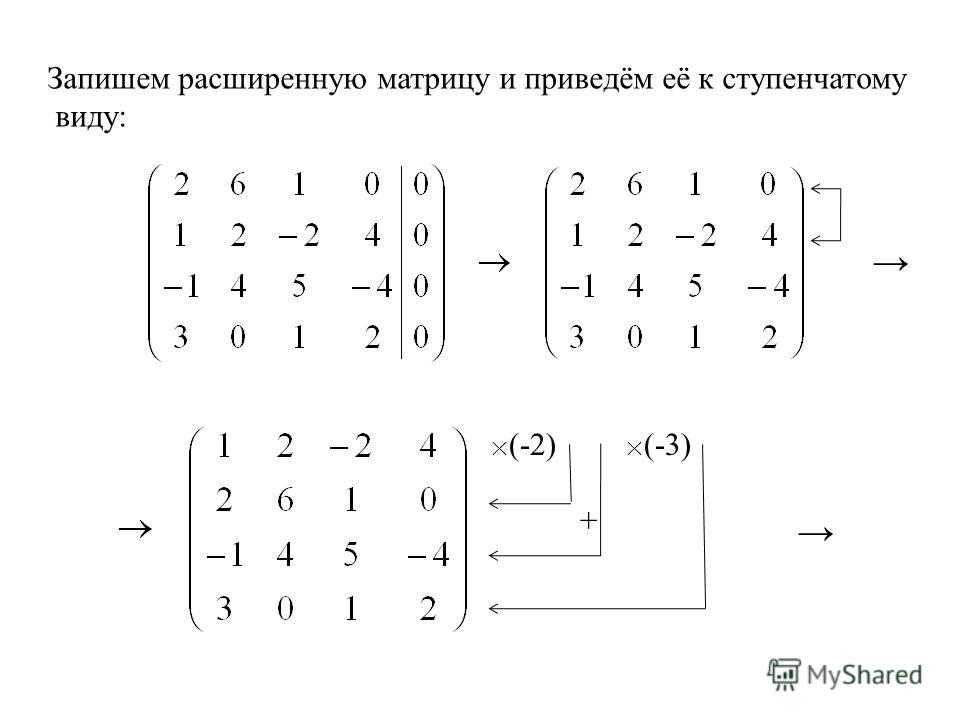

Доказательство. . Пусть

где — матрицы порядка m . Тогда множество векторов , где , инвариантно относительно матриц , т.е. если , то . Пусть V состоит из всех векторов вида , . Из инвариантности матриц следует, что. Следовательно,

 .

 Пусть существует нетривиальное подпространство V , инвариантное относительно матриц . Пусть  базис подпространства V . Пусть  является его дополнением к базе . Пусть столбцы матрицы S — векторы . Из правил умножения матриц следует, что равенство эквивалентно преобразованию подобия , и это равенство можно записать в виде

,                            (4)

, где  элементы матрицы , A произвольная матрица.

Условие инвариантности подпространства V означает, что любой элемент базиса после умножения на любую из матриц остается в подпространстве V и, следовательно, представляет собой линейную комбинацию элементов:

.

Сравнивая последнее равенство с (4) и учитывая линейную независимость векторов, получаем . Эти уравнения выполняются вообще. Следовательно, соответствующие элементы матриц равны нулю, т.е. модифицированные матрицы имеют блочно-треугольную форму.

Составим матрицу преобразования S из базисных векторов этого подпространства и подпространства, являющегося прямым дополнением к нему. Мы располагаем векторы столбцами (см. доказательство теоремы 7).

Прямая сумма в подпространство может быть найдена как общее решение x линейных однородных алгебраических уравнений

.

Здесь T — знак транспонирования.

Для нахождения общего решения можно использовать программу SLAU5 [1].

5. Теорема единственности

Существует теорема единственности.

Теорема 8. Приведем матрицы , i = 1, 2, к блочно-треугольному виду

некоторым преобразованием подобия и дальнейшим сокращением для каждой пары блоков { B _{1 kk} , B _{2 kk} } невозможно. Если существует другое преобразование подобия такое, что для результирующих блоков дальнейшее сокращение невозможно:

, то и мы можем определить соответствие между номерами блоков так, что блоки B _ikk подобны блокам .

Доказательство . Эта теорема следует из теоремы Жордана — Гёльдера (см. также [12, теорема 1]).

6. Частный случай

Рассмотрим случай, когда в базе централизатора содержится более одной матрицы ( r > 1), но каждая из этих матриц не имеет различных собственных значений. Есть предположение, что в этом случае все матрицы централизатора не имеют различных собственных значений и, соответственно, исходные матрицы не приводятся к блочно-диагональному виду одновременно. Оказывается, это предположение справедливо, если алгебра имеет ранг r ≤ 3 и неверно, если rank r = 4 (см. [1, теорема 6.6]).

В этом разделе показано, как в этом случае привести матрицы к блочно-треугольному виду, не обсуждая возможности приведения их к блочно-диагональному виду.

Теорема 9. Если ранг централизатора матриц больше единицы: r >1, то матрицы приводятся к блочно-треугольному виду.

Доказательство. Пусть W ₁ ,…, _{W r — основа алгебры, а W 1 = E . Если матрица W 2 имеет два (или более) различных собственных значения, то можно привести исходные матрицы к блочно-диагональному виду методом коммутативной матрицы. В противном случае собственное значение уникально. Следовательно, матрица нильпотентна. Матрица G нильпотентна и отлична от нуля, поэтому подпространство  нетривиально. Кроме того , т.е. подпространство L инвариантен относительно матриц . Следовательно, мы можем привести матрицы  к блочно-треугольному виду и в этом случае (теорема 7).}

Нам необходимо создать матрицу  и найти векторы  как основу матрицы ядра G для построения матрицы преобразования S. Дальнейшее построение такое же, как в подразделе 4. 4.

Примечание. Условие  не обязательно для приведения матриц к блочно-треугольному виду.

7. Примеры

7.1. Первый пример

 (см. [1], пример 1.6).

Используем метод коммутативной матрицы. Все элементы х _ij матрицы х считаются неизвестными. Составим систему алгебраических уравнений, соответствующую матричным уравнениям B ₁ Х = ХB ₁ , B ₂ Х = ХB _{2 90. Его общее решение выглядит следующим образом:}

, где x ₁₁ и x ₂₁ — свободные неизвестные. Или другим способом

Если x ₁₁ = 0, x ₂₁ = 1 Собственные значения x : L ₁ = L ₂ = — 0,25; л ₃ = 0,25. Затем получаем собственные векторы матрицы X и строим матрицу преобразования

Исходная матрица приводится к блочно-диагональному виду:

                        (5)

Далее рассмотрим блоки  Для них набор коммутирующих матриц  есть a E , где a — произвольное число. Поэтому приведение этих блоков к диагональному виду невозможно (теорема 2). Проверим возможность редукции методом инвариантного подпространства. Матрицы E , B ₁₁₁ и B ₂₁₁ линейно независимы. Произведения любой из этих матриц на единичную матрицу E принадлежат линейному диапазону первых трех матриц. Matrix  также входит в этот набор. Считаем произведение U = B ₁₁₁ B ₂₁₁ . Используя равенство a E + b B ₁₁₁ + g B ₂₁₁ + l U = 0, получаем: a = b = g = l = 0, т.е. матрица U не принадлежит линейная оболочка первых трех матриц. Получаем, что r = 4 и условие r < n ² не выполняется.

Дальнейшее упрощение матриц невозможно (см. п. 4.1). Поэтому окончательным результатом являются матрицы (5).

7.2. Второй пример

,  (см. [1], пример 7.3).

Прямая проверка показывает, что соответствующий централизатор состоит только из матриц. Следовательно, приведение матриц к диагональному виду невозможно.

Построим алгебру. Матрицы Е , B ₁ , B ₂ линейно независимы. Обозначим эти матрицы W ₁ , W ₂ , W ₃ соответственно. Рассмотрим все возможные произведения матриц W _k W _j и проверим, являются ли полученные матрицы линейной комбинацией исходной. Поскольку умножение на W ₁ = E не меняет матрицы, считаем произведения W _k W _j for k , j = 2, 3. Вычислим: . Проверяем, является ли матрица линейной комбинацией первых двух: . Это уравнение соответствует системе уравнений. Ее решение: β = 3, a = – 2. Следовательно, матрица представляет собой линейную комбинацию матриц W ₁ и W ₂ . Далее вычисляем:

Мы нашли, что все произведения принадлежат линейной оболочке матриц Вт ₁ , Вт ₂ , Вт ₃ . Следовательно, эти матрицы составляют основу алгебры. Число элементов базы r = 3, т.е. Это означает, что возможно приведение к треугольной форме.

Составим матрицу D = {Sp( W _j W _k )}. Все продукты W _j W _k уже рассчитаны. Получаем

Составим систему уравнений D а = 0. Общее решение этой системы включает: а ₁ = –6 , где a ₃ — свободная переменная. Пусть а ₃ = 1. Получаем. Вычислим матрицу G : Уравнения  имеют вид:  Отсюда: . Ставим: . Следовательно, базис Z-множества состоит из одного вектора: . Этот вектор и вектор линейно независимы. Поэтому: . Тогда получаем

; ;

;

7.3. Третий пример

. Эти матрицы описывают движение системы из [13].

Ясно, что матрицу B ₂ можно привести к жордановой форме.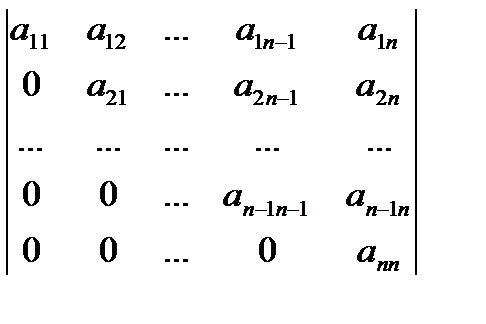 Но давайте рассмотрим подход, изложенный выше.

Найдем матрицу X , коммутирующую с исходными матрицами. В результате вычислений получаем: X = a E , где a — произвольный параметр. Поскольку матрица X не имеет различных собственных значений, приведение исходных матриц к блочно-диагональному виду невозможно.

Далее воспользуемся методом инвариантного подпространства.

Действуем как в предыдущем примере. Получаем: r = 2. Условие выполнено. Далее: D = .

Система уравнений D y = 0 принимает вид: 2 y ₁ + 2 y ₂ = 0

4,

0003 у ₁ + 2 у ₂ = 0. В результате получаем: у = . Основой радикального идеала является матрица G :

.

Уравнение G х = 0 принимает вид: х ₁ – х ₂ = 0, х _{12 – х1 2 состоит из вектора . Этот вектор и вектор линейно независимы. Поэтому, . Получаем треугольные матрицы:}

, .

Особенность этого примера в том, что здесь существует некомпактная группа матриц, коммутирующих с исходными матрицами.

8. Обобщения

Задачу получения наилучшей блочно-треугольной формы можно сформулировать и по-другому: найти такую ​​матрицу преобразования S, что максимум порядков диагональных блоков будет наименьшим из возможных. Из теоремы единственности следует, что, решая задачу получения максимального количества блоков, мы одновременно получаем блок с наименьшим возможным порядком.

Понятно, что исходных матриц может быть больше двух. В этом случае ход решения не изменится. Увеличится только количество матричных уравнений (2) или количество исходных матриц для композиции алгебры j( Â _n ).

Рассмотрим задачу приведения матриц  к блочно-треугольному виду преобразованием , где H и S — невырожденные квадратные матрицы. Это преобразование более эффективно, чем преобразование подобия (1). Задача решается в случае, когда одна из исходных матриц невырождена.

Далее нам понадобится теорема 10 А.К. Лопатин. Уточненная формулировка и доказательство результата состоят в следующем (см. [1; теорема 7.4]).

Теорема 10. Существует преобразование подобия, приводящее матрицу  к блочно-треугольному виду с l блоков на главной диагонали, тогда и только тогда, когда 6)

где .

Доказательство . Пусть матрицы блочно-треугольные. Пусть блоки на главной диагонали имеют порядок и . Мы выбираем набор матриц в виде , где матрицы имеют тот же тип блока, что и ; все блоки переменных матриц, стоящие выше главной диагонали, заполнены параметрами , а остальные элементы этой матрицы равны нулю. Затем

,

где .

Понятно, что . После преобразований , ,  это равенство остается в силе.

 Условие  означает, что , т.е. подпространство  инвариантно относительно матрицы .

Обозначим  как количество блоков на главной диагонали матриц  , приведенных к блочно-треугольному виду. Пусть

.

Теорема 11. Пусть  — матрицы. Если , то , где N — любая невырожденная матрица.

Доказательство. Пусть  и  – матрицы преобразования, при которых исходные матрицы  приводятся к блочно-треугольному виду по формуле  и имеют максимально возможное количество блоков на главной диагонали. В этом случае матрицы имеют одинаковую блочно-диагональную форму. Согласно теореме 10 должны существовать такие матрицы, что

,

, ,

, где .

Выполним преобразование подобия , и замену векторов  в . Уравнения (6) сохраняются. Более того:

.

Используя теорему 10, получаем .

Для нахождения преобразования  с максимально возможным числом блоков на главной диагонали достаточно решить эту задачу преобразованием подобия для опорных матриц , , .

9. Заключение

Таким образом, задача полностью решена. Разработан метод приведения набора матриц к наилучшему блочно-треугольному виду.

Этот результат имеет практическое значение. Этот метод позволяет упростить систему линейных дифференциальных уравнений, содержащую несколько матриц коэффициентов [1,14]. Развязка уравнений на независимые подсистемы соответствует приведению матриц к блочно-диагональному виду. Приведение матриц к блочно-треугольному виду соответствует «иерархической» (вертикальной) развязке. Таким образом, первая подсистема не содержит переменных других подсистем. Во второй подсистеме присутствуют только переменные первой и второй подсистем и т. д. Количество таких подсистем может быть больше, чем при обычном разделении.

10. Следующие направления исследований

Также было бы полезно решить следующие проблемы.

• Решение той же задачи для матриц над другими полями (действительные числа, рациональные числа и т.д.).

• Более подробное изучение частного случая рассмотрено в разделе 6.

• Использование преобразования без требования невырожденности одной из матриц.

• Приведение к наилучшей блочно-треугольной форме n n -матрица A и n n -матрица m -матрица B преобразованием. Здесь S ₁ и S ₂ — неособые квадратные матрицы соответствующих порядков. Эта и подобные ей задачи необходимы для иерархического разделения систем уравнений с прямоугольными матрицами коэффициентов (см. [1], гл. 8 и [12]).

Ссылки

1. Базилевич Ю.В. Н., Численные методы развязки в линейных задачах механики, Киев, Наукова думка, 1987.
2. Базилевич Ю.А. Н., Коротенко М.Л. и Швец И.В., Решение задачи иерархического разделения линейных математических моделей механических систем, Техническая механика , 2003, № 1, 135–141.
3. Базилевич Ю.А. Н., Точная развязка линейных систем,Электронный журнал «Исследовано в России», 2006, 018, 182–190, http://www. sci-journal.ru/articles/2006/018.pdf.
4. Дрозд Ю.А. A., Проблемы с ручными и дикими матрицами, Lect. Notes Math., 832, 242-258 (1980).
5. Ферми Энрико, Заметки по квантовой механике/ The University of Chicago Pres
6. Лопатин А.К., Алгебраическая сводимость систем линейных дифференциальных уравнений. I, Дифференц. Уравн. , 1968, т.4, 439–445 (на русском языке).
7. Якубович Е.Д., Построение систем замены для одного класса многомерных линейных систем автоматического управления, Изв. Вузов, Радиофизика , 1969, т. 12, № 3, 362–377.
8. Гантмахер Ф. Р., Теория матриц / Челси: Нью-Йорк. 1960.
9. Базилевич Ю.В. Н., Бульдович А.Л., Алгоритм нахождения общего решения системы линейных однородных алгебраических уравнений в случае очень крупномасштабных разреженных матричных коэффициентов // Математические модели и современная техника. Сб. научный. тр. / НАН. Институт математики. — Киевская, 1998. — 12, 13.
10. Van Der Waerden Algebra.vols.IandII. Спрингер-Верлаг.
11. Чеботарев Н.Г., Введение в теорию алгебр, М.: Едиториал УРСС, 2003.
12. Белозеров В.Е., Можаев Г. В., Единственность решения задач развязки и агрегации линейных систем автоматического управления // Теория сложных систем и методов их моделирования.— М: ВНИИСИ, 1982.— 4-13 (на русском языке).
13. Базилевич Ю.В. N. Скрытая симметрия Экспозиция. Механические системы с жесткой структурой сил// Труды Института математики НАН Украины. — Т. 50. — Ч. 3. — Киев: Ин-т математики НАН Украины, 2004 /—С.1261—1265.
14. Павловский Ю.А. Н., Смирнова Т.Г., Проблема декомпозиции в математическом моделировании.— М.: ФАЗИС, 1998. VI+266.

ПРИВОД К ТРЕУГОЛЬНОЙ ФОРМЕ БЛОКА

Рассмотрены алгоритмы приведения разреженной матрицы общего вида к блочно-треугольному виду. Эта форма позволяет решать соответствующую систему линейных уравнений как последовательность подзадач. Мы обсуждаем задачу о назначении элементов по диагонали как часть процесса нахождения блочной треугольной формы, хотя эта задача представляет интерес сама по себе. Мы также рассматриваем распространение блочной треугольной формы на прямоугольные и сингулярные матрицы. Если мы решаем систему линейных уравнений , матрица которого имеет блочную треугольную форму, за счет использования этой формы может быть достигнута экономия как вычислительной работы, так и объема памяти. Наша цель в этой главе — объяснить, как данную матрицу можно преобразовать в эту форму, и продемонстрировать, что эта форма (по существу) уникальна. Для этой задачи существуют удивительно экономичные алгоритмы, обычно требующие O(n) + 0(τ ) операций для матрицы порядка n с τ элементами. Нам удобно рассматривать перестановки к блочной нижней треугольной форме , хотя верхнюю треугольную форму блока можно было получить лишь с небольшой модификацией (см. упражнение 6.1). Матрица, которую можно переставить к виду (6.1.2), с N > 1, называется приводимой. Если никакая блочная треугольная форма, кроме тривиальной (N = 1), не может быть Прямые методы для разреженных матриц, второе издание. И. С. Дафф, А. М. Эрисман и Дж. К. Рид. © Oxford University Press, 2017 г. Опубликовано Oxford University Press, 2017 г. найдено, матрица называется неприводимой 1 . Мы ожидаем, что каждое B n будет неприводимым, иначе возможна более тонкая декомпозиция. Преимущество использования блочных треугольных форм, таких как (6.1.2), состоит в том, что система уравнений (6.1.1) может быть решена простой прямой подстановкой (где сумма равна нулю для i = 1) и перестановка Мы должны разложить на множители только диагональные блоки В a, i =1, 2,…, N. Недиагональные блоки Bj, i > j , используются только в умножениях Bj yj. Обратите внимание, в частности, что вся заливка ограничивается диагональными блоками. Если в каждом диагональном блоке для устойчивости и разреженности выполняется перестановка строк и столбцов, это не повлияет на треугольную структуру блока. Существуют классы задач, для которых алгоритмы этой главы бесполезны. Для некоторых приложений может быть заранее известно, что матрица неприводима. Матрицы, возникающие в результате дискретизации уравнений в частных производных, часто имеют такую ​​природу. В других случаях разложение может быть известно заранее из базовой физической структуры. Если A симметричен с ненулевыми диагональными элементами, сводимость означает, что A можно преобразовать в блочно-диагональную форму. Хотя методы этой главы найдут эту форму, вероятно, будет эффективнее найти ее с помощью дерева исключения, см. Раздел 12.4. Даже когда форма известна, автоматические методы все же могут быть полезны, чтобы избежать необходимости явного ввода проблемы в требуемой форме или проверки того, что она не была изменена ошибками ввода данных. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт