Что такое логарифм? Зачем нужны логарифмы?
Логарифмы — традиционная головная боль для многих учеников старших классов. Особенно — уравнения и неравенства с логарифмами. Не любят старшеклассники логарифмы почему-то. И поэтому боятся. И совершенно зря.) Ибо сам по себе логарифм — это очень и очень простое понятие. Не верите? Убедитесь сами! В сегодняшнем уроке.
Итак, поехали знакомиться.)
Для начала решим в уме вот такое очень простенькое уравнение:
2х = 4
Это простейшее показательное уравнение. Оно так называется из-за того, что неизвестное икс находится в показателе степени. Даже если вы не в курсе, как решаются показательные уравнения, просто в уме подберите икс так, чтобы равенство выполнилось. Ну же?! Ну, конечно же, х = 2. Два в квадрате — это четыре.)
А теперь я изменю в нём всего одно число. Вот такое уравнение теперь решим:
2х = 5
И снова пробуем подобрать икс…
Что, никак не подбирается? Два в квадрате — это четыре. Два в кубе — это уже восемь. А у нас — пятёрка. Мимо проскочили… Что делать? Только не говорите мне, что нету такого икса! Не поверю.)
Два в кубе — это уже восемь. А у нас — пятёрка. Мимо проскочили… Что делать? Только не говорите мне, что нету такого икса! Не поверю.)
Согласитесь, что это как-то несправедливо: с четвёркой уравнение решается в уме, а с пятёркой — уже не решается никак. Математика не приемлет такой дискриминации! Для неё все числа — равноправные партнёры.)
На данном этапе мы можем лишь грубо прикинуть, что икс — какое-то дробное число между двойкой (22 = 4) и тройкой (23 = 8). Можем даже немного повозиться с калькулятором и приближённо подобрать, найти это число. Но такая возня каждый раз… Согласен, как-то грустно…
Математика решает данную проблему очень просто и элегантно — введением понятия логарифма.
Итак, что же такое логарифм? Вернёмся к нашему загадочному уравнению:
2х = 5
Осмысливаем задачу: нам надо найти некое число х, в которое надо возвести 2, чтобы получить 5. Понятна эта фраза? Если нет, перечитайте ещё раз. И ещё… Пока не осознаете. Ибо это очень важно!
Понятна эта фраза? Если нет, перечитайте ещё раз. И ещё… Пока не осознаете. Ибо это очень важно!
Вот и назовём это загадочное число х логарифмом пятёрки по основанию два! В математической форме эти слова выглядят так:
x = log25
А произносится эта запись вот так: «Икс равен логарифму пяти по основанию два.»
Число внизу (двойка) называется основанием логарифма. Пишется снизу так же, как и в показательном выражении 2х. Запомнить очень легко.)
Ну, вот, собственно, и всё! Мы решили ужасное на вид показательное уравнение!
2х = 5
x = log25
И всё! Это правильный и совершенно полноценный ответ!
Может быть, вас смущает, что вместо конкретного числа я пишу какие-то непонятные буковки и значки?
Ну что ж, ладно, уговорили… Специально для вас:
x = log25 = 2,321928095…
Имейте в виду, что число это никогда не кончается. Да-да! Иррациональное оно…
Да-да! Иррациональное оно…
Вот вам и ответ на вопрос, для чего нужны логарифмы. Логарифмы нам нужны, в первую очередь, для решения показательных уравнений! Таких, которые без логарифмов и не решаются вовсе…
Например, решая показательное уравнение
3x = 9,
про логарифмы можно не вспоминать. Сразу ясно, что х = 2.
А вот, решая уравнение, скажем, такое
3х = 7,
вы приближённо получите вот такой лохматый ответ:
х ≈ 1,77124375
Зато через логарифм даётся абсолютно точный ответ:
х = log37.
И все дела.) Вот поэтому и пишут логарифмы вместо некрасивых иррациональных чисел. Кому нужен числовой ответ — посчитает на калькуляторе или хотя бы в Excel.) А раньше, когда калькуляторов и компьютеров не было и в помине, существовали специальные таблицы логарифмов. Объёмные и увесистые. Так же, как и таблицы Брадиса для синусов и косинусов. И даже инструмент такой был — логарифмическая линейка. Которая позволяла с хорошей точностью вычислять массу полезных вещей. И не только логарифмы.)
Объёмные и увесистые. Так же, как и таблицы Брадиса для синусов и косинусов. И даже инструмент такой был — логарифмическая линейка. Которая позволяла с хорошей точностью вычислять массу полезных вещей. И не только логарифмы.)
Ну вот. Теперь, незаметно для себя, мы научились решать все показательные уравнения такого зверского типа.
Например:
2х = 13
Никаких проблем:
x = log213
5х = 26
Тоже элементарно!
x = log526
11x = 0,123
И тут не вопрос:
x = log110,123
Это всё верные ответы! Ну как? Заманчиво, правда?
А теперь вдумаемся в смысл самой операции нахождения логарифма.
Как мы знаем, на каждое действие математики стараются найти противодействие (т.е. обратное действие). Для сложения это вычитание, для умножения это деление. А какое обратное действие есть для возведения в степень?
Для сложения это вычитание, для умножения это деление. А какое обратное действие есть для возведения в степень?
Давайте посмотрим. Какие у нас основные действующие фигуры при возведении в степень? Вот они:
an = b
a — основание,
n — показатель,
b — собственно сама степень.
А теперь подумаем: если нам известна степень (b) и известен показатель этой самой степени (n), а найти надо основание (a), то что мы обычно делаем? Правильно! Извлекаем корень n-й степени! Вот так:
А теперь посмотрим на другую ситуацию: нам снова известна степень (b), но на этот раз вместо показателя n нам известно основание (a), а найти как раз надо этот самый показатель (n). Что делать будем?
Вот тут-то на помощь и приходят логарифмы! Прямо так и пишут:
«Эн» (n) — это число, в которое надо возвести «a», чтобы получить «b». Вот и всё. Вот и весь смысл логарифма. Операция нахождения логарифма — это всего лишь поиск показателя степени по известным степени и основанию.
Вот и всё. Вот и весь смысл логарифма. Операция нахождения логарифма — это всего лишь поиск показателя степени по известным степени и основанию.
Таким образом, для возведения в степень в математике существует два разных по природе обратных действия. Это извлечение корня и нахождение логарифма. А вот, скажем для умножения обратное действие только одно — деление. Оно и понятно: любой из неизвестных множителей — что первый, что второй — ищется с помощью одной операции — деления.)
Простейшие примеры с логарифмами.
А теперь новость не очень хорошая. Если логарифм считается ровно, то его надо считать, да.
Скажем, если где-то в уравнении вы получили
x = log39,
то такой ответ никто не оценит. Надо логарифм посчитать и записать:
х = 2
А как мы поняли, что log39=2? Переводим равенство с математического языка на русский: логарифм девяти по основанию три — это число, в которое надо возвести три, чтобы получить девять. И в какое же число надо возвести тройку, чтобы получить девятку? Ну, конечно! В квадрат надо возвести. То есть, в двойку.)
И в какое же число надо возвести тройку, чтобы получить девятку? Ну, конечно! В квадрат надо возвести. То есть, в двойку.)
А чему равен, скажем, log5125? А в какой степени пятёрка даёт нам 125? В третьей, разумеется (т.е. в кубе)!
Стало быть, log5125 = 3.
Идём дальше.
log77 = ?
В какую степень надо возвести 7, чтобы получить 7? В первую!
Вот вам и ответ: log77 = 1
А вот такой пример как вам?
log31 = ?
И в какую же степень надо возвести тройку, чтобы получить единицу? Неужели не догадались? А вы вспомните свойства степеней.) Да! В нулевую! Вот и пишем:
log31 = 0
Уловили принцип? Тогда тренируемся:
log216 = …
log464 = …
log1313 = …
log3243 = …
log151 = …
Ответы (в беспорядке): 1; 3; 5; 0; 4.
Что? Забыли, в какой степени 3 даёт 243? Что ж, ничего не поделаешь: степени популярных чисел надо узнавать. В лицо! Ну, и таблица умножения — надёжный спутник и помощник. И не только в логарифмах.)
Ну вот, совсем простенькие примеры порешали, а теперь шагаем на ступеньку выше. Вспоминаем отрицательные и дробные показатели.)
Решаем вот такой пример:
log40,25 = ?
Мда… И в какую же степень надо возвести четвёрку, чтобы получить 0,25? Так с ходу и не скажешь. Если работать только с натуральными показателями. Но степени в математике, как известно, бывают не только натуральными. Самое время подключить наши знания об отрицательных показателях и вспомнить, что
0,25 = 1/4 = 4-1
Стало быть, можно смело записать:
log40,25 = log44-1 = -1.
И всё.)
Ещё пример:
log42 = ?
В какую такую степень надо возвести четвёрку, чтобы получить двойку? Для ответа на этот вопрос придётся подключать наши знания о корнях. И вспомнить, что двойка — это корень квадратный из четырёх:
И вспомнить, что двойка — это корень квадратный из четырёх:
А корень квадратный математика позволяет представить в виде степени! С показателем 1/2. Так и пишем:
Поэтому наш логарифм будет равен:
Ну что, поздравляю! Вот мы с вами и познакомились с логарифмами. На самом примитивном начальном уровне.) И вы сами лично убедились, что они вовсе не так страшны, как, возможно, вам казалось раньше. Но у логарифмов, как и у любых других математических понятий, есть свои свойства и свои особые фишки. О том и о другом (о свойствах и о фишках) — в следующем уроке.
А теперь решаем самостоятельно.
Вычислить:
Ответы (в беспорядке): 4,4; 0; 1; 6; 4; 2.
Для чего нужны логарифмы?
Слово «логарифм» многие бывшие ученики общеобразовательных учреждений помнят со школьных уроков математики. Эта тема некоторым из них казалась сложной и непонятной. Не все из них действительно поняли, что такое логарифмы и для чего они нужны. Попробуем разобраться в этом вместе с вами.
Попробуем разобраться в этом вместе с вами.
Конечно, в математике есть определение этого слова, но оно не всем может показаться понятным. Логарифмирование – это действие, которое обратно возведению в степень. Неподготовленному человеку трудно понять, что означают эти слова, и какая от всего этого польза.
Что же это такое и как с этим можно работать?
Допустим, нужно найти х в уравнении 5х = 12. В этом случае х будет равен числу, в которое надо возвести 5, чтобы получилось 12. Используя логарифм, этот пример будет звучать так: х равен логарифму 12 по основанию 5. А выгладит уравнение так: х = log512. Если произвести вычисление на калькуляторе или компьютере, то получается иррациональное число. Чтобы было легче работать с такими числами, и создали такую математическую конструкцию, как логарифм.
Говоря простым языком, они нужны для упрощения трудных вычислений. Логарифмы обладают важными свойствами, благодаря которым умножение можно заменить простым сложением, а извлечение корня и его возведение в степень можно преобразовать в умножение и в деление.
Применение свойств логарифмов в жизнедеятельности человека
Если логарифмы имеют одинаковое основание, то их сумма равна логарифму произведения, а разность – частного. И получается, что при математических действиях со сложными иррациональными числами, результатом становятся привычные всем натуральные числа. Если основания логарифма разные, то их можно преобразовать по формулам перехода к новому основанию.
Для упрощения подобных вычислений были созданы логарифмические таблицы. С их помощью можно было легко умножать числа, складывая их логарифмы. Более 300 лет такие таблицы расширялись и уточнялись многими математиками. С появлением возможности электронных вычислений, пользоваться логарифмами стало ещё проще. Таблицы теперь используют только в узкоспециализированных сферах.
Свойства логарифмов на практике пригодятся многим людям, занятым на производстве и в научных сферах, в которых необходимы трудоёмкие вычисления. С их помощью можно сравнивать величины, значительно отличающиеся друг от друга.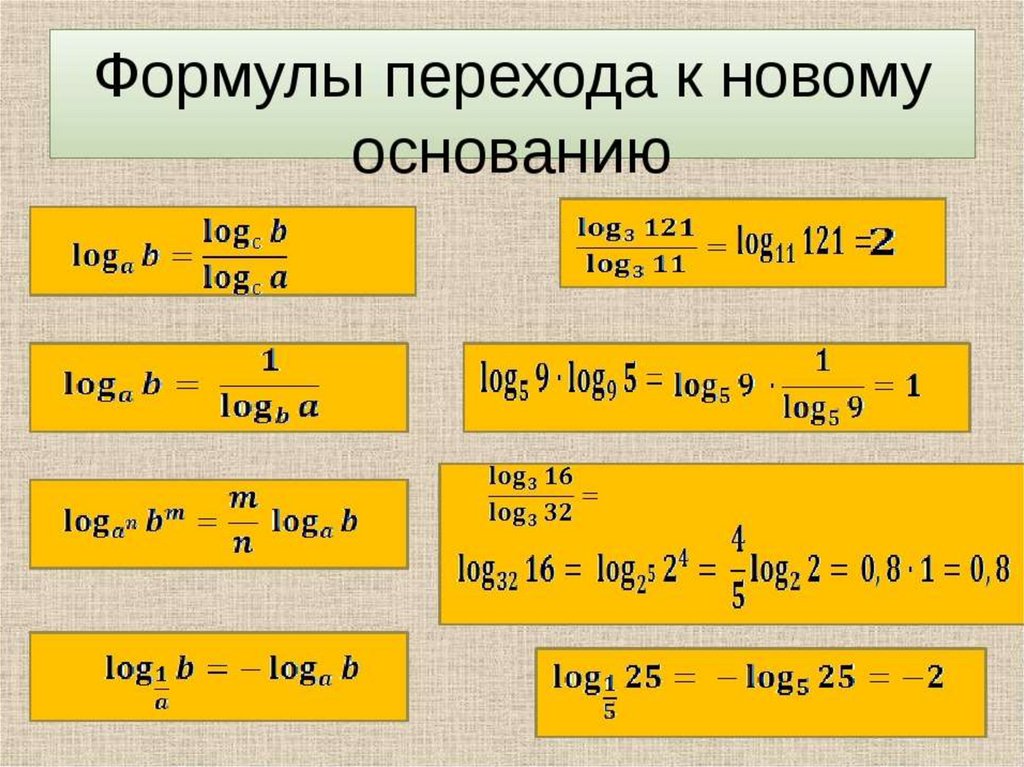 Если вы нарисуете обычный график, на котором отмечены значения 10, 100 и 100 000, то маленькие значения будут практически около ноля. Но логарифмическая линейка позволяет сделать изображение таких чисел более наглядным. С помощью подобных схем часто проводится анализ сравнения шумов, что бывает полезным во многих сферах.
Если вы нарисуете обычный график, на котором отмечены значения 10, 100 и 100 000, то маленькие значения будут практически около ноля. Но логарифмическая линейка позволяет сделать изображение таких чисел более наглядным. С помощью подобных схем часто проводится анализ сравнения шумов, что бывает полезным во многих сферах.
Где можно получить больше информации о свойствах логарифмов?
Пропустили занятие в школе, готовитесь к ЕГЭ или просто интересуетесь математикой? Тогда вам может пригодиться видеоурок на тему «Свойства логарифмов. Логарифм степени», который можно найти, перейдя по ссылке .
В рамках занятия преподаватель не только расскажет о формуле логарифма степени, но и докажет её и напомнит некоторые важные свойства логарифмов. Также можно узнать, как использовать свойства логарифма при решении распространенных примеров. Видеоурок дополнен иллюстрированным текстовым конспектом, в котором также можно найти необходимую информацию.
Стоит отметить, что на образовательном портале можно найти видеоуроки и конспекты не только по алгебре и геометрии, но и по остальным предметам школьной программы, включая обществознание, географию, биологию, и многим другим.
Наука, учеба, религия
Дата: 15/09/16
Комментариев: 0
Brilliant Math & Science Wiki
Хеманг Агарвал, Броди Аккилано, танвин дингра, и
способствовал
Содержимое
- Свойства логарифмов — основные
- Примеры работы с использованием свойств
- Свойства логарифмов — средний уровень
- Решение проблем — базовое
- Решение проблем — средний уровень
- Решение проблем — продвинутый уровень
 Кроме того, log\loglog без базы является сокращением для общего log\loglog базы 10.10.10. Теперь, когда мы это знаем, мы можем манипулировать журналами:
Кроме того, log\loglog без базы является сокращением для общего log\loglog базы 10.10.10. Теперь, когда мы это знаем, мы можем манипулировать журналами:В математике В английском языке Пример logab+logac=logabc\log_a b + log_a bclogab+logac=logabc При добавлении логов с одинаковой базой можно объединить в один лог и умножить их аргументы. 92}{e}=\frac{1}{2}\log_{\pi}{e}logπ2e=21logπe logab=logcblogca\log_a b = \ frac{\log_c b}{\log_c a}logab=logcalogcb Это изменение базовой формулы. Вы можете изменить любой журнал, составив дробь с журналом аргумента в числителе и журналом основания в знаменателе. Для логов можно выбрать любую базу, но базы должны быть одинаковыми для обоих логов. log2π=logπlog2\log_2 \pi = \frac{\log \pi}{\log 2}log2π=log2logπ 92\справа)\\ &=2 \cdot ( 5 \cdot \log_2 2 — 2 \cdot \log_2 3)\\ &=2 \cdot ( 5 \cdot 1 -2 \cdot \log_2 3)\\ &=10- 4 \log_2 3.  \end{выровнено}log2(932)2=2⋅log2(932)=2⋅(log232-log29)=2⋅(log225-log232)=2⋅( 5⋅log22−2⋅log23)=2⋅(5⋅1−2⋅log23)=10−4log23.
\end{выровнено}log2(932)2=2⋅log2(932)=2⋅(log232-log29)=2⋅(log225-log232)=2⋅( 5⋅log22−2⋅log23)=2⋅(5⋅1−2⋅log23)=10−4log23.Примечание: log23\log_2 3log23 нельзя упростить дальше. В строке 1 использовалось второе свойство, в строке 2 фигурки приводились в экспоненциальную форму, в строке 3 использовалось третье свойство, а в строках 4 и 5 выполнялось базовое упрощение. □_\квадрат□ 92}+\frac{1}{2}(4)(\log_2{5})+\log_2{5}\\ &=2\frac{\frac{1}{2}\log 5}{2\log 2}+2\log_2{5}+\log_2{5}\\ &=\frac{1}{2}\frac{\log 5}{\log 2}+3\log_2{5}\\ &=\frac{1}{2}\log_2{5}+3\log_2{5}\\ &=\frac{7}{2}\log_2{5}. \end{выровнено}2log(22)(521)+21log2(54)−log2(5−1)=2log22log521+21(4)(log25)+log25 =22log221log5+2log25+log25=21log2log5+3log25=21log25+3log25=27log25.
Первая строка показывает, что лучше всего (обычно) преобразовывать числа так, чтобы они были целыми числами в степени. Обратите внимание, что строки 4 обращают процесс четвертого свойства. □_\квадрат□ 9{ б } } = б \ журнал { а } \ большой) \\ &= 4.
 \ _\square &&\qquad (\text{по свойству 1})
\end{align}log216=log224=4log22=4. □(16=24)(logab=bloga)(по свойству 1)
\ _\square &&\qquad (\text{по свойству 1})
\end{align}log216=log224=4log22=4. □(16=24)(logab=bloga)(по свойству 1)3. loga(b×c)=logab+logac3.~\log _{ a }{ (b \times c) } = \log _{ a }{ b }+ \log _{ a }{ c } 3. loga(b×c)=logab+logac
Найдите значение log90\log { 90 }log90, предполагая, что log3=0,47\log{3} =0,47log3=0,47.
У нас есть
лог90=лог(9×10)(90=9×10)=лог9+log10(loga(b×c)=logab+logac)=2log3+1(по свойствам 2 и 1)=2×0,47+1=0,94+1=1,94. □\begin{выровнено} \лог {90} &= \log { (9\times 10) } &&\qquad (90= 9 \times 10)\\ &=\log { 9 } + \log { 10 } &&\qquad \big(\log _{ a }{ (b\times c) } =\log _{ a }{ b } +\log _{ a } {с} \большой)\\ &=2\log { 3 } +1 &&\qquad \text{(по свойствам 2 и 1)}\\ &=2\умножить на 0,47+1\\ &=0,94+1\\ &=1,94. \ _\квадрат \end{выровнено}log90=log(9×10)=log9+log10=2log3+1=2×0,47+1=0,94+1=1,94. □(90=9×10)(loga(b×c)=logab+logac) (по свойствам 2 и 1)
4.
 logabc=logab−logac4.~\displaystyle{\log _{a} {\frac {b}{c}} = \log _{a}{b} — \log _{ а }{ в }}4. logacb=logab-logac
logabc=logab−logac4.~\displaystyle{\log _{a} {\frac {b}{c}} = \log _{a}{b} — \log _{ а }{ в }}4. logacb=logab-logacВычислите log0,27\log { 0,27}log0,27, предполагая, что log3=0,47\log{3} =0,47log3=0,47.
У нас есть
log0,27=log27100=log27−log100=3log3−2=1,41−2=−0,59. □\begin{выровнено} \лог {0,27} &= \log { \frac { 27 }{ 100 } } \\ &= \log {27} — \log{100} \\ &=3\лог{ 3 } — 2\\ &=1,41 — 2\\ &=-0,59. \ _\квадрат \end{выровнено}log0.27=log10027=log27-log100=3log3-2=1.41-2=-0.59. □
5.5.5. logab=logcblogca\displaystyle{\log_{a}{b} = \frac{\log_{c}{b}}}{\log_{c}{a}}} logab=logc alogcb
Найдите значение log322\log_{ 32 }{ 2 }log322.
У нас есть
log322=log22log232=15log22=15=0,2. □\begin{выровнено} \log_{ 32 }{ 2 } &=\frac { \log_{ 2 }{ 2 } }{ \log_{ 2 }{ 32 } } \\ &=\frac { 1 }{ 5\log_{ 2 }{ 2 } } \\ &=\фракция { 1 }{ 5 }\\ &={0,2}. \ _\квадрат \end{выровнено} log322=log232log22=5log221=51=0,2.
 □
92-2x-3 &= 0 \\
(х+1)(х-3) &= 0 \\
х &= -1, 3.
\end{выровнено} log2x+log(x−1)log2x(x−1)⇒2x(x−1)x2−2x−3(x+1)(x−3)x=log(x2+3) =log(x2+3)=x2+3=0=0=-1,3.
□
92-2x-3 &= 0 \\
(х+1)(х-3) &= 0 \\
х &= -1, 3.
\end{выровнено} log2x+log(x−1)log2x(x−1)⇒2x(x−1)x2−2x−3(x+1)(x−3)x=log(x2+3) =log(x2+3)=x2+3=0=0=-1,3.Поскольку логарифмические функции log(x−1) \log(x-1)log(x−1) и log2x \log 2xlog2x определены для положительных чисел, должно быть верно, что x−1>
0 ⟹ x >1x-1>0 \подразумевает x>1x−1>0⟹x>1 и 2x>0 ⟹ x>0,2x>0 \подразумевает x>0,2x>0⟹x>0. Таким образом, −1-1−1 не может быть значением x,x,x, из чего следует, что значение xxx, удовлетворяющее данному уравнению, равно x=3.x=3.x=3. □_\квадрат□ 92-2\log_{3} х — 3 &= 0 \\ (\log_{3} x +1)(\log_{3} x — 3) &= 0 \\ \log_{3} х &= -1, 3. \end{выровнено} xlog3x−2⇒(log3x−2)log3x(log3x)2−2log3x−3(log3x+1)(log3x−3)log3x =27=log327=0=0=−1,3.Так как logab+logba \log_{a} b + \log_{b} a logab+logba можно выразить как log3blog3a+log3alog3b\frac{\log_{ 3} b}{\log_{3} a} + \frac{\log_{3} a}{\log_{3} b}log3alog3b+log3blog3a, используя log с основанием 3,
logab+logba=log3blog3a+log3alog3b=−13+3−1=−103.
 □ \begin{выровнено}
\log_{a} b + \log_{b} a &= \frac{\log_{3} b}{\log_{3} a} + \frac{\log_{3} a}{\log_{3} б} \\
&= \frac{-1}{3} + \frac{3}{-1} \\
&= -\фракция{10}{3}. \ _\квадрат
\end{выровнено} logab+logba=log3alog3b+log3blog3a=3−1+−13=−310. □
92 — b \log_{2} \frac{1}{8} + 3a &= 0 \\
\Стрелка вправо 9+3b+3a &=0. \qquad (3)
\end{выровнено} (log22)2-blog22+3a⇒1-b+3a(log281)2-blog281+3a⇒9+3b+3a=0=0,( 2)=0=0.(3)
□ \begin{выровнено}
\log_{a} b + \log_{b} a &= \frac{\log_{3} b}{\log_{3} a} + \frac{\log_{3} a}{\log_{3} б} \\
&= \frac{-1}{3} + \frac{3}{-1} \\
&= -\фракция{10}{3}. \ _\квадрат
\end{выровнено} logab+logba=log3alog3b+log3blog3a=3−1+−13=−310. □
92 — b \log_{2} \frac{1}{8} + 3a &= 0 \\
\Стрелка вправо 9+3b+3a &=0. \qquad (3)
\end{выровнено} (log22)2-blog22+3a⇒1-b+3a(log281)2-blog281+3a⇒9+3b+3a=0=0,( 2)=0=0.(3)Решение уравнений (2)(2)(2) и (3)(3)(3) дает a=-1a= -1a=-1 и b=-2.b = -2.b=-2 . □_\квадрат□
Следующие логарифмы представляют собой арифметическую прогрессию:
log24+log216+log264+⋯+x=42.\log_{2}4 + \log_{2}{16} + \log_ {2}{64} + \cdots + x = 42.log24+log216+log264+⋯+x=42.
Если xxx может быть выражено как log2a,\log_{2}a,log2a, найдите значение a.a.a.
Каковы решения уравнения
logxxy×logyxy+logx(x−y)×logy(x−y)=0? \log_{x} xy \times \log_{y} xy + \log_{x}(xy) \times \log_{y} (xy) = 0?logxxy×logyxy+logx(x−y )×логия(x−y)=0?
У нас есть
log(x−y)logy=0(logxy)2+(log(x−y))2logx⋅logy=0(logxy)2+(log(x− y))2=0⇒logxy=0 и log(x−y)=0.
 2 &= 0 \\
\стрелка вправо \log xy &= 0 \text{ и } \log(x-y)= 0. \\
\end{выравнивание} logxxy×logyxy+logx(x−y)×logy(x−y)logxlogxy×logylogxy+logxlog(x–y)×logylog(x–y)logx ⋅логия(logxy)2+(log(x−y))2(logxy)2+(log(x−y))2⇒logxy=0=0=0=0=0 и log(x−y )=0,
2 &= 0 \\
\стрелка вправо \log xy &= 0 \text{ и } \log(x-y)= 0. \\
\end{выравнивание} logxxy×logyxy+logx(x−y)×logy(x−y)logxlogxy×logylogxy+logxlog(x–y)×logylog(x–y)logx ⋅логия(logxy)2+(log(x−y))2(logxy)2+(log(x−y))2⇒logxy=0=0=0=0=0 и log(x−y )=0,Поскольку xxx и yyy оба положительны, это означает, что
xy=1 и x−y=1⇒x=5+12,y=5−12. □ \begin{выровнено} ху &= 1 \текст{ и } х-у=1 \\ \Rightarrow x&= \frac{\sqrt{5} +1}{2}, y=\frac{\sqrt{5}-1}{2}. \ _\квадрат \end{выровнено} xy⇒x=1 и x−y=1=25+1,y=25−1. □
Шкала Рихтера:
Шкала Рихтера была разработана Чарльзом Рихтером в 1935 году для сравнения силы землетрясений. Количество энергии, высвобождаемой при землетрясении, очень велико, поэтому логарифмическая шкала позволяет избежать использования больших чисел.
Для этих расчетов используется следующая формула:
M=log10(II0),M= \log_{10}\left(\frac{I}{I_0}\right),M=log10(I0I ),
, где MMM — магнитуда по шкале Рихтера, III — интенсивность измеряемого землетрясения, а I0I_0I0 — интенсивность эталонного землетрясения.

Давайте сделаем быстрый пример, чтобы прояснить, как это работает.
Землетрясение в Сан-Франциско в 1906 году имело магнитуду 8,3 балла по шкале Рихтера. В то же время в Южной Америке произошло землетрясение магнитудой 4,1, причинившее лишь незначительные разрушения. Во сколько раз сильнее было землетрясение в Сан-Франциско, чем в Южной Америке? 9M \ приблизительно 15848,9319210M≈15848,93192 раза!
Обратите внимание, что вы можете просто вычесть 4,1 из 8,3 и получить тот же результат. Но если ваши учителя математики такие же, как мои, они захотят, чтобы вы использовали логарифмы, и вот как это делается. Причина, по которой вычитание величин работает, заключается в правиле экспоненты для деления экспонент с одним и тем же основанием.
Шкала децибел:
Один децибел равен одной десятой бела, назван в честь Александра Грэхема Белла. Бел редко используется без префикса деци-, означающего одну десятую. Шкала децибел используется для расчета разницы в интенсивности между двумя звуками:
L=10log10(II0),L=10\log_{10}\left(\frac{I}{I_0}\right),L=10log10(I0I),
где L LL — громкость звука, измеряемая в децибелах, III — интенсивность измеряемого звука, I0I_0I0 — интенсивность звука на пороге слышимости, равном нулю децибел.

Шкала pH\text{pH}pH:
Шкала pH\text{pH}pH была изобретена в 1910 году доктором Сореном Соренсоном, руководителем лаборатории Carlsberg Beer Company. Буква «H» в слове pH\text{pH}pH обозначает водород, а значение «p» в слове pH\text{pH}pH, хотя и оспаривается, обычно считается означающим силу водорода. Эта шкала используется для измерения кислотности или щелочности воды или водорастворимых веществ, включая почву или дождевую воду, но не ограничиваясь ими. Шкала pH\text{pH}pH колеблется от 1 до 14, где семь — нейтральная точка. Значения ниже 7 указывают на кислотность, при этом 1 является наиболее кислой. Значения выше 7 указывают на щелочность, причем 24 является самой щелочной:
pH=-log10[HX+],\text{pH}=-\log_{10}\ce{[H+]},pH=-log10[HX+],
где pH\text{pH} pH – это число pH\text{pH}pH в диапазоне от 111 до 141 414, а [HX+]\ce{[H+]}[HX+] – концентрация ионов водорода.
- Решение логарифмических уравнений
- Графики логарифмических функций
- Решение логарифмических неравенств
Процитировать как: Логарифмы.
 Brilliant.org .
Полученное из
https://brilliant.org/wiki/логарифмы/
Brilliant.org .
Полученное из
https://brilliant.org/wiki/логарифмы/Логарифм | Вики по математике | Фэндом
в: Функции, анализ, предварительное исчисление, логарифмы
английский
Просмотреть источникЛогарифмы — это алгебраические понятия, которые завершают «экспоненциальный круг» (изображенный справа), метафору трех переменных в общем экспоненциальном выражении.
Используя логарифмы, можно найти любую переменную через две другие.
Обратите внимание, что синий текст и стрелки указывают на возведение в степень, а красный указывает на типичное обратное — корни. Логарифмическая зависимость, выделенная зеленым цветом, показывает, как одно может быть разрешено с точки зрения других.
Алгебраически это то, что делают логарифмы. Это очень полезный инструмент для перестановки и обработки алгебраических выражений.
Подстрочное число является основанием логарифма, поскольку оно также является основанием экспоненты.

Содержимое
- 1 Пример
- 2 Ограничения
- 3 приближения
- 4 Примечание о логарифмах
- 5 Графики логарифмических функций
- 6 Обратное возведение в степень
- 7 Свойства логарифмов
Пример
Зная, что и, следовательно, что , мы можем выразить одни и те же три числа с одной экспоненциальной зависимостью двумя разными способами: один решить для 9, а другой решить для 3.
Но если вы хотите найти 2 или любую другую степень, вы должны сделать это с помощью логарифмов:
Аналогично, как показано на рисунке выше, если тогда и .
Теперь можно решать уравнения в форме без необходимости угадывать и проверять, теперь есть систематический и алгебраический метод получения правильного решения в явном виде.
Ограничения
Логарифмы с основанием 0 или 1 не определены.
Логарифмы отрицательных значений не являются действительными комплексными числами.
 (см. комплексный анализ).
(см. комплексный анализ).Приближения
Чтобы начать работу с логарифмическими приближениями, аппроксимируйте логарифм простых чисел следующим образом:
Тогда ознакомьтесь с приближениями логарифмической шкалы для получения дополнительной информации.
Замечание о логарифмах
Для логарифмов требуется базовое число, потому что, в конце концов, функция имеет два входа, которые определенным образом связаны друг с другом и дают один выход. Было бы невозможно прийти к единственному решению, зная только вход или базу, но не то и другое. Следовательно, для всех логарифмов требуется как введенное значение, так и его базовый индекс. Логарифмы — это функция с двумя входами и одним выходом.
Однако общепринятым правилом является пренебрежение записью основания с индексом при обращении к логарифмам с основанием десять. Логарифмы по основанию десять могут быть записаны одним из трех способов и специально называются десятичным логарифмом.


 Кроме того, log\loglog без базы является сокращением для общего log\loglog базы 10.10.10. Теперь, когда мы это знаем, мы можем манипулировать журналами:
Кроме того, log\loglog без базы является сокращением для общего log\loglog базы 10.10.10. Теперь, когда мы это знаем, мы можем манипулировать журналами: \end{выровнено}log2(932)2=2⋅log2(932)=2⋅(log232-log29)=2⋅(log225-log232)=2⋅( 5⋅log22−2⋅log23)=2⋅(5⋅1−2⋅log23)=10−4log23.
\end{выровнено}log2(932)2=2⋅log2(932)=2⋅(log232-log29)=2⋅(log225-log232)=2⋅( 5⋅log22−2⋅log23)=2⋅(5⋅1−2⋅log23)=10−4log23. \ _\square &&\qquad (\text{по свойству 1})
\end{align}log216=log224=4log22=4. □(16=24)(logab=bloga)(по свойству 1)
\ _\square &&\qquad (\text{по свойству 1})
\end{align}log216=log224=4log22=4. □(16=24)(logab=bloga)(по свойству 1) logabc=logab−logac4.~\displaystyle{\log _{a} {\frac {b}{c}} = \log _{a}{b} — \log _{ а }{ в }}4. logacb=logab-logac
logabc=logab−logac4.~\displaystyle{\log _{a} {\frac {b}{c}} = \log _{a}{b} — \log _{ а }{ в }}4. logacb=logab-logac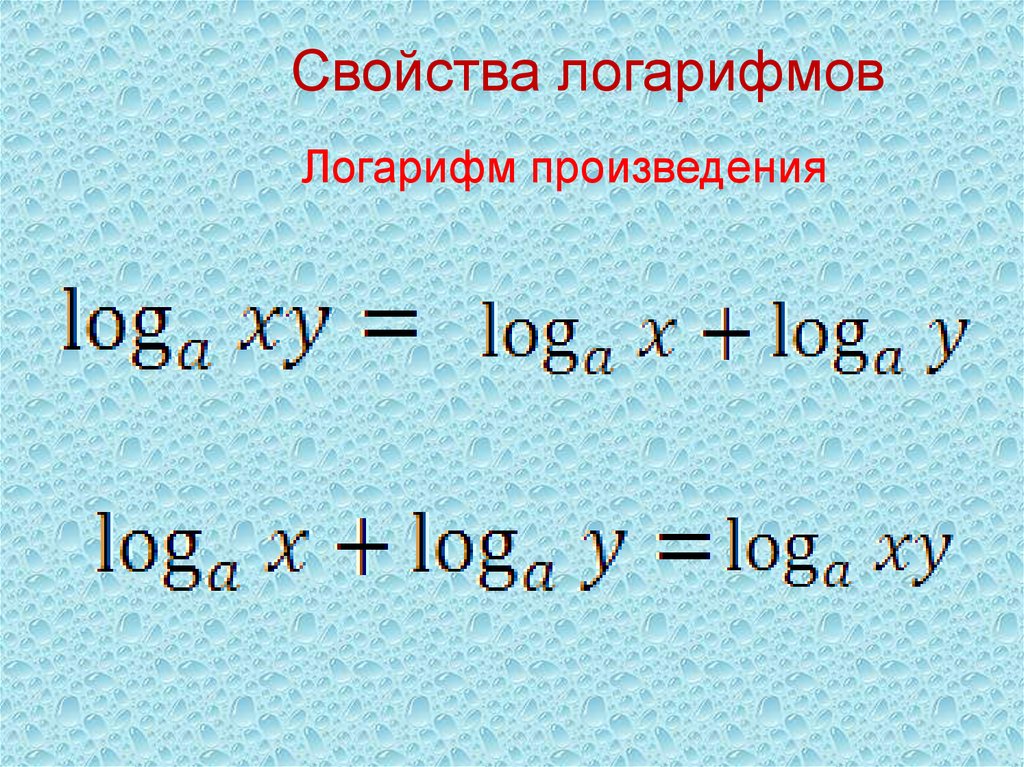 □
92-2x-3 &= 0 \\
(х+1)(х-3) &= 0 \\
х &= -1, 3.
\end{выровнено} log2x+log(x−1)log2x(x−1)⇒2x(x−1)x2−2x−3(x+1)(x−3)x=log(x2+3) =log(x2+3)=x2+3=0=0=-1,3.
□
92-2x-3 &= 0 \\
(х+1)(х-3) &= 0 \\
х &= -1, 3.
\end{выровнено} log2x+log(x−1)log2x(x−1)⇒2x(x−1)x2−2x−3(x+1)(x−3)x=log(x2+3) =log(x2+3)=x2+3=0=0=-1,3. □ \begin{выровнено}
\log_{a} b + \log_{b} a &= \frac{\log_{3} b}{\log_{3} a} + \frac{\log_{3} a}{\log_{3} б} \\
&= \frac{-1}{3} + \frac{3}{-1} \\
&= -\фракция{10}{3}. \ _\квадрат
\end{выровнено} logab+logba=log3alog3b+log3blog3a=3−1+−13=−310. □
92 — b \log_{2} \frac{1}{8} + 3a &= 0 \\
\Стрелка вправо 9+3b+3a &=0. \qquad (3)
\end{выровнено} (log22)2-blog22+3a⇒1-b+3a(log281)2-blog281+3a⇒9+3b+3a=0=0,( 2)=0=0.(3)
□ \begin{выровнено}
\log_{a} b + \log_{b} a &= \frac{\log_{3} b}{\log_{3} a} + \frac{\log_{3} a}{\log_{3} б} \\
&= \frac{-1}{3} + \frac{3}{-1} \\
&= -\фракция{10}{3}. \ _\квадрат
\end{выровнено} logab+logba=log3alog3b+log3blog3a=3−1+−13=−310. □
92 — b \log_{2} \frac{1}{8} + 3a &= 0 \\
\Стрелка вправо 9+3b+3a &=0. \qquad (3)
\end{выровнено} (log22)2-blog22+3a⇒1-b+3a(log281)2-blog281+3a⇒9+3b+3a=0=0,( 2)=0=0.(3) 2 &= 0 \\
\стрелка вправо \log xy &= 0 \text{ и } \log(x-y)= 0. \\
\end{выравнивание} logxxy×logyxy+logx(x−y)×logy(x−y)logxlogxy×logylogxy+logxlog(x–y)×logylog(x–y)logx ⋅логия(logxy)2+(log(x−y))2(logxy)2+(log(x−y))2⇒logxy=0=0=0=0=0 и log(x−y )=0,
2 &= 0 \\
\стрелка вправо \log xy &= 0 \text{ и } \log(x-y)= 0. \\
\end{выравнивание} logxxy×logyxy+logx(x−y)×logy(x−y)logxlogxy×logylogxy+logxlog(x–y)×logylog(x–y)logx ⋅логия(logxy)2+(log(x−y))2(logxy)2+(log(x−y))2⇒logxy=0=0=0=0=0 и log(x−y )=0,

 Brilliant.org .
Полученное из
https://brilliant.org/wiki/логарифмы/
Brilliant.org .
Полученное из
https://brilliant.org/wiki/логарифмы/
 (см. комплексный анализ).
(см. комплексный анализ).