Геометрическая фигура параллелограмм: ПАРАЛЛЕЛОГРАММ | это… Что такое ПАРАЛЛЕЛОГРАММ?

Геометрическая фигура, четырёхугольник, противоположные стороны которого параллельны, 14 (четырнадцать) букв

Вопрос с кроссворда

Ответ на вопрос «Геометрическая фигура, четырёхугольник, противоположные стороны которого параллельны «, 14 (четырнадцать) букв:
параллелограмм

Альтернативные вопросы в кроссвордах для слова параллелограмм

Четырёхугольник, который может и коситься, и прямо смотреть

Четырехугольник, противоположные стороны которого равны и параллельны

Скошенный прямоугольник

Четырёхугольник с параллельными сторонами

Определение слова параллелограмм в словарях

Толковый словарь русского языка. Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
параллелограмма, м. (от греч. parallelos — параллельный и gramma — начертание) (мат.). Четыреугольник, противоположные стороны к-рого равны и параллельны. Параллелограмм сил или скоростей (геом.) — способ нахождения равнодействующей двух сил, скоростей.

Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова. Значение слова в словаре Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
м. Четырехугольник, противоположные стороны которого равны и параллельны.

Энциклопедический словарь, 1998 г. Значение слова в словаре Энциклопедический словарь, 1998 г.
ПАРАЛЛЕЛОГРАММ (от греч. parallelos — параллельный и gramme — линия) четырехугольник, у которого стороны попарно параллельны.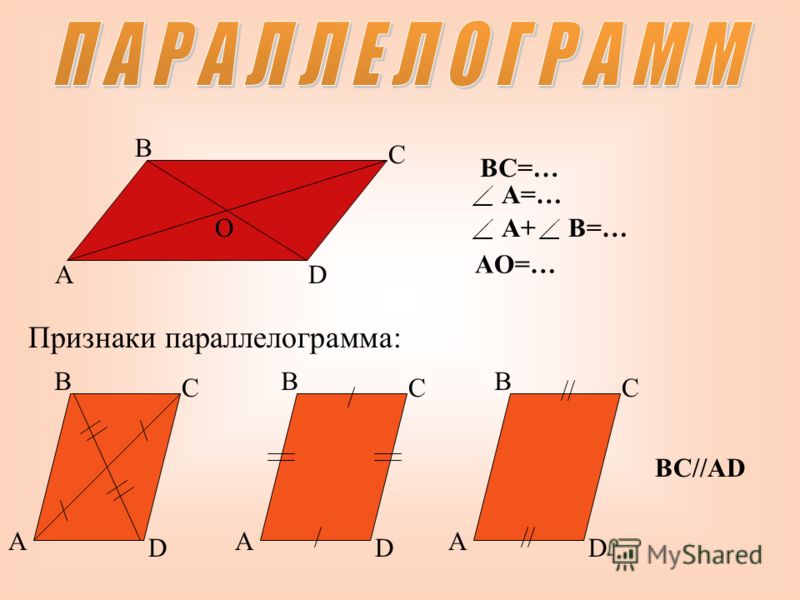

Частные виды параллелограммов: прямоугольник — параллелограмм, все углы которого прямые; ромб — параллелограмм, все стороны которого …

Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова. Значение слова в словаре Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
-а, м. В математике: четырехугольник, у к-рого стороны попарно параллельны.

Большая Советская Энциклопедия Значение слова в словаре Большая Советская Энциклопедия
(греч. parallelógrammon, от parállelos≈параллельный и grámma ≈ линия), четырёхугольник, у которого стороны попарно параллельны (см. рис. а≈г). П. может быть также охарактеризован как выпуклый четырёхугольник при любом из следующих признаков: та и другая .

..

Примеры употребления слова параллелограмм в литературе.

На западе этот параллелограмм на пространстве от Александретты до Адена ограничен гористым поясом, именовавшимся на севере Сирией, который, постепенно опускаясь к югу, последовательно назывался Палестиной, Мидианом, Хиджазом и наконец Йеменом.

Буфет находился в соседней комнате под абстракционистской картиной с нарисованным фуксином подобием женщины о трех грудях, восседающей на параллелограмме.

Уродливое окошко оказалось доступным закату: сбоку по стене пролег пламенистый параллелограмм.

Если при решении какой-нибудь динамической задачи чертится параллелограмм, которого стороны и диагональ представляют силы, и посредством замещения масс силы массами протяжения устанавливается измеряемое отношение между количествами, которые иначе не даются в руки, — то можно смело сказать, что геометрия играет ту же самую роль относительно механики, какую играет огонь литейщика относительно металла, который он готовится плавить.

Если до этого построение кораблей напоминало ромб, то после второй стадии строй принял очертания параллелограмма, на острых углах которого располагались Джеймс и Паладин.

Сильно укрепило его в этом мнении то, что стол, имевший форму узенького параллелограмма, представлял Йорику, сидевшему как раз против Футатория, прекрасный случай ввернуть ему каштан — и что, следовательно, он так и сделал.

Источник: библиотека Максима Мошкова

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

• Четырехугольник (общее для всех четырехугольников)

• Квадрат

• Прямоугольник

• Параллелограмм

• Ромб

• Трапеция

• Треугольник

• Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

 

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если

суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат —  правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a²или S=d²/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

• Все стороны равны, все углы равны и составляют 90°;
• Диагонали квадрата равны и перпендикулярны;
• У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
• Квадрат является одновременно частным случаем ромба и прямоугольника

Калькулятор для квадрата поможет вычислить все характеристики квадрата по одной из известных величин. .

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S =  d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a²+b²)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a²+b²)/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a²+b²) – корень квадратный из (a²+b²).

Свойства:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

.

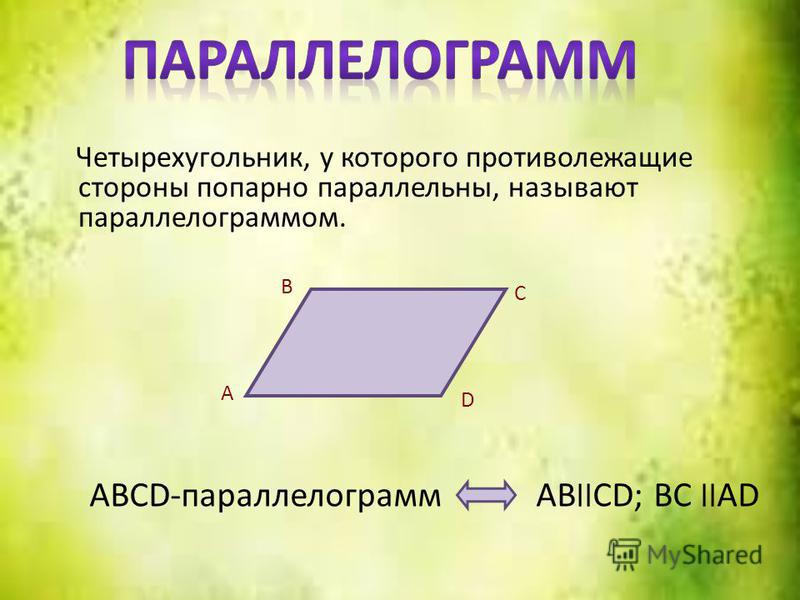
Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁)²+(d₂)²=(a²+b²)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте:  S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними:  S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

• У параллелограмма противоположные стороны равны и противоположные углы равны.
• Сумма любых двух соседних углов параллелограмма равна 180°.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Каждая диагональ делит параллелограмм на два равных треугольника.
• Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
• Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
• Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или  r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a² · sin α

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба

Свойства:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.  
• Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника
  — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними:  S=(a*b)/2* sin γ
                        по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
                        по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c²=a²+b² (Теорема Пифагора)

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ  — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
• Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
• Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
• В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
• Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b² (Теорема Пифагора). В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d).  Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует. 
• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r² или S = π*d²/4

где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

 

 

Калькулятор для окружности и круга поможет вычислить все характеристики круга по одной из известных величин.

В заключении

Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте newlesson.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.

 

Параллелограмм | Encyclopedia.com

gale

просмотров обновлен 27 июня 2018

Обратная сторона. Эта четырехсторонняя фигура называется многоугольником (двумерная [2D] фигура, состоящая из трех или более прямых сторон) или, точнее, четырехугольником (двумерная фигура, состоящая из четырех прямых сторон).

Во всех типах параллелограммов диагонали делят друг друга пополам (или делят пополам) в месте пересечения. (Диагональ — это линия, соединяющая два противоположных угла геометрической фигуры, например параллелограмма. )

Три особых типа параллелограммов называются ромбами, прямоугольниками и квадратами.

Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину, но стороны не обязательно пересекаются под прямым углом друг к другу.

Прямоугольник представляет собой параллелограмм, смежные стороны которого перпендикулярны (встречаются под прямым углом) друг к другу, а противоположные стороны равны по длине.

Квадрат представляет собой параллелограмм, смежные стороны которого перпендикулярны (под углом 90°) и равны по длине. То есть все четыре стороны равны по длине, а стороны, содержащие общую точку, находятся под прямым углом друг к другу.

Площадь (А) параллелограмма равна расстоянию (длине) одной стороны, называемой его основание b, умноженное на кратчайшее расстояние (длину) до противоположной стороны, называемое его высотой или высотой h. Это можно записать как A = bh. Поскольку все четыре стороны (s) квадрата равны, то b= h= s, и его уравнение можно записать как A= 2s. Окружность (С) параллелограмма (или расстояние вокруг него) обозначается: С= 2b+ 2H. В случае квадрата (где все четыре стороны равны по длине) уравнение принимает вид: C = 4s.

Научная энциклопедия Гейла

Гейл

просмотров обновлено 11 мая 2018

Параллелограмм — это плоскость четырехсторонней фигуры, противоположные стороны которой параллельны . Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину; прямоугольник является параллелограммом, смежные стороны которого перпендикулярны ; а квадрат — это параллелограмм, смежные стороны которого перпендикулярны и равны по длине.

Площадь параллелограмма равна длине его основание в раз больше длины его высоты .

Научная энциклопедия Гейла

Оксфорд

просмотра обновлено 11 июня 2018 г. н. четырехсторонняя плоская прямолинейная фигура, противоположные стороны которой параллельны.

параллелограммы

Оксфордский карманный словарь современного английского языка

oxford

просмотров обновлено 18 мая 2018 г.

параллелограмм Четырехугольник (четырехсторонняя плоская фигура), у которого каждая пара противоположных сторон параллельна и равна. Оба противоположных угла параллелограмма также равны. Его площадь равна произведению одной стороны на перпендикулярное расстояние от противоположной стороны. Параллелограмм, у которого все четыре стороны равны, является ромбом.

Всемирная энциклопедия

9 наиболее распространенных форм и способы их идентификации

Вы, вероятно, многое узнали о формах, даже не задумываясь о том, что они из себя представляют. Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.

В этой статье мы рассмотрим, что такое фигура, а также несколько распространенных форм, как они выглядят и основные формулы, связанные с ними.

 

Что такое форма?

Если кто-нибудь спросит вас, что такое фигура, вы, вероятно, сможете назвать несколько из них. Но «форма» имеет и особое значение — это не просто название кругов, квадратов и треугольников.

Форма — это форма объекта, а не то, сколько места он занимает или где он находится физически, а реальная форма, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее фактической круглой формой, которую он принимает.

Фигура может быть любого размера и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места. Это довольно сложно уловить, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например, пирамидальная подставка для книг или цилиндрическая банка из-под овсяных хлопьев, или он может быть двухмерным и не занимать физической комнаты , например треугольник, нарисованный на листе бумаги.

Тот факт, что он имеет форму, отличает форму от точки или линии.

Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни какого бы то ни было измерения.

Линия, напротив, одномерна. Он простирается бесконечно в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.

Хотя мы можем представлять точки или линии в виде фигур, потому что нам нужно их видеть, на самом деле они не имеют никакой формы. Вот что отличает форму от других геометрических фигур — она двумерна или трехмерна, потому что имеет форму.

 

Кубы, подобные тем, что показаны здесь, представляют собой трехмерные формы квадратов — и то, и другое — формы!

 

6 основных типов двумерных геометрических фигур

Трудно изобразить форму только на основе определения— что значит иметь форму , но не занимать место? Давайте рассмотрим несколько различных форм, чтобы лучше понять, что именно означает быть формой!

Мы часто классифицируем фигуры по количеству сторон. «Сторона» — это отрезок линии (часть линии), который составляет часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.

 

Тип 1: Эллипсы

Эллипсы представляют собой круглые овальные формы, в которых заданная точка ( p ) имеет одинаковую сумму расстояний от двух разных фокусов.

 

Овал

Овал немного похож на смазанный круг — он не совсем круглый, а в некотором роде вытянутый. Однако классификация неточная. Есть много, много видов овалов, но общее значение состоит в том, что они имеют круглую форму, которая является удлиненной, а не идеально круглой, как круг. Овал — это любой эллипс, фокусы которого находятся в двух разных положениях.

Поскольку овал не идеально круглый, формулы, которые мы используем для их понимания, должны быть скорректированы.

Также важно отметить, что вычисление длины окружности довольно сложно, поэтому ниже нет уравнения длины окружности. Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией измерения окружности, потому что даже самые лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.

Определения

• Большой радиус : расстояние от начала овала до самого дальнего края
• Малый радиус : расстояние от начала овала до ближайшего края

Формулы

• Площадь = $\Major \Radius*\Minor \Radius*π$

 

Круг

Сколько сторон у круга? Хороший вопрос! К сожалению, хорошего ответа нет, потому что «стороны» больше связаны с многоугольниками — двумерной формой, по крайней мере, с тремя прямыми сторонами и, как правило, по крайней мере с пятью углами. Самые известные фигуры — это многоугольники, но у кругов нет прямых сторон и явно не хватает пяти углов, поэтому они не являются многоугольниками.

 

Итак, сколько сторон у круга? Нуль? Один? На самом деле это не имеет значения — вопрос просто не относится к кругам.

Круг — это не многоугольник, но что это такое? Окружность — это двумерная фигура (у нее нет толщины и глубины), состоящая из кривой, которая всегда находится на одном и том же расстоянии от точки в центре. У овала есть два фокуса в разных положениях, тогда как у круга фокусы всегда находятся в одном и том же положении.

Определения

• Начало: центр окружности
• Радиус: расстояние от начала координат до любой точки на окружности
• Окружность: 92$

 

Тип 2: Треугольники

Треугольники — это простейшие многоугольники. У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.

Поскольку существует много видов треугольников, существует лота важных формул треугольника , многие из них сложнее других. Основы приведены ниже, но даже основы основаны на знании длины сторон треугольника. Если вы не знаете стороны треугольника, вы все равно можете вычислить его различные аспекты, используя углы или только некоторые из сторон.

Определения

• Вершина : точка пересечения двух сторон треугольника
• Основание : любая из сторон треугольника, обычно нижняя сторона
• Высота : расстояние по вертикали от основания до вершины, с которой оно не связано

Формулы

• Площадь = ${\основание*\высота}/2$
• Периметр = $\сторона a + \сторона b + \сторона c$

 

Тип 3: Параллелограммы

Параллелограмм — это фигура с равными противоположными углами, параллельными противоположными сторонами и параллельными сторонами одинаковой длины. Вы могли заметить, что это определение применимо к квадратам и прямоугольникам, потому что квадратов и прямоугольников также являются параллелограммами ! Если вы можете вычислить площадь квадрата, вы можете сделать это с любым параллелограммом.

Определения

• Длина : мера нижней или верхней стороны параллелограмма
• Ширина : мера левой или правой стороны параллелограмма

Формулы

• Площадь : $\длина*\высота$
• Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4$
• В качестве альтернативы, Периметр : $\Сторона*4$

 

Прямоугольник

Прямоугольник — это фигура с параллельными противоположными сторонами и всеми углами в 90 градусов. Как тип параллелограмма, он имеет противоположные параллельные стороны. В прямоугольнике один набор параллельных сторон длиннее другого, что делает его похожим на вытянутый квадрат.

Поскольку прямоугольник является параллелограммом, вы можете использовать те же самые формулы для вычисления его площади и периметра.

 

Квадрат

Квадрат очень похож на прямоугольник, за одним заметным исключением: все его стороны имеют одинаковую длину. Как и прямоугольники, квадратов имеют все углы 90 градусов и параллельны противоположным сторонам. Это потому, что квадрат на самом деле является типом прямоугольника, который является типом параллелограмма!

По этой причине вы можете использовать те же формулы для вычисления площади или периметра квадрата, что и для любого другого параллелограмма.

 

Ромб

Как вы уже догадались, ромб — это разновидность параллелограмма. Отличие ромба от прямоугольника или квадрата в том, что его внутренние углы только такие же, как и их диагональные противоположности.

Из-за этого ромб немного похож на квадрат или прямоугольник, немного скошенный в сторону . Хотя периметр вычисляется таким же образом, это влияет на способ вычисления площади, поскольку высота уже не такая, как в квадрате или прямоугольнике.

Определение

• Диагональ : длина между двумя противоположными вершинами

Формулы

• Площадь = ${\Диагональ 1*\Диагональ 2}/2$

 

Тип 4: Трапеции

Трапеции — четырехсторонние фигуры с двумя противоположными параллельными сторонами. В отличие от параллелограмма, трапеция имеет только две противоположные параллельные стороны, а не четыре , что влияет на способ вычисления площади и периметра.

Определения

• Основание : любая из параллельных сторон трапеции
• Ножки : любая из трапеций с непараллельными сторонами
• Высота : расстояние от одной базы до другой

Формулы

• Площадь : $({\Base_1\length + \Base_2\length}/2)\altitude$
• Периметр : $\Base + \Base + \Leg + \Leg$

 

Тип 5: Пятиугольники

Пятиугольник — это пятиугольник. Обычно мы видим правильные пятиугольники, у которых все стороны и углы равны , но существуют и неправильные пятиугольники. Неправильный пятиугольник имеет неравные стороны и неравные углы и может быть выпуклым — без углов, направленных внутрь — или вогнутым — с внутренним углом более 180 градусов.

 

Поскольку форма более сложная, ее необходимо разделить на меньшие фигуры, чтобы вычислить ее площадь.

Определения

• Апофема : линия, проведенная из центра пятиугольника к одной из сторон, пересекающая сторону под прямым углом.

Формулы

• Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4 + \Сторона 5$
• Площадь : ${\Perimeter*\Apothem}/2$

 

Тип 6: Шестиугольники

Шестиугольник — это шестиугольник, очень похожий на пятиугольник. Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.

Также как и пятиугольники, формула площади шестиугольника значительно сложнее, чем у параллелограмма.

Формулы

• Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4 + \Сторона 5 + \Сторона 6$
• Зона : ${3√3*\Сторона*2}/2$
• В качестве альтернативы, Зона : ${\Perimeter*\Apothem}/2$

 

Как насчет трехмерных геометрических фигур?

Существуют также трехмерные формы, которые имеют не только длину и ширину, но и глубину или объем. Это формы, которые вы видите в реальном мире, например, сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.

Трехмерные фигуры, естественно, более сложны, чем двумерные, с дополнительным измерением — количеством места, которое они занимают, а не только формой, — которое необходимо учитывать при расчете площади и периметра.

Математика, включающая двумерные формы, такие как приведенные выше, называется плоскостной геометрией, поскольку она имеет дело конкретно с плоскостями или плоскими формами . Математика, связанная с трехмерными формами, такими как сферы и кубы, называется твердотельной геометрией, потому что она имеет дело с твердыми телами, другими словами для трехмерных форм .

 

2D-формы составляют 3D-фигуры, которые мы видим каждый день!

 

3 основных совета по работе с фигурами

Существует так много типов фигур, что бывает сложно запомнить, какие из них есть какие, и как вычислить их площади и периметры. Вот несколько советов и приемов, которые помогут вам их запомнить!

 

#1: определение многоугольников

Некоторые фигуры являются многоугольниками, а некоторые нет. Один из самых простых способов определить, к какому типу формы относится предмет, – выяснить, является ли он многоугольником.

Многоугольник состоит из прямых линий, которые не пересекаются. Какие из фигур ниже являются многоугольниками, а какие нет?

 

Круг и овал не являются многоугольниками, а значит, их площадь и периметр вычисляются по-разному. Узнайте больше о том, как вычислить их с помощью $π$ выше!

 

#2: Проверка на наличие параллельных сторон

Если фигура, на которую вы смотрите, является параллелограммом, обычно проще вычислить его площадь и периметр, чем если это не параллелограмм. Но как определить параллелограмм?

В названии указано — параллельно. Параллелограмм — это четырехсторонний многоугольник с двумя наборами параллельных сторон . Квадраты, прямоугольники и ромбы являются параллелограммами.

Квадраты и прямоугольники используют одни и те же базовые формулы для площади — длина умножается на высоту. Для них также очень легко найти периметр, так как вы просто складываете все стороны вместе.

С ромбами все становится сложнее, потому что диагонали перемножаются и делятся на два.

Чтобы определить, на какой вид параллелограмма вы смотрите, спросите себя, имеет ли он все углы по 90 градусов.

Если да, то это либо квадрат, либо прямоугольник .