Частные случаи простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений вида: sin x = a , cos x = a, tg x = a , ctg x = a, где a – произвольное число.
Решите уравнение sin x = a, a ∈ [–1; 1].
| Уравнение | Решение |
| sin x = -1 | |
| sin x = -√3/2 | |
| sin x = -√2/2 | |
| sin x = -1/2 | |
| sin x = 0 | |
| sin x = 1/2 | |
| sin x = √2/2 | |
| sin x = √3/2 | |
| sin x = 1 |
Решите уравнение cos x = a, a ∈ [–1; 1].
| Уравнение | Решение |
| cos x = -1 | |
| cos x = -√3/2 | |
| cos x = -√2/2 | |
| cos x = -1/2 | |
| cos x = 0 | |
| cos x = 1/2 | |
| cos x = √2/2 | |
| cos x = √3/2 | |
| cos x = 1 |
Решите уравнение tg x = a
| Уравнение | Решение |
| tg x = -√3 | |
| tg x = -1 | |
| tg x = -√3/3 | |
| tg x = 0 | |
| tg x = √3/3 | |
| tg x = 1 | |
| tg x = √3 |
Решите уравнение сtg x = a
| Уравнение | Решение |
| сtg x = -√3 | |
| сtg x = -1 | |
| сtg x = -√3/3 | |
| сtg x = 0 | |
| сtg x = √3/3 | |
| сtg x = 1 | |
| сtg x = √3 |
Все эти значения удобно находить по тригонометрическому кругу:
Ключевые слова: синус, косинус, тангенс, котангенс, tan, cot, от икс, чему равен, минус, корень из, пи, pi, π, делить на, равно.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:08.08.2021
- Рубрика записиТеория
- Автор записи:Andrei Maniakin
Частные случаи простых тригонометрических уравнений.
Алгебра. 10 класс. Глава VI. Тест 3.
Вариант 1.
1. Решите уравнение: 2cos x=0.
A) π+2πn, n∈Z; B) π/2+πn, n∈Z;
C) π+πn, n∈Z; D) π/2+2πn, n∈Z.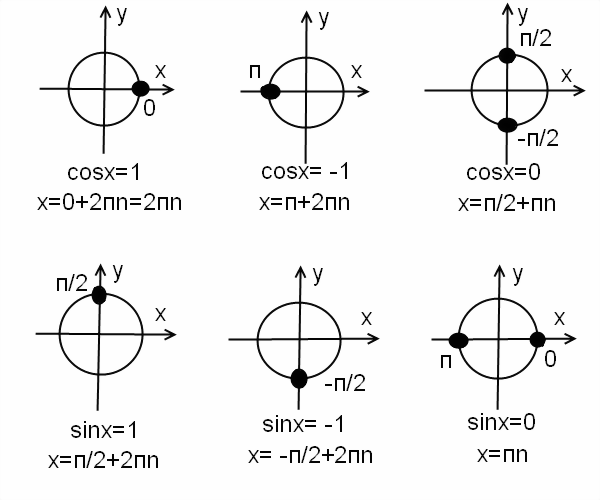
2. Решите уравнение: sin x -1 = 0.
A) π/2+2πn, n∈Z; B) π+2πn, n∈Z;
C) π/2+πn, n∈Z; D) 2πn, n∈Z.
3. Решить уравнение: tg3x=0.
4. Решить уравнение:
5. Решить уравнение:
6. Решить уравнение: cos(π+x) = sin(π/2).
A) π+2πn, n∈Z; B) π+πn, n∈Z;
7. Решите уравнение: sin 5x ∙ sin 4x + cos 5x ∙ cos 4x = 0.
A) π/9 + πn, n∈Z; B) π/2 + 2πn, n∈Z; C) π/4 + πn, n∈Z; D) π/2 + πn, n∈Z.
8. Решить уравнение: cos x + cos 3x = 0.
9. Решите уравнение: 1- cos 2x = 2 sin x.
A) πn; π/2 + 2πn, n∈Z; B) π/2 + 2πn, n∈Z;
C) 2πn, n∈Z; D) 2πn; π/2 + πn, n∈Z.
10. Решить уравнение: 1+cos4x=2cos2x.
11. Решить уравнение: cos22x = 1.
12. Решить уравнение: sin2 2x = 1.
A) π/2 + πn; n∈Z; B) π/2 + 2πn; n∈Z;
C) π/4 + πn; n∈Z; D) π/4 + πn/2; n∈Z.
Вариант 2.
1. Решите уравнение: 3sin x=0.
A) π+2πn, n∈Z; B) πn, n∈Z;
C) π+πn, n∈Z; D) π/2+2πn, n∈Z.
2. Решите уравнение: sin x +1 = 0.
A) -π/2+2πn, n∈Z; B)π+2πn, n∈Z;
C) π/2+πn, n∈Z; D) πn, n∈Z.
3. Решить уравнение: tg5x=0.
4. Решить уравнение:
5. Решить уравнение:
6. Решить уравнение: cos(π+x) = — sin(π/2).
A) π+2πn, n∈Z; B) 2πn, n∈Z; C) π/2+2πn, n∈Z;
7. Решите уравнение: sin 3x ∙ sin 2x + cos 2x ∙ cos 3x = 0.
A) π + πn, n∈Z; B) π/5 + 2πn, n∈Z; C) π/2 + πn, n∈Z; D) π/3 + πn, n∈Z.
8. Решить уравнение: cos 2x — cos 6x = 0.
9. Решите уравнение: 1+ cos 2x = 2 cos x.
A) 2πn; π/2 + πn, n∈Z; B) π/2 + 2πn, n∈Z;
C) 2πn, n∈Z; D) πn; π/4 + 2πn, n∈Z.
10. Решить уравнение: 1-cos4x=2sin2x.
11. Решить уравнение: cos23x = 1.
12. Решить уравнение: sin2 4x = 1.
Сверить ответы.
СПРАВОЧНЫЕ МАТЕРИАЛЫ
Частные формулы для решения простейших тригонометрических уравнений.
1) sin t = 0; t = πn, nϵZ.
2) sin t = 1; t = π/2 +2πn, nϵZ.
3) sin t = -1; t = -π/2 +2πn, nϵZ.
4) cos t = 0; t = π/2 + πn, nϵZ.
5) cos t = 1; t = 2πn, nϵZ.
6) cos t = -1; t = π +2πn, nϵZ.
7) tg t = 0; t = πn, nϵZ.
8) ctg t = 0; t = π/2 +πn, nϵZ.
Рекомендации.
4. Обозначить х-π/3 (х-π/6) через t и решить уравнение cost=0.
5. Сделать замену: пусть 2x+π/7=t (пусть 3x-π/5=t).
6. Использовать формулу приведения cos(π+α)=-cosα.
7. Свернуть выражение с помощью формулы косинуса разности двух углов:
cos(α-β)=cosαcosβ+sinαsinβ.
8. Заменить сумму косинусов произведением по формуле:
Заменить разность косинусов произведением:
Функция косинуса чётная, поэтому cos(-α)=cosα.
Функция синуса нечётная, поэтому sin(-α)= -sinα.
9-10. Применить формулу: 1-cos2α=2sin2α. (*)
(*)
или формулу: 1+cos2α=2cos2α. (**)
11-12. Понизить степень выражения в левой части равенства с помощью формулы (*) или (**) .
Поделиться новостью в соцсетях
Метки: алгебра 10 класс, решить тригонометрическое уравнение тесты, решить уравнение 1-cos4x=2sin2x, тригонометрические формулы, уравнение
4.2: Закон синусов — неоднозначный случай
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 37225
- Ричард В. Беверидж
- Общественный колледж Клэтсопа
Во всех примерах и задачах в разделе \(4. 1,\) обратите внимание, что нам всегда даны два угла и одна сторона, хотя мы могли бы использовать закон синусов, если бы нам были даны один угол и две стороны (пока одна сторон, соответствующих данному углу). Это связано с тем, что когда мы используем закон синусов для нахождения угла, может возникнуть неоднозначность из-за того, что функция синуса положительна в квадранте I и квадранте II.
1,\) обратите внимание, что нам всегда даны два угла и одна сторона, хотя мы могли бы использовать закон синусов, если бы нам были даны один угол и две стороны (пока одна сторон, соответствующих данному углу). Это связано с тем, что когда мы используем закон синусов для нахождения угла, может возникнуть неоднозначность из-за того, что функция синуса положительна в квадранте I и квадранте II.
В главе 3 мы видели, что при использовании обратных тригонометрических функций возникает несколько ответов. Для задач, в которых мы используем закон синусов для одного угла и двух сторон, может быть один возможный треугольник, два возможных треугольника или ни одного возможного треугольника. Есть шесть различных сценариев, связанных с неоднозначным случаем закона синусов: три приводят к одному треугольнику, один приводит к двум треугольникам и два приводят к отсутствию треугольника. 9{\circ}, \quad b=7,6, \quad c=7,1\)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Ричард В.
 Беверидж
Беверидж
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- нет
-
- Теги
- закон синусов
Неоднозначный случай закона синусов
Главная > Математика > Исчисление > Неоднозначный случай закона синусов
При использовании закона синусов для нахождения неизвестного угла вы должны следить за неоднозначным случаем. Это происходит, когда с использованием данной информации можно создать два разных треугольника.
Например, взгляните на эту картинку:
Если вам говорят, что b = 10 дюймов и c = 6 дюймов, есть два разных треугольника, которые соответствуют этому критерию. Как вы можете видеть на рисунке, можно создать как остроугольный, так и тупоугольный треугольник, потому что сторона c может поворачиваться либо внутрь, либо наружу вдоль неизвестной стороны a.
Как вы можете видеть на рисунке, можно создать как остроугольный, так и тупоугольный треугольник, потому что сторона c может поворачиваться либо внутрь, либо наружу вдоль неизвестной стороны a.
Когда вам даны две стороны и угол не между этими сторонами, вам нужно быть настороже в случае неоднозначного случая.
Для определения наличия 2 nd допустимый угол:
1. Посмотрите, даны ли вам две стороны и угол не между ними (SSA). Это ситуация, которая может иметь 2 возможных ответа.
2. Найдите значение неизвестного угла.
3. Как только вы найдете значение своего угла, вычтите его из 180°, чтобы найти возможный второй угол.
4. Добавьте новый угол к исходному углу. Если их сумма меньше 180°, у вас есть два правильных ответа. Если сумма больше 180°, то второй угол недействителен.
Примеры:
1. Используйте закон синусов, чтобы найти меру угла B из нашего примера, в котором , b = 10 дюймов и c = 6 в
Во-первых, мы знаем, что этот треугольник является кандидатом на неоднозначный случай, поскольку нам даны две стороны и угол 90 276, а не 90 277 между ними.
Нам нужно найти угол B, используя закон синусов:
Теперь перекрестим умножим и решим уравнение:
Мы нашли одно значение угла B, но нам нужно посмотреть, есть ли другое возможное значение. Для этого мы вычтем 65,2° из 180°.
180° — 65,2° = 114,8°
Чтобы убедиться, что 114,8° является правильным ответом, мы должны добавить его к другому существующему углу. Если их сумма меньше 180°, мы знаем, что треугольник может существовать. Однако, если он больше 180°, то это неверный ответ (поскольку три угла треугольника в сумме должны давать 180°).
114,8° + 33° = 147,8°
Поскольку 147,8° меньше 180°, мы знаем, что 114,8° — правильный ответ
Окончательный ответ: и
2. Используйте закон синусов, чтобы найти меру угла A в следующем сценарии: c = 10 футов. a = 8 футов.
Если это поможет, вы можете нарисовать грубый набросок, чтобы рассмотреть этот треугольник, но это необязательно. Мы знаем, что этот треугольник является кандидатом на неоднозначный случай, поскольку нам даны две стороны и угол не между ними.
Мы знаем, что этот треугольник является кандидатом на неоднозначный случай, поскольку нам даны две стороны и угол не между ними.
Нам нужно найти угол B, используя закон синусов:
Теперь перекрестим умножим и решим уравнение:
Мы нашли одно значение угла А, но нам нужно посмотреть, есть ли другое возможное значение. Для этого мы вычтем 46,0° из 180°.
180° — 46° = 134°
Чтобы увидеть, является ли 134° допустимым ответом, мы должны добавить его к другому существующему углу. Если их сумма меньше 180°, мы знаем, что треугольник может существовать. Однако если он превышает 180°, то это неверный ответ.
134° + 64° = 198°
Поскольку 198° больше 180°, мы знаем, что второе измерение 134° не является правильным ответом.
Окончательный ответ:
Практика: Используйте закон синусов, чтобы найти угол.

 Беверидж
Беверидж