Что такое тупой угол: определение, примеры задач
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое тупой угол: определение, примеры задач
В данной публикации мы рассмотрим, что такое тупой угол, а также разберем примеры задач, в которых он участвует.
- Определение тупого угла
- Примеры задач
Определение тупого угла
Угол является тупым, если его градусная мера находится между 90 и 180 градусами.
∠α – тупой, если 90° < α < 180°.
То есть тупой угол больше прямого (90°), но меньше развернутого (180°).
Примеры задач
Задание 1
Дан треугольник, у которого известны два угла – 34° и 27°. Найдем третий и определим, является ли он тупым.
Решение:
Примем неизвестную величину за “α“. Как мы знаем, сумма углов треугольника равняется 180 градусам, значит:
α = 180° – 34° – 27° = 119°.
Следовательно, угол α – тупой.
Задание 2
Дан ромб, площадь (
Решение:
Синус угла ромба (α) можно найти следующим образом (выведено из формулы расчета площади фигуры):
Следовательно, α = 30° (arcsin 0,5), является острым.
Как мы знаем, сумма соседних углов ромба составляет 180 градусов, значит второй угол β равен 150° (180° – 30°), и он является тупым.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Тупые углы: краткое описание и особенности
Треугольник – это геометрическая фигура, имеющая три соединенные между собой линиями точки, которые лежат не на единой прямой в плоскости.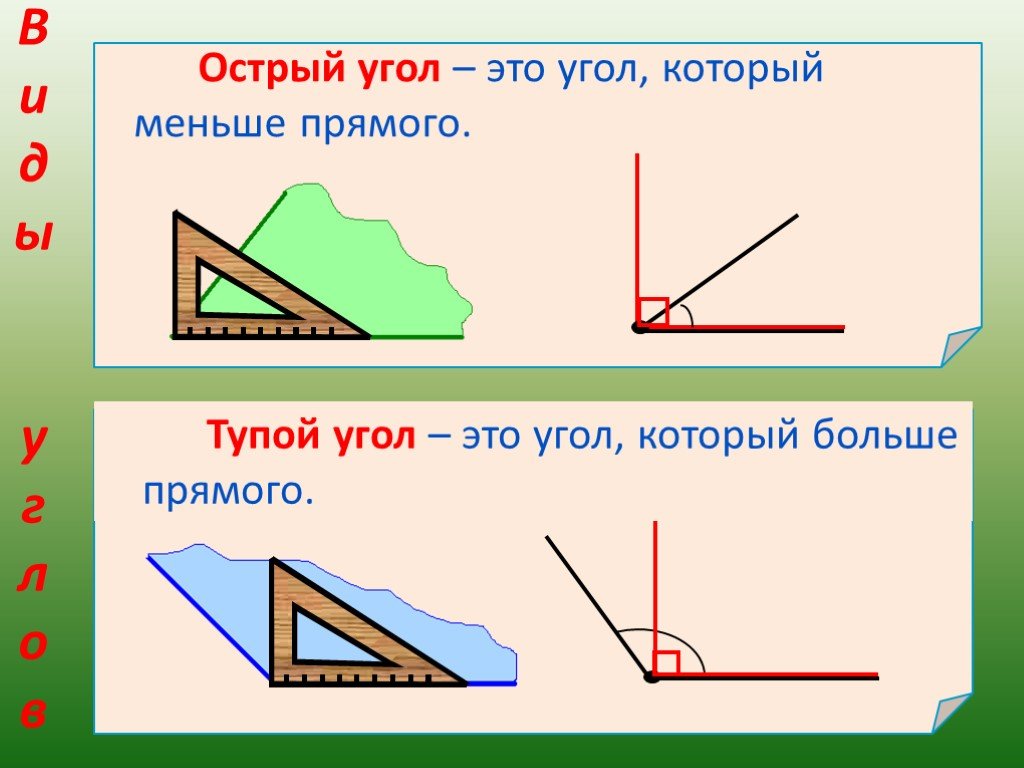 Вершины треугольника – точки в основании углов, а линии, соединяющие их, называют сторонами треугольника. Чтобы определить площадь такой фигуры, часто используют внутреннее пространство треугольника.
Вершины треугольника – точки в основании углов, а линии, соединяющие их, называют сторонами треугольника. Чтобы определить площадь такой фигуры, часто используют внутреннее пространство треугольника.
Классификация
Кроме треугольников, имеющих неодинаковые стороны, существуют равнобедренные, то есть обладающие двумя одинаковыми сторонами. Их называют боковыми, а еще одну сторону – основанием фигуры. Существует еще один вид таких многоугольников – равносторонние. Все три их стороны имеют одинаковую длину.
Для треугольников присуща градусная система измерения. Эти фигуры могут иметь разные углы, поэтому их классифицируют так:
- Прямоугольные – имеющие угол 90 градусов. Две стороны, прилежащие к этому углу, называют катетами, а третью – гипотенузой;
- Остроугольные – это треугольники, обладающие всеми острыми углами, не превышающими 90 градусов;
- Тупоугольные – один угол больше 90 градусов.
Определение и параметры треугольника
Как уже было отмечено, треугольник – это один из видов многоугольников, имеющий три вершины и столько же прямых, их объединяющих.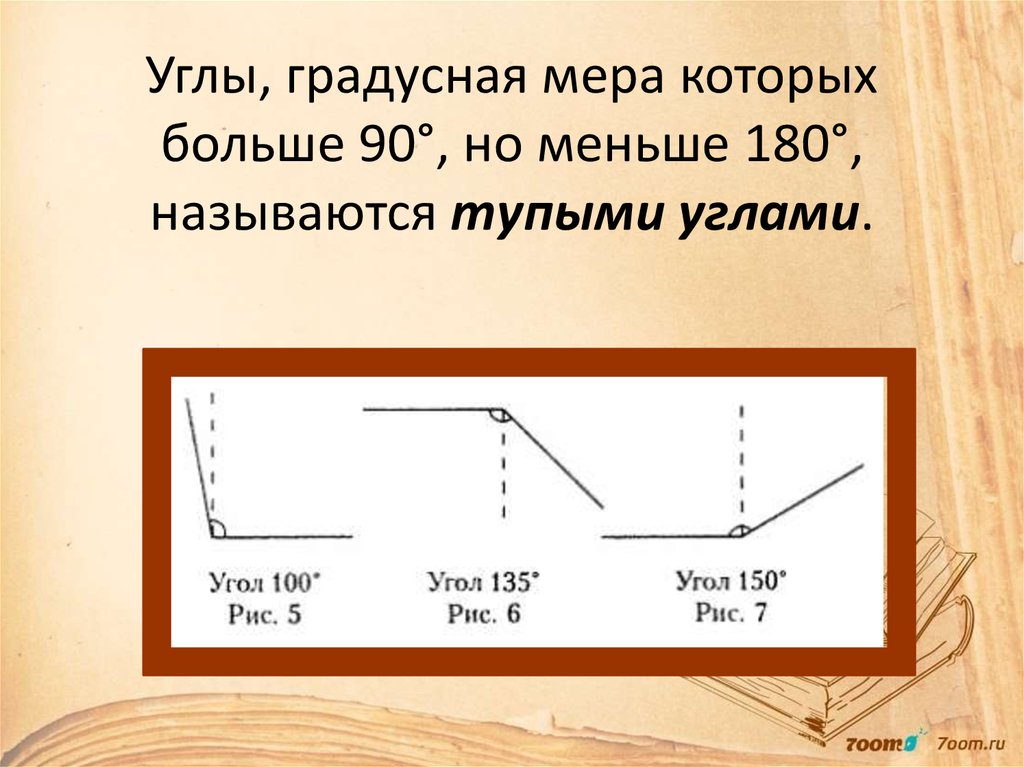 Обозначают линии, как правило, одинаково: углы – маленькими латинскими буквами, а противоположные стороны каждого – соответствующей большой буквой.
Обозначают линии, как правило, одинаково: углы – маленькими латинскими буквами, а противоположные стороны каждого – соответствующей большой буквой.
Если сложить все углы какого-либо треугольника, получится сумма в 180 градусов. Чтобы узнать внутренний угол, нужно из 180градусов вычесть величину внешнего угла треугольника. Для того чтобы узнать, чему равняется угол, находящийся снаружи, стоит сложить два раздельных от него угла внутри.
В каждом треугольнике, имеет он острые или тупые углы, противоположно большому углу находится наибольшая сторона. Если же прямые между вершинами одинаковы, то, соответственно, и каждый угол равняется 60 градусам.
Тупоугольный треугольник
Тупой угол треугольника всегда больше 90-градусного угла, но меньше развернутого. Таким образом, тупой угол равен от 90 до 180 градусов.
Возникает вопрос: бывает ли более одного тупого угла в такой фигуре? Ответ находится на поверхности: нет, потому что сумма углов должна быть менее 1800. Если два угла будут иметь, например, по 95 градусов, то третьему просто не найдется места.
Если два угла будут иметь, например, по 95 градусов, то третьему просто не найдется места.
Два тупоугольных многоугольника равны:
- если равны обе их стороны и угол, находящийся между ними;
- если одна сторона и два угла, находящиеся рядом с ней, равны;
- если три стороны тупоугольных треугольников имеют равенство.
Замечательные линии тупоугольного треугольника
Во всех треугольниках, имеющих тупые углы, есть линии, называемые замечательными. Первая из них – высота. Она представляет собой перпендикуляр из одной из вершин на соответствующую ей сторону. Все высоты сталкиваются в точке, которая именуется как ортоцентр. В треугольнике с тупыми углами он будет находиться за пределами самой фигуры. Что касается острых углов, то центр там находится в самом треугольнике.
Еще одна линия – медиана. Это черта, проведенная от вершины к центру соответствующей стороны. Все медианы сходятся в треугольнике, а место их совмещения – это центр тяжести такого многоугольника.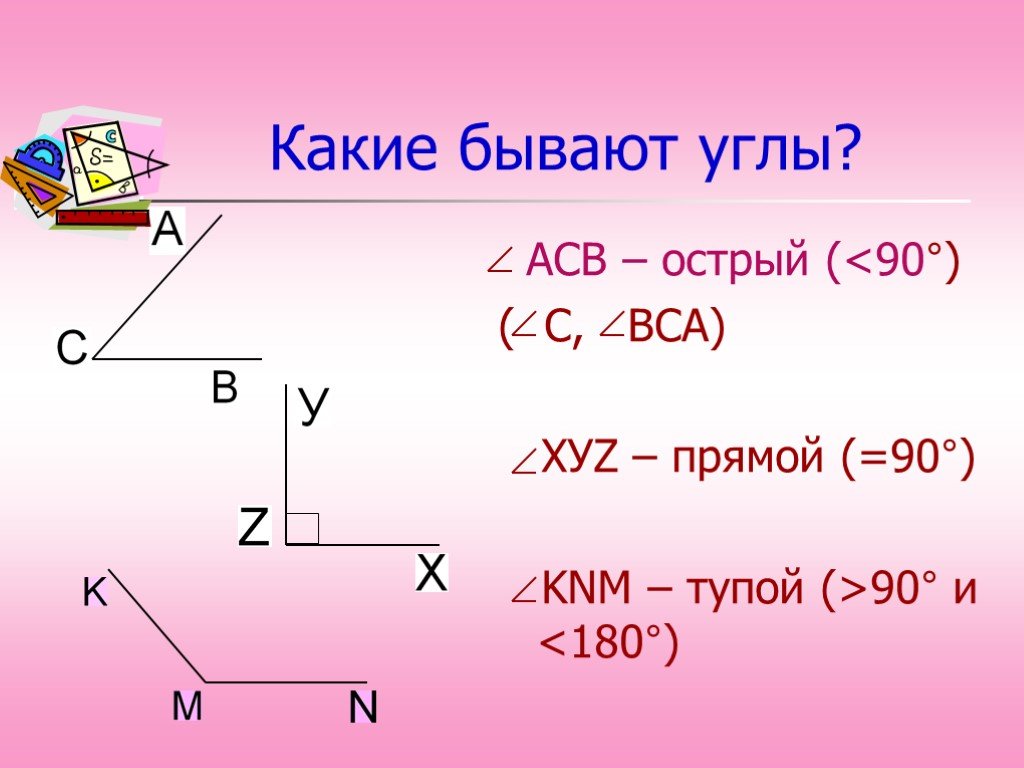
Биссектриса – линия, делящая пополам как тупые углы, так и остальные. Пересечение трех таких линий всегда бывает только в самой фигуре и определяется как центр круга, вписанного в треугольник.
В свою очередь, центр круга, описанного вокруг фигуры, можно получить из трех срединных перпендикуляров. Это линии, которые были опущены из середин прямых, соединяющих вершины. Место пересечения трех срединных перпендикуляров в треугольнике, имеющем тупые углы, находится снаружи фигуры.
Тупой угол Определение и значение
- Основные определения
- Викторина
- Примеры
- Научная
- Культурная
Показывает уровень оценки в зависимости от сложности слова.
Сохрани это слово!
Показывает уровень оценки в зависимости от сложности слова.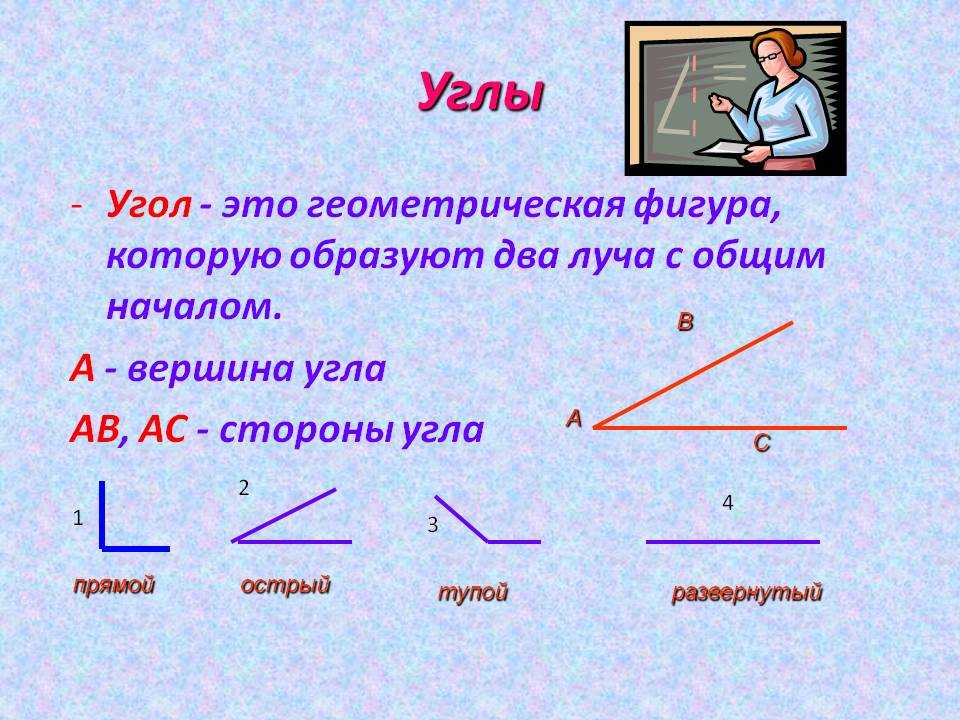
сущ.
угол больше 90°, но меньше 180°.
ВИКТОРИНА
ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?
Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!
Вопрос 1 из 7
Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.
Происхождение тупого угла
Впервые записано в 1560–1570 гг.
ДРУГИЕ СЛОВА ОТ ТУПОЙ УГОЛ , -tyoos], /əbˈtusˈæŋ gyə lər, -ˈtyus/, прилагательное
Слова рядом с тупым углом
навязчивый, тупой, тупой, тупой, тупой, тупой угол, тупой треугольник, Obuda, OBulg., тупой, выпуклый
Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
Как использовать тупой угол в предложении
Мой капитан на лодке, Бразакка, он хотел, чтобы я сделал этот бит Хемингуэя с белой щетиной , и он хотел ракурс героя.
История улыбки Ли Марвина Liberty Valance Smile|Роберт Уорд|3 января 2015 г.
 |DAILY BEAST
|DAILY BEASTЕще один ракурс, который Робинов предлагает в качестве возможного для Питера Паркера/Человека-паука, — это перезагрузка франшизы, в которой Спайди становится… взрослым.
Эксклюзив: Sony Hack раскрывает подробные планы студии по еще одной перезагрузке «Человека-паука»|William Boot|13 декабря 2014 г.|DAILY BEAST
как и иранцы.
Катар, союзник США, укрывает джихадистов-манименов|Джейми Деттмер|10 декабря 2014 г.|DAILY BEAST
Мы видим протопланетный диск вокруг него под углом, но почти «лицом к лицу».
Самый потрясающий вид рождения планет | Мэтью Р. Фрэнсис | 9 ноября, 2014|DAILY BEAST
Какое счастье: мы можем видеть щели в диске более четко, чем если бы диск находился под более крутым углом.
Самое потрясающее зрелище рождения планет|Мэттью Р. Фрэнсис|9 ноября 2014|DAILY BEAST
Ни одна тропа не была настолько тупой, не было таких густых зарослей, чтобы солдаты этого полка не проследили бы их до их логова .

Курьер Озарков|Байрон А. Данн
В центре многих комнат бил небольшой фонтан; в других их было четыре, по одному в каждом углу.
Blackwood’s Edinburgh Magazine, Volume 60, No. 372, October 1846|Various
Остальное делается путем срезания двух верхних и четырех нижних зубов и замены вставных под нужным углом.
Мат|Джозеф Шеридан Ле Фаню
Потому что весь вопрос тогда перевернулся в его уме, так что он вдруг увидел его под новым углом.
Волна|Алджернон Блэквуд
Он прицелился в зевающего бегемота и выстрелил, попав ему в череп, но под таким углом, что мяч отскочил.
Охота на львов|Р.М. Ballantyne
Научное определение тупого угла
тупой угол
[ ŏb-tōōs′ ]
Угол, градусная мера которого лежит в пределах от 90° до 180°. Сравните острый угол.
Научный словарь American Heritage®
Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company.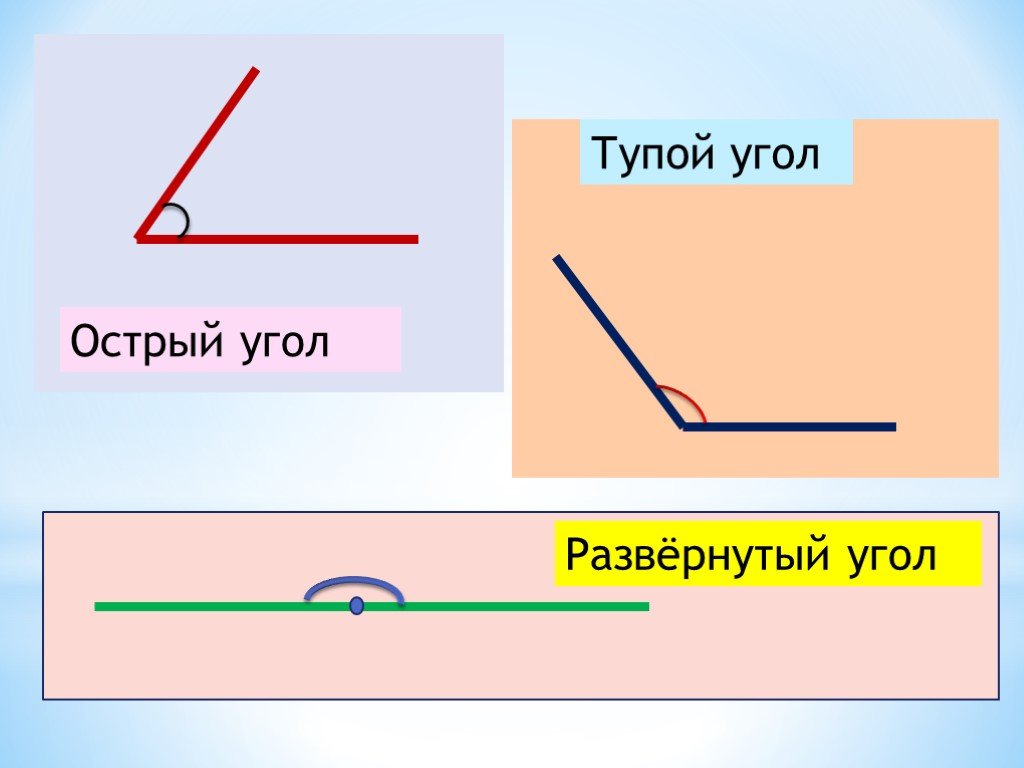 Все права защищены.
Все права защищены.
Культурные определения тупого угла
тупой угол
Угол, размер которого больше 90 градусов, но меньше 180 градусов. (Сравните острый угол и прямой угол.)
Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Тупой угол — Математические монахи
Что такое тупой угол
Тупой угол определяется как угол, который больше 90° и меньше 180°. Другими словами, любой угол, лежащий между 90° и 180° — тупой угол.
Тупой уголНиже приведены еще несколько примеров тупого угла:
Примеры тупого углаТупые углы в реальной жизни
- Один угол в тупоугольном треугольнике
- Все углы правильного многоугольника с пятью или более сторонами
- Лопасти потолочного вентилятора
- Вешалка для одежды
- Стрелки настенных часов, показывающие 8 часов
- Фасад или лестница
- Потолок дома
- Полностью открытая дверца шкафа
- Угол на дне горшка с растением
- Угол на дне кофейной кружки
- Широко раскрытая книга
- Большинство углов нашей комнаты
Выберите из предложенных вариантов тупые углы.
Решение:
Как известно,
Тупые углы — это углы, имеющие размеры больше 90° и меньше 180°,
Следовательно, варианты (b), (c) и (d) являются тупыми углами.
Какая из следующих опций, заданных в часах, соответствует тупому углу?
Решение:
Как мы знаем,
Тупые углы — это углы с размерами больше 90° и меньше 180°,
Следовательно, варианты (a), (b), (c) и (d) тупые углы.
Найдите x в заданном треугольнике и укажите, является ли он тупоугольным0182 Таким образом,
In △ABC,
∠ABC + ∠BCA + ∠CAB = 180°, здесь ∠ABC = 44°, ∠BCA = 32°
44° + 32° + ∠CAB = 180°
∠CAB = 180 ° – (44° + 32°)
∠CAB = (x°) = 104°
Так как ∠CAB измеряет больше 90° и меньше 180°, △ABC является тупоугольным треугольником
Определите тупые углы в данном многоугольнике ABCDEF.
Решение:
Как известно,
Сумма внутренних углов шестиугольника = 720°
Таким образом,
∠ABC +∠BCD + ∠CDE + ∠DEF + ∠EFA +∠FAB =
132° + 82° + ∠CDE + 88° + 107° + 142° = 720°
∠CDE = 720° – 551°
∠CDE = (x°) = 169°
Таким образом, ∠ABC, ∠EFA и ∠FAB — тупые углы.
Острый и тупой углы
Основное различие между острым и тупым углом заключается в том, что острый угол всегда меньше 90°, тогда как тупой угол больше 90° и меньше 180°.
Часто задаваемые вопросы
Q1.Сколько тупых углов в тупоугольном треугольнике?
Ответ . В тупоугольном треугольнике только один тупой угол.
Q2. Может ли треугольник иметь два тупых угла?
Ответ . Нет, в треугольнике не может быть двух тупых углов, потому что сумма трех углов треугольника всегда равна 180°. Если два тупых угла больше 90°, то третий угол будет иметь отрицательное значение, что невозможно.
Q3. Может ли четырехугольник иметь 4 тупых угла?
Ответ . Нет, у четырехугольника не может быть четырех тупых углов.

 |DAILY BEAST
|DAILY BEAST