Построить график y 3cosx: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

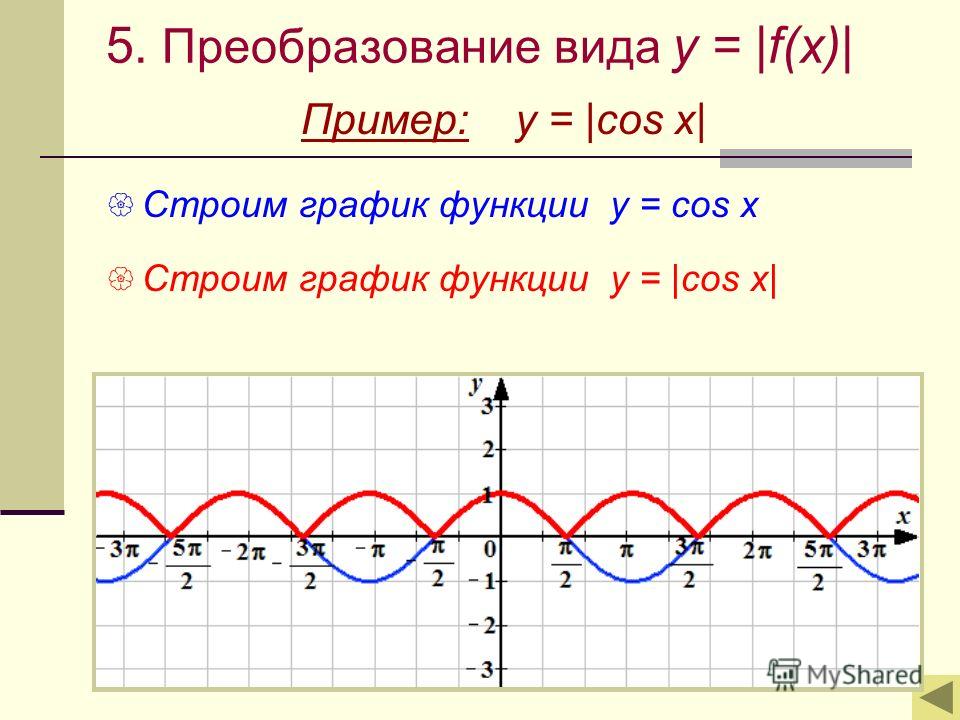
1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )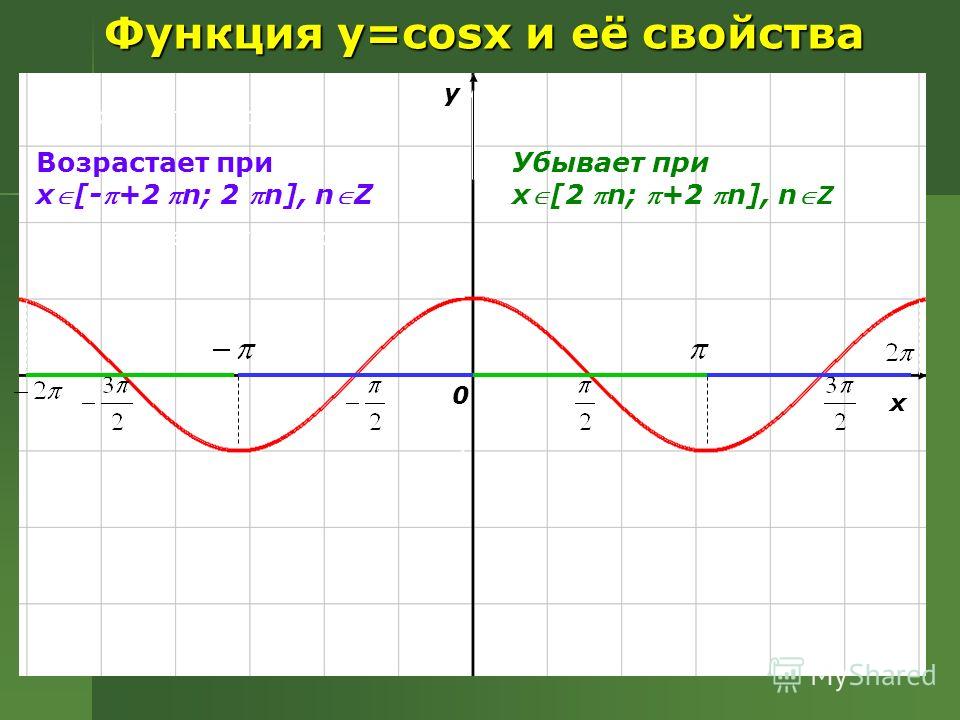
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28 Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )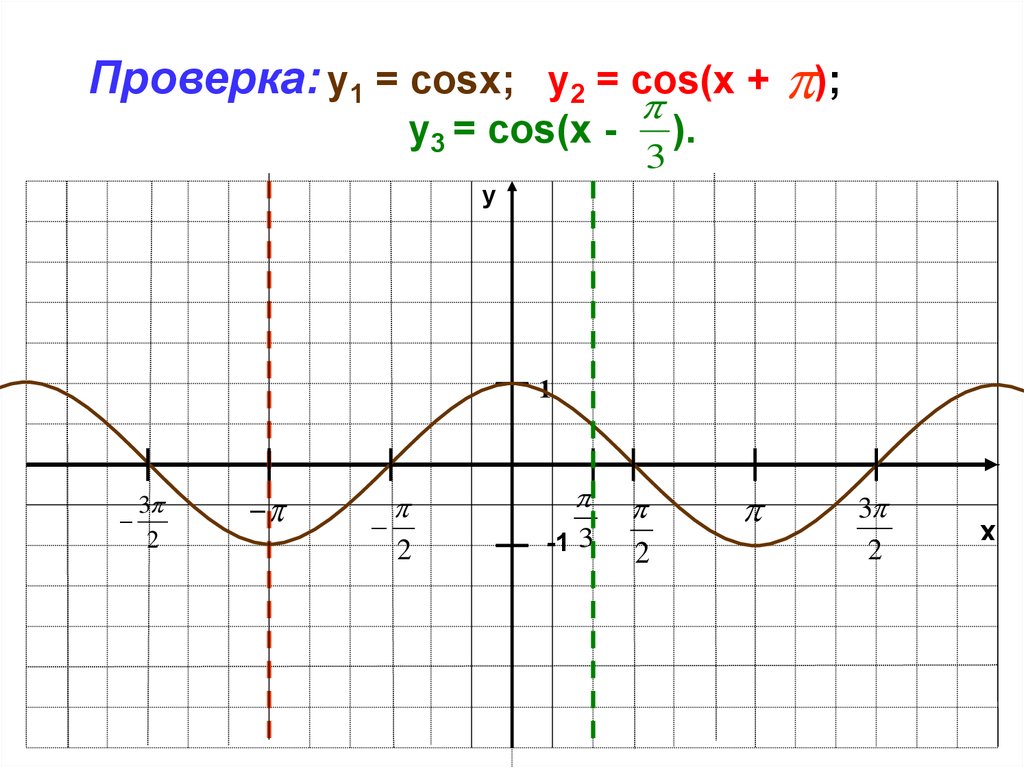
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )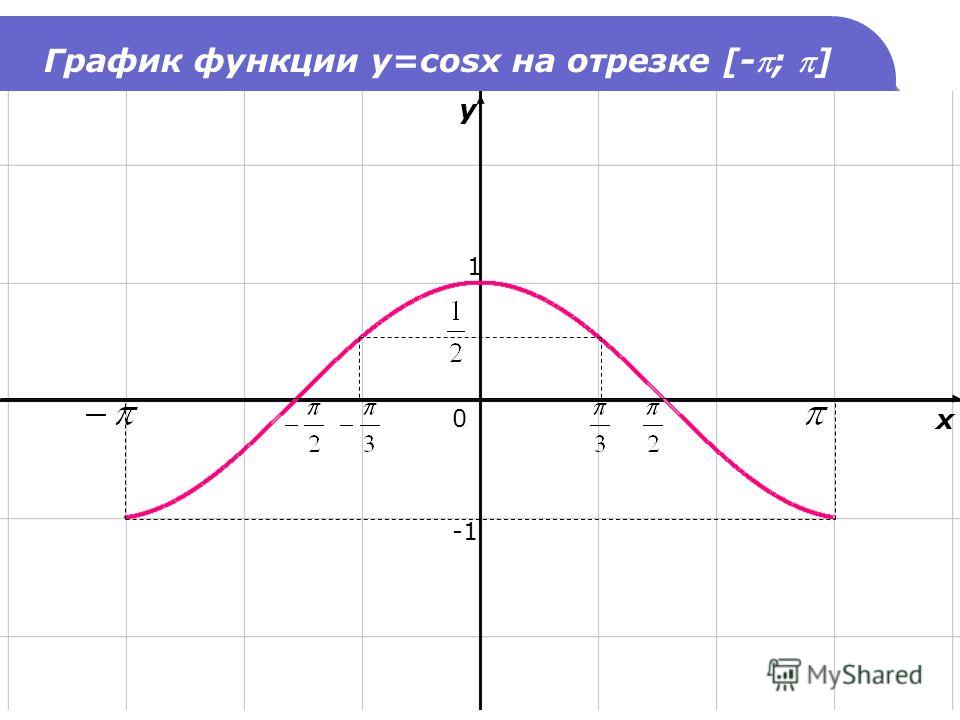
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Рисунки из графиков функций — 74 фото

Рисование графиками функций


Красивые математические графики


График функции рисунок


Рисунки с помощью графиков


Построение графиков функций в эксель рисунки


Математический цветник: розы Гвидо Гранди


Графики рисунки в эксель


Построение графиков по функции формулы


Бабочка по координатам



Математические графики — узоры


График в виде сердечка


Десмос изоклины


Фигуры по координатным точкам


Сердечко математическая функция


График функции sinx+1


График функции


Математический график


Рисунки в Десмос


Рисунки по координатам с координатами


Координатная плоскость (-7, 5;4, 5) , (-8;5)


График функции в виде сердца


График функции сердечко


Красивые математические графики


Рестнуи по координатам


Алгебра графики функций


Моделирование в матлаб


Графики различных функций


Графический нуль функции это


Графики четных функций


Квадратичная парабола y x2


Рисунки на координатной плоск



График функции


Графики функций для исследования свойств


Рисунок производной


Функции Алгебра 10 класс


Построение графиков с ограничениями онлайн


Шаблоны Алгебра 9 класс график функции y x2


График функции y 3cosx период


Quadratic Electro-Optic coefficients


Графики функций


Бабочка по координатам


Декартова система координат на плоскости рисунки животных


Функции в алгебре и их графики формулы


Математические графики


Красивые графики функций Tex


Формулы Графика функции


Как строить график производной функции


Функции Графика функции формулы


Парабола функции y x2


Какая из линий не является графиком функции


На одном из рисунков изображен график функции


Парабола 2×2


На одном из рисунков изображен график функции .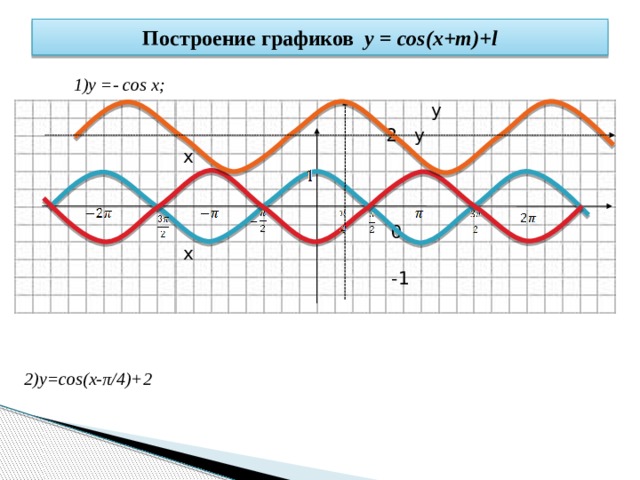 Укажите номер это


Графики квадратичной функции в зависимости от коэффициентов


Y x2 2x график функции


Рисование по координатам


График производной функции

[thumb=|График функции промежуток [- 5 2]]https://flomaster.club/uploads/posts/2022-07/1658190070_58-flomaster-club-p-risunki-iz-grafikov-funktsii-krasivo-61.png[/thumb]

Как определить график функции по формуле


Декартова система координат на плоскости рисунки


Векторная функция Графическое изображение


График функции y x в квадрате



График произвольной функции


График линейной функции


Функция 1/х


Построить график функции y 1 5sinx


Соответствие между графиками функций параболы


Математическая функция конопля


Y B график функции


График функции


График функции вида y KX+B коэффициенты


Функция y=x4


Эскизы графиков функций


Рафик Нечётной функции


Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

косинусоидальный график с фазовым сдвигом|y=a cos(bx + c)

Стандартная форма косинусоидального графика с фазовым сдвигом: $\frac{2\pi }{b} $ = период

$\frac{-c}{b} $ = сдвиг по горизонтали

d = сдвиг по вертикали
Как b, так и c на этих графиках влияют на фазовый сдвиг по косинусу график (или смещение).
Фазовый сдвиг — это величина, на которую кривая смещается в горизонтальном направлении от ее нормального положения. Если фазовый сдвиг отрицательный, то смещение будет двигаться влево, а если фазовый сдвиг положительный, то смещение будет двигаться вправо.
Фазовый сдвиг получается путем решения выражения
bx + c = 0
bx = — c
x = -c/b
‘d’ влияет на вертикальный сдвиг графика косинуса. Если «d» положительное, то график сдвинется вверх на d единиц, а если «d» отрицательное, то график сдвинется на d единиц вниз.
Примечание. Период косинусоидального графика равен $2\pi$.

Как расположить точки на оси x косинусного графика?
Разделите период на 4 Назовем его «а».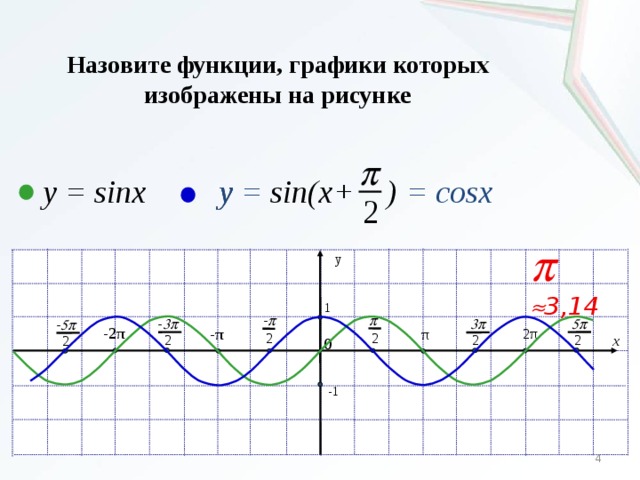
Первая точка: Отметить фазовый сдвиг по оси X. Если фазовый сдвиг отрицательный, то постройте его слева от нуля, а положительный — справа от нуля.
Вторая точка: Добавьте фазовый сдвиг и a.

Пример 1: График y = 3 cos ( x + $\frac{\pi }{4}$)
Решение: сравните y = a cos ( bx + c ) + d и y = cos( x + $\frac{\pi }{6}$)
a = амплитуда = 3
b = 1
$\frac{2\pi }{b}$ = $\frac{2\pi }{1}$ = $2\pi $ = период
Для фазового сдвига решите x + $\frac{\pi }{4}$ = 0
x = $\frac{-\pi }{4}$ = фазовый сдвиг
Поскольку фазовый сдвиг отрицателен, график будет перейти на $\frac{\pi}{4}$ единицу влево.
d = 0 = сдвиг по вертикали, поэтому смещения по вертикали нет.
Поскольку фазовый сдвиг отрицателен, первая точка на оси X — это $\frac{-\pi }{4}$, которую мы наносим слева от нуля.

2-я точка: $\frac{-\pi }{4}$ + $\frac{period}{4}$

= $\frac{-\pi }{4}$ + $\frac{ 2\pi}{4}$ = $\frac{\pi }{4}$

3-я точка: $\frac{\pi }{4}$ + $\frac{2\pi}{4}$ = $\frac{3\pi}{4}$

4-я точка: $\frac{3\pi}{4}$ + $\frac{2\pi}{4}$ = $\frac{5\pi}{4}$

5-я точка: $\frac{ 5\pi}{4}$ + $\frac{2\pi}{4}$ = $\frac{7\pi}{4}$
Примечание.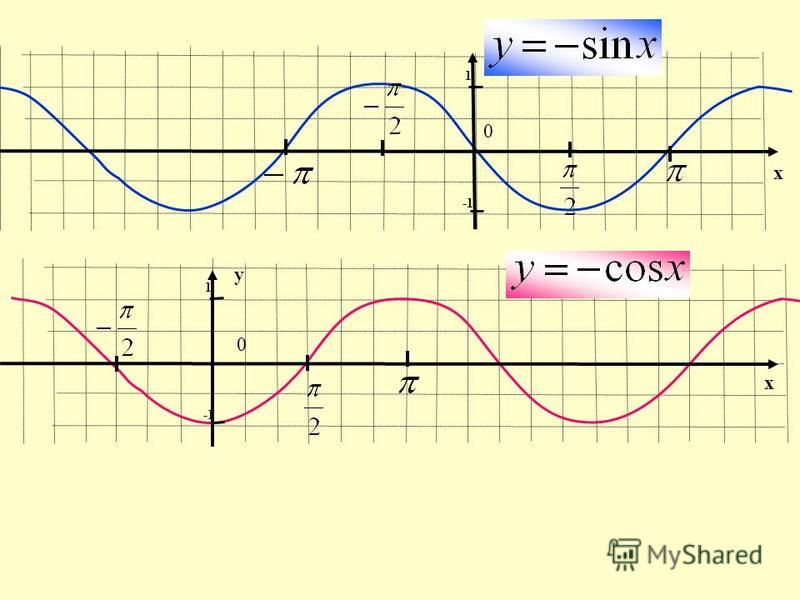 Ниже показан только один цикл косинусоидального графика.

Пример 2: График y = cos ( x — $\frac{2\pi }{5}$) + 1
Решение: сравните y = a cos ( bx + c ) + d и y = 3 потому что ( х — $\frac{2\pi }{5}$)+1
a = амплитуда = 3
b = 1
$\frac{2\pi }{b}$ = $\frac{2\pi }{1}$ = $2\pi $ = период
Для фазового сдвига решите x — $\frac{2\pi }{5}$ = 0
x = $\frac{2\pi }{5}$ = фазовый сдвиг
Поскольку фазовый сдвиг положителен, график переместится в $\frac{ 2\pi {5}$ единицы вправо.
d = 1 = сдвиг по вертикали, поэтому график сдвинется на 1 единицу вверх, поскольку ‘d’ положителен.
Таким образом, новая ось X равна y = 1. Поскольку фазовый сдвиг отрицателен, поэтому 1-я точка на оси X — это $\frac{2\pi }{5}$, которую мы наносим справа от нуля.

2-я точка: $\frac{2\pi }{5}$ + $\frac{period}{4}$

= $\frac{2\pi }{5}$ + $\frac{ 2\pi}{4}$ = $\frac{9\pi }{10}$

3-я точка: $\frac{9\pi }{10}$ + $\frac{2\pi}{ 4}$ = $\frac{14\pi}{10}$

4-я точка: $\frac{14\pi}{10}$ + $\frac{2\pi}{4}$ = $ \frac{19\pi}{10}$

5-я точка: $\frac{19\pi}{10}$ + $\frac{2\pi}{4}$ = $\frac{24\ pi}{10}$
Примечание.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *