Решение тригонометрических функций ⋆ Компьютерные технологии
Домой Калькулятор онлайн Решение тригонометрических функций
Онлайн калькулятор на нашем сайте легко и быстро решает тригонометрические функции, вам не понадобится таблица тригонометрических функций. С нашим калькулятором можно навсегда забыть, что такое таблица Брадиса! Наш бесплатный калькулятор позволяет решать и самые простые задачи (например, найти косинус или синус угла), и сложные выражения с использованием обратных и гиперболических функций тригонометрии.
Кнопки калькулятора для решения тригонометрических функций:
Наш тригонометрический калькулятор может осуществлять вычисления как в градусах, так и в радианах. Таким образом, найти косинус угла можно вне зависимости от единицы измерения, в которой он задан. Это очень удобно и экономит массу времени при емких расчетах. Прежде чем приступить к вычислениям, нужно на панели управления указать, какая единица измерения углов будет использоваться: градусы (Deg) или радианы (Rad).
Выбор единицы измерения угла:
Обратите внимание, что в одной операции нельзя использовать разные единицы измерения углов, другими словами выражение «сумма синус 30 градусов и косинус пи =» — будет посчитано неверно!
Ниже перечислены способы решений различных тригонометрических функций в нашем онлайн калькуляторе.
Простые тригонометрические функции
Простые тригонометрические функции: синус — sin(α), косинус — cos(β) и тангенс — tan(y). Рядом указаны их обозначения так, как они используются в калькуляторе (в зарубежной литературе тангенс сокращенно обозначается tan, в русской — tg).
Кнопки калькулятора, отвечающие за простые тригонометрические функции:
Функция косинуса является четной, поэтому ее значение для отрицательного угла будет положительным. Синус, тангенс и котангенс — нечетные тригонометрические функции, соответственно, значения тригонометрических функции для отрицательных углов также будут отрицательными.
Онлайн калькулятор сам учитывает четность тригонометрических функций при умножении и делении. Вам не потребуется постоянно обращать внимание на соблюдение правила знаков.
Пример вычислений с простыми тригонометрическими функциями:
Обратные тригонометрические функции
Обратные тригонометрические функции: арксинус — asin(), арккосинус — acos() и арктангенс — atan().
Кнопки калькулятора, отвечающие за обратные тригонометрические функции:
Если не вдаваться в формулы и подробности относительно единичной окружности, то обратные тригонометрические функции можно объяснить на простом примере: арккосинус x — это угол, косинус которого равен x. Обратные тригонометрические функции являются многозначными, и одному значению аргумента принадлежит множество значений самой функции.
Пример выражения с обратными тригонометрическими функциями:
Гиперболические функции
Гиперболические функции: гиперболический синус — sinh(), гиперболический косинус — cosh() и гиперболический тангенс tanh().
Гиперболические (круговые) функции — семейство элементарных тригонометрических функций, выраженных через экспоненту.
Кнопки калькулятора, отвечающие за гиперболические функции:
Пример решения гиперболической функции:
Обратные гиперболические функции: гиперболический арксинус — asinh(), гиперболический арккосинус — acosh() и гиперболический арктангенс — atanh().
Кнопки калькулятора, отвечающие за обратные гиперболические функции:
Пример решения обратной гиперболической функции:
Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>
ЭТО ИНТЕРЕСНО
ЭТО ПОПУЛЯРНО
Калькулятор тригонометрии — простой расчет Sin, Cos, Tan
Попробуйте этот тригонометрический калькулятор, который позволяет вычислять функции тригонометрического угла (sin, cos, tan, sec, csc, tan) в градусах или радианах. Не только это, но и калькулятор sohcahtoa с шагами будет применять эту конкретную мнемонику для точного определения тригонометрических отношений углов, тем самым также представляя график.
Давайте перейдем к статье ниже и узнаем, как использовать sohcahtoa для нахождения значений функции угла с помощью этого тригонометрического калькулятора или вручную.
Сосредоточься!
Что такое тригонометрия?
Изучение трех углов треугольника называется тригонометрией.
Рис…
Наш бесплатный треугольник калькулятора триггеров также подходит для определения всех взаимосвязанных угловых соотношений за пару мгновений.
Тригонометрические соотношения:
Ниже приведены стандартные соотношения тригонометрических функций, которые также можно вычислить для любого угла с помощью нашего онлайн-калькулятора тригонометрических соотношений:
Синус:
Отношение длины перпендикуляра к гипотенузе называется синусом.
Формула:
Синус = Перпендикуляр/Гипотенуза
Точное значение синусоиды углов можно вычислить с помощью треугольника тригонометрического калькулятора.
Косинус:
В тригонометрии отношение основания треугольника к гипотенузе известно как функция косинуса, которую можно в деталях понять с помощью бесплатного калькулятора косинуса.
Формула:
Косинус = Основание/Гипотенуза
Тангенс:
Отношение перпендикуляра к основанию треугольника называется функцией тангенса.
Формула:
Тангенс = Перпендикуляр/Основание
Секанс:
Секанс прямо противоположен синусу. Другими словами, оно соответствует отношению гипотенузы к перпендикуляру.
Формула:
Секанс = гипотенуза/перпендикуляр
Косеканс:
Подобно синусу и секансу, косеканс представляет собой отношение, обратное отношению косинуса. Проще говоря, отношение гипотенузы к основанию треугольника называется косекансом.
Формула:
Косеканс = гипотенуза/основание
Котангенс:
Отношение основания треугольника к перпендикуляру называется функцией котангенса.
Формула:
Котангенс = Основание/Перпендикуляр 9{-1}x
Все эти триггерные функции дают разные значения в градусах или радианах для разных мер азимуталей. И довольно сложно рассчитать для каждого значения отдельно. Но здесь на помощь приходит наш бесплатный калькулятор тригонометрии прямоугольного треугольника. Так что используйте этот калькулятор и начните решать для разных углов.
Сводка тригонометрических функций:
| Функция | Описание | Отношения | |
| в радианах 9{\ circ} -x \ right) = {\ frac {1} {\ sin x}}} $ $ | |||
Иллюстрации:
Теперь мы решим пару связанных примеров, чтобы сделать вашу концепцию достаточно ясной!
Утверждение:
Найдите значение каждого тригонометрического соотношения для треугольника, указанного ниже:
Решение:
Синус(θ) = Перпендикуляр/Гипотенуза
Синус(θ) = 0,8 (для расчета угла нажмите калькулятор синуса)
Косинус(θ) = основание/гипотенуза
Косинус (θ) = 0,6 (для расчета угла коснитесь калькулятора косинуса)
Тангенс (θ) = перпендикуляр/основание
Тангенс (θ) = 1,33 (для расчета угла коснитесь калькулятора тангенса)
Секанс (θ) = Гипотенуза/перпендикуляр
Секанс(θ) = 1,25 (для расчета угла нажмите калькулятор секанса)
Косеканс(θ) = гипотенуза/основание
Косеканс(θ) = 1,67 (для расчета угла нажмите калькулятор секанса)
Котангенс (θ) = основание/перпендикуляр
Котангенс(θ) = 0,75 (для расчета угла нажмите калькулятор котангенса)
Требуемые тригонометрические соотношения для данного треугольника, которые также можно дважды проверить с помощью онлайн-калькулятора точного значения тригонометрической функции.
Утверждение:
Вычислите следующие тригонометрические отношения для различных мер треугольника, указанных ниже:
Секанс(θ) = ?
Косинус(θ) = ?
Приведены данные:
Гипотенуза = 5,5
Перпендикуляр = 4
Основание = 2,4
Решение:
Secant (θ) = гипотенуза/перпендикулярный
Secant (θ) = 5,5/4
Secant (θ) = 1,375
Cosin
Косинус (θ) = 2,4 / 5,5
Косинус (θ) = 0,436
Работа с калькулятором тригонометрии прямоугольного треугольника:
Теперь мы рассмотрим приведенное ниже руководство, которое поможет вам определить любые соотношения тригонометрических функций с помощью этого Онлайн-калькулятор шести тригонометрических функций.
Ввод:
- В первое поле введите из первого выпадающего списка выберите триггерную функцию, чтобы я вычислил
- В следующем поле введите угол
- Теперь нажмите кнопку расчета
Вывод:
Наш калькулятор коэффициента триггера выполняет следующие вычисления:
- Вычисляет коэффициент триггерного угла как в градусах, так и в радианах
- Показывает графическую интерпретацию угловой функции
Помимо углов, вы также можете определить стороны прямоугольного треугольника, используя другой калькулятор закона синусов.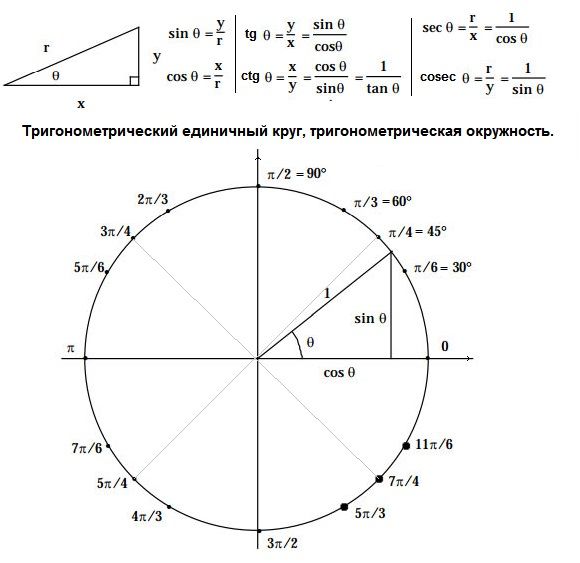
Часто задаваемые вопросы:
Как тригонометрия используется в реальной жизни?
Ниже приведены реальные применения тригонометрии:
- Спутниковые системы
- Картография
- Астрофизика
- Проекты наклона крыши
- Машиностроение
- Химия
В каждой отличительной области
Почему важно изучать тригонометрию?
Тригонометрия считается одним из лучших разделов математики. Это потому, что это помогает ученикам или профессионалам понимать сложные угловые размеры для разработки карт.
Тригонометрия сложнее исчисления?
Тригонометрия — это изучение природы углов в любом треугольнике. В то время как, с другой стороны, исчисление соответствует сложной и продвинутой математике запросов, которая позволяет вам столкнуться со многими сложными функциями.
Кто отец тригонометрии?
Греческий математик Гиппрак ввел понятие тригонометрии.
Заключение:
Мы окружены бесчисленными приложениями тригонометрии.
И функции отношения углов, используемые в этом предмете, очень важны для понимания теории карт, анализа дизайна и сложных расчетов конструкции. Вот почему мы разработали этот тригонометрический калькулятор с шагами, чтобы вы могли решать эти функции без каких-либо препятствий.
Ссылки:
Из источника Википедии: Тригонометрия, соотношения, Мнемоника, Тригонометрические функции действительных или комплексных переменных, Обратные тригонометрические функции, Приложения
Из источника Академии Хана: Радианы и градусы
Из источника Люмен Обучение: алгебра и тригонометрия, аналитическая геометрия
Калькулятор синуса онлайн, решение любого угла
Калькулятор синуса позволит вам рассчитать это тригонометрическое значение, просто введя угол и выбрав его единицы измерения (углы или радианы). Когда вы заполнили эти данные, нажмите кнопку расчета, и вы автоматически получите значение синуса введенного угла.
Если вам это нужно, у нас также есть другие тригонометрические калькуляторы для расчета следующих функций:
- Косинус угла
- Тангенс
Разделы статей
- Определение синуса угла
- Вычисление синуса числа в Excel
- График функции синуса
- Таблица функции синуса
- Синус 9 Теорема 3 двойной угол 3 Синусоидальная производная
- Цельная грудь
- Вычислить синус на калькуляторе
Определение синуса угла
Когда мы говорим о функции синуса, мы должны представить себе прямоугольный треугольник, как на рисунке, чтобы вычислить синус угла угла θ, мы должны разделить противолежащую сторону на гипотенузу.
Это может быть представлено следующей математической формулой:
sin θ = противолежащий угол / гипотенуза
На примере , Давайте представим, что диаметр противоположного катета составляет 3 сантиметра, а размер гипотенузы 5 см. С этими данными синус будет рассчитываться следующим образом:
sin θ = противоположный угол / гипотенуза = 3 см / 5 см = 0,6
Помните, что значение синуса может быть только в следующем диапазоне между -1 и 1 поэтому, если мы получим какое-либо значение за пределами этого диапазона, какой-то расчет неверный. Вы можете проверить это самостоятельно, потренировавшись с функцией обратного синуса, к которой вы можете получить доступ, нажав на ссылку, которую мы только что оставили вам.
Вычислить синус числа в Excel
Как иначе и быть не могло, мы тоже можем вычислить синус угла в радианах в Excel .
Просто введите эту формулу в пустую ячейку:
=SENO()
и напишите в скобках угол в радианах, для которого вы хотите вычислить его синус. Если вы хотите вычислить синус угла в градусах , тогда вам следует написать следующую функцию: по ячейке, в которой вы это написали.
График синусоидальной функции
На этой диаграмме вы можете увидеть, как представляет синусоидальную функцию во всем диапазоне ее значений:
Некоторые значения, такие как угол 45 градусов или не очень хорошо отображаются на графике, но дают следующие результаты:
- Грудь 60 лет º = 0,866
- Грудь 45 º = 0,707
Для других значений вы можете использовать наш онлайн-калькулятор сенны или взгляните на таблицу типичных значений ниже.
Таблица функции синуса
В следующей таблице вы найдете, насколько эквивалентен синус наиболее распространенных углов .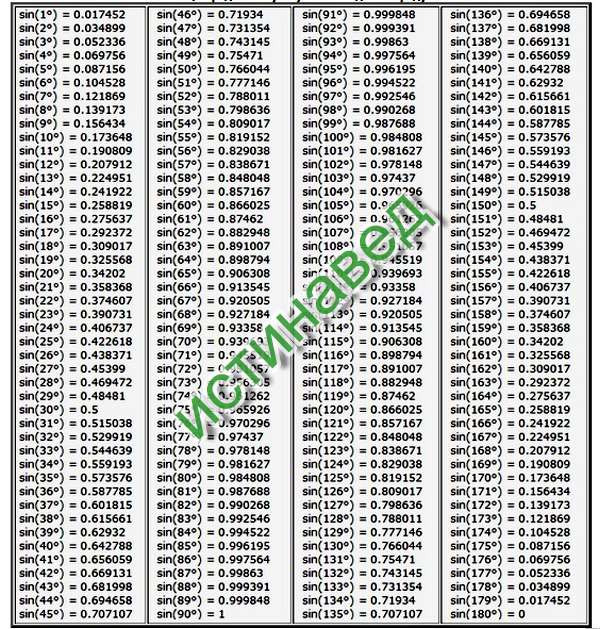
Помните, что функция синуса может принимать значения только между -1 и 1, поэтому любой результат за пределами этого диапазона неверен.
С помощью этой таблицы вы сможете получить синус 0, синус 30 и другие типичные углы, которые мы обычно не помним, если только не занимаемся тригонометрическими задачами часто.
| Классы | Радианы | Синус |
|---|---|---|
| 0º | 0 | 0 |
| 30º | π/6 | 0,5 |
| 45º | π/4 | 0,707 |
| 60º | π/3 | 0,866 |
| 90º | π/2 | 1 |
| 180º | π | 0 |
| 270º | 3π/2 | -1 |
| 360º | 2π | 0 |
Теорема синусов
Теорема синусов говорит нам, что каждая сторона треугольника пропорциональна синусу значения противоположного угла.
Теорема синусов особенно полезна для решения задач, в которых дает нам два угла треугольника и одну из противоположных сторон. Мы также можем применить его, если мы знаем две стороны и они дают нам противоположный угол.
С этими данными мы можем решить полный треугольник, особенно в сочетании с теоремой косинусов, которая имеет очень интересные приложения, такие как возможность вычислить высоту горы, здания или дерева. Мы также можем рассчитать уклон подъема и многие другие приложения.
Синус двойного угла
Синус двойного угла рассчитывается по-другому, и для его вычисления следует следовать следующей процедуре:
sin(2a)=sen(a+a) = sin(a)cos(a) + sin(a)cos(a) =2 sin(a)cos(a)
Синусоидальная производная
Если вы не помните что такое производная синуса это вам поможет:
- f(x) = sinx
- f'(x) = x’ cosx
То есть производная синуса функции равна производной этой функции, умноженной на косинус функции .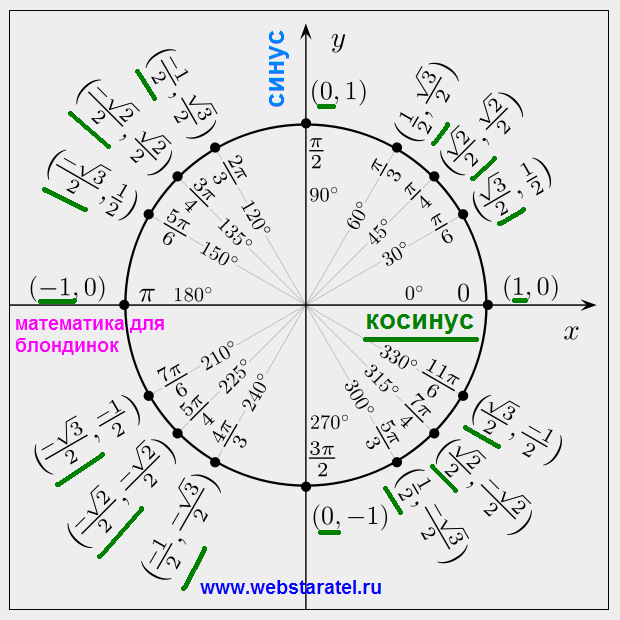
Например, производная f(x) = sin4x равна f'(x) = 4cox4x
Целостная грудь
Интеграл от синуса функции, умноженной на производную этой функции, равен отрицательному косинусу функции. Математически то, что мы только что сказали, выражается следующим образом:
∫sen f
f’ = -cos f
Если вместо функции мы имеем простой интеграл от синуса x, то:
∫sen x = -cos x
Рассчитать синус на калькуляторе
Функция синуса является одним из наиболее часто используемых, и по этой причине большинство калькуляторов имеют специальный ключ, который позволяет вам вычислять его автоматически.
Если у вас есть под рукой калькулятор, найдите tecla etiquetada con las letras «sin» , и это то, что вы должны нажать, чтобы удалить грудь.
Правильно, проверьте, настроен ли у вас калькулятор в градусах или радианах. , так как это радикально изменит результат, который вы получите на экране.