Как найти вероятность в математике егэ: Теория вероятностей на ЕГЭ по математике. Формулы, теория, решения

Решение задач по теории вероятностей (по материалам открытого банка задач ЕГЭ по математике)

Решение задач по
теории вероятностей
(по материалам открытого банка
задач ЕГЭ по математике)
Марова Светлана Николаевна,
МБОУ «Обоянская СОШ №2»,
учитель математики, высшая категория

2. «Сочетая строгость научных доказательств с неопределенностью случая и примиряя казалось бы противоположные вещи, и, извлекая ее

имя из того и другого, можно
по праву присвоить ей ошеломляющее
название геометрия случая»
Блез Паскаль
Термин «геометрия» в те времена употреблялся также в смысле «математика».
Решение задач по
теории вероятностей
профильный уровень
задание № 4
Цель:
• повторить и обобщить основные знания по данной теме;
• повторить классическое определение вероятности события, а
также основные свойства вероятности события, формулы
сложения и умножения вероятностей событий, формулу полной
вероятности;
• применить данные теоретические сведения к решению задач.
профильный уровень
задание № 4
Требования к уровню
подготовки выпускников
Уметь моделировать реальные ситуации на языке
теории вероятностей и статистики, вычислять в
простейших случаях вероятности событий
профильный уровень
задание № 4
• Примерное время выполнения задания –
3-5 мин;
• Максимальный балл за задание – 1.
Теоретические сведения
Классическое определение вероятности
Вероятностью события А называется отношение
числа благоприятных для него исходов испытания к
числу всех равновозможных исходов.
где m — число исходов, благоприятствующих осуществлению
события, а n — число всех возможных исходов.
Теоретические сведения
Некоторые свойства и формулы
1. Вероятность достоверного события равна 1.
2. Вероятность невозможного события равна 0.
3. Сумма вероятностей противоположных событий
равна 1.
4. Формула сложения вероятностей совместных
событий: P(A U B) =P(A) + P(B) – P(A∩B)
5. Вероятность появления одного из двух несовместных
событий равна сумме вероятностей этих событий.
P(A U B) =P(A) + P(B)
Теоретические сведения
Некоторые свойства и формулы
6. Вероятность произведения независимых событий
А и В (наступают одновременно) вычисляется по
формуле:
P(A∩B) = P(A) ∙ P(B).
7. Формула умножения вероятностей:
P(A∩B) = P(A) ∙ P(B\A),
где P(B\A) – условная вероятность события В,
при условии, что событие А наступило.
8. Формула полной вероятности:
P(A) = P(В) ∙ P(А\В)+ P(С) ∙ P(А\С),
где события В и С несовместны, а событие А
происходит вместе с одним из событий В или С.
Теоретические сведения
Некоторые свойства и формулы
9. Формула вероятности k успехов в серии из n
испытаний Бернулли:
P(A) = Cnk p k q n k , где
Cnk
n!
k!(n k )!
р – вероятность успеха, q=1-p – вероятность
неудачи в одном испытании.
Теоретические сведения
Две группы задач
1. Опыты с равновозможными элементарными
событиями.
2. Простейшие правила и формулы вычисления
вероятностей.
Теоретические сведения
Опыты с равновозможными
элементарными событиями
Схема решения задач:
1. Определить, в чем состоит случайный
эксперимент и какие у него элементарные события
(исходы). Убедиться, что они равновозможные.
2. Найти общее число элементарных событий (n).
3. Определить, какие элементарные события
благоприятствуют событию А, и найти их число (m).
4. Найти вероятность события А по формуле
Задача 1.
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США,
остальные − из Китая. Порядок, в котором выступают гимнастки, определяется
жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется
из Китая.
Решение:
Событие состоит в том, что выбрана спортсменка, которая выступает первой. Первой
может оказаться любая.
Всего участвует 20 спортсменок – это общее количество (n).
из которых 20 – 8 – 7 = 5 спортсменок из Китая. (это количество исходов
благоприятных данному событию, т.е. m)
Вероятность того, что спортсменка, выступающая первой, окажется из Китая
p=m/n , т.е. p=5/20 = 1/4 = 0,25.
Ответ: 0,25
Задача 2.
В среднем из 600 садовых насосов, поступивших в продажу, 3 подтекают. Найдите
вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение:
Событие состоит в том, выбирают хороший насос из 600.
Общее количество n=600.
Количество исходов, благоприятных данному событию:
m=600 – 3 = 597, т.е. это количество насосов, которые не
подтекают.
Вероятность того, что один случайно выбранный для
контроля насос не подтекает, равна p=597/600 = 0,995.
Другой способ решения.
Вероятность того, что один случайно выбранный для контроля насос подтекает,
равна p=3/600 = 1/200 = 0,005.
События: «насос подтекает» и «насос не подтекает» — противоположные события,
тогда р=1-0,005=0,995
Ответ: 0,995
Задача 3.
Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь
сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка
окажется качественной. Результат округлите до сотых.
Решение:
Событие состоит в том, купленная сумка окажется качественной. По условию
известно, что таких сумок 100, т.е. это количество благоприятных исходов.
Общее количество сумок: 100 + 8 = 108 (качественных и со скрытыми дефектами).
Вероятность того, что купленная сумка окажется качественной, равна
р=100/108 = 25/27=0,925… ≈ 0,93.
Ответ: 0,93
Задача 4.
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые
три дня по 17 докладов, остальные распределены поровну между четвертым и пятым
днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад
профессора М. окажется запланированным на последний день конференции?
Решение:
Событие состоит в том, доклад профессора М.
окажется запланированным на последний день
конференции. Всего докладов – 75 (общее
количество исходов).
В последний день конференции запланировано
(75 – 17 × 3) : 2 = 12 докладов (количество
благоприятных исходов).
Вероятность того, что доклад профессора М. окажется запланированным на
последний день конференции, равна р=12/75 = 4/25 = 0,16.
Ответ: 0,16
Задача 5.
Всего в группе туристов 21 человек, в том числе Женя и Саша. Группу случайным
образом делят на три подгруппы по 7 человек для посадки в три микроавтобуса. Какова
вероятность того, что Женя и Саша случайно окажутся в одном автобусе?
Решение:
Пусть один из мальчиков, например, Женя, находится в одном из автобусов.
Вместе с ним в этом автобусе окажутся 7-1=6 человек из 21-1=20 оставшихся.
Вероятность того, что Саша окажется среди этих 6 человек, равна
р = 6 : 20 = 3 : 10 = 0,3.
Ответ: 0,3
Задача 6.
Перед началом первого тура чемпионата по бадминтону участников разбивают на
игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует
26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов.
Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо
бадминтонистом из России?
Решение:
Нужно учесть, что Руслан Орлов должен играть с
каким-либо бадминтонистом из России. И сам
Руслан Орлов тоже из России.
В паре с ним могут оказаться 10-1=9 человек из
России из 26-1=25 оставшихся бадминтонистов.
Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо
бадминтонистом из России, равна р=9:25 = 36:100 = 0,36.
Ответ: 0,36
Задача 7.
За круглый стол на 11 стульев в случайном порядке рассаживаются 9 мальчиков и 2
девочки. Найдите вероятность того, что девочки окажутся на соседних местах.
Решение:
Допустим, первая девочка уже села на какое-то
место. Осталось 11-1=10 мест. Число всех
возможных исходов n=10.
Чтобы вторая девочка оказалась рядом с первой, она
может сесть либо слева, либо справа от нее. Получаем
число благоприятных исходов m=2.
р = 2 : 10 = 0,2.
Ответ: 0,2
Задача 8.
Клиент получает в банке кредитную карту. Четыре последние цифры номера карты
случайные. Какова вероятность того, что последние четыре цифры состоят из двух
повторяющихся групп по 2 различные цифры, например 0404 или 5252?
Решение:
Цифры стоят на четырех позициях и могут быть любыми из 10 различных (от 0 до 9),
т.е. число всех исходов n=10∙10∙10∙10 = 10 000.
Число благоприятных исходов m=10∙9∙1∙1=90.
р = 90 : 10 000 = 9:1000 = 0,009.
Ответ: 0,009
Задача 9.
Какова вероятность того, что последние три цифры телефонного номера случайного
абонента совпадают?
Решение:
Цифры меняются от 0 до 9, значит, это комбинации: 000, 111, 222, …, 999. Количество
таких комбинаций 10 и число благоприятных исходов m = 10.
Число всех исходов n=10∙10∙10= 1000
р = 10 : 1000 = 1:100 = 0,01.
Ответ: 0,01
Теоретические сведения
Задачи с монетами и кубиком
Задачи с монетами (и игральной костью) при небольшом
количестве подбрасываний удобно решать методом
перебора комбинаций.
Метод перебора комбинаций:
1. Выписываем все возможные комбинации орлов и
решек. Например, если две монеты: ОО,ОР,РО, РР. Число
таких комбинаций – n.
2. Среди полученных комбинаций выделяем те, которые
требуются по условию задачи (благоприятные исходы),
число благоприятных исходов – m.
Теоретические сведения
Задачи с монетами и кубиком
При решении задач с монетами число всех возможных
N
исходов можно посчитать по формуле n 2 ,
где N – количество бросков, 2 – число равновозможных
исходов (выпадение орла или решки).
При бросании кубика n 6 , где N – количество
бросков, 6 – число равновозможных исходов (выпадение
1, 2, 3, 4, 5 или 6 очков).
N
Задача 10.
Перед началом футбольного матча судья бросает монету, чтобы определить, какая из
команд будет первая владеть мячом. Команда «Меркурий» по очереди играет с
командами «Марс», «Юпитер», «Уран». Найдите вероятность того, что во всех матчах
право владеть мячом выиграет команда «Меркурий»?
Решение:
Обозначим право владения первой мячом
команды «Меркурий» в матче с одной из других
трех команд как «Решка». Тогда право владения
второй мячом этой команды – «Орел». Итак,
напишем все возможные исходы бросания
монеты три раза. «О» – орел, «Р» – решка.
«Марс»
«Юпитер»
«Уран»
О
О
О
О
О
Р
О
Р
О
О
Р
Р
р = 1 : 8 = 0,125
Р
О
О
Ответ: 0,125
Р
О
Р
Р
Р
О
Р
Р
Р
Число всех исходов получилось n=8,
благоприятных – m=1.
Задача 11.
Марина и Диана бросают кубик по одному разу. Выигрывает та, у которой выпадет
больше очков. Если очков выпало поровну, то наступает ничья. Первым бросила
Марина, у нее выпало 3 очка. Найдите вероятность того, что Диана выиграет.
Решение:
При условии, что у Марины выпало 3 очка,
возможны следующие варианты:
Всего вариантов n=6. Подсчитаем количество
исходов, в которых Диана выиграет, т.е. наберет 4, 5
или 6 очков. Таких вариантов m=3.
р=3:6 = 0,5
Ответ: 0,5
3
3
3
3
3
3
и
и
и
и
и
и
1
2
3
4
5
6
Задача 12.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того,
что одновременно хотя бы на одном кубике выпало число 1 и ни на одном кубике не
выпало число 6.
Решение:
Общее число исходов
n 62 36
Благоприятных исходов m=9.
р=9:36 =1: 4=0,25
Ответ: 0,25
1
1
1
1
1
и
и
и
и
и
1
2
3
4
5
2
3
4
5
и
и
и
и
1
1
1
1
Задача 13.
Монету бросают 10 раз. Во сколько раз событие «орел выпадет ровно 5 раз» более
вероятно, чем событие «орел выпадет ровно 7 раз»?
Решение:
m1
p1
n
m2
p2
n
Количество всех исходов первого и второго события одинаково:
p1 m1
p2 m2
n 210
n!
m C
k! (n k )!
k
n
10!
10 9 8 7 6
252
5!(10 5)!
5 4 3 2
p1
10! 10 9 8
7
m2 C10
120
7! 3!
3 2
p2
m1 C105
252
2,1
120
Ответ: 2,1
Теоретические сведения
Задачи из второй группы требуют
знания правил и формул сложения и
умножения вероятностей.
Задача 14.
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с
вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3.
Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет
фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Пусть событие С – «выигрыш гроссмейстера А., когда он играет белыми», р(С)=0,52.
Событие D – «выигрыш гроссмейстера А., когда он играет черными», р(D)=0,3.
Событие F – гроссмейстера А. выиграет обе партии.
Событие F является произведением событий C и D, т.к. гроссмейстер А. выиграет оба
раза, играя и белыми, и черными.
События C и D независимы друг от друга, поэтому р(F)=р(С∙D)=р(С)∙р(D)=0,52∙0,3=0,156.
Ответ: 0,156.
Задача 15. В магазине три продавца. Каждый из них занят с клиентом с
вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три
продавца заняты одновременно (считайте, что клиенты заходят независимо друг от
друга).
Решение:
Пусть событие А – «продавец занят с клиентом», р(А)=0,3.
Необходимо найти вероятность события С, когда занят первый продавец, при этом
занят второй, и при этом (занятости первого и второго) ещё занят и третий.
Используется правило умножения. Вероятность произведения независимых событий
равна произведению вероятностей этих событий.
Значит, вероятность того, что все три продавца заняты, равна:
р(С)= р(А)∙р(А)∙р(А)=0,3∙0,3∙0,3 = 0,027.
Ответ: 0,027.
Задача 16. По отзывам покупателей, Иван Иванович оценил надёжность двух
интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А,
равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван
Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины
работают независимо друг от друга, найдите вероятность того, что ни один магазин не
доставит товар.
Решение:
Пусть событие F – «товар доставят из магазина А»,
тогда событие — «товар не доставят из магазина А», р( )=1– 0,89 = 0,2.
Событие G – «товар доставят из магазина Б»,
тогда событие — «товар не доставят из магазина Б», р( )=1– 0,9 = 0,1.
Эти события независимы. Вероятность совершения независимых событий
одновременно (событие C – «оба магазина не доставят товар»), равна произведению
вероятностей этих событий: р(С)=0,1∙0,2 = 0,02.
Ответ: 0,02.
Задача 17. Биатлонист три раза стреляет по мишеням. Вероятность попадания в
мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист
первые два раза попал в мишени, а последний раз промахнулся. Результат округлите
до сотых.
Решение:
Пусть событие А – «биатлонист попадает в мишени», р(А)=0,8, тогда событие
«биатлонист промахнулся», р( )= 1 – 0,8 = 0,2.
—
Попадание в мишень при стрельбе является независимым событием. Вероятность
произведения независимых событий равна произведению их вероятностей.
Таким образом, вероятность события «попал, попал, промахнулся» равна:
0,8∙0,8∙0,2 = 0,128.
Округляем до сотых, получаем 0,13.
Ответ: 0,13.
Задача 18. На экзамене по геометрии школьнику достаётся один вопрос из списка
экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная
окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм»,
равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет.
Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из
этих двух тем.
Решение:
Пусть событие А – школьнику достанется вопрос по теме «Вписанная окружность»,
р(А)=0,2. Событие B – школьнику достанется вопрос по теме «Параллелограмм»,
р(B)=0,15.
Событие С – школьнику достанется вопрос по одной из двух тем.
Вопросов, которые одновременно относятся к этим двум темам, нет, т.е. события А и
В несовместны. *Несовместные (независимые) события – это события, которые не
могут произойти одновременно.
В данном случае вероятности складываются: р(С)=0,2 + 0,15 = 0,35.
Ответ: 0,35.
Задача 19. Вероятность того, что новый электрический чайник прослужит больше
года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89.
Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение:
Событие А – «чайник прослужит больше года», В – «чайник прослужит
больше двух лет», С – «чайник прослужит меньше двух лет, но больше
года»
Обратите внимание, что событие «В» включено в событие «А».
Графически это можно выразить так:
Таким образом, р(А)=р(В)+р(С). Искомая вероятность события С будет равна
разности: Р(С)=Р(А)–Р(В)= 0,97–0,89 = 0,08.
Ответ: 0,08.
Задача 20. Из районного центра в деревню ежедневно ходит автобус. Вероятность
того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94.
Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите
вероятность того, что число пассажиров будет от 15 до 19.
Решение:
Событие А – «в автобусе меньше 20 пассажиров» состоит из двух несовместных
событий: В – «в автобусе меньше 15 пассажиров» и события С – «в автобусе от 15 до 19
пассажиров». р(А)=0,94, р(В)=0,56.
Таким образом, р(А)=р(В)+р(С). Искомая вероятность события С будет равна
разности: Р(С)=Р(А)–Р(В)=0,94–0,56=0,38.
Ответ: 0,38.
Задача 21. При изготовлении подшипников диаметром 67 мм вероятность того, что
диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965.
Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше
чем 66,99 мм или больше чем 67,01 мм.
Решение:
Событие А – «при изготовлении подшипников диаметр будет отличаться от заданного
не больше, чем на 0,01 мм», т.е. диаметр подшипника будет лежать в пределах от 66,99
до 67,01 мм, р(А)=0,965.
Событие «подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем
67,01 мм» является противоположным событию А.
Значит, необходимо найти вероятность противоположного события.
р( ) =1 – 0,965 = 0,035.
Ответ: 0,035.
Задача 22. В торговом центре два одинаковых автомата продают кофе. Вероятность
того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что
кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу
дня кофе останется в обоих автоматах.
Решение:
Пусть событие А – кофе закончится в первом автомате, р(А)=0,3. Событие В – кофе
закончится во втором автомате, р(В)=0,3.
Обратите внимание, что события А и В совместны, т.к. кофе может закончиться в
обоих автоматах.
Событие А∙В – кофе закончится и в первом, и во втором автоматах, р(А∙В) = 0,12.
А+В – кофе закончится хотя бы в одном автомате.
События A и B совместные, вероятность суммы двух совместных
событий находится по формуле:
Р(А + В) =Р(АUВ)=Р(А) + Р (В) – Р(А∙В) = 0,3 + 0,3 – 0,12 = 0,48.
Задача 22. (продолжение)
Решение:
Все варианты событий, которые могут быть:
ОСТАЛСЯ В ПЕРВОМ – ОСТАЛСЯ ВО ВТОРОМ
ЗАКОНЧИЛСЯ В ПЕРВОМ – ОСТАЛСЯ ВО ВТОРОМ
ОСТАЛСЯ В ПЕРВОМ – ЗАКОНЧИЛСЯ ВО ВТОРОМ
ЗАКОНЧИЛСЯ В ПЕРВОМ – ЗАКОНЧИЛСЯ ВО ВТОРОМ.
Выражению – «кофе закончится хотя бы в одном» соответствуют три события из
представленных.
Значит, событие «кофе останется в обоих автоматах» противоположно
событию «кофе закончится хотя бы в одном». И его вероятность равна:
1 – 0,48 = 0,52.
Ответ: 0,52.
Задача 23. В магазине стоят два платёжных автомата. Каждый из них может быть
неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность
того, что хотя бы один автомат исправен.
Решение:
Пусть событие А – «хотя бы один автомат исправен», тогда событие «оба автомата неисправны». Они противоположны, т.к.
«неисправен-неисправен»
«исправен-неисправен»
«неисправен-исправен»
«исправен-исправен».
Найдем вероятность того, что неисправны оба автомата.
Эти события независимые, значит, вероятность будет равна произведению
вероятностей этих событий: р( )=0,05∙0,05=0,0025.
Значит вероятность того, что исправен хотя бы один автомат: р(А)=1– 0,0025 = 0,9975.
Ответ: 0,9975.
Задача 24. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет
из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера,
то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них
только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый
попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон
промахнётся.
Решение:
Пусть событие С – «Джон попадет в муху». Вероятность этого события найдем по
формуле полной вероятности: р(С)=р(А)∙р(С\А)+р(В)∙р(С\В),
где событие А – «Джон схватит пристрелянный револьвер», р(А)=
;
событие В – «Джон схватит непристрелянный револьвер», р(В)=1-0,4=0,6;
р(С\А) – вероятность того, что Джон попадет в муху, если возьмет
пристрелянный револьвер, р(С\А)=0,9;
р(С\В) – вероятность того, что Джон попадет в муху, если возьмет
непристрелянный револьвер, р(С∙В)=0,2.
р(С)=0,4∙0,9+0,6∙0,2=0,48.
«Джон попадет» и «Джон промахнется» — противоположные события,
значит р( )=1-0,48=0,52.
Ответ: 0,52.
Задача 25. Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу
выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на
рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он
придет в точку G.
Решение:
Выбор пути на каждой развилке происходит
наудачу, поэтому вероятность того, что пенсионер
выберет дорожку АВ р=
, дорожку ВG р=
.
Пусть событие G – «пенсионер пришел в точку G»,
АВG – «маршрут пенсионера».
Значит, по правилу умножения вероятность того, что пенсионер придет в точку G,
равна: Р(G) = Р(АВG) = 1/2·1/4= 0,125.
Ответ: 0,125.
Задача 26. Две фабрики выпускают одинаковые стекла для автомобильных фар.
Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает
3% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно
купленное в магазине стекло окажется бракованным.
Решение:
Событие С – случайно купленное в магазине стекло окажется бракованным.
Первая фабрика выпускает 45% стёкол, значит, вероятность купить стекло первой
фабрики р(А)=0,45. Вероятность купить бракованное стекло первой фабрики р=0,03.
Вторая фабрика выпускает 55% стёкол, значит, вероятность купить стекло второй
фабрики р(В)=0,55. Вероятность купить бракованное стекло второй фабрики равна
р=0,01.
Вероятность того, что стекло куплено на первой фабрике И при этом оно окажется
бракованным равна: 0,45∙ 0,03=0,0135.
Вероятность того, что стекло куплено на второй фабрике И при этом оно окажется
бракованным равна 0,55∙0,01=0,0055.
Покупка в магазине бракованного стекла подразумевает, что оно (бракованное
стекло) куплено с первой фабрики ИЛИ со второй. Это независимые события, то
есть полученные вероятности складываем: 0,0135 + 0,0055 = 0,019.
Ответ: 0,019.
Задача 27. Чтобы пройти в следующий круг соревнований, футбольной команде
нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3
очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того,
что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой
игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Решение:
Вероятность событий «проигрыш», «выигрыш», «ничья» составляют полную
вероятность. Значит, р(3)+ р(0)+р(1)=1, отсюда р(1)=1-0,3-0,3=0,4.
Команда может получить не меньше 4 очков в двух играх тремя способами:
3 + 1, 1 + 3, 3 + 3.
Эти события несовместны, вероятность их суммы равна сумме их вероятностей.
Каждое из этих событий представляет собой произведение двух независимых событий
– результата в первой и во второй игре.
Получаем: р(N ≥ 4) = р(3+1) + р(1+3) + р(3+3) =
= р(3) · р(1) + р(1) · р(3) + р(3) · р(3) =
= 0,3 · 0,4 + 0,4 · 0,3 + 0,3 · 0,3=
= 0,12 + 0,12 + 0,09 = 0,33.
Ответ: 0,33.
Задача 28. На фабрике керамической посуды 10% произведённых тарелок имеют
дефект. При контроле качества продукции выявляется 70% дефектных тарелок.
Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно
выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Решение:
10%=0,1
70%=0,7
Пусть завод произвел t тарелок. В продажу поступят все качественные тарелки, т.е.
(1-0,1)t=0,9t, и 30% невыявленных дефектных тарелок, т.е 0,3∙0,1t.
Количество всех тарелок n=0,9t + 0,3 · 0,1t = 0,9t + 0,03t = 0,93t.
Поскольку качественных из них (количество благоприятных исходов) m=0,9t,
то вероятность купить качественную тарелку равна: р = 0,9t/0,93t = 0,967 …≈0,97
Ответ: 0,97.
Марова Светлана Николаевна
[email protected]
Если вы хотите научиться
плавать, то смело входите в воду,
а если хотите научиться решать
задачи, то решайте их!
Д. Пойа
Удачи на ЕГЭ!
Список источников основного содержания:
Вероятность и комбинаторика в заданиях ЕГЭ по математике.
Фрундин В.Н. Учебное пособие. — Курск: ЦР «Лоцман»,
2013. – 96 с.
ЕГЭ: 4000 задач с ответами по математике. Все задания
«Закрытый сегмент». Базовый и профильный уровни / И.В.
Ященко., И.Р. Высоцкий и др. – М.: Издательство «Экзамен»,
2016. – 640 с.;
https://ege.sdamgia.ru/ − Сайт Дмитрия Гущина;
https://fipi.ru/ege/otkrytyy-bank-zadaniy-ege#!/tab/173765699-2 открытый банк заданий ФИПИ.
Список источников иллюстраций:
https://ru.123rf.com/ — фотобанк бесплатных фотографий;
https://www.freepng.ru/ — прозрачные иллюстрации для
компьютера;
https://ru.depositphotos.com/ — фотосток фотографий,
иллюстраций, векторных изображений.

Шпаргалка по теории вероятности — Без Сменки

11 ноября, 2021

4 мин

Мтмт 📈

Случайности не случайны… Всё решает вероятность событий!

В ЕГЭ по математике целых два задания на теорию вероятностей, поэтому стоит уделить ей в два раза больше внимания! Первое решается по основной формуле вероятности, а вот над вторым придётся подумать и вспомнить, какие бывают события.

Мы структурировали типы задач, которые могут попасться на экзамене, и сделали эту полезную шпаргалку с формулами и теорией — сохраняйте карточки, чтобы подготовка к ЕГЭ по математике была ещё продуктивнее.

 

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Редакция Без Сменки

Честно. Понятно. С душой.

44 подписчиков

+ Подписаться

Редакция Без Сменки

15 июня, 2022

1 мин

Инф 💻

ВЫИГРЫШНАЯ И ПРОИГРЫШНАЯ СТРАТЕГИЯ

👉 Рассмотрим задачу: Два игрока (Петя и Ваня) играют в игру.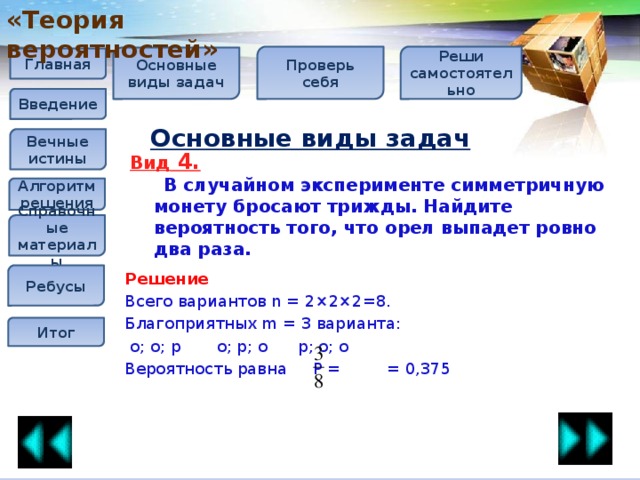

Перед игроками лежит 1 камень. У…

Редакция Без Сменки

15 июня, 2022

1 мин

Инф 💻

Структуры данных

Рассмотрим основные структуры данных: ▪️Список(list) Список в Python представляет собой…

Редакция Без Сменки

03 мая, 2022

1 мин

Ист 🤴

Портрет Екатерина II

А сегодня познакомимся поближе с Екатериной II! Ей удалось укрепить власть империи в мире,…

Редакция Без Сменки

07 июня, 2022

1 мин

Англ 🇬🇧

Stative verbs

❗️ Итак, мы должны помнить, что статичные глаголы относятся к глаголам состояния и их нельзя. 3$. Это возможно, если рассматривать только следующие случаи:

1. Он сдал первый и второй экзамен.
2. Он сдал первый экзамен, провалил второй, но сдал третий экзамен.
3. Он не сдал первый, сдал второй и третий экзамены.

Но я думаю, что это неправильно, так как минимум два из трех экзаменов означают, что сдача первого, второго и третьего экзамена является включительной. Кто-нибудь, пожалуйста, разрешите этот парадокс.

• вероятность

$\endgroup$

4 93$. Проблема поставлена, кстати, плохо.

$\endgroup$

0

$\begingroup$

Обозначим через $E_i$ событие «Экзамен $i$ сдан», а $\overline{E}_i$ — его дополнение. Тогда вы знаете, что $P(E_1)=p$, $P(E_2| \overline{E}_1 ) = P(E_3| \overline{E}_1 \cap \overline{E}_2 ) = P(E_3| \overline{E}_1 \cap E_2 ) = P(E_3| E_1 \cap \overline{E}_2 ) = р/2$ и $P(E_2|E_1) = P(E_3|E_1\cap E_2) = p$. 93 $$

$\endgroup$

ВЕРОЯТНОСТЬ С ЗАМЕНОЙ/БЕЗ ЗАМЕНЫ — Mathtec

Вероятностные задачи и

выборка с заменой и без нее

Выберите соответствующий ответ из строки вероятности выше для следующих событий: очень маловероятно или почти наверняка. Некоторые ответы могут зависеть от ваших собственных обстоятельств.

1) Солнце завтра не взойдет
2) Ты вернешься в свою нынешнюю школу в следующем году
3) Завтра будет дождь
4) Моцарт выступит на собрании
5) Вы получите отработку на обед
6) Вы выиграете в лотерею
                                          количество возможных исходов

Например, найдите вероятность выпадения орла при подбрасывании монеты. У монеты только один орел и есть два возможных исхода: орел или решка. Следовательно, вероятность равна:

Вероятность (P) = 1 = 1/2 или 0,5 или 50%
2

Найдите вероятность получения 6 на рулоне матрицы (Die Singloculal, кубики во множественном числе).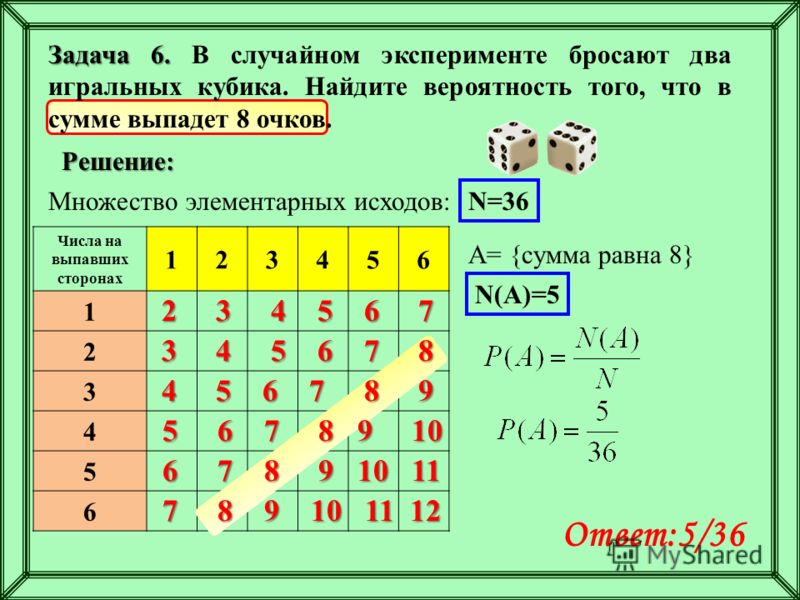

Вероятность (P) = 1 = 1/6 или 0,17 или 17%

6

Символ P или (P) используется в качестве короткого ручного способа написания «вероятность».

Моделирование и инструменты вероятности

Иногда наши действия практичны. Математики часто используют различные инструменты, которые помогают им изучать и понимать, как работает вероятность. Весь смысл в том, чтобы иметь что-то, что может имитировать случайное событие . Вот некоторые из этих инструментов:

1) Игра в кости (или кубик — единственное число). они бывают разных форм и размеров, а не только 6 сторон!
2) Игральные карты — очень популярны, так как их можно комбинировать с играми.
3) Спиннеры (колеса с маркировкой) еще один случайный инструмент
4) Калькуляторы и компьютерные генераторы случайных чисел – полезные, но более дорогие
5) Программные пакеты, такие как Microsoft Excel и онлайн-приложения, такие как Random. Org

примечание по игральные карты

Рис.1 Стандартная колода из 52 игральных карт

Обучение вероятности с использованием игральных карт очень популярно, и все же многие ученики не понимают, как они работают, так что давайте рассмотрим это прямо.

1) Есть 4 масти: (Рис.1 сверху вниз)
     Треф x 13
     Пик x 13
     Червей x 13
     Бубен x 13

Всего получается 52 карты.

2) В каждой масти по 13 карт: на рис.2 показана масть червей:      Туз, 2,3,4,5,6,7,8,9,10, валет, дама и король. 3) Из 13 карт Валет, Дама и Король называются королевскими картами или фигурными картами. Хорошей новостью является то, что когда карточные комбинации используются в математике, вопрос объясняет типы карт, составляющих комбинацию.

Рис.2 «Червовый валет украл эти тарталетки и с ними убежал…»

ВЕРОЯТНОСТЬ С ЗАМЕНОЙ

Рис. 3 Вероятность с заменой — «поставь обратно»

«С заменой» означает, что вы кладете шары обратно в коробку, чтобы количество шаров на выбор было одинаковым для всех розыгрышей при удалении более 1 шара.

вероятность Основы

Выше в коробке 10 цветных шаров: 4 красных, 3 зеленых, 2 синих и 1 черный. Мяч выбирается случайным образом. После каждого выбора шары будут возвращаться в коробку.
Какова вероятность того, что при случайном выборе шара или шаров мы выберем:
1) красный шар?
2) черный шар?
3) не синий шар?
4) сине-зеленый шар?
5) красный шар и 2 зеленых шара?

Вероятность = Общее количество красного = 4
Общее количество шариков 10

1) В коробке есть 4 красных шарика, поэтому вероятность выбора красного шарика составляет 4 из 10 или 4/10, которые можно выразить как 40%
 
2) В коробке только один черный шар, поэтому вероятность равна 1/10 или 10%.
3) Есть 8 не синих шаров, поэтому вероятность того, что выпадет не синий шар, составляет 8/10 или 80%. Это имеет смысл, потому что большинство мячей не синего цвета.
 
4) Вероятность того, что выпадет синий шар, равна 2/10, а вероятность того, что он вытащит зеленый шар, равна 3/10. Таким образом, вероятность выпадения обоих равна:
 2/10 x 3/10 = 6/100 = 0,06 или 6%
 
5) Вероятность выпадения красного шара равна 4/10, а вероятность выпадения зеленого шара равна 3. /10, а так как мяч возвращается в коробку, второй грин тоже 3/10. Таким образом, вероятность равна:
4/10 x 3/10 x 3/10 = 36/1000 = 0,036 или 3,6%
 

вероятность без замены

Рис.4 Вероятность выпадения первого шара без возврата «не класть обратно»

Рис.5 Вероятность выхода второго шара без замены.

«Без замены » означает, что вы не кладете шар или шары обратно в коробку, чтобы количество шаров в коробке уменьшалось по мере удаления каждого шара. Это меняет вероятности. Давайте посмотрим на вопрос 4 выше.

Какова вероятность того, что при случайном выборе шара или шаров мы выберем:
синий и зеленый шар?

Вероятность выбора синего шара составляет 2/10, а вероятность выбора зеленого шара – 3/9, потому что после того, как вынули первый шар, осталось 9 шаров. Таким образом, вероятность равна:
2/10 x 3/9 = 6/90 или 1/15 = 6,7 % (сравните это с заменой 6/100 или 6%)

Карточный домик с использованием вероятности без замены

Рис.6 Карточный домик Пример использования вероятности без замены.

На рис.6 показано 7 карт, 3 красных и 4 черных. Те же самые карты можно использовать для объяснения вероятностей Карточного домика Пример 3. Числа могут быть разными (6 красных и 8 черных), но процесс тот же.

Помните, что тип задачи был «Интересно, насколько вероятно, что я смогу вытянуть 3 красные карты из колоды из 7 карт».