Площадь определение в математике: Что такое площадь? Как её найти?

Площадь | это… Что такое Площадь?

У этого термина существуют и другие значения, см. Площадь (значения).

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры^[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.

Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.

Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.

Содержание 1 Свойства 2 Общий метод определения площади 2. 1 Площадь плоской фигуры 2.1.1 Декартовы координаты 2.1.2 Полярные координаты 2.2 Площадь поверхности 3 Единицы измерения площади 3.1 Метрические единицы 3.2 Русские устаревшие 3.3 Античные 4 Формулы вычисления площадей простейших фигур 4.1 Планиметрические фигуры 4.2 Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур 4.3 Формулы для вычисления площади поверхности тел в пространстве 5 См. также 6 Литература 7 Ссылки 8 Примечания

Свойства

• Площадь единичного квадрата равна 1.
• Площадь аддитивна.
• Площадь неотрицательна.
• Площади конгруэнтных фигур равны.

Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими

[2].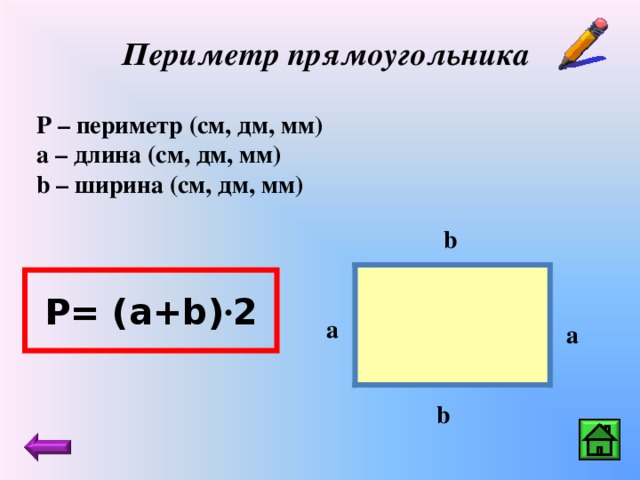

Общий метод определения площади

Площадь плоской фигуры

Декартовы координаты

Определённый интеграл как площадь фигуры

Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования

Площадь, заключённая между графиком непрерывной функции на интервале и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

Площадь, заключённая между графиками двух непрерывных функций на интервале находится как разность определённых интегралов от этих функций:

Полярные координаты

В полярных координатах: площадь, ограниченная графиком функции и лучами вычисляется по формуле:

.

Площадь поверхности

Основная статья: Площадь поверхности

Площадь искривлённой поверхности A, заданной вектор-функцией , даётся двойным интегралом:

То же в координатах:

Здесь .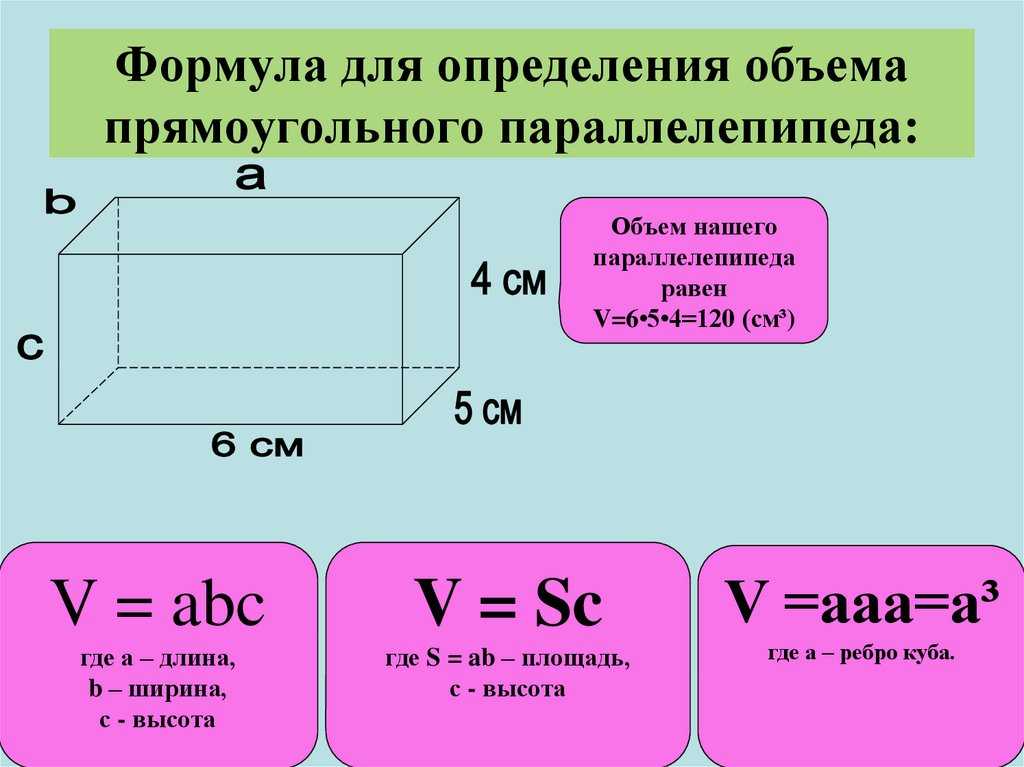

Единицы измерения площади

Метрические единицы

• Квадратный километр, 1 км² = 1 000 000 м²
• Гектар, 1 га = 10 000 м²
• Ар (сотка), 1 а = 100 м²
• Квадратный метр, производная единица системы СИ 1 м² = 1 са (сантиар)
• Квадратный дециметр, 100 дм² = 1 м²;
• Квадратный сантиметр, 10 000 см² = 1 м²;
• Квадратный миллиметр, 1 000 000 мм² = 1 м².

Русские устаревшие

• Квадратная верста = 1,13806 км²
• Десятина = 10925,4 м²
• Копна = 0,1 десятины — сенные покосы меряли копнами
• Квадратная сажень = 4,55224 м²

Мерами земли при налоговых расчетах были выть, соха, обжа

, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.

Античные

• Арура

Формулы вычисления площадей простейших фигур

Планиметрические фигуры

Фигура	Формула	Переменные
Квадрат		— длина стороны квадрата.
Правильный треугольник		— длина стороны треугольника.
Правильный шестиугольник		— длина стороны шестиугольника.
Правильный восьмиугольник		— длина стороны восьмиугольника.
Правильный многоугольник		— периметр, а  — количество сторон.
Прямоугольный треугольник		и  — катеты треугольника.
Произвольный треугольник		— сторона треугольника,  — высота, проведенная к этой стороне.
		,  — любые две стороны,  — угол между ними.
	(формула Герона)	, ,  — стороны треугольника,  — полупериметр .
		в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный.
Прямоугольник		и  — длины сторон прямоугольника (его длина и ширина).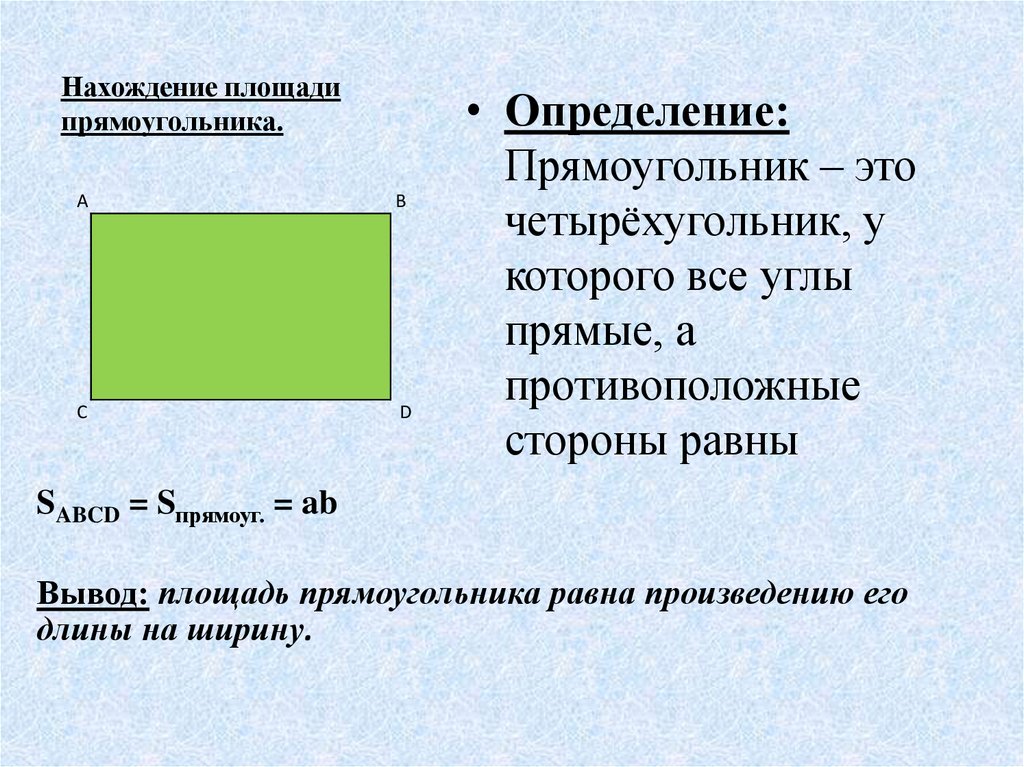
Параллелограмм		и  — длина стороны и опущенной на неё высоты соответственно.
		и  — соседние стороны параллелограмма,  — угол между ними.
Ромб		и  — длины диагоналей ромба.
Эллипс		и  — длины малой и большой полуосей.
Трапеция		та  — параллельные стороны, и  — расстояние между ними (высота трапеции).

Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур

Фигура	Формула	Переменные
Круг	или	— радиус, а  — диаметр круга.
Сектор круга		— радиус круга,  — центральный угол сектора (в радианах).
Сегмент		— радиус круга,  — центральный угол сегмента (в радианах).
Треугольник, вписанный в окружность		, ,  — стороны треугольника,  — радиус описанной окружности.
Произвольный многоугольник, описанный вокруг окружности		— радиус окружности, вписанной в многоугольник, и  — периметр многоугольника.

Формулы для вычисления площади поверхности тел в пространстве

Тело	Формула	Переменные
Полная площадь поверхности цилиндра		и  — радиус и высота соответственно.
Площадь боковой поверхности цилиндра		и  — радиус и высота соответственно.
Полная площадь конуса		и  — радиус и высота боковой поверхности соответственно.
Площадь боковой поверхности конуса		и  — радиус и образующая боковой поверхности соответственно.
Площадь поверхности сферы (шара)	или	и радиус и диаметр, соответственно.

См. также

• Площадь фигуры — математические аспекты понятия.
• Длина кривой
• Квадратура (математика)
• Объём
• Поверхность

Литература

• Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2

Ссылки

• Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977.
• Рохлин В. А. Площадь и объём. Энциклопедия элементарной математики, Книга 5, Геометрия.

Примечания

1. ↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
2. ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186-224. — 800 с.

формула в математике 5 класса, методика ее нахождения

Математика

12.11.21

16 мин.

При решении задач иногда возникает необходимость в определении площади прямоугольника. Формула для математики 5 класса довольно простая и позволяет находить не один параметр геометрической фигуры, а также широко применяется в строительстве, электротехнике и других отраслях человеческой жизни.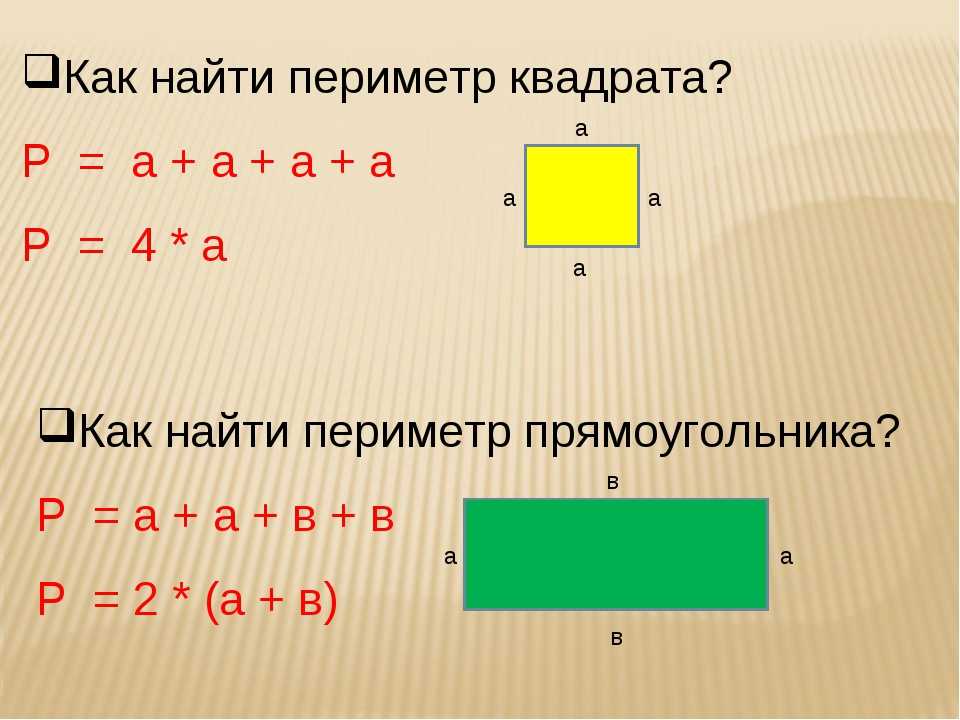

Специалисты разработали специальный алгоритм, позволяющий не только выполнять правильно расчеты, но и контролировать размерность величин.

Общие сведения

Прямоугольник — геометрическая фигура, состоящая из четырех взаимно перпендикулярных и равных между собой сторон. Следует отметить, что у него углы между смежными сторонами равны 90 градусов. У любой фигуры есть понятие размерности, а прямоугольник не является исключением.

Найти площадь прямоугольника можно по очень простой формуле. Она имеет следующий вид: S=k*l, где S — площадь (искомая величина), k и l — длины наибольшей и наименьшей сторон соответственно. Формулировка формулы имеет следующий вид: размерность прямоугольника прямо пропорциональна произведению его сторон. Однако это не единственное соотношение для вычисления этого параметра.

Если неизвестны стороны, то можно найти площадь через диагонали. Для этого потребуется знать их длину, а также острый угол между ними (y). Следует отметить, что диагонали прямоугольника равны между собой, поэтому можно обозначить их одной литерой «q».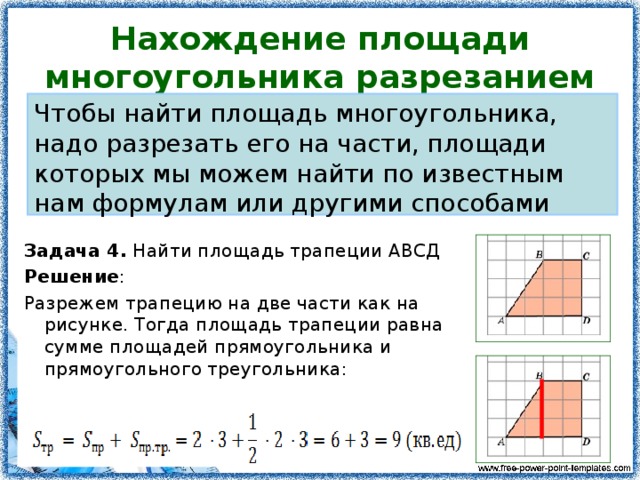 В результате формула записывается следующим образом: S=q ² * sin (y).

Звучит соотношение следующим образом: площадь прямоугольника эквивалентна произведению квадрата его диагонали на синус острого угла между диагоналями.

Применение формулы площади

Вычисление размерности прямоугольника применяется не только при решении задач, но и в строительстве. Например, чтобы выложить пол плиткой, нужно знать площадь комнаты, в которой будет выполняться эта операция. Следует отметить, что плитка в магазине продается в метрах квадратных.

Исходя из этого, требуется вычислить площадь комнаты, предварительно замерив стороны «прямоугольника». Однако на этом расчеты не заканчиваются, поскольку необходимо доказать, что пол комнаты является прямоугольником. Доказательство является очень простым, поскольку достаточно измерить диагонали.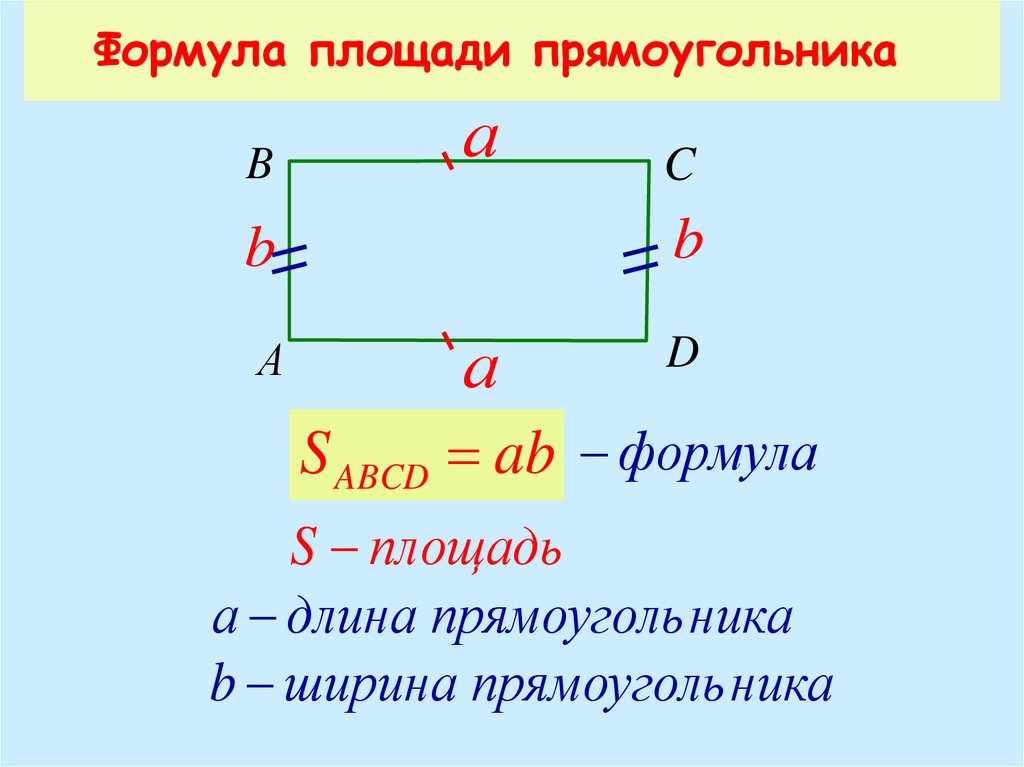 Если последние равны между собой, то плитку можно выкладывать от стены (ровно). В противном случае следует начинать работы с центра, и следить, чтобы углы изделия не совпадали с углами комнаты.

Следующий пример — расчет площади земельных участков. Вычисление происходит на основании базового соотношения определения площади через стороны.

Измеряется величина в сотках или гектарах, в которые нужно переводить метрические величины (длина и ширина участка — в метрах). Для правильности выполнения вычислений специалисты предлагают простой алгоритм измерения размерности.

Алгоритм нахождения размерности

Для вычисления площади прямоугольника нужно использовать специальный алгоритм, разработанный специалистами. Он имеет такой вид:

1. Определить тип фигуры: у нее противолежащие стороны и диагонали не должны быть разными и углы внутри прямоугольника, образованные сторонами, — прямыми.
2. Записать формулу площади: S=k*l=d ² * sin (y).
3. Определить размерность, то есть сантиметры, метры или километры.
4. Подставить известные величины в одно из тождеств во втором пункте.
5. Записать результат, вычислив величину размерности, которая может находиться по одной из формул.

Следует отметить, что каждый алгоритм должен быть реализован на практическом примере. Последний имеет следующий вид:

1. Условие: диагонали четырехугольника и противоположные стороны равны (5 м и 7 м). Следовательно, фигура является прямоугольником.
2. Формула размерности: S=l*k.
3. Единица измерения — м², поскольку стороны равны 5 м и 7 м.
4. S=5*7=35 (м²).
5. Результат: площадь прямоугольника со сторонами 5 и 7 метров эквивалентна 35 м².

Следует отметить, что при отсутствии единицы измерения сторон необходимо указывать условные величины, то есть ед². Далее необходимо рассчитать размерность фигуры на практическом примере при решении задачи.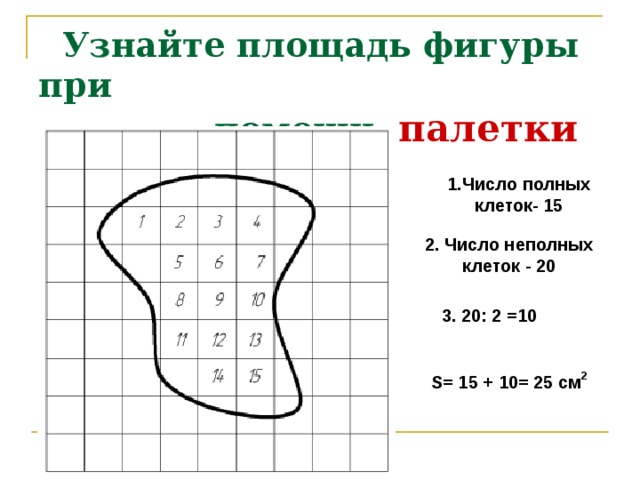

Пример решения задачи

Для закрепления теоретического материала необходимо решить задачу. Она имеет следующее условие:

1. Фигура состоит из прямоугольных треугольников, которые равны между собой.
2. Периметр одного треугольника: 12.
3. Разница между катетами составляет 1.
4. Гипотенуза больше первого катета на 1, а второго — на 2.

Необходимо узнать площадь фигуры. Решение задачи выглядит следующим образом:

1. Первый катет нужно приравнять к переменной m, тогда второй будет эквивалентен величине «m+1», а гипотенуза — «m+2».
2. Составить уравнение для нахождения периметра: m+m+1+m+2=12. Его корень (значение переменной) равен 1, то есть m=3. Тогда второй катет эквивалентен числу 4, а гипотенуза — 5.
3. Фигура является прямоугольником, так как состоит из равных треугольников.
4. На основании третьего пункта алгоритма стороны прямоугольника эквивалентны 3 и 4.
5. Площадь вычисляется по формуле: S=k*l=3*4=12 (ед²).

Cледует отметить, что фигура имеет одинаковые значения площади и периметра. Этот факт свидетельствует о том, что она была образована при помощи египетских треугольников (каждая сторона на единицу больше предыдущей).

Таким образом, определение площади прямоугольника необходимо осуществлять по алгоритму, предложенному специалистами. Кроме того, нужно внимательно следить за единицами измерения размерности.

При решении задач иногда возникает необходимость в определении площади прямоугольника. Формула для математики 5 класса довольно простая и позволяет находить не один параметр геометрической фигуры, а также широко применяется в строительстве, электротехнике и других отраслях человеческой жизни.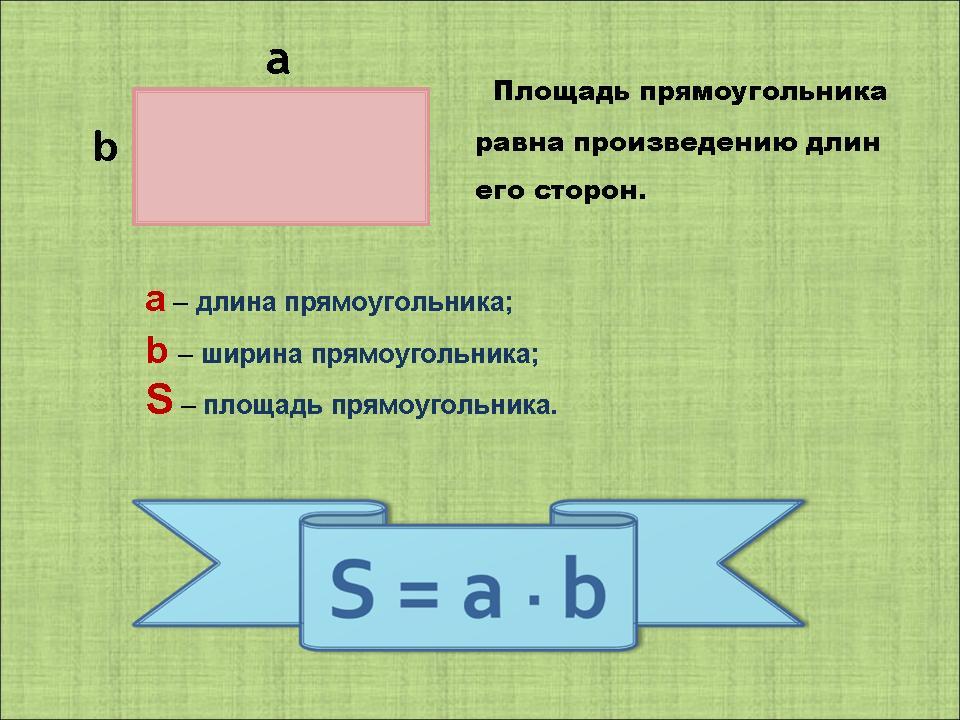 Специалисты разработали специальный алгоритм, позволяющий не только выполнять правильно расчеты, но и контролировать размерность величин.

Общие сведения

Прямоугольник — геометрическая фигура, состоящая из четырех взаимно перпендикулярных и равных между собой сторон. Следует отметить, что у него углы между смежными сторонами равны 90 градусов. У любой фигуры есть понятие размерности, а прямоугольник не является исключением.

Найти площадь прямоугольника можно по очень простой формуле. Она имеет следующий вид: S=k*l, где S — площадь (искомая величина), k и l — длины наибольшей и наименьшей сторон соответственно. Формулировка формулы имеет следующий вид: размерность прямоугольника прямо пропорциональна произведению его сторон. Однако это не единственное соотношение для вычисления этого параметра.

Если неизвестны стороны, то можно найти площадь через диагонали. Для этого потребуется знать их длину, а также острый угол между ними (y). Следует отметить, что диагонали прямоугольника равны между собой, поэтому можно обозначить их одной литерой «q». В результате формула записывается следующим образом: S=q ² * sin (y).

Звучит соотношение следующим образом: площадь прямоугольника эквивалентна произведению квадрата его диагонали на синус острого угла между диагоналями.

Применение формулы площади

Вычисление размерности прямоугольника применяется не только при решении задач, но и в строительстве. Например, чтобы выложить пол плиткой, нужно знать площадь комнаты, в которой будет выполняться эта операция. Следует отметить, что плитка в магазине продается в метрах квадратных.

Исходя из этого, требуется вычислить площадь комнаты, предварительно замерив стороны «прямоугольника». Однако на этом расчеты не заканчиваются, поскольку необходимо доказать, что пол комнаты является прямоугольником. Доказательство является очень простым, поскольку достаточно измерить диагонали. Если последние равны между собой, то плитку можно выкладывать от стены (ровно). В противном случае следует начинать работы с центра, и следить, чтобы углы изделия не совпадали с углами комнаты.

Следующий пример — расчет площади земельных участков. Вычисление происходит на основании базового соотношения определения площади через стороны.

Измеряется величина в сотках или гектарах, в которые нужно переводить метрические величины (длина и ширина участка — в метрах). Для правильности выполнения вычислений специалисты предлагают простой алгоритм измерения размерности.

Алгоритм нахождения размерности

Для вычисления площади прямоугольника нужно использовать специальный алгоритм, разработанный специалистами. Он имеет такой вид:

1. Определить тип фигуры: у нее противолежащие стороны и диагонали не должны быть разными и углы внутри прямоугольника, образованные сторонами, — прямыми.
2. Записать формулу площади: S=k*l=d ² * sin (y).
3. Определить размерность, то есть сантиметры, метры или километры.
4. Подставить известные величины в одно из тождеств во втором пункте.
5. Записать результат, вычислив величину размерности, которая может находиться по одной из формул.

Следует отметить, что каждый алгоритм должен быть реализован на практическом примере. Последний имеет следующий вид:

1. Условие: диагонали четырехугольника и противоположные стороны равны (5 м и 7 м). Следовательно, фигура является прямоугольником.
2. Формула размерности: S=l*k.
3. Единица измерения — м², поскольку стороны равны 5 м и 7 м.
4. S=5*7=35 (м²).
5. Результат: площадь прямоугольника со сторонами 5 и 7 метров эквивалентна 35 м².

Следует отметить, что при отсутствии единицы измерения сторон необходимо указывать условные величины, то есть ед². Далее необходимо рассчитать размерность фигуры на практическом примере при решении задачи.

Пример решения задачи

Для закрепления теоретического материала необходимо решить задачу. Она имеет следующее условие:

1. Фигура состоит из прямоугольных треугольников, которые равны между собой.
2. Периметр одного треугольника: 12.
3. Разница между катетами составляет 1.
4. Гипотенуза больше первого катета на 1, а второго — на 2.

Необходимо узнать площадь фигуры. Решение задачи выглядит следующим образом:

1. Первый катет нужно приравнять к переменной m, тогда второй будет эквивалентен величине «m+1», а гипотенуза — «m+2».
2. Составить уравнение для нахождения периметра: m+m+1+m+2=12. Его корень (значение переменной) равен 1, то есть m=3. Тогда второй катет эквивалентен числу 4, а гипотенуза — 5.
3. Фигура является прямоугольником, так как состоит из равных треугольников.
4. На основании третьего пункта алгоритма стороны прямоугольника эквивалентны 3 и 4.
5. Площадь вычисляется по формуле: S=k*l=3*4=12 (ед²).

Cледует отметить, что фигура имеет одинаковые значения площади и периметра. Этот факт свидетельствует о том, что она была образована при помощи египетских треугольников (каждая сторона на единицу больше предыдущей).

Таким образом, определение площади прямоугольника необходимо осуществлять по алгоритму, предложенному специалистами. Кроме того, нужно внимательно следить за единицами измерения размерности.

1.1 Давайте проясним: что мы подразумеваем под ОБЛАСТЬЮ?

Грубо говоря, площадь геометрической фигуры — это количество пространства внутри нее. Такое определение обращается к нашему интуитивному пониманию. Что это за интуитивное понимание?

 

Изучение площади обычно начинается с объявления площади квадрата шириной в одну единицу равной одной квадратной единице. Мы называем это базовой единицей площади.

Так как четыре из этих основных единиц плотно укладываются в квадрат со стороной два, без наложения друг на друга, мы говорим, что квадрат \(2 \times 2\) имеет площадь четыре. Точно так же квадрат \(3 \times 3\) имеет площадь девять, квадрат \(4 \times 4\) — площадь \(16\) и так далее.

Прямоугольник \(3 \times 6\) содержит \(18\) основных единиц квадратов и, следовательно, имеет площадь \(18\). В общем, прямоугольник, длина которого составляет \(a\) единиц, а ширина – \(b\) единиц, в котором есть как \(a\), так и \(b\) целые числа, имеет площадь \(a \×b\). Молодые студенты изучают эту идею в учебной программе K-5.

Поскольку четыре \(\frac{1}{2}\times\frac{1}{2}\) квадрата плотно помещаются в единичный квадрат, мы говорим, что площадь такого маленького квадрата равна \(\ frac{1}{4}\) квадратных единиц.

И дальнейшие исследования по сокращению долей единичных квадратов, по-видимому, указывают на то, что площадь прямоугольника \(a\) на \(b\) равна \(a \times b\) квадратных единиц, даже если \ (a\) и \(b\) имеют дробные части.

Это похоже на общий фундаментальный факт. Это кажется таким естественным и правильным, что мы могли бы счесть это отправной точкой общей теории площади.

ОПРЕДЕЛЕНИЕ: Площадь прямоугольника определяется как произведение его длины и ширины.

Комментарий для нас, взрослых:  Это определение взято как наблюдение в учебной программе K-5 (все обсуждаемые величины представляют собой либо целые числа, либо дроби). Но для тех, кто знает о существовании иррациональных чисел, это определение выводит дело на новый уровень: хотя невозможно уместить целое число или даже дробное число единичных квадратов в прямоугольник, равный \(5 \frac{3 {4}\) единиц длины и \(\sqrt{7}\) единиц ширины, тем не менее мы объявляем, что площадь такого прямоугольника есть произведение этих двух чисел. Это смело! К счастью, это утверждение соответствует нашему интуитивному представлению о том, что с помощью ножниц в этот прямоугольник поместится около \(5\frac{3}{4} \times \sqrt{7} \приблизительно 15,213\) единичных квадратов. (Однако мы, люди, никогда не увидим действительно правильной пропорции единичных квадратов, соответствующих этой форме. Тогда это утверждение действительно смело.)

 

Для правильной теории площади мы также должны сделать некоторые фундаментальные предположения о том, как работает площадь. Посмотрите это парадоксальное видео, чтобы увидеть, как я мотивирую следующие две сухие идеи с помощью причудливой интриги.

Кажется разумным сказать, что два прямоугольника, которые перекрываются только вдоль общего края , образуют фигуру, площадь которой равна сумме площадей прямоугольников.

Многие считают это фундаментальным постулатом геометрии:

Постулат сложения площадей: Если фигуру можно рассматривать как объединение двух меньших фигур, перекрывающихся только вдоль отрезков, то общая площадь фигуры равна сумме площадей меньших фигур.

Это, конечно, при условии, что у нас есть осмысленное представление о том, что означает площадь для этих двух меньших фигур.

Нам также хочется верить:

Постулат о совпадении площадей : Две конгруэнтные фигуры имеют одинаковую площадь.

То есть площадь фигуры не меняется при перемещении, вращении или отражении.

Этих двух убеждений, взятых в качестве наблюдений в учебной программе K-5 и принятых в качестве аксиом в геометрии средней школы, вместе с определяющим определением площади прямоугольника достаточно, чтобы разработать осмысленную теорию площади для всех средних классов. школьная и средняя школа математики: теперь мы можем вывести формулы площадей параллелограммов, треугольников, правильных многоугольников и т. д. (См. видео и мои тексты по ГЕОМЕТРИИ для получения подробной информации о разработке всей этой работы).

 

Пример: Смесь соков состоит из 60 % яблочного сока, 30 % грушевого сока и 10 % смешанного ягодного сока. Соковый коктейль содержит 50% яблочного сока, 10% вишневого сока и 40% воды. Если два галлона соковой смеси смешаны с тремя галлонами сокового коктейля, укажите процентное содержание каждого типа сока и воды в пятигаллонной смеси.

Ответ :

Мы видим, что пять галлонов состоят из \(6+6+5+5+5=27\) частей из пятидесяти, то есть \(54\%\), яблока сок, \(\frac{6}{50}=12\%\) грушевый сок, \(\frac{2}{50}=4\%\) ягодный сок, \(\frac{3}{50} =6\%\) вишневого сока и \(\frac{12}{50}=24\%\) воды.

     

Упражнение: В предыдущем вопросе, сколько галлонов сокового коктейля, смешанного с двумя галлонами смеси соков, даст смесь, состоящую из 45% яблочного сока? 30% яблочный сок?

 

Пример:   В определенном колледже \(60\%\) студентов составляют женщины и  \(40\%\) — мужчины. Из женщин \(50\%\) работают над получением степени по математике; мужчин, \(25\%\). Какой процент студентов колледжей изучает математику?

Ответ:

Мы видим, что \(40\%\) студентов колледжа изучают математику.

 

Упражнение: Предположим, мы поменяем местами числа в предыдущем вопросе: В некотором колледже \(60\%\) студентов составляют женщины и \(40\%\) мужчины, но на этот раз скажем, это \(50\%\) мужчин, работающих над получением степени по математике, и \(25\%\) женщин. Ожидаете ли вы, что новое количество специальностей по математике будет больше или меньше предыдущего?

 

Учащиеся классов K–5 должны развить глубокое, интуитивное и гибкое понимание местности.

Конечно, сначала они должны увидеть \(4 \x 6\) прямоугольник, например, как сумму \(24\) единичных квадратов, расположенных в виде массива четыре на шесть, построить, нарисовать и отразить на многих подобных примерах.

Складывая или разрывая бумагу или рисуя линии по всей фигуре, учащиеся должны искать структуру в этих картинках, например, видеть \(4 \x 4 + 4 \time 2\) внутри \(4 \раз 6\).

В конце концов мы должны отвлечь учащихся от буквального и перейти к концептуальному, рассматривая фигуру, подобную приведенной ниже, по-прежнему представляющую прямоугольник площадью \(24\) квадратных единиц (без необходимости рисовать их на самом деле) и играть с разделенным прямоугольником.

Для этого см. работу Джери Лоруэй. (Вот несколько более подробных примечаний: нажмите Geri Lorways PDF .)0002 Я как математик не могу не прокомментировать наше вступительное, расплывчатое определение:

Грубо говоря, площадь геометрической фигуры — это количество пространства внутри нее.

Да, такое определение обращается к нашему интуитивному пониманию. Но если мы хотим быть точными в нашем определении, мы быстро погрязнем в глубокой концептуальной неясности. Что именно мы подразумеваем под «количеством» и «пространством»? Даже слово «внутри» проблематично.

Упражнение: Нам нравится верить, что каждая кривая, которую мы рисуем в двумерном пространстве, делит пространство на две области: конечную, называемую внутренней частью петли, и бесконечную, называемую внешней. Это очевидно верно? Каждая ли кривая, нарисованная на плоскости, обладает этим свойством? Каждая ли петля, нарисованная на поверхности Земли, обладает этим свойством? (Если да, то что значит «внутри»?)

Это серьезные вопросы. Если бы Земля имела форму пончика, то на планете были бы изгибы, которые не делят поверхность на две части.

Конечно, чтобы выбраться из этого тумана, нужно следовать маршруту , который мы описали в этом уроке.

1. Сначала объявите значение «площади» прямоугольника, что бы это ни значило, равное произведению его длины на ширину.

2. Затем сделайте две декларации о том, как должна вести себя «область», что бы это ни значило. Возьмем постулат сложения площадей и постулат совпадения площадей.

3. Теперь проследите логические следствия этого вступительного заявления и двух заявленных убеждений.

Этот подход никогда не дает ответа на вопрос, что такое площадь на самом деле (и никогда не устанавливает, что мы подразумеваем под «пространством», «количеством» и «внутри»). И вся проблема разработки всеобъемлющего определения была полностью отодвинута на второй план. Но поскольку вступительные заявления основаны на наших интуитивных убеждениях, последующая теория кажется всегда соответствующей нашей интуиции. Это хорошо и правильно.

(Сказав это, я не должен упоминать парадокс Банаха-Тарского!)

 

Присоединяйтесь к обсуждению в Facebook и Twitter и поделитесь этой страницей, используя кнопки ниже.

Facebook

Twitter

область математических словосочетаний | значения и примеры использования

Эти слова часто используются вместе. Нажмите на ссылки ниже, чтобы изучить значения. Или посмотрите другие словосочетания с математикой или области.

Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.

Не все в районе математика учение уныние и уныние.

Из архива

Hansard

Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3. 0

.

Перестановки происходят более или менее заметным образом почти в каждой области из математики .

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

В области из математики он входит в число 150 лучших университетов мира.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Вопросы, касающиеся области математика развивать привычку логически и объективно.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Целью этой награды является признание выдающихся достижений в любой области из математика образование, следует понимать в самом широком смысле.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Такая ситуация, когда одно слово имеет много значений в одной и той же области математике , может сбивать с толку.

От

Википедия

Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.

Теория групп является важной областью математики для физиков.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Это область из математика является частью фундамента топологии и до сих пор по-новому применяется в математической физике.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Возникновение геометрической теории групп как отдельной области из математики обычно прослеживается до конца XIX в.80-х и начала 1990-х годов.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Проект в первую очередь предусматривал проведение поиска талантов с целью выявления одаренной молодежи, в частности, по направлениям из математика .

Из

Википедия

Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.

Ороско говорит, что работа представляет собой упражнение в топологии, области из математики , связанной с изучением непрерывности и связности.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Некоторые читатели могут быть заинтересованы только в том, как методы расщепления работают в одной из этих областей математики/науки, в частности.

Из Кембриджского корпуса английского языка

Доказательства включают различные области математики, которые не всегда считаются непосредственно связанными.

Из Кембриджского корпуса английского языка

Дифференциальная алгебра относится также к области из математики , состоящей в изучении этих алгебраических объектов и их использовании для алгебраического изучения дифференциальных уравнений.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Это область математика касается свойств пространства, сохраняющихся при непрерывных деформациях, в том числе при растяжении и изгибе, но не при разрыве или склеивании.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Отвечая на этот вопрос, упомянем прежде всего три классические избыточные системы, которые используются в разных областях математики.

Из Кембриджского корпуса английского языка

Алгебраическая комбинаторика стала рассматриваться более широко как область математики , где взаимодействие комбинаторных и алгебраических методов особенно сильно и значимо.

From

Wikipedia

Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.

Однако идея явного описания частичных элементов является гораздо более фундаментальной и может быть успешно использована в других областях математики и информатики.

No related posts.