Длина дуги кривой — вычисление с примерами решения
Содержание:
- Длина дуги в прямоугольных координатах
- Длина дуги кривой, заданной параметрически
Длина дуги кривой вычисляется по формуле или (10.18) Длина дуги кривой, заданной параметрически
определяется формулой
Если кривая задана уравнением в полярных координатах
Длина дуги в прямоугольных координатах
Длина s дуги гладкой кривой содержащейся между двумя точками с
абсциссами равна
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Примеры с решением
Пример 1.
Найти длину астроиды
Решение:
Дифференцируя уравнение астроиды, получим:
Поэтому для длины дуги одной четверти астроиды имеем:
Отсюда
Длина дуги кривой, заданной параметрически
Если кривая задана уравнениями в параметрической форме и непрерывно дифференцируемые функции), то длина дуги кривой равна
где —значения параметра, соответствующие концам дуги
Возможно вам будут полезны данные страницы:
Изменить порядок интегрирования |
Непрерывность функции |
фундаментальная система решений |
Метод Ньютона |
Найти длину одной арки циклоиды (рис. 50)
Пределы интегрирования соответствуют крайним точкам арки циклоиды. Если гладкая кривая задана уравнением в полярных координатах то длина дуги s равна
где — значения полярного угла в крайних точках дуги.
Пример 3.
Найти длину всей кривой (рис. 51). Вся кривая описывается точкой при изменении
Решение:
Имеем поэтому длина всей дуги кривой
Пример 4.
Найти длину дуги астроиды Чему равна длина астроиды при Поскольку астроида симметрична относительно координатных осей (см. рис. 1.36), нам достаточно вычислить длину дуги АВ и полученный результат умножить на 4.
Дифференцируя функцию как неявную, получим
Найдем выражение для подынтегральной функции, входящей в формулу (10.18). Имеем
По формуле (10.18) находим
При получаем при
Пример 5.
Вычислить длину дуги полукубической параболы отсекаемой прямой
Указанная дуга состоит из двух частей, симметричных относительно оси (см.
рис. 10.8).
Вычислим длину одной из них. Находя производную функции и подставляя ее в формулу (10.18), получим 4хт)!</х = //и-|хЛ =
Пример 6.
Найти длину дуги одной арки циклоиды
Движущаяся точка описывает одну арку циклоиды (рис. 1.35) когда меняется от Следовательно, в формуле (10.19)
выражение для подынтегральной функции в формуле (10.19). Дифференцируя уравнения циклоиды, получим:
Таким образом,
Подставляя это выражение в формулу (10.19), находим
Итак, Например, при
Пример 7.
Найти длину дуги эвольвенты (развертки) окружности: до произвольной точки
По формуле (10.19) получаем
Развертка окружности изображена на рис. 1.37.
Пример 8.
Найти длину дуги спирали Архимеда г — а<р от полюса О до любой точки М.
По формуле (10.20) получаем
Так как
то
Пример 9.
Вычислить длину кривой
Вся кривая описывается точкой при изменении (рис.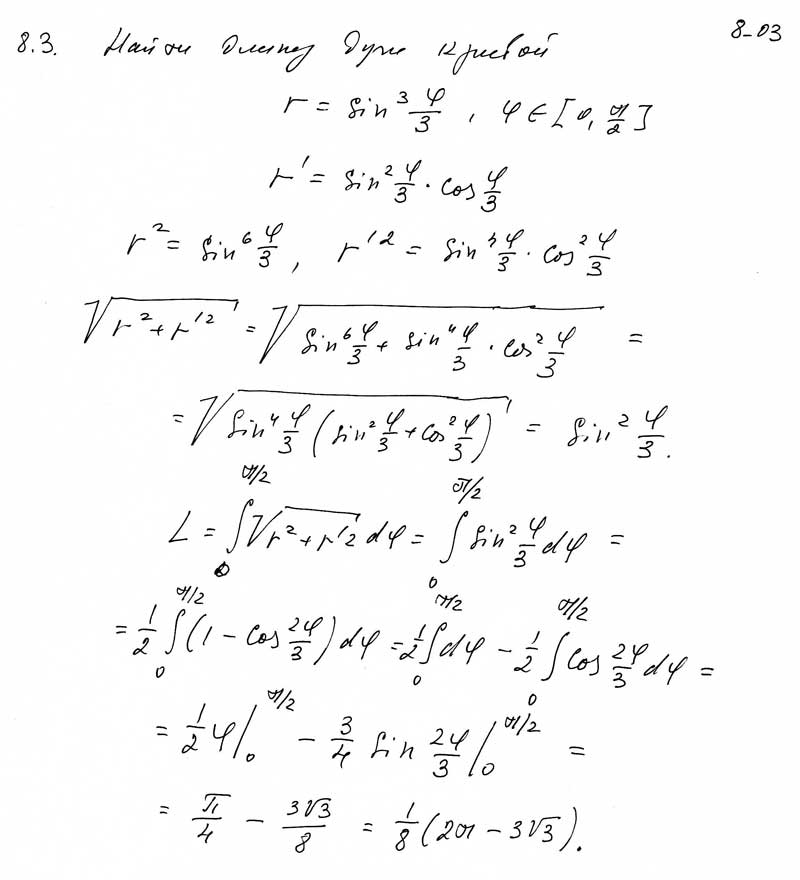
10.11).
Так как находим
Как найти длину дуги кривой линии в Wolfram|Alpha
1При помощи интегралов, кроме прочего, можно находить длину дуги кривой линии или площадь кривой поверхности. Длина дуги — это длина кривой, если ее «выпрямить», превратить прямую линию. Также ее можно представить, как расстояние, которое вы бы могли пройти, если бы шли от одной точки к другой, двигаясь вдоль кривой, а не непосредственно по прямой между точками.
Для вычисления длины дуги Wolfram|Alpha использует функцию arc length.
Длина дуги плоской кривой
Чтобы понять, для чего это нужно, задумайтесь над тем, сколько троса может понадобится, чтобы построить подвесной мост. Форма, которую принимает провисающий трос, называется «цепная линия» (catenary), но с подвесом, он принимает форму более знакомой кривой — параболы (parabola).
Мост Золотые Ворота. 2 / 8820 — (10x) / 21 + 500, x = 0..4200Таким образом, длина каждого троса составляет около 4354 футов в длину, чуть больше, чем расстояние между башнями. Обратите внимание, что Wolfram | Alpha показывает также интеграл, который нужно вычислить для нахождения длины дуги, а не только ответ. Длина дуги пространственной кривой Одно из обычных упражнений в стандартном курсе интегрального исчисления — найти длину дуги спирали. С прикладной точки зрения, это может быть, например, длина проволоки в катушке или количество ленты, которое потребуется, чтобы обернуть цилиндр, не оставляя промежутков. Спираль может быть выражена как параметрическая кривая, в которой координаты х и у определяют круг, а координата z линейно возрастает. Например: arc length (x, y, z) = (sin(t), cos(t), 2t), t =0..10 Длина дуги в полярных координатах Можно также находить длину дуги кривых в полярных координатах. В приведенном ниже примере, использование переменных r, θ позволяет Wolfram | Alpha догадаться, что данная кривая задана уравнением в полярных координатах: arc length r = theta*sin(theta), theta = 2. На рисунке выше, Wolfram | Alpha автоматически выбрал второе значение значение t=2. Изменяя это значение, можно подобрать, что при t=3.571 получим такой результат: 1По материалам: by Peter Barendse От себя Просто запросу arc length Wolfram|Alpha выводит калькулятор для вычисления длины дуги, где можно задать произвольную функцию и указать пределы интегрирования: Надеюсь, что вам понравилась функция arc length, и я с нетерпением ожидаю следующей возможности доставить вам удовольствием рассказом об интересных и полезных применениях Wolfram|Alpha. Калькулятор длины дуги — примеры, Калькулятор длины дуги онлайнКалькулятор длины дуги — это онлайн-инструмент, который вычисляет длину дуги, зная радиус окружности и центральный угол дуги. Дуга определяется как часть окружности окружности, которая лежит между любыми двумя точками. Что такое калькулятор длины дуги? Калькулятор длины дуги вычисляет длину дуги, используя различные формулы в зависимости от единицы измерения заданного центрального угла. Калькулятор длины дугиКак пользоваться калькулятором длины дуги?Чтобы найти длину дуги с помощью калькулятора длины дуги, выполните указанные ниже действия.
Как работает калькулятор длины дуги?Для расчета длины дуги нам нужно знать два параметра. Они следующие:
Чтобы найти длину дуги, мы можем использовать две разные формулы в зависимости от единицы измерения центрального угла. 1. Центральный угол дается в радианах.
Формула дается как: L = θ × r. 2. Центральный угол указывается в градусах.
Формула выглядит следующим образом: L = θ × (π/180) × r Здесь L — длина дуги, r — радиус окружности, θ — центральный угол, а π ( pi) — константа со значением 3,14 или 22/7. Хотите найти сложные математические решения за считанные секунды? Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. Записаться на бесплатный пробный урок Решенные примеры длины дугиПример 1: Найдите длину дуги, радиус которой равен 5 единицам, а центральный угол равен 4 радианам. Проверьте результат с помощью калькулятора длины дуги. Решение: Поскольку центральный угол дается в радианах, мы используем формулу L = θ × r L = 4 × 5 L = 20 единиц. Таким образом, длина дуги составляет 20 единиц. Пример 2: Найдите длину дуги, радиус которой равен 3,5 единицы, а центральный угол равен 6 градусам. Проверьте результат с помощью калькулятора длины дуги. Решение: Поскольку центральный угол дан в радианах, мы используем формулу L = θ × (π/180) × r L = 6 × (3,14 / 180) × 3,5 л = 0,37 ед. Таким образом, длина дуги составляет 0,37 единицы. Теперь используйте калькулятор длины дуги, чтобы найти длину дуги с заданными размерами:
☛ Математические калькуляторы: Калькулятор длины дуги Выберите параметры и введите их значения. РЕКЛАМА Рассчитайте: Центральный угол и радиусрадий и сегмент Heightradius и сектор ареарадиус и длина хорды и диаметр и диаметр угловой угол сектора (θ). * π рад Радиус (r)
mmcmmkminftydminmi Diameter
mmcmmkminftydminmi Sector area (A)
mm²cm²dm²m²km²in²ft²yd²mi²adahaacsoccer fields Chord length (c)
mmcmmkminftydminmi Segment Height (h )
ммкммкминфтидминми РЕКЛАМА РЕКЛАМА Содержание
Получите виджет! Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты. Получить код Обратная связь Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам! ОБРАТНАЯ СВЯЗЬ Онлайн-калькулятор длины дуги помогает найти длину дуги, центральный угол, радиус, диаметр, площадь сектора, высоту сегмента и длину хорды окружности. Когда дело доходит до определения длины дуги окружности, этот калькулятор дуги сообщает нам значение длины дуги вместе с другими соответствующими измерениями только в соответствии с выбранным полем. Что такое длина дуги?Длину дуги можно определить как общее расстояние между двумя точками на участке любой кривой. Вычисление длины сегмента дуги неправильной формы называется выпрямлением кривой. Меру дуги можно рассчитать с помощью обоих: • Уравнение длины дуги Вершина или вершина центрального ангела является центром \(O \) любой круг. Формулу длины дуги можно понять из следующего изображения: Если угол равен \(360\) градусов или \(2π\), то длина дуги будет быть равным окружности. Кроме того, пропорция между углом и длиной дуги остается постоянной, поэтому уравнение длины дуги будет: • \(L / θ = C / 2π\) В радианах: • Чтобы найти длину арки с радиусом, формула будет: \(s = ϴ × r\). В градусах: • Чтобы найти градусы длины арки, формула будет выглядеть так:\( s = 2 π r (θ/360°)\). Определение длины дуги больше не является сложным методом, так как вы можете использовать калькулятор длины дуги для быстрых вычислений. Кроме того, формула длины дуги является лучшим, но трудоемким способом определения длины дуги. Посмотрите приведенные примеры для лучшего понимания: Пример:Если радиус данного круга равен \(50 см \), а его центральный угол равен \(π/4 \), то какова будет площадь дуги? • Поскольку даны две меры; радиус и центральный ангел. Поэтому мы применим формулу, чтобы найти длину дуги в радианах: \ ( s = ϴ × r \). просто поместите в него значения. Этот онлайн-калькулятор дуги предлагает очень простой интерфейс, с помощью которого вы можете легко определить длину дуги и различные связанные параметры. Шаги: Ввод: Калькулятор поможет вам рассчитать длину дуги по:  |
2} from 0
Центральный угол может быть выражен как в градусах, так и в радианах. Чтобы использовать Калькулятор длины дуги , введите значения в соответствующие поля ввода.
С Cuemath находите решения простыми и легкими шагами.
Инструмент рассчитает длину дуги, диаметр, площадь, радиус, центральный угол, высоту сегмента и хорду заданного круга с отображением шагов.
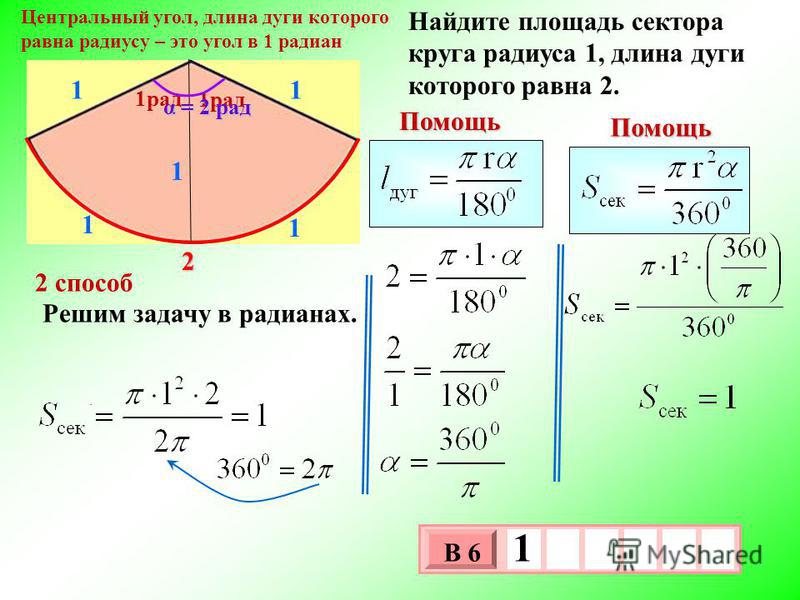Его стороны представляют собой радиусы, пересекающие окружность в двух дискретных точках, скажем, A и B. Кроме того, она опирается на дугу между точками A и B.