Пример по математике сложный: Сложные примеры по математике, которые вгоняют в краску неучей

Более сложные примеры уравнений | Математика

52. Более сложные примеры уравнений.
Пример 1.

5/(x – 1) – 3/(x + 1) = 15/(x² – 1)

Общий знаменатель есть x² – 1, так как x² – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x² – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

или

5x + 5 – 3x + 3 = 15

или

2x = 7 и x = 3½

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x² – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

Пример 2.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

или

2x² + 6x – 2x – 6 = 2x² + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x². Однако, мы можем от обеих частей уравнения вычесть по 2x² — от этого уравнение не нарушится; тогда члены с x² уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

3x = 3 или x = 1

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

что невозможно.

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

6x + 10 = 2x + 18

или

4x = 8 и x = 2

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x² + 4x – 10 = 2x² + 16x – 18.

Здесь уже члены с x² не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

4x² – 12x = –8

или

x² – 3x = –2

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2² – 3 · 2 = –2 и 2) 1² – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Пример 3.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x² – 5x + 6 = x² – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x² – x – 2 = x² – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x² – 2x – 3 = x² – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1).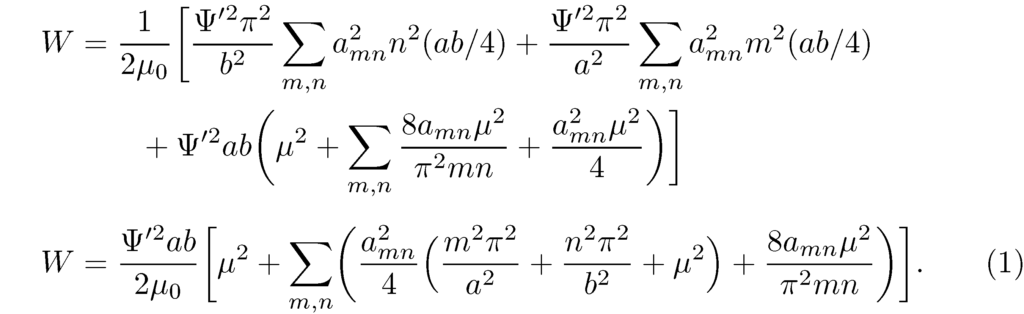 Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Отсюда получим:

–x = –13 и x = 13.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

или

3x + 3 – 2x + 6 = x – 2

или

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

0 = –11,

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Сложные примеры — легкие решения

• Авторы
• Руководители
• Файлы работы
• Презентация
• Наградные документы

Татаурова Н.И. 1

---

1МБОУ Гимназия № 17 4 класс

Сунцова Е.В. 1

---

1МБОУ Гимназия № 17

---

---

Автор работы награжден дипломом победителя II степени

Диплом школьникаСвидетельство руководителяДиплом участника II этапаДиплом за подготовку участника II этапаДиплом лауреата II этапаДиплом за подготовку лауреата II этапа

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Тема моей научно-практической работы – «Сложные примеры – легкие решения». Я выбрала эту тему для своей работы, так как для меня очень интересна и увлекательна математика. Чем дольше я учусь в школе и чем больше изучаю математику, тем чаще задаюсь вопросом: «Как можно решать такие сложные задачи и примеры быстро и, не прибегая к помощи калькулятора или компьютера». Интерес к этим вопросам побудил меня искать информацию в интернете, читать статьи и книги с этим связанные, спрашивать своих одноклассников и друзей, что они используют, чтобы облегчить себе изучение математики. Оказалось, что существует масса приемов устного счета, зная которые можно очень быстро считать в уме. Владение такими приемами не только облегчает изучение математики, но и значительно помогает в простой жизни. Мне захотелось поделиться со всеми найденной информацией, но для того, чтоб все легко запомнилось, появилась идея изложить в стихах алгоритмы решения примеров.

Цель моей работы – разработать свое пособие-напоминание, в котором изложены основные алгоритмы решения примеров на умножение и деление двузначных и трехзначных чисел. Это пособие выполнить в виде брошюры с примерами, объяснениями решений в стихах, которые я сочинила сама и иллюстрациями.

Моя гипотеза – с помощью моего пособия дети проявят большой интерес к математике, научатся быстро решать в уме сложные примеры, в том числе благодаря стихотворной форме изложения алгоритма.

Задачи моей работы:

Ознакомиться с алгоритмами решений сложных математических решений в уме.

Выяснить, что знают мои одноклассники о таких приемах.

Сочинить стих – объяснение про каждый пример, используемый в моем пособии.

Составить пособие и распечатать его в виде брошюры.

2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Каждый день каждый человек десятки, а то и сотни раз сталкивается с математикой. Начиная с момента пробуждения, мы весь день применяем в жизни наши математические навыки, иногда не замечая этого (как для приготовления завтрака и измерения пропорций), а иногда (как в магазине, например) вполне осознанно.

Чтобы что-то посчитать, человек применяет свои вычислительные навыки. И навыки эти нужно развивать. А развить их может каждый человек, независимо от его феноменальных математических способностей, хотя бы для того, чтобы не стать жертвой обмана в магазине или на рынке.

Развивать их можно, в том числе и с помощью применения различных техник и приемов устного счета.

С давних времен люди изобретали или находили все новые такие приемы.

Когда я начала изучать этот вопрос, поняла, что мало знать о таких методах, их надо разобрать, запомнить, и тогда ты сможешь их активно применять в жизни. Разбираться с приемами устного счета оказалось не так уж сложно. Но вот запомнить столько различных задач сразу не удалось.

Так мне пришло в голову, что наиболее понравившиеся мне методы нужно зарифмовать. Ведь стихи запоминаются всегда лучше прозы. Пока я сочиняла стихи, все, используемые мной для работы математические примеры запомнились сами собой. Тогда и возникла идея поделиться своими стихами со своими друзьями, чтобы они тоже смогли легко запомнить алгоритмы решения сложных примеров.

Вас может удивит, но такая смесь математики и литературы дала очень хорошие результаты.

В ходе работы над своим проектом я ознакомилась со множеством подобных работ других учеников и пришла к выводу, что во всех случаях, когда ученики целенаправленно в счете использовали общеизвестные алгоритмы устного счета, скорость вычислений значительно увеличивалась, иногда даже в два раза. В просмотренных мною работах приводились таблицы с результатами таких экспериментов. Поэтому, я не стала доказывать в своей работе результативность применения различных методов устного счета. Это факт общепризнанный.

Моей задачей стало облегчить сам способ запоминания этих методов. Поскольку я очень люблю стихи и в повседневной жизни часто что-нибудь рифмую, выбор способа запоминания стал очевиден.

Вот что у меня получилось.

ПРАКТИЧЕСКАЯ ЧАСТЬ

3.1 Умножение на 11 числа, сумма цифр которого не превышает 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр.

63 х 11 = 693

26 х 11 = 286

Сложи числа две половинки

Помести их в серединку

3. 2 Умножение на 11 числа, сумма цифр которого больше или равна 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр. Единицы числа записываем в середину, а десяток прибавляем к первой цифре.

78 х 11 = 858

64 х 11 = 704

Сложи числа две половинки

Помести их в серединку.

Про десяток не забудь,

Прибавь к началу, Умным будь!

3.3 Умножение на 111 (если сумма чисел множимого меньше 10).

Также мысленно раздвигаем цифры этого числа, находим сумму цифр данного двузначного числа и ставим ее в середину дважды.

36 х 111 = 3996

3 + 6 = 9

42 х 111 = 4662

4 + 2 = 6

Опять сложи две половинки

Помести их в серединку.

Только дважды повтори,

Так как единицы три.

3.4 Умножение на 111 (если сумма чисел множимого больше 10).

Опять мысленно раздвигаем это число, складываем цифры и вставляем их в середину числа. Но поскольку сумма цифр составляет двузначное число, прибавляем его к первым цифрам.

76 х 111 = 8436

(7+6=13)

7136

13

8436

И вновь сложи две половинки

Снова вставь их в серединку

Ну, а так как число двузначное

нужно вставить в ответ два раза

Мы прибавим его однозначно

К первым цифрам. И без отказа!

3.5 Умножение на 25.

Чтобы умножить число на 25 , надо данное число (36) умножить на 100 и произведение разделить на 4:

37 х 25 = 900

(37 х 100) : 4 = 925

Если множимое делится на 4, то сначала можно разделить множимое на 4 и полученное частное умножить на а 100.

48 х 25 = 1200

(48 : 4) х 100 = 1200

При умножении на двадцать пять

Число на сто нам надо умножать,

Потом разделим на четыре,

Вот и ответ мы получили

3.6 Деление на 25.

Чтобы разделить число на 25, надо разделить его на 100 (если делится на 100) и полученное частное умножить на 4, или сначала делимое умножить на 4, а потом полученное произведение разделить на 100:

800 : 25 = (800 : 100) х 4 = 32

225 : 25 = (225 х 4) : 100 = 9

Сделаем наоборот от предыдущего примера

При делении на двадцать пять

Число на сто нам нужно разделять

Потом уже умножим на четыре

Вот снова и ответ мы получили

А если разделить на сто нельзя

То мы пойдем другим путем, друзья

Сначала на четыре мы умножим

Потом на сто поделим и отложим.

3.7 Умножение чисел от 11 до 19.

Умножать такие числа можно используя следующую формулу, которую стоит запомнить.

100 + 10 х (а + в) + а х в

Где а и в это единицы множителей

Формула только на первый взгляд кажется сложной

Любое число из диапазона от 11 до 19 представляем как десятки и единицы.

Получаем формулу: (10+a)×(10+b).

Раскрываем скобки: 100+10×b+10×a+a×b.

Выносим за скобки общий множитель и получаем окончательную формулу, по которой можно считать и которую есть смысл запомнить: 100+10×(a+b)+a×b.

14 х 18 = 252

100 + 10 х (4 + 8) + 4 х 8 =

= 100 + 120 + 32 = 252

Чтобы перемножить два числа

Между десятью и двадцатью

Единицы перемножь сперва

И запомни как свою семью.

А еще сложи их и умножь

На десятку. Это тоже впрок.

Вот теперь сложи все результаты

И еще плюс сто. И весь урок.

3.8 Старинный русский способ умножения.

Умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа.

32 х 13

16 х 26

8 х 52

4 х 104

2 х 208

1 х 416

32 х 13 = 416

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Первое число дели на два,

Второе же, напротив, умножай.

Дели до единицы и тогда

Записывай ответ и отдыхай!

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Немного усложняется, если делимое нечётное число, то нужно откинуть единицу и делить остаток пополам, но в результате прибавить все те числа, которые стоят напротив нечётных чисел левого столбца.

19 х 17

((19-1):2) = 9 х 34

((9-1):2) = 4 х 68

2 х 136

1 х 272

19 х 17 = 272 + 17 + 34 = 323

А если разделить на 2 нельзя,

То просто единицу убирай

Все делать точно так же продолжай

А то, что не делил — к ответу прибавляй

3. 9 Умножение двузначных чисел на 9, 99, 999.

К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель.

28 х 9 = 280 — 28 = 152.

18 х 99 = 1800 — 18 = 1782.

23 х 999 = 23000 — 23=22977.

Так как 10а-а=9а, то для умножения числа а на 9 достаточно от увеличенного в 10 раз числа а отнять само число. Аналогично умножение на 99 и на 999. Число а умножают на 100 и на 1000 и отнимают само число.

Сколько девяток – столько нулей

Пусть даже три, ты не робей

Смело нули к числу припиши,

Ну, а потом, число отними.

3.10 Умножение трёхзначного числа на 999.

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только на уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9.

385 х 999 = 384615

Но в принципе, здесь работает тот же принцип, что и в предыдущем примере.

385 х 999 = 385000 – 385 = 384615

Даже, если множитель трехзначный

Три нуля к нему прибавить можно

И само число из цифры этой

Вычесть для тебя совсем не сложно.

3.11 Умножение чисел от 91 до 99 друг на друга.

Первый множитель вычесть из 100, второй множитель вычесть из 100, результаты сложить. Сумму вычесть из 100 и записать ответ первыми цифрами ответа. Далее перемножить ответы и записать следующими цифрами ответа.

97 х 96 = 9312

100 – 97 = 3, 100 – 94 = 4.

4 + 3 = 7, 100 – 7 = 93, 4 х 3 = 12.

Из ста вычесть и второй и первый

Все сложить, поверьте, это верно.

Результат опять от ста отнимем

И началом для ответа примем.

А в конец ответа – очень просто,

Перемножим отнятое от ста.

3.12 Умножение трёхзначных чисел от 101 до 109.

Если к одному из чисел прибавить единицы второго числа, то это

будут первые цифры ответа, затем перемножить единицы — это будут

последние цифры ответа.

105 х 107=11235.

105 + 7 = 112, 5 х 7 = 35.

Целое число плюс единицы

И отправим их за знак «равно»

Только единицы перемножим

И поставим рядом заодно.

3.13 Умножение двузначного числа на 101.

Самое простое правило: припишите число к самому себе.

57 х 101 = 5757

На сто один умножить просто

Число ставь рядом как по росту.

3.14 Применение моего пособия.

Стихи получились не сложными и легкими в запоминании. Я раздала своим одноклассникам брошюры, в которых объясняются сами методы устного счета и рядом располагаются стихи для запоминания метода.

Спустя месяц, я провела исследование способом анкетирования и получила такие результаты. Из 29 опрошенных 20 человек сказали, что мои стихи им очень помогли в запоминании способов быстрого счета.

ЗАКЛЮЧЕНИЕ

В заключение я бы хотела сказать, что выбранная мной тема мне очень понравилась, мне было очень интересно искать разные возможности облегчения устного счета. Оказалось очень интересно и захватывающе самой разбираться в примерах, проверять и перепроверять работает ли алгоритм, сочинять стихи и разрабатывать свое пособие, а потом раздать его друзьям.

В ходе работы над проектом мне удалось кратко познакомиться с историей появления различных приемов устного счета и узнать, как человечество развивалось в этом направлении.

Цель моей работы было создание своего пособия по запоминанию некоторых методов устного счета. Указанное пособие основано на стихах про математические примеры, которые я сочинила сама. Цель моей работы достигнута.

После знакомства с моей брошюрой, ребята стали интересоваться математикой и, в частности, исследованием алгоритмов устного счета. А это, в свою очередь, развивает память, мышление, другие умственные способности, приучает к поиску решений в любых жизненных ситуациях. Таким образом, казалось бы простая тема получила большой отклик у моих одноклассников и все получили новые знания.

СПИСОК ЛИТЕРАТУРЫ

Арутюнян Е., Левитас Г. «Занимательная математика» -М.:АСТ-пресс,1999г.

Владимиров, А. И. Интересные способы быстрого счета / А. И. Владимиров, В. В. Михайлова, С. П. Шмелева. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 15-17. — URL: https://moluch.ru/young/archive/9/633/ (дата обращения: 27.10.2020).

Гарднер М.  «Математические чудеса и тайны.»  М. 1978.

ГлейзерГ.И.» История математики в школе.» — М,1981.

«Библиотечка Первого сентября»,серия «Математика».Вып.3(15).  http//portfolio 1 September ru/subjest

ПРИЛОЖЕНИЕ

Просмотров работы: 1052

Сложные примеры для 2. Сообщение темы урока

В математике, конечно же, важно уметь думать и мыслить логически, но не менее важна в ней практика. Половина ошибок на экзаменах по математике делается из-за неправильного вычисления простых действий с числами — сложение, вычитание, умножение, деление. А отработать эти навыки важно еще в начальной школе. Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям — тренажерам. Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение.

Математика. Решаем примеры с переходом через десяток.

Тетрадь для отработки навыков сложения и вычитания с переходом через десяток. Не просто примеры, а интересные игры и задания.

Карточки-задания. Математика. Сложение и вычитание. 2 класс

Удобные карточки для учителя второклашек. 2 варианта на сложение и вычитание одного вида. Подойдут для организации самостоятельной работы по математике в зависимости от продвижения по программе.

Математика. Сложение и вычитание в пределах 20. 1-2 классы. Е.Э.Кочурова

В разных курсах математике тема сложения и вычитание в пределах 20 изучается или в конце 1 класса, или в начале 2-го. В любом случае пособие поможет закрепить изученные способы манипуляций с числами, в некоторых заданиях эти способы представлены в виде своеобразных подсказок. В ходе самостоятельной работы с тетрадью ребенок ориентируется на образец выполнения и алгоритмические предписания. Умение пользоваться такими подсказками в учебе позволит ученику не только находить и использовать нужную информацию в ходе выполнения задания, но и осуществлять самопроверку.

Начинается тетрадь с отработки навыков сложения и вычитание в пределах 10, эта часть подойдет и для первоклашек.

Математика тренажерная тетрадь для 2 класса

Тетрадь содержит не только примеры на сложение и вычитание, но и перевод единиц друг в друга, и сравнение результатов вычисления (больше-меньше).

3000 примеров по математике (счет в пределах 100 часть 1)

Тренажер со счетом на время. Время засекать на решение одной колонки примеров и записывать внизу в окошечке. Обратите внимание на колонки, которые ребенок решал более 5 минут, значит у него возникли сложности по этому виду примеров. Приведены примеры на сложение и вычитание в пределах десяти и с переходом через десяток, сложение и вычитание десятков, манипуляции в пределах сотни.

Счет от 0 до 100

В этой прописи дается много примеров на сложение и вычитание, чтобы закрепить навыки устного счета в пределах 100.

Считаем правильно. Рабочая тетрадь по математике. Г.В.Белых

Тетрадь также выполнена в виде тренажера, сплошные примеры и уравнения. Начинается со счета в пределах десяти, далее — в пределах сотни (сложение, вычитание, умножение и деление), заканчивается сравнением уравнений (примеры со знаками больше, меньше, равно).

Пособия пригодятся и учителям начальных классов в их работе, и родителям для занятий дома с детьми, в частности, в летние каникулы. Задания разных уровней сложности позволят осуществить дифференцированный подход к обучению.

Великие математики

Евклид. (ок. 365 — 300 до н. э.).

Древнегреческий математик. Работал в Александрии в 3 в. до н. э. Главный труд «Начала» (15 книг), содержащий основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов, оказал огромное влияние на развитие математики. Работы по астрономии, оптике, теории музыки. Евклид доказал множество теорем и гипотез.

Исаак Ньютон.

Родился 4 января 1643 года, механик, астроном и физик, создатель классической механики, член, затем президент Лондонского королевского общества. Один из основоположников современной физики, сформулировал основные законы механики и был фактическим создателем единой физической программы описания всех физических явлений на базе механики, открыл закон всемирного тяготения, объяснил движение планет вокруг Солнца и Луны вокруг Земли, а также приливы в океанах, заложил основы механики сплошных сред, акустики и физической оптики. Фундаментальные труды «Математические начала натуральной философии» и «Оптика». Ньютон разработал дифференциальное и интегральное исчисления. Открыл дисперсию света, хроматическую аберрацию, исследовал интерференцию и дифракцию, развивал корпускулярную теорию света, высказал гипотезу, сочетавшую корпускулярные и волновые представления.

Примеры по математике для 2 класса

Примеры по математике 2 класс

25 — 3 = 51 + 4 = 75 — 1 =

73 + 1 = 26 — 4 = 55 — 3 =

35 — 4 = 38 — 6 = 37 — 4 =

21 + 7 = 37 + 2 = 59 — 5 =

35 — 4 = 43 + 6 = 21 + 7 =

75 + 2 = 66 — 2 = 54 — 1 =

23 + 5 = 43 + 6 = 78 + 1 =

34 — 3 = 54 + 3 = 28 — 6 =

22 + 3 = 44 + 5 = 78 + 1 =

54 + 3 = 36 + 3 = 76 + 2 =

64 — 3 = 33 + 5 = 68 — 2 =

Цель: научить решать примеры в два действия.

Задачи:

1. Совершенствовать устные и письменные вычислительные навыки при решении примеров в два действия;
2. Развивать и обогащать речь учащихся терминологией при чтении математических выражений; слуховое и зрительное восприятие, внимание, память на устном счете при использовании дидактических игр, коррекционных и кинезиологических упражнений, развивать логическое мышление при решении задач;
3. Воспитывать целеустремленность, самостоятельность, взаимопомощь, аккуратность и соблюдение орфографического режима в тетрадях.

Оборудование:

• машина из геометрических фигур;
• учебник, картинки зверей;
• карточки с домашним заданием.

Ход урока:

1. Организационный момент.

Учитель:

Добрый день, добрый час!
Как я рада видеть вас!
Друг на друга посмотрели
И тихонечко все сели.
Долгожданный дан звонок
Все на месте? Все в порядке?
Ручки, книжки и тетрадки
Начинается урок математики.

Чем мы будем заниматься?

Ученики:

2. Учитель: Согреем руки и по массажируем мочки ушей.

Выполним упражнение «Ухо-нос» (кинезеологическое).

3. Сообщение темы урока.

Сегодня мы проведем необычный урок математики, мы отправимся в путешествие, а куда, вы узнаете, если:

А) правильно исключите лишнее число и объясните почему,

Б) расположите числа в порядке возрастания и прочтете зашифрованное слово:

11		14		8		17
Л		Е		В		С

Правильно, мы отправляемся в лес по теме «Решение примеров в два действия».

Цель нашего путешествия: обработка знаний, умений и навыков при решении примеров в два действия.

Задача нашего путешествия: работать быстро, четко, правильно.

4. Прежде чем отправимся в путешествие нам надо пройти подготовку:

Начинаем тренировку,
Чтобы умным стать и ловким (устный счет):

Прочтите выражение различными способами: 8 + 3 = 11.

(Первое слагаемое – 8, второе – 3, сумма – 11. Сумма чисел 8 и 3 равна 11.)

Следующее задание:

Что значит 5 увеличить на 2?

Что значит 7 увеличить на 3?

А теперь проверим вашу внимательность:

Нужно хлопнуть в ладоши, если число однозначное: 9 12 16 5 3 2 14 20.

Какое число я отстучу: 4 2 7 3 8.

Молодцы ребята, с заданиями хорошо справились! Теперь мы готовы к путешествию.

5. Геометрический материал.

Отгадав загадку, вы узнаете, на чем мы отправимся в путешествие.

Не летает, не жужжит,
Жук по улице бежит.
И горят в глазах жука
Два блестящих огонька. (Машина.)

Посмотрите на машину и скажите, их каких геометрических фигур она состоит.

Молодцы, с задачами справились, отправляемся в путешествие по лесу.

Обратить внимание на посадку, пристегнуть ремни, выполнить упражнение «Зайка» (пальчиковая гимнастика, кинезиологическое упражнение).

Открыли тетрадки: мы прибыли в лес. Первое задание вам даст тот, о ком загадка:

Под соснами,
Под елками
Лежит мешок
С иголками. (Ёжик.)

Правильно, ежик. Ежик предлагает вам прописать красиво и аккуратно числа 4 и 14.

Ребята, сравните свой показ с показом учителя и подчеркните лучший (каллиграфическая минутка)

По веткам скачет, а не птица,
Рыжая, а не лисица. Кто это? (Белка.)

Правильно, белочка. Она приготовила для вас задание – откройте учебник на стр. 223, №196 (решение примеров в два действия у доски и в тетрадях).

Поработали, ребятки, а теперь все на зарядку! А проведет зарядку отгадайте кто…

Чуткий нос
Пушистый хвост.
Ее не тронь,
Шубка как огонь. (Лиса.)

Правильно, лисичка. Проведение физкультурной минутки.

Встаньте дружно, улыбнитесь,
Все в зверюшек превратитесь!
Пойдем мягко, как лисята,
И как мишка косолапый.
Зайчик белый прыг да скок.
Серый еж собрался весь в клубок,
Лучик ежика коснулся,
Ежик сладко потянулся.

Решение задачи №195, стр. 223 (чтение задачи, работа над условием, анализ задачи, запись краткой записи, решение задачи).

Молодцы, ребята! Все задания выполнены, все звери остались довольны вашей работой! И домашнее задание они вам приготовили на карточках.

6. Подведение итога урока, выставление оценок.

Примеры онлайн на сложение и вычитание в пределах 10000

Примеры онлайн на сложение и вычитание в пределах 10000

ПримерОнлайн. ru

Генератор примеров по математике 1-3 класс

Онлайн Примеры на сложение трёхзначных чисел позволяют вывести большое количество неповторяющихся примеров с трёхзначными числами.

Примеры можно разделить по степени сложности: лёгкие – это примеры без перехода через десяток, сложные – с обязательным переходом, обычные – слагаемые выбираются случайным образом.

 



Настройка генератора примеров



Файл для печати В файле 1234567891012152025303540455060708090100 стр. Скачать: файл заданий, файл ответов

Свой формат страницы Выводить 153050100200300500 примеров Распечатать страницу

Интерактивные примеры Выводить 153050100200300500 примеров Показать страницу

Образец примеров



4155 + 4436

3680 + 4364

6693 — 3308

4486 — 2702

9753 — 8495

5639 — 2322

9471 — 7207

1724 + 4671

1743 + 5770

8150 — 6412

7736 — 2288

5609 — 3549

1104 + 3969

8093 — 4323

1698 + 3793

2257 + 2675

4036 — 2505

4903 + 1021

1550 + 7440

7468 — 1220

3004 + 6409

4404 + 4215

4225 — 3059

9817 — 5250

6298 + 2099

5988 + 3814

2879 + 3027

9889 — 7125

1653 + 2760

2547 + 1631

6224 — 2338

1899 + 4546

2407 + 6512

8364 — 2758

2812 + 1077

3444 — 1055

7201 — 4435

1726 + 4065

8616 — 1049

8508 — 6005

2092 + 2815

9695 — 3234

8985 — 1451

5090 — 3978

8779 — 1564

2099 + 3702

9328 — 4891

7137 + 2614

4094 — 1277

2652 + 3481

4127 — 3778

6561 — 2600

2775 + 2136

9359 — 5926

7741 — 7291

6547 — 5140

8233 — 4519

7783 — 2356

6766 + 2640

5789 + 2396

2511 — 1152

2661 + 3025

7959 — 1514

5772 — 3688

7751 — 5519

7469 — 2763

3491 + 3139

1502 — 1498

5074 + 4483

8312 — 2375

1877 + 5286

3732 + 5944

9498 — 4728

5376 + 1543

7411 — 1359

1775 + 8146

8529 — 4155

6505 — 6205

8334 — 8162

3408 + 1446

9221 — 7174

8144 — 7724

6369 — 2012

7283 — 1952

1699 + 2495

7851 — 3186

9153 — 6083

7076 + 2036

7917 — 1155

8901 — 2860

2656 + 6887

1317 + 2564

2509 + 6762

6940 — 6147

5739 + 4187

3670 + 4861

6784 + 2527

4835 — 4267

1768 + 4361

6501 — 4324

3196 + 5774

7598 + 1074

3136 + 1655

4476 + 2694

7234 — 4207

3246 + 6158

4627 — 2702

9860 — 1889

9175 — 6380

2794 — 1112

5651 — 3017

6429 + 1387

6671 — 5926

9782 — 2523

8324 — 4339

1919 + 5255

4358 — 1539

8641 — 2137

1163 + 5149

4368 + 2705

4677 — 1678

4617 + 2103

5673 — 4737

8439 — 3842

3986 + 2735

3705 + 3630

1740 + 6349

1732 + 8045

1187 + 6470

2805 + 1540

2833 — 2111

9046 — 5654

2785 — 1449

1251 + 3133

5298 — 2927

4839 + 4527

9877 — 6438

9227 — 3721

6351 — 4967

5421 + 1337

1083 + 4590

1965 + 1244

6665 + 1362

5223 — 1108

4048 + 3876

4025 + 5103

4980 + 4628

3408 + 5306

4970 + 2400

1004 + 6818

4933 — 2369

5125 + 3120

2963 + 7029

4333 — 1933

5192 — 4216

5345 — 4273

5038 + 1077

1751 + 6000

5004 — 2733

6745 — 6252

4994 + 1763

1838 + 2500

5586 — 2900

5092 + 2754

2656 + 7267

4325 + 5069

3314 + 2735

6810 + 2935

2987 + 1474

3980 + 5842

6240 — 2531

5095 — 3340

5501 + 1831

6104 — 2423

8125 — 2735

9702 — 1755

6160 + 3279

7515 — 3420

2184 + 4759

8089 — 6066

2544 + 3272

1579 + 4797

4122 + 4486

2410 — 1692

7705 — 3365

4948 + 4324

4339 + 3351

6847 — 2462

3559 + 1494

6852 — 4754

7159 — 6838

3332 + 5590

5826 + 1775

5704 — 4398

1182 + 8006

9229 — 2131

8282 — 5406

7317 — 1624

1089 + 2522

9075 — 7276

1579 + 5805

1672 + 2631

4859 + 3588

4795 + 2145

1268 + 7267

6117 — 1468

4421 + 4280

5074 — 3773

1064 + 7881

4367 + 4059

4344 + 5505

5854 + 1095

5808 + 1075

2800 + 6149

5376 — 4406

1568 + 4119

2376 — 1082

6559 — 2001

1209 + 6847

8000 — 4745

7668 — 2852

9797 — 6436

7654 + 1596

9990 — 8208

4084 — 1267

7671 — 7340

9706 — 1825

4824 + 1903

1096 + 7438

2775 + 2052

1095 + 8339

7947 — 1883

9606 — 6449

6947 — 2329

3470 + 1804

3620 + 2131

7241 + 2253

8336 + 1660

5123 + 2624

6191 — 2740

1888 + 3531

7649 + 1452

7767 + 2059

1316 + 6202

6236 — 3571

5704 — 2237

2416 + 3857

4243 + 5376

2078 + 7262

1110 + 1558

6164 — 2469

5037 — 5006

9849 — 1512

1427 + 4435

1083 + 3085

4670 — 4227

6726 — 3780

3461 + 2176

3996 + 5601

6989 — 1852

8974 — 5517

5809 — 5295

1276 + 6741

2719 + 6546

6549 — 6316

1533 + 4944

7289 + 1306

3955 + 3036

6168 — 2354

8913 — 8706

3503 + 2447

9423 — 7741

1395 — 1180

7648 + 1036

7575 — 6485

5564 — 3156

8502 — 3862

3844 + 3855

8264 — 7235

6585 — 1325

1071 + 3782

4230 — 1676

6792 — 1913

6049 — 1465

5372 + 4613

2970 — 2181

9314 — 6614

7014 — 6708

6397 — 1229

5558 + 1141

5537 — 2501

4273 + 1729

5643 — 3433

4106 + 2099

6479 + 2382

4496 + 3456

3886 — 1252

4829 + 4176

1287 + 8686

9373 — 8913

2811 + 5879

3777 — 1877

9669 — 2755

2616 + 5224

4041 + 4127

4498 — 1979

9544 — 5545

7759 — 1502

8127 — 3368

5531 — 3825

1893 + 4093

3812 + 2151

6926 + 2458

5480 + 2451

2484 + 4646

6856 + 1090

2555 + 5639

5812 — 4256

1862 + 5972

1561 + 5297

8668 — 1064

2739 — 2544

3232 + 2994

6011 + 3403

3560 + 5621

2643 + 7092

8589 — 6163

5772 — 3540

4747 + 5016

8177 — 1283

3340 — 2245

9646 — 1945

3484 + 1526

3646 — 2530

5744 — 2737

2625 + 6398

3710 + 4936

2176 + 3094

8881 — 2011

4160 + 3721

4268 + 1330

3944 + 5379

9672 — 5063

8157 — 1703

5503 + 2417

8958 — 4499

1694 + 8277

2772 + 5302

1640 + 5222

2570 + 2629

6352 — 3966

3155 + 4748

3409 — 1820

4728 + 2588

4722 + 5118

7208 + 2022

4483 + 3176

8578 — 7849

1360 + 2333

8090 — 2841

1696 — 1621

3343 + 6475

7789 — 3905

3659 — 1625

1428 + 3248

9935 — 7270

7192 — 3180

3383 — 3052

6259 — 2938

6885 + 2621

8866 — 7750

2243 + 4390

7756 — 3302

8891 — 7476

7208 — 6349

9036 — 5161

1977 + 2317

5527 + 4203

3074 + 1983

2820 + 2358

5511 — 5006

9515 — 8585

9682 — 4010

5384 + 2864

4856 + 4429

4135 — 3816

7265 — 2373

2996 — 2611

9863 — 2434

1394 + 6763

3096 + 5824

1664 + 6700

1034 + 5094

8101 — 3380

3067 + 2052

3356 + 3847

1657 + 3086

6881 — 2336

1092 + 3527

9374 — 9095

7913 + 1105

7619 — 5766

2830 — 2444

6334 — 3546

5122 — 1719

2480 + 1171

9914 — 1619

6625 — 3244

8366 — 8249

9457 — 1415

4619 + 2593

8177 — 8162

4810 + 4786

2838 + 2027

8396 — 4524

4679 — 3692

9270 — 1810

1184 + 5152

3702 — 1693

5906 — 1526

1807 + 3926

7908 + 1245

3421 + 6389

4820 — 3698

4605 — 3595

4313 + 2577

1105 + 4557

1761 + 1963

5652 + 3951

2386 + 3920

5813 — 3979

8046 — 3383

5268 + 1585

3909 — 2812

8144 — 6992

5230 — 5065

1447 + 3357

7737 — 4919

1213 + 1761

9472 — 2461

8571 — 1947

9080 — 7771

5542 + 1530

4643 — 4118

9376 — 9071

6614 + 2339

4405 + 4810

3550 + 2371

5253 — 4543

1006 + 2472

8371 — 3430

2221 + 6978

9045 — 4093

8213 — 4491

2256 + 1284

4411 + 2092

4924 + 1181

4685 — 1714

9440 — 1259

3570 — 3462

4463 + 2962

4594 + 1305

8657 + 1275

2262 + 1119

5735 — 1325

9585 — 6897

3152 + 1443

5004 + 2529

1495 + 2413

1996 + 6432

4413 + 3621

1941 + 7237

5724 + 2329

3949 + 5193

6639 — 2286

5585 — 2090

5093 + 2217

4308 — 1930

1355 + 3694

1988 — 1948

5810 + 2736

3934 + 4778

8698 — 5324

2795 + 2714

9074 — 6991

7251 — 6072

2096 + 3850

2024 + 6352

7165 — 1926

4470 + 1028

4819 — 2315

1648 + 1479

3913 — 1674

3359 + 2841

5469 — 3630

2839 + 2694

8270 — 7917

2837 + 5066

 

Задачи на пропорции по математике — примеры с ответами

Понятие пропорции

Чтобы решать задачи на тему пропорции, вспомним главное определение.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Главное свойство пропорции: Произведение крайних членов равно произведению средних. a : b = c : d, где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.

Вывод из главного свойства пропорции:

• Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
  
  
• Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:
  
  

Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.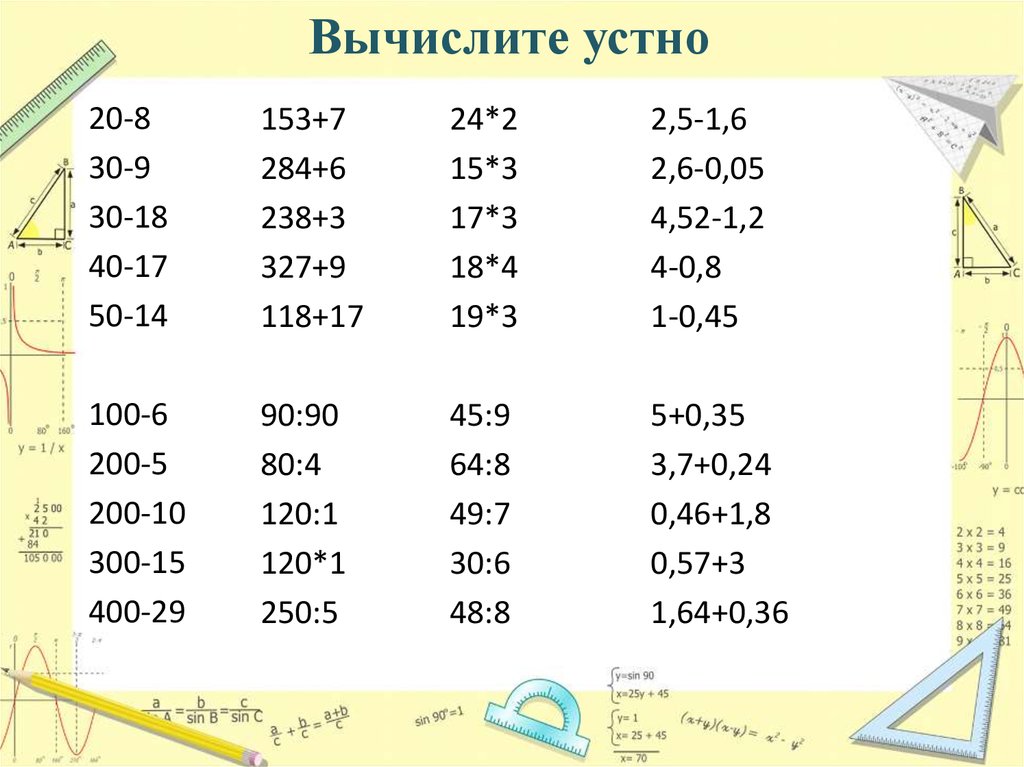

Запомним!

Равенство двух отношений называют пропорцией.

Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

Как решаем:

В этом примере неизвестен крайний член, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

x = (2 * 3)/1 = 6

Ответ: x = 6.

Задание 2. Найти неизвестный член: 1/3 = 5/y

Как решаем:

y = (3 * 5)/1 = 15

Ответ: y = 15.

Задача 3. Решить пропорцию: 30/x = 5/8

Как решаем:

x = (30 * 8)/5 = 48

Ответ: x = 48.

Задание 4. Решить: 7/5 = y/10

Как решаем:

y = (7 * 10)/5 = 14

Ответ: y = 14.

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Как решаем:

• Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.

  Получим: 3x = 2y.

• Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.
• После сокращения отношений получилось: x/y = 2/3.

Ответ: 2 к 3.

На следующем примере мы узнаем как составить пропорцию по задаче💡

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Как решаем:

• Примем всех подписчиков за 100% и запишем условие задачи кратко:

  300 — 100%

  108 — ?%

• Составим пропорцию: 300/108 = 100/x.
• Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

Как решаем:

• Составим пропорцию: 5/2 = x/450.
• Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Как решаем:

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Составим пропорцию:

5 : 100 = х : 98

х = (5 * 98) : 100

х = 4,9

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

• v1 = 75 км/ч
• v2 = 52 км/ч
• t1 = 13 ч
• t2 = х

Как решаем:

1. Составим пропорцию: v1/v2 = t2/t1.

   Соотношения равны, но перевернуты относительно друг друга.



2. Подставим известные значения: 75/52 = t2/13

   t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.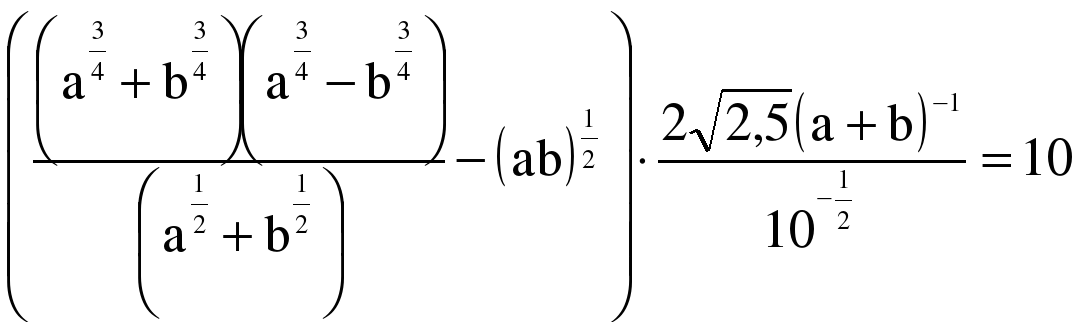

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

1. Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:

   30 : 24 = 5 : х



2. Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

   х = 24 * 5 : 30

   х = 4



3. Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

в картинках и текстовые, для взрослых и детей

Занимательная математика и логика / Математические игры

Знакомим с популярными головоломками, увлекательными заданиями от ЛогикЛайк, которые нравятся детям и их родителям. Разбираем решение известных числовых и логических головоломок.

17 категорий числовых и логических математических головоломок

2 варианта занятий, выбор сложности

• Пройдите 3 стартовые главы курса логики – и откройте доступ к разным категориям. Попробуйте «Логические задачи», «Истина и ложь», «Умный счёт», «3D‑мышление».
• Попробуйте задания разного уровня сложности: «Новичок», «Опытный», «Эксперт».

Попробуйте курс ЛогикЛайк в игровой форме!

Выберите возраст для старта

4-6 лет

1 класс

2 класс

3 класс

4-5 класс

старше

На платформе LogicLike.com дети и взрослые с удовольствием развивают логику и мышление. У нас 3500 занимательных заданий с ответами и пояснениями!

9 знаменитых математических головоломок, о которых будет интересно узнать вашим детям

Математические головоломки как способ помериться интеллектуальными силами всегда увлекали людей. ЛогикЛайк рассказывает о нескольких широко известных задачках, над которыми ломали голову десятки поколений.

Разберите подборку головоломок вместе с детьми: «разомнете» мозги, весело проведете время и знание истории «прокачаете»! Мы выбрали интересные задачки, дошедшие до наших дней из «древности», и приближенные к «нашему» времени.

• Папирус Ахмеса
• Задача о переправе
• Печать царя Соломона
• Головоломка Фибоначчи о кроликах
• Задача Тартальи «Трудное наследство»
• Головоломка Льюиса Кэрролла
• «Безумный разрез» Мартина Гарднера
• Сингапурская головоломка
• Танграм

Папирус Ахмеса

Древние египтяне были не только опытными строителями пирамид, но и прекрасными математиками. Доказательством этому служит древнеегипетский папирус, автором которого был некий Ахмес. Как выяснили исследователи-египтологи, папирус Ахмеса — копия очень древнего математического сборника, составленного во времена фараона Аменемхета III (приблизительно 1853-1806 гг. до н.э.). Задач в сборнике много — ниже одна из них.

Показать решение

Задача о переправе

Не только древние египтяне упражнялись в решении задач на сообразительность. Историки обнаружили книгу, написанную на латыни, под названием «Задачи для развития молодого ума». Ирландский богослов, ученый и просветитель Алкуин, живший в IX веке, собрал в книге 53 задачи. Предлагаем одну из них — настолько «бородатую», что ее знают школьники во всем мире.

Как крестьянину перевезти все в целости и сохранности?

Показать решение

Печать царя Соломона

На гробнице мудрого легендарного библейского царя Соломона потомки изобразили знаменитую печать правителя.

Попробуйте сосчитать, сколько равносторонних треугольников изображено на печати.

Проверить себя

Попробуйте курс ЛогикЛайк «ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ»

• Развиваем мышление Решая задачи и головоломки дети развивают смекалку, а взрослые тренируют «извилины».
• Строим фундамента успеха Учим грамотно работать с информацией, тренируем память и развиваем логико‑математический интеллект. Повышаем познавательный интерес и уверенность в себе.
• Глоток «свежего воздуха» Можно потратить 20-30 минут на себя, пока ребёнок развивается. Заниматься на ЛогикЛайк одинаково интересно детям и взрослым.

Начать курс!

Задача Фибоначчи о размножении кроликов

Леонардо Пизанский (около 1170 г.р.), по прозвищу Фибоначчи, — один из первых именитых математиков средневековой Европы. Он успешно участвовал в математических турнирах, а, создав себе имя, придумывал для них занимательные задачи. Ниже одна из самых известных.

«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца.
Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов».

Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения?

Подсказка Вспомните последовательность Фибоначчи или запаситесь терпением — и считайте.

Смотреть ответ

Задача Тартальи «Трудное наследство»

Никколо Тарталья (1499 г.р.), итальянский математик, обнаруживший общий алгоритм решения кубических уравнений. Описанный Никколо метод вошел в историю математики как Формула Кардано, по имени первого публикатора метода, до которого независимо друг от друга додумались Тарталья и Сципион дель Ферро.

Предлагаем решить ставшую известной задачу Тартальи о дележе лошадей.

Как выполнить завещание?

Показать решение

Головоломка Льюиса Кэрролла

Известный писатель Льюис Кэрролл, тот самый, который создал истории об Алисе и ее приключениях в Стране Чудес и Зазеркалье, еще и очень любил придумывать головоломки и преподавал логику.

Своим маленьким поклонникам Кэрролл часто предлагал такую головоломку:

Задача усложняется особыми условиями ее выполнения:

• карандаш от бумаги отрывать нельзя;
• дважды проводить карандашом в одном месте нельзя;
• пересекать линии нельзя.

Показать решение

Отгадывайте головоломки

и решайте задания на логику от ЛогикЛайк!

Классические логические вопросы и головоломки

Числовые ребусы, магические квадраты

Взвешивания и&nbspпереливания

Комбинаторные задачи

Пространственные головоломки

Шестерёнки (вращение)

Алгоритмические задачи

Нестандартные шахматные задания

Начать занятия! Начать занятия!

«Безумный разрез» Мартина Гарднера

Мартин Гарднер — известный американский писатель, математик-любитель, автор множества статей и книг по занимательной математике, научно-популярных этюдов, математических фокусов, головоломок и задач на сообразительность и множества других публикаций.

Предлагаем решить одну из самых популярных головоломок Гарднера.

Сделайте один разрез (или нарисуйте одну линию) — не обязательно, прямую — чтобы разделить нарисованную фигуру на две одинаковые части.

Показать ответ

Сингапурская головоломка

Благодаря социальным сетям некоторые головоломки распространяются, как вирус, и становятся известными. Так случилось с головоломкой, которую телеведущий Кеннет Конг из Сингапура разместил на своей странице в фейсбуке, и вскоре ею поделились 4400 человек.

Альфред и Бернард только что познакомились с Шерил и хотят выяснить, когда у нее день рождения.

Шерил показала поклонникам 10 возможных дат:

Затем она показала Альфреду месяц своего рождения, а Бернарду — день.

Чтобы решить головоломку, друзья обменялись парой реплик:

Так когда же у Шерил день рождения?

Смотреть решение и ответ

Танграм

Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древнекитайскими мудрецами для сына императора. Правитель хотел чтобы через простую игру его сын постиг начала математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и осознал, что сложные вещи состоят из простых.

Так появился «Ши-Чао-Тю» — квадрат, разрезанный на семь частей:
5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.

Суть «свободной» игры в танграм — собирать из имеющихся деталей по принципу мозаики всевозможные фигурки: животных, птиц, человека, что угодно. Младшим дошкольникам предлагают простой вариант развивающей игры, когда фигурки танграма нужно просто наложить на готовый образец-ответ.

Многие дети в 5-7 лет складывают модели из фигурок рядом с изображением-ответом, даже если размеры вырезанных фигур и деталей на картинке отличаются.

Танграм как головоломка обычно по силам ребенку начиная с 6-7 лет. Все так же — из элементов танграма нужно сложить готовую модель, но на карточке изображен лишь силуэт фигуры.

Вырежьте элементы танграма из бумажного, картонного или другого квадрата, и для начала предлагаем собрать одну из популярных фигурок — бегущего человека, как на рисунке выше.

Помните 2 правила головоломки:
1) необходимо использовать все 7 фигурок головоломки;
2) фигуры не должны накладываться друг на друга.

Показать готовую фигурку

Среди поклонников танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что именно «танграмом» назвал игру американский шахматист, изобретатель «пятнашек» и многих других головоломок, Самюэль Лойд.
В 21 веке самые интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном дизайне и архитектуре.

Ответы и решения к головоломкам

1. Папирус Ахмеса: решение

Пусть w — количество зерна для первого работника,
d — разница в количестве зерна между двумя работниками, следующими по порядку.
Составим два равенства.
5w + 10d = 100
7*(2w + d) = 3w + 9d
Остается только решить уравнение с двумя неизвестными.

Ответ:
1-ый работник = 10/6 мер зерна,
2-ой = 65/6 мер зерна,
3-ий = 120/6 (то есть 20) мер зерна,
4-ый = 175/6 мер зерна,
5-ый = 230/6 мер зерна.

Вернуться к условию.

2. Переправа: решение

Рассуждаем логически!

• Крестьянин перевозит козу (иначе потеряет часть имущества).
• Возвращается.
• Перевозит капусту (или волка), а козу увозит обратно.
• Козу оставляет на первом берегу.
• Перевозит волка (или капусту) на другой берег.
• Возвращается.
• Перевозит козу.

Вернуться к условию.

3. Печать царя Соломона: ответ

31 треугольник.

Вернуться к условию.

4. Задача Фибоначчи: решение

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …, …, …

Ответ:
233 пары.

Вернуться к условию.

5. Задача Тартальи: решение

Сам Тарталья предложил следующее решение.
Для раздела имеющихся лошадей необходимо заимствовать еще одну, после чего их общее количество станет 18. Раздел этого количества даст 2, 6 и 9 лошадей, которых в сумме окажется 17.
Одна лошадь из 18 оказалась как бы «лишней» — это заимствованная лошадь, которую следует вернуть владельцу после раздела имущества.

Можно решить головоломку и арифметическим способом:
пропорцию 1/2 : 1/3 : 1/9 достаточно умножить на 18 и получится тот же результат.

Ответ:
2, 6 и 9 лошадей.

Вернуться к условию.

6. Головоломка Льюиса Кэрролла: ответ

Ниже мы изобразили 2 варианта решения. Возможно, вам удастся найти и другие.

Вернуться к условию.

7. «Безумный разрез» Гарднера: ответ

Намёк был верен. Линия действительно изогнутая.

Вернуться к условию.

8. Сингапурская головоломка: решение

Даты находятся в промежутке от 14 до 19. Числа 18 и 19 встречаются по разу. Если день рождения в эти даты, то Бернард сразу бы сказал месяц.

Если Шерил сказала Альфреду, что родилась в мае или июне, значит, день рождения может быть 19 мая или 18 июня. Раз Альфред точно знает, что Бернард не знает ответ, значит, речь не о мае или июне. Остаются июль или август.

В июле и августе остались даты в диапазоне от 15 до 17, а 14 встречается дважды. Если бы день рождения был 14-го, то Бернард после реплики Альфреда еще не мог бы дать точного ответа. Значит, речь не о 14-ом. Остаются 16 июля, 15 августа и 17 августа.

Если бы Шерил сказала Альфреду, что родилась в августе, то после ответа Бернарда, Альфред не мог бы точно узнать дату рождения — ведь целых 2 даты приходятся на август.
Значит, Шерил родилась 16 июля.

Ответ:
16 июля.

Эту задачку Конгу показала племянница друга. Она же разыграла телеведущего, сказав, что головоломка предназначена для 10-летних школьников.

Дебаты о том, как решить «простую» задачку, развернулись нешуточные. Спустя 2 дня, когда большинство участников сдались, выяснилось, что задача — олимпиадная, для 14-летних школьников.

Вернуться к условию.

9. Танграм: ответ

Можно предварительно раскрасить элементы танграма и получится такой человечек:

Вернуться к условию.

Со всеми головоломками успешно справились? Великие математики и логики мира гордились бы вами!

10 сложных математических задач | Самые сложные математические задачи с ответами

В 2019 году математики наконец решили математическую головоломку, которая десятилетиями ставила их в тупик. Это называется диофантовым уравнением, и его иногда называют «суммированием трех кубов»: найти x, y и z такие, что x³+y³+z³=k, для каждого k от одного до 100.

На поверхности, кажется легко. Можете ли вы придумать целые числа для x, y и z, чтобы x³+y³+z³=8? Конечно. Один из ответов: x = 1, y = -1 и z = 2. Но как насчет целых чисел для x, y и z, чтобы x³+y³+z³=42?

Это оказалось намного сложнее — например, никто не мог решить эти целые числа в течение 65 лет, пока суперкомпьютер, наконец, не нашел решение для 42. (Для протокола: x = -80538738812075974, y = 80435758145817515 , и z = 12602123297335631. Очевидно.)

В этом прелесть математики: на все всегда есть ответ, даже если на его поиск уйдут годы, десятилетия или даже столетия. Итак, вот еще девять чрезвычайно сложных математических задач, которые когда-то казались неразрешимыми, пока математики не нашли прорыв.

ПЛЮС:

1

Гипотеза Пуанкаре

Popular Science Monthly Volume 82 [общественное достояние]Wikimedia Commons

В 2000 году Математический институт Клэя, некоммерческая организация, занимающаяся «расширением и распространением математических знаний», попросила мир решить семь математических задач и предложила каждому миллион долларов. кто мог взломать хотя бы один. Сегодня они все еще не решены, за исключением гипотезы Пуанкаре.

Анри Пуанкаре был французским математиком, который на рубеже 20-го века проделал фундаментальную работу в том, что мы сейчас называем топологией. Вот идея: топологам нужны математические инструменты для различения абстрактных форм. 3», что, по сути, говорит: «Простейшая 4D-форма — это 4D-эквивалент сферы».

Все еще с нами?

Столетие спустя, в 2003 году, русский математик Григорий Перельман опубликовал доказательство гипотезы Пуанкаре на современном открытом математическом форуме arXiv. Доказательство Перельмана содержало несколько небольших пробелов и основывалось непосредственно на исследованиях американского математика Ричарда Гамильтона. Это было новаторским, но скромным.

После того, как математический мир потратил несколько лет на проверку деталей работы Перельмана, начались награждения. Перельману предложили Премию Тысячелетия в миллион долларов, а также Филдсовскую медаль, которую часто называют Нобелевской премией по математике. Перельман отверг оба. Он сказал, что его работа была на благо математики, а не на личную выгоду, а также что Гамильтон, заложивший основу для его доказательства, по крайней мере, заслуживает наград.

2

Великая теорема Ферма

Wikimedia Commons

Пьер де Ферма был французским юристом и математиком 17-го века. Математика, по-видимому, была для Ферма скорее хобби, и поэтому один из величайших математических умов в истории передал многие из своих теорем посредством случайной переписки. Он делал утверждения, не доказывая их, оставляя их для доказательства другим математикам спустя десятилетия или даже столетия. Самая сложная из них стала известна как Великая теорема Ферма.

Это просто написать. Существует множество троек целых чисел (x,y,z), удовлетворяющих условию x²+y²=z². Они известны как пифагорейские тройки, такие как (3,4,5) и (5,12,13). Теперь, любые трио (x,y,z) удовлетворяют условию x³+y³=z³? Ответ — нет, и это Великая теорема Ферма.

Ферма, как известно, написал Великую теорему от руки на полях учебника вместе с комментарием о том, что у него есть доказательство, но он не может поместить его на поля. На протяжении веков математический мир задавался вопросом, действительно ли Ферма на самом деле имел в виду действительное доказательство.

Перенесемся через 330 лет после смерти Ферма в 1995 год, когда британский математик сэр Эндрю Уайлс наконец решил одну из старейших открытых задач в истории. За свои усилия Уайлс был посвящен в рыцари королевой Елизаветой II и был награжден уникальной почетной табличкой вместо Филдсовской медали, поскольку он был чуть выше официального предельного возраста для получения Филдсовской медали.

Уайлсу удалось объединить новые исследования в самых разных областях математики, чтобы решить классический вопрос теории чисел Ферма. Одна из этих тем, эллиптические кривые, была совершенно не открыта во времена Ферма, что заставило многих поверить в то, что у Ферма никогда не было доказательства его Великой теоремы.

3

Классификация конечных простых групп.

Wikimedia Commons

От сборки кубика Рубика до доказательства факта обмена телами на Futurama , абстрактная алгебра имеет широкий спектр приложений. Алгебраические группы — это наборы, которые следуют нескольким основным свойствам, таким как наличие «элемента идентичности», который работает как добавление 0.

Группы могут быть конечными или бесконечными, и если вы хотите знать, как выглядят группы определенного размера n, это может стать очень сложным в зависимости от вашего выбора п .

Если n равно 2 или 3, эта группа может выглядеть только одним способом. Когда n достигает 4, есть две возможности. Естественно, математикам нужен был исчерпывающий список всех возможных групп любого заданного размера.

На завершение полного списка ушли десятилетия из-за трудностей с уверенностью в том, что он действительно полный. Одно дело описать, как выглядит бесконечное множество групп, но еще сложнее быть уверенным, что список охватывает все. Вероятно, величайший математический проект 20-го века, классификация конечных простых групп была организована гарвардским математиком Дэниелом Горенштейном, который в 1972 изложил чрезвычайно сложный план.

К 1985 году работа была почти завершена, но она занимала так много страниц и публикаций, что было немыслимо, чтобы один человек рецензировал ее. Часть за частью многие аспекты доказательства были в конечном счете проверены, и полнота классификации была подтверждена.

К 1990-м годам доказательство получило широкое признание. Последующие усилия были предприняты для упрощения титанического доказательства до более управляемого уровня, и этот проект все еще продолжается сегодня.

4

Теорема о четырех цветах

Индуктивная нагрузка [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)]Wikimedia Commons

Это так же легко заявить, как и трудно доказать.

Возьмите любую карту и четыре карандаша. Можно раскрасить каждый штат (или страну) на карте, следуя одному правилу: штаты, имеющие общую границу, не окрашиваются в один и тот же цвет.

Тот факт, что любую карту можно раскрасить пятью цветами — теорема о пяти красках, — был доказан в XIX веке.век. Но сокращение этого числа до четырех заняло время до 1976 года.

Два математика из Университета Иллинойса, Урбана-Шампейн, Кеннет Аппель и Вольфганг Хакан, нашли способ свести доказательство к большому, конечному числу случаев. С помощью компьютера они тщательно проверили почти 2000 случаев и получили доказательства беспрецедентного стиля.

Доказательство Аппеля и Хакана, вероятно, спорное, поскольку оно было частично задумано в уме машины, в конечном итоге было принято большинством математиков. С тех пор доказательство стало гораздо более распространенным, если его часть была проверена компьютером, но Аппель и Хакан проложили путь.

5

(Независимость) гипотезы континуума

Wikimedia Commons

В конце 19 века немецкий математик по имени Георг Кантор поразил всех, выяснив, что бесконечности бывают разных размеров, называемых мощностями. Он доказал фундаментальные теоремы о количестве элементов, которые современные математики обычно изучают на уроках дискретной математики.

Кантор доказал, что множество действительных чисел больше, чем множество натуральных чисел, которое мы записываем как |ℝ|>|ℕ|. Было легко установить, что размер натуральных чисел, |ℕ|, является первым бесконечным размером; никакое бесконечное множество не меньше ℕ.

Настоящие числа больше, но являются ли они вторым бесконечным размером? Это оказалось гораздо более сложным вопросом, известным как гипотеза континуума (CH).

Если CH истинно, то |ℝ| является вторым бесконечным размером, и нет бесконечных множеств меньше ℝ, но больше ℕ. И если CH ложно, то между ними есть хотя бы один размер.

Так какой же ответ? Здесь дело принимает оборот.

CH доказал свою независимость относительно базовых аксиом математики. Оно может быть истинным, и логических противоречий не последует, но может быть и ложным, и логических противоречий не последует.

Это странное положение вещей, но не такое уж редкое в современной математике. Возможно, вы слышали об аксиоме выбора, еще одном независимом утверждении. Доказательство этого результата растянулось на десятилетия и, естественно, разделилось на две основные части: доказательство непротиворечивости CH и доказательство непротиворечивости отрицания CH.

Первая половина написана благодаря Курту Гёделю, легендарному австро-венгерскому логику. Его математическая конструкция 1938 года, известная как конструируемая Вселенная Гёделя, доказала совместимость CH с базовыми аксиомами и до сих пор является краеугольным камнем классов теории множеств. Вторая половина преследовалась еще два десятилетия, пока Пол Коэн, математик из Стэнфорда, не решил ее, изобретя целый метод доказательства в теории моделей, известный как «вынуждение».

Половины доказательства, полученные Гёделем и Коэном, требуют изучения теории множеств с высшим образованием, поэтому неудивительно, что эта уникальная история была эзотерической за пределами математических кругов.

6

Теоремы Гёделя о неполноте

Алехандро Маллеа/Из книги Герберта Эндертона «Математическое введение в логику». Помимо доказательств, Гёдель также любил доказывать, возможно ли доказательство . Его теоремы о неполноте часто понимают неправильно, так что у вас есть прекрасная возможность их прояснить.

Первая теорема Гёделя о неполноте утверждает, что в любом языке доказательств всегда есть недоказуемые утверждения. Всегда есть что-то истинное, что вы не можете доказать правдой. Можно понять (не математически строгую) версию рассуждения Гёделя, если хорошенько подумать. Так что пристегнитесь, вот оно: рассмотрите утверждение: «Это утверждение не может быть доказано».

Подумайте над каждым случаем, чтобы понять, почему это пример истинного, но недоказуемого утверждения. Если оно ложно, то и то, что оно говорит, ложно, и тогда можно доказать, что оно истинно, а это противоречиво, поэтому этот случай невозможен. С другой стороны, если бы у него было доказательство, то это доказательство доказывало бы его истинность… делая истинным то, что у него нет доказательств, что противоречиво, убивая это дело. Таким образом, мы логически остаемся со случаем, когда утверждение истинно, но не имеет доказательства. Да, у нас тоже голова кружится.

Но следуйте этому почти-но-не-совсем-парадоксальному трюку, и вы проиллюстрируете справедливость первой теоремы Гёделя о неполноте.

Вторая теорема Гёделя о неполноте так же странна. В нем говорится, что математические «формальные системы» не могут доказать свою непротиворечивость. Последовательная система — это та, которая не вызовет у вас никаких логических противоречий.

Вот как вы можете это представить. Представьте, что Аманда и Боб имеют в виду набор математических аксиом — базовых математических правил. Если Аманда может использовать свои аксиомы, чтобы доказать, что система аксиом Боба свободна от противоречий, то Боб не может использовать свои аксиомы, чтобы доказать, что система Аманды не приводит к противоречиям.

Поэтому, когда математики обсуждают наилучший выбор основных аксиом математики (это происходит гораздо чаще, чем вы можете себе представить), очень важно знать об этом явлении.

7

Теорема о простых числах

Пользователь:Dcoetzee [CC0]

Существует множество теорем о простых числах. Один из самых простых фактов — что существует бесконечно много простых чисел — можно даже очаровательно вписать в форму хайку.

Теорема о простых числах более тонкая; он описывает распределение простых чисел вдоль числовой прямой. Точнее, там говорится, что для натурального числа N число простых чисел меньше N приблизительно равно N/log(N)… с обычными статистическими тонкостями к слову «приблизительно».

Опираясь на идеи середины XIX века, два математика, Жак Адамар и Шарль Жан де ла Валле Пуссен, независимо друг от друга доказали теорему о простых числах в 1898 году. и упрощения. Но влияние теоремы только возросло.

Полезность теоремы о простых числах огромна. Современные компьютерные программы, работающие с простыми числами, полагаются на него. Это основа методов проверки простоты и всей связанной с этим криптологии. 92-4ac))/(2a), которое, возможно, было трудно запомнить в старшей школе, но вы должны признать, что это удобное решение в закрытой форме.

Теперь, если мы подойдем к ax³+bx²+cx+d=0, можно найти замкнутую форму для «x=», хотя она намного объемнее, чем квадратичная версия. Также возможно, хотя и некрасиво, сделать это для полиномов степени 4: ax⁴+bx³+cx²+dx+f=0.

Цель сделать это для многочленов любой степени была отмечена еще в 15 веке. Но начиная с 5-й степени закрытая форма невозможна. Написание форм, когда они возможны, — это одно, но как математики доказали, что это невозможно, начиная с 5?

Мир только начал осознавать гениальность французского математика Эвариста Галуа, когда он умер в возрасте 20 лет в 1832 году. Его жизнь включала в себя месяцы, проведенные в тюрьме, где он был наказан за свою политическую активность, написав остроумные, но необработанные математические ученым, и это закончилось роковой дуэлью.

Идеи Галуа были полностью поняты спустя десятилетия после его смерти, но в конечном итоге они превратились в целую теорию, которая теперь называется теорией Галуа. Основная теорема этой теории дает точные условия, когда многочлен можно «решить в радикалах», то есть он имеет замкнутую форму, подобную квадратичной формуле. Все полиномы до степени 4 удовлетворяют этим условиям, но начиная со степени 5 некоторые не удовлетворяют, поэтому нет общей формы для решения любой степени выше 4.

9

Трисекция угла

Сам [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]Wikimedia Commons

Чтобы закончить, давайте вернемся в историю.

Древние греки задавались вопросом построения линий и форм в различных соотношениях, используя такие инструменты, как циркуль без опознавательных знаков и линейку. Если кто-то нарисует перед вами угол на листе бумаги и даст вам линейку без пометок, обычный циркуль и ручку, вы сможете провести линию, которая делит этот угол ровно пополам. Это быстрые четыре шага, хорошо проиллюстрированные вот так, и греки знали их две тысячи лет назад.

Что ускользнуло от них, так это разрезание угла на три части. Он оставался неуловимым буквально 15 столетий, с сотнями тщетных попыток найти сооружение. Оказывается, такая конструкция невозможна.

Современные студенты-математики изучают задачу о трисекции угла и способы доказательства ее невозможности на занятиях по теории Галуа. Но, учитывая вышеупомянутый период времени, который потребовался математическому миру для обработки работы Галуа, первое доказательство проблемы было сделано другим французским математиком, Пьером Ванцелем. Он опубликовал свою работу в 1837 году, через 16 лет после смерти Галуа, но за девять лет до того, как была опубликована большая часть работ Галуа.

В любом случае, их взгляды схожи, что превращает вопрос построения в вопрос о свойствах некоторых репрезентативных многочленов. С помощью этих методов стали доступны многие другие вопросы древнего строительства, что закрыло некоторые из старейших открытых математических вопросов в истории.

Так что, если вы когда-нибудь отправитесь в древнюю Грецию, вы можете сказать им, что их попытки решить проблему трисекции угла тщетны.

Дэйв Линклеттер Дэйв Линклеттер — доктор философии.

Сложные математические задачи, от которых у вас закружится голова

Эти сложные математические задачи сложны, но они дадут вашему мозгу тренировку — и они действительно вознаграждают, когда вы решаете одну из них!

Усилители разума

Время проверить свой мозг!

Эти сложные математические задачи не являются простой арифметикой. Они бросят вам вызов посмотреть на «проблемы» по-другому и проверят вашу логику и навыки решения проблем, пока вы их решаете. И если математика не является вашей сильной стороной, наберитесь мужества — в большинстве этих сложных математических задач используются очень простые числа с простейшими операциями — сложением, вычитанием, умножением и делением. Что делает их сложной задачей, так это изучение проблемы, чтобы найти «хитрость» или закономерность и то, как числа соотносятся друг с другом. Другие требуют техники «заполнения пробелов», которая требует от вас использования метода проб и ошибок и работы в обратном направлении. Пора включить мозги в работу! Может быть, вы освежите в памяти эти простые математические трюки, о которых вам хотелось бы знать до того, как вы начнете.

Усилители разума

Легкая атлетика

Если каждый из этих бегунов преодолеет указанное количество клеток за одинаковое время, в какой пронумерованной точке все бегуны окажутся рядом друг с другом?

Растягиватели разума

Ответ: Космос 19

Поначалу кажется, что это займет целую вечность, но на самом деле все бегуны выстроятся в линию всего за шесть «ходов»! Составьте схему, указывающую, где будет находиться каждый бегун после каждого «хода». Чтобы понять это, все, что вам действительно нужно сделать, это добавить! Просто прибавьте количество делений, на которые продвигается каждый бегун — три, два, один и пять — к числу, на котором он уже находится, возвращаясь к ячейке 1 после 30. Конечно же, все они доберутся до ячейки 19.в то же время.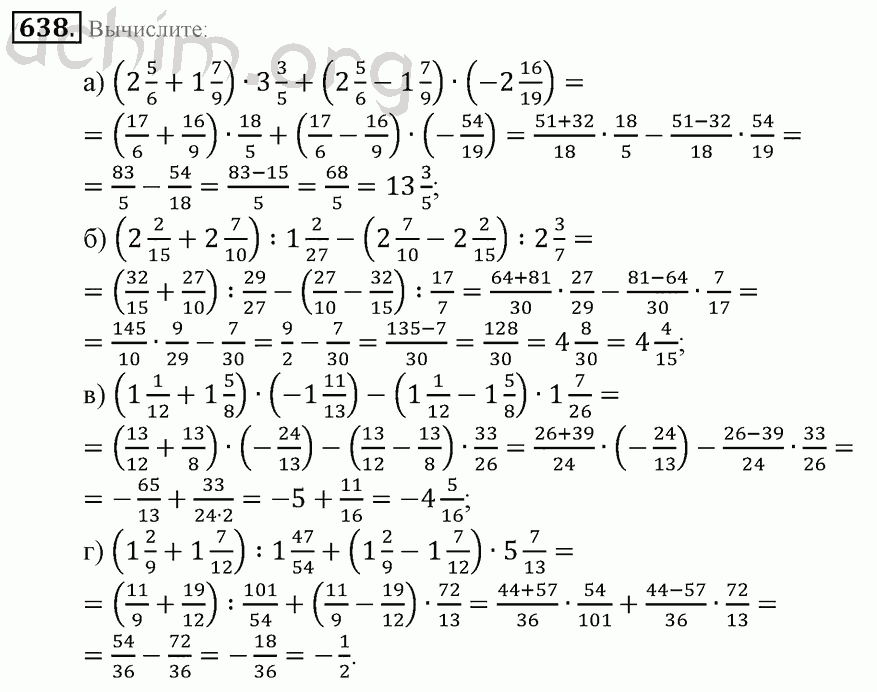 В настроении для чего-то более сложного? Продолжайте или попробуйте эти сложные головоломки, которые поставят вас в тупик.

Усилители разума

Единицы и нули

Ниже вы увидите двоичное представление десятичных чисел от 1 до 7. Следуя образцу, какое двоичное представление используется для десятичного числа 12? Как только вы решите это, освежите некоторые числовые факты, о которых вы никогда не знали.

Усилители разума

Ответ: 1100

Если вы набрали пять цифр, значит, вы ошиблись (и это нормально, я так и сделал с первой попытки)! Что делает это сложным и отличается от большинства сложных математических задач, так это то, что это так не похоже на то, как мы привыкли смотреть на числа, особенно в последовательности. По сути, вы перебираете все числа, которые можете составить из , всего единиц и нулей, начиная с наименьшего (0, представленного четырьмя нулями) и увеличивая его. Но у вас всегда будет четыре цифры, поэтому, пока у вас не будет четырехзначного числа (1000), цифра (цифры) слева от старшего разряда будет нулем. Таким образом, вопрос дает вам 111 (записывается как 0111, что означает четыре цифры), и, поскольку он представляет 7, а вы пытаетесь достичь 12, просто пройдите через следующие самые большие числа, которые используют только 1 и 0. Так 8 будет 1000, 9будет 1001, 10 будет 1010, 11 будет 1011, а 12 будет 1100.

Усилители разума

Номинальная стоимость

Какой номер должен быть на нижней левой марке? (Подсказка: это однозначное число.)

Растягиватели разума

Ответ: 1

Многие из этих сложных математических задач не столько требуют сложных математических вычислений, сколько требуют определения взаимосвязей между группами чисел. В этом случае смотрите не на горизонтальные ряды марок, а на вертикальные пары марок. Число в разряде десятков верхней марки, деленное на число в разряде единиц верхней марки, равно числу на нижней марке (8, деленное на 2, равно 4 в крайней левой паре марок). Итак, для последней пары 2 разделить на 2 равно 1,9.0003

Усилители разума

Энергосбережение

Транспортная компания значительно сокращает количество потребляемой нефти, но насколько? Какое число должно быть под последним баррелем? Кроме того, попробуйте эти игры для мозга, которые улучшат ваши умственные способности.

Усилители разума

Ответ: 2

Хитрость — здесь вообще не нужны арифметические операции! И, к счастью, из-за того, что это какие-то дурацкие вычисления, с большими числами было бы неинтересно вычислять. Вместо этого ищите закономерности в самих числах. Представляется следующая закономерность: каждое число (за исключением первого, которое является произвольным) представляет собой цифры числа перед ним минус первая, перевернутые. Например, первое число 19.247. Отнимите первую цифру, 1, и переверните ее, и вы получите 7429, что, конечно же, является вторым числом. Число перед пустым местом состоит только из двух цифр, поэтому, когда вы удаляете первую, 4, у вас остается только 2. Не нужно «переворачивать» число только с одной цифрой, так что вот ваш ответ.

Усилители разума

Код сейфа

Какую цифру нужно ввести в поле со знаком вопроса, чтобы завершить код от сейфа? Вот подсказка, чтобы избавить вас от стресса: текст «Safe A08» внизу бессмысленен, поэтому не тратьте время на попытки выяснить, поможет ли это вам получить ответ!

Растягиватели разума

Ответ: 4

Вот еще одна вещь, которую вам нужно знать, чтобы получить этот ответ: только группы из четырех чисел, два сверху и два снизу, связаны друг с другом; например, целые верхняя и нижняя строки не являются последовательностью. Думайте об этом как о трех парах двузначных чисел.

Итак, что за шаблон? Что ж, числа в разряде десятков умножаются на два, чтобы получить число в разряде единиц 9.0030 другое  двузначное число. Например, в первой паре вы умножаете 2 на два, чтобы получить 4 по диагонали от него, и 3, чтобы получить соответствующие 6.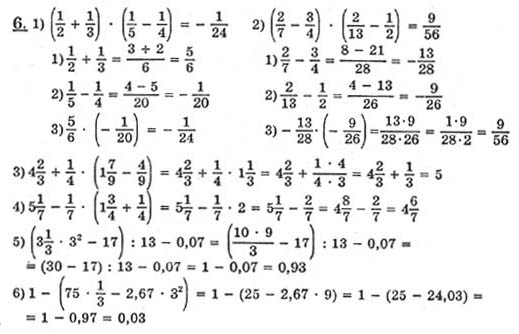 И последняя пара фактически отражает первую пару; вы также умножаете 2, чтобы получить 4!

Усилители разума

Суммы символов

Как сделать это уравнение точным, используя три из этих четырех математических символов: + – × ÷  (сложение, вычитание, умножение и деление)? ПРИМЕЧАНИЕ. Для этой задачи порядок операций не применяется; на самом деле вы будете выполнять каждую операцию слева направо (вам не нужно сначала умножать или делить и т. д.).

Усилители разума

Ответ: – ,  + ,  ÷

Вот правильное уравнение:  21 – 3 + 18 ÷ 6 = 6. Двадцать один минус 3 равно 18, затем прибавьте к этому 18, чтобы получить 36. Затем разделите это на 6, чтобы получить правильный ответ, 6! Если вы предпочитаете слова цифрам, попробуйте решить эти сложные словесные головоломки.

Усилители разума

Сложите их

Поместите эти бильярдные шары снаружи в правильные места соответствующих цветов, чтобы сумма каждого столбца, строки, 9Диагональ 0030 и равна 49. Пока вы размышляете над этим, попробуйте этот тест на определение цвета, который может пройти только 1 процент людей.

Усилители разума

Ответ:

Иногда сложные математические задачи решаются путем проб и ошибок и исключения неработающих возможностей; в этом смысле это немного похоже на судоку. Но в этом есть маленькая часть стратегии; например, для крайнего левого столбца и самой нижней строки у вас уже есть число, оканчивающееся на 3, поэтому вам нужно, чтобы сумма трех других чисел оканчивалась на 6. И занимаемся диагональю снизу вверх первый действительно поможет; не хватает только одного шарика, так что вы можете сразу понять, что это за пустое место. Вы также знаете, что вы не можете поставить шар 25 или 31 в любой ряд, столбец или диагональ с шаром 23; они немедленно сделают вашу сумму слишком большой.

Усилители разума

Музыка с цифрами

В этом математическом упражнении вы увидите, как быстро вы сможете решать эти несложные математические задачи, слушая любимую музыку.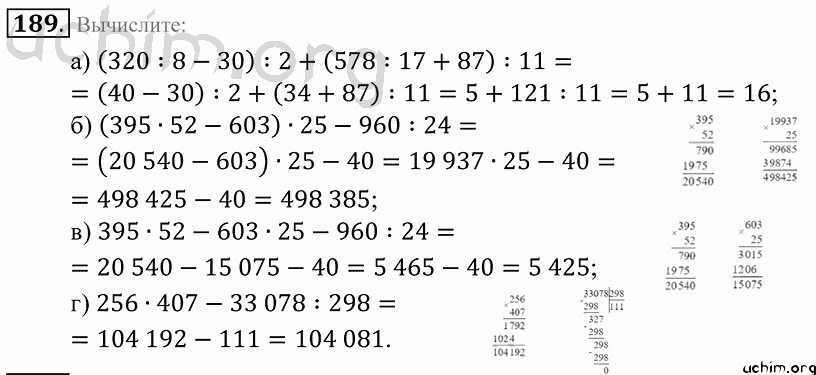 О, и постарайтесь не пользоваться калькулятором!

Растягиватели разума

Ответы:

Большинство из них — это простая математика или даже общеизвестная информация (четверть из 100)!

Усилители разума

Посчитайте

Для этого введите цифры от 1 до 9, используя каждый только один раз, чтобы сделать все вертикальные и горизонтальные уравнения правильными.

Растягиватели разума

Ответы:

Вот еще один, который, вероятно, требует некоторого времени и нескольких неверных предположений.

Усилители разума

Удар

Какие кегли нужно сбить, чтобы получить 100 очков?

Усилители разума

Ответ: 13, 39 и 48

Это сложный вопрос, потому что он не говорит вам, сколько кеглей вам нужно сбить, так что это может быть любая комбинация кеглей.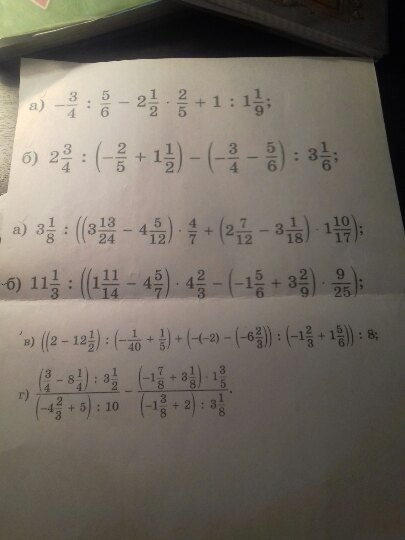 Но это единственная комбинация, которая в сумме дает ровно 100! Проверьте свои визуальные способности, посмотрев, сможете ли вы идентифицировать эти предметы повседневного обихода по их крупным планам.

Усилители разума

Увеличить

Какими тремя числами (от 0 до 9) нужно заменить вопросительные знаки, чтобы ответ был максимально возможным? (Без повторяющихся номеров.)

Растягиватели разума

Ответ:

Наибольшее возможное решение этой математической задачи — 44418, и чтобы получить этот результат, вам нужно прибавить 128 к 79894, а затем вычесть 35604. Хотя эта задача может показаться ошеломляющей на первый взгляд, ответы действительно имеют смысл; вы хотите получить наибольшую возможную сумму, а затем вычесть из нее наименьшее возможное число. Если вам нужно отвлечься от цифр, разгадайте эти хитрые загадки, чтобы проверить свою сообразительность.

Усилители разума

Дневник

Во сколько последняя встреча?

Усилители разума

Ответ: 19.

50

Для этого ответа вы быстро заметите закономерность, если каждый раз будете складывать цифры; игнорировать десятичные точки. Цифры в первом «времени» в сумме дают 11; второй, 12; третий, 13; и, ну, теперь у вас есть очень простой шаблон. Итак, вы знаете, что цифры в пятом разе должны составлять в сумме 15. И когда вы их складываете… они уже делают! Поэтому вопросительный знак нужно заменить на 0, чтобы сумма оставалась равной 15. Знаете ли вы об этих уроках математики, которые вы действительно будете использовать в реальной жизни?

Усилители разума

То же самое

Просто сложив символы  + – × ÷ √ (сложение, вычитание, умножение, деление и квадратный корень), сможете ли вы сделать все эти уравнения верными? Символы не обязательно должны быть там, где находятся многоточия; они могут быть и перед первым числом (хотя отрицательных чисел быть не может). И в каждом месте многоточия может быть более одного символа. Наконец, вам разрешено группировать пары операций вместе со скобками.

Растягиватели разума

Ответы:

Хорошо, да, возможно, это была самая сложная из этих сложных математических задач! Квадратные корни могут сделать вещи еще более запутанными, и требуется немалый ум и изобретательность, чтобы понять, где разместить эти скобки. Хотите отдохнуть от этих сложных математических задач? Получите смех от этих умных математических шуток.

Усилители разума

Собери

Какие блоки должны быть в ячейках А и В?

Растягиватели разума

Ответ: Блок 2 в пространстве A и блок 0 в пространстве B

Это одна из самых простых из этих сложных математических задач (и, честно говоря, хороший перерыв после последней задачи)! Вы можете заметить, что все полные горизонтальные строки и полных вертикальных столбцов в сумме дают 8. Затем вы точно знаете, какие числа вам нужны, чтобы неполные строки также равнялись 8. Посмотрите, как вы справитесь с этим тестом по математике для начальной школы.

Усилители разума

Блоки с цифрами

Какое число должно заменить вопросительный знак в нижней правой петле?

Усилители разума

Ответ: 9

И мы вернулись к действительно сложному! Число на каждой петле — это количество блоков, которые могут поместиться в середине. Это было очень сложно — точно так же, как этот «простой» математический вопрос для детей, который поставил Интернет в тупик.

Растягиватели разума

Место 100

Не выписывая каждую цифру, сможете ли вы определить, под какой буквой будет цифра 100?

Усилители разума

Ответ: Буква d

Я понял это, подумав о восьми столбцах, поэтому после восьми чисел новая строка снова начинается с буквы «а». Поэтому я подумал о числах, кратных десяти (поскольку 100 — это единица). Поскольку строки начинаются заново после восьми чисел, каждое число, кратное десяти, будет на две «буквы» после предыдущего числа, кратного десяти. Например, в таблице уже видно, что 10 стоит под буквой «б», а 20 — под буквой «д». Таким образом, 30 будет находиться под «f», 40 — под «h», 50 — под «b» и так далее.

Растягиватели разума

Это знак

Какое число должно стоять на нижнем правом знаке?

Растягиватели разума

Ответ: 11

В этом случае все, что вы делаете, это ставите знаки минус между верхним и вторым знаками и между вторым и третьим знаками, а затем знак равенства между третьим и нижним знаками. Итак, вы вычитаете, а затем вычитаете еще раз, чтобы получить нижние числа. Таким образом, в первом столбце вы выполняете 41 – 17 – 14, чтобы получить 10. (Вы также можете представить это как сложение второго и третьего знаков, а затем вычитание этого из первого знака.) В последнем столбце вы вычитаете 21. из 37, а затем вычтите из него 5, чтобы получить пропущенное число 11. Если вы можете решить их, попробуйте решить несколько хитрых математических загадок, которые могут решить только самые умные.

Первоначально опубликовано: 29 октября 2019 г.

Меган Джонс

Меган Джонс — помешанная на словах, которая пишет для RD.com с 2017 года. Вы можете найти ее авторство в материалах о грамматике, забавных фактах, значениях различных головокружительных слов и фраз и многом другом. Меган окончила Marist College со степенью бакалавра искусств по английскому языку в 2017 году; ее творческая научно-популярная работа «Предчувствие» была опубликована в весеннем номере литературного журнала «Angles» за 2017 год.

20 каверзных, но забавных вопросов по математике для начальной школы

Если вы не выросли инженером, банкиром или бухгалтером, то, скорее всего, математика в начальной и средней школе была проклятием вашего существования. Вы бы неделями неустанно готовились к этим дурацким стандартизированным тестам — и все же, наступая в день экзамена, вы все равно не имели бы ни малейшего представления о том, для чего нужны какие-либо уравнения или сложные математические задачи.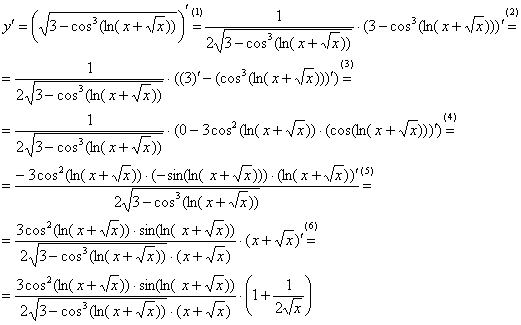 Поверьте нам, мы поняли.

Хотя логика может привести вас к мысли, что ваши математические способности естественным образом улучшились с возрастом, к сожалению, реальность такова, что если вы не решаете задачи по алгебре и геометрии ежедневно, скорее всего, произойдет обратное. кейс.

Не верите нам? Затем испытайте свою мудрость в вычислении чисел с помощью этих хитрых математических вопросов, взятых прямо из школьных тестов и домашних заданий, и убедитесь в этом сами.

1. Вопрос: Какой номер парковочного места занимает автомобиль?

Эта сложная математическая задачка стала вирусной несколько лет назад после того, как появилась на вступительном экзамене в Гонконге… для шестилетних детей. Предположительно, у студентов было всего 20 секунд, чтобы решить задачу!

Ответ: 87.

Хотите верьте, хотите нет, но этот «математический» вопрос вообще не требует математики. Если вы перевернете изображение вверх ногами, то увидите, что имеете дело с простой числовой последовательностью.

2. Вопрос: Замените вопросительный знак в приведенной выше задаче соответствующим номером.

Эта проблема не должна быть слишком сложной для решения, если вы много играете в судоку.

Ответ: 6.

Все числа в каждой строке и столбце в сумме дают 15! (Кроме того, 6 — единственное число, не представленное среди чисел от 1 до 9..)

3. Вопрос: Найдите эквивалентное число.

Эта задача взята прямо из стандартного теста, проведенного в Нью-Йорке в 2014 году.

Ответ: 9.

Shutterstock

Простите, если вы не помните точно, как работают экспоненты. Чтобы решить эту задачу, вам просто нужно вычесть показатели степени (4-2) и решить для 3 ² , что расширяется до 3 x 3 и равняется 9.ae0fcc31ae342fd3a1346ebb1f342fcb

4. Вопрос: Сколько маленьких собак подписано участвовать в выставке собак?

Изображение через Imgur/zakiamon

Этот вопрос взят непосредственно из домашнего задания по математике второклассника.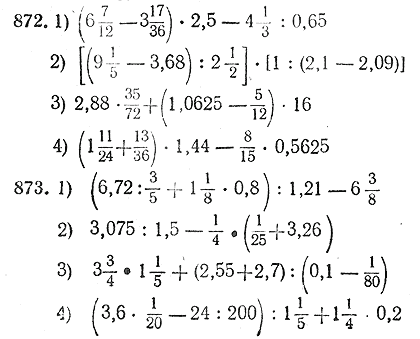 Угу.

Ответ: 42,5 собаки.

Чтобы вычислить, сколько маленьких собак участвует в соревнованиях, вы должны вычесть 36 из 49, а затем разделить результат, 13, на 2, чтобы получить 6,5 собак, или количество больших собак, участвующих в соревнованиях. Но вы еще не закончили! Затем вам нужно прибавить 6,5 к 36, чтобы получить количество соревнующихся маленьких собак, которое равно 42,5. Конечно, на самом деле половина собаки не может участвовать в выставках собак, но ради решения этой математической задачи давайте предположим, что это возможно.

5. Вопрос: Найдите площадь красного треугольника.

Изображение с YouTube

Этот вопрос использовался в Китае для выявления одаренных пятиклассников. Предположительно, некоторые из сообразительных студентов смогли решить это менее чем за одну минуту.

Ответ: 9.

Чтобы решить эту задачу, вам нужно понять, как работает площадь параллелограмма. Если вы уже знаете, как связаны площадь параллелограмма и площадь треугольника, то сложите 79 и 10, а затем вычтите 72 и 8, чтобы получить 9. должно иметь смысл, но если вы все еще запутались, посмотрите это видео на YouTube для более подробного объяснения.

6. Вопрос: Какой высоты стол?

Изображение с YouTube

YouTuber MindYourDecisions адаптировал этот умопомрачительный математический вопрос из похожего вопроса, найденного в домашнем задании ученика начальной школы в Китае.

Ответ: 150 см.

Изображение с YouTube

Поскольку одно измерение включает рост кошки и вычитает рост черепахи, а другое делает противоположное, вы можете просто вести себя так, как будто двух животных здесь нет. Поэтому все, что вам нужно сделать, это сложить два измерения — 170 см и 130 см — вместе и разделить их на 2, чтобы получить высоту стола, 150 см.

7. Вопрос: Если стоимость биты и бейсбольного мяча вместе взятых составляет 1,10 доллара, а бита стоит на 1 доллар больше, чем мяч, сколько стоит мяч?

Shutterstock

Эта задача с математической точки зрения очень похожа на одну из других в этом списке.

Ответ: 0,05 доллара США.

Вспомните задачу о собаках на выставке собак и используйте ту же логику для решения этой задачи. Все, что вам нужно сделать, это вычесть 1,00 доллара из 1,10 доллара, а затем разделить этот результат, 0,10 доллара, на 2, чтобы получить окончательный ответ, 0,05 доллара.

8. Вопрос: Когда у Шерил день рождения?

Изображение через Facebook/Kenneth Kong

Если вам трудно это прочитать, см. здесь:

«Альберт и Бернард только что подружились с Шерил, и они хотят знать, когда у нее день рождения. Шерил дает им список из 10 возможных Даты.

мая 15 мая 16 мая 19

июня 17 июня 18

14 июля 16

августа 15 августа 17 августа

Затем Шерил рассказывает Альберту и Бернарду отдельно в месяц и день своего дня рождения соответственно.0003

Альберт: Я не знаю, когда день рождения Шерил, но я знаю, что Бернард тоже не знает.

Бернард: Сначала я не знал, когда день рождения Шерил, но теперь я знаю.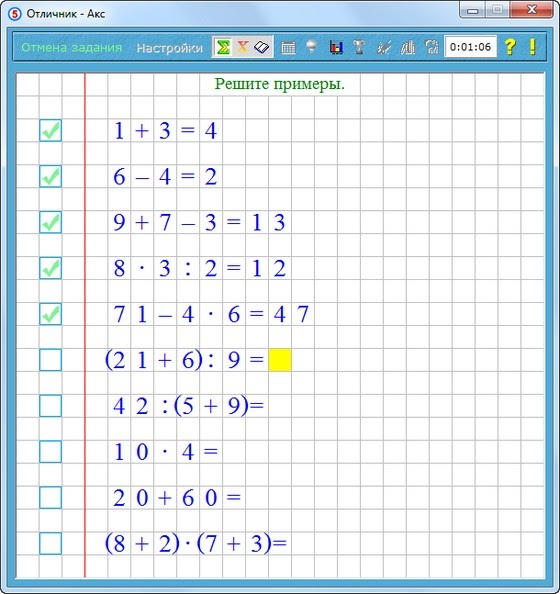

Альберт: Тогда я также знаю, когда у Шерил день рождения.

Итак, когда у Шерил день рождения?»

Непонятно, почему Шерил не могла просто сказать Альберту и Бернарду месяц и день своего рождения, но это не имеет отношения к решению этой проблемы.

Ответ: 16 июля.

Запутался о том, как можно найти какой-либо ответ на этот вопрос? Не волнуйтесь, так было в большинстве стран мира, когда несколько лет назад этот вопрос, взятый из олимпиады по математике среди школьников Сингапура и Азии, стал вирусным. New York Times  шаг за шагом объясняет, как добраться до 16 июля, и вы можете прочитать их подробный вывод здесь.

9. Вопрос: Найдите пропущенную букву.

Изображение из Facebook/The Holderness Family

Это взято из домашнего задания первоклассника .

Ответ: пропущена буква J.

Если сложить вместе значения, указанные для S, B и G, сумма получится равной 40, а добавление пропущенной буквы J (которая имеет значение 14) дает сумма других диагоналей такая же.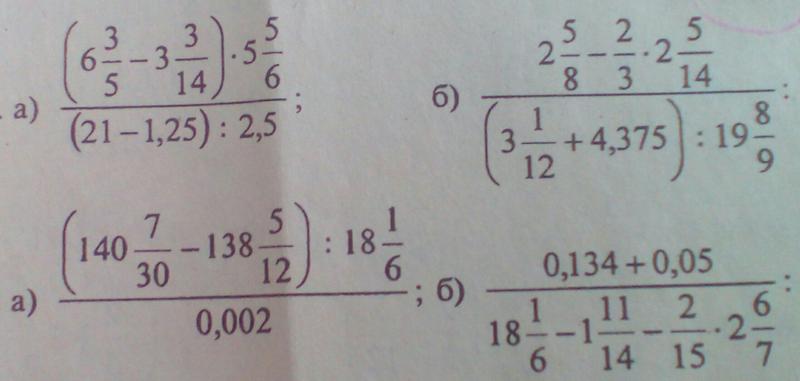

10. Вопрос: Решите уравнение.

Изображение с YouTube

Эта задача может показаться простой, но удивительное количество взрослых не могут решить ее правильно.

Ответ: 1.

Начните с решения части уравнения, относящейся к делению. Для этого, если вы забыли, вам нужно перевернуть дробь и перейти от деления к умножению, получив таким образом 3 x 3 = 9. Теперь у вас есть 9 – 9 + 1, и оттуда вы можете просто работать слева направо. вправо и получите окончательный ответ: 1.

11. Вопрос: Где следует провести линию, чтобы приведенное ниже уравнение было точным?

5 + 5 + 5 + 5 = 555.

Ответ: Над знаком «+» следует провести черту.

Когда вы проводите наклонную линию в верхнем левом квадранте знака «+», она становится цифрой 4, и таким образом уравнение принимает вид 5 + 545 + 5 = 555.

12. Вопрос: Решите незаконченное уравнение.

Попробуйте выяснить, что общего у всех уравнений.

Answer: 4 = 256.



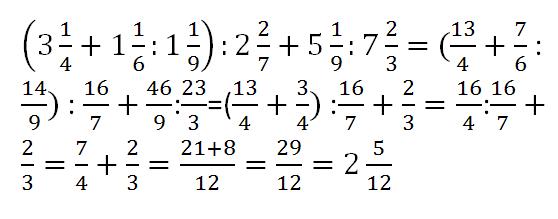
The formula used in each equation is 4 ^x  = Y. So, 4 ¹  = 4, 4 ²  = 16, 4 ³ = 64 и 4 ⁴  = 256.

13. Вопрос: Сколько треугольников на изображении выше?

Когда Best Life впервые написали об этом обманчивом вопросе, нам пришлось просить математика объяснить ответ!

Ответ: 18.

Некоторых людей смущают треугольники, спрятанные внутри треугольников, а другие забывают включить гигантский треугольник, в котором заключены все остальные. В любом случае, очень немногим людям — даже учителям математики — удалось найти правильный ответ на эту проблему. А чтобы получить дополнительные вопросы, которые проверят ваше предыдущее образование, ознакомьтесь с этими 30 вопросами, которые вам нужно будет ответить на высший балл, чтобы сдать экзамен по географии в 6-м классе.

14. Вопрос: Добавьте 8,563 и 4,8292.



Сложить два десятичных знака проще, чем кажется.

Ответ: 13.3922.

Пусть вас не смущает тот факт, что 8.563 имеет меньше номеров, чем 4.8292. Все, что вам нужно сделать, это добавить 0 в конце 8,563, а затем добавить, как обычно.

15. Вопрос: На озере есть кувшинки. Каждый день заплата удваивается в размере…

Shutterstock

… Если заплата покроет все озеро за 48 дней, сколько времени потребуется, чтобы заплата покрыла половину озера?

Ответ: 47 дней.

Большинство людей автоматически предполагают, что половина озера будет покрыта за половину времени, но это предположение неверно. Поскольку участок площадок удваивается в размере каждый день, озеро будет покрыто наполовину всего за один день до того, как оно покроется полностью.

16. Вопрос: Сколько футов в миле?

Эта задачка для начальной школы требует не столько решения задач, сколько запоминания.

Ответ: 5280.

Это был один из вопросов, представленных в популярном шоу  Вы умнее пятиклассника?

17.

Вопрос: При каком значении «x» приведенное ниже уравнение верно? Shutterstock

-15 + (-5x) = 0

Ответ: -3.

Вам простительно думать, что ответ равен 3. Однако, поскольку число рядом с x отрицательное, нам нужно, чтобы x также было отрицательным, чтобы получить 0. Следовательно, x должно быть -3.

18. Вопрос: Сколько 1,92 разделить на 3?

Возможно, вам придется попросить помощи у детей.

Ответ: 0,64.

Чтобы решить эту, казалось бы, простую задачу, нужно убрать десятичную дробь из числа 1,92 и вести себя так, будто ее нет. После того, как вы разделили 192 на 3, чтобы получить 64, вы можете вернуть десятичную запятую на место и получить окончательный ответ 0,64.

19. Вопрос: Решите приведенное выше математическое уравнение.

Изображение с YouTube

Не забывайте о PEMDAS!

Ответ: 9.

Используя PEMDAS (аббревиатура, указывающая порядок, в котором вы решаете: «круглые скобки, показатели степени, умножение, деление, сложение, вычитание»), вы сначала должны решить сложение внутри скобок (1 + 2 = 3), и оттуда закончите уравнение, как оно написано слева направо.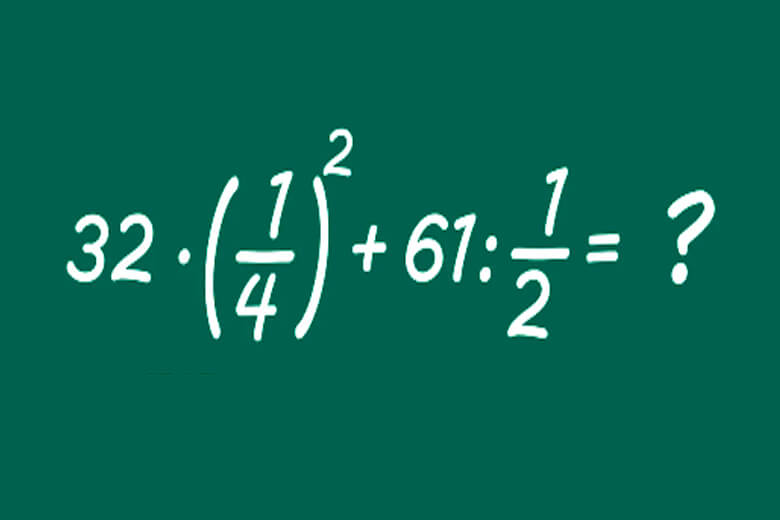

20. Вопрос: Сколько здесь зомби?

Чтобы найти ответ на этот последний вопрос, нужно использовать дроби.

Ответ: 34.

Поскольку мы знаем, что на каждых трех человек приходится два зомби и что 2 + 3 = 5, мы можем разделить 85 на 5, чтобы вычислить, что всего существует 17 групп людей и зомби. Отсюда мы можем умножить 17 на 2 и 3 и узнать, что существует 34 зомби и 51 человек соответственно. Не так уж плохо, верно?

Чтобы узнать больше удивительных секретов о том, как прожить свою лучшую жизнь,  нажмите здесь  , чтобы подписаться на нас в Instagram!

7 самых сложных математических задач в мире (нерешенных)

Сложная математика трудна и подробна. И сложные математические задачи, несомненно, являются самыми сложными математическими задачами. Многие из которых остаются нерешенными.

Это самые сложные в мире:

7. Большой кардинальный проект

Немецкий математик Георг Кантор выяснил, что бесконечность может быть разной величины, и некоторые бесконечные множества содержат больше элементов, чем другие:

Математики продолжают открывать все большие и большие числа или размеры, известные как Большие кардиналы. Таким образом, процесс идет так, что определение кардинала достигается до тех пор, пока кто-то не докажет, что другой кардинал больше, чем все другие известные кардиналы. Затем, в зависимости от их доказательства, это становится новым наибольшим кардиналом.

На протяжении всего прошлого века известные крупные кардиналы неуклонно продвигались вперед. Хотя кажется, что вершина большой количественной иерархии уже видна, многие вопросы о том, насколько большим будет это окончательное большое кардинальное число, остаются открытыми.

ПРОВЕРКА: 10 необъяснимых древних артефактов со всего мира

6. Задача о распутывании

На сегодняшний день простейшая версия задачи о распутывании решена, но полная версия остается нерешенной. Основа этой задачи вытекает из математической темы Knot Theory:

Существующий алгоритм может распутывать узлы любой сложности, но когда узлы становятся более сложными, алгоритмы начинают решать невероятно много времени.

Итак, что еще предстоит увидеть, так это то, что если кто-то сможет разработать алгоритм, способный распутывать любое количество узлов за так называемое полиномиальное время, это, наконец, решит проблему распутывания раз и навсегда.

(Впрочем, при этом кто-то мог даже доказать, что эта задача неразрешима).

5. Задача с числом поцелуев

В пятерку самых сложных математических задач входит задача с числом поцелуев:

Задача с числом поцелуев определяет следующее: когда в области находится множество сфер, каждая сфера считается есть число поцелуев, которое является числом других сфер, с которыми оно соприкасается.

Например, если вы касаетесь шести соседних сфер, то число поцелуев равно шести.

У упакованной группы сфер будет среднее число поцелуев, что поможет описать ситуацию с точки зрения математики. Однако именно тогда, когда проблема пересекает три измерения или большие числа, проблемы поцелуев остаются нерешенными.

CHECK OUT: 7 самых ценных иностранных монет: от Европы до Африки

4. Гипотеза Римана

Одной из наиболее важных открытых проблем в математике является гипотеза Римана. За ее решение даже предусмотрена награда в миллион долларов:

(верно, это одна из тех математических задач на миллион долларов, о которых вы наверняка слышали).

Гипотеза Римана фокусируется на том, что все нетривиальные нули дзета-функции Римана находятся в действительной части 1/2.

В терминах комплексных чисел это означает, что функция имеет определенное поведение вдоль вертикальной линии, и гипотеза утверждает, что это поведение будет продолжаться вдоль этой линии бесконечно.

Понимание простых чисел значительно расширилось за последние 160 лет, но гипотеза Римана до сих пор не решена.

3. Гипотеза о простых числах-близнецах

Гипотеза о простых числах-близнецах — одна из самых известных нерешенных математических задач:

Это одна из многих задач теории чисел, связанных с простыми числами. Когда два простых числа имеют разность в два, они называются простыми числами-близнецами.

Например, 11 и 13 — простые числа-близнецы, как и 59.9 и 601.

Теория чисел утверждает, что существует бесконечное количество простых чисел, поэтому должно быть верным, что существует бесконечно много простых чисел-близнецов. Соответственно, гипотеза о простых числах-близнецах предсказывает, что существует бесконечное число простых чисел-близнецов.

Хотя математики добились прогресса в решении этой проблемы за последнее десятилетие, они все еще далеки от ее решения.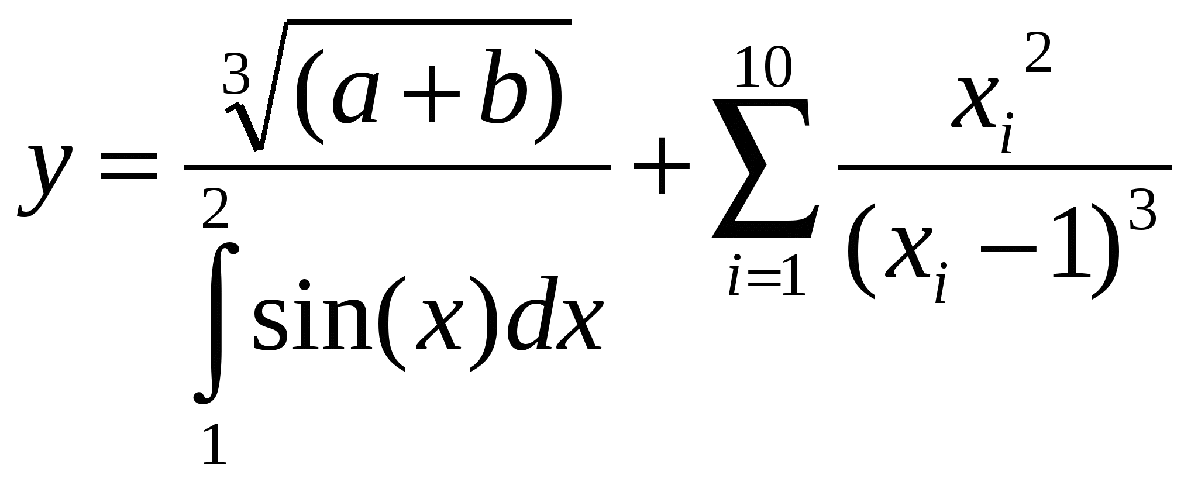 Это делает ее одной из самых сложных математических задач в мире.

ПРОВЕРКА: 5 самых странных дней в истории человечества

2. Гипотеза Гольдбаха

Гипотеза Гольдбаха остается одной из самых сложных математических задач на сегодняшний день:

Проще говоря, Гипотеза Гольдбаха утверждает, что каждое четное число, большее двух, является суммой двух простых чисел. Хотя компьютеры проверили гипотезу для нескольких чисел, доказательство все еще необходимо для всех натуральных чисел.

Многие считают, что гипотеза Гольдбаха является преуменьшением для очень больших чисел. Тем не менее, эта проблема долгое время продолжала озадачивать математиков.

1. Гипотеза Коллатца

Этот математический вопрос 82-летней давности продолжает смущать математиков всего мира:

Хотя в сентябре 2019 года Теренс Тао сделал некоторые прорывы в решении этой проблемы, тем не менее, она до сих пор остается нерешенной. .

Гипотеза Коллатца касается функции f(n), которая учитывает четные числа и делит их пополам. В то же время нечетные числа утраиваются и прибавляются к 1. Гипотеза утверждает, что это верно для всех натуральных чисел.

Гипотеза происходит от математической дисциплины, известной как Динамические Системы, что означает изучение ситуаций, которые меняются с течением времени каким-то полупредсказуемым образом.

Читайте также:
5 изобретений Николы Теслы, которые навсегда изменили мир

сложных математических задач, которые стали вирусными в 2018 году Значок поискаУвеличительное стекло.

Это означает: «Нажмите, чтобы выполнить поиск». Значок шевронаОн указывает на расширяемый раздел или меню, а иногда и на предыдущие/следующие параметры навигации.ДОМАШНЯЯ СТРАНИЦА

образ жизни

Значок «Сохранить статью» Значок «Закладка» Значок «Поделиться» Изогнутая стрелка, указывающая вправо.

Скачать приложение

Какие числа обозначают шарики и конусы мороженого? Предоставлено Гергели Дудасом
• Люди с переменным успехом пытались решить вирусные математические задачи в этом году.
• Некоторым родителям было трудно отвечать на домашние вопросы своих детей.
• Британский математик представил решение 160-летней математической задачи, которая может сделать его миллионером.

Кажется, у Интернета отношения любви и ненависти к математике.

В этом году люди не могли насытиться математическими вопросами, поскольку они обсуждали ответы в темах Твиттера и на родительских форумах. Но они также сетовали на то, как сильно сложные проблемы причиняют боль их мозгам.

Вот 11 математических задач, головоломок и вопросов SAT, которые стали вирусными в этом году.

Только 2% людей смогли разгадать эту загадку менее чем за 60 секунд.

Сможете ли вы определить, какие числа пропущены? ИНСАЙДЕР

Адам Спенсер, комик, математик и автор «Игр с числами», придумал загадку, которую, по данным «Ридерз дайджест», смогли решить только 2% людей за одну минуту.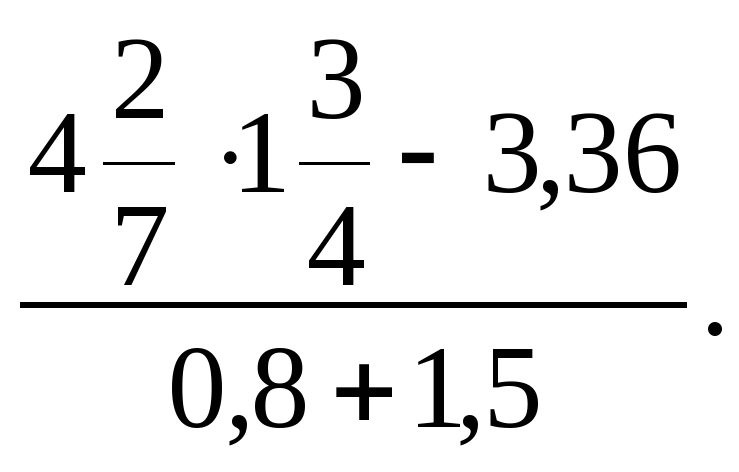

Он записал числа от 1 до 19 в следующем порядке:

8, 18, 11, 15, 5, 4, 14, 9, 19, 1, 7, 17, 6, 16, ?, ?, ? , ?, ?

Чтобы разгадать загадку, нужно выяснить, как он упорядочил первые 14 чисел, и закончить загадку, добавив последние пять.

Пять отсутствующих чисел: два, три, 10, 12 и 13. Схема такова, что существующие числа перечислены в алфавитном порядке.

Полный набор чисел выглядит так:

8, 18, 11, 15, 5, 4, 14, 9, 19, 1, 7, 17, 6, 16, 10, 13, 3, 12, 2

Этот вопрос по китайской математике для пятиклассников поставил в тупик взрослых.

Вопрос был к пятиклассникам. Вейбо

Вопрос по математике для пятиклассников в китайском районе Шуньцин поставил в тупик взрослых по всему миру.

Задача переводится так: «Если на борту корабля 26 овец и 10 коз, сколько лет капитану корабля?»

Каким образом количество груза на корабле должно помочь вам выяснить, сколько лет капитану?

Интернет много говорил об этом, казалось бы, невозможном математическом вопросе, который стал популярной темой в Твиттере.

После того, как тестовый вопрос стал вирусным, Департамент образования Шуньцин опубликовал заявление, в котором говорилось, что вопрос предназначен для оценки «критической осведомленности и способности мыслить независимо», согласно переводу BBC.

Эта задача по математике для второго класса привела Интернет в замешательство.

Эту задачу должны решить второклассники. ИНСАЙДЕР

Вопрос: «Для участия в выставке зарегистрировалось 49 собак. Маленьких собак заявлено на 36 больше, чем крупных собак. Сколько маленьких собак заявлено для участия в соревнованиях?»

Популярное рассуждение состояло в том, что если всего 49 собак, а маленьких собак на 36 больше, чем больших, то из 49 нужно вычесть 36. По этой мере есть 13 больших собак и 36 маленьких собак, а это означает, что ответ таков: 36. Но учитывая, что это означает, что маленьких собак на 23 больше, чем больших, это неверно.

Учитель, задавший вопрос, позже сказал Popsugar: «Округ неправильно сформулировал вопрос». Но в нынешнем виде ответ равен 42,5: 49 — 36 = 13, 13/2 = 6,5 и 36 + 6,5 = 42,5. Судя по всему, на выставке собак соревновалась половина собаки.

Люди не смогли сойтись в ответе на вопрос о купле-продаже лошадей.

Сколько денег он заработал? ПириБрикс

Пользователь Mumsnet PeerieBreeks поделился загадкой на сайте для родителей, где она собрала почти 500 комментариев, а другие пользователи обсуждали ответ.

Вот вопрос: «Человек покупает лошадь за 60 долларов. Он продает лошадь за 70 долларов. Затем он покупает лошадь обратно за 80 долларов. И снова продает лошадь за 90 долларов. заработать или проиграть? Или он безубыточен?»

Ответы в ветке Mumsnet варьировались от получения 10, 20 и 30 долларов до безубыточности. Итак, каково решение?

Кажется, людей сбивает с толку тот факт, что мужчина продает лошадь за 70 долларов, а затем покупает ее обратно за 80 долларов, создавая впечатление, что он потратил на 10 долларов больше. Но правильный способ решить эту проблему состоит в том, чтобы рассматривать две транзакции как отдельные: -60 + 70 = 10 и -80 + 90 = 10.

Человек зарабатывает 10 долларов с каждой продажи, следовательно, он зарабатывает в общей сложности 20 долларов.

Автор Эд Саутхолл поделился в Твиттере математической задачей, которую некоторым людям удалось решить правильно.

Можете ли вы решить это? Solvemymaths/Twitter

Эд Саутхолл, автор книги «Геометрические закуски», поделился фотографией розового треугольника внутри квадрата и предложил людям выяснить, какая часть квадрата закрашена розовым цветом. Некоторые пользователи Twitter сразу же сдались, но другие приняли вызов.

По словам Энди Кирса, корреспондента Business Insider, ключом к решению проблемы является высота розового треугольника.

Площадь треугольника равна 1/2 (основание х высота). Если мы предположим, что квадрат представляет собой единицу 1 x 1, мы увидим, что основание розового треугольника равно 1, длине квадрата. Все, что нам нужно выяснить, это высота.

«Главная хитрость в том, что маленький треугольник наверху похож на розовый треугольник, а это значит, что маленький треугольник — это просто уменьшенная версия розового треугольника», — сказал Кирш.

«Свойство подобных треугольников состоит в том, что отношение высот треугольников будет таким же, как отношение их оснований», — сказал он. «Поскольку основание розового треугольника в два раза больше основания маленького треугольника, его высота также в два раза больше высоты маленького треугольника. Но мы знаем, что высота маленького треугольника плюс высота розового треугольника равна 1, значит, высота розового треугольника равна 2/3. . Подключите это, и мы получим площадь = 1/2 x основание x высота = 1/2 x 1 x 2/3 = 1/3».

Саутхолл подтвердил, что ответ действительно равен 1/3.

Математическая задача, предназначенная для 8-летних детей, стала вирусной после того, как родители не смогли ее решить.

Этот вопрос был слишком сложным для родителей. Помните о своих решениях/YouTube

Пользователь Mumsnet lucysmam обратился в Интернет за помощью с заданием по математике для своей дочери.

Задача звучит так:

«На берегу три маяка.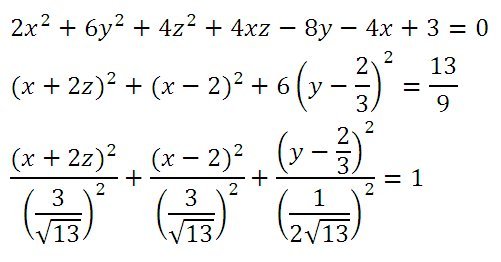

Первый свет горит 3 секунды, затем гаснет на 3 секунды.

Второй свет горит 4 секунды, затем гаснет на 4 секунды

Третий индикатор горит 5 секунд, затем выключается на 5 секунд

Все три индикатора только что загорелись вместе

1) Когда в первый раз все три индикатора будут выключены одновременно №

2) Когда в следующий раз все три индикатора загорятся одновременно?»

К счастью, математический гений YouTube Преш Талвалкар предложил объяснение на своем канале MindYourDecisions.

Согласно Талвалкару, самый простой способ Ответ на первый вопрос о том, когда погаснут все огни, состоит в том, чтобы наметить интервалы для каждого маяка и посмотреть, где перекрываются их «выключенные» участки. второй свет все еще не горит.

Чтобы определить, когда загорятся все лампочки одновременно, нужно найти наименьшее общее кратное интервалов, когда загорятся лампочки. Ответ на этот вопрос заключается в том, что все маяки зажгутся вместе через 120 секунд или две минуты.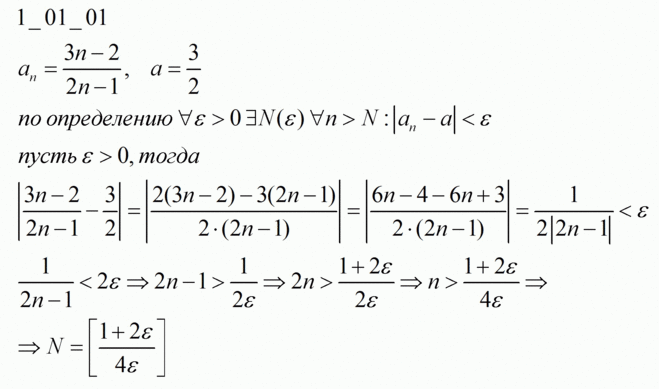

Для получения более подробной информации нажмите здесь.

В сложной математической задаче, созданной Гергели Дудасом, вместо переменных использовались рожки мороженого.

Какие числа обозначают шарики и конусы мороженого? Предоставлено Гергели Дудасом

Художник Гергели Дудас, известный своими хитрыми головоломками со скрытыми предметами, поделился на своей странице в Facebook математической задачей, которую он проиллюстрировал конусами мороженого.

Головоломка состоит из четырех математических уравнений, каждое из которых складывает или умножает числовую сумму или произведение.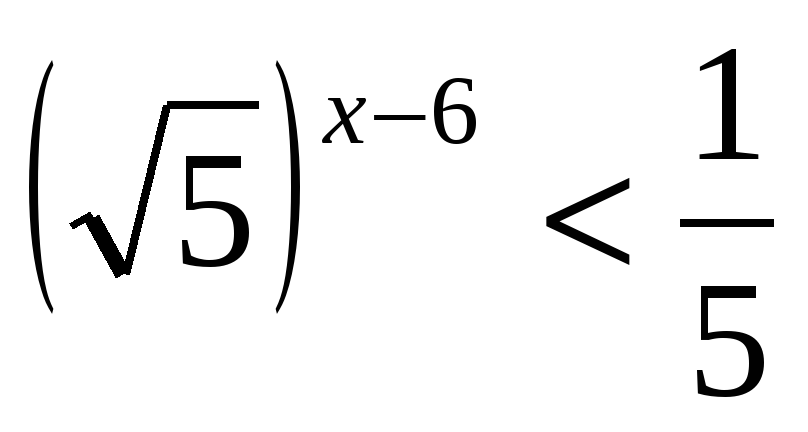 Однако вместо таких переменных, как x или y, головоломка заменяет рожки мороженого, которые либо пусты, либо имеют шарики белого мороженого, розового мороженого или того и другого.

Чтобы решить головоломку, вам нужно выяснить, какое число обозначают пустые рожки для мороженого, белые и розовые шарики для мороженого.

Ответ заключается в том, что пустой рожок для мороженого представляет цифру три, белая ложка мороженого представляет цифру два, а розовая ложка мороженого представляет цифру один.

В ветке сложных математических вопросов SAT на Quora был один человек, которого назвали «самой серьезной тестовой задачей».

Что такое п/н? Помните о своих решениях/YouTube

В ветке Quora, посвящённой самым сложным математическим задачам SAT, один вопрос был назван «самой сложной тестовой задачей».

Он гласит:

«В классе из учащихся из среднее (среднее арифметическое) баллов за тест равно 70.

равно 92.

Если объединить баллы двух классов, среднее значение тестов равно 86.

Каково значение p / n ? имел средний балл 70. Это на 16 баллов ниже среднего балла 86. Другими словами, 86 — 70 = 16. Поскольку в классе p учеников, разница со средним значением составляет 16 p .

Второй класс имел средний балл 92. Это на 6 баллов больше, чем в среднем 86. Другими словами, 9 баллов.2 — 86 = 6. В этом классе n учеников, поэтому разница со средним значением составляет 6 n .

Поскольку эти классы усредняются вместе — как говорится в задаче, «когда баллы двух классов суммируются», — дефицит баллов должен быть равен избытку баллов. Следовательно, 16 p равно 6 n .

Превратив это в уравнение, мы можем легко вычислить, что такое p / n :

16 p = 6 n

p/n = 6/16 или 3/8.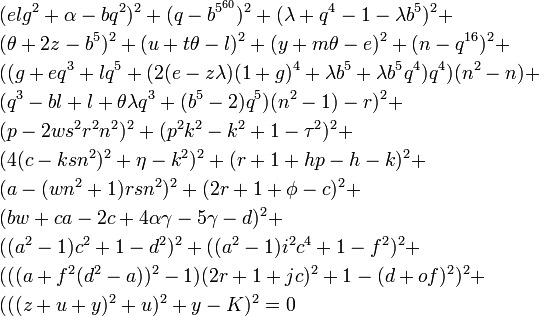

Значок сделкиЗначок в виде молнии.

Продолжай читать

LoadingЧто-то загружается. Функции Математика Головоломки

Подробнее…

Более 35 сложных математических задач и задач для будущих гениев

Никто не оставит равнодушным сложную математическую задачу с начальной строкой: «67 человек едут на запад со скоростью 45 миль в час».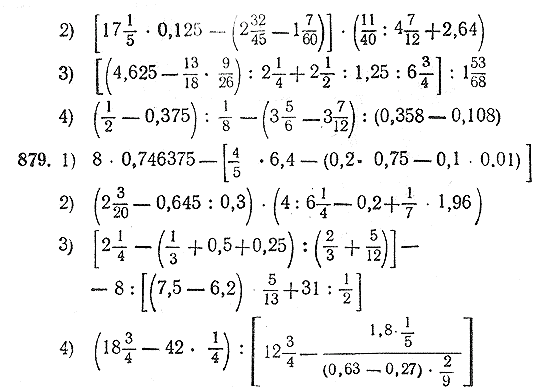 Эти словесные уравнения имеют тенденцию либо волновать нас, либо внушать страх. В то время как мы все без усилий сталкиваемся с ежедневными встречами с простой арифметикой, иногда математические загадки и задачи со словами останавливают нас на пути. Часто они представляют собой сложное и восхитительное сочетание абстрактного и реального мира, поэтому они идеально подходят для детей.

Чтобы решить математическую загадку, дети должны преобразовать несколько предложений о реальном сценарии в правильную комбинацию математических уравнений. Используя логику, творческое решение задач и здравый смысл, дети могут разгадать любой код, включая математические загадки. Несмотря на сложность, более сложные из них особенно доставляют удовольствие детям (и, будем откровенны, взрослым).

Хорошая новость заключается в том, что скрыть сложное уравнение за веселой и увлекательной загадкой — лучший способ заинтересовать вашего ребенка математикой задолго до того, как он столкнется с большим разрывом в восьмом классе, вызванным квадратичной формулой. Эти хитрые математические загадки развлекают детей, развивая их логику и математические навыки. Скорее всего, вы тоже чему-то научитесь.

Лучшие математические загадки для детей

1. Загадка: Если есть четыре яблока, и вы уберете три, сколько у вас останется? / Ответ: Ты взял три яблока, значит, у тебя их три!

2. Загадка : Бабушка, две мамы и две дочери вместе пошли на бейсбольный матч и купили по одному билету. Сколько всего билетов они купили? / Ответ : Три билета / Объяснение: Бабушка тоже мать, а мать тоже дочь.

3. Загадка: Яйца стоят 12 центов за дюжину. Сколько яиц можно получить за доллар? / Ответ: 100 яиц по пенни каждое

4. Загадка: Как сложить восемь четверок, чтобы в сумме получилось 500? / Ответ: 444 + 44 + 4 + 4 + 4 = 500

5. Загадка: Если семь человек встречаются друг с другом и каждый пожимает друг другу руку только один раз, сколько рукопожатий произошло? / Ответ: 21

Загадки по математике для средней школы

1. Загадка: Поезд длиной 300 футов движется со скоростью 300 футов в минуту и ​​должен пройти через туннель длиной 300 футов. За какое время поезд проедет тоннель? / Ответ: Две минуты. Передней части поезда требуется одна минута, а остальной части поезда требуется две минуты, чтобы пройти туннель.

2. Загадка: Мобильный телефон и чехол для телефона стоят в общей сложности 110 долларов. Сотовый телефон стоит на 100 долларов больше, чем чехол для телефона. Сколько стоил мобильник? / Ответ: 105 долларов (не 110 долларов)

3. Загадка: Роберт и Дэвид сыграли друг с другом несколько матчей в гольф за неделю. На каждом матче они играли за пиццу, но до конца недели пиццы не покупали. Если у Роберта и Дэвида было одинаковое количество побед в любое время, эти пиццы отменялись. Роберт выиграл четыре матча (но ни одной пиццы), а Дэвид выиграл три пиццы. Сколько раундов в гольф было сыграно? / Ответ: 11 / Объяснение: Дэвид выиграл семь матчей — четыре, чтобы свести на нет четыре победы Роберта, и еще три, чтобы выиграть пиццу.

4. Загадка: Я трехзначное число. Моя вторая цифра в четыре раза больше, чем третья цифра. Моя первая цифра на три меньше моей второй цифры. Кто я? / Ответ: 141

5. Загадка: Я прибавляю пять к девяти и получаю два. Ответ правильный, но как? / Ответ: Когда будет 9 часов утра, прибавьте к этому пять часов, и вы получите 2 часа дня.

6. Загадка: Половина — это треть. Что это? / Ответ: 1 1/2

7. Загадка: Когда Мигелю было 6 лет, его младшая сестра Лейла была вдвое моложе его. Если Мигелю сегодня 40 лет, то сколько лет Лейле? / Ответ: Ей 37 лет.

8. Загадка: Тома попросили закрасить числа за пределами 100 квартир, а это значит, что ему нужно будет закрасить числа от 1 до 100. Сколько раз ему придется закрасить число восемь? / Ответ: 20 раз / Объяснение: (8, 18, 28, 38, 48, 58, 68, 78, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 98)

9. Загадка: Что можно поставить между семеркой и восьмеркой так, чтобы результат был больше семерки, но меньше восьмерки? / Ответ: Десятичное число, потому что 7,8 больше семи, но меньше восьми.

10. Загадка: «Сколько стоит этот мешок картошки?» — спросил мужчина. «Тридцать два фунта разделить на половину собственного веса», — сказал бакалейщик. Сколько весил картофель? / Ответ: 8 фунтов

11. Загадка: Когда Лизе было 6 лет, ее сестра Люси была вдвое моложе ее. Если Лизе сегодня 40 лет, то сколько лет Люси? / Ответ: 37 / Пояснение: Люси на три года младше Лизы.

12. Загадка: Вам даны три положительных числа. Вы можете сложить эти числа и умножить их вместе. Результат, который вы получите, будет таким же. Какие числа? / Ответ: Раз, два и три.

Математические загадки о животных

1. Загадка: В зоопарке 100 пар собак; у каждой собаки рождается пара малышей. К сожалению, 23 собаки не выжили. Сколько всего собак осталось? / Ответ: 977 собак / Объяснение: 100 х 2 = 200; 200 + 800 = 1000; 1000 – 23 = 977

2. Загадка: Если полторы курицы снесут полтора яйца за полтора дня, сколько яиц снесут полдюжины кур за полдюжины дней? / Ответ: Две дюжины

3. Загадка: Леон работает в аквариуме. Когда он пытается поместить каждую черепаху в отдельный аквариум, у него на одну черепаху слишком много. Но если он поставит по две черепахи на один аквариум, то у него будет на один танк слишком много. Сколько черепах и сколько танков у Леона? / Ответ: У него три танка и четыре черепахи.

4. Загадка: Утке дали 9 долларов, пауку дали 36 долларов, а пчеле дали 27 долларов. Основываясь на этой информации, сколько денег дадут кошке? / Ответ: 18 долларов (4,50 доллара за ногу)

5. Загадка: Если вы покупаете петуха, чтобы он нес яйца, и рассчитываете получать три яйца каждый день на завтрак, сколько яиц у вас будет через три недели? / Ответ: Нет. Петухи не несут яиц.

6. Загадка: У фермера на земле 19 овец. Однажды налетает сильный шторм, и все, кроме семерых, убегают. Сколько овец осталось у фермера? / Ответ: Семь. Все, кроме семи, убежали.

Забавные математические загадки

1. Загадка: Группа студентов стояла под палящим солнцем лицом прямо на запад, маршируя мимо мероприятия. Вождь крикнул им: направо! О повороте! Левый поворот! В конце этих команд, в каком направлении теперь смотрят ученики? / Ответ: Восток / Объяснение: Они повернутся на 90 градусов при повороте направо, затем на 180 градусов при развороте и, наконец, на 90 градусов при повороте налево. Таким образом, студенты теперь смотрят на восток.

2. Загадка: Что тяжелее: 16 унций газировки или фунт чистого золота? / Ответ: Ни то, ни другое. Они оба весят одинаково!

3. Загадка: Во время отправки Том может поместить в коробку 10 маленьких коробок или восемь больших коробок. Всего было отправлено 96 коробок одной партией. Маленьких ящиков было меньше, чем больших. Каково общее количество коробок, которые он отгрузил? / Ответ: 11 коробок / Объяснение: Четыре маленьких коробки (410 = 40 коробок) + семь больших коробок (78 = 56 коробок). Итак, 96 коробок и всего 11 коробок.

4. Загадка: Какое максимальное количество раз можно вычесть пять из 25? / Ответ: Только один раз. Это потому, что когда вы вычитаете пять в первый раз, 25 становится 20, затем 15 и так далее.

5. Загадка: Общая стоимость пары туфель и худи составляет 150 долларов. Толстовка стоила на 100 долларов больше, чем пара туфель. Сколько стоит каждый предмет? / Ответ: Толстовка стоит 125 долларов, а туфли — 25 долларов.

6. Загадка: У вас есть две монеты США общей стоимостью 30 центов. Один из них не пятак. Какие две монеты? / Ответ: Одна четверть, а одна пятак.

7. Загадка: Я трехзначное число. Моя цифра десятков на шесть больше, чем моя цифра единиц. Моя цифра сотен на восемь меньше моей цифры десятков. Какой я номер? / Ответ: 193

8. Загадка: Мужчина вдвое старше своей младшей сестры. Он также вдвое моложе своего отца. Через 50 лет возраст его сестры станет вдвое меньше возраста их отца. Сколько лет мужчине сейчас? / Ответ: 50 лет

8. Загадка: Если четыре человека могут построить четыре стола за четыре часа, сколько восемь человек могут построить за восемь часов? / Ответ : 16 столов

9. Загадка : В Далласе есть магазин одежды. Владелец сделал свой собственный метод ценообразования предметов. Жилет стоит 20 долларов, носки — 25 долларов, галстук — 15 долларов, а блузка — 30 долларов. Используя этот метод, сколько будет стоить пара нижнего белья? / Ответ: $45 / Объяснение: Метод ценообразования заключается в взимании 5 долларов за каждую букву, необходимую для написания элемента.

10. Загадка: Если вы идете в кино и платите, дешевле будет сводить одного друга в кино дважды или двух друзей в кино одновременно? / Ответ: Дешевле взять двух друзей одновременно. / Объяснение: В этом случае вы покупаете только три билета, тогда как если вы берете одного и того же друга дважды, вы покупаете четыре билета.

11. Загадка: Маленький мальчик ходит по магазинам и покупает 12 помидоров. По дороге домой все, кроме девяти, раздавлены и раздавлены. Сколько помидоров осталось в хорошем состоянии? / Ответ: Девять помидоров.

No related posts.