Как правильно умножать отрицательные числа?
В 6 классе каждый школьник знает отличие между положительным и отрицательным числом и правила умножения. В этой статье объединим эти две темы и попрактикуемся в умножении отрицательных чисел.
Записывайтесь на онлайн-фестиваль для родителей SmartFest!
Ждём вас 8 октября в 13:00. Вместе с педагогами, психологами и другими экспертами в образовании и воспитании ответим на главные вопросы мам и пап.
Бесплатный урок по математике
Записаться
Основные определения
Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:
Два главных определения:
Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.
Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.
Запоминаем!
Положительные числа — это те, что больше нуля, а отрицательные — меньшие.
Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».
Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!
Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).
Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения
|
Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Умножение отрицательных чисел
Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:
Это значит, что для любых отрицательных чисел -a, -b верно равенство:
- (-а) * (-b) = a * b
А вот как умножить два числа с разными знаками:
- перемножить модули этих чисел
- перед полученным числом поставить знак минус
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
- «—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс - «-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус - «+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус - «++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.
Примеры умножения отрицательных чисел
Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)
Как решаем:
Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:
Считаем:
- (-2)∗(-2) = 4
- (-3)∗(-7) = 21
Ответ: 4; 21.
Пример 2. Вычислить: (-11)∗11 и (-20)∗2
Как решаем:
Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:
- -11 * 11 = -121
- (-20) * 2 = -40
Ответ: -121; -40.
Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)
Как решаем:
Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:
- 5 ∗ (-5)= -25
- 12 ∗ (-8)= -96
Ответ: -25; -96.
Пример 4. Вычислить произведение: (-0,125 ) * (-6)
Как решаем:
- Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6.
- Выполним умножение десятичной дроби на натуральное число столбиком:
Ответ: 0,75.
Шпаргалки по математике родителей
Все формулы по математике под рукой
При делении минуса на минус что получается
При делении минус на минус дает плюс – Умножения и деление отрицательных чисел. Решение примеров.
Если подположить, что минус на минус даёт минус, многие алгебраические вычисления будут приводить к абсурду.
Это обычный здравый смысл. Возьми аналог на примере слов. Предложение «я люблю чай с сахаром» — содержит как бы два множителя: «я люблю» и «с сахаром». «Минус» — это отрицательное число. Отрицание. Если в нашей фразе приписать «минус» к одному из множителей, то получится «я НЕ люблю чай с сахаром». А если приписать к другому, то «я люблю чай БЕЗ сахара». Если же минусы окажутся у обоих множителей, то получится фраза «я не люблю чай без сахара» — как видишь, она содержит тот же самый смысл, что и исходная фраза без отрицаний. Видишь? Иными словами, если ты отрицаешь отрицание — то ты тем самым утверждаешь. Простой здравый смысл!
Видишь? Иными словами, если ты отрицаешь отрицание — то ты тем самым утверждаешь. Простой здравый смысл!
если умножать минус на минус в результате будет плюс?
Если умножать отрицательное число на отрицательное, то да Минус на минус даёт плюс Например (-3) * (-3) = +9 Однако, если отрицательных множетелей нечётное количество, то уже будет минус! Например (-2) * (-2) * (-2) = -8 (потому, что при первом перемножении получился плюс, а при втором снова минус)
Это смотря как умножпть 8) Вожет получиться Три и более Минусов))
Да. В математике.. .
а это смотря в чем. в деньгах минус на минус дает еще больший минус. долговую яму. а в алгебре да. дает плюс. но вот в отношениях минус на минус дает вражду. а в математике да. плюс. но это не значит что тебе поставят плюс на уроке. ты ни умножать ни считать не можешь. а то бы не спрашивал здесь
В математике, если умножать минус на минус, получается плюс. В жизни если умножать минус, получается громадный МИНУС.
да! всегда так было, есть и будет!
ДА!)) ) Минус умножить на минус=+
Минус на минус дает плюс.
 Почему?
Почему?Как известно, уже в школе всем говорят, что минус на минус дает плюс. Можно даже привести примеры:
$$x-(-y)=x+y; (-x)\cdot (-y)=x\cdot y; -x/\left(-y \right)=x/y$$ Но самое интересное в другом. Если у кого угодно спросить а почему так, то мало кто сможет ответить. Вам скажут — так принято или так должно быть по правилам. А ответить почему такие правила и откуда они появились еще труднее. И даже если задать такой же вопрос в поисковой системе, то можно прочитать все что угодно, начиная с дурацких примеров и заканчивая попытками объяснения из области теории групп. Ну как школьнику или даже студенту можно объяснить что такое кольца из теории групп? Поэтому требуется нормальное объяснение, основанное на понятных и легко проверяемых понятиях и правилах. Как оказалось, это можно сделать фактически в одну строку. Смотрите выкладки: $$A-(-B)=X\Rightarrow A=X+(-B)\Rightarrow A=X-B\Rightarrow A+B=X\Rightarrow A-(-B)=A+B$$ Тут тоже могут возникать вопросы: «Почему при переносе слагаемого меняется знак на противоположный?» Ответ будет такой: «Мы ничего никуда не переносим, а просто добавляем в левую и правую части выражения одну и ту же величину»: $$A-(-B)=X\Rightarrow A-\left(-B \right)+(-B)=X+(-B)$$ А вот теперь обозначим: $$-B=Z$$ и после подстановки все становится очевидным: $$A-Z=X\Rightarrow A-Z+Z=X+Z\Rightarrow A=X+Z$$ Теперь осталось вернуться к старой (заменной переменной), используя выражение: $$-B=Z$$ И в результате получим, что при «переносе вправо слагаемого его знак поменялся на противоположный»: $$ A=X-B$$ Вот и все преобразования, объясняющие почему если в выражении идет два минуса подряд, то в итоге их надо заменить на плюс. Теперь займемся случаем умножения двух отрицательных чисел. $$(-A)\cdot (-B)=X\Rightarrow (-A)\cdot (-B)+\left(A\cdot B \right)-\left(A\cdot B \right)=X\Rightarrow …$$ $$… \Rightarrow (-A)\cdot (-B)+\left(A\cdot B \right)+ \left(-A \right) \cdot B=X\Rightarrow …$$ $$…\Rightarrow \left(-A \right)\left[\left(-B \right)+B \right]+A\cdot B=X\Rightarrow \left(-A\ \right) \cdot 0+A\cdot B=X\Rightarrow A\cdot B=X$$ Теперь осталось приравнять, с одной стороны: $$\left(-A \right)\cdot \left(-B \right)=X$$ а с другой стороны: $$A \cdot B =X$$ Тогда, окончательно: $$\left(-A \right)\cdot \left(-B \right)=A \cdot B$$ Как вам понятно, с делением двух отрицательных чисел уже не возникает проблем, так как операцию деления можно легко заменить операцией умножения на обратное. Остается выяснить почему минус из знаменателя можно поднимать в числитель. Один из вариантов: $$\frac=\frac=\frac$$ Предлагаем все высказываться в комментариях, если что кому не понравилось. Эта статья подготовлена студенческой лабораторией для любознательных школьников и их учителей.
Теперь займемся случаем умножения двух отрицательных чисел. $$(-A)\cdot (-B)=X\Rightarrow (-A)\cdot (-B)+\left(A\cdot B \right)-\left(A\cdot B \right)=X\Rightarrow …$$ $$… \Rightarrow (-A)\cdot (-B)+\left(A\cdot B \right)+ \left(-A \right) \cdot B=X\Rightarrow …$$ $$…\Rightarrow \left(-A \right)\left[\left(-B \right)+B \right]+A\cdot B=X\Rightarrow \left(-A\ \right) \cdot 0+A\cdot B=X\Rightarrow A\cdot B=X$$ Теперь осталось приравнять, с одной стороны: $$\left(-A \right)\cdot \left(-B \right)=X$$ а с другой стороны: $$A \cdot B =X$$ Тогда, окончательно: $$\left(-A \right)\cdot \left(-B \right)=A \cdot B$$ Как вам понятно, с делением двух отрицательных чисел уже не возникает проблем, так как операцию деления можно легко заменить операцией умножения на обратное. Остается выяснить почему минус из знаменателя можно поднимать в числитель. Один из вариантов: $$\frac=\frac=\frac$$ Предлагаем все высказываться в комментариях, если что кому не понравилось. Эта статья подготовлена студенческой лабораторией для любознательных школьников и их учителей.
Отрицательные дроби
Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус можно ставить перед дробью, перед числителем или перед знаменателем:
| — | 2 | = | -2 | = | 2 | . |
| 7 | 7 | -7 |
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
| — | 2 | + (- | 1 | ) | . |
| 5 | 4 |
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | . |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | — | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Математика для блондинок
Математикой должны заниматься блондинки — они врать не умеют.
Страницы
четверг, 31 декабря 2020 г.
Минус на плюс что дает?
Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.
Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.
Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.
| Минус на плюс, плюс на минус. |
Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился. Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.
Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.
alt=»Минус на минус, плюс на плюс. Умножение и деление отрицательных или положительных чисел в результате дает положительное число. Математика для блондинок.или» width=»654″ height=»848″ /> Математика для блондинок.или» width=»654″ height=»848″ /> |
| Минус на минус, плюс на плюс. |
Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.
Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?
Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.
Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.
Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.
Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает.
Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.
Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.
Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.
В чем же отличие качественных изменений от количественных? В единицах измерения, которые в математике предпочитают игнорировать. Вот смотрите. Если мы к метрам длины прибавим метры ширины, мы получим метры периметра. А если мы умножим метры длины на метры ширины, то в результате будут метры квадратные площади. Теперь вопрос к математикам: сколько метров длины или ширины нужно сложить, чтобы получить один метр квадратный площади? Или вопрос к вам: сколько метров ниток вам нужно намотать на себя, чтобы одеться? Ведь ткань — это те же самые нитки, только в совершенно другом качестве. Ну и наглядный пример из алгебры:
Ну и наглядный пример из алгебры:
В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?
Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.
Кто придумал что минус на минус дает плюс?
Содержание
- — Что значит минус на минус дает плюс?
- — Как будет минус или плюс?
- — Чему равняется минус на минус?
- — Что будет если делить на отрицательное число?
- — Что способствовало появлению отрицательных чисел?
- — Почему при умножении двух отрицательных чисел получается положительное?
- — Какое действие выполняется первым плюс или минус?
- — Что дает плюс на минус при сложении?
- — Что значит +- в математике?
- — Как делить отрицательные числа?
- — Как складывать отрицательные числа?
- — Что такое минус?
- — Какой знак будет если минус делить на минус?
- — Можно ли разделить на минус?
- — Как складывать и вычитать отрицательные и положительные числа?
В трактате 1494 года Сумма арифметики итальянский математик Лука Пачоли вводит символы P с чертой — p̄ для più, то есть «плюс» и M с чертой — m̄ для meno, то есть «минус».
Что значит минус на минус дает плюс?
Этих принципов достаточно, чтобы вывести правило для «минус на минус». Разумно устроить умножение на отрицательные числа так, что произведение любого числа и нуля дает ноль. … Получается, это первое произведение должно быть положительным. Это и значит, что «минус на минус» дает «плюс».
Как будет минус или плюс?
Умножение. Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс».
Чему равняется минус на минус?
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. … Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Что будет если делить на отрицательное число?
В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число.
Что способствовало появлению отрицательных чисел?
Впервые отрицательные числа были частично узаконены в классическом китайском трактате «Математика в девяти книгах» (II в до н. э.), а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или, как у Диофанта (III в н. э.), признавались как временные значения.
Почему при умножении двух отрицательных чисел получается положительное?
Чтобы перемножить два отрицательных числа, надо умножить их модули. Таким образом, при умножении двух отрицательных чисел получается положительное число.
Таким образом, при умножении двух отрицательных чисел получается положительное число.
Какое действие выполняется первым плюс или минус?
действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Что дает плюс на минус при сложении?
В этом случае получается та же ситуация, что при сложении двух отрицательных чисел. Так как, “минус” на “плюс” дает “минус”. Получившиеся числа складываются по модулю, а потом к результату возвращают “минус”.
Что значит +- в математике?
Знак плюс-минус (±) — математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и отрицательным. Часто используется, например, для указания: . .. интервала значений результата в приближённых математических вычислениях.
.. интервала значений результата в приближённых математических вычислениях.
Как делить отрицательные числа?
Чтобы разделить отрицательное число на отрицательное (два отрицательных числа), надо разделить модуль делимого на модуль делителя.
Как складывать отрицательные числа?
Чтобы сложить положительное и отрицательное число, нужно:
- Найти модули слагаемых — то есть этих чисел.
- Сравнить полученные числа. …
- Из большего модуля вычесть меньший.
- Перед полученным числом поставить знак того слагаемого, модуль которого больше.
29 дек. 2020 г.
Что такое минус?
Минусовая фонограмма («минус», «минусовка»; от «запись минус один голос») — запись музыкального произведения, в котором отсутствует одна или более партий, обычно вокал или солирующий инструмент. Под такую запись музыкант (профессионал или любитель) имеет возможность сам исполнять отсутствующую партию.
Какой знак будет если минус делить на минус?
Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс.
Можно ли разделить на минус?
Итак, правило деления чисел с разными знаками имеет следующую формулировку: чтобы разделить положительное число на отрицательное или отрицательное число на положительное, надо модуль делимого разделить на модуль делителя, и перед полученным числом поставить знак минус.
Как складывать и вычитать отрицательные и положительные числа?
Как видим, чтобы вычесть из положительного числа отрицательное число, нужно просто сложить их модули. Таким образом, при вычитании отрицательного числа из отрицательного мы действуем по правилу сложения чисел с разными знаками, и у нас может получиться как положительное, так и отрицательное число.
Интересные материалы:
Сколько грамм весит креветка?
Сколько грамм весит один пирожок?
Сколько грамм весит одна шаурма?
Сколько калорий в 1 кг лишнего веса?
Сколько килограмм весит литр меда?
Сколько килограмм весит рога оленя?
Сколько может весить бобер?
Сколько примерно весит 1 гранат?
Сколько ребенок набирает вес в 3 триместре?
Сколько ребенок весит в 3 месяца?
Умножение чисел с разными знаками (6-й класс)
Цели урока:
Обучающие:
- формулирование правил умножения чисел с одинаковыми и разными знаками;
- овладение и совершенствование навыков умножения чисел с разными знаками.
Развивающие:
- развитие мыслительных операций: сравнение, обобщение, анализ, аналогия;
- развитие навыков самостоятельной работы;
- расширение кругозора учащихся.
Воспитательные:
- воспитание культуры оформления записей;
- воспитание ответственности, внимания;
- воспитание интереса к предмету.

Тип урока: изучение нового материала.
Оборудование: компьютер, мультимедиапроектор, карточки для игры «Математический бой», тесты, карты учёта знаний.
На стенах плакаты:
- Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит.
Ал-Бируни - Во всём мне хочется дойти до самой сути…
Б. Пастернак
План урока
- Организационный момент (1 мин).
- Вступительное слово учителя (3 мин).
- Устная работа (10 мин).
- Изложение материала (15 мин).
- Математическая цепочка (5 мин).
- Домашнее задание (2 мин).
- Тест (6 мин).
- Итог урока (3 мин).
готовность учащихся к уроку.
II. Вступительное слово учителя
Ребята, мы сегодня с вами встретились не зря, а для плодотворной работы: получения знаний.
С тех пор, как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы не возьмём язык и век,
Всегда стремился к знанью человек…
Рудаки
На уроке мы будем изучать новый материал, закреплять его, работать самостоятельно, оценивать себя и своих товарищей. У каждого на столе лежит карта учета знаний, в которой наш урок разделён на этапы. Заработанные вами баллы на разных этапах урока вы сами будете заносить в эту карту. А в конце урока подведём итоги. Положите эти карты на видное место.
| Карта учета знаний | ||||
| Фамилия, имя учащегося | ||||
| Игра «Математический бой» | Математическая цепочка | Тест | Итог урока | |
| баллы | оценка | |||
 Устная работа (в виде игры «Математический бой»)
Устная работа (в виде игры «Математический бой»)Ребята, прежде чем приступить к новой теме, повторим ранее изученное. У каждого на парте лежит лист с игрой «Математический бой». В вертикальных и горизонтальных столбцах записаны числа, которые необходимо сложить. Эти числа отмечены точками. Ответы запишем в те клеточки на поле, где и стоят точки.
Три минуты на выполнение. Начали работу.
А теперь обменялись работами с соседом по парте и проверяем их друг у друга. Если вы считаете, что ответ неправильный, то аккуратно зачеркните его и рядом впишите правильный. Проверяем.
А сейчас сверим ответы с экраном (на экран проектируются правильные ответы).
За правильно решенные
5 заданий ставим 5 баллов;
4 задания – 4 балла;
3 задания – 3 балла;
2 задания – 2 балла;
1 задание – 1 балл.
Молодцы. Отложили всё в сторону. Ребята, в свои карты учета знаний занесём количество баллов, набранное за «Математический бой» (Приложение 1).
IV. Изложение материала
Открываем рабочие тетради. Записываем число, классная работа.
- Какие действия над положительными и отрицательными числами вы знаете?
- Как сложить два отрицательных числа?
- Как сложить два числа с разными знаками?
- Как вычесть числа с разными знаками?
- Вы всегда употребляете слово «модуль». А что называется модулем числа а?
Сегодняшняя тема урока также связана с действием над числами разных знаков. Но она спряталась в анаграмме, в которой необходимо поменять местами буквы и получить знакомое слово. Попробуем разгадать.
ЕНОЖЕУМНИ
Записываем тему урока: «Умножение».
Цель нашего урока: познакомиться с умножением положительных и отрицательных чисел и сформулировать правила умножения чисел как с одинаковыми, так и с разными знаками.
Всё внимание на доску. Перед вами таблица с задачами, решив которые мы сформулируем правила умножения положительных и отрицательных чисел.
| Начальная температура | 0°С | 0°С | 0°С | 0°С |
| Изменение температуры за час | 2°С | –2°С | –2°С | 2°С |
| Время | 3ч | 3ч | –3ч | –3ч |
| Результат | 6°С | –6°С | 6°С | –6°С |
- 2*3 = 6°С;
- –2*3 = –6°С;
- –2*(–3) = 6°С;
- 2*(–3) = –6°С;
1. Температура воздуха повышается каждый час на 2°С. Сейчас термометр показывает 0°С (Приложение 2 – Градусник) (слайд 1 на компьютере). Какую температуру воздуха будет показывать термометр через 3 часа?
Температура воздуха повышается каждый час на 2°С. Сейчас термометр показывает 0°С (Приложение 2 – Градусник) (слайд 1 на компьютере). Какую температуру воздуха будет показывать термометр через 3 часа?
- Сколько получили? (6°С).
- Кто-то запишет решение на доске, а мы все в тетрадях.
- Давайте посмотрим на термометр, верный мы получили ответ? (слайд 2 на компьютере).
2. Температура воздуха понижается каждый час на 2°С. Сейчас термометр показывает 0°С (слайд 3 на компьютере). Какую температуру воздуха будет показывать термометр через 3 часа?
- Сколько получили? (–6°С).
- Запишем соответствующее решение на доске и в тетрадях. Аналогия с задачей 1.
- Сравним результат с показанием термометра. (слайд 4 на компьютере).

3. Температура воздуха понижается каждый час на 2°С. Сейчас термометр показывает 0°С (слайд 5 на компьютере). Какую температуру воздуха показывал термометр 3 часа назад?
- Сколько получили? (6°С).
- Запишем соответствующее решение на доске и в тетрадях. Аналогия с задачами 1 и 2.
- Сравним результат с показанием термометра. (слайд 6 на компьютере).
4. Температура воздуха повышается каждый час на 2°С. Сейчас термометр показывает 0°С (слайд 7 на компьютере). Какую температуру воздуха показывал термометр 3 часа назад?
- Сколько получили? (–6°С).
- Запишем соответствующее решение на доске и в тетрадях. Аналогия с задачами 1-3.
- Сравним результат с показанием термометра. (слайд 8 на компьютере).

Посмотрите на свои результаты. При умножении чисел с одинаковыми знаками (примеры 1 и 3) какой по знаку получили ответ? (положительный).
Хорошо. Но вот в примере 3 оба множителя отрицательные, а ответ получили положительный. Какое математическое понятие позволяет от отрицательных чисел переходить к положительным? (модуль).
Внимание правило: Чтобы умножить два числа с одинаковыми знаками, надо умножить их модули и поставить перед полученным результатом знак «плюс». (2 человека повторяют).
Вернёмся к примеру 3. Чему равны модули (–2) и (–3)? Перемножим эти модули. Сколько получили? С каким знаком?
Далее при вычислениях мы будем говорить проще: умножение «минуса» на «минус» даёт «плюс». (кто-то повторяет).Но, ребята, это не правило.
При умножении чисел с разными знаками (примеры 2 и 4) какой по знаку получили ответ? (отрицательный).
Сформулируйте сами правило умножения чисел с разными знаками.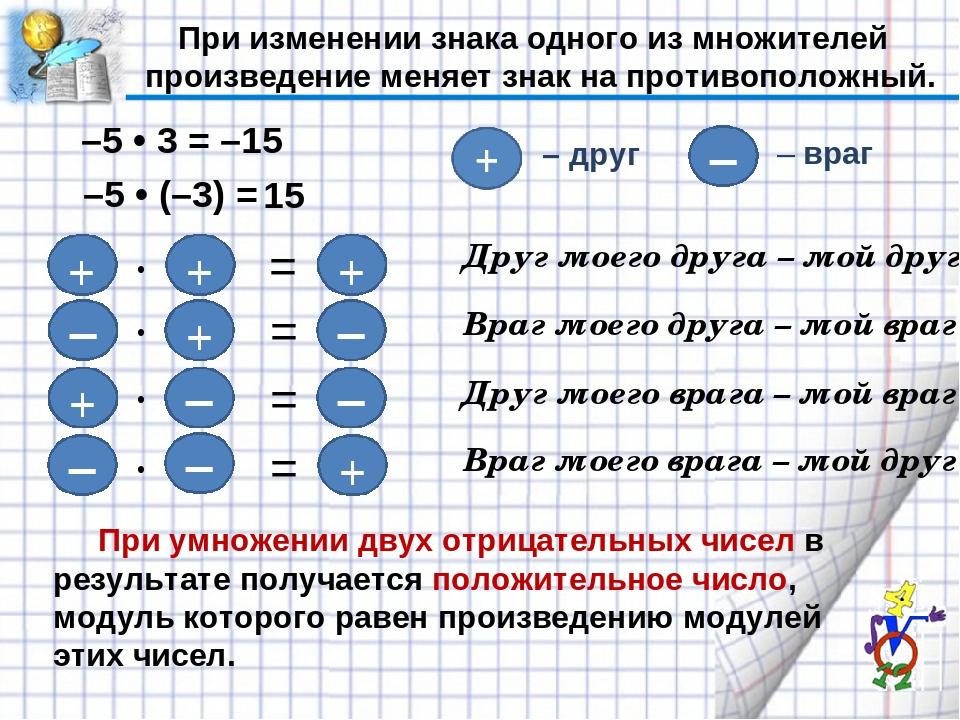
Правило: При умножении чисел с разными знаками, надо умножить их модули и поставить перед полученным результатом знак «минус». (2 человека повторяют).
Вернёмся к примерам №2 и №4. Чему равны модули их множителей? Перемножим эти модули. Сколько получили? Какой знак необходимо поставить в результате?
Далее при вычислениях мы будем говорить: умножение «минуса» на «плюс» даёт «минус», умножение «плюса» на «минус» даёт «минус». (кто-то повторяет).
С помощью этих двух правил можно умножать и дроби: десятичные, смешанные, обыкновенные.
Перед вами, на доске, несколько примеров. Три решим вместе со мной, а остальные самостоятельно. Обратите внимание на запись и оформление.
- = 96;
- = –21,2;
- = 14,7;
- = -6,5;
- = 66.
Молодцы. Откроем учебники и отметим правила, которые необходимо выучить к следующему уроку (страница 190, §7(пункт 35)). Знание этих правил поможет в дальнейшем быстро освоить деление положительных и отрицательных чисел.
Откроем учебники и отметим правила, которые необходимо выучить к следующему уроку (страница 190, §7(пункт 35)). Знание этих правил поможет в дальнейшем быстро освоить деление положительных и отрицательных чисел.
V. Математическая цепочка
А сейчас Незнайка хочет проверить, как вы усвоили новый материал, и задаст вам несколько вопросов. Решение и ответы обязательно записываем в тетрадях (Приложение 3 – Математическая цепочка).
Компьютерная презентация
Здравствуйте ребята. Я вижу вы очень умные и любознательные, поэтому хочу задать вам несколько вопросов. Будьте внимательны, особенно со знаками.
Первый мой вопрос: умножить (–3) на (–13).
Второй вопрос: умножить то, что получили в первом задании на (–0,1).
Третий вопрос: результат второго задания умножить на (–2).
Четвёртый вопрос: умножить (-1/3) на результат третьего задания.
И последний, пятый вопрос: вычислите температуру замерзания ртути, умножив результат четвертого задания на 15.
Спасибо за работу. Желаю успеха.
Ребята, давайте проверим, как мы справились с заданиями. Встали все.
Сколько получили в первом задании?
У кого другой ответ, сели, и кто сел, в карту учета знаний ставим себе за математическую цепочку 0 баллов. Остальные ничего не ставят.
Сколько получили во втором задании?
У кого другой ответ, сели, и ставим себе в карту учета знаний за математическую цепочку 1 балл.
Сколько получили в третьем задании?
У кого другой ответ, сели, и ставим себе в карту учета знаний за математическую цепочку 2 балла.
Сколько получили в четвертом задании?
У кого другой ответ, сели, и ставим себе в карту учета знаний за математическую цепочку 3 балла.
Сколько получили в пятом задании?
У кого другой ответ, сели, и ставим себе в карту учета знаний за математическую цепочку 4 балла. Оставшиеся ребята решили правильно все 5 заданий. Садитесь, вы ставите себе в карту учета знаний 5 баллов за математическую цепочку.
Оставшиеся ребята решили правильно все 5 заданий. Садитесь, вы ставите себе в карту учета знаний 5 баллов за математическую цепочку.
Чему же равна температура замерзания ртути? (–39°С).
VI. Домашнее задание
§7(пункт 35, страница 190), №1121– учебник: Математика. 6 класс: [Н.Я.Виленкин и др.]
Творческое задание: Составить задачу на умножение положительных и отрицательных чисел.
VII. Тест
Переходим к следующему этапу урока: выполнению теста (Приложение 4).
Вам необходимо решить задания и обвести кружком номер правильного ответа. За первые два верновыполненных задания вы получите по 1 баллу, за 3 задание – 2 балла, за 4 задание – 3 балла. Начали работу.
Δ –1 балл;
o –2 балла;
–3 балла.
А теперь номера правильных ответов запишем в таблицу под тестом. Проверим полученные результаты. У вас в пустых клеточках должно получиться число 1418 (записываю на доске). Кто получил его – ставит в карту учета знаний 7 баллов. Кто допустил ошибки, то в карту учета знаний ставит количество баллов, набранное только за верновыполненные задания.
У вас в пустых клеточках должно получиться число 1418 (записываю на доске). Кто получил его – ставит в карту учета знаний 7 баллов. Кто допустил ошибки, то в карту учета знаний ставит количество баллов, набранное только за верновыполненные задания.
Именно 1418 дней длилась Великая Отечественная война, победа в которой русскому народу досталась тяжелой ценой. И 9 мая 2010 года мы будем отмечать 65-летие Победы над фашистской Германией.
VIII. Итог урока
А теперь подсчитаем общее количество баллов, набранных вами за урок, и результаты занесем в карту учета знаний учащихся. После сдаем эти карты.
15 – 17 баллов – оценка «5»;
10 – 14 баллов – оценка «4»;
менее 10 баллов – оценка «3».
Поднимите руки, кто получил «5», «4», «3».
- Какую тему мы рассмотрели сегодня?
- Как умножить числа с одинаковыми знаками; с разными знаками?
Итак, наш урок подошел к концу. Я хочу сказать вам СПАСИБО за работу на уроке.
Я хочу сказать вам СПАСИБО за работу на уроке.
Сколько будет плюс на минус? — IronSet
Plan
- 1 Сколько будет плюс на минус?
- 2 Как вычитать положительные и отрицательные числа?
- 3 Как вычитать отрицательные дроби?
- 4 Как вычитать дроби с целым числом?
- 5 Можно ли разделить на минус?
- 6 Как умножать и делить положительные и отрицательные числа?
- 7 Что нужно сделать чтобы вычесть числа с разными знаками?
- 8 Что необходимо знать чтобы правильно выполнить сложение или вычитание чисел?
- 9 Как вычитать дроби с одинаковым числителем?
- 10 Как сложить или вычесть дроби с разными знаменателями?
- 11 Как решать Сложение смешанных дробей?
Сколько будет плюс на минус?
Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число. В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус.
Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус.
Когда минус на минус дает плюс?
Иначе говоря, чтобы умножение было осмысленным, «минус на плюс» должен давать «минус». Этих принципов достаточно, чтобы вывести правило для «минус на минус». Разумно устроить умножение на отрицательные числа так, что произведение любого числа и нуля дает ноль. Это и значит, что «минус на минус» дает «плюс».
Как вычитать положительные и отрицательные числа?
Как видим, чтобы вычесть из положительного числа отрицательное число, нужно просто сложить их модули. Таким образом, при вычитании отрицательного числа из отрицательного мы действуем по правилу сложения чисел с разными знаками, и у нас может получиться как положительное, так и отрицательное число.
Как считать числа с минусом?
Правило вычитания отрицательных чисел формулируется так: чтобы из числа a вычесть число b со знаком минус, необходимо к уменьшаемому a прибавить число −b , которое является противоположным вычитаемому b .
Как вычитать отрицательные дроби?
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел. Пример. Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Как Минусовать дроби?
Чтобы вычесть из одной обыкновенной дроби другую, следует:
- привести дроби к наименьшему общему знаменателю;
- из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменений;
- сократить полученную дробь.
Как вычитать дроби с целым числом?
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа. Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.
Как разделить дробь на отрицательное число?
Итак, правило деления чисел с разными знаками имеет следующую формулировку: чтобы разделить положительное число на отрицательное или отрицательное число на положительное, надо модуль делимого разделить на модуль делителя, и перед полученным числом поставить знак минус. Запишем это правило деления с помощью букв.
Запишем это правило деления с помощью букв.
Можно ли разделить на минус?
Правило знаков при делении Поэтому в конце результат получится со знаком «минус». Частное от деления нуля на число, отличное от нуля, равно нулю. Делить на ноль НЕЛЬЗЯ!
Как разделить отрицательное число на отрицательное?
Чтобы разделить отрицательное число на отрицательное (два отрицательных числа), надо разделить модуль делимого на модуль делителя. Пример 3. − 35 : − 7 = − 35 : − 7 = 5 .
Как умножать и делить положительные и отрицательные числа?
Умножение положительных и отрицательных чисел (то есть чисел с разными знаками) выполняется по следующему правилу: Чтобы перемножить два числа с разными знаками (положительное и отрицательное число), надо перемножить их модули и перед полученным произведением поставить знак «минус».
Что нужно сделать чтобы сложить два числа с разными знаками?
Вспомним, как складывают два числа с разными знаками. Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший и полученную разность взять со знаком того слагаемого, модуль которого больше.
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший и полученную разность взять со знаком того слагаемого, модуль которого больше.
Что нужно сделать чтобы вычесть числа с разными знаками?
Правило вычитания чисел с разными знаками дословно совпадает с правилом вычитания отрицательных чисел. Его формулировка такова: вычесть из числа a число b – это все равно, что к числу a прибавить число −b, где b и −b – противоположные числа.
Как вычитать числа с разными степенями?
Вычитание чисел с одинаковыми степенями Если степени одинаковые, а основания разные, то нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
Что необходимо знать чтобы правильно выполнить сложение или вычитание чисел?
Первым делом нужно сравнить числа между собой.
- Если уменьшаемое меньше вычитаемого, то результатом будет отрицательное число.
- Если уменьшаемое больше вычитаемого, то результат будет положительным.

- Если уменьшаемое равняется вычитаемому, то результатом будет число ноль. При вычитании нуля из числа, получится то же число.
Как вычесть две дроби с разными знаками?
Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби. Чтобы вычесть две дроби с одинаковым положительными знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Как вычитать дроби с одинаковым числителем?
Определение: Чтобы найти разность дробей с разными знаменателями нужно привести дроби к общему знаменателю, затем вычесть дроби так же, как дроби с одинаковыми знаменателями.
Как вычесть смешанные дроби с разными знаменателями?
Вычитание смешанных дробей производится по тому же принципу: целая часть вычитается из целой части, дробная вычитается из дробной. Результаты этих разностей складываются. В приведённом выражении вычитаем целые и дробные части. Разность целых чисел равна 3, разность дробных чисел равна тём седьмым.
Разность целых чисел равна 3, разность дробных чисел равна тём седьмым.
Как сложить или вычесть дроби с разными знаменателями?
Правило. Чтобы сложить или вычесть дроби с разными знаменателями, нужно их сначала привести к наименьшему общему знаменателю, а потом производить действия сложения или вычитания как с дробями с одинаковыми знаменателями.
Как сложить дроби с разными знаменателями 5 класс?
Чтобы сложить две дроби с разными знаменателями, их надо привести к общему знаменателю, а затем применить правило сложения дробей с общим знаменателем.
Как решать Сложение смешанных дробей?
Чтобы сложить смешанные числа, надо сложить отдельно их целые и их дробные части и полученные результаты сложить. Пример. Условились считать, что любое натуральное число имеет дробную часть, равную нулю, а любая правильная дробь имеет целую часть, равную нулю.
Как складывать и вычитать смешанные числа с разными знаменателями?
Чтобы сложить смешанные числа нужно.
- Отдельно сложить их целые части. Пример.
- Отдельно сложить дробные части.
- Сложить полученные результаты из пунктов 1 и 2.
- Если при сложении дробных частей получилась неправильная дробь, то нужно выделить целую часть из этой дроби и прибавить к полученной в пункте 1 целой части.
Мнимые числа реальны — Наутилус
Мнимые числа вовсе не мнимые. Правда в том, что они оказали гораздо большее влияние на нашу жизнь, чем что-либо воображаемое. Без воображаемых чисел и жизненно важной роли, которую они играли в обеспечении электричеством домов, фабрик и интернет-ферм, современный мир не существовал бы. Студенты, которые могут жаловаться своему учителю математики на то, что никому нет смысла учиться пользоваться мнимыми числами, должны будут отложить телефон, выключить музыку и выдернуть провода из своего широкополосного маршрутизатора. Но, пожалуй, нам следует начать с объяснения того, что такое мнимое число.
Теперь мы знаем, как возвести число в квадрат (умножить его само на себя), и мы знаем, что отрицательные числа при возведении в квадрат дают положительное число; минус, умноженный на минус, — это плюс, помните? Таким образом, (–2) × (–2) = 4. Мы также знаем, что извлечение квадратного корня является обратным действием возведения в квадрат. Таким образом, возможные квадратные корни из 4 равны 2 и -2. Мнимое число возникает из вопроса, каким будет квадратный корень из -4.
Мы также знаем, что извлечение квадратного корня является обратным действием возведения в квадрат. Таким образом, возможные квадратные корни из 4 равны 2 и -2. Мнимое число возникает из вопроса, каким будет квадратный корень из -4.
То, что мы здесь открываем, не является какой-то глубокой тайной Вселенной.
Неужели вопрос бессмысленный? Если возвести в квадрат число, положительное или отрицательное, ответ положительный. Таким образом, вы не сможете выполнить обратную операцию, если начнете с отрицательного числа. Именно так, казалось, думал Герон Александрийский. Герон был египетским архитектором, чьи математические трюки, написанные в Stereometrica , дали нам купол собора Святой Софии. В том же томе он показал, как вычислить объем усеченной квадратной пирамиды; то есть пирамида с отрубленной вершиной. Его решение для одного примера заключалось в том, чтобы вычесть 288 из 225 и найти квадратный корень из результата. Результат, однако, является отрицательным числом: -63. Таким образом, ответ будет найден через √–63.
Таким образом, ответ будет найден через √–63.
По какой-то причине — будь то ощущение, что была какая-то ошибка, или кто-то скопировал что-то неправильно, или потому что это было настолько абсурдно — рукописи, которые у нас есть, показывают, что Герон проигнорировал знак минус и вместо этого дал ответ как √63.
Квадратные корни отрицательных чисел — это то, что мы теперь называем мнимыми числами. Первым, кто предположил, что их не следует игнорировать, был итальянский астролог 16-го века Джером Кардано, который приступил к грандиозному проекту: книге, подробно излагающей все алгебраические знания того времени. Решая кубические уравнения, он остановился и уставился на проблему. Сначала он назвал их «невозможными случаями». В своей книге по алгебре 1545 г. Великое искусство , он привел пример попытки разделить 10 на два числа, которые умножаются вместе, чтобы получить 40. В процессе нахождения этих чисел вы сталкиваетесь с 5 + √–15.
Кардано не уклонился от этой неожиданной встречи. На самом деле, он даже записал несколько мыслей по этому поводу. Однако он писал на латыни, и переводчики спорят о том, что он имел в виду на самом деле. Для некоторых он называет это «ложной позицией». Для других это «фиктивное» число. Третьи говорят, что он характеризует ситуацию как «неразрешимую». Одно из его дальнейших замечаний о том, как действовать в такой ситуации, переводится как «отказ от душевных мук» и как «потеря воображаемых частей». В другом месте он называет это «арифметической тонкостью, конец которой… столь же утончен, сколь и бесполезен». Он говорит, что это «действительно сложно… невозможно выполнить другие операции, которые можно выполнить в случае чистого негатива». Под чистым отрицанием он подразумевает стандартное отрицательное число, что-то вроде -4. Он был доволен отрицательными числами и написал, что «√9равно +3 или -3, если плюс [умножить на плюс] или минус, умноженный на минус, дает плюс». И затем он продолжил: «√–9 — это не +3 и не —3, а нечто непонятное третьего рода».
На самом деле, он даже записал несколько мыслей по этому поводу. Однако он писал на латыни, и переводчики спорят о том, что он имел в виду на самом деле. Для некоторых он называет это «ложной позицией». Для других это «фиктивное» число. Третьи говорят, что он характеризует ситуацию как «неразрешимую». Одно из его дальнейших замечаний о том, как действовать в такой ситуации, переводится как «отказ от душевных мук» и как «потеря воображаемых частей». В другом месте он называет это «арифметической тонкостью, конец которой… столь же утончен, сколь и бесполезен». Он говорит, что это «действительно сложно… невозможно выполнить другие операции, которые можно выполнить в случае чистого негатива». Под чистым отрицанием он подразумевает стандартное отрицательное число, что-то вроде -4. Он был доволен отрицательными числами и написал, что «√9равно +3 или -3, если плюс [умножить на плюс] или минус, умноженный на минус, дает плюс». И затем он продолжил: «√–9 — это не +3 и не —3, а нечто непонятное третьего рода».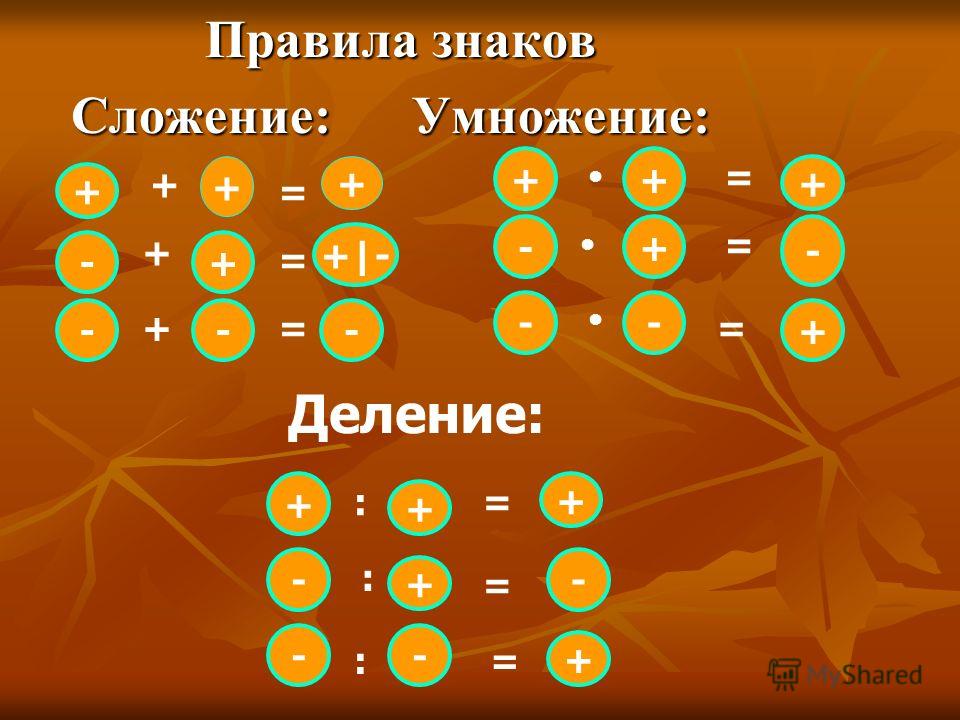 Кардано явно думал, что квадратные корни из отрицательных чисел были чем-то заумным и абстрактным, но в то же время он знал, что они были чем-то вроде и — чем-то, чем должен заниматься математик. Однако эта задача была не для него; ни в одном из последующих сочинений Кардано не упоминаются квадратные корни из отрицательных чисел. Он предоставил своему соотечественнику Рафаэлю Бомбелли обратиться к ним через пару десятилетий или около того.
Кардано явно думал, что квадратные корни из отрицательных чисел были чем-то заумным и абстрактным, но в то же время он знал, что они были чем-то вроде и — чем-то, чем должен заниматься математик. Однако эта задача была не для него; ни в одном из последующих сочинений Кардано не упоминаются квадратные корни из отрицательных чисел. Он предоставил своему соотечественнику Рафаэлю Бомбелли обратиться к ним через пару десятилетий или около того.
В том, что он назвал «дикой мыслью», Бомбелли предположил в 1572 году, что два члена в 5 + √–15 можно рассматривать как две отдельные вещи. «Кажется, все дело зиждется на софистике, а не на истине», — сказал он, но все же сделал это. И мы все еще делаем это сегодня, потому что это работает.
Полное математическое описание природы требует существования мнимых чисел.
Две отдельные вещи Бомбелли были тем, что мы теперь называем действительными числами и мнимыми числами. Их комбинация известна как «комплексное число» (оно сложное, как в «военно-промышленном комплексе», если говорить о комбинации — реальной и мнимой частей — а не о сложности). Но давайте проясним. Если и есть что-то, чему мы научились в наше время, пересматривая математику, так это тому, что все числа воображаемы. Это просто обозначения, которые помогают понять понятие «сколько». Поэтому применение названия «мнимые числа» к квадратным корням из отрицательных чисел является уничижительным и бесполезным.
Но давайте проясним. Если и есть что-то, чему мы научились в наше время, пересматривая математику, так это тому, что все числа воображаемы. Это просто обозначения, которые помогают понять понятие «сколько». Поэтому применение названия «мнимые числа» к квадратным корням из отрицательных чисел является уничижительным и бесполезным.
Тем не менее, мы должны признать различие. То, что математики называют «настоящими» числами, — это числа, с которыми вы лучше знакомы. «Двойка» в двух яблоках; 3,14… в пи; дробь. И точно так же, как положительные числа в некотором смысле дополняются отрицательными числами, то, что мы называем действительными числами, дополняется тем, что мы теперь называем мнимыми числами. Думайте о них как об инь и ян, или орел и решка. И уж точно не так, как на самом деле воображаемый.
Бомбелли в своей дикой мысли продемонстрировал, что это новое числовое племя может сыграть свою роль в реальном мире. Он решил решить кубическое уравнение, от которого отказался Кардано: x 3 = 15 x + 4. Решение Кардано требовало, чтобы он имел дело с выражением, содержащим квадратный корень из –121, и он просто не знал, что с ним делать. Бомбелли, с другой стороны, подумал, что может попробовать применить к квадратному корню обычные правила арифметики. Итак, сказал он, возможно, √–121 равно √121 × √–1, что дает 11 × √–1.
Решение Кардано требовало, чтобы он имел дело с выражением, содержащим квадратный корень из –121, и он просто не знал, что с ним делать. Бомбелли, с другой стороны, подумал, что может попробовать применить к квадратному корню обычные правила арифметики. Итак, сказал он, возможно, √–121 равно √121 × √–1, что дает 11 × √–1.
Великий прорыв Бомбелли состоял в том, что он увидел, что эти странные, кажущиеся невозможными числа подчиняются простым арифметическим правилам, когда они отделяются от других, более привычных типов чисел во время вычисления. Все после этого просто хватались за крапиву.
Продолжая кубическое уравнение Кардано, он в конце концов пришел к решению:
x = (2 + √–1) + (2 – √–1)
Разделите их на то, что мы теперь назвали бы их реальными и мнимых частей, и это упрощается до 2 плюс 2 и √–1 минус √–1. Мнимая часть исчезает, остается только 2 + 2. Таким образом, x = 4 является одним из решений x 3 = 15 x + 4. Подставьте его и проверьте сами.
Подставьте его и проверьте сами.
В наши дни принято использовать i для представления √–1. Первым к этому пришел швейцарский математик Леонард Эйлер. Легко предположить, что i означает мнимое, но на самом деле, как и в случае со своим e , Эйлер мог просто выбрать его наугад. Какова бы ни была причина, ход Эйлера закрепил i как мнимое число весьма бесполезным образом.
Чтобы лучше понять, что такое мнимое число, давайте представим себе стандартную числовую прямую, которая идет от –1 до 1 (вы можете думать о ней как о линейке, расположенной на столе перед вами, идущей от –1 слева до +1 справа). Мы называем процесс движения по строке сложением и вычитанием (у меня 0,3, и я добавлю еще 0,3, что приведет меня к 0,6). Но мы также можем представить себе выполнение некоторых ходов путем умножения. Если я начну с 1, как мне добраться до –1? Умножаю на -1. Итак, давайте представим умножение на –1 как половину оборота против часовой стрелки по окружности (в нашем случае окружность проходит через 1 и –1). На самом деле это поворот на 180 градусов. В предпочитаемых математиками единицах измерения углов 180 градусов составляют π радиан (360°, полный круг, равен 2π радианам).
На самом деле это поворот на 180 градусов. В предпочитаемых математиками единицах измерения углов 180 градусов составляют π радиан (360°, полный круг, равен 2π радианам).
Что произойдет, если мы сделаем только половину этого вращения? Это на полпути к умножению на –1, что можно представить как умножение на √–1. Этот поворот всего на π/2 радиана (или 90°) оставляет наше число в верхней части окружности, в стороне от стандартной числовой линии. Таким образом, мы можем думать о квадратном корне из –1 как о расположении на числовой прямой, которая проходит под прямым углом к знакомой нам числовой прямой. Это просто еще один набор чисел, на этот раз на линейке, которая совпадает с другой линейкой на отметке 9.0°, образуя крест, с +1 на самом дальнем от вас конце и –1 прямо перед вами.
Это приводит нас в интересное место. Связь с вращением по кругу означает, что и связаны с π и синусом и косинусом углов. Эта связь опосредована странным числом e , которое часто называют числом Эйлера.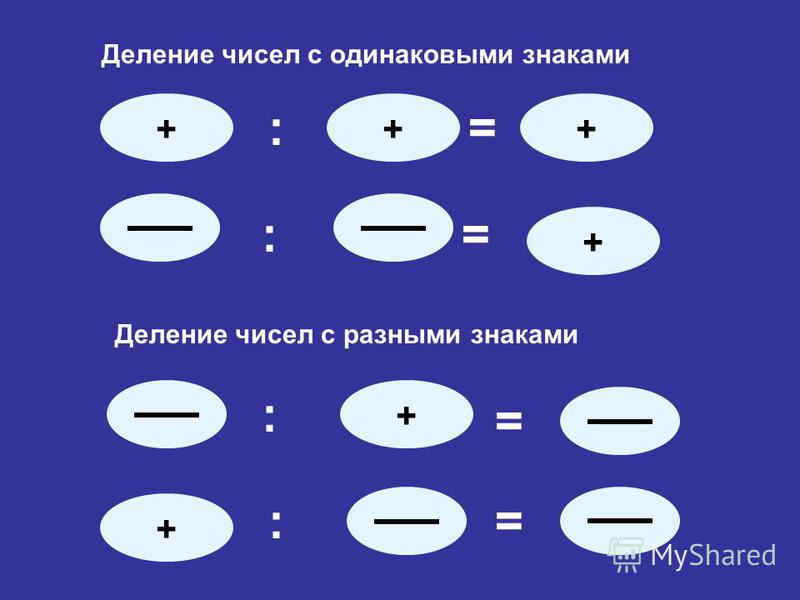 Это «иррациональное» число начинается с последовательности 2,71828… и продолжается вечно. Он широко распространен в математике и жизненно важен для статистики, математических вычислений, натуральных логарифмов и ряда арифметических вычислений. Эйлер точно определил, как это выглядит, взяв бесконечный ряд определенного типа (он называется рядом Тейлора) и выведя формулу Эйлера:0003
Это «иррациональное» число начинается с последовательности 2,71828… и продолжается вечно. Он широко распространен в математике и жизненно важен для статистики, математических вычислений, натуральных логарифмов и ряда арифметических вычислений. Эйлер точно определил, как это выглядит, взяв бесконечный ряд определенного типа (он называется рядом Тейлора) и выведя формулу Эйлера:0003
e ±iθ = cosθ ± i sinθ
Это показывает, что существует фундаментальная связь между основанием натурального логарифма и мнимым числом. Более того, вы можете свести это к соотношению, известному как тождество Эйлера:
e iπ + 1 = 0
Для некоторых это почти мистическая формула. Здесь у нас есть основание натуральных логарифмов e ; числа 0 и 1, которые являются уникальными случаями во всей числовой строке; мнимое число, особый случай; и π, которое, как мы знаем, является источником силы в математике. Несмотря на то, что они были обнаружены в разное время разными людьми, изучающими разные области математики, оказывается, что они взаимосвязаны, сосуществуя в этом элегантном простом уравнении.
Взглянув немного с другой точки зрения, возможно, мы не должны удивляться. Как и в случае с самим числом π, в этой формуле нет ничего мистического. Это происходит от того, что числа изменяются и трансформируются сами и друг в друга посредством вращения. Это происходит только из-за того, чем являются числа: представлением отношений между величинами. Мы не находим ничего мистического в перемещении по привычной «действительной» числовой прямой путем сложения и вычитания. И на самом деле нет ничего особенного в преобразованиях, происходящих посредством умножения и деления. Помните, что синусы и косинусы — это просто отношения — одно число, деленное на другое, — которые связаны с углами внутри треугольников, и вы можете представить эти углы как доли или кратные π в единицах, известных как радианы. Итак, то, что мы здесь обнаруживаем, — это не какая-то глубокая тайна Вселенной, а ясный и полезный набор взаимосвязей, которые являются следствием различных способов определения чисел.
На самом деле, эти отношения более чем полезны — их можно назвать жизненно важными. Возьмем, к примеру, их применение в науке: полное математическое описание природы, по-видимому, требует существования мнимых чисел. «Настоящих» чисел, о которых мы так много узнали, недостаточно. Их нужно комбинировать с мнимыми числами, чтобы получить «комплексные» числа, которые впервые создал Бомбелли. В результате, по словам математика Роджера Пенроуза, получается прекрасная полнота. «Комплексные числа, как и действительные, а может быть, и в большей степени, обнаруживают поистине замечательное единство с природой», — говорит он в своей книге 9.0011 Дорога к реальности . «Это как если бы сама Природа была так же впечатлена масштабом и последовательностью системы комплексных чисел, как и мы сами, и доверила этим числам точные операции своего мира в его мельчайших масштабах». Другими словами, необходимо было открыть мнимые числа, потому что они составляют существенную часть описания природы.
Возьмем, к примеру, их применение в науке: полное математическое описание природы, по-видимому, требует существования мнимых чисел. «Настоящих» чисел, о которых мы так много узнали, недостаточно. Их нужно комбинировать с мнимыми числами, чтобы получить «комплексные» числа, которые впервые создал Бомбелли. В результате, по словам математика Роджера Пенроуза, получается прекрасная полнота. «Комплексные числа, как и действительные, а может быть, и в большей степени, обнаруживают поистине замечательное единство с природой», — говорит он в своей книге 9.0011 Дорога к реальности . «Это как если бы сама Природа была так же впечатлена масштабом и последовательностью системы комплексных чисел, как и мы сами, и доверила этим числам точные операции своего мира в его мельчайших масштабах». Другими словами, необходимо было открыть мнимые числа, потому что они составляют существенную часть описания природы.
Майкл Брукс — научный писатель из Соединенного Королевства. Его последняя книга — « Искусство большего: как математика создала цивилизацию 9». 0011 .
0011 .
Отрывок из книги Майкла Брукса «Искусство большего: как математика создала цивилизацию ». Copyright © 2022 Майкл Брукс. Взято с разрешения Pantheon Books, подразделения Penguin Random House LLC. Все права защищены. Никакая часть этого отрывка не может быть воспроизведена или перепечатана без письменного разрешения издателя.
Главное изображение: agsandrew / Shutterstock
Получить информационный бюллетень Nautilus
Самые новые и самые популярные статьи доставляются прямо на ваш почтовый ящик!
По какому правилу вычитаются отрицательные числа?
Алгебра — раздел математики, занимающийся арифметическими операциями и связанными с ними символами. Символы называются переменными, которые могут принимать разные значения при различных ограничениях. Переменные в основном обозначаются как x, y, z, p или q, которыми можно манипулировать с помощью различных арифметических операций сложения, вычитания, умножения и деления для вычисления значений.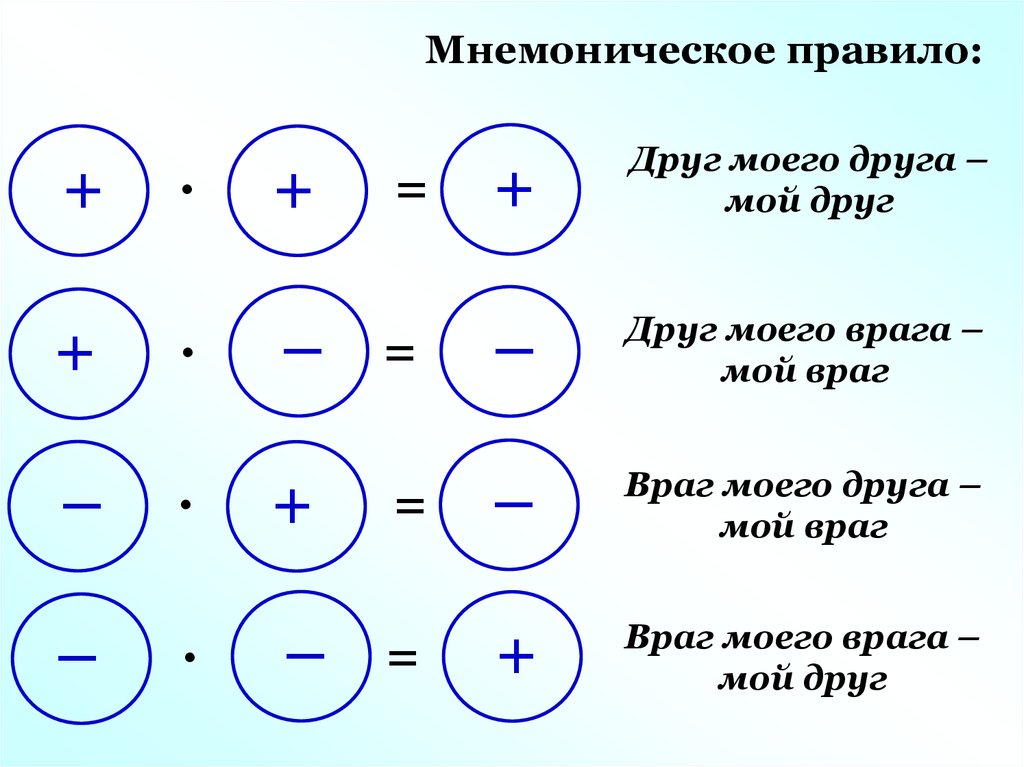
Отрицательные числа
Отрицательные числа обозначаются целыми числами, перед которыми стоит знак минус. Например, -4, -2 — отрицательные числа. Отрицательные числа лежат слева от числовой прямой, они отделены от положительных чисел 0. Можно сказать, что отрицательные числа являются дополнением положительных чисел. Отрицательные числа можно легко складывать или вычитать, используя оба отрицательных операнда. Давайте узнаем, как специально вычитать отрицательные числа с правильными случаями,
По какому правилу вычитаются отрицательные числа?
Решение:
Правило 1: Вычитание отрицательного числа из отрицательного числа (-) со знаком минус, за которым следует знак минус, превращает два знака в знак плюс.
Вычитание отрицательного числа из другого отрицательного числа — это просто сложение отрицательных и положительных чисел. Это потому, что по известному правилу – (-4) становится +4. Результирующая операция приобретает положительный характер.
Заключительная операция может носить положительный или отрицательный характер. Однако величина конечного вывода больше, чем оба операнда, если ни один из операндов не равен 0. В случае вычитания отрицательных чисел могут возникнуть следующие сценарии, когда мы вычитаем второй операнд из первого операнда:
- Второй операнд > первый операнд
Если величина второго операнда больше, чем величина первого операнда, окончательный результат имеет положительный знак, связанный с ним. Например, у нас есть, -2 – (-4). Это уравнение эквивалентно -2 + 4, что сводится к добавлению 4 к -2. На числовой прямой он начинается с -2.Затем продвигаемся вперед с 4 единицами: +4.
Ответ: -2 – (-4) = 2.
- Второй операнд < первого операнда
В случае, если величина второго операнда больше первого операнда, окончательный вывод имеет связанный с ним отрицательный знак. Например, у нас есть -4 – (-2).Это уравнение эквивалентно -4 + 2, что сводится к добавлению 2 к -4. На числовой прямой он начинается с -4. При добавлении 2 результат становится -2.
- Второй операнд = первый операнд
В случае, если величина второго операнда равна первому операнду, окончательный вывод равен 0. Например, у нас есть, -2 – (-2). Это уравнение эквивалентно -2 + 2, которое сводится к добавлению 2 к -2 и дает 0,
Примеры задач
Вопрос 1: Оцените -4 – (-10) – 2 – (-25).
Решение:
-4 – (-10) – 2 – (-25)
- Сначала откройте скобки.
= -4 + 10 – 2 + 25
- Сложите положительные и отрицательные целые числа отдельно.
= -4 – 2 + 10 + 25
= -6 + 35
= 29
Вопрос 2: Найдите решение для: (2 × 2) – (3 × 3) – (4 × 4)
Решение:
(2 × 2) – (3 × 3) – (4 × 4)
- Сначала разгадайте скобки.
= (4) – (9) – (16)
- Теперь раскроем скобки.
= 4 – 9 – 16
- Сложите положительные и отрицательные целые числа отдельно.
= 4 – 25
= -21
Вопрос 3: Вычтите (2x + 3y) 2 из (4x – 5y) 2 .
Решение:
(4x – 5 лет) 2 – (2x + 3 года) 2
- Раскройте скобки.
Использование алгебраической идентичности,
(x + y) 2 = x 2 + y 2 + 2xy
= (16x 2 + 25y 2 — 40xy) — (4x 2 25y 2 — 4036) + 9y 2 + 12xy)
- Теперь раскройте скобки
= 16x 2 + 25y 2 – 40xy – 9 0 – 3y – 4x 0036 – 12xy
- Now add or subtract the like terms
= 16x 2 – 4x 2 + 25y 2 – 9y 2 – 40xy – 12xy
= 12x 2 + 16y 2 — 52xy
Вопрос 4: Вычитание (6x — 8y) 2 из 2x 2 — 4y 2 — 12x
Решение:
9000 2 9000 2 9003 2 9003 2 9003 2 9003 29003 2 9003 2 9003 2 9003 2 9003 2 9003 2 9003 2 9003 2 9003 9003 2 9003 2 9003 2 9003 9003 2 9003 9003 2 9003 9003 9003 2 9003 9003 2 . – 12xy – (6x – 8y) 2
– 12xy – (6x – 8y) 2
- Решите скобку.
Using algebraic identity,
(x + y) 2 = x 2 + y 2 + 2xy
= 2x 2 – 4y 2 – 12xy – (36x 2 + 64y 2 – 96xy)
- Откройте кронштейн.
= 2x 2 – 4y 2 – 12xy – 36x 2 – 64y 2 + 96xy
- Сложите или вычтите подобные члены.
= 2x 2 – 36x 2 – 4y 2 – 64y 2 – 12xy + 96xy
= -34x 2 – 68y 2 + 84xy
plus, minus, times, divided на, проценты… – LearnAmo
Кто любит математику? Ах да… Это правда… Многие люди не любят математику… Однако на сегодняшнем уроке мы не будем учить вас математике (мы не умеем), а научим вас говорить о математике на итальянском языке! Это урок, о котором вы, возможно, никогда не задумывались, но он будет очень полезен в вашей повседневной жизни! Оставайтесь с нами! Оно того стоит!
youtube.com/embed/ej1P9BMl1uU?rel=0″ frameborder=»0″ allowfullscreen=»allowfullscreen»>
Первое, что вам нужно знать, это 4 основные операции: сложение, вычитание, умножение и деление.
Чтобы спросить кого-нибудь о результате вычисления, для любой из 4-х операций, мы используем выражение « Quanto fa…? » (Сколько стоит…?), а для ответа используем « Fa… » (Это…).
Например:
– Quanto fa 147 + 345? (Сколько будет 147+345?)
– Fa 492! (Это 492!)
Просмотрите номера на итальянском языке !
ДОБАВЛЕНИЕ по-итальянски
Сложение – это сумма, то есть мы прибавляем одну (или несколько) величин к другой.
Символ, который характеризует сложение, таков: + , что читается как « più » (плюс). Причем перед результатом мы обычно добавляем символ = , то есть читается « uguale » (равно).
Например:
12 + 5 = 17 равно « dodici più cinque uguale diciassette ”(двенадцать плюс пять равно семнадцати)
Результат сложения называется “ somma ” (сумма).
ВЫЧИТАНИЕ на итальянском языке
Вычитание означает получение количества (или большего количества) из другого.
Его символ: – , что читается как « мено » (минус).
Например:
120 – 34 = 86 равно « centoventi meno trentaquattro uguale ottantasei » (сто двадцать минус тридцать четыре равно восьмидесяти шести)
Результат вычитания называется « Differentenza » или « Resto » (разность).
САМОРОДОК СЕГОДНЯ:
«Parlare del più e del meno»: поболтать.
УМНОЖЕНИЕ по-итальянски
Умножение означает повторение количества (или более) столько раз, сколько указано другим.
Его символ: x , который не читается как «икс», как если бы это была буква алфавита, а в математике читается как «9».0133 на ” (раз).
Per esempio:
56 x 45 = 2520 равно « cinquantasei per quarantacinque uguale duemilacinquecentoventi » (пятьдесят шесть раз сорок пять, умножение равно двум тысячам пятистам двадцати)
prodotto ” (продукт).
ДЕЛЕНИЕ на итальянском языке
Деление означает делить количество столько раз, сколько указано другим.
Его символ: : , то есть читается как « diviso » (делится на). Иногда, однако, это также пишется с тире между двумя точками: ÷
Например:
36 : 3 = 12 это « trentasei diviso tre uguale dodici » (тридцать шесть разделить на три равняется двенадцати)
Если результат деления не имеет остатка (как в примере выше), он называется « quoto »; вместо этого он называется « quoziente », если у подразделения есть остаток.
Посетите наш интернет-магазин: Коллекция LearnAmo ! Вы найдете много интересных товаров на любой возраст и вкус! Чего ты ждешь? Выбери свой товар и расскажи друзьям!
ПРОЦЕНТ на итальянском
Теперь мы увидим еще один проблематичный аспект, исходящий из математики: % . Этот символ читается как « percento » (проценты).
Например:
25% это « venticinque percento » (двадцать пять процентов)
Однако, когда вам нужно добавить процентные данные к тексту или во время разговора, вам нужно добавить определенный артикль… и глагол в единственном числе! На самом деле, даже если процент относится к более чем одной вещи или человеку, мы думаем о нем как о целом (как это происходит со словами «gruppo», «gente», «classe» и т. д.), по этой причине глагол в единственном числе!
Например:
Il 50% dei candidati non ha superato il colloquio. (50% кандидатов не прошли собеседование)
РАЗМЕРЫ на итальянском языке
Предположим, вам нужно купить рамку для картины… Как вы сообщите размеры продавцу? В итальянском языке, когда мы говорим о высоте , длине и ширине , мы используем символ « x » ( на ), чтобы разделить их!
Например:
– Mi servirebbe una cornice da 18×7 см .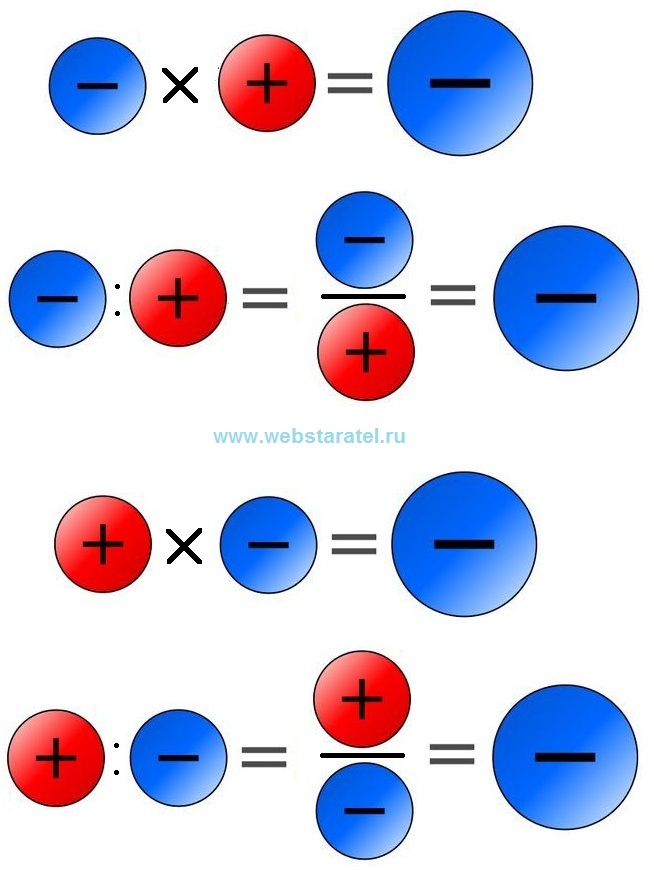 Се л’авете? (Хочу рамку 18×7 см. Есть?)
Се л’авете? (Хочу рамку 18×7 см. Есть?)
— Mi dispiace, ma ne abbiamo solo da 18×9 см . Le va bene lo stesso? (Извините, у нас только рамки 18х9 см. Вас это устраивает?)
А теперь, перед завершением нашего урока, мы решили сделать краткий конспект о…
Основные и самые проблемные узлы Мера по-итальянски!
1. В связи с этим следует писать «хилометр» или «километр» (километр)?
Аббревиатура KM , потому что CM — это сантиметры, но когда мы хотим написать его полностью, мы можем использовать либо « хилометро », то есть основная форма, или « км », что встречается реже!
То же самое относится к «хилограмм» и «килограмм» (килограмм), сокращение которых KG .
Рекомендуем всегда использовать версию с CH!
2. Вы, наверное, не знаете, особенно если вы не живете в Италии, что когда мы говорим об экранах телевизоров, смартфонов, компьютеров и т. д., мы используем pollici (дюймы)!
д., мы используем pollici (дюймы)!
Например:
Il nostro televisore è 20″ (20 опросов). (у нас 20-дюймовый телевизор)
3. Когда рядом с метрами или километрами вы найдете маленькую цифру 2, она читается как «quadrato» (квадрат) в единственном числе и «quadrati» (квадрат) в множественное число!
Например:
1 м² = 1 metro quadrato (один квадратный метр)
10 км² = 10 chilometri quadrati (десять квадратных километров)
Наконец, для обозначения размеров земли в сельском хозяйстве мы использовать ettaro (га)! Один гектар равен 10 000 м²!
Если есть другие сомнения по математике, напишите их в комментариях и мы ответим как можно скорее!
Знаете ли вы все способов сказать «ДОБРО ПОЖАЛОВАТЬ» по-итальянски?
[qsm quiz=149]
Отрицательный результат, часть 1 |
Минус, умноженный на минус, дает плюс. / Причину этого мы обсуждать не будем.
/ Причину этого мы обсуждать не будем.
— У. Х. Оден вспоминает популярный стих из школьных лет
Вы когда-нибудь пробовали смешивать два самых нелюбимых продукта? Я подозреваю, что нет. Никто не смешивает два вредных ингредиента и не ожидает, что результат будет вкусным. Так почему же числа должны вести себя иначе в числовом рецепте, называемом умножением? Какая мистическая алхимия «две ошибки превращают в правду» устраняет налет негатива и делает произведение двух отрицательных чисел положительным? Это просто не имеет смысла!
Первый алгебраист шестнадцатого века Джироламо Кардано сомневался в этой алхимии и забавлялся идеей определить произведение двух отрицательных чисел как отрицательное. За прошедшие века легионы школьников соблазнились пойти по этому пути. Но математическое сообщество упорно настаивает на том, что это неверный путь. Почему?
Закон знаков восходит по крайней мере к индийскому математику седьмого века Брахмагупте, который писал: «Произведение отрицательного и положительного отрицательно, двух отрицательных положительных и положительных положительных; произведение нуля и отрицательного, нуля и положительного или двух нулей равно нулю». К концу тринадцатого века, если не раньше, китайские математики тоже восприняли эти идеи без особой суеты. Но в то время как азиатские математики относились к публичным спариваниям чисел со знаком и к природе их мультипликативных потомков (как эндогамных, так и экзогамных), как ни в чем не бывало, европейцы, и особенно англичане, были встревожены. Они знали, что могут использовать отрицательные числа, чтобы получить правильные положительные ответы на задачи, но беспокоились, неужели это право сделать это? Отрицательные числа казались им глубоко неестественными, и даже сегодня англоязычные математики сохраняют термин «натуральные» за обычными счетными числами. Мне вспоминается беспокойное отношение ученых-магистов в начале замечательного романа Сюзанны Кларк «, Джонатан Стрэндж и мистер Норрелл, »: в Англии Кларка вопрос о том, работают ли заклинания, подчинен вопросу о том, можно ли их использовать. их без ущерба для своего аристократизма.
К концу тринадцатого века, если не раньше, китайские математики тоже восприняли эти идеи без особой суеты. Но в то время как азиатские математики относились к публичным спариваниям чисел со знаком и к природе их мультипликативных потомков (как эндогамных, так и экзогамных), как ни в чем не бывало, европейцы, и особенно англичане, были встревожены. Они знали, что могут использовать отрицательные числа, чтобы получить правильные положительные ответы на задачи, но беспокоились, неужели это право сделать это? Отрицательные числа казались им глубоко неестественными, и даже сегодня англоязычные математики сохраняют термин «натуральные» за обычными счетными числами. Мне вспоминается беспокойное отношение ученых-магистов в начале замечательного романа Сюзанны Кларк «, Джонатан Стрэндж и мистер Норрелл, »: в Англии Кларка вопрос о том, работают ли заклинания, подчинен вопросу о том, можно ли их использовать. их без ущерба для своего аристократизма.
В конце семнадцатого века, в нашей Англии (не в Англии Сюзанны Кларк), математик Джон Уоллис попытался рассеять дым вокруг отрицательных чисел: правильно понял. И хотя, что касается голой алгебраической нотации, она означает количество меньше, чем ничего: тем не менее, когда дело доходит до физического приложения, она обозначает как реальную величину, как если бы знак был +; но толковаться в противоположном смысле».
И хотя, что касается голой алгебраической нотации, она означает количество меньше, чем ничего: тем не менее, когда дело доходит до физического приложения, она обозначает как реальную величину, как если бы знак был +; но толковаться в противоположном смысле».
В соответствии со своей физической интерпретацией отрицательного количества Уоллис дал Европе числовую прямую. Это отличный инструмент для понимания сложения положительных и отрицательных чисел, но в некотором смысле он может способствовать неправильному пониманию умножения: поскольку законы естественного мира (за небольшими исключениями) двусторонне симметричны, и поскольку умножение является естественным, не должно умножение тоже симметрично? Одни числа идут вправо, а другие — влево; нет причин отдавать предпочтение правому перед левым, не так ли?
Моя главная цель в этом месяце (и в следующем месяце) — пролить свет на то, почему математики определяют умножение отрицательных чисел именно так, как они это делают, и обсудить девиантную альтернативу стандартному закону знаков.
Триггерное предупреждение: появится злой клоун. Также воздушные шары.
ЗАКЛАДЫВАЯ ОСНОВУ
Количество раз, когда я рассказывал учащимся подготовительных курсов об отрицательных числах, хотя это и не совсем отрицательное число само по себе, приближается к этому. Так что особого опыта у меня нет. Но мой опыт математика позволяет мне признать, что вопрос «Почему -1 умножить на -1 равно +1?» является глубоким. Такой глубокий вопрос заслуживает того, чтобы на него ответили более одного раза и более чем одним способом. Хорошая образовательная система заложит основу для ответа за годы до того, как вопрос будет задан.
В моем случае фундамент для понимания закона знаков был заложен дошкольным опытом, таким как просмотр «Семейки Аддамс» — в частности, эпизода, в котором у Гомеса случилась амнезия. В этом эпизоде используются два распространенных телевизионных образа 1960-х годов: амнезия личности и вера в то, что то же самое, что вызывает состояние (в данном случае удар по голове), лечит его. С медицинской точки зрения это ерунда; математически он воплощает идею о том, что во многих ситуациях выполнение операции дважды имеет тот же эффект, что и ее полное отсутствие. (Смотри, мама: я сказал вам, что шоу носило образовательный характер.)
С медицинской точки зрения это ерунда; математически он воплощает идею о том, что во многих ситуациях выполнение операции дважды имеет тот же эффект, что и ее полное отсутствие. (Смотри, мама: я сказал вам, что шоу носило образовательный характер.)
Мортиша Аддамс собирается либо вылечить амнезию Гомеса Аддамса, либо повторно вызвать ее.
Кроме того, в вестибюле многоквартирного дома моей бабушки на Манхэттене было два зеркала, образующих вогнутый угол в 90 градусов. Если я пройду мимо него, то увижу себя идущим в другую сторону, а если присмотрюсь, то увижу, что двойное зеркало — Джим разделил волосы слева так же, как и я (в отличие от однозеркального Джима, который пробор справа).
Позже, когда я начал получать пособие, соотношение между минус и больше прояснилось практическим пониманием того, что потратить меньше значит сэкономить больше . На том этапе я недостаточно знал алгебру, чтобы понять такое уравнение, как a − ( b − c ) = a − b + c , но на каком-то уровне я думаю, что у меня было проблески, которые спустя годы станут пониманием того, откуда взялся этот знак плюс.
В конце концов я узнал об отрицательных числах, которые были крутыми, но загадочными. В отличие от числа 2, которое имеет смысл во всех контекстах, где ожидаются числовые ответы, -2 иногда имеет смысл («Какая температура?»), а иногда нет («Сколько печенья вы хотите?»). Я уже не помню, как освоился с законом знаков. Я полагаю, что мне дали некоторые частичные объяснения, но поскольку лучшее обоснование закона исходит из алгебры, а поскольку я еще не знал алгебры, я полагаю, что сыграл свою роль прыжок веры с моей стороны. Мне помогли учителя, которым я доверял. Кроме того, хотя я был любознательным и легко раздражающимся ребенком, я не был настолько жестким, чтобы требовать понимания каждого шага во всех деталях, прежде чем переходить к следующему. Наконец, я нашел закон знаков забавным; Я хотел, чтобы это было правдой. Даже если это было похоже на волшебство, это была хорошая магия, и я хотел посмотреть, к чему это приведет.
Что должен сказать учитель, когда явно возникает вопрос, почему отрицательное умножение на отрицательное равно положительному? Наиболее удовлетворительным ответом была бы конкретная демонстрация, как это можно сделать с помощью таких формул, как 6 умножить на 1/2, равно 3. Обсуждая закон знаков, математик Дэвид Мамфорд пишет: «Одна из трудностей при аргументации этого правила заключается в том, что в мире не так много простых случаев величин, когда единицы двух множимых позволяют нам вывести правило умножения, используя нашу физическую интуицию о мире».
Обсуждая закон знаков, математик Дэвид Мамфорд пишет: «Одна из трудностей при аргументации этого правила заключается в том, что в мире не так много простых случаев величин, когда единицы двух множимых позволяют нам вывести правило умножения, используя нашу физическую интуицию о мире».
Их немного, но есть. Вот несколько физических примеров закона знаков.
МОДЕЛИ
Клоуны: Вы в цирке, держите два гелиевых шара, каждый из которых поднимает на 3 унции. Клоун вручает вам два цветка по 3 унции. На сколько увеличился ваш вес? Он дал вам 2 цветка, каждый из которых весит 3 унции, поэтому ваш вес увеличивается в 2 раза по 3 унции или 6 унций. Но теперь коварный клоун обнаруживает, что его кажущаяся щедрость была лишь предлогом для кражи, замаскированной под торговлю, и выхватывает у вас два воздушных шарика. На сколько увеличился ваш вес? Клоун дал вам -2 воздушных шарика, каждый из которых весит -3 унции, поэтому ваш вес увеличивается на -2 умножить на -3 унции, или на 6 унций.
Фильмы: Если вы воспроизведете видео с удвоенной скоростью, а затем сделаете из него видео и воспроизведете его с тройной скоростью, результатом будет ускорение в шесть раз. Таким образом, умножение — хороший способ описать ускорение видео (и звукозаписей, если на то пошло). Умножение на 1/2 означает замедление в 2 раза. Но что значит воспроизводить фильм с отрицательной скоростью? Ну, конечно, играть задом наперёд! (Этот ответ мог быть более интуитивным для тех, кто вырос, играя с фонографом во времена виниловых пластинок, когда можно было влиять на скорость воспроизведения, поворачивая диск вручную, по часовой стрелке или против часовой стрелки. Если на то пошло, некоторые кинетоскопы позволяли вы воспроизводите фильмы с целым диапазоном скоростей, как положительных, так и отрицательных.) Если вы возьмете фильм из фильма, воспроизводимого в обратном направлении, и воспроизведете его в обратном направлении, вы получите исходный фильм, воспроизводимый вперед.
Линзы: Если вы увеличите изображение в два раза, а результат в три раза, вы получите увеличение в шесть раз. Таким образом, умножение — хороший способ описать увеличение изображений. Умножение на 1/2 означает уменьшение в 2 раза. Но что значит увеличить изображение в отрицательную сторону? Здесь ответ менее очевиден, но законы оптики подсказывают, что при отрицательном увеличении получается перевернутое изображение, то есть такое, которое повернуто на угол 180 градусов. (Посмотрите в вогнутое зеркало и переместите голову так, чтобы она проходила с одной стороны фокальной точки на другую, и вы поймете, что я имею в виду.) Если вы перевернете перевернутое изображение, вы получите неперевернутое изображение.
Таким образом, умножение — хороший способ описать увеличение изображений. Умножение на 1/2 означает уменьшение в 2 раза. Но что значит увеличить изображение в отрицательную сторону? Здесь ответ менее очевиден, но законы оптики подсказывают, что при отрицательном увеличении получается перевернутое изображение, то есть такое, которое повернуто на угол 180 градусов. (Посмотрите в вогнутое зеркало и переместите голову так, чтобы она проходила с одной стороны фокальной точки на другую, и вы поймете, что я имею в виду.) Если вы перевернете перевернутое изображение, вы получите неперевернутое изображение.
Ливни: Это не так количественно, как другие, но, возможно, вам понравится. Реальная история: несколько недель назад, когда я начал писать это эссе, я принимал душ в квартире моих родителей и вдруг понял, что вода слишком горячая. Я открыл два крана в душе, не обращая внимания на то, какой кран какой и в какую сторону я их повернул (когда кран в душе закрыт, его можно повернуть только в одну сторону, так что можно делать это на автопилоте). Я хотел более прохладный душ, но я не знал, какую ручку повернуть или в какую сторону. Если бы я уменьшил поток горячей воды или увеличил поток холодной воды, все было бы в порядке; но если бы я уменьшил поток холодной воды или увеличил поток горячей воды, я бы обжегся. К счастью, я дважды угадал (или дважды ошибся). Жизнь полна таких ситуаций, если мы будем внимательны к ним.
Я хотел более прохладный душ, но я не знал, какую ручку повернуть или в какую сторону. Если бы я уменьшил поток горячей воды или увеличил поток холодной воды, все было бы в порядке; но если бы я уменьшил поток холодной воды или увеличил поток горячей воды, я бы обжегся. К счастью, я дважды угадал (или дважды ошибся). Жизнь полна таких ситуаций, если мы будем внимательны к ним.
ДРУГИЕ ОТВЕТЫ
Мои примеры клоунов, фильмов, линз и душ не удовлетворят всех. Некоторые учащиеся могут вообще не захотеть такого ответа; вместо этого они говорят: «Этот способ мышления вредит моему мозгу, поэтому не могли бы вы объяснить мне, почему он полезен?» Этим учащимся может понравиться то, как закон знаков в сочетании с составным распределительным законом ( a + b ) ( c + d ) = ac + ad + bc + bd, дает нам ярлыки для выполнения вычислений. Хотите возвести 999 в квадрат в своей голове? Думайте об этом как (1000 + (-1)) × (1000 + (-1)). Тогда мы можем представить его как 1000 × 1000, плюс 1000 × (−1), плюс (−1) × 1000, плюс (−1) × (−1), или 1 000 000 плюс −1000 плюс −1000 плюс 1, или 1 000 000 минус 1000 минус 1000 плюс 1 или 998 001. Это намного проще, чем делать это стандартным способом, умножая все эти 9 и складывая все эти 81. Это утилитарное обоснование закона знаков.
Тогда мы можем представить его как 1000 × 1000, плюс 1000 × (−1), плюс (−1) × 1000, плюс (−1) × (−1), или 1 000 000 плюс −1000 плюс −1000 плюс 1, или 1 000 000 минус 1000 минус 1000 плюс 1 или 998 001. Это намного проще, чем делать это стандартным способом, умножая все эти 9 и складывая все эти 81. Это утилитарное обоснование закона знаков.
Другие учащиеся могут быть более уверены, увидев, что согласно обычному закону знаков гобелен таблицы умножения очень упорядочен, а записи в каждой строке и столбце постоянно увеличиваются или уменьшаются. На рис. 1 показана неполная таблица обычной операции умножения × ; На рис. 2 показана соответствующая таблица для операции девиантного умножения, которую я обозначу как ❎. (На обоих рисунках слагаемые возрастают слева направо и сверху вниз, так что обычное умножение 0,1,2 на 0,1,2 появляется внизу справа.) Рядом с таблицей на рис. Мы указали величину увеличения в каждой строке при чтении слева направо и величину увеличения в каждом столбце при чтении сверху вниз.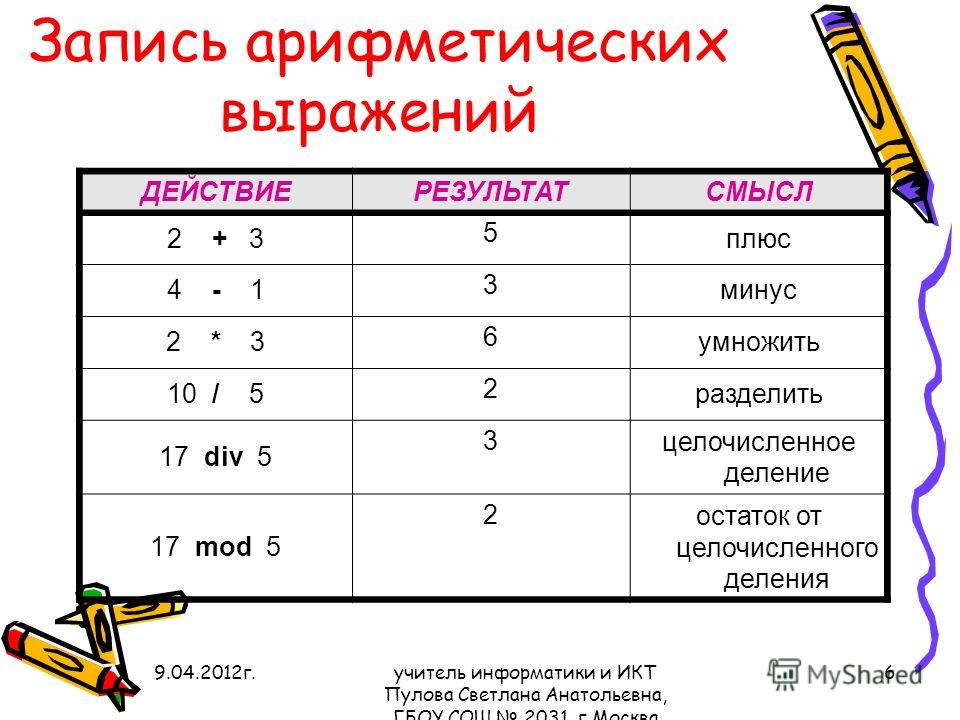 Я попытался сделать то же самое с рис. 2, но с некоторыми строками и столбцами это сделать не удалось, так как величина увеличения непостоянна. это эстетическое обоснование стандартного определения умножения.
Я попытался сделать то же самое с рис. 2, но с некоторыми строками и столбцами это сделать не удалось, так как величина увеличения непостоянна. это эстетическое обоснование стандартного определения умножения.
Рисунок 1. Обычное умножение.
Рис. 2. Девиантное умножение.
Одно из величайших удовольствий математики и одна из величайших загадок — это то, как эстетика и полезность толкают нас в одном направлении.
Вот еще одна мысль о педагогике: я подозреваю, что многие студенты оценят тот факт, что умножение на −1 — это та же операция, которую они уже освоили, а именно отрицание; услышать, как учитель говорит: «Вы уже знаете, как умножать на минус один, даже если вы не знали, что знаете это», скорее всего, вас обнадеживает. И если вы уже знакомы с формулой −(− a ) = a , тогда, объединив это с формулой (−1) × a = − a , вы, вероятно, согласитесь с тем, что (−1) × (−1) × a = (−1) × (− a ) = −(− a ) = a = 1 × a , что облегчает проглатывание −1 × −1 = 1 .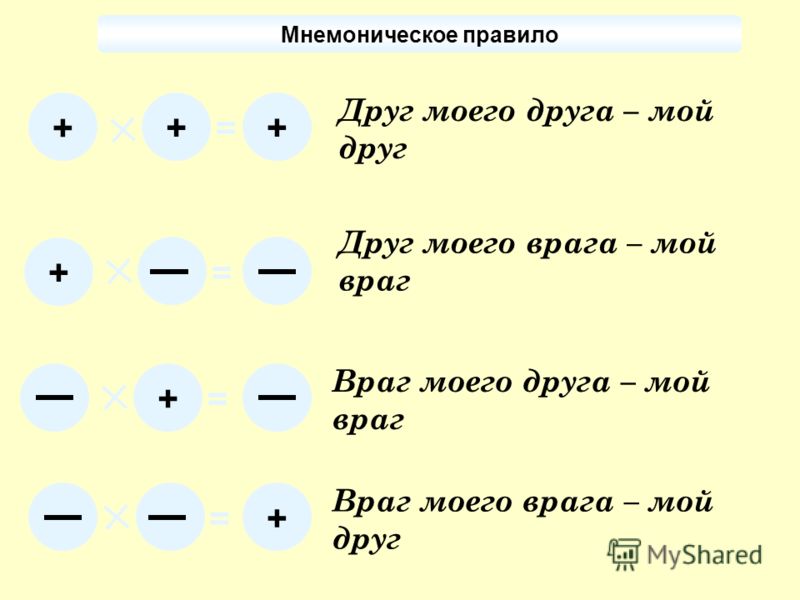
Что сработало для вас? А если вы учитель, что работает для ваших учеников?
Вот некоторые ресурсы, которые, по моему мнению, могут оказаться полезными:
- Веб-страница и видео, состоящее из двух частей, от главного учителя Джеймса Тантона
- Веб-страница mathisfun.com, посвященная умножению отрицаний
- Способ Майка Лоулера объяснить закон знаков своему сыну
- Лист с заданиями гуру математики Анри Пиччиотто «Два негатива»
У меня есть еще что сказать (включая ответ на вопрос «Почему закон знаков по-разному трактует право и лево?»), но это придется подождать до следующего месяца.
Спасибо Йоргу Арндту, Джону Баезу, Санди Губину, Тому Карзесу, Майку Лоулеру, Альберто Мартинесу, Дэвиду Мамфорду, Анри Пиччиотто, Майку Стаю, Джеймсу Тантону и Глену Уитни.
В следующем месяце (17 октября): отрицательный результат, часть 2.
КОНЕЧНЫЕ ПРИМЕЧАНИЯ
в связи с составным распределительным законом ( a + b )( c + d ) = ac + ad + bc + bd для определения a1 e2, 900−11 bd )(−1) = +1. Также можно мысленно возвести в квадрат 999 без использования множества девяток и без использования отрицательных чисел: просто используйте вариантный закон распределения ( a − b )( c − d ) = ac − ad − bc + bd . Действительно, как отмечает Мартин Гарднер в своем эссе «Отрицательные числа»: «Греческие математики знали, что (10−4)(8−2) равно (10×8)−(4×8)−(2×10)+( 2×4). Признать такое равенство — значит неявно принять то, что позже было названо законом знаков: произведение любых двух чисел с одинаковыми знаками положительно, а произведение любых двух чисел с разными знаками отрицательно. Просто греки предпочитали не звонить − n номер». Упомянутое мной видео Майка Лоулера показывает, как думать о ( a − b )( c − d ) = ac − ad − bc + bd геометрически и демонстрирует мощность площадной модели умножения.
Также можно мысленно возвести в квадрат 999 без использования множества девяток и без использования отрицательных чисел: просто используйте вариантный закон распределения ( a − b )( c − d ) = ac − ad − bc + bd . Действительно, как отмечает Мартин Гарднер в своем эссе «Отрицательные числа»: «Греческие математики знали, что (10−4)(8−2) равно (10×8)−(4×8)−(2×10)+( 2×4). Признать такое равенство — значит неявно принять то, что позже было названо законом знаков: произведение любых двух чисел с одинаковыми знаками положительно, а произведение любых двух чисел с разными знаками отрицательно. Просто греки предпочитали не звонить − n номер». Упомянутое мной видео Майка Лоулера показывает, как думать о ( a − b )( c − d ) = ac − ad − bc + bd геометрически и демонстрирует мощность площадной модели умножения.
#2: Отличным примером силы «негативного мышления» является классическая проблема, описанная Мартином Гарднером в его эссе «Обезьяна и кокосы». Оказывается (внимание, спойлер!), что один из способов решения проблемы — позволить переменной, представляющей неизвестное количество кокосов, принимать отрицательное значение, даже если это не имеет физического смысла. Этот трюк часто приписывают физику Полю Дираку, и заманчиво предположить, что он придумал его из-за той же предрасположенности к негативному мышлению, которая привела его к предсказанию существования античастиц, но Дирак сказал, что он перенял этот трюк от другого математика. , который сказал, что фокус у него не оригинальный, а там след стынет.
Оказывается (внимание, спойлер!), что один из способов решения проблемы — позволить переменной, представляющей неизвестное количество кокосов, принимать отрицательное значение, даже если это не имеет физического смысла. Этот трюк часто приписывают физику Полю Дираку, и заманчиво предположить, что он придумал его из-за той же предрасположенности к негативному мышлению, которая привела его к предсказанию существования античастиц, но Дирак сказал, что он перенял этот трюк от другого математика. , который сказал, что фокус у него не оригинальный, а там след стынет.
А откуда взялась сама проблема? Мы не знаем, но задачи такого рода обсуждал индийский математик IX века Махавира. Я не могу не задаться вопросом, знал ли Махавира (который, несомненно, читал Брахмагупту) о негативных решениях таких проблем и их полезности для поиска позитивных решений.
№ 3: Еще одним прекрасным примером головоломки об обычных числах, которую можно упростить, допустив появление на сцене отрицательных чисел, является задача о сумме лестниц, также известная как задача о трапециевидных числах, чьи педагогические достоинства были использованы Анри Пиччиотто, Джеймс Тантон и Пол Зейтц (и, возможно, другие учителя). См. описание Picciotto, указанное в Справочнике.
См. описание Picciotto, указанное в Справочнике.
ССЫЛКИ
Мартин Гарднер, «Обезьяна и кокосы» (глава 9 во «Второй научной американской книге математических головоломок и диверсий»). См. также онлайн-обсуждения проблемы Гэри Антоником и Эриком Вайсштейном.
Мартин Гарднер, «Отрицательные числа» (глава 11 книги «Плитки Пенроуза к шифрам с лазейками и возвращение доктора Матрицы»).
Дэвид Мамфорд, «Что такого непонятного в отрицательных числах?: Межкультурное сравнение».
Анри Пиччиотто, «Лестничные суммы» (урок 5.9 его «Алгебры»). См. также его версию для учителей.
Нравится:
Нравится Загрузка…
Добавить или вычесть время
Excel
Формулы и функции
Дополнительные функции
Дополнительные функции
Добавить или вычесть время
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019Excel 2016 Excel 2013 Excel 2010 Excel 2007 Больше. ..Меньше
..Меньше
Допустим, вам нужно сложить два разных значения времени, чтобы получить сумму. Или вам нужно вычесть одно значение времени из другого, чтобы получить общее время, затраченное на работу над проектом.
Как вы увидите в следующих разделах, Excel позволяет легко прибавлять или вычитать время.
Добавить время
Предположим, вы хотите узнать, сколько часов и минут потребуется для выполнения двух задач. Вы оцениваете, что первая задача займет 6 часов 45 минут, а вторая задача займет 9часов 30 минут.
Вот один из способов настроить это на рабочем листе.
Введите 6:45 в ячейку B2 и введите 9 :30 в ячейку B3 .
org/ListItem»>
В ячейке B4 введите =B2+B3 и нажмите клавишу ВВОД.
Результат 16:15 — 16 часов 15 минут — на выполнение двух задач.
Совет: Вы также можете суммировать время, используя функцию AutoSum для суммирования чисел. Выберите ячейку B4, а затем на вкладке Главная выберите Автосумма . Формула будет выглядеть так: =СУММ(B2:B3). Нажмите Enter, чтобы получить тот же результат, 16 часов и 15 минут.
Ну, это было достаточно просто, но есть дополнительный шаг, если ваши часы в сумме превышают 24. Вам нужно применить специальный формат к результату формулы.
Чтобы суммировать более 24 часов:
В ячейке B2 введите 12:45 , а в ячейке B3 введите 15:30 .
Введите =B2+B3 в ячейку B4 и нажмите клавишу ВВОД.
Результат 4:15, что не соответствует ожиданиям. Это связано с тем, что время задачи 2 указано в 24-часовом формате. 15:30 это то же самое, что и 3:30.
Чтобы отобразить время более 24 часов, выберите ячейку B4.
На вкладке Главная в группе Ячейки выберите Формат , а затем выберите Формат ячеек .
В поле Format Cells выберите Custom в Список категорий .
В поле Введите в верхней части списка форматов введите [h]:mm;@ , а затем выберите OK .
Обратите внимание на двоеточие после [ч] и точку с запятой после мм .
Результат 28 часов 15 минут. Формат будет в Введите список в следующий раз, когда он вам понадобится.
Вычесть время
Вот еще один пример: допустим, вы и ваши друзья знаете время начала и окончания волонтерского проекта и хотите знать, сколько времени вы потратили в целом.
Выполните следующие действия, чтобы получить прошедшее время, которое представляет собой разницу между двумя значениями времени.
В ячейке B2 введите время начала и включите « a » для AM или « p » для PM. Затем нажмите Enter.
В ячейке C2 введите время окончания, включая « a » или « p », в зависимости от ситуации, а затем нажмите Enter.

Введите другое время начала и окончания для ваших друзей, Джой и Лесли.
В ячейке D2 вычтите время окончания из времени начала, введя формулу =C2-B2 , а затем нажмите клавишу ВВОД.
В поле Формат ячеек щелкните Пользовательский в категории 9.Список 0917.
В списке Введите щелкните ч:мм (для часов и минут), а затем щелкните OK .

Теперь мы видим, что Ричард работал 3 часа 45 минут.
Чтобы получить результаты для Джой и Лесли, скопируйте формулу, выбрав ячейку D2 и перетащив ее в ячейку D4.
Форматирование в ячейке D2 копируется вместе с формулой.
Чтобы вычесть время, превышающее 24 часа:
Необходимо создать формулу для вычитания разницы между двумя значениями времени, которые в сумме превышают 24 часа.
Выполните следующие шаги:
- org/ListItem»>
В поле Формат ячеек щелкните Пользовательский в списке Категория .
В поле Введите вверху списка форматов введите м/д/гггг ч:мм AM/PM .
Обратите внимание на пустое место в конце гггг и в конце мм .
Новый формат будет доступен, когда он вам понадобится, в списке Type .
org/ListItem»>В ячейке B2 сделайте то же самое для конечной даты.
В ячейке B3 введите формулу =(B2-B1)*24 .
Ссылаясь на приведенный выше пример, выберите ячейку B1 и перетащите в ячейку B2, чтобы вы могли применить формат к обеим ячейкам одновременно.
В ячейке B1 введите дату начала, включая месяц/день/год и время, используя « a » или « p » для AM и PM.
Результат 31,5 часа.
Примечание. В Excel для Интернета можно складывать и вычитать более 24 часов, но нельзя применять пользовательский формат чисел.
Добавить время
Предположим, вы хотите узнать, сколько часов и минут потребуется для выполнения двух задач. Вы оцениваете, что первая задача займет 6 часов 45 минут, а вторая задача займет 9часов 30 минут.
Вы оцениваете, что первая задача займет 6 часов 45 минут, а вторая задача займет 9часов 30 минут.
В ячейке B2 введите 6:45 , а в ячейке B3 введите 9:30 .
Введите =B2+B3 в ячейку B4 и нажмите клавишу ВВОД.
На выполнение двух заданий уйдет 16 часов 15 минут.
Совет: Вы также можете суммировать время с помощью функции автосуммирования. Щелкните в ячейке B4. Затем нажмите Главная > Автосумма . Формула будет выглядеть так: =СУММ(B2:B3). Нажмите Enter, чтобы получить результат, 16 часов и 15 минут.
Нажмите Enter, чтобы получить результат, 16 часов и 15 минут.
Вычесть время
Допустим, вы и ваши друзья знаете время начала и окончания волонтерского проекта и хотите знать, сколько времени вы потратили. Другими словами, вам нужно прошедшее время или разница между двумя временами.
В ячейке B2 введите время начала, введите пробел, а затем введите « a » для AM или « p » для PM и нажмите Enter. В ячейке C2 введите время окончания, включая « a » или « p », в зависимости от ситуации, и нажмите Enter. Введите другое время начала и окончания для ваших друзей Джой и Лесли.
org/ListItem»>Чтобы получить результаты для Джой и Лесли, скопируйте формулу, щелкнув ячейку D2 и перетащив ее в ячейку D4. Форматирование в ячейке D2 копируется вместе с формулой.
В ячейке D2 вычтите время окончания из времени начала, введя формулу: =C2-B2 и нажав Enter. Теперь мы видим, что Ричард работал 3 часа 45 минут.
Исчисление I — Типы бесконечности
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 7-7: Типы Infinity
Большинство студентов сталкивались с бесконечностью в какой-то момент времени перед уроком математического анализа. Однако, когда они имели дело с этим, это был просто символ, используемый для представления очень, очень большого положительного или очень, очень большого отрицательного числа, и это было его пределом. Как только они попадают в класс исчисления, студентов просят выполнить базовую алгебру с бесконечностью, и здесь у них возникают проблемы. Бесконечность НЕ является числом и по большей части не ведет себя как число. Однако, несмотря на это, в этом разделе мы будем думать о бесконечности как о очень, очень, очень большом числе, которое настолько велико, что нет другого числа, большего, чем оно.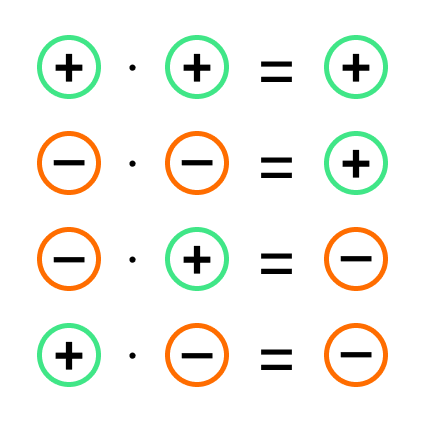 Это, конечно, неверно, но может помочь в обсуждении в этом разделе. Также обратите внимание, что все, что мы будем обсуждать в этом разделе, относится только к действительным числам. Например, если вы перейдете к комплексным числам, все может измениться и действительно изменится.
Это, конечно, неверно, но может помочь в обсуждении в этом разделе. Также обратите внимание, что все, что мы будем обсуждать в этом разделе, относится только к действительным числам. Например, если вы перейдете к комплексным числам, все может измениться и действительно изменится.
Итак, давайте начнем думать о сложении с бесконечностью. Когда вы добавляете два ненулевых числа, вы получаете новое число. Например, \(4 + 7 = 11\). С бесконечностью это не так. С бесконечностью у вас есть следующее.
\[\begin{align*}\infty + a & = \infty \hspace{0,25 дюйма}{\mbox{где }}a \ne — \infty \\ \infty + \infty & = \infty \end{align *}\]
Другими словами, очень-очень большое положительное число (\(\infty \)) плюс любое положительное число, независимо от размера, все равно будет очень-очень большим положительным числом. Точно так же вы можете добавить отрицательное число ( , т. е. \(a < 0\)) в очень, очень большое положительное число и останется очень, очень большим и положительным. Таким образом, сложением, включающим бесконечность, можно заниматься интуитивно, если вы будете осторожны. Также обратите внимание, что \(a\) НЕ должно быть отрицательной бесконечностью. Если это так, есть некоторые серьезные проблемы, с которыми нам нужно разобраться, как мы вскоре увидим.
Таким образом, сложением, включающим бесконечность, можно заниматься интуитивно, если вы будете осторожны. Также обратите внимание, что \(a\) НЕ должно быть отрицательной бесконечностью. Если это так, есть некоторые серьезные проблемы, с которыми нам нужно разобраться, как мы вскоре увидим.
Вычитание с отрицательной бесконечностью в большинстве случаев также может быть реализовано интуитивно. Очень, очень большое отрицательное число за вычетом любого положительного числа, независимо от его размера, все равно будет очень, очень большим отрицательным числом. Вычитание отрицательного числа ( т. е. \(a < 0\)) из действительно очень большого отрицательного числа все равно будет очень, очень большим отрицательным числом. Или
\[\begin{align*} — \infty — a & = — \infty \hspace{0.25in}{\mbox{где}}a \ne — \infty \\ — \infty — \infty & = — \infty \конец{выравнивание*}\]
Опять же, \(a\) не должно быть отрицательной бесконечностью, чтобы избежать некоторых потенциально серьезных трудностей.
С умножением также можно справиться довольно интуитивно. Очень, очень большое число (положительное или отрицательное), умноженное на любое число, независимо от размера, все равно будет очень, очень большим числом, нам просто нужно быть осторожным со знаками. В случае умножения имеем
\[\begin{array}{c}\left( a \right)\left( \infty \right) = \infty \hspace{0,25 дюйма}{\mbox{if}}a > 0\hspace{0,75 дюйма} \left( a \right)\left( \infty \right) = — \infty \hspace{0.25in}{\mbox{if}}a < 0\\ \\ \left( \infty \right)\left( \infty \right) = \infty \hspace{0.5in}\left( { - \infty } \right)\left( { - \infty } \right) = \infty \hspace{0.75in}\left( { - \infty } \right)\left( \infty \right) = - \infty \end{массив}\]
То, что вы знаете о произведениях положительных и отрицательных чисел, остается здесь верным.
С некоторыми формами деления можно работать и интуитивно. Действительно, очень большое число, деленное на не слишком большое число, все равно остается очень, очень большим числом.
\[\begin{align*}\frac{\infty}{a} & = \infty & \hspace{0,25in} & {\mbox{if}}a > 0,a \ne \infty & \hspace{0,75 in}\frac{\infty} {a} & = — \infty & \hspace{0,25in}{\mbox{if}}a < 0,a \ne - \infty \\ \frac{{ - \infty} }{a} & = - \infty & \hspace{0,25in} & {\mbox{ if }}a > 0,a \ne \infty & \hspace{0,75in}\frac{{ — \infty}}{ a} & = \infty & \hspace{0,25in}{\mbox{, если }}a < 0,a \ne - \infty \end{align*}\]
Деление числа на бесконечность несколько интуитивно понятно, но есть пара тонкостей, о которых нужно знать. Когда мы говорим о делении на бесконечность, мы на самом деле говорим об ограничивающем процессе, в котором знаменатель стремится к бесконечности. Таким образом, число, которое не слишком велико, деленное на все большее число, является все более малым числом. Другими словами, в нашем пределе
\[\frac{a}{\infty} = 0\hspace{0,5 дюйма}\hspace{0,5 дюйма}\hspace{0,25 дюйма}\frac{a}{{ — \infty}} = 0\]
Итак, мы рассмотрели почти все основные алгебраические операции с бесконечностью. Есть два случая, которые мы еще не рассмотрели. Это
Есть два случая, которые мы еще не рассмотрели. Это
\[\infty — \infty = {\mbox{?}}\hspace{0,5 дюйма}\hspace{0,5 дюйма}\frac{{ \pm \,\infty}}{{ \pm \,\infty}} = ?\]
Проблема этих двух случаев в том, что интуиция здесь не особо помогает. Очень, очень большое число минус очень, очень большое число может быть чем угодно (\( — \infty \), константой или \(\infty \)). Точно так же очень, очень большое число, деленное на очень, очень большое число, также может быть чем угодно (\( \pm \infty \) — это зависит от проблем со знаком, 0 или ненулевой константы).
Здесь мы должны помнить, что есть очень, очень большие числа и есть очень, очень, очень большие числа. Другими словами, одни бесконечности больше других бесконечностей. Со сложением, умножением и первым набором деления, с которым мы работали, это не было проблемой. Общий размер бесконечности просто не влияет на ответ в этих случаях. Однако в случаях вычитания и деления, перечисленных выше, это имеет значение, как мы увидим.
Вот один из способов понять идею о том, что одни бесконечности больше других. Это довольно сухой и технический способ думать об этом, и ваши задачи по исчислению, вероятно, никогда не будут использовать этот материал, но это хороший способ взглянуть на это. Кроме того, обратите внимание, что я не пытаюсь дать здесь точное доказательство чего-либо. Я просто пытаюсь дать вам небольшое представление о проблемах с бесконечностью и о том, как некоторые бесконечности можно считать большими, чем другие. Более подробное (и определенно более точное) обсуждение см. в 9.0003
http://www.math.vanderbilt.edu/~schectex/courses/infinity.pdf
Начнем с того, сколько существует целых чисел. Ясно, надеюсь, что их бесконечное множество, но давайте попробуем лучше понять «размер» этой бесконечности. Итак, выберите любые два целых числа совершенно случайным образом. Начните с меньшего из двух и перечислите в порядке возрастания все целые числа, которые следуют за ним. В конце концов мы достигнем большего из двух целых чисел, которые вы выбрали.
В зависимости от относительного размера двух целых чисел перечисление всех целых чисел между ними может занять очень, очень много времени, и в действительности это не имеет смысла. Но это можно было бы сделать, если бы мы захотели, и это важная часть.
Поскольку мы могли бы перечислить все эти целые числа между двумя случайно выбранными целыми числами, мы говорим, что целые числа счетно бесконечны . Опять же, нет никакой реальной причины делать это, это просто то, что можно сделать, если мы захотим это сделать.
В общем случае набор чисел называется счетно бесконечным, если мы можем найти способ перечислить их все. В более точной математической постановке это обычно делается с помощью функции особого типа, называемой биекцией, которая связывает каждое число в наборе ровно с одним из положительных целых чисел. Чтобы увидеть более подробную информацию об этом, см. PDF-файл, приведенный выше.
Можно также показать, что множество всех дробей также счетно бесконечно, хотя это немного сложнее показать, и это не является целью данного обсуждения. Чтобы увидеть доказательство этого, см. pdf, приведенный выше. У него есть очень хорошее доказательство этого факта.
Чтобы увидеть доказательство этого, см. pdf, приведенный выше. У него есть очень хорошее доказательство этого факта.
Давайте сравним это, попытавшись выяснить, сколько чисел содержится в интервале \( \left(0,1\right) \). Под числами я подразумеваю все возможные дроби, которые лежат между нулем и единицей, а также все возможные десятичные дроби (которые не являются дробями), которые лежат между нулем и единицей. Следующее похоже на доказательство, приведенное в pdf выше, но оно было достаточно хорошим и достаточно простым (надеюсь), поэтому я хотел включить его сюда.
Для начала предположим, что все числа в интервале \( \left(0,1\right) \) счетно бесконечны. Это означает, что должен быть способ перечислить их все. У нас может быть что-то вроде следующего:
. \[\begin{align*}{x_1} & = 0,692096 \cdots \\ {x_2} & = 0,171034 \cdots \\ {x_3} & = 0,993671 \cdots \\ {x_4} & = 0,045908 \cdots \\ \vdots \,\, & \hspace{0,6 дюйма} \vdots \end{align*}\]
Теперь выберите \(i\) -й десятичный из \({x_i}\), как показано ниже
\[\begin{align*}{x_1} & = 0. \underline 6 92096 \cdots \\ {x_2} & = 0.1\underline 7 1034 \cdots \\ {x_3} & = 0.99\underline 3 671 \cdots \ \ {x_4} & = 0.045\underline 9 08 \cdots \\ \vdots \,\, & \hspace{0.6in} \vdots \end{align*}\]
\underline 6 92096 \cdots \\ {x_2} & = 0.1\underline 7 1034 \cdots \\ {x_3} & = 0.99\underline 3 671 \cdots \ \ {x_4} & = 0.045\underline 9 08 \cdots \\ \vdots \,\, & \hspace{0.6in} \vdots \end{align*}\]
и сформируйте из этих цифр новый номер. Итак, для нашего примера у нас будет номер
. \[х = 0,6739\cdots\]
В этом новом десятичном числе замените все тройки на 1 и замените все остальные числа на 3. В нашем примере это даст новое число
\[\overline x = 0,3313 \cdots \]
Обратите внимание, что это число находится в интервале \( \left(0,1\right) \), а также обратите внимание, что, учитывая то, как мы выбираем цифры числа, это число не будет равно первому числу в нашем списке, \({x_1}\), потому что первая цифра каждого из них гарантированно не будет одинаковой. Точно так же это новое число не будет совпадать со вторым в нашем списке, \({x_2}\), потому что вторая цифра каждого из них гарантированно не будет одинаковой. Продолжая в том же духе, мы можем видеть, что это новое число, которое мы построили, \(\overline x \), гарантированно не будет в нашем списке. Но это противоречит первоначальному предположению, что мы можем перечислить все числа в интервале \( \left(0,1\right) \). Следовательно, не должно быть возможности перечислить все
числа в интервале \( \left(0,1\right) \).
Продолжая в том же духе, мы можем видеть, что это новое число, которое мы построили, \(\overline x \), гарантированно не будет в нашем списке. Но это противоречит первоначальному предположению, что мы можем перечислить все числа в интервале \( \left(0,1\right) \). Следовательно, не должно быть возможности перечислить все
числа в интервале \( \left(0,1\right) \).
Наборы чисел, такие как все числа в \( \left(0,1\right) \), которые мы не можем записать в список, называются несчетно бесконечными.
Причина перехода по следующему. Бесконечность, неисчислимо бесконечная, значительно больше, чем бесконечность, которая только счетно бесконечна. Итак, если мы возьмем разницу в две бесконечности, у нас будет пара возможностей.
\[\begin{align*}\infty \left( {{\mbox{uncountable}}} \right) — \infty \left( {{\mbox{countable}}} \right) & = \infty \\ & \\ \infty \left( {{\mbox{countable}}} \right) — \infty \left( {{\mbox{uncountable}}} \right) & = — \infty \end{align*}\]
Обратите внимание, что мы не записали разность двух бесконечностей одного типа.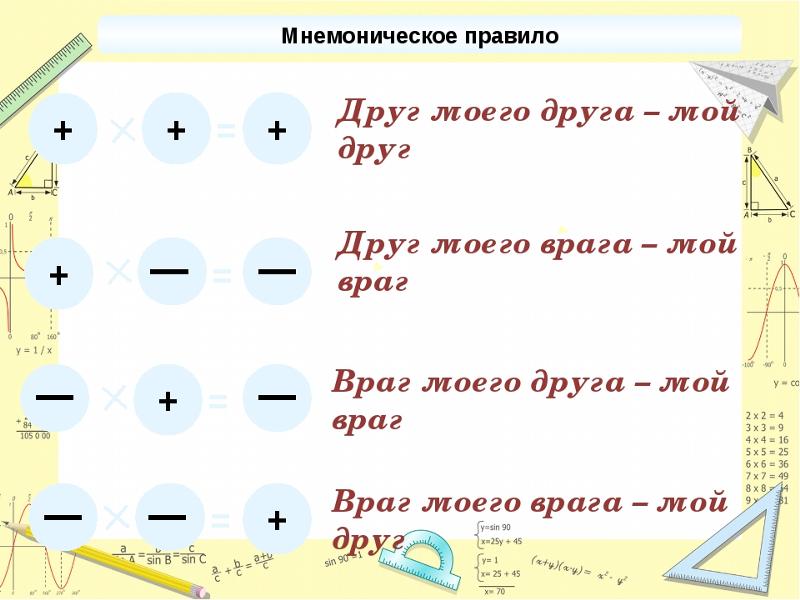







 Заключительная операция может носить положительный или отрицательный характер. Однако величина конечного вывода больше, чем оба операнда, если ни один из операндов не равен 0. В случае вычитания отрицательных чисел могут возникнуть следующие сценарии, когда мы вычитаем второй операнд из первого операнда:
Заключительная операция может носить положительный или отрицательный характер. Однако величина конечного вывода больше, чем оба операнда, если ни один из операндов не равен 0. В случае вычитания отрицательных чисел могут возникнуть следующие сценарии, когда мы вычитаем второй операнд из первого операнда:  Это уравнение эквивалентно -4 + 2, что сводится к добавлению 2 к -4. На числовой прямой он начинается с -4. При добавлении 2 результат становится -2.
Это уравнение эквивалентно -4 + 2, что сводится к добавлению 2 к -4. На числовой прямой он начинается с -4. При добавлении 2 результат становится -2.

