A 1 в квадрате: Таблица квадратов натуральных чисел.

alexxlab / / Разное

Содержание

Что значит 1 в квадрате. Быстрое возведение чисел в квадрат без калькулятора

Квадрат числа — это результат математической операции, которая возводит это число во вторую степень, то есть однократно умножает это число на само себя. Обозначать такую операцию принято так: Z2, где Z — наше число, 2 — степень «квадрат». О том, как вычислить квадрат числа, расскажет наша статья.

Вычисляем квадрат

Если число простое и маленькое, то сделать это просто или в уме, или воспользовавшись таблицей умножения, которая нам всем хорошо известна. Например:

42 = 4х4 = 16; 72 = 7х7 = 49; 92 = 9х9 = 81.

Если число большое или «громадное», то можно воспользоваться или таблицей квадратов, которую все учили в школе, или калькулятором. Например:

122 = 12х12 = 144; 172 = 17х17 = 289; 1392 = 139х139 = 19321.

Также для получения необходимого результата по двум вышеприведенным примерам, можно умножить эти числа в столбик.

Для того чтобы получить квадрат любой дроби, необходимо:

  1. Перевести дробь (если дробь имеет целую часть или же она десятичная) в неправильную дробь. {2}}+n+(n+1) \\\end{align}\]

    — аналогичная формула для чисел, больших на 1.

    Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!

    Формулы сокращенного умножения.

    Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

    Применение формул сокращенного умножения при решении примеров.

    Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

    Пусть а, b R. Тогда:

    1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

    (a + b) 2 = a 2 + 2ab + b 2

    2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

    (a — b) 2 = a 2 — 2ab + b 2

    3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

    a 2 — b 2 = (a -b) (a+b)

    4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

    (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

    5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

    (a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

    6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

    a 3 + b 3 = (a + b) (a 2 — ab + b 2)

    7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

    a 3 — b 3 = (a — b) (a 2 + ab + b 2)

    Применение формул сокращенного умножения при решении примеров.

    Пример 1.

    Вычислить

    а) Используя формулу квадрата суммы двух выражений, имеем

    (40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

    б) Используя формулу квадрата разности двух выражений, получим

    98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

    Пример 2.

    Вычислить

    Используя формулу разности квадратов двух выражений, получим

    Пример 3.

    Упростить выражение

    (х — у) 2 + (х + у) 2

    Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

    (х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

    Формулы сокращенного умножения в одной таблице:

    (a + b) 2 = a 2 + 2ab + b 2
    (a — b) 2 = a 2 — 2ab + b 2
    a 2 — b 2 = (a — b) (a+b)
    (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
    (a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
    a 3 + b 3 = (a + b) (a 2 — ab + b 2)
    a 3 — b 3 = (a — b) (a 2 + ab + b 2)

    Mathway | Популярные задачи

    1Множительx^2-4
    2Множитель4x^2+20x+16
    3Графикy=-x^2
    4Вычислить2+2
    5Множительx^2-25
    6Множительx^2+5x+6
    7Множительx^2-9
    8Множительx^3-8
    9Вычислитьквадратный корень из 12
    10Вычислитьквадратный корень из 20
    11Вычислитьквадратный корень из 50
    12Множительx^2-16
    13Вычислитьквадратный корень из 75
    14Множительx^2-1
    15Множительx^3+8
    16Вычислить-2^2
    17Вычислитьквадратный корень из (-3)^4
    18Вычислитьквадратный корень из 45
    19Вычислитьквадратный корень из 32
    20Вычислитьквадратный корень из 18
    21Множительx^4-16
    22Вычислитьквадратный корень из 48
    23Вычислитьквадратный корень из 72
    24Вычислитьквадратный корень из (-2)^4
    25Множительx^3-27
    26Вычислить-3^2
    27Множительx^4-1
    28Множительx^2+x-6
    29Множительx^3+27
    30Множительx^2-5x+6
    31Вычислитьквадратный корень из 24
    32Множительx^2-36
    33Множительx^2-4x+4
    34Вычислить-4^2
    35Множительx^2-x-6
    36Множительx^4-81
    37Множительx^3-64
    38Вычислить4^3
    39Множительx^3-1
    40Графикy=x^2
    41Вычислить2^3
    42Вычислить(-12+ квадратный корень из -18)/60
    43Множительx^2-6x+9
    44Множительx^2-64
    45Графикy=2x
    46Множительx^3+64
    47Вычислить(-8+ квадратный корень из -12)/40
    48Множительx^2-8x+16
    49Вычислить3^4
    50Вычислить-5^2
    51Множительx^2-49
    52Вычислить(-20+ квадратный корень из -75)/40
    53Множительx^2+6x+9
    54Множитель4x^2-25
    55Вычислитьквадратный корень из 28
    56Множительx^2-81
    57Вычислить2^5
    58Вычислить-8^2
    59Вычислить2^4
    60Множитель4x^2-9
    61Вычислить(-20+ квадратный корень из -50)/60
    62Вычислить(-8+ квадратный корень из -20)/24
    63Множительx^2+4x+4
    64Множительx^2-10x+25
    65Вычислитьквадратный корень из -16
    66Множительx^2-2x+1
    67Вычислить-7^2
    68Графикf(x)=2^x
    69Вычислить2^-2
    70Вычислитьквадратный корень из 27
    71Вычислитьквадратный корень из 80
    72Множительx^3+125
    73Вычислить-9^2
    74Множитель2x^2-5x-3
    75Вычислитьквадратный корень из 40
    76Множительx^2+2x+1
    77Множительx^2+8x+16
    78Графикy=3x
    79Множительx^2+10x+25
    80Вычислить3^3
    81Вычислить5^-2
    82Графикf(x)=x^2
    83Вычислитьквадратный корень из 54
    84Вычислить(-12+ квадратный корень из -45)/24
    85Множительx^2+x-2
    86Вычислить(-3)^3
    87Множительx^2-12x+36
    88Множительx^2+4
    89Вычислитьквадратный корень из (-8)^2
    90Множительx^2+7x+12
    91Вычислитьквадратный корень из -25
    92Множительx^2-x-20
    93Вычислить5^3
    94Множительx^2+8x+15
    95Множительx^2+7x+10
    96Множитель2x^2+5x-3
    97Вычислить квадратный кореньквадратный корень из 116
    98Множительx^2-x-12
    99Множительx^2-x-2
    100Вычислить2^2

    Таблица квадратов

    Таблица квадратов

    Определение Калькулятор — квадрат числа Таблица квадратов

    Скачать таблицу квадратов

    Определение. Квадрат числа — есть данное число, возведенное во вторую степень (число умноженное само на себя).

    a2 = a · a

    «Квадратом» оно называется, потому что такая операция аналогична вычислению площади квадрата.

    Калькулятор для вычисления квадрата числа

    2 = 49 ≈ 0.4444444444444444

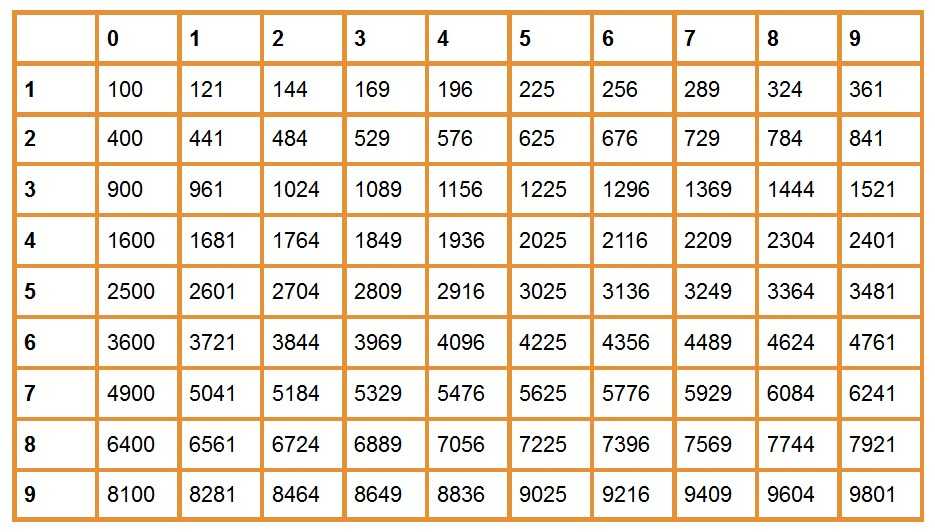
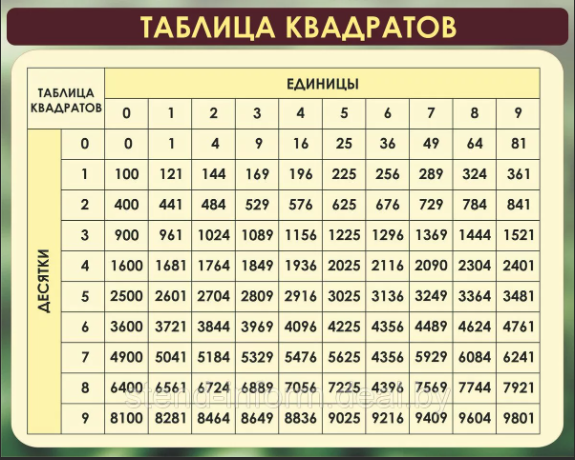
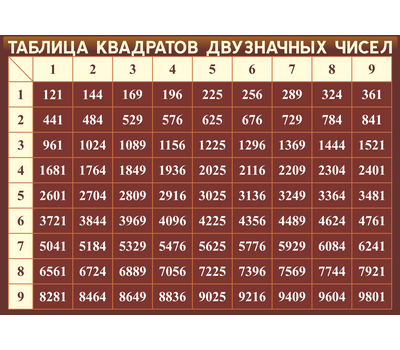
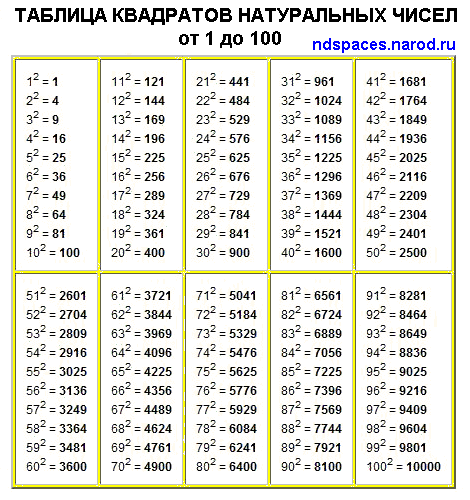
    Ниже приведены две удобные таблицы квадратов натуральных чисел от 1 до 100.


    Таблица квадратов чисел от 1 до 100

    12 = 1

    22 = 4

    32 = 9

    42 = 16

    52 = 25

    62 = 36

    72 = 49

    82 = 64

    92 = 81

    102 = 100

    112 = 121

    122 = 144

    132 = 169

    142 = 196

    152 = 225

    162 = 256

    172 = 289

    182 = 324

    192 = 361

    202 = 400

    212 = 441

    222 = 484

    232 = 529

    242 = 576

    252 = 625

    262 = 676

    272 = 729

    282 = 784

    292 = 841

    302 = 900

    312 = 961

    322 = 1024

    332 = 1089

    342 = 1156

    352 = 1225

    362 = 1296

    372 = 1369

    382 = 1444

    392 = 1521

    402 = 1600

    412 = 1681

    422 = 1764

    432 = 1849

    442 = 1936

    452 = 2025

    462 = 2116

    472 = 2209

    482 = 2304

    492 = 2401

    502 = 2500

    512 = 2601

    522 = 2704

    532 = 2809

    542 = 2916

    552 = 3025

    562 = 3136

    572 = 3249

    582 = 3364

    592 = 3481

    602 = 3600

    612 = 3721

    622 = 3844

    632 = 3969

    642 = 4096

    652 = 4225

    662 = 4356

    672 = 4489

    682 = 4624

    692 = 4761

    702 = 4900

    712 = 5041

    722 = 5184

    732 = 5329

    742 = 5476

    752 = 5625

    762 = 5776

    772 = 5929

    782 = 6084

    792 = 6241

    802 = 6400

    812 = 6561

    822 = 6724

    832 = 6889

    842 = 7056

    852 = 7225

    862 = 7396

    872 = 7569

    882 = 7744

    892 = 7921

    902 = 8100

    912 = 8281

    922 = 8464

    932 = 8649

    942 = 8836

    952 = 9025

    962 = 9216

    972 = 9409

    982 = 9604

    992 = 9801

    1002 = 10000

     Распечатать таблицу квадратов

    Таблица квадратов

    0123456789
    00149162536496481
    1100121144169196225256289324361
    2400441484529576625676729784841
    390096110241089115612251296136914441521
    41600168117641849193620252116220923042401
    52500260127042809291630253136324933643481
    63600372138443969409642254356448946244761
    74900504151845329547656255776592960846241
    86400656167246889705672257396756977447921
    98100828184648649883690259216940996049801

     Распечатать таблицу квадратов

    © 2011-2022 Довжик Михаил
    Копирование материалов запрещено.

    Добро пожаловать на OnlineMSchool.
    Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

    Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]

    Квадрат суммы двух выражений.

    Алгебра. 7 класс. Параграф 12. Тест 1.

    (a+b)²=a²+2ab+b². Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

    Вариант 1.

    1. Дописать равенство: (3a+2b)²=9a²+12ab+… .

    A) 4b²;   B)16b²;   C) 8b;   D) 2b².

    2. Раскрыть скобки: (2a+5)².

    A) 4a²+20a+10;      B) 4a²+10a+25;

    C) 4a²+20a+25;      D) 2a²+20a+25.

    3. Заменить звездочку (*) одночленом так, чтобы получилось верное равенство. (7x+1)²=(

    *)+14x+1.

    A) 7x²;   B) 49x²;   C) 14x²;   D) 14x.

    4. Представить в виде степени: 25x²+40xy+16y².

    A) (25x+4y)²;   B)(5x+4y)²;   C) (25x+16y)²;   D) (5x4y)².

    5. Свернуть трехчлен:

    6. Представить в виде суммы: (x+2y)²+(3x+y)².

    A) 10x²+25xy+5y²;    B) 10x²+10xy+10y²;

    C) 25x²+10xy+5y²;    D) 10x²+10xy+5y².

    7.  Представить в виде многочлена: (5a+3)² -(3a+1)².

    A) 16a+24a+8;       B) 16a²+24a+8;

    C) 16a²+24a+9;    

    D) 20a²+24a+8.

    8. Раскрыть скобки: (2x³+3y²)².

    A) 4x6+12x3y2+9y4;    B) 4x6+6x3y2+9y4;  

    C) 4x3+12x3y2+9y4;    D) 4x6+12x3y2+9y2.

    9. Представить в виде квадрата двучлена: 32x² -30y²+46xy+94y²+50xy+4x².

    A) (16x+18y)²;  B)(18x+32y)²;  C) (6x+4y)²;  D) (6x+8y)².

    10. Решить уравнение: (x+4)² = x(x-8).

    A) 4;    B) -4;    C) -1;    D) 1.

    11. Найти корень уравнения: (0,2x+1)² -x(0,04x+0,3)=0.

    A) -1;    B) 1;    C) 0,2;    D) -10.

    12. Сократить дробь:

    Вариант 2.

    1. Дописать равенство: (2a+3b)2=4a2+12ab+… .

    A) 3b2; B) 6b2; C) 9b2; D) 9b.

    2. Раскрыть скобки: (3a+5)2.

    A) 9a2+25;  B) 3a2+30a+5;  C) 9a2+15a+25;  D) 9a2+30a+25.

    3. Заменить звездочку (*) одночленом так, чтобы получилось верное равенство. (4x+1)2=(*)+8x+1.

    A) 16x2; B) 4x2; C) 16x; D) 4x.

    4. Представить в виде степени: 9x2+12xy+4y2.

    A) (2x+3y)2; B) (3x+2y)2; C) (9x+4y)2; D) (3x2y)2.

    5. Свернуть трехчлен:

    6. Представить в виде суммы: (2x+y)2+(x+3y)2.

    A) 5x2+10xy+10y2;  B) 4x2+10xy+25y2;

    C) 5x2+10xy+5y2; D) 10x2+10xy+10y2.

    7. Представить в виде многочлена: (4a+3)2-(2a+3)2.

    A)

    12a+18;  B) 12a2+12a+18;

    C) 12a2+24a+9;  D) 12a2+12a.

    8. Раскрыть скобки: (5x3+2y2)2.

    A) 5x6+20x3y2+2y4;  B) 25x6+10x3y2+4y4;  

    C) 25x6+20x3y2+4y4; D) 25x6+40x3y2+4y2.

    9. Представить в виде квадрата двучлена: 42xy-30y2+16x2+48xy+55y2+65x2.

    A) (6x+5y)2; B) (9x+5y)2; C) (9x+7y)2; D)  (9x+4y)2.

    10. Решить уравнение: (2x+1)2 = x(4x-1).

    A) -0,1; B) -0,2; C) -0,3; D) -0,5.

    11. Найти корень уравнения: (0,3x+2)2-x(0,09x+0,2)=0.

    A) -4; B)-3; C) -2; D) -1.

    12. Сократить дробь:

    Сверить ответы.

    Поделиться новостью в соцсетях