Натуральные и целые числа действительные числа: Числа: натуральные, целые, рациональные, иррациональные, действительные

Содержание

Какие числа называются Рациональными? Примеры и Определение

Определение рациональных чисел

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.

Рациональные числа — это те, которые можно представить в виде

где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

десятичная дробь 1,15 — это 115/100;
десятичная дробь 0,5 — это 1/2;
целое число 0 — это 0/1;
целое число 6 — это 6/1;
целое число 1 — это 1/1;
бесконечная периодическая дробь 0,33333. .. — это 1/3;
смешанное число — это 25/10;

отрицательная десятичная дробь -3,16 — это -316/100.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Свойства рациональных чисел

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Основные свойства действий с рациональными числами

Переместительное свойство сложения: a + b = b + a.
Сочетательное свойство сложения: (a + b) +c = a + (b + c).
Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a.
У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0.
Переместительное свойство умножения: ab = ba.
Сочетательное свойство умножения: (a * b) * c = a * (b * c).
Произведение рационального числа и едины не изменяет это число: a * 1 = a.
У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1.
Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.

Кроме основных перечисленных есть еще ряд свойств:

Правило умножения рациональных чисел с разными знаками: (-a) * b = -ab. Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».

Правило умножения отрицательных рациональных чисел: (−a) * (−b) = ab. Запомнить поможет фраза: «минус на минус есть плюс».

Правило умножении произвольного рационального числа на нуль: a * 0 = 0 или 0 * a = 0. Докажем это свойство.
Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).

Распределительный закон позволяет переписать выражение:
a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d + (-ad).
Так получилась сумма двух противоположных чисел, которая в результате дает нуль, что доказывает равенство a * 0 = 0.

Мы перечислили только свойства сложения и умножения. На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a — b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Определение иррационального числа

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби

Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры:

π = 3,1415926. ..
√2 = 1,41421356…
e = 2,71828182…
√8 = 2.828427…
-√11= -3.31662…

Обозначение множества иррациональных чисел: латинская буква I.

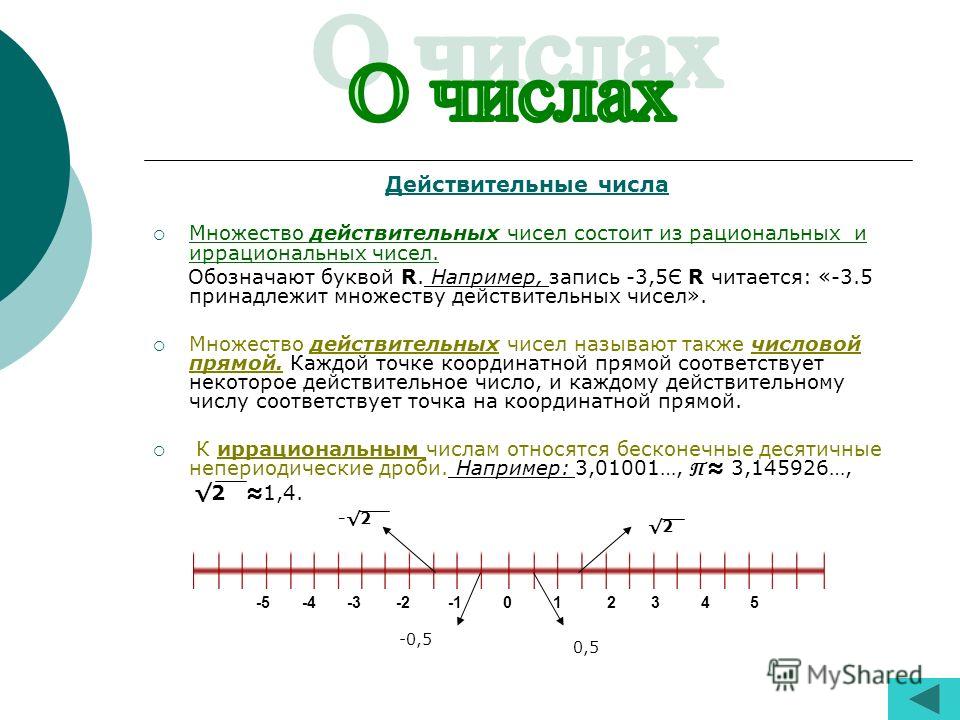
Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Свойства иррациональных чисел:

результат суммы иррационального числа и рационального равен иррациональному числу;
результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;

результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Различие между целыми, натуральными и рациональными числами

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.

А вот, что точно не является натуральным числом:

Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.
Отрицательные числа: -1, -2, -3, -4.
Дроби: 1/2, 3/4, 5/6.

Целые числа — это натуральные числа, противоположные им и нуль.

Если два числа отличаются друг от друга знаком — их называют противоположными: +2 и -2, +7 и -7. Знак «плюс» обычно не пишут, и если перед числом нет никакого знака, значит оно положительное. Числа, перед которыми стоит знак «минус», называют отрицательными.

Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.

Рациональные числа — это конечные дроби и бесконечные периодические дроби.

Например:

Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.

Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.

Что такое целое число? Примеры

Определение целых чисел

Что такое целое число — это натуральное число, а также противоположное ему число и нуль. Примеры целых чисел: -7, 222, 0, 569321, -12345 и др.

Что важно знать о целых числах:

Сумма, разность и произведение целых чисел в результате дают целые числа.
Не существует самого большого и самого маленького целого числа. Этот ряд бесконечен. Наибольшего и наименьшего целых чисел — не бывает.
Обыкновенные и десятичные дроби нельзя назвать целыми числами. Но иногда в задачах можно встретить целые числа, у которых дробная часть равна нулю и при этом нет долей.

Целые числа на числовой оси выглядят так:

На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.

В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.

Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.

Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.

Выглядит эти ребята вот так:

Последовательность целых чисел можно записать так:

∞ + . .. -4, -3, -2, -1, 0, 1, 2, 3, 4 … + ∞

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Практикующий детский психолог Екатерина Мурашова

Свойства целых чисел

Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:

Свойство	Сложение	Умножение
Замкнутость	a + b — целое	a × b — целое
Ассоциативность	a + (b + c) = (a + b) + c	a * (b * c) = (a * b) * c
Коммутативность	a + b = b + a	a * b = b * a
Существование нейтрального элемента	a + 0 = a	a * 1 = a
Существование противоположного элемента	a + (−a) = 0	a ≠ ±1 ⇒ 1/a не является целым
Дистрибутивность умножения относительно сложения	a * (b + c) = (a * b) + (a * c)

Пару слов о делении. В стандартном виде невозможно разделить число на множестве целых чисел, но можно делить с остатком. Это правило можно сформулировать так:

Для всяких целых a и b (b ≠ 0), есть один набор целых чисел q и r. При этом:

a = bq + r, где a — делимое, b — делитель, q — частное, r — остаток,

0 ≤ r < |b|, где |b| — абсолютная величина (модуль) числа b.

Положительные и отрицательные целые числа

Ряд целых чисел состоит из положительных и отрицательных чисел. Справа от нуля живут натуральные числа — их еще называют целыми положительными числами. А слева от нуля — целые отрицательные числа.

Отрицательные целые числа — это целые числа со знаком «минус». Они всегда меньше нуля. Примеры целых отрицательных чисел: -944, -1287, -1, -19.

Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 13, 401, 55, 29, 12345.

Бесконечное множество — это ряд целых чисел в положительную и в отрицательную сторону.

Если выбрать два любых целых числа, то те числа, которые находятся между заданными, можно называть конечным множеством.

Например, напишем целые числа от -4 до 3. Все числа, стоящие между этими числами, входят в конечное множество. Данное конечное множество чисел выглядит так:

-3, -2, -1, 0, 1, 2

Пример 1. Сколько целых чисел расположено между числами -30 и 100?

Как рассуждаем:

Можно построить прямую и посчитать сколько отрезков находится между заданными числам.

Или можно посчитать в уме: у нас есть 29 отрицательных числа, нуль и 99 положительных чисел.

29 + 1 + 99 = 129

Ответ: 129.

Пример 2. Сколько нечетных целых чисел расположено между числами -4 и 5?

Как рассуждаем:

Выпишем все целые числа, которые находятся между -4 и 5:
-3, -2, -1, 0, 1, 2, 3, 4

Подчеркнем нечетные числа в данному ряду.

Ответ: -3, -1, 1, 3.

Учёба без слёз (бесплатный гайд для родителей)

Неположительные и неотрицательные целые числа

Неотрицательные целые числа — это положительные целые числа и число нуль. Примеры неотрицательных целых чисел: 43, 878, 0.

Неположительные целые числа — это отрицательные целые числа и число нуль. Примеры неположительных целых чисел: -43, -878, 0.

Нуль — это граница между положительными и отрицательными числами. То есть нуль это ни положительное и ни отрицательное число.

Эти два термина помогают формулировать мысли кратко. Например, вместо того, чтобы говорить, что число a — целое число, которое меньше или равно нулю, можно сказать: a — целое неположительное число.

Целые числа в описании изменения величины

Какие числа называют целыми мы уже знаем. Их удобно использовать, чтобы считать предметы или чтобы сказать, что чего-то стало больше или меньше. А теперь примерчик!

Вы участвуете в конкурсе в инстаграм: нужно написать 5 постов про свои самые заветные мечты. А пока вы это не сделали, можно сказать, что сейчас у вас -5 постов. То есть число 5 описывает сколько вы должны сделать постов, а знак «минус» говорит о том, что вы все еще не выполнили условия конкурса. Постов то нет🙄

А если помимо 5 постов, нужно опубликовать еще 5 сторис — общий долг можно вычислить по правилу сложения отрицательных чисел:

-5 (постов, которых еще нет) + (-5 сториз, которых тоже еще нет) = -10 публикаций

Итого: чтобы участвовать в конкурсе, нужно сделать 10 публикаций в инстаграм.

1-4. Натуральные и целые числа

Натуральные и целые числа. Принцип математической индукции. Пример.

Натуральные числа – числа, возникающие естественным путем.

Перечисление (первый, второй, третий. )
Количество (Один, два, три)

Свойства натуральных чисел:

Свойства сложения:

X+(Y+Z)=(X+Y)+Z — ассоциативность

X+Y=Y+X – коммутативность

Свойства умножения

X(YZ)=(XY)Z- ассоциативность

XY=YX– коммутативность

1X=X

X(Y+Z)=XY+XZ – дистрибутивность

Неарифметические свойства связаны с порядком следования.

Для любого натурального Х существует единственное натуральное число Sx=X+1 следующего за числом X.

Sx ≠1 для всех Х

Отношение порядка натуральных чисел а<b, если существует такое натурально n, что b=a+n->x<Sx<S(Sx)

Если x₁,x₂— различные категории числа, то рассмотрев только те , которые меньше x₁ ивыбрав из них минимальные, получим минимальные из x₁ x₂

Целые числа

Множество целых чисел это Z={-2,-1,0,1,2} определены как замкнутые множества натуральных чисел N относительно арифметических операций сложения и вычитания.

Свойства целых чисел

Свойства сложения:

X+(Y+Z)=(X+Y)+Z — ассоциативность

X+Y=Y+X – коммутативность

Существует единственное число 0, такое что X+0=X

Для любого целого числа X, существует единственное число (-X), называемое противоположным (-X)+(X)=0 (симметритизация)

Свойства умножения

X(YZ)=(XY)Z- ассоциативность

XY=YX– коммутативность

1X=X

X(Y+Z)=XY+XZ – дистрибутивность

Свойства связанные с порядком следованием, распространяемое с натуральных чисел на целые.

Пусть -X<0<Y тогда по определению -Y<-X<0. Также -X<0<Y, где X и Y – произвольные.

Математическая индукция

Один из методов доказательства.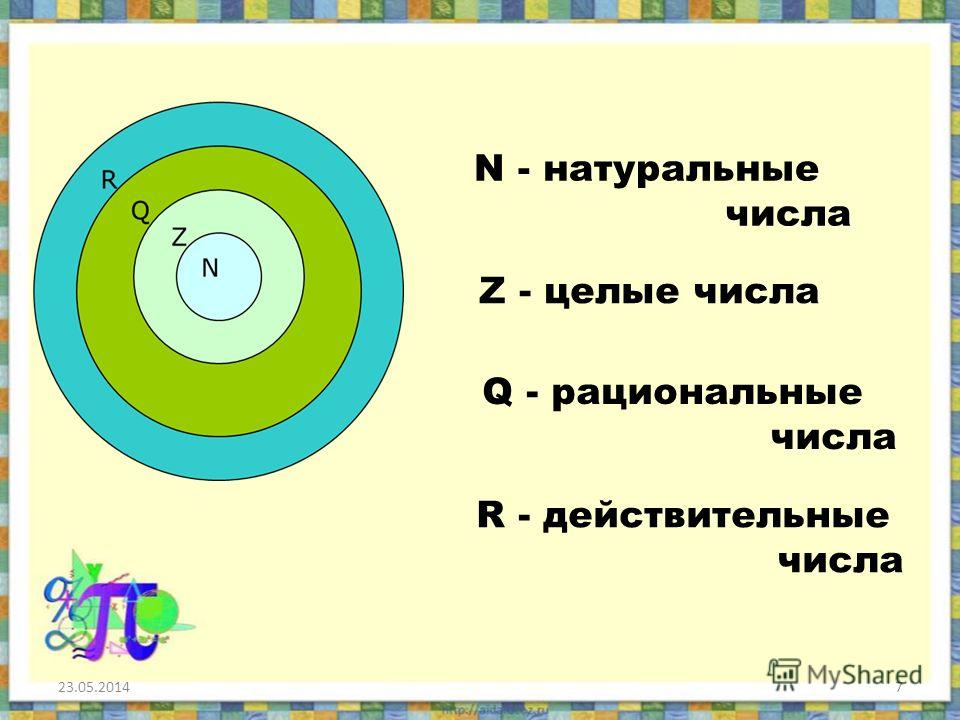 Используется для того, чтобы доказать истинность некого утверждения для всех натуральных чисел.

База индукции верно с номером n
Индуктивный переход верно для n+1

1³+2³+3³…+n³=((n(n+1))/2)²

Проверка для n=1

1³⁼

1=1 – верно

Пусть утверждении верно для всех n<k
Индуктивный переход

1³+2³+3³…+(n+1)³ = + (n+1)³=()+(n+1)³=–верно

Рациональные числа или расширение целых. Соразмерность. Рациональная прямая. Изоморфизм.

Рациональные – числа вида m/n, где m, n – целые, причем n≠0

Равенства и алгебраические операции

Равенства дробей a/b=c/d, если ad=cb (a, b, c, d – целые)

Справедливо m/n=(-m)/(-n)

Умножение. Пусть r=m/n и s=m’/n’, тогда по определению rs=mm’/(nn’)
Сложение. Пусть r=m/n и s=m’/n’, тогда r+s=(mn’+m’n)/(nn’)
Определение порядка для рац. чисел:

Пусть R=m/n и S=m’/nэб тогда R<S, если mn’<nm’.

Арифметические свойства:

Сложения.

x+(y+z)=(x+y)+z
x+y=y+x
сущ. такое число 0, x+0=x
для любого целого x, сущ. одно число (-x), (-x)+x=0.

Умножения.

x(yz)=(xy)z
xy=yx
существует одно число = 1, кот. 1x=x
Для любого целого числа x≠0, сущ. ед. число x^-1, называемое обратным

x*x^-1=1.

Дистрибутивность.

x(y+z)=xy+xz

Если мы представим все рациональные числа в виде k/1, то получится, что рац. вмещают в себя целые.

Если R=m/n и R’=m’/n’ – два произвольных рац. числа, то R=(mn’)s и R’=(m’n)s, где s=1/(nn’)>0.

Соответствующие числа получаются откладыванием отрезка [0,s], соотв. число раз влево и вправо, зависит от знаков R и R’.

Отрезок [0,s] называется общей мерой отрезков [0,|R|] и [0,|R’|].

Рациональная прямая.

R=m/n, где n – натуральное, нужно разделить на отр [0,1], нужно разделить на n частей. Первая справа от нуля точки соответствует дроби 1/n, дробь m/n изображается точкой, получающейся откладыванием 1/n вправо m раз, если m>0, влево (-m) раз m<0.

Для любой рациональной точки R>0 длина отр [0,R] равна R, для R<0 длина отр. То [R,0] равна –R.

Изоморфизм. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.

Сохраняет все алгебраические операции и свойства в задачах алгебры или свойства предельного перехода или непрерывности в началах анализа, то изоморфный образ можно считать копией данного множества.

Иррациональные отрезки. Действительные числа и операции над ними. Порядок. Существование корней.

Иррациональный отрезок несоизмерим, мы не можем отложить его или соизмеримый от нуля.

Предположим, что диагональ и сторона соизмеримы, т. е. их длины равны ns и ms., где s – их общая мера, m,n — натуральные числа. Тогда x=m/n, можем предположить, что m/n – несократимая, 2=m²/n², то m²=2n², т.е. m=2k, т.е. n²=2k², n – четно. X – не может быть представимо в виде m/n => 2^1/2 – не рациональное число.

Вещественные или действительные числа.

Действительные числа – мат. абстракция, возникшая из потребности измерения геометрических и физических величин окруж. мира, а также проведение таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений.

Под множеством понимается произвольная совокупность элементов, которая меняется как единое целое.

Действия над действит. числами:

a+b=b+a
a+(b+c)=(a+b)+с
∃0∈R, a∈R, a+0=a
a+(-a)=0
ab=ba
a(bc)=(ab)c
1∈R, a∈R, a1=a
a∈R, a≠0, a^-1∈R, aa^-1=1
a, b, c∈R, a(b+c)=ab+ac
Нетривиальность поля: 1≠0.

Действия над множествами:

Пересечение: A∩B, A={0,1,2,3}, B={-1,0,1,10}, то A∩B={0,1}

Объединение: A∪B, A={0,1,2}, B={-2,-1,0,1}, то A∪B={-2,-1,0,1,2}

Разность.

Прямое произведение.

Числовая ось или прямая – это прямая, на кот. выбраны:

— некоторая точка 0 – начало отсчета

— положительное направление, указанное стрелкой

— масштаб для измерения длин, еденичный отрезок

Полнота:

Лемма о вложенных отрезках. Принцип вложенных отрезков Коши-Кантора.

Для всякой системы вложенных отрезков

[a₁, b₁]->[a₂, b₂]->…->[a_n, b_n]

Существует хотя бы одна точка с, принадлежащая всем отрезкам данной системы. 2

ТЕМА.1 ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. Преподаватель Гобова — презентация на Slide-Share.ru 🎓

Первый слайд презентации

ТЕМА.1 ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. Преподаватель Гобова Мария Юрьевна

Изображение слайда

Слайд 2: Содержание:

Натуральные числа. Целые числа. Рациональные числа Действительные числа Преобразование выражений с действительными числами.

Изображение слайда

Слайд 3

Для счета предметов используются числа, которые называются натуральными. Для обозначения множества натуральных чисел употребляется буква N -первая буква латинского слова Naturalis, «естественный», «натуральный» Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается Z — первой буквой немецкого слова Zahl — «число».

Изображение слайда

Слайд 4

Натуральные числа 1, 2, 3, 4, 5, 6… Сумма и произведение натуральных чисел есть число натуральное. n — натуральное

Изображение слайда

Слайд 5: Целые числа

Целыми числами называют множество натуральных чисел, им противоположных и число нуль. Z =(1,2,3,4,5,6,7,8… -1,-2,-3,-4,-5,-6,-7,-8…, 0) Целые числа замкнуты относительны суммы, произведения и разности.

Изображение слайда

Слайд 6

Сумма, произведение и разность целых чисел есть число целое. Целые числа …-3;-2;-1;0,1, 2, 3,… m — целое

Изображение слайда

Слайд 7

Отрицательные числа ввели в математический обиход Михаэль Штифель (1487—1567) в книге «Полная арифметика» (1544), и Никола Шюке (1445—1500 )- его работа была обнаружена в 1848 году.

Изображение слайда

Слайд 8

Множество чисел, которое можно представить в виде, называется множеством рациональных чисел и обозначается- Q первой буквой французского слова Quotient — «отношение».

Изображение слайда

Слайд 9: Рациональные числа

Целые и дробные числа составляют множество рациональных чисел. Q =(целые числа, дробные числа) Рациональные числа замкнуты относительно суммы, разности, произведения и частного (исключая деления на нуль)

Изображение слайда

Слайд 10

Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью, где числитель m — целое число, а знаменатель n — натуральное число. Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся.

Изображение слайда

Слайд 11

Выполнить действия Ответы

Изображение слайда

Слайд 12

Вычислите: . ответ 3,5

Изображение слайда

Слайд 13

Дроби естественно возникли при решении задач о разделе имущества, измерении земельных участков, исчислении времени.

Изображение слайда

Слайд 14

Дробные числа Сумма, произведение и частное дробных чисел есть число дробное.

Изображение слайда

Слайд 15

Десятичные дроби в XV веке ввел самаркандский ученый ал — Каши. Ничего, не зная об открытии ал – Коши, десятичные дроби открыл второй раз, приблизительно через 150 лет, после него, фламандский ученый математик и инженер Симон Стевин в труде «Децималь» (1585 г).

Изображение слайда

Слайд 16

Множество рациональных чисел Множество рациональных чисел обозначается и может быть записано в виде: Q = m : n Нужно понимать, что численно равные дроби такие как, например, 3/4 и 9/12, входят в это множество как одно число. Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:

Изображение слайда

Слайд 17

Сумма, произведение, разность и частное рациональных чисел есть число рациональное. Рациональные числа r — рациональное

Изображение слайда

Слайд 18

Замените данные рациональные числа десятичными дробями.

Изображение слайда

Слайд 19

Чтобы обратить чисто периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, образованное из цифр, стоящих в периоде, а в знаменателе – написать цифру 9 столько раз, сколько цифр в периоде. 0,(2)= 2 9 1 цифра 0,(81)= 81 2 цифры 99

Изображение слайда

Слайд 20

Чтобы обратить смешанную периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода ; а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода. 0,4(6)= 4 6 4 1 цифра 9 1 цифра 0

Изображение слайда

Слайд 21: Домашнее задание Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь

1,5(23) = 0,3(18) = 8,3(7) = 1,(72)= 2,9(12)= 1,12(8)=

Изображение слайда

Последний слайд презентации: ТЕМА.1 ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. Преподаватель Гобова

Вариант 1 1. Записать в виде а) б) 2.Представьте в виде а) 15,(3) б) 2,(14) в) 1,6(1) Вариант 2 бесконечной дроби а) б) обыкновенной дроби а) 7,(2) б) 23,(25) в) 3,9(12) Самостоятельная работа

Изображение слайда

множество чисел, определение, свойства и примеры

Понятие и свойства натуральных чисел
Понятие и свойства целых чисел
Примеры

Понятие и свойства натуральных чисел

Натуральные числа – множество чисел, используемых для счёта предметов. b = c$

Незамкнутые операции над натуральными числами (не всегда результаты будут натуральными)

1. Вычитание: a-b = c. Результат натуральный, если $a \gt b$

2. Деление нацело (с остатком): $a/b = (c;r), 0 \le r \lt b,a = bc+r$

Понятие и свойства целых чисел

Целые числа – расширение множества целых чисел, получаемое при добавлении к нему нуля и отрицательных чисел.

Множество целых чисел обозначается Z.

$$Z = \{…,-2,-1,0,1,2,…\}$$

Свойства целых чисел

1. Множество целых чисел бесконечно.

2. На множестве определено отношение порядка

$… \lt -2 \lt -1 \lt 0 \lt 1 \lt 2 \lt ⋯ $

3. Множество содержит ноль («нейтральный элемент»): 0+a = a+0 = a,∀a $\in \Bbb Z$

4. Для каждого целого числа a существует противоположное ему число –a, при этом a+(-a) = 0.

Замкнутые операции над целыми числами

1. Сложение: a+b = c

2. Вычитание: a-b = c

3. Умножение: ab = c

4. Возведение в натуральную или нулевую степень: $a^b = c$

5. 2-xy-x+y = 1$

$$x(x-y)-(x-y) = 1 \Rightarrow (x-1)(x-y) = 1 \Rightarrow x-y = \frac{1}{x-1} \Rightarrow$$

$$ \Rightarrow y = x — \frac{1}{x-1} $$

Дробь $\frac{1}{x-1}$ будет целым числом только для $x-1 = \pm 1 \Rightarrow x = 1 \pm 1 \Rightarrow x_1 = 2,x_2 = 0$

Получаем:

$$ \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x = 2 \\ y = 2 — \frac{1}{2-1} = 1 \end{array} \right.} \\ {\left\{ \begin{array}{c} x = 0 \\ y = 0 — \frac{1}{0-1} = 1 \end{array} \right.} \end{array} \right. $$

Ответ:$\{(2;1),(0;1)\}$

Разница между натуральными числами и целыми числами

LearnPracticeDownload

Основное различие между натуральными числами и целыми числами связано с числом 0, которое является лишь частью множества целых чисел и не присутствует в множестве натуральных чисел. Одним из важнейших аспектов математики являются числа. Нам нужны числа, чтобы считать, измерять и обозначать. Они могут быть представлены в различных формах, таких как цифры, слова и на линии. Числа — это те значения, которые представляют определенную величину. В математике числа бывают разных типов — натуральные числа, целые числа, целые числа, действительные числа, рациональные числа, иррациональные числа и комплексные числа.

В этой статье мы узнаем определение натуральных чисел, определение целых чисел и разницу между натуральными числами и целыми числами на примерах.

1.	Что такое натуральные числа?
2.	Что такое целые числа?
3.	Разница между натуральными числами и целыми числами
4.	Часто задаваемые вопросы

Что такое натуральные числа?

Натуральные числа также известны как счетные числа, потому что эти числа можно сосчитать на руках. Например, числа, которые мы считаем на руках, — это 1, 2, 3, 4, 5, 6 и так далее. По определению, натуральные числа — это часть системы счисления, которая включает только положительные целые числа от 1 и которую можно пересчитать на руках. Число 1 считается самым маленьким натуральным числом. Поэтому 0, отрицательные числа, дроби и десятичные дроби не считаются натуральными числами. Вот несколько примеров натуральных чисел: 46, 72, 25, 888, 560 и т. д.

Что такое целые числа?

Целые числа — это числа, включающие положительные целые числа наряду с 0. Они представлены в правой части числовой строки. 0 считается наименьшим целым числом. Следует отметить, что положительные целые числа и натуральные числа также считаются целыми числами, тогда как дроби и десятичные дроби не подпадают под целые числа. С целыми числами возможны такие арифметические операции, как сложение, вычитание, умножение и деление. Несколько примеров целых чисел: 0, 15, 37, 9.7, 67 и т. д.

Разница между натуральными числами и целыми числами

Основное различие между натуральными числами и целыми числами заключается в том, что натуральные числа не включают число 0, и здесь наименьшее число равно 1. Тогда как целые числа включают 0, и здесь наименьшее число равно 0. Обратите внимание на рисунок, приведенный ниже, который показывает разницу между набором натуральных чисел и целыми числами.

Натуральные числа и целые числа

В следующей таблице показана разница между натуральными и целыми числами.

Натуральные числа	Целые числа
Натуральные числа — это счетные числа, начинающиеся с 1.	Целые числа — это натуральные числа, начинающиеся с цифры 0.
Все положительные целые числа входят в набор натуральных чисел.	Все положительные целые числа и ноль включены в набор целых чисел.
Все натуральные числа считаются целыми числами.	Все целые числа не считаются натуральными числами.
Обозначается буквой «N».	Обозначается буквой «W».
Натуральные числа закрыты при сложении и умножении.	Целые числа закрыты при сложении и умножении.

☛ Связанные статьи

Составные номера
Четные числа
Нечетные числа
Простые числа
Воображаемые числа
Кардинальные числа
Порядковые номера

Примеры различий между натуральными и целыми числами

Пример 1: Определите целые числа из заданных чисел: 7/9, 0, 7, 69,6, 10, -21, -56, 90
Решение: Из данного списка целые числа равны 0, 7, 10 и 90
Пример 2: «Каждое целое число также является натуральным числом.» Это утверждение верно? Обосновать ответ.
Решение: Нет, каждое целое число не является натуральным. По определению, натуральные числа — это часть системы счисления, которая содержит все положительные целые числа, начиная с цифры 1 и заканчивая бесконечностью. Принимая во внимание, что целые числа включают в себя все положительные числа, начиная с цифры 0 и до бесконечности. Число 0 является целым числом, но не натуральным числом. Следовательно, мы можем сказать, что натуральные числа содержат все целые числа, кроме числа 0. Следовательно, утверждение, что каждое целое число также является натуральным числом, неверно.
Пример 3: Определить целые числа и натуральные числа из данного списка включают все положительные целые числа без 0, а целые числа включают положительные целые числа вместе с 0. Из данного списка
- Целые числа 121, 4, 0, 30
- Натуральные числа 121, 4, 30

перейти к слайдуперейти к слайдуперейти к слайду

Разбейте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы о разнице между натуральными и целыми числами

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о разнице между натуральными числами и целыми числами

В чем разница между натуральными числами и целыми числами?

Натуральные числа — это числа, включающие только положительные целые числа, начинающиеся с 1 и продолжающиеся до бесконечности. Принимая во внимание, что целые числа — это те числа, которые включают в себя 0 и натуральные числа, начинаются с 0 и продолжаются до бесконечности.

Натуральные числа и целые числа — одно и то же?

Натуральные числа начинаются с 1, тогда как целые числа начинаются с 0. Все натуральные числа считаются целыми числами, но все целые числа не считаются натуральными числами.

Какое число не является общим между натуральными и целыми числами?

Число, которое не является общим между натуральными и целыми числами, — это 0. Это означает, что целые числа включают 0, а натуральные числа — нет.

Целые числа — это целые или натуральные числа?

Целые числа включают целые числа и натуральные числа. Числа, которые являются положительными, отрицательными и 0, называются целыми числами. Эти числа можно представить на числовой прямой. Все положительные числа и 0 являются целыми числами. Дроби и десятичные дроби не входят в список целых чисел.

Все ли натуральные числа, целые числа?

Да, все натуральные числа являются целыми числами, поскольку натуральные числа начинаются с 1,2,3,4 и так далее, а целые числа начинаются с 0, 1,2,3,4 и так далее. Но не все целые числа являются натуральными числами.

Какие первые пять натуральных чисел?

Первые пять натуральных чисел — это 1, 2, 3, 4 и 5. Натуральные числа — это числа, которые используются для счета и являются частью действительных чисел.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по числам

Рабочие листы по математике и
наглядный учебный план

Разница между натуральными и целыми числами

Существуют различные типы чисел, такие как целые числа, натуральные числа, целые числа, рациональные числа, иррациональные числа, действительные числа и комплексные числа. числа. И чаще всего студенты могут найти это запутанным, то есть студент может спутать одно с другим. Особенно в натуральных числах и целых числах, потому что они оба кажутся похожими. И поэтому учащимся важно иметь четкое представление о целых числах и натуральных числах.

Понимание целых чисел

Прежде чем углубляться в различие между целыми числами и натуральными числами, учащимся важно сначала понять оба термина, целые числа и натуральные числа по отдельности. Потому что основное различие между ними заключается в их значении. Поэтому начнем с целых чисел.

Возможно, вы знакомы с термином «целые числа», если нет, вот краткий обзор. Целые числа — это те числа, которые могут быть выражены без использования дробей, короче говоря, числа, не являющиеся дробями, являются целыми числами. Например, числа 1, 25, 124, 5624, -54 являются целыми числами, поскольку они не требуют дробей. А вот числа ¾, ½ не являются целыми числами, потому что они выражены дробью.

Теперь, что касается целых чисел, все положительные целые числа вместе с 0 называются целыми числами. Это означает десятичные дроби, такие как 5,2, 3,2; Отрицательные, такие как -5, -6; а дроби не целые числа.

Если вы хотите узнать больше о целых числах, перейдите по этой ссылке.

Понимание натуральных чисел

Теперь, что касается натуральных чисел, это так же просто, как и целые числа. Потому что все, что вам нужно сделать, это удалить 0 из целых чисел, и вы получите натуральные числа. Да, все положительные целые числа системы счисления называются натуральными числами. Это означает, что целые числа, такие как 1, 5, 8, 541 и т. д., являются натуральными числами. Но, как и в случае с целыми числами, здесь снова не учитываются десятичные, отрицательные и дробные числа. Вы можете неопределенно сказать, что все числа, которые мы обычно используем для счета, являются натуральными числами 9.0003

Difference Between Natural Numbers and Whole Numbers

Sr No	Natural Numbers	Whole Numbers
1	Natural Numbers are those numbers которые мы обычно используем для счета.	Целые числа включают все натуральные числа, кроме нуля.
2	Все положительные целые числа, отличные от нуля, называются натуральными числами.	Все положительные целые числа, включая ноль, называются целыми числами.
3	Все натуральные числа от 1 до бесконечности также являются целыми числами.	Все целые числа, кроме 0, что означает от 1 до бесконечности, являются натуральными числами.

Жизнь без чисел невообразима. Есть многочисленные свойства чисел, которые привели к их категоризации. Прежде всего следует отметить, что все натуральные числа являются целыми числами. Однако есть и другие категории чисел, например, 9.0003

Whole Numbers
Natural Numbers
Integers
Rational Numbers
Irrational Numbers
Real Numbers
Complex Numbers

These categories differ from each другие по своим свойствам. Давайте рассмотрим разницу между натуральными и целыми числами.

0 — наименьшее целое число. В математике самым основным набором являются целые числа. Эти целые числа являются неотъемлемой частью набора действительных чисел, который включает в себя различные другие наборы чисел, такие как целые числа, рациональные числа и другие.

За исключением 0, у каждого целого числа есть ровно один непосредственный предшественник, то есть число, стоящее перед целым числом. У каждого целого числа есть только один непосредственный преемник, т. е. число, следующее за целым числом.

Основное различие между натуральными числами и целыми числами заключается в том, что набор целых чисел включает 0. Вместо этого набор натуральных чисел не включает 0. Давайте поговорим о других различиях, как показано ниже.

Разница между натуральными и целыми числами

Целое число

Все целые числа представлены буквой «W»
В целых числах счет начинается с «0» НОЛЬ

9 Прибавляется к числу 0 ответ — это просто число, с которого вы начинаете: 24 + 0 = 24.

По этой причине 0 называется элементом идентичности для сложения. Элемент идентичности отсутствует в натуральных числах из-за дополнительного свойства.

Все целые числа также являются целыми числами. Каждому целому числу соответствует отрицательное число. Например, -5 соответствует целому числу 5, а -120 соответствует целому числу 120.

В наборе целых чисел сумма двух чисел может быть 0. 20+(-20)=0 и 135+(-135)=0.

20 и -20 будем называть аддитивными инверсиями.

Натуральное число

Все натуральные числа представлены буквой ‘N’
В натуральных числах счет начинается с 1
При сложении двух или более натуральных чисел снова получается натуральное число.
Когда вы умножаете два или более натуральных числа, вы снова получаете натуральное число

Математический способ сказать это так: «Система натуральных чисел замкнута относительно сложения и умножения». Это означает, что при выполнении вычитания или деления натуральных чисел результатом может быть не всегда натуральное число.

Примеры целых чисел и натуральных чисел

Пример 1. Найдите целые числа из данных чисел. 14,0,8,48,-6,-9,2

Сол. Целые числа: 14,0,8,48,2

Пример 2. Из заданных чисел найти натуральные числа.

24,(0,6),6,40,-60,0,-2

Сол. натуральные числа: 24,6,40

Объяснение свойства сложения натуральных и целых чисел

При сложении двух натуральных чисел получается только натуральное число.

Например: 34+45 = 79

Если сложить два целых числа, получится целое число.

Например: 6+0= 6

Объяснение свойства вычитания натуральных и целых чисел

Вычитание двух натуральных чисел не обязательно дает натуральное число

– 5 = Например: 902: 3 является натуральным числом

Но 5 – 8 = -3 не является натуральным числом

Аналогично условие для целых чисел. Вычитание двух целых чисел не обязательно должно давать целое число.

Объяснение свойства умножения натуральных и целых чисел

Умножение натурального числа на натуральное число и целого числа на другое целое число дает натуральное число и целое число соответственно.

Например: 4 x 3 = 12 — натуральное число

8 x 5 = 40 — целое число, где 8 и 0 также являются целыми числами.

Объяснение свойства деления для натуральных и целых чисел

Свойство деления также не действует, например, для натуральных и целых чисел.

Например: 10/2 = 5 является натуральным, как и все число

Но 7/2 = 3,5 не является ни натуральным, ни целым числом.

Точно так же разницу между натуральными числами и целыми числами можно понять, представив их на числовой прямой.

Целые числа расположены справа от числовой строки, включая ноль.

Натуральные числа расположены справа, за исключением нуля.

2.1 — Типы чисел

Давайте рассмотрим типы чисел. Мы рассмотрим натуральные и целые числа, целые числа, рациональные числа, иррациональные числа, действительные числа, мнимые числа и комплексные числа.

Натуральные и целые числа

Начнем с натуральных чисел . Это числа 1, 2, 3, … (Символ … означает, что последовательность продолжается вечно.) Они используются для счета. Если мы включим ноль, то получим целых чисел , 0, 1, 2, 3, ….

Натуральные и целые числа обычно считаются точными (например, у автомобиля 4 шины, у паука 8 ног). Но иногда они приблизительны (например, в толпе было 1000 человек).

Вот целые числа, показанные в числовой строке :

Целые числа

Теперь для каждого из чисел 1, 2, 3, … создадим его противоположное или отрицательное и положим на противоположное стороне числовой прямой, например:

. Мы говорим, что 1 и −1 являются противоположностями, 2 и −2 являются противоположностями и т. д., а также мы говорим, что −1 противоположно 1, а 1 противоположно −1.

Отрицательные числа используются для описания долгов, а не активов, температуры ниже нуля, а не температуры выше нуля, высоты ниже уровня моря, а не высоты над уровнем моря, и так далее.

Набор чисел …, −3, −2, −1, 0, 1, 2, 3, … (целые числа и их противоположности) называется целых чисел .

Рациональные числа

Далее идут рациональные числа. Они представляют собой обобщение обыкновенные дроби, поэтому давайте сначала рассмотрим их. Помните, что запись дроби a / b означает, что мы разбиваем что-то на b равных частей и что у нас есть a этих частей. Например, если мы разделим пирог на 4 части и у нас будет 1 часть, то у нас будет 1/4 части пирога:

Рациональное число определяется как любое число, которое может быть выражено как частное или отношение из два целых числа . Мы используем то же обозначение дроби для выражения рациональных чисел:

Целое число a называется числителем, а целое число b называется знаменателем. Знаменатель не может быть равен нулю.

Обратите внимание, что если a и b являются натуральными числами (1, 2, 3 и т. д.), то мы получаем обыкновенную дробь. Таким образом, рациональные числа включают обыкновенные дроби.

Обратите внимание, что 3/1 = 3 и −5/1 = −5, поэтому рациональные числа включают все целые числа.

Рациональные числа также можно записывать в десятичном виде вместо дробного. Например:

1/4 = 0,25

Десятичная запись 0,25 буквально означает «25/100», а 25/100 и 1/4 — эквивалентные дроби.

Обратите внимание, что некоторые рациональные числа не имеют точного десятичного эквивалента. Например 1/3 примерно равно 33/100, но не точно:

1/3 ≈ 0,33

(Символ ≈ означает « приблизительно равно ».) Рациональные числа обычно считаются точными . По этой причине программа Algebra Coach не будет преобразовывать дроби в десятичные, когда она работает в точном режиме.

Иррациональные числа

Иррациональные числа — это те, которые нельзя представить в виде отношения двух целых чисел.

Примеры, а также квадратные корни многих других чисел, и специальные числа, такие как e и π. Оказывается, иррациональных чисел столько же как рациональное. Иррациональные числа не имеют точных десятичных эквивалентов. Записать любое иррациональное число в десятичной системе счисления потребовало бы бесконечного числа десятичных цифр. Таким образом, это только приблизительные значения:

≈ 1,732, e ≈ 2,718 и π ≈ 3,14,

По этой причине программа Algebra Coach не будет преобразовывать иррациональные числа в десятичные. когда он работает в точном режиме.

Реальные цифры

Рациональные числа и иррациональные числа вместе составляют действительных чисел . Реальные цифры считается плотным . Они включают в себя каждое отдельное число, которое находится на числовой прямой.

Числовая строка полезна для понимания порядка чисел . Меньшие числа расположены левее и большие числа дальше вправо.

Мы используем символ < для обозначения « меньше » и символ > означает « больше, чем ». Вот несколько примеров использования этих символов:

5 < 8, потому что 5 левее 8.
−5 < 2, потому что −5 находится слева от 2. На самом деле любое отрицательное число меньше любого положительного числа.
5 < 8 и 8 > 5 — два способа констатировать один и тот же факт.
3,14 < π < 3,15 Я называю это «меньше, чем бутерброд». Это означает, что 3,14 < π, а также π < 3,15. Другими словами, число π находится где-то между 3,14 и 3,15.

Реальные числа часто получаются в результате измерений, а измерения всегда приблизительны. Например, с помощью одной единицы оборудования длина объекта может быть измерена как 5,28. (в некоторых единицах). Это не означает, что длина ровно 5,28. Это просто означает, что это ближе к 5,28, чем к 5,27 или 5,29. При более точном (и, как правило, гораздо более дорогом оборудовании) длина может быть измерено как 5,283, что просто означает, что оно ближе к 5,283, чем к 5,282 или 5,284 и так далее.

Если выражение содержит приблизительное число, то оно все выражение также является приблизительным.

Щелкните здесь для получения дополнительной информации о точности и значащих цифрах.

Мнимые числа и комплексные числа

Если действительные числа включают в себя каждое отдельное число на числовой прямой, то какие еще могут быть числа? Чтобы ответить на этот вопрос, рассмотрим, как мы до сих пор строили систему счисления:

Мы начали с целых чисел (например, 3)
Мы хотели, чтобы эти числа были обратными, поэтому мы создали целые числа (числа вроде −3)
Мы хотели разделить эти числа, но нам нужны были рациональные числа для описания некоторые результаты (цифры вроде 3/4)
Мы хотели извлечь квадратный корень из этих чисел, но нам нужны были иррациональные числа, чтобы описать некоторые результаты (например, )

Теперь мы хотим извлечь квадратный корень из отрицательных чисел, но нам понадобится новый тип числа.

чтобы описать результат. Определяем квадратный корень из отрицательного числа быть воображаемым числом . Насколько дальше может продолжаться этот процесс создание новых типов номеров идет? Ответ — еще один шаг. Мы можем добавить действительное число к мнимому числу. Результат называется комплексным числом . Это конец строки, потому что оказывается, что любая возможная операция со всеми возможными комплексными числами приводит только к другим комплексным числам. Мы говорим, что комплексные числа делают числа полными.

Где на числовой прямой располагаются мнимые и комплексные числа? Ответ: нет. На этой картинке изображено сложный самолет . Он содержит числовую строку (которая теперь называется реальной осью ) и новой осью, называемой мнимая ось , перпендикулярная ей. Действительные числа лежат на действительной оси, мнимые числа лежат на мнимой оси, а комплексные числа обычно лежат вне действительной оси, либо над ним, либо под ним.

Программа Algebra Coach может работать в реальном или сложном режиме. В реальном режиме не будет выполнять любую операцию, которая приводит к недействительному числу (например, извлечение квадратного корня отрицательного числа).

Щелкните здесь для получения дополнительной информации о комплексных числах.

Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.

Документ без названия

Все бесконечности одного размера?

До сих пор мы в основном сосредоточивали наше внимание на конечных множествах (то есть множествах, которые не являются бесконечными). Но вы, возможно, заметили, что большинство множеств, с которыми мы работаем в математике: множество целых чисел, множество рациональных чисел, множество действительных чисел и т. д., НЕ являются конечными! Все эти наборы имеют БЕСКОНЕЧНОЕ количество элементов, поэтому они называются БЕСКОНЕЧНЫМИ НАБОРАМИ.

Бесконечность может быть очень сложной концепцией, но очень интересной. Если вы начнете думать о бесконечностях, то в конце концов столкнетесь с вопросом:

«Все бесконечности одного размера?»

Ответ, как оказалось, «нет». Так что некоторые бесконечности «больше» других!

Является ли мощность набора действительных чисел «больше», чем мощность набора целых чисел?

Например, набор целых чисел (помните, что набор целых чисел включает в себя все положительные и отрицательные целые числа, включая ноль) продолжается вечно. Если бы я спросил вас, сколько существует целых чисел, вы бы ответили: «бесконечно много». Но множество действительных чисел также продолжается вечно, а множество целых чисел равно 9.0064 PROPER подмножество множества действительных чисел. Значит, действительных чисел должно быть на больше, чем целых , или, другими словами, мощность набора действительных чисел должна быть «большей бесконечностью», чем мощность набора целых чисел, верно?

С другой стороны, мы могли бы утверждать, что добавление дополнительных элементов к уже бесконечному количеству элементов не меняет это бесконечное количество. Да, мы могли бы сказать, что действительных чисел больше, чем целых, но поскольку и число действительных чисел, и число целых чисел бесконечно, мощность этих двух множеств одинакова, потому что у вас не может быть одной бесконечной величины, которая больше другого! Другими словами, вы можете утверждать, что добавление чего-либо или умножение чего-либо на бесконечность не изменит эту бесконечность.

Итак, какой из этих аргументов правильный? Что ж, они оба делают важные и правильные выводы, но в этом случае мощность набора действительных чисел на самом деле «больше», чем мощность набора целых чисел, даже если они оба являются бесконечными величинами. Однако причины этого несколько сложнее, чем кажется на первый взгляд.

Давайте посмотрим, сможем ли мы понять, как отличить один вид бесконечности от другого:

Начнем с множества натуральных чисел. Ясно, что множество натуральных чисел имеет бесконечную мощность, потому что целые числа продолжаются вечно. (Помните, что слово «мощность» относится только к количеству элементов в множестве. ) Мы можем безнаказанно называть бесконечность числом, если понимаем, что это новый, странный вид «числа», который не следует правилам. что следуют регулярные конечные числа. (Технически мы вообще не должны называть бесконечные количества числами, потому что технически числа включают только конечные количества, но чтобы сделать язык этой лекции более читабельным, мы будем продолжать называть бесконечные количества «числами», заключая их в кавычки. математики на самом деле относятся к бесконечным количествам как бесконечных количества , а не бесконечных «числа». )

Мы еще не знаем никаких бесконечных «чисел», но мы можем видеть, что должно существовать некоторое бесконечное «число», чтобы описать количество элементов в множестве натуральных чисел. Поэтому мы решили просто дать этому бесконечному «числу» имя. Мы называем это ℵ ₀. Мы называем этот символ ℵ ₀ «алеф-нулевой». Алеф — это просто первая буква еврейского алфавита, а ноль — это просто индекс 0. ℵ ₀ не является числом в том смысле, в каком 5 или 12 миллионов или 3,79384509 являются числом. Мы не можем сосчитать ℵ ₀ на пальцах или измерить его; нам нужно просто привыкнуть к идее, что ℵ ₀ просто ОПРЕДЕЛЯЕТСЯ как мощность натуральных чисел, которая является неким бесконечным «числом» . Поскольку ℵ ₀ бесконечно, оно очень велико — настолько велико, что мы не можем его записать, кроме как написать ℵ ₀ .

Чем бесконечные «числа» отличаются от обычных конечных чисел?

Мы должны быть осторожны с бесконечными «числами». Они могут вести себя не так, как обычные конечные числа. Например, если вы добавите 1 к любому обычному конечному числу, вы получите новое число, отличное от числа, с которого вы начали. Формально мы бы написали так:

Для любого конечного числа n , n +1 ≠ n .

Чтобы убедиться, что это так, предположим, что n = n +1.

Вычитание n с каждой стороны дает нам 0=1.

Это явно неверно, поэтому наше предположение, что n = n +1, должно быть ложным.

Следовательно, мы можем заключить, что для любого конечного числа n , n +1 ≠ n .

Это НЕ соответствует действительности с БЕСКОНЕЧНЫМИ «числами», такими как ℵ ₀ !

Еще одним важным свойством конечных чисел является то, что если умножить любое ненулевое конечное число на 2, вы получите новое число, отличное от исходного числа. Формально мы бы написали так:

Для любого конечного ненулевого числа n , 2 n≠n .

Чтобы убедиться, что это так, предположим, что n = 2 n .

Разделив обе части на n , мы получим 1=2.

Это явно неверно, поэтому наше предположение, что n = 2 n , должно быть ложным.

Следовательно, мы можем заключить, что для любого конечного ненулевого числа n , 2 n ≠ n .

Это также оказывается НЕ верным с БЕСКОНЕЧНЫМИ «числами», такими как ℵ ₀ !

Так как же мы можем решить, равны две бесконечности или нет? Ответ на этот вопрос возвращает нас к бесконечным множествам и их мощностям.

Как узнать, что две бесконечности имеют одинаковый «размер»?

Вот как математики решили решить эту проблему определения того, когда два бесконечных количественных «числа» имеют одинаковый размер:

Если два набора имеют одинаковое количество элементов, то мы должны быть в состоянии установить то, что мы называем ОДИН НА ОДИН СООТВЕТСТВИЕ между двумя наборами. ДОПОЛНИТЕЛЬНОЕ СООТВЕТСТВИЕ — это процесс, в котором мы берем каждый элемент из первого набора и соединяем его с одним уникальным элементом из второго набора. По сути, это означает, что мы соединяем каждый элемент в первом наборе с элементом во втором наборе, так что каждого числа в каждом наборе соединяется с одним и только с одним другим числом в другом наборе .

Если мы можем установить однозначное соответствие между двумя множествами, то мы доказали, что эти два множества имеют одинаковую мощность.

Например:

Пример 1 (установка однозначного соответствия между двумя конечными множествами):

Если мы возьмем множества {1,2,3} и {1/4, 1/3, 1/2}, мы можем установить однозначное соответствие несколькими различными способами. Одним из способов было бы установить это взаимное соответствие:

1 → 1/4

2 → 1/3

3 → 1/2

Итак, числа 2 и 1/4 составляют пару, 2 и 1/3 составляют пару, а 3 и 1/2 составляют пару. Каждому элементу первого набора соответствует ровно один элемент второго набора. Ни один элемент ни в одном из наборов не был пропущен, и ни один элемент ни в одном из наборов не использовался в паре более одного раза. Таким образом, множества {1,2,3} и {1/4, 1/3, 1/2} имеют одинаковую мощность. Поскольку эти два множества конечны, мы можем, очевидно, сказать, что это верно; очевидно, что оба набора имеют мощность 3.

Заметьте, однако, что однозначное соответствие, которое мы использовали здесь, — это не , а только способ установить взаимно однозначное соответствие между двумя наборами; есть несколько других возможных однозначных соответствий. Например, другим способом было бы установить взаимно однозначное соответствие между этими двумя множествами:

1 → 1/3

2 → 1/2

3 → 1/4

Для этих двух наборов на самом деле существует 6 возможных способов установить однозначное соответствие между двумя наборами. Мы показали вам два возможных пути. Сможете ли вы найти 4 других возможных способа установить однозначное соответствие между этими двумя множествами?

Пример 2 (установка однозначного соответствия между двумя конечными множествами):

Если мы возьмем множества {1,2,3} и {2, 3, 4, 5}, мы не сможем установить однозначное соответствие между этими двумя множествами. Чтобы убедиться в этом, попробуйте выровнять каждый элемент первого набора с одним элементом второго набора. Если мы соединим один из элементов первого набора с числом 2 во втором наборе, а затем соединим второй элемент первого набора с числом 3 во втором наборе, а затем соединим в пару третий элемент первого набор с номером 4 во втором наборе, в первом наборе больше не будет элементов для соединения с номером 5 во втором наборе! Таким образом, мы не можем поставить множества во взаимно однозначное соответствие, и два множества не имеют одинаковой мощности. Это ясно, так как первое множество имеет мощность 3, а второе множество имеет мощность 4, и, очевидно, 3 не равно 4!

Установление взаимно-однозначных соответствий между двумя конечными множествами не очень интересно, потому что мы всегда можем сказать, имеют ли два конечных множества одинаковую мощность, просто подсчитав количество элементов в каждом множестве. Но с бесконечными множествами мы не можем сосчитать все элементы в каждом множестве, потому что они продолжаются вечно! Итак, , чтобы найти мощность бесконечных множеств, мы должны попытаться поставить их во взаимно однозначное соответствие с другими бесконечными множествами!

Приведение бесконечных множеств во взаимно однозначное соответствие друг другу

Что касается бесконечных множеств, нас на самом деле интересует следующее: имеет ли данное бесконечное множество ту же мощность, что и множество натуральных чисел? Чтобы ответить на этот вопрос, мы просто пытаемся поставить множество во взаимно однозначное соответствие с множеством натуральных чисел; если это возможно, то рассматриваемое бесконечное множество имеет ту же мощность, что и множество натуральных чисел.

Мощность множества целых чисел

Начнем с набора целых чисел. Пока единственное известное нам бесконечное «число» — это ℵ ₀ . Это описывает мощность множества натуральных чисел . Но ясно, что мощность множества целых чисел тоже бесконечна, потому что целые числа продолжаются вечно. Множество натуральных чисел является собственным подмножеством множества целых чисел, потому что число 0 — это целое число, но не натуральное число. Значит, мощность набора целых чисел должна быть больше мощности набора натуральных чисел, верно? Вообще-то, нет! Если мы можем поставить два множества во взаимно однозначное соответствие, то их мощности равны, даже если кажется, что одно множество имеет «больше» элементов, чем другое! Мы вернемся к этой идее позже.

А пока посмотрим, сможем ли мы установить однозначное соответствие между набором натуральных чисел и набором целых чисел:

Мы можем начать с записи натуральных чисел в виде N ={1,2,3,4,…}, а целых чисел в виде Z ^* ={0,1,2,3,4,…} .

Теперь настраиваем следующую корреспонденцию:

1 → 0

2 → 1

3 → 2

4 → 3

Давайте проверим, действительно ли это взаимно однозначное соответствие. Помните, что взаимно-однозначное соответствие связывает каждый элемент первого набора с одним и только одним элементом второго набора и наоборот.

Таким образом, чтобы показать, что спаривание является взаимно однозначным соответствием, нам нужно только показать, что:

Здесь есть ОБЫЧНАЯ РЕЗУЛЬТАТ, который мы можем продолжать ВЕЧНО.
Если мы продолжим этот шаблон, у нас НИКОГДА НЕ ИСЧЕЗАЮТ НОМЕРА для составления пар из каждого набора, и мы НИКОГДА не будем ПРОПУСКАТЬ числа в любом наборе.

Удовлетворяет ли эта пара этим двум критериям?

Есть ли здесь закономерность? Да. Шаблон заключается в том, что каждое натуральное число отправляется целому числу, которое на единицу меньше, чем натуральное число. Формально, если мы позволим n символизировать натуральное число, которое мы пытаемся соединить в пару, то n всегда будут в паре с n -1. Это определенно четкая закономерность. Может ли эта закономерность продолжаться вечно? Другими словами, для произвольного натурального числа возникнут ли у нас проблемы с поиском целого числа, которое меньше его на единицу? Нет. Ясно, что для любого натурального числа число, которое мы получаем, когда мы вычитаем 1, всегда будет целым числом. Таким образом, мы можем продолжать этот шаблон навсегда.
Если мы продолжим в том же духе, не закончатся ли когда-нибудь числа для составления пар из каждого набора? Нет. Поскольку оба набора бесконечны, мы не можем исчерпать числа ни в одном из наборов. Если мы продолжим этот шаблон, мы когда-нибудь пропустим какие-либо числа в любом наборе? Нет. Поскольку мы начали с начала каждого набора, и число, выбранное из каждого набора на любом данном шаге жеребьёвки, будет на единицу больше, чем предыдущее число, мы не можем пропустить какие-либо числа в любом наборе, используя этот образец спаривания.

Так что у нас переписка один на один!

Таким образом, мощность множества целых чисел равна ℵ ₀ !

Почему? Потому что множество натуральных чисел и множество целых чисел можно поставить во взаимно-однозначное соответствие друг другу. Следовательно, они имеют одинаковую мощность. Мощность множества натуральных чисел определяется как бесконечное количество ℵ ₀ . Поэтому мощность набора целых чисел должна быть ℵ ₀ .

(Это может занять некоторое время, чтобы вникнуть в суть. Может помочь вспомнить, что ключевая идея здесь такова: если в одном множестве на один элемент больше, чем в другом, и эти два множества конечны, у нас в конце концов закончатся числа для сопряжения. с элементами большего множества. Но когда два множества бесконечны, у нас никогда не закончатся числа для спаривания, поэтому в этом случае мы можем установить однозначное соответствие, даже если одно множество явно имеет на один элемент больше, чем на другой. )

Что это говорит нам о природе бесконечных «чисел»?
Здесь интересно отметить, что, поскольку в множестве целых чисел ровно на один элемент больше (ноль), чем в множестве натуральных чисел, можно сказать, что мощность множества целых чисел равна ℵ ₀ + 1, или, другими словами, n( Z ^* )=ℵ ₀ +1. Но поскольку мы только что поставили множество натуральных чисел и множество целых чисел во взаимно однозначное соответствие, мы знаем, что мощность множества целых чисел равна ℵ ₀ , или, другими словами, n( Z ^* )=ℵ ₀ . Таким образом, эти две величины должны быть равными , и поэтому мы должны иметь ℵ ₀ +1 = ℵ ₀!
Сначала это кажется противоречием, потому что мы знаем, что для любого правильного конечного числа n мы не можем иметь n +1 = n .
Однако ℵ ₀ — это , а не — обычное конечное число. Это бесконечно. И поскольку мы видим, что у нас должно быть ℵ ₀ +1 = ℵ ₀ , что ℵ ₀ НЕ ведет себя как обычные конечные числа!
На самом деле, если подумать об этом еще более внимательно, мы можем заметить, что если у нас есть ℵ ₀ +1 = ℵ ₀ , то мы можем добавить 1 к обеим частям этого уравнения, чтобы получить ℵ ₀ +2 = ℵ ₀ +1, но поскольку ℵ ₀ +1 = ℵ ₀ , мы можем заменить ℵ ₀ на ℵ ₀ +1 в правой части уравнения, чтобы получить ℵ 0 _{2 = ℵ ₀ _. Тогда, поскольку у нас есть ℵ ₀ +2 = ℵ ₀ , мы можем добавить 1 к обеим частям этого уравнения, чтобы получить ℵ ₀ +3 = ℵ ₀ +2, но так как ℵ ₀ +2 = ℵ ₀ , мы можем заменить ℵ ₀ на ℵ ₀ +2 в правой части уравнения, чтобы получить ℵ ₀ +3 = ℵ ₀ _. Обратите внимание, что мы можем продолжать этот шаблон вечно, так что мы можем видеть, что для любого регулярного конечного числа n мы имеем:}
ℵ ₀ + n = ℵ ₀
Таким образом, добавление любого обычного конечного числа к ℵ ₀ меняет , а не ! (В основном идея здесь в том, что бесконечное «число» ℵ ₀ настолько велико, что добавление чего-либо еще, что не является бесконечным, будет недостаточно, чтобы изменить его. Любое конечное число будет настолько «маленьким» по сравнению с ℵ _{. 0} что это не изменит.)

Мощность множества целых чисел

Теперь давайте рассмотрим набор целых чисел и посмотрим, сможем ли мы поставить набор целых чисел во взаимно однозначное соответствие с набором натуральных чисел. Если мы сможем установить это однозначное соответствие, то множество целых чисел также будет иметь мощность ℵ ₀ .

Очевидно, что мощность набора целых чисел бесконечна, потому что целые числа продолжаются вечно в обоих направлениях. Множество натуральных чисел и множество целых чисел являются собственными подмножествами целых чисел.

Здесь мы запишем целые числа как Z = {…-3,-2,-1,0,1,2,3,…} и снова мы запишем натуральные числа как N = {1,2 ,3,…}.

Но вот проблема, с которой мы сталкиваемся:

Если мы попытаемся настроить взаимное соответствие, как в предыдущем примере, мы можем попробовать что-то вроде этого:

1 → -3

2 → -2

3 → -1

4 → 0

5 → 1

6 → 2

7 → 3

Но нам нужно проверить, является ли эта пара соответствием один к одному:

Есть ли здесь закономерность? Да. Шаблон заключается в том, что каждое натуральное число передается целому числу, которое на четыре меньше натурального числа. Формально, если мы позволим n символизировать натуральное число, которое мы пытаемся соединить в пару, то n всегда будут в паре с n -4. Это определенно четкая закономерность. Может ли эта закономерность продолжаться вечно? Другими словами, для произвольного натурального числа возникнут ли у нас проблемы с поиском целого числа, которое меньше его на четыре? Нет. Ясно, что для любого натурального числа число, которое мы получим, вычитая 4, всегда будет целым числом. Таким образом, мы можем продолжать этот шаблон навсегда.
Если мы продолжим в том же духе, не закончатся ли когда-нибудь числа для составления пар из каждого набора? Нет. Поскольку оба набора бесконечны, мы не можем исчерпать числа ни в одном из наборов. Если мы продолжим в том же духе, пропустим ли мы какие-либо числа в любом наборе? Да! Обратите внимание, что в этой паре мы пропускаем все целые числа меньше -3!

Таким образом, это сопряжение , а не взаимно-однозначное соответствие!

Будьте осторожны — это НЕ означает, что между набором натуральных чисел и набором целых чисел НЕ существует однозначного соответствия. Все это означает, что ЭТА КОНКРЕТНАЯ пара НЕ является взаимно-однозначным соответствием. Но может быть ДРУГОЙ способ спаривания чисел из двух наборов, который даст однозначное соответствие!

Можем ли мы найти другой способ соединить набор целых чисел с набором натуральных чисел, которые и дадут нам однозначное соответствие? Давайте попробуем разобраться, что пошло не так с нашей последней парой, и посмотрим, сможем ли мы извлечь из этого уроки. В нашей последней попытке соединить все элементы из этих двух наборов в пары шаблон, который мы использовали для выбора целых чисел, начинался с одного целого числа, которое было в середине набора (-3), а затем продолжалось вправо, выбирая следующее. номер вверх от предыдущего. Проблема с этой логикой заключается в том, что она оставляет любые целые числа слева от -3 вне нашей пары.

Как мы можем попытаться это исправить?

Можно попробовать начать, например, с целого числа, которое находится левее. Предположим, что мы начинаем с -10, соединяя 1 в наборе натуральных чисел с целым числом -10. Затем мы соединим 2 в наборе натуральных чисел с целым числом -9 и т. д. Но в наборе целых чисел слева от -10 все еще будут целые числа, которые не включены в эту пару! Так это не сработает! Простого переноса числа, с которого мы начинаем, в целые числа недостаточно, чтобы решить нашу проблему!

Мы могли бы попробовать изменить шаблон выбора целых чисел, начав с числа в правой части набора и двигаясь влево по набору, чтобы установить пары — создаст ли это однозначное соответствие? Например, что, если мы попробуем следующее соединение:

1 → 3

2 → 2

3 → 1

4 → 0

5 → -1

6 → -2

7 → -3

В этой паре по-прежнему пропущены некоторые целые числа? Да! Эта пара пропускает все целые числа, которые больше 3! Так что это сопряжение тоже не будет работать как тет-а-тет!

В чем здесь настоящая проблема?

Если мы присмотримся повнимательнее, то увидим, что реальная трудность, с которой мы сталкиваемся, когда пытаемся соединить элементы множества целых чисел с элементами множества натуральных чисел, заключается в том, что множество натуральных чисел бесконечно только в в одном направлении (вправо), а набор целых чисел бесконечен как влево, так и вправо . Таким образом, мы никогда не сможем установить однозначное соответствие, используя шаблон, который выбирает целые числа, идя только вправо или только влево.

Однако помните, что порядок элементов в наборе не имеет значения ! Итак, если мы можем придумать способ переписать набор целых чисел так, чтобы он выглядел как бесконечный только в одном направлении , тогда мы сможем установить однозначное соответствие между этими двумя наборами. !

Например, мы могли бы написать Z = {0,1,-1,2,-2,3,-3,…}. Ясно {0,1,-1,2,-2,3,-3,…}={…,-3,-2,-1,0,1,2,3,…} потому что эти два набора содержат одни и те же элементы; элементы только что были переставлены. Итак, мы нашли способ переупорядочить целые числа так, чтобы они выглядели так, как будто они бесконечны только в одном направлении.

Другой способ взглянуть на это переупорядочение состоит в том, чтобы просто оставить набор целых чисел таким, какой он есть, но «перескакивать» по набору следующим образом:

Начинаем с 0, который находится в середине набора, затем идем на единицу вправо, затем возвращаемся к следующей цифре слева, которую мы не использовали, затем к следующей цифре справа, которую мы не использовали , затем следующее число слева, которое мы не использовали, и т. д.

Теперь настроить личную переписку легко:

Например, теперь мы можем установить следующую корреспонденцию:

1 → 0

2 → 1

3 → -1

4 → 2

5 → -2

6 → 3

7 → -3

Давайте проверим, что это взаимно-однозначное соответствие:

Есть ли здесь закономерность? Да. Шаблон таков, что каждое четное натуральное число передается следующему целому числу в порядке, который мы установили. Поскольку порядок включает в себя начало с 0, а затем чередование следующего неиспользованного числа справа и следующего неиспользованного числа слева, это, безусловно, четкий шаблон. Может ли эта закономерность продолжаться вечно? Другими словами, для произвольного натурального числа возникнут ли у нас когда-нибудь проблемы с поиском целого числа, которое можно было бы связать с ним, используя порядок целых чисел, который мы установили здесь? Нет. Шаблон таков, что каждое четное натуральное число передается следующему целому числу в порядке, который мы установили. Поскольку порядок целых чисел включает в себя начало с 0, а затем чередование между следующим неиспользованным числом справа и следующим неиспользованным числом слева, и поскольку целые числа продолжаются вечно в обоих этих направлениях, мы можем продолжать этот шаблон вечно.
Если мы продолжим в том же духе, не закончатся ли когда-нибудь числа для составления пар из каждого набора? Нет. Поскольку оба набора бесконечны, мы не можем исчерпать числа ни в одном из наборов. Если мы продолжим этот шаблон, мы когда-нибудь пропустим какие-либо числа в любом наборе? Нет. Поскольку порядок, который мы установили в целых числах, начинается в середине, а затем чередуется между движением влево и вправо, и поскольку мы всегда выбираем следующее неиспользованное число в этом шаблоне, мы не будем оставлять целые числа вне порядка. .

Итак, это спаривание взаимно-однозначное соответствие!

Так как у нас есть однозначное соответствие между набором натуральных чисел и набором целых чисел, мы можем заключить, что мощность набора целых чисел равна ℵ ₀ !

Будьте осторожны — это НЕ ЕДИНСТВЕННЫЙ способ установить однозначное соответствие между набором целых чисел и набором натуральных чисел. Существует несколько РАЗНЫХ способов установить взаимно однозначное соответствие, которые предполагают РАЗНОЕ упорядочение целых чисел. Можете ли вы придумать ОТЛИЧНУЮ личную переписку, чем та, что приведена здесь? (На самом деле, существует БЕСКОНЕЧНОЕ количество правильных способов установить однозначное соответствие между целыми и натуральными числами, каждый из которых следует своему образцу!)

Что это говорит нам о природе бесконечных «чисел»?
Интересно, что ℵ ₀ описывает как количество натуральных чисел, так и количество целых чисел. Это интересно, потому что количество целых чисел должно быть , умноженное на , число натуральных чисел, потому что для каждого положительного натурального числа существует положительное И отрицательное целое число. Целые числа также имеют 0, чего нет у натуральных чисел. Таким образом, это говорит нам о том, что мощность множества целых чисел должна быть 2ℵ 9.0697 0 +1, или, другими словами, n( Z )=2ℵ ₀ +1.
Но поскольку мы можем поставить множество целых чисел во взаимно однозначное соответствие с множеством натуральных чисел, мы знаем, что мощность множества целых чисел должна быть ℵ ₀ , или, другими словами, n( Z )=ℵ ₀ . Таким образом, эти две величины должны быть равными , а это означает, что 2ℵ ₀ +1 = ℵ ₀!
Сначала это может показаться противоречием, потому что мы знаем, что для любого конечного числа н , 2 н +1 ≠ н . Но помните, что ℵ ₀ означает, что , а не ведет себя как обычное конечное число, потому что это бесконечное !
Давайте посмотрим на это более внимательно: если у нас есть 2ℵ ₀ +1 = ℵ ₀ , и мы знаем из нашего предыдущего обсуждения, что добавление 1 к ℵ ₀ не меняет его, то мы можем заменить ℵ ₀ с ℵ ₀ +1 справа, чтобы получить 2ℵ ₀ +1 = ℵ ₀ +1. Затем вычитание 1 с каждой стороны дает нам: 2ℵ ₀ = ℵ ₀ .
На самом деле, если подумать об этом еще более внимательно, мы можем заметить, что если у нас есть 2ℵ ₀ = ℵ ₀ , то мы можем умножить обе части этого уравнения на 2, чтобы получить 4 ℵ ₀ = 2ℵ ₀ . Но так как 2ℵ ₀ = ℵ ₀ , мы можем заменить 2ℵ ₀ на ℵ ₀ в правой части уравнения, чтобы получить 4ℵ ₀ = ℵ 7 _{0 906.} И с 2ℵ ₀ ≤ 3ℵ ₀ ≤ 4ℵ ₀, и мы знаем, что 2ℵ ₀ и 4ℵ ₀ оба равны ℵ ₀, мы можем заменить ℵ ₀ для обоих 2ℵ ₀ и 4068 и 406 88 и 406 88 и 406 88 и 4068. чтобы получить ℵ ₀ ≤ 3ℵ ₀ ≤ ℵ ₀ , следовательно, мы также должны иметь 3ℵ ₀ = ℵ ₀.
Затем, если мы умножим это уравнение на 2 с обеих сторон, мы получим 6ℵ ₀ = 2ℵ ₀ . Но так как 2ℵ ₀ = ℵ ₀ , мы можем заменить ℵ ₀ на 2ℵ ₀ в правой части уравнения, чтобы получить 6ℵ ₀ = ℵ ₀ _. и с 4ℵ ₀ ≤ 5ℵ ₀ ≤ 6ℵ ₀, и мы знаем, что 4ℵ ₀ и 6ℵ ₀ Оба равны ℵ ₀, мы сможем подбадривать ℵ _{_{_{_{_{_{_{_. и 6ℵ ₀ в этом неравенстве получаем ℵ ₀ ≤ 5ℵ ₀ ≤ ℵ ₀ , а значит, мы должны иметь 5ℵ ₀ = ℵ ₀ также.}}}}}}}
Обратите внимание, что мы можем продолжать этот шаблон вечно, так что мы можем видеть, что для любого регулярного конечного числа n мы имеем:
п ℵ ₀ = ℵ ₀
Итак, умножение ℵ ₀ на любое правильное конечное число меняет , а не ! (По сути, идея здесь в том, что бесконечное «число» ℵ ₀ настолько велико, что умножения его на что-то еще, что не является бесконечным, будет недостаточно, чтобы изменить его.)

У нас еще есть несколько других бесконечных множеств, на которые нужно обратить внимание: рациональные числа Q , действительные числа R и иррациональные числа. Начнем с рациональных чисел. Можем ли мы поставить их во взаимно однозначное соответствие с натуральными числами?

Мощность множества рациональных чисел

Напомним, что множество рациональных чисел определяется как множество всех чисел, которые можно записать в виде дробей. Можем ли мы поставить это множество во взаимно однозначное соответствие с натуральными числами?

Это кажется сложным — чтобы упростить это, давайте сначала просто выпишем все положительных рациональных чисел.

Если мы попытаемся выписать все положительные рациональные числа дважды, нам придется начать так:

Этот набор действительно грязный. Это совсем не похоже на множество натуральных чисел. На самом деле, этот набор продолжается вечно в куче разных направлений. Каждая строка бесконечно уходит вправо, а каждый столбец вечно уходит вниз. Как мы вообще можем надеяться найти способ поставить это во взаимно-однозначное соответствие с натуральными числами, если натуральные числа всегда идут в одном направлении?

Из наших исследований с целыми числами мы можем видеть, что пока мы можем выстроить элементы множества в определенном порядке, мы можем поставить элементы во взаимно-однозначное соответствие с натуральными числами . Это заставляет нас называть бесконечные множества с мощностью ℵ ₀ СЧЕТНЫМИ, потому что их всегда можно выстроить в определенном порядке и «сосчитать». Эти множества бесконечны, но их можно «сосчитать», если мы готовы продолжать считать вечно.

Итак, давайте посмотрим, есть ли способ выстроить положительные рациональные числа в ряд. Хорошо, если мы нарисуем следующую диаграмму, а затем пройдемся по рациональным числам в порядке, указанном стрелками, мы сможем выстроить все рациональные числа в определенном порядке:

Поскольку рациональные числа всегда идут вправо и всегда вниз, мы можем просто двигаться вперед и назад по диагонали, чтобы выстроить их все в ряд. Так вот как начнется переписка:

1 → 0/1

2 → 1/1

3 → 1/2

4 → 1/3 (мы не отправляем 4 в 2/2, потому что 2/2=1 и мы уже отправили 2 в 1…)

5 → 1/4

Проверим, что это взаимно однозначное соответствие:

Есть ли здесь закономерность? Да. В этом порядке есть логика, которую мы можем видеть на картинке; он включает в себя зигзагообразные движения вперед и назад по диагональным линиям. Обратите внимание, что мы не можем увидеть этот шаблон, если просто начнем перечислять фактическую пару; здесь гораздо проще увидеть закономерность, если мы нарисуем картинку. Может ли эта закономерность продолжаться вечно? Да. Мы сможем вечно продолжать это зигзагообразное движение по положительным рациональным числам.
Если мы продолжим в том же духе, не закончатся ли когда-нибудь числа для составления пар из каждого набора? Нет. Поскольку оба набора бесконечны, мы не можем исчерпать числа ни в одном из наборов. Если мы продолжим этот шаблон, мы когда-нибудь пропустим какие-либо числа в любом наборе? Нет. Так как порядок, который мы установили в положительных рациональных числах, начинается с одного угла, а затем проходит зигзагом по каждой диагонали в наборе, мы не оставим в порядке ни одного целого числа; опять же, это действительно ясно, когда мы смотрим на нарисованную нами картинку, хотя очень трудно понять, если мы просто перечислим порядок чисел. Часто лучший способ показать закономерность — это просто нарисовать картинку!

Итак, это спаривание взаимно-однозначное соответствие!

Поскольку у нас есть однозначное соответствие между множеством положительных рациональных чисел и множеством натуральных чисел, мы можем заключить, что мощность множества положительных рациональных чисел равна ℵ ₀ !

А как насчет множества всех рациональных чисел? Помните, что Q — это символ множества рациональных чисел, и поэтому Q ⁺ — это символ множества положительных рациональных чисел, а Q ^— — это символ множества отрицательных рациональных чисел. Мы уже знаем, что n( Q ⁺ ) = ℵ ₀. А поскольку отрицательных рациональных чисел должно быть столько же, сколько и положительных рациональных чисел, мы также должны иметь n( Q-) = ℵ ₀. Поскольку множество рациональных чисел включает в себя все положительные рациональные числа и все отрицательные рациональные числа, а также число 0 (которое не является ни положительным, ни отрицательным), то общее количество элементов в множестве рациональных чисел должно быть: n( Q ) = n( Q ⁺ )+n( Q ^— )+1. Таким образом, заменить в ℵ ₀ для N ( Q ⁺ ) и N ( Q ^— ) дает N ( Q ) = ℵ ₀ +ℵ ₀ +168 +168 +168 +1698 +168 +2 +1698 +2 +1698 +2 +1698 +2 +1698. +1. Но мы знаем, что добавление или умножение ℵ ₀ на конечные числа, такие как 1 и 2, ничего не меняет! Таким образом, мы можем написать: n( Q ) = 2ℵ ₀ +1 = ℵ ₀ , и поэтому мы имеем n( Q ) = ℵ ₀ .

Таким образом, мощность рациональных чисел равна ℵ ₀ !

Что это говорит нам о природе бесконечных «чисел»?
Интересно, что ℵ ₀ описывает как количество натуральных чисел, так и количество рациональных чисел. Это интересно, потому что количество рациональных чисел должно быть много-много раз количество натуральных чисел. Сколько еще раз? Давайте снова посмотрим на нашу картину положительных рациональных чисел:
Здесь мы видим, что положительные рациональные числа составляют своего рода квадрат, который имеет бесконечную высоту и бесконечную ширину. Поскольку каждую строку и каждый столбец можно поставить во взаимно однозначное соответствие с натуральными числами, мы можем видеть, что высота этого квадрата должна быть ℵ ₀, а ширина этого квадрата должна быть ℵ ₀ . Поскольку мы знаем, как найти площадь квадрата (это просто длина, умноженная на высоту), мы знаем, что число рациональных чисел должно быть ℵ 9.0697 0 × ℵ ₀ , что совпадает с ℵ ₀ ² .
Итак, мощность множества положительных рациональных чисел должна быть ℵ ₀ ² , или, другими словами, n( Q ⁺ )=ℵ ₀ ² .
Но поскольку мы можем поставить множество положительных рациональных чисел во взаимно однозначное соответствие с множеством натуральных чисел, мы знаем, что мощность множества рациональных чисел должна быть ℵ ₀ , или, другими словами, n( Q ⁺ )=ℵ ₀ . Таким образом, эти две величины должны быть равными , а это означает, что ℵ ₀ ² = ℵ ₀!
Сначала это может показаться противоречием, потому что мы знаем, что для любого конечного числа n , отличного от 0 или 1, n ² ≠ n . Но помните, что ℵ ₀ ведет себя , а не как обычное конечное число, потому что это бесконечность !
Давайте посмотрим на это более внимательно: если у нас есть ℵ ₀ ² = ℵ ₀ , то мы можем умножить обе части этого уравнения на ℵ ₀, чтобы получить ℵ _{0 _{ℵ 609874 ^{3 0}} ² . Но с момента ℵ ₀ ² = ℵ ₀, мы можем заменить ℵ ₀ для ℵ ₀ ² С правой стороной уравнения до получения ₀ 3}
3
3
3
3
3
. _. Затем, если мы умножим это уравнение на ℵ ₀ с обеих сторон, мы получим ℵ ₀ ⁴ = ℵ ₀ ² . But since ℵ ₀ ² = ℵ ₀ , we can substitute ℵ ₀ for ℵ ₀ ² on the right side of the equation to get _{ℵ ₀ ⁴ = ℵ ₀ .}
Обратите внимание, что мы можем продолжать этот шаблон вечно, так что мы можем видеть, что для любого правильного ненулевого конечного числа н , у нас:
ℵ ₀ ⁿ = ℵ ₀
Итак, возведение ℵ ₀ в степень любого правильного конечного числа, отличного от нуля, меняет , а не ! (В основном идея здесь в том, что бесконечное «число» ℵ ₀ настолько велико, что возведения его в любую небесконечную степень будет недостаточно, чтобы изменить его. )

Мощность множества действительных чисел:

Теперь давайте посмотрим на реальные числа:

Множество действительных чисел, очевидно, тоже бесконечно, но имеет ли оно ту же бесконечную мощность, что и множество натуральных чисел? Трудно сказать.

Помните, что к действительным числам относятся любые числа, которые можно записать в виде десятичной дроби. Поэтому, чтобы даже начать перечислять их все, нам нужно перечислить все возможные десятичные дроби. С чего бы мы начали? Как только мы выберем одно десятичное число для начала, какое десятичное число мы выберем следующим?

Получается, что множество действительных чисел НЕ имеет той же мощности, что и множество натуральных чисел, но нам нужно уметь это ДОКАЗАТЬ. Как вы докажете, что это не можно ли установить любое однозначное соответствие между данным набором и набором натуральных чисел? Просто показать, что одно конкретное соответствие не является взаимно-однозначным соответствием, недостаточно, потому что может существовать другое взаимно-однозначное соответствие, которое работает. Вместо этого мы должны придумать общий аргумент , который показывает, почему нет пары между двумя множествами будет однозначное соответствие.

Одним из очень распространенных методов ДОКАЗАТЕЛЬСТВА в математике является то, что мы называем 9.0064 ДОКАЗАТЕЛЬСТВО ПРОТИВОРЕЧИЕМ . Если мы хотим доказать, что что-то ложно, мы часто используем этот вид доказательства. В этом методе ДОКАЗАТЕЛЬСТВА мы предполагаем, что то, что мы пытаемся доказать, ложно, на самом деле истинно , и мы показываем, что предположение, что это истинно, приводит к противоречию . Если мы предполагаем, что что-то верно, и это предположение приводит к противоречию, то мы должны заключить, что наше первоначальное предположение было ложным. Вы уже видели, как я использую этот метод доказательства. Помните это доказательство из предыдущей лекции?:

Мы хотим доказать, что для любого конечного числа n , n ≠ n +1.
Начнем с предположения, что n = n +1.
Вычитание n с каждой стороны дает нам 0 = 1.
Это явно неверно — утверждение, что 0=1, является противоречием! Таким образом, наше предположение о том, что n = n +1, которое привело к этому уравнению, должно быть ложным.
Следовательно, мы можем заключить, что для любого конечного числа н , н ≠ н +1.

Это доказательство было доказательством от противного .

Итак, теперь давайте попробуем использовать доказательство от противного, чтобы доказать, что мощность множества действительных чисел равна , а не ℵ ₀ :

Начнем с предположения, противоположного тому, что мы хотим доказать: мы предполагаем, что мощность действительных чисел равна ℵ ₀ .

Это означает, что множество действительных чисел может быть поставлено во взаимно однозначное соответствие с натуральными числами.

Каждое действительное число может быть записано в виде десятичного числа, поэтому это означает, что мы можем составить список действительных чисел, записанных в виде десятичных знаков, так что мы соединим первый элемент списка с натуральным числом один, а второе десятичное число в списке с натуральное число 2 и так далее…

Например, наш список действительных чисел может начинаться так:

2.19456283980…

0,73646556586…

0,74654433322…

5.04

3.33333333333…

Теперь мы хотим показать, что будет проблема с выстраиванием всех десятичных знаков таким образом; лучший способ сделать это — показать, что независимо от того, как мы выстраиваем десятичные дроби, мы всегда будем оставлять десятичную дробь . Потому что, если мы опустим десятичную дробь, у нас не будет однозначного соответствия.

Давайте попробуем найти десятичную дробь, которая не попала в список, выстроив все числа таким образом:

1 → 20. 19456283980…

2 → 0,73646556586…

3 → 0,74654433322…

4 → 5.04

5 → 3,33333333333…

Создадим новую десятичную дробь, которой нет в списке. Для первого десятичного разряда или десятого разряда, чтобы убедиться, что это новое число , а не , то же самое, что и первое действительное число в нашем списке, нам просто нужно выбрать любую цифру, которая будет отличаться от цифры в десятых разрядах действительное число, которое находится в паре с натуральным числом 1. В этом случае наше первое число — 20,19.456283980…. В этом числе стоит 1 на десятом месте. Итак, нам просто нужно выбрать любую цифру, которая НЕ 1, и поставить ее на десятое место нашего нового числа. Давайте выберем 7. Итак, наше новое число начинается с 0,7…. Следовательно, поскольку они имеют разные цифры десятых, это новое число не может быть реальным числом в нашем списке, которое находится в паре с натуральным числом 1.

Теперь нам нужно выбрать второе десятичное или сотое место этого нового числа. Чтобы сделать это таким образом, чтобы наш новый номер был , а не — это то же самое число, что и второе действительное число в нашем списке, нам просто нужно выбрать любую цифру, которая будет отличаться от цифры в сотых долях действительного числа, которое находится в паре с натуральным числом 2. В этом случае, второе число в списке — 0,7364655658…. В этом числе 3 стоит на сотых, поэтому нам просто нужно выбрать любую цифру, НЕ равную 3, и поставить ее на сотые места нашего нового числа. Давайте выберем 5. Итак, наше новое число теперь начинается с 0,75…. Следовательно, поскольку у них разные цифры сотых, это новое число не может быть реальным числом в нашем списке, которое находится в паре с натуральным числом 2.

Мы повторяем эту процедуру для третьего знака после запятой или тысячных, убедившись, что тысячный разряд нашего нового числа отличается от тысячного разряда третьего числа в нашем списке действительных чисел. Так что в этом случае мы можем поставить любую цифру, кроме 6, в тысячном разряде нашего нового числа, потому что 6 — цифра в тысячном разряде третьего числа в списке действительных чисел. Давайте выберем 1. Итак, теперь наше новое число 0,751… и равно 9.0064, а не — третье реальное число в нашем списке.

Мы повторяем эту процедуру для четвертого знака после запятой или десятитысячных, убедившись, что десятитысячный разряд нашего нового числа отличается от десятитысячного разряда четвертого числа в нашем списке действительных чисел. Так что в этом случае мы можем поставить любую цифру, кроме 0, в тысячном разряде нашего нового числа, потому что 0 — это цифра в десятитысячном разряде четвертого числа в списке действительных чисел (поскольку 5,04 можно переписать как 5,0400 без меняя его). Давайте выберем 1. Итак, теперь наше новое число 0,7511… и равно 9.0064, а не , четвертое реальное число в нашем списке.

Мы продолжаем делать это всегда, так что, вообще говоря, n -й десятичный разряд нашего нового числа отличается от n -го десятичного разряда n -го действительного числа в нашем списке.

Если мы продолжим в том же духе, то получим новое действительное число, записанное в виде десятичной дроби, в которой хотя бы одна десятичная цифра полностью отличается от того же десятичного разряда для каждого отдельного числа в нашем списке действительных чисел. Наш новый номер будет иметь другую цифру первого десятичного разряда, чем первое число в списке, другую цифру второго десятичного разряда из второго числа в списке, другую цифру третьего десятичного разряда из третьего числа в списке, другую четвертую цифру. цифра десятичного разряда из четвертого числа в списке и т. д. Поскольку десятичные разряды идут бесконечно, у нас никогда не закончатся десятичные разряды, поэтому мы можем быть уверены, что каждое число в списке действительных чисел имеет по крайней мере один десятичный разряд, который отличается от нашего нового номера. Таким образом, независимо от того, как мы выстраиваем реальные числа, мы всегда можем придумать новое число, которого нет в списке!

Но это противоречие! Если мы выстроим все действительные числа в список, то все действительные числа окажутся в списке, и мы не сможем придумать новое действительное число, которого нет в списке! Поскольку предположение, что все действительные числа могут быть выстроены в определенном порядке, приводит к противоречию, мы должны заключить, что наше предположение неверно, и, следовательно, действительные числа не могут быть выстроены в каком-либо определенном порядке без пропуска некоторых чисел. . Поскольку мы никогда не можем выстроить все действительные числа в определенном порядке, мы не можем установить однозначное соответствие между множеством действительных чисел и множеством натуральных чисел, и, следовательно, мощность множества действительных чисел не может быть быть ℵ ₀ . Мощность набора действительных чисел должна быть другим бесконечным «числом!»

Другое бесконечное «число»: ℵ

₁
Итак, мы нашли другое бесконечное «число!» Бесконечное «число», описывающее количество элементов в множестве действительных чисел, отлично от ℵ ₀, потому что действительные числа нельзя поставить в однозначное соответствие с натуральными числами. Мы назовем это новое бесконечное «число» ℵ ₁ (или с, символ, который используется в книге). Итак, теперь ℵ ₁ является бесконечным «числом», точно так же, как ℵ ₀ , за исключением того, что ℵ ₀ описывает количество элементов в наборе натуральных чисел, ℵ ₁ описывает количество элементов в наборе. действительных чисел. Ясно, что ℵ ₁ должно быть больше бесконечности, чем ℵ 9.0697 0 , потому что множество действительных чисел больше, чем множество натуральных чисел. Точно так же, как мы говорим, что нечто является СЧЕТНЫМ, если оно имеет мощность ℵ ₀, мы говорим, что множество НЕСЧЕТНО, если оно имеет мощность ℵ ₁. Мы описываем множества с мощностью ℵ ₁ как НЕСЧЕТНЫЕ, потому что их нельзя выстроить по порядку и, следовательно, «сосчитать». Если бы эти множества можно было выстроить по порядку и «сосчитать», мы смогли бы создать однозначное соответствие с целыми числами, и это означало бы, что множество имело мощность ℵ ₀ вместо ℵ ₁ .
Вот также способ взглянуть на рисунок рисунка ℵ ₀ по сравнению с ℵ ₁ . Любой набор, мощность которого ℵ ₀, является дискретным, что означает, что он содержит различные отдельные элементы, которые можно выстроить в ряд. Например, если бы мы нарисовали целые числа на числовой прямой, картина этого выглядела бы так:
.
Это последовательность отдельных точек. Любой набор, имеющий мощность ℵ ₀ можно нарисовать таким образом, с его элементами в виде последовательности отдельных упорядоченных точек.
Однако, если бы мы нарисовали действительные числа на числовой прямой, картина этого выглядела бы так:
Это сплошная непрерывная линия. Любое множество, имеющее мощность ℵ ₁, можно нарисовать таким образом, чтобы его элементы представляли собой одну непрерывную линию.
Это дает нам визуальную картину того, насколько эти бесконечности так отличаются друг от друга. Счетная бесконечность может продолжаться вечно в одном или нескольких направлениях, но в ней нет бесконечного числа элементов между любыми двумя элементами, как в действительных числах. Элементы счетного множества дискретны. Однако в несчетном множестве элементов так много, что все пространство между любыми двумя элементами заполнено бесконечным числом других элементов, что делает множество непрерывным.
Мощность множества иррациональных чисел
Итак, теперь у нас есть последнее бесконечное множество для рассмотрения, которое мы еще не рассматривали: множество иррациональных чисел. (Помните, что это всего лишь набор действительных чисел, которые НЕ являются рациональными числами.) Поскольку иррациональные числа, как и действительные числа, могут иметь десятичные дроби, которые продолжаются вечно без повторения, мы подозреваем, что иррациональные числа имеют мощность ℵ ₁ от действительные числа вместо мощности ℵ ₀ натуральных чисел. Но нам нужно это доказать. Опять же, мы собираемся использовать ДОКАЗАТЕЛЬСТВО ПО ПРОТИВОРЕЧИЮ:
.
Во-первых, предположим, что иррациональные числа имеют мощность ℵ ₀ .
Если мы сложим вместе все рациональные числа со всеми иррациональными числами, то получим действительные числа.
Таким образом, если мы добавим количество рациональных чисел к количеству иррациональных чисел, мы должны получить ℵ ₁ .
Но если мощность иррациональных чисел ℵ ₀ , это даст нам ℵ ₀ + ℵ ₀ = ℵ ₁ .
Но мы уже знаем, что ℵ ₀ + ℵ ₀ = 2ℵ ₀ = ℵ ₀, потому что умножение ℵ ₀ на любое конечное число не меняет его!
Итак, если предположить, что мощность рациональных чисел равна ℵ ₀ , мы в итоге докажем, что ℵ ₀ = ℵ ₁ , что является противоречием!
Таким образом, наше предположение о том, что мощность иррациональных чисел равна ℵ ₀ должно быть ложным.
Следовательно, мощность иррациональных чисел должна быть ℵ ₁ , такая же, как и мощность действительных чисел.
Сводка бесконечных мощностей
Итак, наконец, мы определили мощность всех важных бесконечных множеств: (Помните, что мы записываем мощность множества A как n(A).)
н( Н ) = ℵ ₀
н ( Z ^*) = ℵ ₀
н ( Q ) = ℵ ₀
n( R ) = ℵ ₁ (или c)
n(множество иррациональных чисел) = ℵ ₁ (или c)
Переопределение бесконечных множеств
Теперь мы можем создать новое определение бесконечного множества на основе того, что мы уже узнали о бесконечных мощностях:
Если множество может быть поставлено во взаимно-однозначное соответствие с ПРАВИЛЬНЫМ подмножеством самого себя, то это БЕСКОНЕЧНОЕ МНОЖЕСТВО.
Ясно, что если множество конечно, его нельзя поставить во взаимно однозначное соответствие с собственным подмножеством самого себя, потому что у нас закончатся числа в правильном подмножестве для сопоставления с элементами множества, потому что собственное подмножество Подмножество всегда содержит меньше элементов, чем родительское множество. Но с бесконечным набором у нас не обязательно возникает эта проблема, потому что у нас никогда не заканчиваются числа в любом наборе для объединения в пары, каждый набор бесконечен.
Будьте осторожны, чтобы не прочитать неправильно это определение: оно говорит, что любое бесконечное множество может быть поставлено во взаимно-однозначное соответствие с собственным подмножеством самого себя, но НЕ говорит, что бесконечное множество может быть поставлено во взаимно-однозначное соответствие. соответствие КАЖДОМУ собственному подмножеству. Например, множество действительных чисел МОЖЕТ быть поставлено во взаимно однозначное соответствие с множеством иррациональных чисел, которое является правильным подмножеством (мы знаем это, потому что ранее доказали, что действительные числа и иррациональные числа имеют одинаковую мощность). ℵ ₁ .). Но множество действительных чисел НЕ МОЖЕТ быть поставлено во взаимно однозначное соответствие с множеством рациональных чисел, как мы доказали выше. И набор рациональных, и набор иррациональных чисел являются правильными подмножествами действительных чисел, но действительные числа могут ТОЛЬКО быть поставлены во взаимно однозначное соответствие с иррациональными числами, а НЕ с рациональными числами. Технически, чтобы показать, что множество бесконечно, нам нужно только придумать ОДНО правильное подмножество множества, которое можно поставить во взаимно-однозначное соответствие с множеством.
Например, если я хочу ДОКАЗАТЬ, что множество натуральных чисел бесконечно, все, что мне нужно сделать, это придумать подмножество натуральных чисел, которое можно расположить в определенном порядке, который будет продолжаться вечно, чтобы я мог установить вести индивидуальную переписку. Я выбираю множество четных целых чисел. Этот набор продолжается вечно, потому что четные целые числа продолжаются вечно, и его легко упорядочить. Я только что настроил переписку следующим образом:
1 → 2
2 → 4
3 → 6
4 → 8
.
.
.
Очевидно, что если я просто отправлю каждое натуральное число в его двойное число, я получу взаимно однозначное соответствие. Это показывает мне, что множество четных натуральных чисел можно поставить во взаимно однозначное соответствие с натуральными числами. Множество четных натуральных чисел, очевидно, является ПРАВИЛЬНЫМ подмножеством натуральных чисел, потому что каждое четное натуральное число находится в множестве натуральных чисел, а число 1 (или любое другое нечетное число фактически) является элементом натуральных чисел, но не из четных натуральных чисел. Таким образом, с помощью определения, данного выше, мы доказали, что множество натуральных чисел является БЕСКОНЕЧНЫМ МНОЖЕСТВОМ, показав, что оно имеет собственную подгруппу, с которой оно может быть поставлено во взаимно однозначное соответствие.
Можете ли вы найти другую правильную подгруппу натуральных чисел, которую можно поставить во взаимно однозначное соответствие с натуральными числами?
Что такое целые числа? Определение, примеры, список и символы
Определение целых чисел
В нашей повседневной жизни мы используем числа для счета, такие как 1, 2, 3, …. . и так далее. Целые числа — это совокупность всех основных счетных чисел и 0. В математике счетные числа называются натуральными числами. Таким образом, мы можем определить целое число как набор всех натуральных чисел и 0. Целые числа также включают в себя все положительные целые числа наряду с нулем.

К целым числам относятся натуральные числа, начинающиеся с 1.
Давайте рассмотрим несколько примеров целых чисел.
Целые номера Не целых чисел
0, 14, 97, 345, 8901 и 888888 -5 (отрицательные числа), 7,3 (децимальные), ⅘ (фракции) (отрицательные числа), 7,3 (децимальные), ⅘ (фракции) 9 (отрицательные номера), 7,3 (децимальные), ⅘ (фракции)
Набор целых чисел обозначается буквой ‘ W ‘.
Вт = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,.…}
Целые числа в числовой строке
Набор целых чисел может отображаться в числовой строке, как показано ниже.
Наименьшее и наибольшее целое число
Наименьшее целое число равно 0. В целых числах 0 не имеет предшествующего или предшествующего числа. Не существует «наибольшего» целого числа.
Свойства целых чисел
Основные операции сложения, вычитания, умножения и деления приводят к четырем основным свойствам целых чисел.
Замыкание Свойство:
Сумма и произведение двух целых чисел всегда является целым числом и замкнуто при сложении и умножении.
Рассмотрим два целых числа, 5 и 8.
5 + 8 = 13; целое число
5 × 8 = 40; целое число
Коммутативное свойство:
Сумма и произведение целых чисел одинаковы, даже если порядок чисел поменять местами.
Рассмотрим два целых числа, 2 и 7.
2 + 7 = 7 + 2 = 9
2 × 7 = 7 × 2 = 14
Свойство коммутативности верно для сложения и умножения.
Ассоциативное свойство:
То, как целые числа группируются при сложении или умножении, не меняет сумму или произведение.
Рассмотрим три целых числа 2, 3 и 4.
2 + (3 + 4) = 2 + 7 = 9
(2 + 3) + 4 = 5 + 4 = 9
Таким образом, 2 + (3 + 4) = (2 + 3) + 4
2 × (3 × 4) = 2 × 12 = 24
(2 × 3) × 4 = 6 × 4 = 24
Таким образом, 2 × (3 × 4) = (2 × 3) × 4
Распределяющее свойство:
Умножение целого числа распределяется по сумме или разности целых чисел. Применение распределительного свойства упрощает решение уравнения.
Рассмотрим три целых числа: 9, 11 и 6.
9 × (11 + 6) = 9 × 17 = 153
(9 × 11) + (9 × 6) = 99 + 54 = 153
Таким образом, 9 × (11 + 6) = (9 × 11) + (9 × 6)
Разница между целыми числами и натуральными числами
целые числа Натуральные номера
12
Целые числа включают все натуральные числа и ноль. Натуральные числа обычно используются для счета предметов или вещей.
Набор целых чисел W = {0,1,2,3,…}. Набор натуральных чисел N = {1,2,3,…}.
Наименьшее целое число равно 0. Наименьшее натуральное число равно 1.
Из этих различий мы легко можем сделать вывод, что любое целое число, кроме 0, является натуральным числом. Можно сказать, что множество натуральных чисел является подмножеством целых чисел.
Интересные факты
Не существует «наибольшего» целого числа .
Каждое целое число имеет непосредственного предшественника, кроме 0.
Десятичное число или дробь, расположенная между двумя целыми числами, не является целым числом.
Заключение
В двух словах можно сказать, что целые числа являются основной частью системы счисления, которая включает в себя все положительные целые числа от 0 до бесконечности. Чтобы узнать больше о таких понятиях, как натуральные числа и действительные числа, ознакомьтесь с игровой обучающей платформой SplashLearn. С помощью увлекательных мероприятий и курсов он направлен на то, чтобы преобразовать обучение K-8 и вооружить детей навыками, необходимыми в 21 веке.
Решенные примеры
Q1. Сложите числа тремя различными способами. Укажите используемое свойство.
25 + 36 + 15
Решение:
(а) 25 + 36 + 15 25 + 36) + 15 = 61 + 15 = 76
Метод III: (25 + 15) + 36 = 40 + 36 = 76
Здесь мы использовали свойство ассоциативности.
Q2. Решите 6 × (8 – 3), используя распределительное свойство умножения.
Решение:
Применение формулы закона распределения a(b + c) = ab + ac
6 × (8 – 3)
= 6(8) – 6(3)
= 40 – 18
= 22
Q3. При каком условии произведение двух целых чисел равно нулю?
Решение:
Если произведение двух целых чисел равно нулю, то одно из них обязательно равно нулю.
Например, 0 × 5 = 0 и 19 × 0 = 0
Если произведение двух целых чисел равно нулю, то оба они могут быть равны нулю.
0 × 0 = 0
Произведение двух целых чисел равно нулю при условии, что одно или оба из них равны нулю.
Практические задачи
1100, 1101, 1102
1090, 1010, 1100
1101,1102,1103
1000, 1001, 1002
Правильный ответ: 1100, 1101, 1102
Каждый целый номер. По другому, чем 0. — натуральное число, поэтому следующие три числа после 1099 — натуральные числа.
20
22
12
14
Правильный ответ: 12
Целые числа от 22 до 35: 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34
636 × (10 + 2)
(600 + 30) × 102
636 × (100 + 2)
(600 + 2) × 102
Правильный ответ: 636 × (100 + 2)
636 × (100 + 2) = 636 × 102
172
252
272
300
Правильный ответ: 252
Используя формулу распределения, $6 × (40 + 2) = (6 × 40) + 2 × 0 = 1 252$
Часто задаваемые вопросы
Приведите примеры и не примеры целых чисел.
Целое число — это любое положительное число, не содержащее дробной или десятичной части, и ноль.
Примеры: 0, 1, 2, 3, 4, 5, 6 и 7
Непримеры: 3, 2,7 или 3 ½
Можно ли записать 1/2 как целое число?
Нет, мы не можем записать данную дробь как целое число. Целые числа не включают дробные или десятичные числа.
Мы можем округлить ½ или 0,5 до 1 или вниз до 0.
Для чего используются целые числа?
Целые числа используются в качестве строительных блоков для углубленного понимания более сложных числовых идентификаторов, таких как действительные, рациональные и иррациональные числа. Округляя десятичное число до ближайшего целого числа, мы можем упростить вычисления и быстрее решать задачи.
Классификация вещественных чисел — УРОКИ МАТЕМАТИИ КЕЙТ
Сопроводительный ресурс:
Классификация реальных чисел Boom Cards
Обратите внимание, что в этом уроке используются иррациональные числа. Если вы ищете более простой урок , обязательно ознакомьтесь с моим уроком «Классификация рациональных чисел», который включает в себя целые числа, целые числа и рациональные числа.
Типы номеров
Знаете ли вы, что числа существуют не вечно? Давным-давно у людей не было слов или символов для таких простых чисел, как 1, 2, 3. . . До того, как были изобретены числа и их символы, люди использовали палки и делали отметки на камнях, чтобы следить за вещами. К счастью, со временем система счисления развилась, поэтому нам больше не нужно использовать палочки или поднимать пальцы, чтобы считать! Теперь у нас есть имена и символы, которые мы используем для представления чисел. (Хотите увидеть некоторые из более ранних символов, которые использовались? Прочтите эту статью об истории системы счисления.)
Система счисления, которую мы используем сегодня, имеет много различных типов чисел. В этом уроке мы рассмотрим 6 типов: натуральные числа, целые числа, целые числа, рациональные числа, иррациональные числа и действительные числа. Мы начнем с простейшего набора чисел, натуральных чисел.
Натуральные числа (счетные числа)
1, 2, 3 . . . .
Натуральные числа начинаются с 1 и идут вверх. Их также иногда называют счетными числами, потому что мы начинаем с 1, когда учимся считать. Натуральные числа не включают ноль, отрицательные числа, десятичные дроби или дроби. Скорее всего, это первый тип чисел, о котором вы узнали в детстве.
Примеры натуральных чисел:
6
18
305
Не натуральные числа:
0
-7
24,6
целые числа
0, 1, 3. . .
Целые числа начинаются с нуля и идут вверх. Так же, как и натуральные числа, с добавлением числа 0. Целые числа не включают отрицательные числа, дроби или десятичные дроби.

Примеры целых чисел:
5
23
167
14
НЕ Целые числа:
8.9
-2
3/5
Бонусное примечание: Знаете ли вы, что людям было очень трудно принять 0 как число? Раньше они думали, что это безумие, когда число обозначает «ничего». Я надеюсь, вы рады, что он был изобретен, потому что у нас не было бы компьютеров без числа 0! Прочтите эту историю числа ноль, чтобы узнать больше интересных фактов о нуле (знали ли вы, что кто-то думал, что это зло?).
Целые числа
. . . -3, -2, -1, 0, 1, 2, 3. . .
Этот набор чисел похож на целые числа, но включает и отрицательные числа. Целые числа не включают дроби или десятичные дроби. Все целые числа также являются целыми числами.
Примеры целых чисел:
8
-34
721
-5
Не целых чисел:
6.2
-7/8
Rational Numbers

40064.

Любое число, которое можно представить в виде дроби, считается рациональным числом. Я бы перечислил их для вас, но это невозможно, потому что их так много! Все целые числа также являются рациональными числами, потому что вы можете переписать любое из них в виде дроби, используя 1 в знаменателе (например, 5 можно переписать как дробь 5/1). К рациональным числам также относятся конечные десятичные дроби (десятичные дроби, которые останавливаются в какой-то точке), повторяющиеся десятичные дроби (например, .2323…) и числа, которые уже записаны в виде дробей.

В более техническом определении рационального числа будет сказано, что — это отношение двух целых чисел . Когда рациональное число записывается в виде дроби, числитель и знаменатель будут целыми числами (вы можете записать дробь без десятичных знаков сверху или снизу дроби).

Примеры рациональных чисел:
13,25
-7 (это можно записать в виде дроби -7/1)
2/5
. 4444 . . . . (Это можно записать как дробь 4/9)

НЕРАЦИОНАЛЬНЫЕ Числа:
Десятичная дробь, которая идет бесконечно, не заканчиваясь и не повторяясь, не является рациональной. Вот два примера:

Иррациональные числа

Числа, которые нельзя записать в виде простой дроби.

Другими словами, не рационально. Иррациональные числа нельзя записать в виде отношения двух целых чисел. Десятичные числа, которые не заканчиваются и не повторяются, являются иррациональными числами. Некоторые иррациональные числа используются так часто, что у них есть собственное имя и символ, например пи (3,14159).265. . . ) и число Эйлера e (2,71828…).

Многие квадратные корни, кубические корни и т. д. также являются иррациональными числами. Например, квадратный корень из 41 приблизительно равен 6,40312423. . . Это десятичное число, которое не заканчивается и не повторяется, и является иррациональным числом.

Обратите внимание: не все квадратные корни иррациональны! Например, квадратный корень из 64 равен 8 (что рационально). Вам может понадобиться сначала упростить выражение, чтобы определить тип числа.

Примеры иррациональных чисел:

НЕ Иррациональные числа:

Вещественные числа

Множество всех рациональных и иррациональных чисел.

Все числа, которые мы рассмотрели в этом уроке, называются действительными числами. Таким образом, все натуральные числа, целые числа, целые числа, рациональные числа и иррациональные числа являются действительными числами.

Так все ли числа настоящие числа? Неа. Но большинство чисел, с которыми вы знакомы, являются действительными числами.

Помните, люди думали, что 0 как число — это безумие? Возможно, именно так вы почувствуете, когда я скажу вам, что существуют числа, называемые мнимыми числами. Название «воображаемый» довольно неудачно, так как оно создает у людей впечатление, что они просто воображаемые числа, но они существуют и полезны в таких вещах, как электротехника и квантовая физика (это довольно сложные вещи, поэтому вы можете не узнать о них до тех пор, пока не получите более высокий уровень знаний). уровень курса математики). Посмотрите этот урок «Воображаемые числа», если хотите узнать больше!

Использование графического органайзера для классификации действительных чисел

Вот диаграмма, которая поможет вам понять, как все различные типы чисел связаны друг с другом. Натуральные числа находятся внутри целых чисел, потому что все натуральные числа также являются целыми числами. Целые числа находятся внутри целых чисел, потому что все целые числа также являются целыми числами. Целые числа находятся внутри рациональных чисел, потому что все целые числа можно записать в виде дроби.

Обратите внимание, что рациональные числа и иррациональные числа находятся в совершенно разных полях. Действительное число будет либо рациональным, либо иррациональным, но никогда тем и другим одновременно. Все эти типы чисел составляют то, что мы называем системой действительных чисел, это набор всех рациональных и иррациональных чисел.

Допустим, вам нужно классифицировать следующие числа:

Когда я классифицирую числа, я начинаю с рациональной стороны в самая внутренняя секция и пробираюсь наружу.

Давайте сначала посмотрим на -5. Это натуральное число? Нет, натуральные числа не включают отрицательные числа. -5 — это целое число? Нет, целые числа также не включают отрицательные числа. Это целое число? Да, целые числа включают -1, -2, -3 и т. д., поэтому -5 — это целое число . -5 также является рациональным числом, поскольку его можно записать в виде дроби -5/1, но термин «целое число» является более конкретным.

Теперь давайте посмотрим на квадратный корень из 17. 17 не является полным квадратом, поэтому оно не упрощается до рационального числа.