Урок математики на тему «Дроби и проценты», (6 класс)
Тема урока: « Дроби и проценты».
Цель: обобщить и систематизировать знания по темам: сложение и вычитание обыкновенных дробей, умножение и деление обыкновенных дробей, проценты;
развивать коммуникабельность, креативность, умение анализировать, обобщать, сравнивать, выделять главное;
воспитывать познавательный интерес к предмету и уверенность в своих силах.
Педагогические задачи:
Создать условия для повышения мотивации учащихся в потребности усвоения новых умений;
Организовать ситуацию постановки учебной проблемы;
Помочь учащимся в постановке цели урока и поиске путей решения данной проблемы;
Создать ситуацию самостоятельного поиска новых способов решения в группе, в паре;
Создать условия для самоконтроля и самооценивания.
Планируемые результаты:
предметные: формулировать и применять правила действий с обыкновенными дробями; формировать умение решать задачи на дроби, используя различные стратегии и способы рассуждений;
метапредметные: применять знания в различных ситуациях; предлагать разные варианты в зависимости от предложенной ситуации; применять приёмы самоконтроля при выполнении заданий;
личностные: организовывать свою деятельность, т. е. ставить личные цели, их достигать и оценивать результаты.
е. ставить личные цели, их достигать и оценивать результаты.
Тип урока: урок систематизации и обобщения знаний и умений.
Формы работы: самостоятельная, групповая, фронтальная работа.
Оборудование: мультимедийный проектор, компьютер, доска, задачники.
План урока:
Организационный этап.
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Актуализация знаний.
Обобщение и систематизация знаний
Физкультминутка.
Применение знаний и умений в новой ситуации.
Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
Информация о домашнем задании, инструктаж по его выполнению.
Рефлексия.
Ход урока.
Организационный этап.
Здравствуйте ребята. Посмотрите, какая сегодня замечательная погода, как ярко светит солнце. Я надеюсь, что после сегодняшнего урока ваше настроение будет таким же солнечным. Начнем урок.
Начнем урок.
Отгадайте загадку:
Без чего не могут обойтись математики, барабанщики и даже охотники? (Дробь) (Слайд 3 )
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Ребята, а нужны ли дроби? Может быть, можно обойтись без них?
(Ответы детей)
Вы правы, конечно, нужны. На протяжении всей своей жизни мы постоянно сталкиваемся с дробями. А сейчас на уроках учимся выполнять различные действия с ними. Какова же тема сегодняшнего урока?
(Учащиеся формулируют тему урока).
А сейчас каждый ряд составит кластер: в центре — название дроби, а по сторонам — умения.
Составляют кластеры, передают друг другу по цепочке, дополняют, обсуждают (приложение 1). Вместе с учителем делают вывод, определяют цели урока.
Актуализация знаний.
— Давайте узнаем на деле, насколько дружим с дробями:
Правило вычитания дробей .(Ответы детей)
Соотнесите выражение и его значение: а) ; б) ; в) .
1) ; 2) ; 3). ( Слайд 4)
Правило сложения дробей. (Ответы детей)
Сложите дроби: а) ; б) ; в) . (Слайд 5)
Расставь числа так, чтобы получилось верное равенство. (Слайд 6 )
Как умножить дробь на дробь? (Ответы детей)
Как найти часть от числа? Как найти процент от числа? (Ответы детей)
Найдите: а) четвертую часть от 100; б) пятую часть от 80 ; в) 25% от 100; г)20% от 80.(Ответы детей)
Ответы: а) 25 ; б) 16 ; в) 25 ; г) 16.
Обратить внимание детей на одинаковые ответы в заданиях. Ученики делают вывод: 25% = ; 20% = . (Слайд 7 )
Обобщение и систематизация знаний
Работа по учебнику. Анализируем и рассуждаем.
— Иногда нужное число процентов от величины можно найти совсем просто. Например, чтобы найти 10% от 100, нужно разделить 100 на 10.
Рассматривают таблицу. Приводят свои примеры.
Проценты | Дроби |
10% | |
20% | |
25% | |
50% | |
75% |
Вопрос: Как записать дробь в виде процентов?
стр. 27, № 114.
Решение задач.
Стакан вмещает 200 г молока. В него налили 160 г. Какая часть стакана осталась ненаполненной?
Обсуждается решение задачи. К доске идут два ученика, предложившие разные способы решения.
1 способ. 1) 160 : 200 = стакана наполнено.
2) 1 — стакана не наполнена.
Ответ: стакана.
2 способ. 1) 200 – 160 = 40 (г) – молока не долили в стакан.
2) 40 : 200 = стакана не наполнена.
Ответ: стакана.
— На сколько процентов наполнен стакан? (Ответы детей)
Записать на доске и в тетрадях :
В первый день туристы прошли 40% намеченного пути, во второй день 1/4 пути, а в третий день остальные 14 км. Чему равна длина всего пути?
Один ученик решает задачу у доски с полным объяснением.
Решение: 40% =
пути прошли туристы за два дня.
пути прошли в третий день.
14 : (км) – длина всего пути.
Ответ: 40 км.
— Стр. 28 из учебника № 118.
Физкультминутка.
Ребята, давайте немного отдохнем. Все встали около своих парт. Выполним «Математическую зарядку».
Под музыку выполняют « Математическую зарядку». (Слайд 8 )
«Да» — руки вверх, «нет» — руки вниз.
В дроби знаменатель – 9.
В дроби числитель – 6.
Дробь — неправильная.
1 копейка – 1% рубля.
30 % — .
Молодцы! А теперь продолжим работу.
Применение знаний и умений в новой ситуации.
1. Осваивает алгоритмы.
Заполните самостоятельно таблицу. Затем выполните взаимопроверку.
Дробь | Дробь со знаменателем 100 | Проценты |
2.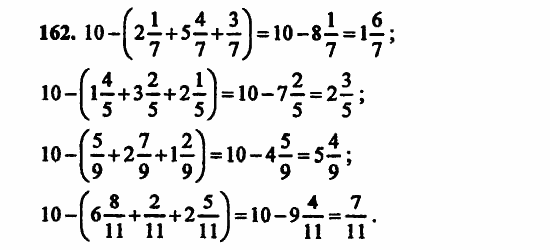 Анализируем и рассуждаем.
Анализируем и рассуждаем.
Следующее задание выполним в группах.
стр. 26 № 97(б)
Ученики работают в группах по 4 человека. Затем проверяется решение .
Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
А сейчас выполним самостоятельную работу по вариантам
(приложение 2). У каждого на столе карточка с заданием. На выполнение работы 10 минут.
Выполняют самостоятельную работу в тетрадях. Четыре человека работают на ноутбуках, выполняют тест по теме «Дроби и проценты». Используется электронное приложение к учебнику.
По окончании выполняется проверка. Дети видят ответы на слайде. (Слайд 9 )
Каждый проверяет свою работу самостоятельно, исправляет ошибки. Проводится анализ наиболее распространенных ошибок.
Информация о домашнем задании, инструктаж по его выполнению.
Урок подходит к концу. Ребята, откройте дневники и запишите задание на дом.
Ребята, откройте дневники и запишите задание на дом.
На доске и слайде записано домашнее задание: Задачник: п. 1.6,
№ 97(а), 101(а-г), 108, 120
(Слайд 10 )
Откройте задачники. Найдите все номера, записанные на доске. Внимательно прочтите задания. Какие правила нужно вспомнить для выполнения домашнего задания? (Ответы детей)
IX.Рефлексия
Закончить урок мне бы хотелось словами знаменитого русского писателя Льва Толстого:
«Человек подобен дроби:
в знаменателе – то, что он о себе думает,
в числителе – то, что он есть на самом деле.
Чем больше знаменатель, тем меньше дробь».
Как вы понимаете эти слова? (Ответы детей)
Да, ребята, можно сказать, что Толстой вывел «формулу» для обозначения человеческого характера.
Из математики мы знаем, что если знаменатель равен числителю, то будет единица. Но также мы знаем, что знаменатель не должен равняться нулю, так как вся дробь не будет иметь смысла. И ещё, чем больше знаменатель, тем меньше дробь.
И ещё, чем больше знаменатель, тем меньше дробь.
Очень редкое явление, когда «знаменатель» равен «числителю» , то есть мнение окружающих не всегда совпадает со своей самооценкой.
Родители с детства учили нас тому, что любить себя плохо, что приличный человек должен думать сначала о других, о потом уже о себе.
Я считаю, что уважать себя должен каждый. Это просто необходимо для сохранения чувства собственного достоинства. Но любить себя надо в меру. Если человек думает только о себе, то он эгоист. Нужно всегда думать о чувствах других.
Я надеюсь, что слова великого писателя запомнятся вам на всю жизнь.
Спасибо за урок! (Слайд 11)
Презентация к уроку математики «Дроби и проценты»
PPTX / 390.49 Кб
Опубликовано в группе «УРОК.РФ: группа для участников конкурсов»
Математика 6 класс.
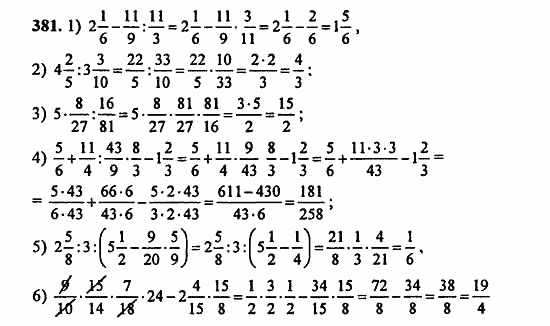 Обыкновенные дроби презентация, доклад
Обыкновенные дроби презентация, докладМатематика 6 класс. Обыкновенные дроби.
Делимость чисел
Сложение и вычитание дробей с разными знаменателями
Признаки делимости на 10, 5, 2
Делители и кратные
Признаки делимости на 9 и 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Основное свойство дроби
Сокращение дробей
Приведение дробей к общему знаменателю
Сравнение, сложение, вычитание дробей
Сложение и вычитание смешанных чисел
ТРЕНАЖЕР
Сложение, вычитание дробей с разными знаменателями
ТРЕНАЖЕР
Сложение и вычитание смешанных чисел
END
Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Д(18): 1, 2, 3, 6, 9, 18
Пример:
Д(37): 1, 37
Д(25): 1, 5, 25
Д(6): 1, 2, 3, 6
Д(19): 1, 19
КОНЕЧНОЕ КОЛИЧЕСТВО
Кратным натурального числа а называют натуральное число, которое без остатка делится на а.
К(8): 8, 16, 24, 32 …
Пример:
К(11): 11, 22, 33, 44 …
К(48): 48, 96 …
К(99): 99, 198, 297 …
БЕСКОНЕЧНОЕ КОЛИЧЕСТВО
Пример:
1. Доказать, что число 70525 кратно числу 217.
70525 : 217=
70525
217
3
651
—
____
54
2
2
434
____
—
108
5
5
1085
____
—
0
325
Делится нацело,
значит 70525 кратно 217.
Пример:
2. Доказать, что число 729 делитель числа 225261.
225261 : 729 =
225261
729
3
2187
—
____
65
6
0
1
____
6561
9
—
0
309
Делится нацело,
значит 729 делитель числа 225261.
На 10: число оканчивается цифрой 0.
Примеры:
На 5: число оканчивается цифрами
0 и 5.
Примеры:
На 2: число должно быть четным (оканчивается на цифры 0, 2, 4, 6, 8).
Примеры:
Нечетные числа оканчиваются цифрами 1, 3, 5, 7, 9.
№38.
чет (4)
неч (3)
неч (7)
чет (6)
чет (2)
чет (8)
неч (5)
чет (4)
неч (9)
неч (1)
неч (7)
чет (8)
чет (4)
неч (3)
неч (1)
чет (6)
чет (2)
чет (4)
неч (5)
чет (4)
неч (1)
неч (7)
неч (1)
чет (6)
Вывод: сумма и разность одинаковых по четности чисел четна, разных по четности чисел – нечетна.
Простые числа имеют только 2 делителя (1 и само число).
(см. таблицу на форзаце учебника)
Число 1 не является ни простым, ни составным.
Составные числа имеют более 2 делителей.
Примеры:
Простые: 2, 3, 5, 7,…
Составные: 4, 6, 8, 9,…
На 9: если сумма цифр числа делится на 9, то и число делится на 9.
На 3: если сумма цифр числа делится на 3, то и число делится на 3.
Примеры: 1) , т.к.
7+5+4+3+2=21, 21 3, 21 9.
2) 2772825 3 ( 9), т.к. 2+7+7+2+8+2+5=33, 33 3, 33 9.
3)5402070 3 ( 9), т.к.
5+4+2+7=18, 18 3, 18 9.
Любое число можно разложить на простые множители.
Примеры:
216 =
216
2
108
2
54
2
27
3
9
3
3
3
1
Примеры:
60 =
60
2
30
2
15
3
5
5
1
НОД (х, у) – это наибольшее натуральное число, на которое числа х и у делятся без остатка.
Пример:
Д(6): 1, 2, 3, 6
Д(12): 1, 2, 3, 4, 6, 12
НОД(6, 12) = 6
План нахождения НОД:
Разложить числа на простые множители.
Обвести в кружок одинаковые множители.
Найти их произведение – это и есть НОД.
Примеры: НОД(12; 18) =
12
2
6
2
3
3
1
18
2
9
3
3
3
1
Примеры: НОД(675; 825) =
675
5
135
5
27
3
11
825
5
165
5
33
3
9
3
3
3
1
11
1
Примеры: НОД(24; 35) =
24
2
12
2
6
3
1
35
5
7
7
2
2
1
Если у чисел нет общих множителей, кроме 1, то они называются взаимно простые (НОД(х, у)=1).
Нет общих делителей, кроме 1.
НОК (х, у)
– наименьшее натуральное число, которое кратно и х, и у.
План нахождения НОК:
Разложить числа на простые множители.
В НОК выписать наибольшее число.
Домножить выписанное число на недостающие множители из другого разложения.
Найти произведение.
Примеры: НОК(6; 8) =
6
2
3
3
1
8
2
4
2
2
2
1
выписали
Недостающий множитель
8
НОК(72; 99) =
72
2
36
3
1
99
3
33
3
11
11
12
99
3
4
2
2
2
1
НОК(34;51;68) =
34
2
17
17
1
51
3
17
17
1
68
68
2
34
2
17
17
1
НОК(a, b) =
=2700
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Примеры:
1)
2)
НОД используется при сокращении дробей
Примеры:
Сократить дробь:
198
2
99
3
33
3
121
1452
2
726
2
363
3
11
11
1
11
1
11
11
НОД(198,1452)=
, значит числитель и
знаменатель можно сократить на 66
Примеры:
Сократить дробь:
56
2
28
2
14
2
7
196
2
98
2
49
7
7
7
1
7
1
НОД(56, 196)=
, значит числитель и
знаменатель можно сократить на 28
Примеры:
Сократить дробь:
Любые две дроби можно привести к одному и тому же знаменателю.
Наименьший общий знаменатель (НОЗ) равен НОК знаменателей дробей.
План приведения к НОЗ:
Найти НОК знаменателей дробей – это НОЗ.
Расставить дополнительные множители для всех дробей (НОЗ делим на знаменатели дробей).
Умножить числители дробей на дополнительный множитель.
НОК(6; 8) =
6
2
3
3
1
8
2
4
2
2
2
1
Примеры:
4
3
НОК(9; 15) =
9
3
3
3
1
15
5
3
3
1
Примеры:
5
3
План:
Привести дроби к НОЗ.
Сравнить (сложить, вычесть) полученные дроби.
НОК(6; 8) =
6
2
3
3
1
8
2
4
2
2
2
1
Примеры: 1. Сравнить
4
3
НОК(6; 8) =
6
2
3
3
1
8
2
4
2
2
2
1
Примеры: 2.
4
3
+
=
+
НОК(6; 8) =
6
2
3
3
1
8
2
4
2
2
2
1
Примеры: 2.
3
4
—
=
—
=
=
План сложения:
Привести дробные части чисел к НОЗ.
Отдельно выполнить сложение целых и дробных частей.
Если нужно – сократить дробь.
Если при сложении дробных частей получилась неправильная дробь, — выделить целую часть и прибавить к полученной целой части.
План вычитания:
Привести дробные части чисел к НОЗ.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на 1 целую часть.
Отдельно выполнить вычитание целых и дробных частей.
Примеры:
3
2
4
5
+
2
3
2
21
10
=
8
3
9
Примеры:
5
3
—
4
28
9
10
7
7
9
7
—
3
3
4
15
8
6 класс.
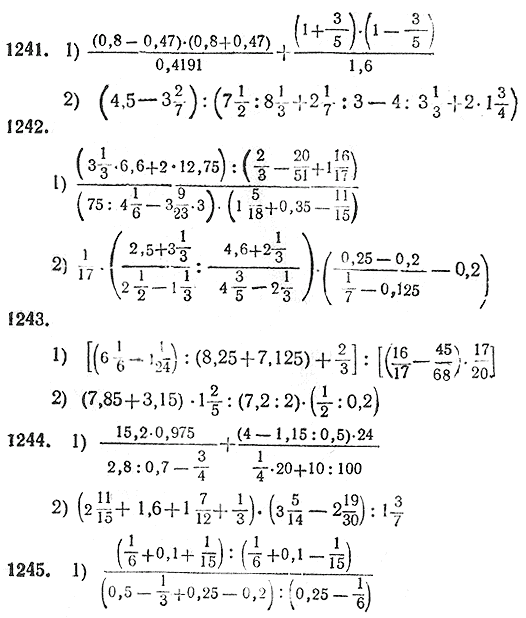 Математика. Никольский. Учебник. Ответы к стр. 89
Математика. Никольский. Учебник. Ответы к стр. 89Рациональные числа
Отрицательные дроби
Ответы к стр. 89
435. Запишите три отрицательные дроби.
— 4/6, — 3/2, — 5/5.
436. Какие числа называют противоположными? Приведите примеры.
Числа, отличающиеся только знаком, называют противоположными: — 4/6 и 4/6, — 3/2, и 3/2, — 5/5 и 5/5.
437. Какое число противоположно:
а) числу нуль;
б) положительному числу;
в) отрицательному числу?
а) нуль противоположен сам себе;
б) положительному числу противоположно отрицательное число;
в) отрицательному числу противоположно положительное число.
438. Что называют модулем:
а) положительной дроби; б) отрицательной дроби; в) нуля?
а) саму эту дробь;
б) противоположную ей (положительную) дробь;
в) число нуль.
439. Какие из дробей являются положительными, какие отрицательными: 1/6, — 1/3, 0/4, — 2/7, 3/1, — 0/2?
Отрицательные дроби: — 1/3, — 2/7, — 0/2.
Положительные дроби: 1/6, 0/4, 3/1.
440. Назовите дроби, противоположные дробям: 1/2, 2/9, — 1/3, — 3/7, -4/11.
дробь — 1/2 противоположна дроби 1/2;
дробь — 2/9 противоположна дроби 2/9;
дробь 1/3 противоположна дроби — 1/3;
дробь 3/7 противоположна дроби — 3/7;
дробь 4/11 противоположна дроби -4/11.
441. Какое число противоположно самому себе?
Число нуль противоположно само себе.
Упростите запись по образцу (442-443):
442. а) |8| = 8; б) |-7| = 7; в) |1/9| = 1/9; г) |-2/3| = 2/3;
д) |2|; е) |-3|; ж) |0|; з) |1/4|;и) |- 1/5|; к) |2/7|.
д) |2| = 2;
е) |-3| = 3;
ж) |0| = 0;
з) |1/4| = 1/4;
и) |- 1/5| = 1/5;
к) |2/7| = 2/7.
443. а) |-1/4|;б) |-2/9|;в) |-1/8|;г) |-8/15|;
д) |- 3/8|;е) |- 8/9|;ж) — |- 1/2|;з) — |- 1/5|.
а) |-1/4| = 1/4;
б) |-2/9| = 2/9;
в) |-1/8| = 1/8;
г) |-8/15| = 8/15;
д) |- 3/8| = 3/8;
е) |- 8/9| = 8/9;
ж) — |- 1/2| = — 1/2;
з) — |- 1/5| = — 1/5.
444. Сравните:
а) |2/3| и |- 2/3|; б) |-5| и |- 1/2|; в) |- 1/5| и |1/4|.
а) |2/3| = 2/3, |- 2/3| = 2/3,
2/3 = 2/3, следовательно, |2/3| = |- 2/3|;
б) |-5| = 5, |- 1/2| = 1/2,
5 > 1/2, следовательно, |-5| > |- 1/2|;
в) |- 1/5| = 1/5, |1/4| = 1/4,
1/5 < 1/4, следовательно, |- 1/5| < |1/4|.
445. Запишите дробь так, чтобы знак «-» стоял в числителе по образцу:
а) — 3/4 = -3/4; б) — 5/7; в) — 7/3; г) — 4/9; д) — 1/9; е) — 13/12.
б) — 5/7 = -5/7;
в) — 7/3 = -7/3;
г) — 4/9 = -4/9;
д) — 1/9 = -1/9;
е) — 13/12 = -13/12.
446. Запишите дробь так, чтобы знак «-» стоял в знаменателе по образцу:
а) — 3/4 = 3/-4; б) — 6/5; в) — 7/8; г) — 8/9; д) — 17/18; е) — 18/17.
б) — 6/5 = 6/-5;
в) — 7/8 = 7/-8;
г) — 8/9 = 8/-9;
д) — 17/18 = 17/-18;
е) — 18/17 = 18/-17.
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 6 класс
Учебная программа по математике для шестого класса и планы уроков – Time4Learning
Посмотрите наши демонстрации уроков!
Для преподавания математики в 6-м классе вам потребуется обширная учебная программа по математике, которая поможет вам эффективно обучать вашего ребенка, делая изучение математики увлекательным.
Чтобы гарантировать, что ваш ребенок достигает своих учебных целей, важно, чтобы выбранная вами программа по математике для 6-го класса соответствовала всем государственным стандартам и предоставляла множество возможностей для практики. Это поможет вашему ребенку обрести уверенность при освоении новых математических понятий.
Какую математику должен знать шестиклассник?
Основными направлениями математики в программе шестого класса являются чувство чисел и операции, алгебра, геометрия и чувство пространства, измерения, функции и вероятность. Хотя эти математические темы могут вас удивить, они охватывают основы того, что шестиклассник должен изучать по математике.
Хотя эти математические темы могут вас удивить, они охватывают основы того, что шестиклассник должен изучать по математике.
Учащиеся 6-го класса уже должны знать математические факты, чтобы понять более сложные математические понятия. Вот некоторые из навыков, которыми ваш ребенок уже должен владеть в шестом классе:
- Сравнение и упорядочивание чисел с использованием таблицы стоимостных значений и числовых строк
- Умножение 2-значных чисел на 2-значные и 3-значных чисел на 3-значные
- Определение наибольшего общего делителя и наименьшего общего кратного
- Чтение и запись чисел до тысячных в письменной и стандартной форме
- Добавление смешанных номеров с перегруппировкой и без нее
- Измерение прямых, острых, тупых и прямых углов с помощью транспортира
- Написание и вычисление алгебраических выражений
Если вашему учащемуся необходимо повторить математические концепции 5-го класса, вы можете легко получить доступ к этим урокам благодаря нашим гибким параметрам уровня обучения, которые дают вам доступ на один уровень выше и на один ниже уровня по умолчанию для вашего ребенка.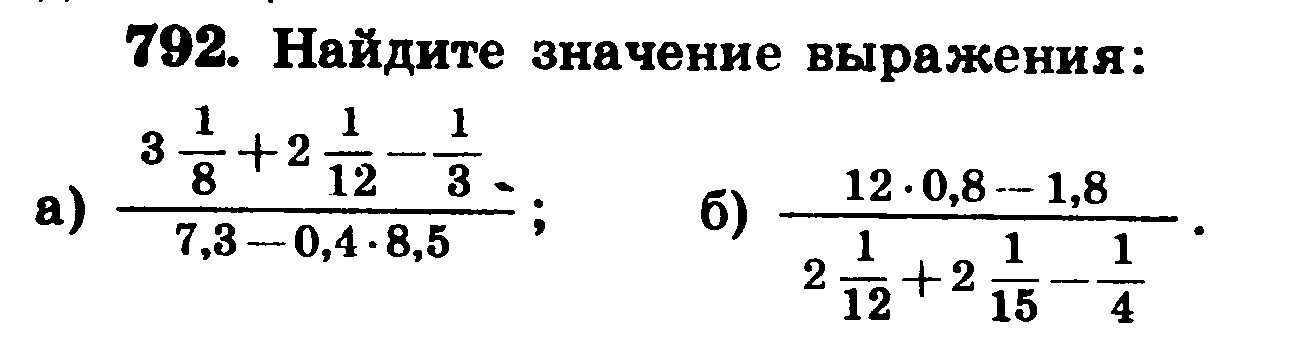
Цели по математике для шестого класса
В начале учебного года вы должны определить для своего ученика цели и задачи по математике в 6-м классе. Ниже приведено общее представление о задачах по математике для 6-го класса, над которыми должен работать ваш ребенок.
- Понимание доалгебраических концепций, таких как использование переменных для упрощения выражений
- Определение десятичного разряда; сравнивать и упорядочивать десятичные числа, используя числовую строку
- Используйте таблицы частот и определите соответствующие интервалы
- Знать, как использовать коэффициенты и ставки для сравнения данных
- Найдите и нанесите точки на график координат, используя упорядоченные пары
- Понимать взаимосвязь между дробями, десятичными знаками и процентами
Математика для шестого класса и последовательность
Глава 1. «Целые числа»
Урок 1. Римские и греческие цифры
Учащиеся будут использовать римские и греческие цифры.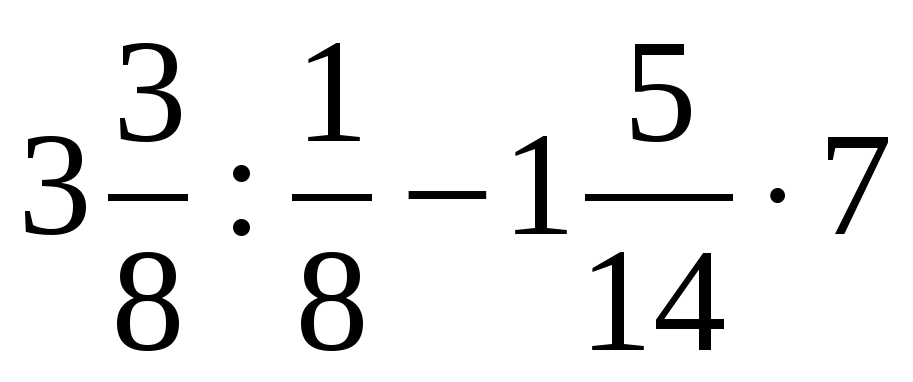
Урок 2. Генерация эквивалентных форм целых чисел
Учащиеся найдут эквивалентные формы для целых чисел.
Урок 3. Сравнение и упорядочивание целых чисел
Учащиеся будут сравнивать и упорядочивать целые числа до одного триллиона.
Урок 4. Округление целых чисел
Учащиеся округляют целые числа до одного триллиона.
Урок 5. Оценка целых чисел
Учащиеся будут оценивать целые числа при решении задач.
Урок 6. Сложение и вычитание целых чисел
Учащиеся будут складывать и вычитать целые числа до одного триллиона.
Урок 7. Умножение и деление целых чисел
Учащиеся будут умножать и делить целые числа до четырех цифр.
Урок 8. Деление целых чисел
Учащиеся будут делить целые числа так, чтобы делимое не превышало пяти цифр, а делитель не превышал трех цифр.
Урок 9. Использование стандартного алгоритма для деления 4-значных дивидендов на двузначные делители
Учащиеся будут использовать стандартный алгоритм для деления 4-значных дивидендов на двузначные делители.
Урок 10: Стратегии решения проблем
Учащиеся будут применять стратегии для решения реальных проблем.
Глава 2. «Операции с целыми числами»
Урок 1. Показатель степени и квадратный корень
Учащиеся будут оценивать выражения, используя показатель степени и квадратный корень.
Урок 2: Порядок действий (GEMDAS)
Учащиеся будут применять порядок действий для решения задач.
Урок 3. Переменные и выражения
Учащиеся будут использовать переменные для упрощения выражений.
Урок 4: Свойства сложения и умножения
Учащиеся будут применять свойства сложения и умножения при решении задач.
Урок 5: Закономерности и последовательности
Учащиеся будут определять закономерности, арифметические и геометрические последовательности.
Урок 6. Одношаговые уравнения с целыми числами
Учащиеся будут решать одношаговые уравнения, используя только целые числа.
Урок 7. Периметр
Учащиеся найдут периметр заданных фигур.
Урок 8. Площадь
Учащиеся определят площадь заданной формы.
Урок 9: Решение задач
Учащиеся будут использовать метод выбора для вычислений и использовать модели и конкретные объекты для решения реальных задач.
Глава 3. «Десятичные дроби»
Урок 1. Генерация эквивалентных форм десятичных дробей
Учащиеся определят десятичное число и запишут число в стандартной, письменной и расширенной форме.
Урок 2. Сравнение и упорядочивание десятичных дробей
Учащиеся будут сравнивать и упорядочивать десятичные дроби, в том числе с помощью числовой строки.
Урок 3. Оценка и округление десятичных дробей
Учащиеся будут округлять и оценивать десятичные дроби при выполнении всех четырех операций.
Урок 4. Сложение и вычитание десятичных дробей
Учащиеся будут складывать и вычитать десятичные дроби, используя деньги.
Урок 5. Умножение десятичных дробей
Учащиеся будут умножать и округлять десятичные дроби.
Урок 6. Деление десятичных дробей
Учащиеся будут делить на целые числа и десятичные дроби.
Урок 7. Научное обозначение
Учащиеся будут сравнивать рациональные числа, используя экспоненциальную запись.
Урок 8. Одношаговые уравнения с десятичными дробями
Учащиеся будут решать одношаговые уравнения с десятичными дробями, используя сложение, вычитание, умножение и деление.
Урок 9: Решение задач
Учащиеся будут использовать стратегии догадок, проверок и обоснования для решения реальных задач.
Глава 4: «Дроби»
Урок 1. Знакомство с дробями
Учащиеся узнают графические и числовые представления дробей и смешанных чисел.
Урок 2. Наименьшее общее кратное
Учащиеся найдут наименьшее общее кратное более чем двух чисел.
Урок 3. Наименьший общий знаменатель
Учащиеся найдут наименьший общий знаменатель для двух или более дробей.
Урок 4. Образцы делимости
Учащиеся узнают правила делимости на 2, 3, 4, 5, 6, 9 и 10 для наборов чисел.
Урок 5: Знакомство с простыми и составными числами
Учащиеся будут решать задачи, используя разложение на простые множители. Урок 6. Факторы и НОД
Урок 7. Упрощение дробей
Учащиеся будут упрощать дроби с помощью разложения на простые множители и наибольшего общего делителя. Учащиеся также покажут остатки от деления в виде упрощенных дробей.
Урок 8. Равнозначные дроби
Учащиеся найдут эквивалентные дроби, найдя недостающую переменную и применяя понятия, используемые для нахождения эквивалентных дробей для неправильных дробей и смешанных чисел.
Урок 9: Дроби и десятичные числа
Учащиеся найдут эквивалентные формы для десятичных и дробных чисел, включая повторяющиеся десятичные числа.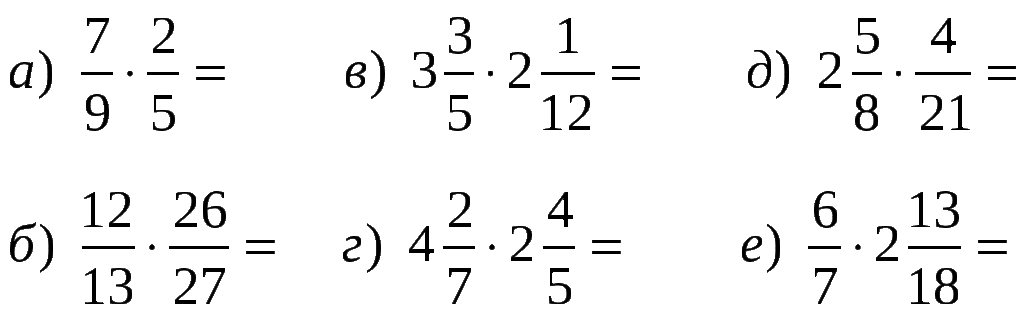
Урок 10. Сравнение и упорядочивание дробей
Учащиеся будут сравнивать и упорядочивать дроби, в том числе с помощью числовой прямой.
Урок 11. Вычисление и округление дробей
Учащиеся будут округлять дроби до ближайшей половины и вычислять суммы, разности, произведения и частные.
Урок 12. Сложение и вычитание дробей с одинаковыми знаменателями
Учащиеся будут складывать и вычитать дроби с одинаковыми знаменателями.
Урок 13. Сложение дробей с разными знаменателями
Учащиеся будут складывать дроби и смешанные числа с разными знаменателями.
Урок 14. Вычитание дробей с разными знаменателями
Учащиеся будут вычитать дроби и смешанные числа с разными знаменателями.
Урок 15. Умножение дробей
Учащиеся будут умножать дроби и смешанные числа.
Урок 16. Деление дробей
Учащиеся будут делить дроби и смешанные числа.
Урок 17. Деление целых чисел на дроби
Учащиеся будут делить целые числа на дроби.
Урок 18. Деление дробей на дроби
Учащиеся будут делить дроби на дроби.
Урок 19. Одношаговые уравнения с дробями
Учащиеся будут решать одношаговые уравнения с дробями и всеми четырьмя операциями. Урок 1: Понимание противоположностей
Урок 2. Использование положительных и отрицательных чисел для представления величин в реальном мире
Учащиеся будут использовать положительные и отрицательные числа для обозначения величин в реальном мире.
Урок 3. Нахождение рациональных чисел на числовой прямой
Учащиеся будут находить рациональные числа на числовой прямой.
Глава 6: «Абсолютное значение»
Урок 1: Понимание абсолютного значения
Учащиеся будут работать, чтобы понять абсолютное значение.
Урок 2. Сравнение абсолютных значений
Учащиеся будут сравнивать абсолютные значения рациональных чисел.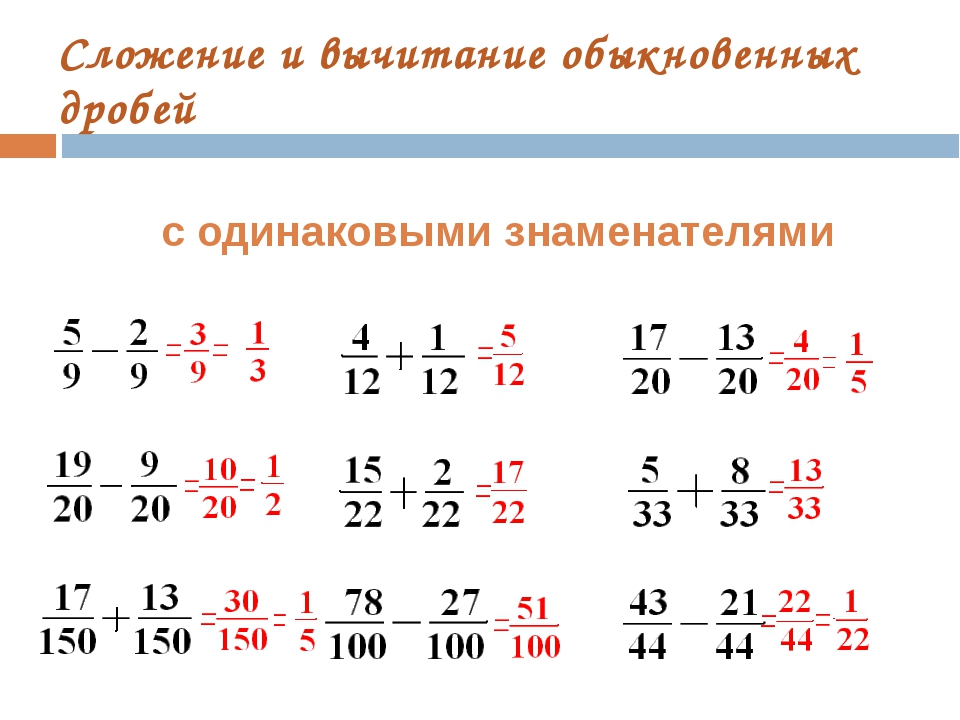 Урок 1. Целые числа в реальном мире
Урок 1. Целые числа в реальном мире
Урок 2. Сравнение и упорядочение целых чисел
Учащиеся будут сравнивать целые и рациональные числа.
Урок 3. Сравнение рациональных чисел
Учащиеся будут сравнивать рациональные числа, которые представляют реальные ситуации.
Урок 4. Сложение и вычитание целых чисел
Учащиеся будут складывать и вычитать целые числа.
Урок 5. Умножение и деление целых чисел
Учащиеся будут умножать и делить целые числа.
Урок 6. Одношаговые уравнения
Учащиеся будут решать одношаговые уравнения с целыми числами, включая дроби и десятичные дроби.
Урок 7. Решение задач
Учащиеся будут использовать дедуктивное или индуктивное рассуждение, процесс исключения или работать в обратном порядке для решения реальных задач.
Глава 8. «Построение графиков»
Урок 1. Знакомство с графиками
Учащиеся должны выбрать соответствующее представление и представить данные, обосновав свой выбор.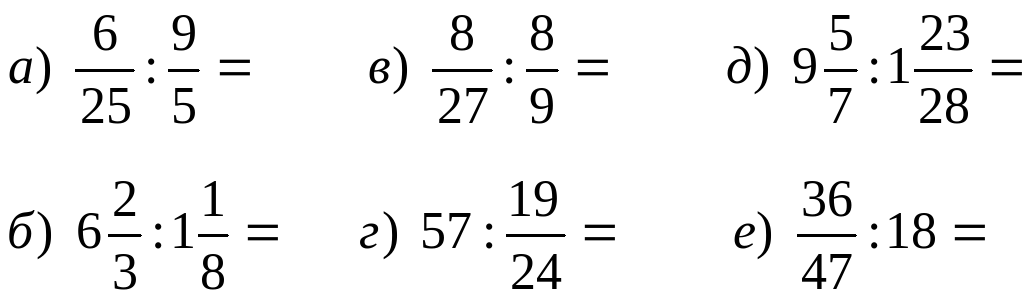
Урок 2. Таблицы частот и линейные графики
Учащиеся будут использовать таблицы частот и определять соответствующие интервалы.
Урок 3. Пиктограммы и диаграммы Венна
Учащиеся будут использовать диаграммы Венна, линейные и линейные графики.
Урок 4. Гистограммы
При ответе на вопросы учащиеся будут использовать гистограммы и гистограммы.
Урок 5. Линейные графики и линейные графики
Учащиеся будут читать и интерпретировать линейные графики, двойные линейные графики и линейные графики.
Урок 6. Двойные гистограммы и двойные линейные диаграммы
Учащиеся будут создавать двойные гистограммы и линейные диаграммы.
Урок 7. Графики координат (Quad. I)
Учащиеся находят и наносят точки на график координат, используя упорядоченные пары.
Урок 8. Показатели центральной тенденции
Учащиеся определят выбросы, диапазон, среднее значение, медиану и моду.
Урок 9: Вводящие в заблуждение графики и статистика
Учащиеся будут работать с честными опросами.
Урок 10: Графики стеблей и листьев
Учащиеся будут читать и интерпретировать графики стеблей и листьев.
Урок 11. Ящичные диаграммы и диаграммы с усами
Учащиеся будут читать, интерпретировать и создавать прямоугольные диаграммы и диаграммы с усами.
Урок 12. Решение задач
Учащиеся составят таблицу, упорядоченный список, нарисуют картинку или будут использовать логику для решения задач. 9Урок 1. Отражение точек по осям
Урок 2. Поиск точек на координатной плоскости
Учащиеся будут находить и располагать пары рациональных чисел на координатной плоскости.
Урок 3: графическое отображение точек для решения задач
Учащиеся рисуют точки для решения задач. Урок 1. Метрическая система
Урок 2: Обычная система
Учащиеся будут использовать правильные инструменты и выполнять преобразования, используя обычную систему измерения.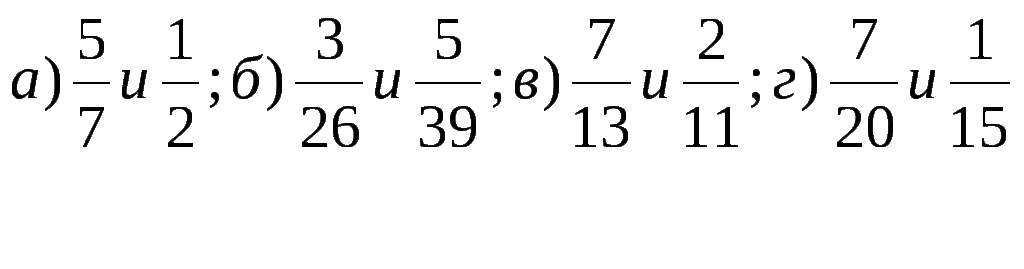
Урок 3. Измерение
Учащиеся найдут приближенное измерение с точностью до ближайшей единицы и, используя разумность, определят наилучшую единицу измерения.
Урок 4: Время и температура
Учащиеся будут оценивать и находить меры времени и прошедшего времени, а также обычную и метрическую температуру.
Урок 5. Площадь и периметр
Учащиеся найдут площадь и периметр четырехугольника.
Урок 6. Решение проблем
Учащиеся объяснят процесс решения задач, опишу шаги и решат более простую задачу из реальной жизни. Урок 1: Отношения и пропорции
Урок 2: Решение пропорций и единиц измерения
Учащиеся будут устанавливать пропорции и решать единицы измерения и задачи, используя геометрические изображения.
Урок 3. Ставки
Учащиеся будут решать задачи со ставками и простыми процентами.
Урок 4: Понимание удельных цен
Учащиеся поймут удельные цены и смогут использовать диаграммы для определения удельных цен.
Урок 5: Проценты
Учащиеся будут показывать эквивалентные формы процентов в дробях и десятичных дробях и решать задачи, которые больше 100%.
Урок 6. Круговые диаграммы
Учащиеся будут читать и интерпретировать круговые диаграммы, а также определять соответствующие диаграммы с заданными процентными значениями.
Урок 7. Решение задач на проценты
Учащиеся находят процент от числа, целое число или процент.
Урок 8. Проценты и реальная жизнь
Учащиеся найдут цену, используя налог с продаж и скидки.
Урок 9. Решение задач
Учащиеся будут делать прогнозы на основе данных и решать многоступенчатые задачи.
Глава 12. «Использование соотношений и коэффициентов для сравнения и решения задач»
Урок 1. Использование таблиц эквивалентных соотношений для решения задач
Учащиеся будут использовать таблицу эквивалентных соотношений для решения задач.
Урок 2. Использование таблицы для сравнения и построения коэффициентов
Учащиеся будут использовать таблицу для сравнения и построения коэффициентов.
Урок 3. Выражение отношений и решение целых чисел с помощью процентов
Учащиеся будут выражать отношения и решать целые числа, используя проценты.
Урок 4. Использование рассуждений о соотношениях для преобразования единиц измерения
Учащиеся будут использовать рассуждения о соотношениях для преобразования единиц измерения.
Глава 13. «Геометрия»
Урок 1. Основные определения геометрии
Учащиеся будут различать точки, лучи, прямые, отрезки и плоскости.
Урок 2: Углы
Учащиеся будут измерять и классифицировать углы, решать задачи с неизвестными углами, находить сумму углов в многоугольниках и определять особые углы.
Урок 3. Классификация линий
Учащиеся будут классифицировать линии как параллельные, перпендикулярные и наклонные.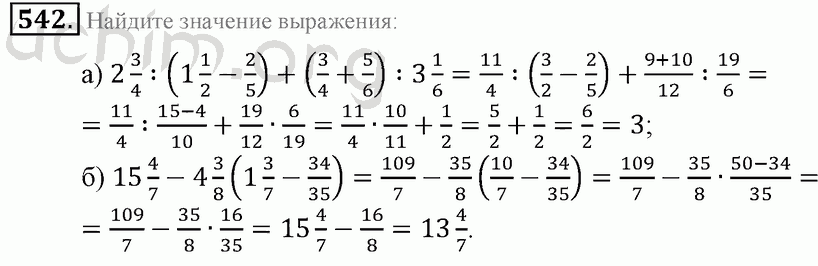
Урок 4. Классификация треугольников
Учащиеся определят пропорции подобных треугольников и классифицируют их по сторонам или углам.
Урок 5. Треугольники
Учащиеся найдут недостающие меры, используя теорему Пифагора.
Урок 6. Классификация многоугольников
Учащиеся определят название фигуры по сторонам.
Урок 7: Трехмерные фигуры
Учащиеся определят характеристики трехмерных фигур с помощью граней, ребер и вершин и определят различные виды.
Урок 8. Классификация четырехугольников
Учащиеся будут классифицировать четырехугольники и находить сечения.
Урок 9: Геометрические узоры
Учащиеся найдут недостающий член в геометрическом узоре и будут использовать мозаику
Урок 10: Сходство, Конгруэнтные фигуры, Линии конгруэнтности Учащиеся будут применять концепции
900 подобия и симметрии. Урок 11.
 Преобразования
Преобразования
Учащиеся определят переносы, повороты и отражения на координатной сетке.
Урок 12. Площадь
Учащиеся оценят и найдут площади правильных и неправильных фигур. Учащиеся также сравнивают диаметр и радиус.
Урок 13. Нахождение площади путем составления и разложения фигур
Учащиеся найдут площадь, составив и разложив фигуры.
Урок 14. Длина окружности
Учащиеся находят площадь и длину окружности.
Урок 15. Пропорциональное изменение
Учащиеся найдут недостающие стороны у подобных треугольников.
Урок 16. Площадь поверхности
Учащиеся найдут площадь поверхности.
Урок 17: Объем
Учащиеся найдут объем призм, кубов и цилиндров.
Урок 18. Решение задач
Учащиеся будут использовать формулу для решения задачи и связывать математические идеи с другими областями содержания в реальных задачах.
Глава 14. «Выражения»
Урок 1. Определение частей алгебраических выражений
Учащиеся будут определять части алгебраических выражений.
Урок 2. Написание и вычисление выражений
Учащиеся будут писать и вычислять выражения.
Урок 3. Использование свойства распределения для записи эквивалентных выражений
Учащиеся моделируют и используют свойство распределения для написания эквивалентных выражений.
Урок 4. Определение эквивалентных выражений
Учащиеся будут определять эквивалентные выражения и объяснять, почему два выражения эквивалентны.
Урок 5. Практический материал: Написание алгебраических выражений с помощью одной операции
Учащиеся будут писать выражения с помощью одной операции для представления реальных ситуаций.
Урок 6. Написание реальных алгебраических выражений с несколькими операциями
Учащиеся будут писать выражения с более чем одной операцией для представления реальных ситуаций.
Глава 15. «Уравнения и неравенства»
Урок 1. Решение уравнений реального мира
Учащиеся будут решать уравнения реального мира.
Урок 2. Написание и решение уравнений реального мира
Учащиеся будут писать и решать уравнения для решения реальных задач.
Урок 3: Написание уравнений с двумя переменными
Учащиеся будут писать уравнения с двумя переменными.
Урок 4: Написание неравенств
Учащиеся будут писать неравенства для представления математических и реальных задач.
Урок 5. Графики решений неравенств
Учащиеся представляют решения неравенств на числовых прямых.
Глава 16: «Функции и вероятность»
Урок 1: Функции
Учащиеся будут определять отношения функций, решать и интерпретировать на графиках.
Урок 2. Графики координат
Учащиеся найдут расстояние между двумя точками и точки графика в 4 квадрантах.
Урок 3. Решение задач
Учащиеся сделают выводы на основе данных и обосновывают обоснованность ответа.
Урок 4. Введение в теорию вероятности
Учащиеся определят возможные результаты и представят вероятность с помощью соотношений.
Урок 5: Экспериментальная и теоретическая вероятность
Учащиеся найдут вероятность события.
Урок 6. Составные события
Учащиеся будут сравнивать события, делать комплименты и перечислять результаты, используя теоретическую вероятность.
Урок 7. Зависимые и независимые события
Учащиеся определят различия между зависимыми и независимыми событиями.
Урок 8. Комбинации и перестановки
Учащиеся найдут комбинации и перестановки.
Урок 9. Решение задач
Учащиеся будут решать задачи, составляя уравнения и упрощая алгебраические выражения.
Почему стоит выбрать программу Time4Learning для шестого класса по математике на дому
Наша учебная программа по математике для 6-го класса может использоваться в качестве основной программы домашнего обучения или в качестве дополнения к другим учебным программам и внеклассным занятиям. Тысячи семей доверяют Time4Learning, чтобы научить всех важнейшим понятиям, которые должны знать учащиеся, и помочь им достичь всех своих целей на год.
Тысячи семей доверяют Time4Learning, чтобы научить всех важнейшим понятиям, которые должны знать учащиеся, и помочь им достичь всех своих целей на год.
Time4Learning позволяет учащимся работать в разных классах. Например, если ваш ученик находится «на уровне» по словесности, но впереди по математике, он может использовать учебную программу по словесности для шестого класса и предлагаемую учебную программу по математике для седьмого класса.
В качестве альтернативы, если ваш шестиклассник посещает обычную школу или использует другую программу домашнего обучения, учебную программу по математике Time4Learning можно использовать в качестве дополнения, чтобы вернуться на правильный путь. Вы можете использовать планы уроков, чтобы найти определенные темы и концепции, и учащиеся могут работать в своем собственном темпе, пропускать и/или повторять уроки.
Дроби в 6-м классе (возраст 10–11 лет)
В 6-м классе ваш ребенок решит множество задач на дроби, десятичные числа и проценты.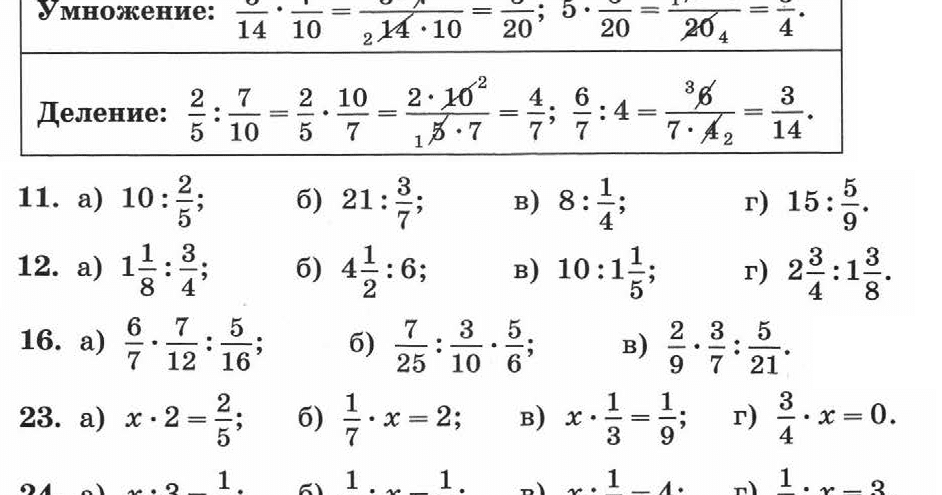 Они будут упрощать дроби, используя общие множители, и будут практиковаться в умножении дробей.
Они будут упрощать дроби, используя общие множители, и будут практиковаться в умножении дробей.
Ключевые слова в этом разделе: общий делитель, числитель, знаменатель, неправильная дробь и смешанное число.
Чему научится ваш ребенок
Взгляните на требования Национальной учебной программы к фракциям для 6-го класса (10–11 лет):
Используйте общие множители для упрощения дробей
Ваш ребенок будет упрощать дроби, используя свои знания об общих множителях. Например, можно упростить до , потому что 4 является множителем как 8, так и 12.
Сравните и упорядочите дроби
Ваш ребенок будет сравнивать дроби и расставлять их по размеру.
Они смогут делать это с правильными дробями (т.е. дробями меньше единицы) и дробями больше единицы (т.е. неправильными дробями или смешанными числами). Например:
больше
больше
Счет со смешанными числами и дробями с разными знаменателями
Ваш ребенок научится складывать и вычитать дроби с разными знаменателями (нижние числа). Они будут делать это, находя эквивалентные дроби с одинаковыми знаменателями. Например:
Они будут делать это, находя эквивалентные дроби с одинаковыми знаменателями. Например:
+ = + =
Ваш ребенок также умеет складывать и вычитать смешанные числа. Смешанное число — это число, записанное как целое и дробное (например, 1 ).
Они будут использовать предметы, диаграммы и символы для решения задач со смешанными числами и дробями, а также для объяснения того, как они решили задачу.
Умножение и упрощение правильных дробей
Ваш ребенок сможет умножать пары правильных дробей (то есть дроби меньше 1) вместе, а затем записывать ответ в простейшей форме.
× = =
Ваш ребенок будет использовать объекты, диаграммы и символы в своих вычислениях.
Разделение правильных дробей на целые числа
Правильные дроби — это дроби со значением меньше 1. Ваш ребенок сможет делить такие дроби на целые числа. Например:
÷ 2 =
Ваш ребенок будет делать это, используя предметы, схемы и символы.
Понимать связь между дробями, делением и десятичными знаками
К 6-му классу очень важно, чтобы дети понимали взаимосвязь между дробями и умножением/делением. Например:
Чтобы найти 36 см, нужно разделить 36 на 4 (36 см ÷ 4 = 9 см).
Если вы знаете, что неизвестная длина равна 36 см, и хотите найти всю длину, умножьте 36 на 4 (36 см × 4 = 144 см).
Ваш ребенок попытается преобразовать простые дроби в десятичные числа (например, = 0,375). Они узнают, что некоторые простые дроби имеют так называемые «повторяющиеся десятичные эквиваленты». Например, имеет повторяющееся десятичное значение 0,333… Это означает, что в нем есть цифры, которые повторяются вечно.
Ваш ребенок также научится округлять десятичные дроби до 3 знаков после запятой.
Использование чисел с 3 знаками после запятой
Ваш ребенок поймет значение каждой цифры в числах с 3 знаками после запятой. Они также смогут умножать и делить числа на 10, 100 и 1000, давая ответы до 3 знаков после запятой. Например:
Они также смогут умножать и делить числа на 10, 100 и 1000, давая ответы до 3 знаков после запятой. Например:
9 ÷ 1000 = 0,009
0·734 × 100 = 73,4
Ваш ребенок будет делить десятичные числа на однозначные целые числа. Сначала они узнают об этом в практических контекстах, связанных с мерами и деньгами (например, 0,65 м ÷ 5 = 0,13 м).
Умножение чисел с десятичными знаками
Ваш ребенок научится умножать однозначные числа с двумя знаками после запятой на целые числа. Например:
2,75 × 2 = 5,5
Они начнут с простых примеров, таких как 0,4 × 2 = 0,8, в практических контекстах, таких как использование денег.
При необходимости используйте письменные методы деления
Ваш ребенок будет использовать письменные методы деления (такие как деление в длинное и короткое деление) в случаях, когда ответ содержит до 2 знаков после запятой. Вы можете узнать больше об этих методах на нашем канале YouTube: см. Как сделать длинное деление и Как сделать короткое деление.
Как сделать длинное деление и Как сделать короткое деление.
Округление чисел для оценки ответов
Ваш ребенок будет округлять числа и оценивать ответы, чтобы проверить свои ответы на десятичные вычисления. Например:
2,56 × 5,3 ≈ 2,5 × 5 = 12,5
Итак, когда ваш ребенок точно ответит на вопрос, он будет ожидать, что его результат будет примерно 12,5. Если они получат ответ типа 1350, они поймут, что что-то пошло не так!
Использование эквивалентов между простыми дробями, десятичными знаками и процентами
Ваш ребенок будет использовать связь между простыми дробями, десятичными знаками и процентами для решения задач. Например, они могут помнить и использовать тот факт, что = 0,5 = 50%, для решения задач.
Как помочь дома
Существует множество способов помочь ребенку понять дроби. Вот лишь несколько идей.
1. Помогите ребенку считать дроби
В 6-м классе ваш ребенок продолжит складывать и вычитать дроби. Теперь они будут использовать дроби с одинаковыми знаменателями (например, + ) и дроби, знаменатели которых кратны одним и тем же числам (например, + ). Теперь они также должны будут складывать и вычитать, используя смешанные числа (например, 2 ).
Теперь они будут использовать дроби с одинаковыми знаменателями (например, + ) и дроби, знаменатели которых кратны одним и тем же числам (например, + ). Теперь они также должны будут складывать и вычитать, используя смешанные числа (например, 2 ).
Ваш ребенок может решать задачи, например 3 + 2 , следующими способами.
Вариант 1
Они могут разделять целые числа и дробные части:
Сначала сложим целые числа: 3 + 2 = 5.
Затем добавьте дробные части: + = .
Наконец, сложите целое число и дробные части вместе, чтобы получить смешанное число: 5.
Вариант 2
Они могли превратить каждое смешанное число в неправильную дробь, затем сложить неправильные дроби и, наконец, преобразовать ответ обратно в смешанное число:
Сначала преобразуйте 3 в неправильную дробь: .
Затем преобразуйте 2 в неправильную дробь: .
Затем сложите неправильные дроби: + = .
Наконец, превратите ответ обратно в смешанное число: = 5 .
Те же стратегии можно применять для вычитания дробей из смешанных чисел.
2. Умножать и делить дроби
Ваш ребенок будет умножать пары простых дробей, например, × = . Их можно познакомить с этой идеей с помощью таких диаграмм:
В этом примере половина показана слева, разделенная по вертикали на две равные части. Затем будет нарисована та же фигура, представляющая четвертей , на этот раз разделенных по горизонтали на четыре равные части. Затем диаграммы будут сложены вместе, чтобы разделить фигуру на восьмые:
Ответ можно найти там, где половина и четверть перекрываются, образуя одну восьмую :
Ваш ребенок сможет увидеть эту из восьми заштриховано, поэтому ответ на × есть . Спросите ребенка о том, что происходит, когда вы умножаете простые дроби. Вы могли бы рассказать о том, что когда мы умножаем дроби, мы можем умножать два числителя и умножать два знаменателя.
Ваш ребенок также научится делить правильные дроби на целые числа, например, ÷ 2 = . Поощряйте ребенка использовать диаграммы, чтобы помочь им. В этом примере ваш ребенок может нарисовать что-то, чтобы изобразить , а затем разделить это на 2:
Напомните ребенку, что деление на 2 — это то же самое, что найти половину чего-либо. Вашему ребенку может быть полезно думать о ÷ 2 как о нахождении половины трети. В качестве альтернативы они могли думать о расчете как об умножении на половину. Они могли бы решить задачу, умножив на . Полезно поощрять множество методов вычисления с дробями.
3. Счет с десятичной дробью
Ваш ребенок продолжит практиковаться в сложении и вычитании десятичных чисел до 3 знаков после запятой. Им нужно будет понять действие умножения и деления десятичных чисел на 10, 100, 1000 и так далее.
Таблицы разрядов — отличный способ визуализировать эти изменения:
Помогите ребенку понять, что деление на 10 означает уменьшение в десять раз, деление на 100 — уменьшение в сто раз и так далее. Та же концепция применима к умножению, но наоборот.
Та же концепция применима к умножению, но наоборот.
Расчет с числами, которые в реальном мире имеют 3 знака после запятой. Например, когда вы заправляете машину бензином, попросите ребенка сказать вам, что это за число, объяснив, сколько в нем десятых, сотых или тысячных долей. Могут ли они округлить общую цену или общее количество бензина до ближайшего целого числа, десятых или сотых? Например:
Если у вас 56,784 литра бензина, вы можете округлить до ближайшего литра (57 л), десятых (56,8 л) или сотых (56,78 л).
Деньги и меры отлично подходят для практики использования чисел с двумя знаками после запятой. Вы можете показать своему ребенку квитанцию о покупках со скрытой суммой. Попросите ребенка подсчитать общую стоимость чека. Сколько сдачи вам дали бы, если бы вы заплатили, например, купюрой в 10 фунтов стерлингов?
4. Связывание дробей, десятичных знаков и процентов
Важно, чтобы ваш ребенок понимал, что десятичные числа и проценты — это просто другие способы представления дробей.
Ожидается, что ваш ребенок будет использовать эквиваленты между простыми дробями, десятичными знаками и процентами (например, 0,5, , и 50%). Чтобы попрактиковаться, поощряйте их указывать дроби, десятичные числа и проценты в реальной жизни и конвертировать между различными формами, где это возможно.
Решения NCERT для класса 6 по математике, глава 7
Математика NCERT, 6 класс, глава 7: Дроби — Как следует из названия, глава посвящена концепции дробей . Это делается с помощью примеров из реальной жизни и небольших игр.
- Дробь — это число, представляющее часть целого числа .
С каждой дробью связана точка на числовой прямой . Это объясняется в следующем разделе под названием Дроби в числовой строке .
В этой главе учащиеся познакомятся с различными типами дробей :
1. Правильные дроби: числитель меньше знаменателя .
Правильные дроби: числитель меньше знаменателя .
2. Неправильные дроби: числитель больше знаменателя
3. Смешанные дроби: Неправильную дробь можно записать как комбинацию целого и части.
4. Подобные дроби: Дроби с одинаковыми знаменателями
5. Отличающиеся дроби: Дроби с разными знаменателями
Кроме этих, понятие 9Объясняется 1238 эквивалентных дробей , что является важной темой.
- Чтобы найти эквивалентную дробь данной дроби , вы можете умножить числитель и знаменатель данной дроби на одно и то же число .
- Чтобы найти эквивалентную дробь , мы можем разделить и числитель, и знаменатель на одно и то же число.
Глава Дроби также содержит тему- Простейшая форма дроби.
- Говорят, что дробь имеет простейшую форму , если ее числитель и знаменатель не имеют общего делителя, кроме 1 .
Узнав о , как и в отличие от дроби , следующим шагом будет понять, как сравнить их с . Сравнивать одинаковые дроби легко, но сравнение непохожих дробей требует особого внимания, когда 9Требуется общий знаменатель 1238 и LCM .
сложение и вычитание дроби объясняются соответствующими примерами и объясняются в разных подразделах:
- Сложение или вычитание одинаковых дробей
- Сложение и вычитание дробей
В конце дается краткое содержание главы.
Страница № 135:
Вопрос 1:
(v)
Запишите дробь, представляющую заштрихованную часть.
(и) | (ii) | (iii) | (iv) |
| (v)
| (ви) | (vii) | (viii) |
| |||
(ix) | (х) |
|
Ответ:
(i) Данная цифра представляет собой 2 заштрихованные части из 4 равных частей.
Следовательно,
(ii) Данная цифра представляет собой 8 заштрихованных частей из 9 равных частей.
Следовательно,
(iii) Данная цифра представляет собой 4 заштрихованные части из 8 равных частей.
Следовательно,
(iv) Данная цифра представляет собой 1 заштрихованную часть из 4 равных частей.
Следовательно,
(v) Данная цифра представляет собой 3 заштрихованные части из 7 равных частей.
Следовательно,
(vi) Данная цифра представляет собой 3 заштрихованные части из 12 равных частей.
Следовательно,
(vii) Данная цифра представляет 10 заштрихованных частей из 10 равных частей.
Следовательно,
(viii) Данная цифра представляет собой 4 заштрихованные части из 9 равных частей.
Следовательно,
(ix) Данная цифра представляет собой 4 заштрихованные части из 8 равных частей.
Следовательно,
(x) Данная цифра представляет собой 1 заштрихованную часть из 2 равных частей.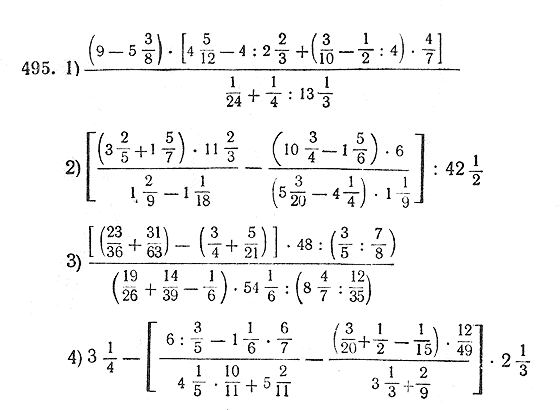
Следовательно,
Страница № 135:
Вопрос 2:
Раскрасьте часть согласно данной дроби.
(и) | (ii) | (iii) |
(iv) | (в) |
Ответ:
(i)
(ii)
(iii)
(iv)
(в)
Страница № 136:
Вопрос 3:
Определите ошибку, если таковая имеется.
Ответ:
Приведенные цифры не являются дробями, так как здесь каждая фигура не делится на равные части.
Видео Решение для дробей (Страница: 136 , Q.No.: 3)
NCERT Решение для 6 класса по математике — дроби 136 , Вопрос 3
Страница № 136:
Вопрос 4:
Что часть суток составляет 8 часов?
Ответ:
Есть 24 часа в сутках. Следовательно, 8 часов в сутках представляют собой.
Страница № 136:
Вопрос 5:
Что доля часа составляет 40 минут?
Ответ:
Есть 60 минут в часе. Следовательно, 40 минут часа составляют
.
Страница № 136:
Вопрос 6:
Арья, Абхиманью и Вивек вместе обедали. Арья принесла два бутерброда, один с овощами, а другой с джемом. Два других мальчика забыли принести обед. Арья согласилась разделить его бутерброды, чтобы каждый человек получил равную долю каждого бутерброда.
(a) Как Арья может разделить свои бутерброды так, чтобы каждый получил поровну?
(b) Какую часть бутерброда получит каждый мальчик?
Ответ:
(a) Арья разделит каждый бутерброд на три равные части. Затем он
Затем он
даст по одной части каждого бутерброда каждому из них.
(b) Каждый мальчик получит часть каждого бутерброда.
Видео Решение для дробей (Страница: 136 , Q.No.: 6)
NCERT Решение для 6 класса по математике — дроби 136 , Вопрос 6
Страница № 136:
Вопрос 7:
Канчан красит платья. Ей пришлось перекрасить 30 платьев. Она пока закончила 20 платья. Какую часть платьев она закончила?
Ответ:
Окрашенное платье пока = 20
Итого платья = 30
Дробь =
Страница № 136:
Вопрос 8:
Напишите натуральные числа от 2 до 12. Какая их доля простые числа?
Ответ:
Натуральный числа от 2 до 12 это 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12.
Простой среди них 2, 3, 5, 7 и 11.
Следовательно, из 11 чисел 5 являются простыми числами. Представляет дробь.
Страница № 136:
Вопрос 9:
Напишите
натуральные числа от 102 до 113. Какая часть из них простые
числа?
Какая часть из них простые
числа?
Ответ:
Натуральный числа от 102 до 113 это 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113
Среди эти числа, простые числа 103, 107, 109, и 113.
Следовательно, из 12 чисел 4 являются простыми числами. Он представляет дробь
Страница № 136:
Вопрос 10:
В каких долях этих кругов есть крестики?
Ответ:
Есть 4 круга из 8, в которых есть крестики. Следовательно, он представляет дробь
.
Видео Решение для дробей (Страница: 136 , Q.No.: 10)
NCERT Решение для 6 класса по математике — дроби 136 , Вопрос 10
Страница № 136:
Вопрос 11:
Кристин получила на день рождения проигрыватель компакт-дисков. Она купила 3 диска и получила 5 других в подарок. Какую часть от общего числа компакт-дисков она купила и какую долю она получила в подарок?
Ответ:
Всего компакт-дисков У Кристин в день рождения было = 3 + 5 = 8
Из 8
компакт-диски, она купила 3 компакт-диска, а также получила 5 компакт-дисков в подарок. Следовательно, она
купили и получили в подарок компакт-диски на долю
соответственно.
Следовательно, она
купили и получили в подарок компакт-диски на долю
соответственно.
Страница № 141:
Вопрос 1:
Розыгрыш пронумеруйте прямые и найдите на них точки:
(а) (б) (в)
Ответ:
(а)
(б)
(в)
Страница № 141:
Вопрос 2:
Экспресс смешанные дроби:
(а) (б) (в)
(г) (д) (е)
)
(г)
(д)
(е)
Страница № 141:
Экспресс Вопрос 3:
45 в виде неправильных дробей:(а) (б) (в)
(г) (д) (е)
Ответ:
(а)
(б)
(в)
( г)
(д)
(е)
Страница № 146:
Вопрос 1:
Запишите дроби. Все эти дроби равнозначны?
(а)
(б)
Ответ:
(а) В данных кружках 1 из 2, 2 из 4, 3 из 6,
и 4 из 8 равных частей заштрихованы соответственно. Следовательно,
эти кружки представляют
Следовательно,
эти кружки представляют
Кроме того, все эти дроби эквивалентны.
(б)
В данных прямоугольниках 4 из 12, 3 из 9, 2 из 6, 1 из 3 и 6 из 15 равных частей (т. е. кругов) заштрихованы соответственно. Следовательно, эти прямоугольники представляют
Нет, не все эти дроби эквивалентны.
Страница № 146:
Вопрос 2:
Напишите дроби и сопоставьте эквивалентные дроби из каждой строки.
Ответ:
(a) Здесь 1 часть заштрихована из 2 равных частей (т. е. прямоугольник). Следовательно, это
цифра представляет дробь.
(б) Здесь, Из 6 равных частей (т. е. прямоугольника) заштрихованы 4 части. Следовательно,
эта цифра представляет дробь
(c) Здесь заштриховано 3 части из 9 равных частей (т.е. квадратов). Следовательно, это
цифра представляет дробь
(г) Здесь, Из 8 равных частей (т. е. прямоугольника) заштрихованы 2 части. Следовательно,
эта цифра представляет дробь
(д) Здесь,
Из 4 равных частей (т. е. квадратов) заштриховано 3 части. Следовательно, это
е. квадратов) заштриховано 3 части. Следовательно, это
цифра представляет дробь .
(i) Здесь заштриховано 6 частей из 18 равных частей (т. е. треугольников). Следовательно, эта цифра представляет собой дробь
(ii) Здесь заштрихованы 4 части из 8 равных частей (т.е. прямоугольники). Следовательно, эта цифра представляет собой дробь
(iii) Здесь заштриховано 12 частей из 16 равных частей (т.е. квадраты). Следовательно, эта цифра представляет собой дробь
(iv) Здесь закрашено 8 частей из 12 равных частей (т.е. прямоугольники). Следовательно, эта цифра представляет собой дробь
(v) Здесь заштриховано 4 части из 16 равных частей (т. е. треугольников). Следовательно, эта цифра представляет собой дробь
Теперь эти цифры можно правильно сопоставить как
(а) (ii), (b) (iv), (c) (i), (d) (v), (e) (iii)
Страница № 147:
Вопрос 3:
Заменить &mnSq2 в каждом из следующих по правильному номеру:
(а) (б)
(в) (г)
(д)
Ответ:
(а)
Следовательно, &mnSq2 можно заменить на
28.
(б)
Следовательно, &mnSq2 можно заменить на 16.
(в)
Следовательно, &mnSq2 можно заменить на 12.
(г)
Следовательно, &mnSq2 можно заменить на 20.
(д)
Следовательно, &mnSq2 можно заменить на 3.
Страница № 147:
Вопрос 4:
Найдите эквивалентная доля имеющий
(a) знаменатель 20 (b) числитель 9
(c) знаменатель 30 (d) числитель 27
Ответ:
(a)
Следовательно, искомая дробь равна.
(б)
Следовательно, искомая дробь равна.
(в)
Следовательно, искомая дробь равна.
(г)
Следовательно, искомая дробь равна.
Страница № 147:
Вопрос 5:
Найдите эквивалентная доля с числителем
(а) 9 (б) знаменатель 4
Ответ:
(а)
Следовательно, искомая дробь равна.
(б)
Следовательно, искомая дробь равна.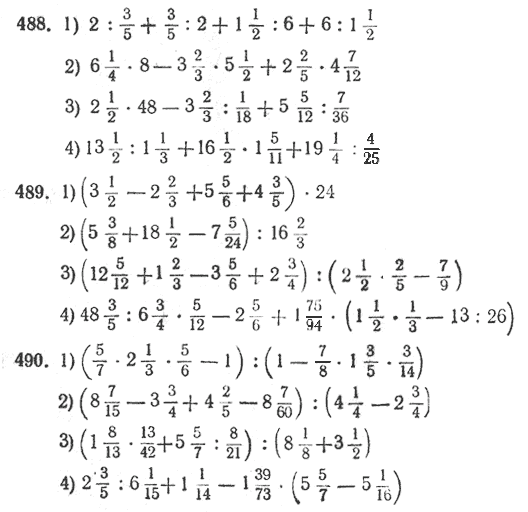
Страница № 147:
Вопрос 6:
Проверить равны ли данные дроби:
(а) (б)
(в)
Ответ:
(а)
Ясно, что обе дроби равны.
(б)
Ясно, что обе дроби не равны.
(в)
Ясно, что обе дроби не равны.
Страница № 147:
Вопрос 7:
Уменьшить
(а) (б)
(в) (г)
(д)
Ответ:
(а)
(б)
(в)
4 (г) )
(e)
Страница № 147:
Вопрос 8:
Рамеш имел 20 карандашей, у Шилу 50 карандашей, а у Джамаала 80 карандашей. Через 4 месяцев, Рамеш израсходовал 10 карандашей, Шилу израсходовал 25 карандашей и Джамаал израсходовал 40 карандашей. Какую часть израсходовал каждый? Проверить, если каждый из них израсходовал равную долю своих карандашей?
Ответ:
Дробь используется Рамешем =
Дробь используется Sheelu =
Дробь используется Джамаалом =
Да, все
из них использовали равную долю карандашей, т. е.
.
е.
.
Страница № 147:
Вопрос 9:
Соедините эквивалентные дроби и напишите еще две для каждой.
(i) (a) (iv) (d)
(ii) (b) (v) (e)
(iii) (c)
Ответ:
(i)
Еще две дроби .
(ii)
Еще две дроби .
(iii)
Еще две дроби .
(iv)
Еще две дроби .
(в)
Еще две дроби .
Теперь их можно сопоставить как
. (я) (г), (ii) (д), (iii) (а), (iv) (резюме) (b)
Стр. № 152:
Вопрос 1:
Заштрихованную часть запишите в виде дроби. Расположите их по возрастанию и в порядке убывания, используя правильный знак «<», «=», «>» между дробями:
(а)
(б)
(с) Показать на числовой ряд. Поставьте соответствующие знаки между данными дробями.
Ответ:
(a)
Здесь 1 st круг представляет 3 закрашенные части из 8
равные части. Следовательно, он представляет дробь
.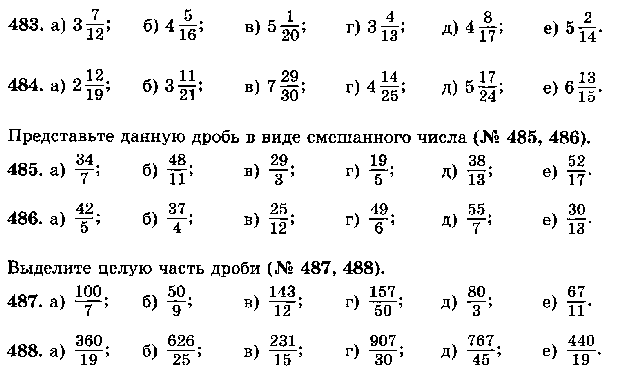
Здесь 2-й круг представляет 6 заштрихованных частей из 8 равных частей. Следовательно, он представляет дробь .
Здесь 3-й круг представляет 4 заштрихованные части из 8 равных частей. Следовательно, он представляет дробь .
Здесь 4 й круг представляет 1 заштрихованную часть из 8 равные части. Следовательно, он представляет дробь .
Теперь эти дроби можно расположить следующим образом:
(b)
Здесь 1 st квадрат представляет 8 заштрихованных частей из 9 равные части. Следовательно, он представляет дробь.
Здесь 2-й квадрат представляет 4 заштрихованные части из 9 равных частей. Следовательно, он представляет дробь .
Здесь 3-й квадрат представляет собой 3 заштрихованные части из 9 равных частей. Следовательно, он представляет дробь .
Здесь 4-й квадрат представляет собой 6 заштрихованных частей из 9 равных частей.
Следовательно, он представляет дробь
.
Теперь эти дроби можно расположить как
(c) Чтобы представить данные дроби на числовой прямой каждая единица длины должна быть разделена на 6 равных частей. Теперь эти дроби можно представить в виде
Страница № 153:
Вопрос 2:
Сравнить дроби и поставить соответствующий знак.
(а) (б)
(в) (г)
Ответ:
(а)
Здесь знаменатели одинаковы. Следовательно, дробь, имеющая большее числитель будет больше.
(б)
Поскольку 4 < 7,
(в)
Здесь знаменатели одинаковы. Следовательно, дробь, имеющая больший числитель будет больше.
(г)
Здесь числители совпадают. Следовательно, дробь, имеющая меньшую знаменатель будет больше.
Страница № 153:
Вопрос 3:
Составьте еще пять таких пар и поставьте соответствующий знак.
Ответ:
(i)
Здесь знаменатели одинаковы. Следовательно, дробь, имеющая
больший числитель будет больше.
(ii)
Здесь знаменатели одинаковы. Следовательно, дробь, имеющая больший числитель будет больше.
(iii)
Здесь числители одинаковые. Следовательно, дробь, имеющая меньшую знаменатель будет больше.
(iv)
Здесь знаменатели одинаковы. Следовательно, дробь, имеющая больший числитель будет больше.
(в)
Здесь числители совпадают. Следовательно, дробь, имеющая меньший знаменатель будет больше.
Страница № 153:
Вопрос 4:
Посмотрите на цифры и напишите «<» или «>», «=» между данными парами дробей.
(а)
(б)
(в)
(г)
(д)
Ответ:
а) Здесь числители одинаковы. Следовательно, дробь, имеющая
меньший знаменатель будет больше.
Следовательно,
(б)
В качестве знаменателей одинаковые, больше та дробь, у которой числитель больше.
Следовательно,
в) Здесь числители одинаковы. Следовательно, дробь, имеющая
меньший знаменатель будет больше.
Следовательно,
(г) Как ,
д) Здесь числители одинаковы. Следовательно, дробь, имеющая меньший знаменатель будет больше.
Следовательно,
Страница № 153:
Вопрос 5:
Как быстро ты можешь это сделать? Заполните соответствующий знак («<», ‘=’, ‘>’)
(a) (b)
(c) (d)
(e) (f)
(g) (h)
(i) (j)
(k)
Ответ:
а) Здесь числители одинаковы. Следовательно, дробь, имеющая
меньший знаменатель будет больше.
Следовательно,
(б)
Следовательно,
(в)
В качестве знаменателей одинаковые, больше та дробь, у которой числитель больше.
Следовательно,
(г)
В качестве знаменателей одинаковые, больше та дробь, у которой числитель больше.
Следовательно,
д) Здесь знаменатели одинаковы. Следовательно, дробь, имеющая больший числитель будет больше.
Следовательно,
(f) Здесь знаменатели одинаковы. Следовательно, дробь, имеющая
больший числитель будет больше.
Следовательно, дробь, имеющая
больший числитель будет больше.
Следовательно,
(г)
Следовательно,
(ч)
В качестве знаменателей одинаковые, больше та дробь, у которой числитель больше.
Следовательно,
(и)
В качестве знаменателей одинаковые, больше та дробь, у которой числитель больше.
Следовательно,
(к)
В качестве знаменателей одинаковые, больше та дробь, у которой числитель больше.
Следовательно,
(к)
Следовательно,
Страница № 154:
Вопрос 6:
следующие дроби представляют всего три разных числа. Отдельный их на три группы эквивалентных дробей, заменив каждую до простейшей формы.
(a) (b)
(c) (d)
(e) (f)
(g) (h)
(i) (j)
(k) (l)
Ответ:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)
(к)
(л)
Есть 3 группы эквивалентных фракций
(а), (д), (з), (к), (л)
(б), (е), (ж)
(в), (d), (i), (l)
Страница № 154:
Вопрос 7:
Найдите ответы на следующие вопросы. Напишите и укажите, как вы их решили.
Напишите и укажите, как вы их решили.
(а) ? (б) ?
(с) ? (г) ?
Ответ:
(a)
. ,
(d)
Страница № 154:
Вопрос 8:
Я прочитал 25 страниц книги, содержащей 100 страниц. Лалита читала ту же книгу. Кто меньше читал?
Ответ:
Количество страниц, прочитанных Лалитой == 40
Количество страниц, прочитанных Илой = 25
Следовательно, Ила прочитала меньше страниц.
Видео Решение для дробей (Страница: 154 , Q.No.: 8)
NCERT Решение для 6 класса по математике — дроби 154 , вопрос 8
Страница № 154:
Вопрос 9:
Рафик тренировался в течение часа, а Рохит тренировался в течение часа.
Кто тренировался дольше?
Ответ:
Рафик упражнялся, а Рохит упражнялся на
Преобразовывая их в одинаковые дроби,
Следовательно, Рохит упражнялся дольше.
Страница № 154:
Вопрос 10:
В классе А из 25 учеников 20 прошли в первый класс; в другом классе B из 30 учеников 24 перешли в первый класс. В каком классе было больше учеников, получивших первый класс?
В каком классе было больше учеников, получивших первый класс?
Ответ:
Доля учеников класса А, перешедших в I класс =
Доля учеников класса В, перешедших в I класс =
Из обоих классов в первый класс перешла равная доля учеников.
Видео Решение для дробей (Страница: 154 , Q.No.: 10)
NCERT Решение для 6 класса по математике — дроби 154 , Вопрос 10
Страница № 157:
Вопрос 1:
Написать эти дроби соответственно как сложения или вычитания:
(а)
(б)
(в)
Ответ:
(a) Здесь можно заметить, что 1 st , 2 nd и 3 прямоугольника rd представляют 1, 2 и 3 заштрихованные части из 5 равных частей соответственно. Ясно, что дробь, представленная по 3 рд прямоугольник это сумма представленных дробей по 1 ст и 2 й прямоугольников.
Следовательно,
(b) Здесь можно заметить, что 1 st , 2 nd и
3 rd кружки обозначают 5, 3 и 2 заштрихованные части
из 5 равных частей соответственно. Ясно, что дробь, представленная
3 рд круг разница между дробями
представлены 1 -й и 2 -й кругами.
Ясно, что дробь, представленная
3 рд круг разница между дробями
представлены 1 -й и 2 -й кругами.
Следовательно,
(c) Здесь можно заметить, что 1 st , 2 nd и 3 прямоугольника rd представляют 2, 3 и 5 заштрихованные части из 6 равных частей соответственно. Ясно, что дробь, представленная к 3 рд прямоугольник это сумма представленных дробей по 1 ст и 2 й прямоугольников.
Следовательно,
Страница № 158:
Вопрос 2:
Решить:
(a) (b)
(c) (d)
(e) (f)
(g) 3 (h)
4 и)
Ответ:
(а)
(б)
(в)
(г)
(д)
(е)
0 (з)
0004 (i)
Страница № 158:
Вопрос 3:
Шубхам окрашенный из стенное пространство в его комнате. Его сестра Мадхави помогала и рисовала из пространство стены. Сколько они рисовали вместе?
Ответ:
Пробел нарисовано Шубхэмом = помещения
Площадь нарисованный Мадхави = комнаты
Следовательно, вместе они рисовали =из номер
= 1 = вся стена
Страница № 158:
Вопрос 4:
Вставьте пропущенные дроби.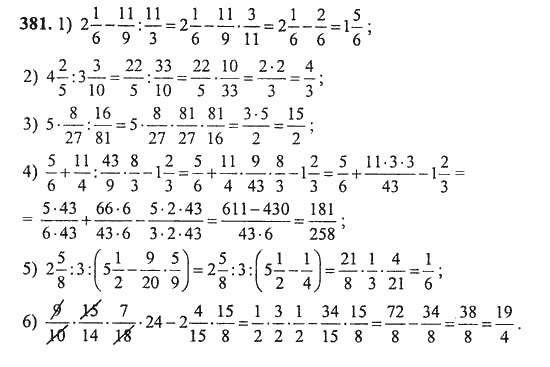
(a) (b)
(c) (d)
Ответ:
(a)
(b)
(c)
(D)
Страница № 158:
Вопрос 5:
Джавед был данный из корзина апельсинов. Какая часть апельсинов осталась в корзине?
Ответ:
Дроби дано Джаведу =
Дробь осталось в корзине = знак равно
Страница № 160:
Вопрос 1:
Решить
(а) (б)
(в) (г)
(д) (е)
(ж) (з)
(и) (к)
(л) (л) )
(м) (н)
Ответ:
(а)
(б)
(в)
(г)
(д)
(ж)
(г)
(ч)
(и)
(к)
(к)
(л)
(м)
(н)
Страница № 160:
Вопрос 2:
Сарита купленный метр ленты и Лалита метр ленты. Какова общая длина ленты, которую они купили?
Ответ:
Длина лента, купленная Саритой =
Длина лента, купленная Лалитой =
Итого длина купленной ими ленты =
Страница № 160:
Вопрос 3:
Наина была
данный
кусок
пирога и Наджме дали
кусок
торт. Найдите общее количество пирога, которое дали им обоим.
Найдите общее количество пирога, которое дали им обоим.
Ответ:
Дробь Наина получила =
Дробь Najma got =
Номер страницы 161:
Вопрос 4:
Заполнить коробки: (a) (b) (c)
Ответ:
(a)
(б)
(в)
Страница № 161:
Вопрос 5:
Заполните поле сложения-вычитания.
(а)
(б)
Ответ:
(а)
Следовательно, данное поле можно заполнить как
(b)
Следовательно, данную коробку можно заполнить как
Страница № 161:
Вопрос 6:
Кусок провод метр давно развалился на две части. Одна часть была метр длинная. Какой длины другая часть?
Ответ:
Длина одна штука =
Длина
другого отрезка проволоки будет разница длин
оригинальный провод и этот кусок провода.

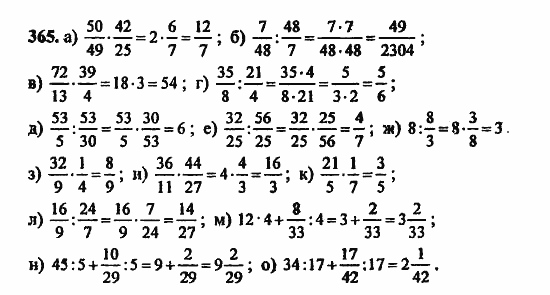 Преобразования
Преобразования