График функции — MathCracker.com
Алгебра Учебники
График функции — это набор упорядоченных пар \((x,y)\). Или график функции — это концептуализация, которую мы делаем набором пар \((x,y)\) в системе координат. Я говорю, что это концептуализация, потому что то, как мы представляем граф, в некоторой степени является оптической иллюзией.
Почему я так говорю? Ну посмотрите.
Итак, это график. Набор пар \((x, y)\), или, как мы их еще называем, точек. Ниже выделен конкретный момент, посмотрите
Уловка, или визуальная иллюзия, заключается в том, что точка теоретически не имеет размеров (ни ширины, ни длины). Итак, эта «кривая», которую мы рисуем для представления графика, это своего рода удобный способ представления графика, но мы обманываем нас, потому что это представление имеет кривую, имеющую толщину.
Итак, это не для вашего парада, это просто для того, чтобы прояснить, что то, что вы понимаете под графиком, это скорее представление
графа, который удобен и заслуживает доверия.
Графики, связанные с функциями
Один действительно простой способ определить график — использовать функцию \(f(x)\). Действительно, график, определяемый функцией \(f(x)\), представляет собой набор всех точек \((x, f(x))\) для \(x \in D\), где \(D\) — это область определения функции \(f\).
Представление такое же, как и на предыдущих графиках, только теперь мы делаем следующее:
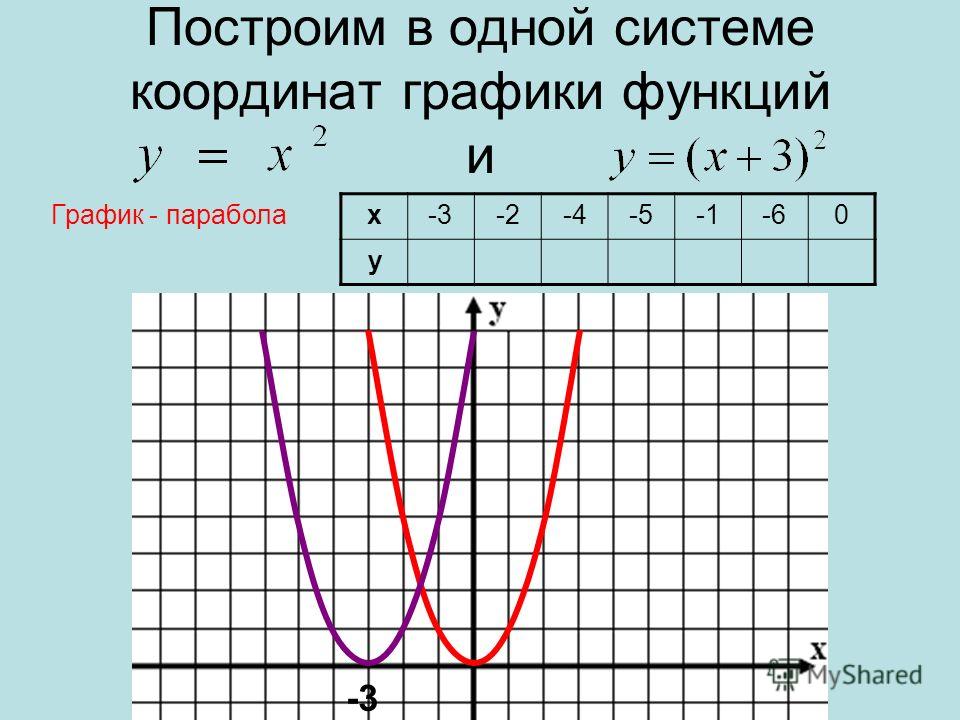2\).
Понятие гладкости функции формально рассматривается в исчислении с понятием непрерывной функции. Но не вдаваясь в подробности, мы можем сказать, что на данный момент мы будем думать, что непрерывная функция — это функция, имеющая «гладкий» график, а прерывистая функция — это функция, которая не является гладкой или имеет «скачки». ".
ПРИМЕР 2
Функция \(f(x) = sin(x)\) непрерывна?
ОТВЕЧАТЬ:
Что ж, опять же, для проверки нам потребуется формальный анализ непрерывности.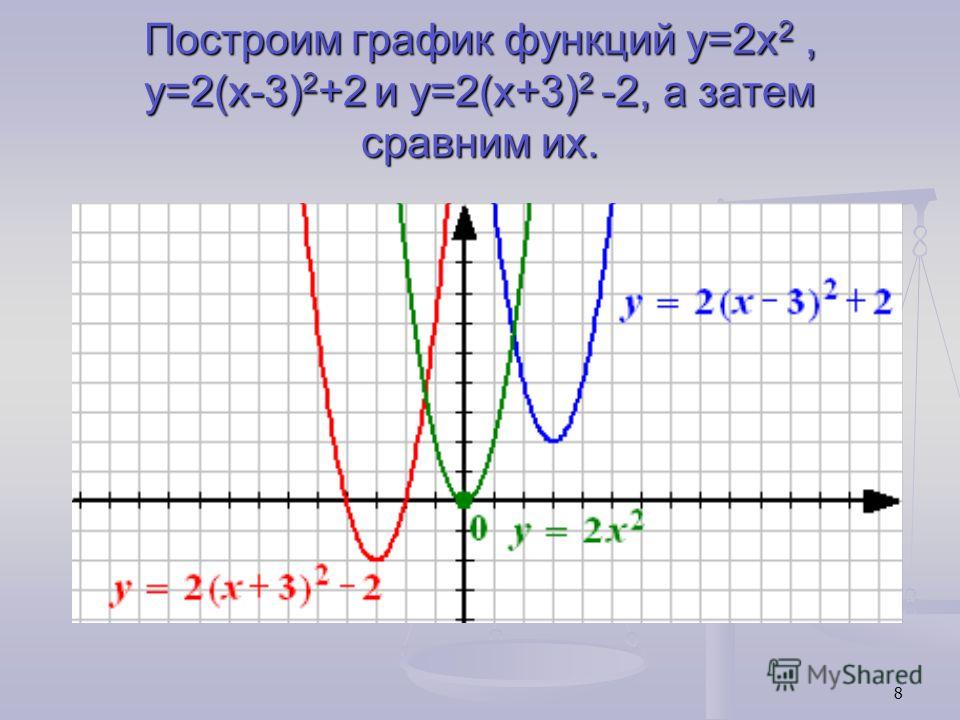
Но в свете приведенного выше неформального определения давайте проверим его график. Компьютер дает нам следующее:
Я бы сказал, что приведенный выше график выглядит очень гладким, без каких-либо скачков, поэтому, используя наше наивное определение, я бы сказал, что \(f(x) = \sin x\) непрерывно.
ПРИМЕР 3
Функция \( f\left( x \right)=\left\{ \begin{array}{cc}-1 &\,\,\,\,\text{for } x\le 1 \\ \\ x & \,\,\,\,\,\,\text{for }x>1 \\ \end{array} \right.\) непрерывна?
ОТВЕЧАТЬ:
Чтобы ответить на вопрос, нам нужно построить график.
Обратите внимание, что есть скачок в точке \(x = 1\), поэтому я бы сказал, что на графике выше есть скачок, и, следовательно, эта функция является прерывистой.
Подробнее о графиках
Использование графиков для представления функции может сыграть решающую роль для понимания поведения функции.
Существует достаточно аналитических инструментов (вычислений), чтобы понять поведение функции \(f(x)\) без необходимости ее построения. Но очень практично видеть график, потому что это действительно быстрый способ получить представление о том, что делает функция.
Если вам нужно построить график, попробуйте график функций чтобы получить хорошее представление о том, как ведет себя функция.
Учебники по алгебре Непрерывные графики Разрывные графы График График функции
2Если вы не укажете знак равенства, предполагается, что вы имеете в виду « =0 »
Он не был хорошо протестирован, поэтому
Если у вас возникнут проблемы, дайте мне знать.
Примечание: завершение может занять несколько секунд, так как необходимо выполнить множество вычислений.
Если вы просто хотите построить график функции в стиле «y=…», вы можете предпочесть Function Grapher and Calculator
Масштабирование
Используйте ползунок масштабирования (влево увеличивает масштаб, вправо уменьшает).
Чтобы сбросить масштаб до исходных границ, нажмите кнопку Reset .
Перетаскивание
Нажмите и перетащите, чтобы переместить график. Если вы просто нажмете и отпустите (без перетаскивания), то место, на которое вы нажали, будет новым центром
.
Примечание: графики используют компьютерных расчетов . Округление может привести к ошибкам или полному отсутствию значений.
Все функции
Операторы
| + | Оператор сложения | |
|---|---|---|
| — | Оператор вычитания | |
| * | Оператор умножения | |
| 9 | Оператор экспоненты (мощности) |
Функции
| кв | Квадратный корень из значения или выражения. | |
|---|---|---|
| синус значения или выражения | ||
| потому что | косинус значения или выражения | |
| желтовато-коричневый | тангенс значения или выражения | |
| как | арксинус (арксинус) значения или выражения | |
| акос | арккосинус (arccos) значения или выражения | |
| атан | арктангенс (арктангенс) значения или выражения | |
| синх | Гиперболический синус (sinh) значения или выражения | |
| кош | Гиперболический косинус (cosh) значения или выражения | |
| танх | Гиперболический тангенс (tanh) значения или выражения | |
| эксп | e (константа Эйлера), возведенная в степень значения или выражения | |
пер. | Натуральный логарифм значения или выражения | |
| журнал | Десятичный логарифм значения или выражения | |
| этаж | Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу. | |
| потолок | Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу. | |
| раунд | Округлить до ближайшего целого числа. Примеры: округление (-2,5) = -2, округление (-0,1) = 0, округление (0,1) = 0, округление (2,5) = 3 | |
| абс | Абсолютное значение (расстояние от нуля) значения или выражения | |
| знак | Знак (+1 или −1) значения или выражения | |
Константы
| пи | Константа π (3,141592654. ..) | |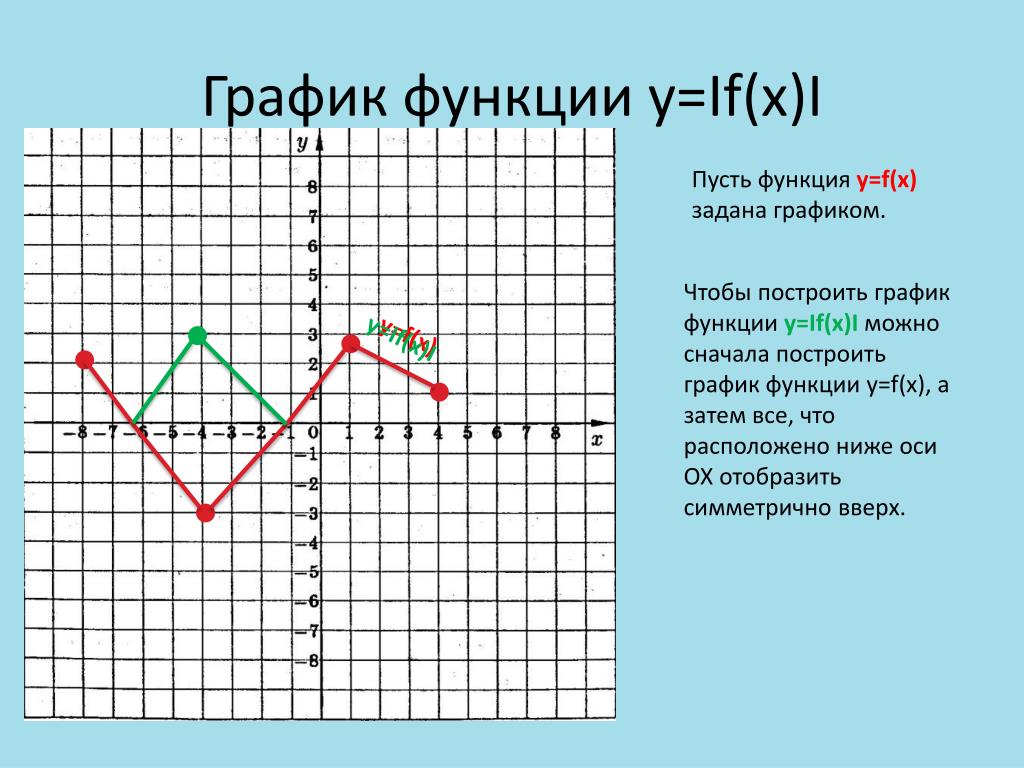
|---|---|---|
| и | Число Эйлера (2,71828…), основание натурального логарифма |
Функции двух переменных
Функции двух переменныхЧасть 1: Функции двух переменных
В предыдущей главе мы распространили дифференциальное исчисление на векторнозначные функции. В этой главе мы расширяем исчисление до функции двух variables , which are functions like f ( x , y ) = x 2 + y 2 and g ( x , y ) = sin( х ) cos( у ) .
В частности, функция двух переменных — это функция, входы которой точек ( x , y ) в плоскости xy и чьи выходные данные действительны числа. Мы часто обозначаем функции двух переменных через ф ( х , и ), что означает «выход со входа ( x , y )», и мы часто определяют эти функции в виде
|
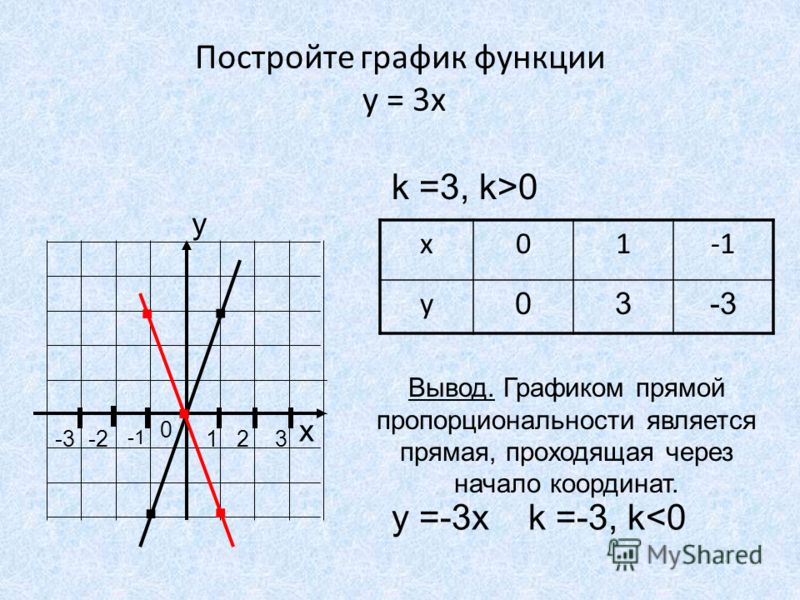
EXAMPLE 1 Evaluate f ( 1,2) and f (2,5) if f ( x , y ) = x 2 +2 xyРешение: Для начала f ( 1,2) = 1 2 +2·1·2 = 5, то есть f ( x , y ) = x 2 +2 xy карты точку ( 1,2) на число 5. Аналогично, f (2,5) = 2 2 +2·2·5 = 24.
График f ( x , y ) представляет собой набор точек в R 3 , которые удовлетворяют z = f ( x , 4 ). То есть график f ( x , y ) является поверхность z = f ( x , y ) и выход z высота поверхности в точке ( x , y ).
Графический калькулятор или система компьютерной алгебры часто используются для получения
аппроксимация графика функции.
ПРИМЕР 2 Используйте систему компьютерной алгебры для построения графика функции ф ( x , y ) = x 2 + y 2 для x и y в [-1,1] .Решение: График f ( x , y ) = x 2 + y 2 для x и y в [-1,1] по определению является набором всех точек ( x,y,z ) с x в [-1,1], y в [-1,1] и z = x 2 + y 2 . Этот набор точек образует поверхность , показанную на рис. четыре различных типа графиков ниже. Патч-график показывает только поверхность, в то время как участок и сетка показывают график вместе с сеткой кривых на поверхности.
Контур показывает поверхность вместе с горизонтальными поперечными сечениями на различных высотах.
Участок патчей Патч и сетка Каркасный график показывает только сетку кривых на поверхность.
Контур Каркас
Каркасный график показывает только сетку кривых на
поверхность. Мы часто принимаем x = x , и – быть
вектор положения точки в xy -плоскости, и тогда мы пишем
|
ПРИМЕР 3 Какая функция f ( x , y ) представлена поРешение: Поскольку x = x , и с, мы имеют
ф ( х ) = || х || 2
f ( x , y ) = || x , и с || 2 = х 2 + у 2
Примечание: Часто мы будем использовать выделенную полужирным шрифтом первую букву
вектор переменных для обозначения вектора.
Например, мы пишем
|
Проверьте свое чтение : Как z = x 2 + y 2 связаны с пример 2?
Рисование графиков математических функций с помощью Math Assistant в OneNote
Одна нота
Записывать
Записывать
Рисование графиков математических функций с помощью Math Assistant в OneNote
OneNote для Интернета OneNote для Windows 10 Math Assistant Дополнительно… Меньше
Создавайте графики рукописных или напечатанных уравнений с помощью Math Assistant в OneNote.
Вы даже можете манипулировать переменными, чтобы увидеть визуальный эффект изменений, превращая Math Assistant в мощного тренера по математике.
Примечание. Эта функция доступна только при наличии подписки Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
Откройте настольное приложение OneNote или войдите в Office.com и выберите OneNote .
Совет: Если вы не видите OneNote сразу, откройте средство запуска приложений , чтобы найти его.
Откройте существующий блокнот или создайте новый блокнот.
Выберите вкладку Draw и напишите или введите свое уравнение.
Используйте инструмент Lasso Select , чтобы нарисовать круг вокруг уравнения.
Выбрать Математика , чтобы открыть панель Math Assistant.
В раскрывающемся меню Выберите действие на панели Math выберите Graph in 2D или Graph Both Sides in 2D .
Чтобы настроить график, созданный Math Assistant, выполните любое из следующих действий, где это возможно:
Примечание. Если вы используете OneNote на устройстве с сенсорным экраном, график можно настроить пальцами. Используйте один палец для перемещения графика. Сведите два пальца, чтобы изменить уровень увеличения. В OneNote для Интернета вы можете использовать стрелки по бокам графика, чтобы изменить его положение.
Выберите или коснитесь значка с двойной стрелкой Сброс , чтобы восстановить исходное состояние графика.
Когда график будет выглядеть так, как вы хотите, выберите или коснитесь Вставить на страницу , чтобы поместить его в виде снимка экрана на текущую страницу.
Примечание. Чтобы изменить способ представления графика (градусы, радианы, граданы), выберите или коснитесь Настройки , когда открыта панель математических вычислений.
Расширенные графические возможности
В зависимости от типа графика могут быть доступны следующие функции:
Чтение значений x-y: Наведите указатель мыши на точку на линии графика, чтобы увидеть значения x и y в OneNote для Windows 10. В OneNote для Интернета — линию, чтобы просмотреть значения.
Управление параметрами: Если у вас есть уравнение с параметрами, такими как ax+b, используйте знаки + и — под графиком, чтобы изменить значения a и b.
Основные функции графика: Математический помощник вычисляет интересную информацию о графике, такую как нули, точки пересечения, минимумы, максимумы и многое другое. Используйте флажки, чтобы выбрать, какие функции вы хотите отобразить на графике.
Узнать больше
Создавайте математические уравнения с помощью рукописного ввода или текста с помощью помощника по математике в OneNote.
Решайте математические уравнения с помощью Math Assistant в OneNote
Типы задач, поддерживаемые Math Assistant
Создайте тренировочную математическую викторину
Типы задач, которые можно отображать в 2D-графике
При использовании Math Assistant в OneNote вы заметите, что раскрывающийся список Выберите действие под уравнением изменяется в зависимости от выбранного вами уравнения.
Следующие типы задач можно изобразить в 2D с помощью Math Assistant.
Примечание. Эта функция доступна только при наличии подписки на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
Выражения (с переменной) | |
Полиномиальные массивы | |
Уравнения | Вы можете График в 2D или График с обеих сторон в 2D при работе с уравнениями. Выберите График в 2D , чтобы увидеть решение уравнения.
Выберите График обеих сторон в 2D , чтобы просмотреть график двух функций по разные стороны от знака равенства. |
Системы уравнений | |
Полярные координаты | Чтобы построить график функции в полярных координатах, r необходимо выразить как функцию тета. |
Неравенства | Вы можете График в 2D или График обеих сторон в 2D при работе с неравенствами. |
