Знаки по математике: ‎Символы, Эмоджи, иероглифы, письменности, алфавиты и весь Юникод

Математические знаки и символы

• Главная
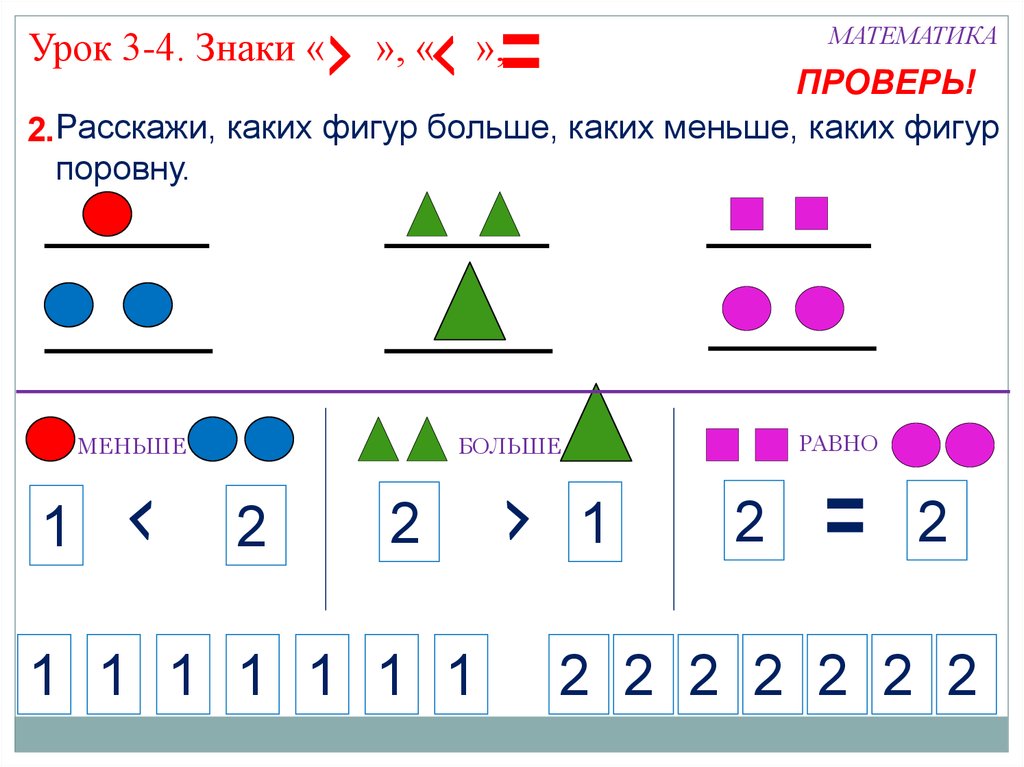
• Математические знаки и символы

Здесь вы можете скачать новогодние задания для детей «Поставь знак больше меньше или равно» во вложениях внизу материала. В заданиях вы найдете четыре упражнения для малышей на счет, а также проверите умение ребенка правильно подбирать для сравнения чисел математические знаки.

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Здесь вы скачаете задания для распечатки «Соседи чисел, математические знаки больше, меньше», в которых ребенку нужно выполнить четыре математических упражнения. Ребенок сможет не только решать примеры, но и составлять их самостоятельно, используя предметы, изображенные на картинке.

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Задачи по математике — Интересные примеры на сравнение — предназначены детям от 6-ти лет. Воспользуйтесь тем, что красочные картинки хорошо привлекают внимание ребенка, поэтому выполнение этих задач не станет для них утомительным и неинтересным занятием.

Чтобы решать задачи необходимы хотя бы минимальные знания математических знаков больше, меньше и знака равенства, а также умения прибавлять и отнимать. И конечно же, здесь понадобится умение ребенка логически мыслить.

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Математическое сравнение «Примеры в картинках» предназначены для детей, которые только начинают осваивать счет и уже запомнили, что означают математические знаки больше, меньше и знак равенста. Такие примеры можно решать как с одним ребенком (в домашних условиях), так и с группой детей (в детских садах и начальных школах).

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Веселые задачи по математике в картинках для детей позволят вашим малышам не только осваивать счет, но и послужат чудесным материалом в развитии их логики и внимания. Любимые сказки, используемые в задачках, сделают занятия более интересными и веселыми.

Не торопите ребенка и не подсказывайте ему, но обязательно проверьте его ответы на правильность.

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Здесь вы встретите задания самым маленьким «Математика в картинках», с помощью которых ребенок научится решать математические задачи. Задания будут интересны детям 4 — 7 лет, они развивают умственные способности малышей, внимание и память.  Объясняйте задачи, помогайте и подсказывайте ребенку то, чего он не может понять. Приводите подобные примеры.

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Здесь вы можете скачать картинки с заданиями на тему «Математические знаки +, -, >,», в которых ребенку нужно будет поставить правильные математические знаки между различными насекомыми на картинке. Такие задания подойдут для дошкольных занятий с детьми, как в домашних условиях, так и в детских садах или школах раннего развития.

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

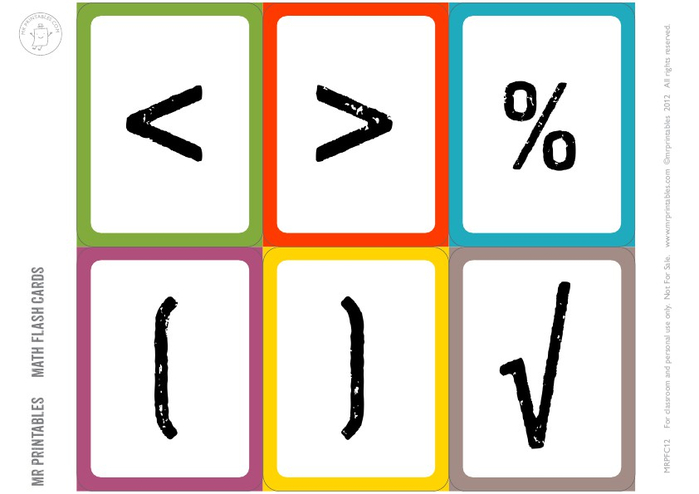
Здесь вы можете скачать карточки по математике, 1 класс с математическими знаками для использования их в качестве обучающего материала в начальной школе, а также дошкольных учреждениях. С помощью карточек можно составлять любые примеры на прибавление, отнимание, умножение, деление, а также выполнять сравнение чисел (используя знаки «больше», «меньше»). 

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Математические задачки на изучение знаков плюс, минус и равно помогут вам в доступной, игровой форме ознакомить малыша с основами математики и счетом. Начните занятие с ребенком со следующих слов: «Знак плюс очень похож на крестик, потому что они с ним братья-близнецы. А еще, это очень щедрый знак, он все цифры складывает вместе — прибавляет. Посмотри, как это происходит на картинке!»

Опубликовано в Математика для детей 4, 5, 6, 7 лет — распечатай и занимайся

Кто придумал значок. Происхождение математических знаков. Проект по математике

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

История происхождения математических знаков Подготовил: Черепанов Иван, ученик 5 В класс Учитель математики: Мосунова О. А. Как нет на свете без ножек столов, Как нет на свете без рожек козлов, Котов без усов и без панцирей раков, Так нет в арифметике действий без знаков!

2 слайд

Описание слайда:

3 слайд

Описание слайда:

Задачи Рассмотреть откуда математические знаки пришли к нам и что они изначально обозначали. Сравнить математические знаки разных народов. Рассмотреть сходство современных математических знаков со знаками наших предков

4 слайд

Описание слайда:

Объект: математические знаки разных народов Основные методы исследования: анализ литературы, сравнение, опрос учащихся, анализ и обобщение полученных в ходе исследования данных.

5 слайд

Описание слайда:

Почему в наше время мы используем именно такие математические знаки: + «плюс»,- « минус», ∙ « умножение» и: « деление», а не какие нибудь другие? Проблема

6 слайд

Описание слайда:

Гипотеза Я думаю, что математические знаки возникли одновременно с появлением цифр и чисел

7 слайд

Описание слайда:

Происхождение математических знаков Происхождение этих знаков не всегда можно точно установить.

Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Существует мнение, что знаки «+» и «–» возникли в торговой практике. Виноторговец чёрточками отмечал, сколько мер вина он продал из бочки. Приливая в бочку новые запасы, он перечёркивал столько расходных чёрточек, сколько мер он восстановил. Так, якобы, произошли знаки сложения и вычитания в ХV веке. Относительно происхождения знака «+» существует и другое объяснение. Вместо «а + b» писали «а и b», по латыни «а et b». Так как слово «et» («и») приходилось писать очень часто, то его стали сокращать: писали сначала одну букву t, которая, в конце концов, превратилась в знак «+»

8 слайд

Описание слайда:

Алгебраического знак “- ” Первое использование современного алгебраического знака “ +” относится к немецкой рукописи по алгебре 1481 г. , которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: + и — . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака + и — (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.

9 слайд

Описание слайда:

Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест “†’’, иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид Видман

10 слайд

Описание слайда:

Первое появление « +» и «-» на английском языке обнаружено в книге по алгебре 1551 г. “The Whetstone of Witte” математика из Оксфорда Роберта Рекорда, который также ввел знак равенства, который был гораздо длиннее, чем нынешний знак. В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется «+» и обозначает больше, а второй «-» и обозначает меньше’’.

11 слайд

Описание слайда:

Знак вычитания Обозначения вычитания были несколько менее причудливыми, но, возможно, более запутанными (для нас, по крайней мере), так как вместо простого знака “- ” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Галлей и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.

12 слайд

Описание слайда:

В Древней Египте В знаменитом египетском папирусе Ахмеса пара ног, идущих вперед, обозначает сложение, а уходящих — вычитание

13 слайд

Описание слайда:

Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полу-эллиптическую кривую для вычитания Индусы, как и греки, обычно никак не обозначали сложение, кроме того, что символы “yu’’ были использованы в рукописи Бахшали “Арифметика’’ (вероятно, это третий или четвертый век).

14 слайд

Описание слайда:

В конце пятнадцатого века французский математик Шюке (1484 г.) и итальянский Пачоли (1494 г.) использовали “p ’’ (обозначая “плюс’’) для сложения “ m’’ (обозначая “минус’’) для вычитания. Шюке

15 слайд

Описание слайда:

В Италии В Италии символы «+» и «-» были приняты астрономом Кристофером Клавиусом (немцем, жившим в Риме), математиками Глориози и Кавальери в начале семнадцатого века Кристофер Клавиус

16 слайд

Описание слайда:

Знак умножения Для обозначения действия умножения одни из европейских математиков XVI века употребляли букву М, которая была начальной в латинском слове, обозначающем увеличение, умножение, – мультипликация (от этого слова произошло название «мультфильм»). В XVII веке некоторые математики стали обозначать умножение косым крестиком «×», а иные употребляли для этого точку. В Европе продолжительное время произведение называли суммой умножения.

Название «множитель» упоминается в работах XI века. На протяжении тысячелетий действие деление не обозначали знаками. Арабы ввели для обозначения деления черту «/». Её перенял от арабов в XIII веке итальянский математик Фибоначчи. Он же первым употребил термин «частное». Знак двоеточия «:» для обозначения деления вошёл в употребление в конце XVII века. В России названия «делимое», «делитель», «частное» впервые ввёл Л.Ф. Магницкий в начале XVIII века. Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560-1621).

17 слайд

Описание слайда:

Знаки деления Отред предпочитал косую черту «/». Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл (John Pell) в середине XVII века.

18 слайд

Описание слайда:

Знаки равенства и неравенства Знак равенства обозначался в разные времена по-разному: и словами, и различными символами. Знак «=», столь удобный и понятный сейчас, вошёл во всеобщее употребление только в XVIII веке. А предложил этот знак для обозначения равенства двух выражений английский автор учебника алгебры Роберт Рикорд в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем. Знак «не равно» впервые встречается у Эйлера. Знаки сравнения ввёл Томас Гарриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше.

Этот символ знаком любому пользователю интернета. Но появился он отнюдь не в век всеобщей компьютерной грамотности, символ который мы называем «собака» был известен еще в средние века, и у него было несколько разных назначений. Версий его происхождения тоже несколько, все они интересны и заслуживают внимания.

Символ @ известен как минимум с XV века , но вполне возможно, что он был придуман и раньше. До сих пор доподлинно не установлено, как и откуда он появился, и время первого упоминания определено лишь приблизительно. По одной из версий, знак @ первыми стали использовать в письме монахи, делавшие переводы трактатов, которые были написаны в том числе и на латыни. В латыни есть предлог «ad», и в шрифте принятом в то время для письма, буква «d» писалась с небольшим хвостиком, закрученным вверх. При быстром письме предлог выглядел как значок @.

Благодаря флорентийским купцам, с XV века значок @ стал использоваться в качестве коммерческого символа. Он обозначал меру веса, равную 12,5 кг. – амфору, и по тогдашней традиции буква «А», которой и обозначался вес, была украшена завитками и выглядела как всем известный сегодня символ. У испанцев, португальцев и французов своя версия происхождения обозначения – от слова «арроба» — староиспанской меры веса около 15 кг, которую обозначали в письме условным знаком @, тоже взятом от первой буквы слова.

В современном коммерческом языке официальное название знака @ — «коммерческое at» произошло из бухгалтерских счетов, где обозначало предлог «в, на, по, к», и в русском переводе выглядело примерно так – 5шт. по 3$ (5 widgets @ $3 each). Так как символ использовался в торговле, то он был размещен на клавиатурах первых пишущих машинок, откуда и перебрался на компьютерную клавиатуру.

В интернете символ @ появился благодаря создателю электронной почты Томлинсону. Почему он выбрал этот знак для разделения имени пользователя и сервера электронной почты Томлинсон объяснил просто – он искал знак, который бы не встречался ни в именах, ни в названиях и не мог внести путаницу в систему. В разных странах символ называют по-разному, как собачка он известен лишь в русском языке. Версий появления этого забавного названия несколько. Согласно одной из них – звучание английского «at» напоминает собачий лай, по другой – сам значок напоминает свернувшуюся калачиком маленькую собачку. Но самая популярная связана с одной из первых текстовых игр. По сюжету, у игрока был помощник, верный пес, который помогал искать клады, защищал от разных монстров, отправлялся в разведку и в катакомбы. И конечно же обозначался пес знаком @.

Кстати, символ @ во многих странах так или иначе пользователи связывают с животными – у немцев и поляков это обезьянка, у итальянцев – улитка, в Америке и Финляндии – кошка, на Тайване и в Китае – мышка. В других странах символ означает что-то вкусное – булочку с корицей у шведов, штрудель у израильтян. Только дисциплинированные японцы далеки от романтичных сравнений и предпочитают называть знак «attomark», так как он звучит в английском языке, и не придумывают для него своих названий.

Первое использование знаков + и — в печати в Behëde und Johannes Widman auff allen Kauffmanschafft, Аугсбург, 1526 г.

Марио Ливио

Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Когда я начал изучать историю этих знаков, я обнаружил, к своему удивлению, что они появились вовсе не в глубокой древности. Многое из того, что нам известно, происходит из всеобъемлющего и впечатляющего исследования 1928–1929 гг., которое до сих пор остается непревзойденным. Это “История математических обозначений’’ швейцарско-американского историка математики Флориана Каджори (1859-1930).

Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полу-эллиптическую кривую для вычитания. В знаменитом египетском папирусе Ахмеса пара ног, идущих вперед, обозначает сложение, а уходящих — вычитание. Индусы, как и греки, обычно никак не обозначали сложение, кроме того, что символы “yu’’ были использованы в рукописи Бахшали “Арифметика’’ (вероятно, это третий или четвертый век). В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания.

Несколько сомнительно, но считается, что наш знак происходит от одной из форм слова “et’’, которое значит “и’’ по-латыни. Первым человеком, который, возможно, использовал знак как аббревиатуру для et, был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ — “Книги неба и мира’’) в середине четырнадцатого века. Рукопись 1417 г. также содержит символ (хотя палочка, направленная сверху вниз, не совсем вертикальна). И это тоже потомок одной из форм et.

Происхождение знака “” гораздо менее ясно, и высказываются гипотезы его появления от иероглифического письма или александрийской грамматики, до черты, которую использовали торговцы, чтобы отделить тару от общей массы товаров.

Первое использование современного алгебраического знака “” относится к немецкой рукописи по алгебре 1481 г. , которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: и . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака и (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.

В Италии символы и были приняты астрономом Кристофером Клавиусом (немцем, жившим в Риме), математиками Глориози и Кавальери в начале семнадцатого века.

Первое появление и на английском языке обнаружено в книге по алгебре 1551 г. “The Whetstone of Witte” математика из Оксфорда , который также ввел знак равенства, который был гораздо длиннее, чем нынешний знак . В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется и обозначает больше, а второй и обозначает меньше’’.

Как исторический курьез, стоит отметить, что даже после принятия знака не все использовали этот символ. Видман сам ввел его как греческий крест (знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест “†’’, иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид “’’.

Обозначения вычитания были несколько менее причудливыми, но, возможно, более запутанными (для нас, по крайней мере), так как вместо простого знака “” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.

В общем, самым впечатляющим в этой истории является то, что символы, которые впервые появились в печати лишь около пятисот лет назад, стали частью того, что является, видимо, наиболее универсальным “языком’’. Занимаетесь ли вы наукой или финансами, живете в Кентукки или в Сибири, все равно вы точно знаете, что означают эти символы.

От индийских значков, показанных в нижней строке (начертание I века н. э.), произошли современные цифры

Для обозначения цифр от 1 до 9 в Индии с VI века до н. э. использовалось написание «брахми», с отдельными знаками для каждой цифры. Несколько видоизменившись, эти значки стали современными цифрами, которые мы называем арабскими , а сами арабы — индийскими .

Десятичная запятая, отделяющая дробную часть числа от целой, введена итальянским астрономом Маджини (1592) и Непером (1617). Ранее вместо запятой ставили иные символы — вертикальную черту: 3|62, или нуль в скобках: 3 (0) 62

«Двухэтажная» запись обыкновенной дроби (например ) использовалась ещёдревнегреческими математиками, хотя знаменатель у них записывался надчислителем, а черты дроби не было. Индийские математики переместили числитель наверх; через арабов этот формат переняли в Европе. Дробную черту впервые в Европе ввёл Леонардо Пизанский (1202), но в обиход она вошла только при поддержке Иоганна Видмана (1489).

Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в учебнике Иоганна Видмана «Быстрый и приятный счёт для всех торговцев», изданном в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus)

Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали чаще всего букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон, 1634), звёздочка (Иоганн Ран,1659). Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x ; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).

Знаки деления. Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц.

Знак плюс-минус появился у Жирара (1626) и Отреда. Правда, Жирар между плюсом и минусом писал ещё словами «или».

Возведение в степень. Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2.

Знак суммы ввёл Эйлер в 1755 году.

Знак произведения ввёл Гаусс в 1812 году.

Букву i как код мнимой единицы: предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый).

Обозначение абсолютной величины и модуля комплексного числа появились уВейерштрасса в 1841 году. В 1903 году Лоренц использовал эту же символику для длины вектора.

=
Первое печатное появление знака равенства (записано уравнение )

Знак равенства предложил Роберт Рекорд в1557 году

Знак «приблизительно равно» придумал немецкий математик С. Гюнтер в 1882 году.

Знак «не равно» впервые встречается у Эйлера.

Автор знака «тождественно равно» — Бернхард Риман (1857). Этот же символ, по предложению Гаусса, используется в теории чисел как знак сравнения по модулю, а в логике — как знак операции эквивалентности.

Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше , меньше .

Символы нестрогого сравнения предложил Валлис в 1670 году.

Символы «угол» и «перпендикулярно» придумал в 1634 году французский математик Пьер Эригон. Символ угла у Эригона напоминал значок , современную форму ему придал Уильям Отред (1657).

Современные обозначения угловых единиц (градусы, минуты, секунды) встречаются ещё в «Альмагесте» Птолемея. Радианную меру углов, более удобную для анализа , предложил в 1714 году английский математик Роджер Котс . Сам термин радиан придумал в 1873 году Джеймс Томсон, брат известного физика лорда Кельвина .

Общепринятое обозначение числа 3,14159… впервые образовал Уильям Джонс в1706 году, взяв первую букву слов греч. περιφρεια — окружность и περμετρος —периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно.

Сокращённые обозначения для синуса и косинуса ввёл Отред в середине XVII века.

Сокращённые обозначения тангенса и котангенса: введены Иоганном Бернулли в XVIII веке, они получили распространение в Германии и России. В других странах употребляются названия этих функций , предложенные Альбером Жираром ещё ранее, в начале XVII века.

Манера обозначать обратные тригонометрических функции с помощью приставки arc (от лат. arcus , дуга) появилась у австрийского математика Карла Шерфера (нем. Karl Scherffer ; 1716—1783) и закрепилась благодаряЛагранжу. Имелось в виду, что, например, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: , но они не прижились.

Символ частной производной сделали общеупотребительным сначала Карл Якоби (1837), а затем Вейерштрасс, хотя это обозначение уже встречалось ранее в одной работе Лежандра (1786).

Символ предела появился в 1787 году у Симона Люилье и получил поддержку Коши (1821) . Предельное значение аргумента сначала указывалось отдельно, после символа lim , а не под ним. Близкое к современному обозначение ввёл Вейерштрасс, однако вместо привычной нам стрелки он использовал знак равенства . Стрелка появилась в начале XX века сразу у нескольких математиков — например, у Харди (1908).

Символ этого дифференциального оператора придумал Уильям Роуэн Гамильтон(1853), а название «набла» предложил Хевисайд (1892).

находящейся на интернете в свободном доступе

http://goo.gl/WcU0Ss

Всем привычный значок @ не был известен в нашей стране до наступления компьютерной эры. Обычно при заимствовании названия из другого языка новое не изобретается, а просто копируется (так в русский язык пришли слова «почта» и «табак», а слова «водка» и «спутник» пересекли границу в обратном направлении). Но иногда исходное название может оказаться непроизносимым, неприличным или не соответствующим правилам языка. Видимо, это и произошло с символом @ — его официальное название «коммерческое эт» русскому уху кажется совершенно бессмысленным. Название должно быть таким, чтобы его хотелось запомнить и применять. В 1990-е годы, когда значок @ впервые пытались перевести на русский, существовало множество равноправных вариантов — «кракозябра», «закорючка», «лягушка», «ухо» и другие. Правда, в настоящее время они практически исчезли, а «собака» распространилась по всему Рунету и осталась, потому что любой язык стремится иметь только одно универсальное слово для обозначения чего бы то ни было. Остальные названия остаются маргинальными, хотя их может быть очень много. Например, в английском языке символ @ называют не только словами commercial at, но и mercantile symbol, commercial symbol, scroll, arobase, each, about и т. д. Откуда взялась ассоциация между главным компьютерным значком и другом человека? Для многих символ @ действительно напоминает свернувшуюся калачиком собаку. Существует экзотическая версия, что отрывистое произношение английского at может напомнить собачий лай. Однако гораздо более вероятная гипотеза связывает наш символ с очень старой компьютерной игрой Adventure. В ней нужно было путешествовать по лабиринту, сражаясь с разными малоприятными подземными тварями. Поскольку игра была текстовая, сам игрок, стены лабиринта, монстры и клады обозначались различными символами (скажем, стены были постоены из «!», «+» и «-»). Игрока в Adventure сопровождал пес, которого можно было посылать с разведывательными миссиями. Обозначался он символом @. Возможно, именно благодаря этой ныне забытой компьютерной игре в России укоренилось название «собака». В современном мире знак @ присутствует повсюду, особенно с того момента, как он стал неотъемлемой частью адреса электронной почты. Но этот символ задолго до компьютерной эры входил в раскладку стандартной американской пишущей машинки, а компьютерным стал лишь потому, что сравнительно мало использовался. Значок @ применяется в коммерческих расчетах — в значении «по цене» (at the rate). Скажем, 10 галлонов масла по цене в 3,95 доллара США за галлон будет кратко записываться: 10 gal of oil @ $3.95/gal. В англоязычных странах символ применяется и в науке в значении «при»: например, плотность 1,050 г/см при 15°C будет записана: 1.050 g/cm @ 15°C. Кроме того, знак @ полюбили и часто используют анархисты ввиду его сходства с их символом — «А в круге». Однако его изначальное происхождение окутано тайной. С точки зрения лингвиста Ульмана, символ @ был изобретен средневековыми монахами для сокращения латинского ad («на», «в», «в отношении» и так далее), что очень напоминает его нынешнее использование. Другое объяснение дает итальянский ученый Джорджо Стабиле — он обнаружил этот символ в записях флорентийского купца Франческо Лапи за 1536 год в значении «амфора»: например, цена одной @ вина. Интересно, что испанцы и португальцы называют символ в электронных письмах именно «амфорой» (arroba) — словом, которое французы, исказив, превратили в arobase. Впрочем, в разных странах существуют самые разные названия для символа @, чаще всего зоологические. Поляки называют его «обезьянкой», тайваньцы — «мышкой», греки — «уточкой», итальянцы и корейцы — «улиткой», венгры — «червячком», шведы и датчане — «слоновым хоботом», финны — «кошачьим хвостом» или «знаком мяу», а армяне, подобно нам, — «песиком». Есть гастрономические названия — «штрудель» в Израиле и «рольмопс» (сельдь под маринадом) в Чехии и Словакии. Кроме того, часто этот символ называют просто «скрюченным А», или «А с завитком», или, как сербы, «чокнутым А». Впрочем, самая удивительная из современных историй, связанных с символом @, произошла в Китае, где знак банально называется «А в круге». Несколько лет назад китайская пара дала такое имя новорожденному. Возможно, знак стали воспринимать как иероглиф, символизирующий технический прогресс, и решили, что он принесет счастье и успех юному обитателю Срединной державы.

Список из 20+ полезных математических символов

Математические символы — это универсальные представления понятий, идей и чисел, которые можно использовать для выражения отношений между величинами. Их можно использовать в различных типах уравнений, и они образуют универсальный язык математики, на который можно ссылаться в любое время. Учащиеся также могут научиться решать более сложные математические уравнения, интуитивно понимая значения символов, таких как число пи, римские цифры, деление, дроби и т. д. 

Почему мы используем математические символы?

Математические символы используются различными способами, чтобы помочь извлечь максимальную пользу из уравнений, расчетов и формул. Они упрощают определение математических величин, а также устанавливают отношения между величинами, которые могут быть выражены уникальным образом. Они помогают нам создать логическую последовательность, которую можно использовать для представления любого физического события.

SplashLearn пробуждает любознательность на протяжении всей жизни благодаря своей обучающей программе PreK-5, основанной на играх, которую полюбили более 40 миллионов детей. С более чем 4000 веселых игр и занятий, это идеальный баланс между обучением и игрой для вашего малыша.

Попробуйте бесплатно

Символы также используются для обозначения предопределенных значений, таких как число Пи или постоянная Эйлера. Они используются для обеспечения согласованного стандарта, а также для упрощения расчетов, которые требуют регулярного использования этих чисел. Символы остаются неизменными с течением времени, что делает их лучшим способом представления идеи или стандарта для использования в любых расчетах.

   Похожие чтения:    Лучшие математические трюки, которые превратят ваших детей в математических гениев  

Вы также можете использовать символы для создания основы базовых знаний для учащихся. Математические символы, такие как знаки равенства, знаки больше, скобки и круглые скобки, формируют большую часть предварительных практических знаний обо всех сложных математических уравнениях. Учащиеся должны быть в состоянии привыкнуть к символам, чтобы уверенно решать математические задачи.

Математические символы также значительно облегчают работу со ссылками, так как вы можете вернуться к этим символам, чтобы выяснить взаимосвязь между величинами. Каждый символ, от производных до логарифмов, содержит историю информации, которую можно использовать для решения математических уравнений. Их можно использовать на разных языках, поскольку они являются постоянным справочником для любого математика во всем мире.

Основные математические символы

Начнем с основных математических символов, используемых для выражения отношений между величинами.

1. Сложение (+) используется для сложения двух чисел. 9+10 = 19

2. Вычитание (-) используется для вычитания одного числа из другого. 11-2 = 9

3. Знак равенства (=) используется для выражения двух одинаковых значений. X = 33

4. Приближение (≈) используется для обозначения приблизительного равенства. π (пи) ≈3,14

5. Не равно (≠) используется для выражения неравноправия. 15 ≠ Z

6. Умножение (x) используется для умножения двух чисел. 12 x 2 = 24

7. Деление (÷) используется для отделения одного числа от другого. 15 ÷ 5 = 3

Ознакомьтесь с более распространенными математическими символами здесь.

Хотите узнать больше о сложении и вычитании? Эта приключенческая игра учит детей, как использовать дополнение для освещения пещер в темноте – https://www.splashlearn.com/addition-games

Теория множеств и символы диаграммы Венна

Теория множеств и представление диаграмм Венна ключ к решению проблемы.

1. Пересечение (∩) обозначает общие числа между множествами.

2. Союз (U) обозначает объединение двух наборов.

3. Равенство (A = B) означает равные элементы в обоих множествах.

4. Декартово произведение (A X B) используется для обозначения наборов упорядоченных пар.

Доступ к другим символам теории множеств и диаграмм Венна здесь.

Римские цифры Математические символы

Вы также можете встретить римские цифры, особенно в сложных математических уравнениях.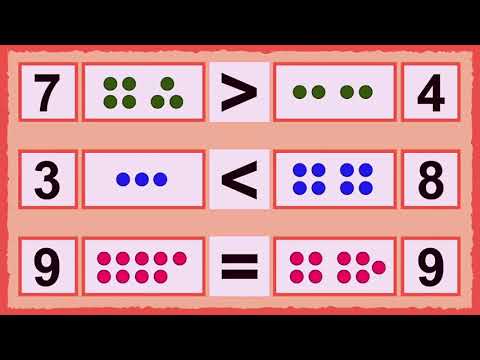

1. I — римская цифра со значением 1. II = 2

2. V — римская цифра со значением 5. V = 5

3. X — римская цифра со значением 10 , XX = 20

4. L — римская цифра со значением 50. L = 50

Чтобы увидеть больше римских цифр, нажмите здесь.

Неизменяемые математические константы

Время от времени вам также может понадобиться использовать математические константы, которые можно выразить, как показано ниже.

1. Квадратный корень из двух (√2) используется как положительное число с прибл. значение 1,41421.

2. Постоянная Эйлера (е) используется как основание натурального логарифма.

3. Пи (π) используется как символ для обозначения отношения длины окружности к диаметру круга.

4. Мнимая единица (i), используемая как корень из минус 1 для обозначения комплексных чисел.

Получите доступ к дополнительным математическим константам и их значению.

Алгебраические математические символы

Алгебраические символы — одни из наиболее часто используемых символов в математике и естественных науках.

1. Переменные (x, y), используемые для обозначения заполнителей для переменных чисел. х = у + 10,

2. Пропорционально (∝) используется для обозначения пропорционального отношения. X ∝ y ⟹ x = ky

3. Сложение (+) используется для добавления переменных. 2x + 3y = 4z

4. Функциональная карта f(x), используемая для обозначения функции. f(x) = 2x – 9

Узнайте больше математических символов алгебры здесь.

Нужна дополнительная помощь в решении алгебраических уравнений? Помогите детям обрести интуитивное понимание предмета, нажмите здесь.

Улучшите успеваемость вашего ребенка по математике, записавшись на обширную библиотеку викторин и игр SplashLearn

Вы можете получить доступ к забавным играм, исследовательским викторинам и творческим рабочим листам, позволяющим учащимся раскрыть свой потенциал в математике. С 2046 математическими играми и 51 математическим курсом SplashLearn охватывает весь спектр математических знаний для детей от Pre-K до 5 класса. Используя научно разработанные игры и курсы, созданные в сотрудничестве с ведущими преподавателями, наша программа повышает успеваемость и уверенность в своих математических способностях.

   Связанные чтения:    Как стать лучше в математике за 10 эффективных шагов
  

Узнайте больше, посетив – https://www.splashlearn.com/math-games

Есть вопрос? Отправьте нам электронное письмо по адресу [email protected]

Часто задаваемые вопросы

Что означает ∈ ø в математике?

Символ означает, что элемент этого набора является объектом, содержащимся в нем. Он широко используется в теории множеств и является ключевым математическим символом, используемым для описания отношений.

Что означает U в математике?

Когда два набора имеют объединение, его можно использовать для представления себя как U. В каждом наборе присутствуют значения, которые можно объединить с помощью символа «U». Вы можете узнать больше о союзах, посетив математические игры SplashLearn.

Что такое x и y в математике?

Строчные буквы могут использоваться для обозначения переменных в математике. Буквы x и y широко используются как общие переменные, которые могут быть выражены, чтобы помочь решить проблему. Они также используются в более сложных уравнениях, чтобы установить базовый стандарт для нахождения неизвестных величин.

Какой большой символ Е используется в математике?

В. Что такое большой символ Е, используемый в математике?

A. Знак Σ (сигма) используется для обозначения суммирования нескольких элементов. Он также широко используется в математике и является основным символом, с которым все учащиеся должны быть знакомы интуитивно.

Как мне улучшить понимание символов моим ребенком?

Прямые методы обучения могут быть неэффективными, поскольку символы являются абстрактными и обозначают отношения между величинами. Вы можете использовать игры, онлайн-платформы обучения и видеоинструменты, чтобы помочь детям визуализировать, что представляет собой символ.