Y x 2 y 4 вычислите площадь фигуры ограниченной линиями: 1.вычислите площадь фигуры ограниченной линиями y=x^2 и y=4 2.вычислите площадь фигуры ограниченной линиями y=x^2-6x+7 и…

4 и y=2 — Учеба и наука

Содержание

Ответы

31.

03.14

Ответ не понравился автору вопроса

Михаил Александров

Читать ответы

Андрей Андреевич

Читать ответы

Eleonora Gabrielyan

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

В гараже в одном ряду было 25 машин,а в другом -32.

2, y=4-x

Лучший ответ по мнению автора

19.

12.17

Лучший ответ по мнению автора

Ответ понравился автору вопроса

Михаил Александров

Читать ответы

Андрей Андреевич

Читать ответы

Eleonora Gabrielyan

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно

Решено

Помогите пожалуйста решить задачу 4-го класса. Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько

В прямоугольнике ABCD AB=24 см, AC=25 см. Найдите площадь прямоугольника

Сколько существует 2016-значных чисел таких, что при вычёркивании его любой одной цифры получается 2015-значное число, и это 2015-значное число является делителем исходного числа (Напомним, что

Решено

Высота цилиндра равна 16 см. На расстоянии 6 см от оси цилиндра проведено сечения, параллельное оси цилиндра и имеющее форму квадрата. Найдите радиус цилиндра

Пользуйтесь нашим приложением

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

1.

5: Площадь между кривыми — Mathematics LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 91709

Джоэл Фельдман, Эндрю Рехнитцер и Элиз Йегер
Университет Британской Колумбии

Прежде чем мы продолжим изучение различных методов интегрирования функций, у нас теперь есть достаточно инструментов для изучения некоторых простых приложений определенных интегралов. Одним из мотивов нашего определения «интеграла» была проблема нахождения площади между некоторой кривой и осью $x$ для $x$, проходящей между двумя заданными значениями. Точнее

9б f(x) \, d{x} \end{gather*}

равно площади со знаком между кривой $y=f(x)\text{,}$ и осью $x$ и вертикальными линиями $x=a$ и $x =б\текст{. }$

Мы нашли площадь этой области, аппроксимировав ее объединением высоких тонких прямоугольников, а затем нашли точную площадь, взяв предел, когда ширина аппроксимирующих прямоугольников стремится к нулю. Мы можем использовать ту же стратегию, чтобы найти области более сложных областей в $xy$-плоскости.

В качестве превью следующего материала пусть $f(x) \gt g(x) \gt 0$ и $a \lt b$ и предположим, что нас интересует площадь области 9b \big(f(x)-g(x)\big)\,\, d{x} \end{align*}

Это вычисление основывалось на предположении, что $f(x) \gt g(x)$ и, в частности, что кривые $y=g(x)$ и \(y=f(x)\ ) не пересекался. Если они пересекаются, как на этом рисунке

, то мы должны быть намного осторожнее. Идея состоит в том, чтобы разделить область интегрирования в зависимости от того, где $f(x) — g(x)$ меняет знак, т.е. где пересекаются кривые. Мы проиллюстрируем это в примере 1.5.5 ниже.

Начнем с примера, который делает связь с суммами Римана и определенными интегралами совершенно явной.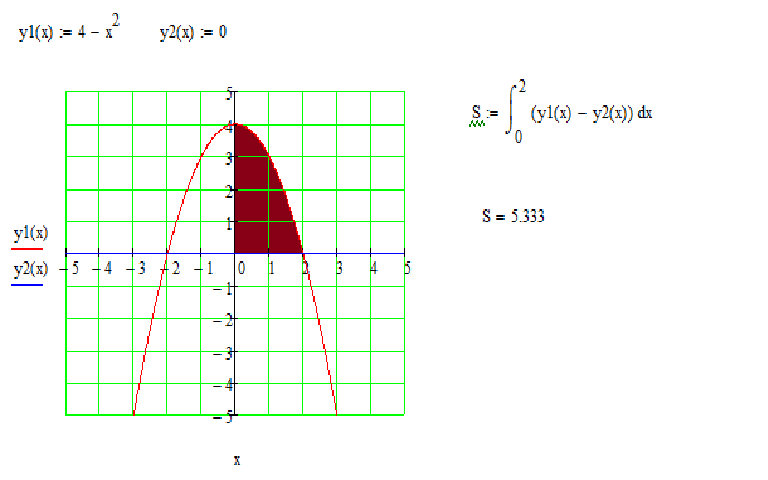 *)\text{.}\) 91\\ &= \left(4 — \frac{1}{2}-\frac{1}{3} \right) — \left(-4-\frac{1}{2}+\frac{1 {3} \right)\\ &= \frac{24-3-2}{6} — \frac{-24-3+2}{6}\\ &= \frac{19}{6} + \frac{25}{6}\\ &= \frac{44}{6} = \frac{22}{3}. \end{выравнивание*}

Уф! К счастью, нам обычно не нужно проходить этапы вычисления суммы Римана, чтобы получить ответ. Обычно, при условии, что мы тщательно проверяем, где пересекаются кривые и какая кривая находится выше какой, мы можем просто сразу перейти к интегралу 9.2\text{.}\)

Решение

Это немного отличается от предыдущего вопроса, так как нам не заданы ограничивающие линии $x=a$ и $x=b$ — вместо этого мы должны определить минимальные и максимальные допустимые значения $х$, определив, где пересекаются кривые. Следовательно, наша самая первая задача — получить хорошее представление о том, как выглядит регион, зарисовав его.

Начните с наброска области:
Это приводит нас к наброску
.

Решение

Мы показываем два разных решения этой задачи. Первый использует подход, который мы использовали в примере 1.5.3, но приводит к запутанной алгебре. Второй требует немного размышлений в начале, но затем довольно прост. Прежде чем мы доберемся до этого, мы должны начать с наброска области.

Как отмечалось выше, мы можем найти площадь этой области, аппроксимировав ее объединением узких вертикальных прямоугольников, как мы сделали в примере 1.5.3, хотя это немного сложнее. Самый простой способ — аппроксимировать его объединением узких горизонтальных прямоугольников. Просто для практики, вот жесткое решение. Простое решение после него.

Более сложное решение:

Как и раньше, мы аппроксимируем область объединением узких вертикальных прямоугольников, каждый шириной $\Delta x\text{.}$ Два из этих прямоугольников показано на эскизе
В этой области $x$ проходит от $a=-3$ до $b=5\text{. 2-6)\le x \le y+1\text{.}$
Давайте использовать
- $c$ для обозначения наименьшего допустимого значения $y\text{,}$
- $d$ для обозначения максимального допустимого значения $y$
- $L(y)$ («$L$» означает «слева») для обозначения наименьшего допустимого значения $x\text{,}$, когда $y$-координата $г\текст{,}$ и
- $R(y)$ («$R$» означает «право») для обозначения наибольшего допустимого значения $x\text{,}$, когда $y$-координата равна $г\текст{.}$
- Теперь наша стратегия почти такая же, как в примере 1.5.1:
  - Выберите натуральное число $n$ (которое мы позже отправим в бесконечность), затем
  - разделить интервал $c\le y\le d$ на $n$ узких подинтервалов, каждый шириной $\Delta y=\frac{d-c}{n}\text{. }$ Каждый подинтервал вырезает из региона тонкий горизонтальный срез (см. рисунок ниже). 94\\ &=-\tfrac{1}{6}\big(64-(-8)\big)+\tfrac{1}{2}(16-4)+4(4+2)\\ & =-12+6+24\\ &=18 \end{выравнивание*}
  Последний пример.
  Пример 1.5.5 Другая область
  Найдите площадь между кривыми $y=\dfrac{1}{\sqrt{2}}$ и $y=\sin(x)$ с $x\ ) выполняется от \(0$ до $\frac{\pi}{2}\text{.}$
  Решение:
  Это немного сложнее, поскольку (как мы увидим) область разделен на две части, и мы должны рассматривать их отдельно.
  - Снова начнем с наброска области.
    Нам нужна заштрихованная область.
  - В отличие от наших предыдущих примеров, ограничивающие кривые $y=\frac{1}{\sqrt{2}}$ и $y=\sin(x)$ пересекаются в середине интересующей области. Они пересекаются, когда $y=\frac{1}{\sqrt{2}}$ и $\sin(x)=y=\frac{1}{\sqrt{2}}\text{,}\ ) т.е. когда \(x=\frac{\pi}{4}\text{.}$ Итак
    - слева от $x=\frac{\pi}{4}\text{,}$ верхняя граница является частью прямой линии $y=\frac{1}{\sqrt{2} }$, а нижняя граница является частью кривой $y=\sin(x)$
    - , а справа от $x=\frac{\pi}{4}\text{,}$ верхняя граница является частью кривой $y=\sin(x)$, а нижняя граница часть прямой линии $y=\frac{1}{\sqrt{2}}\text{. }$
  - Таким образом, формулы для верхней и нижней границ равны
    \begin{align*} T(x) & =\left.\begin{cases} \frac{1}{\sqrt{2}} & \text{if $0\le x\le \frac{\pi} {4}$}\\ \sin(x)& \text{if $\frac{\pi}{4}\le x\le \frac{\pi}{2}$} \end{cases}\right \}\\ B(x) & =\left.\begin{cases} \sin(x) & \text{if $0\le x\le \frac{\pi}{4}$}\\ \frac{ 1}{\sqrt{2}}& \text{if $\frac{\pi}{4}\le x\le \frac{\pi}{2}$} \end{cases}\right\} \ конец{выравнивание*} 9{\ frac {\ pi} {2}} \\ & = \ Big [\ frac {1} {\ sqrt {2}} \ frac {\ pi} {4} + \ frac {1} {\ sqrt {2 }}-1\Big] +\Big[\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}\frac{\pi}{4}\Big]\\ &=\frac{2}{\sqrt{2}}-1\\ &=\sqrt{2}-1 \end{align*}
  Стадия 1
  1
  Мы хотим аппроксимировать площадь между графиками $y=\cos x$ и $y=\sin x$ от $x=0$ до $x =\pi$ с помощью левой суммы Римана с $n=4$ прямоугольниками.
  1. На графике ниже нарисуйте четыре прямоугольника.
  2. Вычислите приближение Римана.
  2
  Мы хотим аппроксимировать ограниченную область между кривыми $y=\arcsin\left(\dfrac{2x}{\pi}\right)$ и $y=\sqrt{\dfrac{\ pi x}{2}}$ с помощью прямоугольников $n=5$.
  1. Нарисуйте пять (вертикальных) прямоугольников на рисунке ниже, соответствующих правой сумме Римана.
  2. Нарисуйте пять прямоугольников на картинке ниже, которые мы могли бы использовать, если бы использовали горизонтальные прямоугольники.
  3 (✳) 9b \big|f(x) — g(x)\big|\,\, d{x}\text{.}\) Чтобы убедиться, что два интеграла совпадают, разделим область интегрирования, где $f (x)-g(x)$ меняет знак.