в картинках и текстовые, для взрослых и детей
Математические головоломки как способ помериться интеллектуальными силами всегда увлекали людей. ЛогикЛайк рассказывает о нескольких широко известных задачках, над которыми ломали голову десятки поколений.
Разберите подборку головоломок вместе с детьми: «разомнете» мозги, весело проведете время и знание истории «прокачаете»! Мы выбрали интересные задачки, дошедшие до наших дней из «древности», и приближенные к «нашему» времени.
Папирус Ахмеса
Древние египтяне были не только опытными строителями пирамид, но и прекрасными математиками. Доказательством этому служит древнеегипетский папирус, автором которого был некий Ахмес. Как выяснили исследователи-египтологи, папирус Ахмеса — копия очень древнего математического сборника, составленного во времена фараона Аменемхета III (приблизительно 1853-1806 гг. до н.э.). Задач в сборнике много — ниже одна из них.

Задача о переправе
Не только древние египтяне упражнялись в решении задач на сообразительность. Историки обнаружили книгу, написанную на латыни, под названием «Задачи для развития молодого ума». Ирландский богослов, ученый и просветитель Алкуин, живший в IX веке, собрал в книге 53 задачи. Предлагаем одну из них — настолько «бородатую», что ее знают школьники во всем мире.

Как крестьянину перевезти все в целости и сохранности?
Печать царя Соломона
На гробнице мудрого легендарного библейского царя Соломона потомки изобразили знаменитую печать правителя.

Попробуйте сосчитать, сколько равносторонних треугольников изображено на печати.
Задача Фибоначчи о размножении кроликов
Леонардо Пизанский (около 1170 г.р.), по прозвищу Фибоначчи, — один из первых именитых математиков средневековой Европы. Он успешно участвовал в математических турнирах, а, создав себе имя, придумывал для них занимательные задачи. Ниже одна из самых известных.
«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца.
Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов».
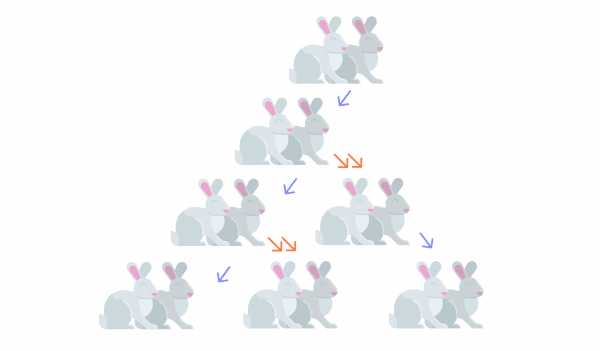
Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения?
Подсказка Вспомните последовательность Фибоначчи или запаситесь терпением — и считайте.
Задача Тартальи «Трудное наследство»
Никколо Тарталья (1499 г.р.), итальянский математик, обнаруживший общий алгоритм решения кубических уравнений. Описанный Никколо метод вошел в историю математики как Формула Кардано, по имени первого публикатора метода, до которого независимо друг от друга додумались Тарталья и Сципион дель Ферро.
Предлагаем решить ставшую известной задачу Тартальи о дележе лошадей.

Как выполнить завещание?
Головоломка Льюиса Кэрролла
Известный писатель Льюис Кэрролл, тот самый, который создал истории об Алисе и ее приключениях в Стране Чудес и Зазеркалье, еще и очень любил придумывать головоломки и преподавал логику.
Своим маленьким поклонникам Кэрролл часто предлагал такую головоломку:
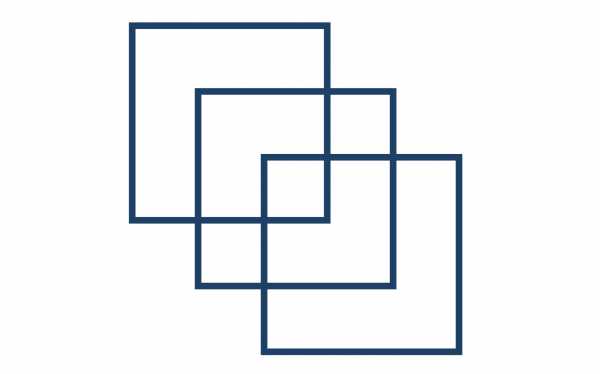
Задача усложняется особыми условиями ее выполнения:
- карандаш от бумаги отрывать нельзя;
- дважды проводить карандашом в одном месте нельзя;
- пересекать линии нельзя.
«Безумный разрез» Мартина Гарднера
Мартин Гарднер — известный американский писатель, математик-любитель, автор множества статей и книг по занимательной математике, научно-популярных этюдов, математических фокусов, головоломок и задач на сообразительность и множества других публикаций.
Предлагаем решить одну из самых популярных головоломок Гарднера.

Сделайте один разрез (или нарисуйте одну линию) — не обязательно, прямую — чтобы разделить нарисованную фигуру на две одинаковые части.
Сингапурская головоломка
Благодаря социальным сетям некоторые головоломки распространяются, как вирус, и становятся известными. Так случилось с головоломкой, которую телеведущий Кеннет Конг из Сингапура разместил на своей странице в фейсбуке, и вскоре ею поделились 4400 человек.
Альфред и Бернард только что познакомились с Шерил и хотят выяснить, когда у нее день рождения.
Шерил показала поклонникам 10 возможных дат:
Затем она показала Альфреду месяц своего рождения, а Бернарду — день.
Чтобы решить головоломку, друзья обменялись парой реплик:
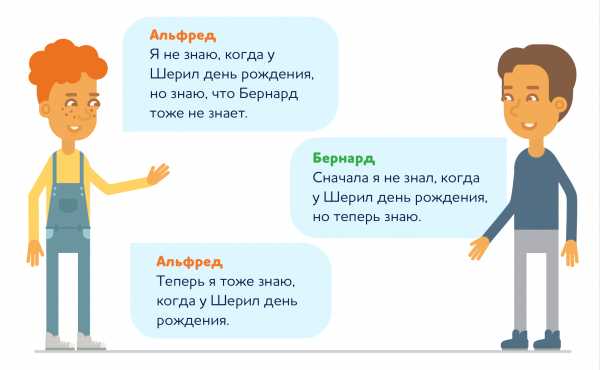
Так когда же у Шерил день рождения?
Танграм
Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древнекитайскими мудрецами для сына императора. Правитель хотел чтобы через простую игру его сын постиг начала математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и осознал, что сложные вещи состоят из простых.
Так появился «Ши-Чао-Тю» — квадрат, разрезанный на семь частей:
5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.
Суть «свободной» игры в танграм — собирать из имеющихся деталей по принципу мозаики всевозможные фигурки: животных, птиц, человека, что угодно. Младшим дошкольникам предлагают простой вариант развивающей игры, когда фигурки танграма нужно просто наложить на готовый образец-ответ.
Многие дети в 5-7 лет складывают модели из фигурок рядом с изображением-ответом, даже если размеры вырезанных фигур и деталей на картинке отличаются.
Танграм как головоломка обычно по силам ребенку начиная с 6-7 лет. Все так же — из элементов танграма нужно сложить готовую модель, но на карточке изображен лишь силуэт фигуры.
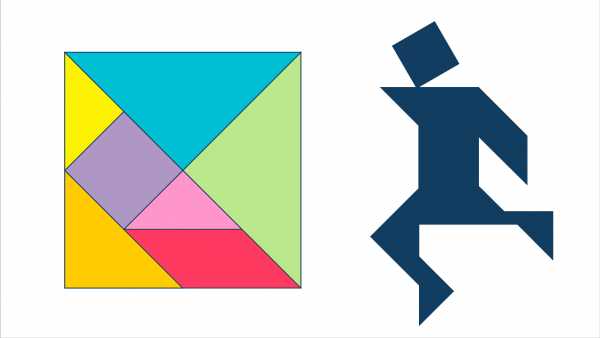
Вырежьте элементы танграма из бумажного, картонного или другого квадрата, и для начала предлагаем собрать одну из популярных фигурок — бегущего человека, как на рисунке выше.
Помните 2 правила головоломки:
1) необходимо использовать все 7 фигурок головоломки;
2) фигуры не должны накладываться друг на друга.
Среди поклонников танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что именно «танграмом» назвал игру американский шахматист, изобретатель «пятнашек» и многих других головоломок, Самюэль Лойд.
В 21 веке самые интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном дизайне и архитектуре.
logiclike.com
Занимательные задачи по математике для начальной школы
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ

1. Из гнезда вылетели три ласточки. Какова вероятность того, что через 15 секунд они будут находиться в одной плоскости? (Ответ: 100%, так как три точки всегда образуют одну плоскость)
2. На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты? (Ответ: 2 рубля и 1 рубль. Одна-то не 1 рубль, а вот другая — 1 рубль)
3. С какой скоростью должна бежать собака, чтобы не слышать звона сковородки, привязанной к ее хвосту? (Ответ: Если вы думаете, что ей нужно бежать со сверхзвуковой скоростью, то вы ошибаетесь — собаке достаточно стоять на месте)
4. Один оборот вокруг Земли спутник делает за 1 час 40 минут, а другой — за 100 минут. Как это может быть? (Ответ: 1 ч 40 мин = 100 мин)
5. Крыша одного дома не симметрична: один скат ее составляет с горизонталью угол 60 градусов, другой — угол 70 градусов. Предположим, что петух откладывает яйцо на гребень крыши. В какую сторону упадет яйцо — в сторону более пологого или крутого ската? (Ответ: Петухи не кладут яйца)
6. В 12-этажном доме есть лифт. На первом этаже живет всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. Какая кнопка в лифте этого дома нажимается чаще других? (Ответ: Независимо от распределения жильцов по этажам, кнопка «1»)
7. В двух кошельках лежат две монеты, причем в одном кошельке монет вдвое больше, чем в другом. Как такое может быть? (Ответ: Один кошелек лежит внутри другого)
8. Сын отца профессора разговаривает с отцом сына профессора, причем сам профессор в разговоре не участвует. Может ли такое быть? (Ответ: Да, может, если профессор — женщина).
9. Два сына и два отца съели 3 яйца. Сколько яиц съел каждый? (По одному яйцу каждый)
10. На складе было 5 цистерн с горючим, по 6 тонн в каждой. Из двух цистерн горючее выдали. Сколько цистерн осталось? (5)
11. Вообрази, что ты капитан футбольной команды. В районе 8 футбольных команд, по 11 человек в каждой. Игроки вашей команды на 2 года моложе своего капитана, а игроки других — только на 1 год. Сколько лет капитану вашей команды? (Столько, сколько лет отвечающему)
12. Пара лошадей пробежала 20 км. Сколько километров пробежала каждая лошадь? (20 км)
13. Когда сороке исполнится 4 года, что с ней произойдет? (Будет жить пятый год)
14. Если в 11 часов ночи идет дождь, то возможно ли через 48 часов солнечная погода? (Нет, так как будет ночь)
15. Чтобы сварить 1 кг мяса, требуется один час. Сколько времени потребуется для варки х кг мяса? (1 час)
16. У Марины было целое яблоко, две половинки и 4 четвертинки. Сколько было у нее яблок? (3)
17. На грядке сидели 6 воробьев, к ним прилетели еще 5. Кот подкрался и схватил одного воробья. Сколько воробьев осталось на грядке? (Один, которого схватил кот. Остальные улетели)
18. Мальчик написал на бумажке число 86 и говорит своему товарищу: «Не производя никакой записи, увеличь это число на 12 и покажи мне ответ». Недолго думая, товарищ показал ответ. А вы это сделать сумеете? (Перевернуть бумажку «вверх ногами»)
19. В клетке находились 4 кролика. Четверо ребят купили по одному из этих кроликов и один кролик остался в клетке. Как это могло получиться? (Одного кролика купили вместе с клеткой)1
20. Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток? (Три утки, одна за другой)
21. У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. Как это могло быть? (Этот человек родился 29 февраля, т. е. день рождения у него бывает один раз в четыре года)
22. Что это такое: две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги, схватив три, бросили их в четыре, чтобы четыре оставили одну? (Повар сидел на стуле, имеющем три ножки, пришла собака и утащила куриную ногу. Повар бросил стул в собаку, чтобы она оставила куриную ногу)
23. Часы бьют каждый час и отбивают столько ударов, сколько показывает часовая стрелка. Сколько ударов отобьют часы в течение 12 часов? (Количество ударов равняется 1+2+3+…+12…= 78. Суммы членов, равноотстоящих от концов (1+12, 2+11, 3+10,…) равны между собой — 13. Таких пар, равноотстоящих от концов чисел, имеется 6. Значит, 1+2+3+…+12=6 х 13=78).
24. Летели скворцы и встретились им деревья. Когда сели они по одному на дерево, то одному скворцу не хватило дерева, а когда на каждое дерево сели по два скворца, то одно дерево осталось не занятым. Сколько было скворцов и сколько деревьев? (Предположим, что, после того как скворцы сели на деревья по два, с каждого дерева взлетело по одному скворцу. Один из взлетевших скворцов может сесть на незанятое дерево, тогда на каждом дереве будет сидеть по одному скворцу. По условию если на каждое дерево сядет по одному скворцу, то один скворец останется в воздухе. Значит, взлетело 2 скворца. Тогда общее число скворцов равно 4, а число деревьев 3.
Задачи-эксперименты.
Задача 1. Предложите учащимся взять произвольно три различные цифры, кроме нуля, а затем составить из них всевозможные трехзначные числа, сложить их и полученную сумму разделить на сумму первоначально взятых цифр. Учащимся можно сразу сообщить ответ — 222.
Например, учащиеся взяли цифры 2, 3, 7. Они составили из них шесть трехзначных чисел: 237, 273, 327, 372, 723, 732. Сумма их равна: 237 + 273 + 327 + 372 + 723 + 732 = (237 + 723) + (273 + + 327) + (372 + 732) = 960 + 600+1104 = 2664.
Разделив это число на сумму цифр 7 + 3 + 2, учащиеся получают ответ: 2664 : 12 = 222.
Эта задача очень интересна. Удивление вызывает угадывание ответа учителем. Особенно удивительно то, что учитель угадал ответ у каждого из учеников. Несмотря на то, что цифры были взяты ими совершенно произвольно и в весьма разнообразных сочетаниях. Но это эмоциональная сторона дела, хотя ее роль в обучении математике младших школьников представляется весьма важной. В задаче немало и поучительных математических моментов.
Во-первых, обратим внимание учащихся на то, что из трех цифр можно составить именно шесть чисел. Это несложно, на первое место можно поставить любую из трех цифр, а на оставшиеся — две другие в разном порядке. Значит, всего таких чисел 3×2 = 6.
Во-вторых, при сложении чисел чрезвычайно полезными оказываются навыки рационального выполнения действий, что приводит к результату значительно быстрее, и уменьшает возможность допущения ошибок.
В-третьих, и это главное, весьма интересно решение задачи в общем виде. Итак, пусть взяты цифры a, b, с (различные, ни одна из цифр не равна нулю). Составим из них шесть трехзначных чисел. Каждая цифра, например, а, будет дважды означать число сотен, дважды — десятков, дважды — единиц. Значит, сумма всех шести чисел будет равна.
100 (2а + 2b + 2с) + 10 (2а + 2b + 2с) + (2а + 2b + 2с) = 222 (а + b + с), и результат от деления этой суммы на сумму цифр (а + b + с) будет равен 222.
Учащимся будут интересны и другие задачи такого типа.
Задача 2. Возьмите любое трехзначное число, не оканчивающееся нулем. Переставьте в нем цифры в обратном порядке. ц3 большего числа вычтите меньшее и полученную разность разделите на разность первых цифр слева этих двух чисел. У вас получится 99. Почему?
Например, взяли число 285, переставили в нем цифры, получили 582. Из большего вычли меньшее 582 — 285 = 297 и разделили на разность первых цифр 5-2 = 3, получили 297 : 3 = 99.
Задача 3. Задумайте число, которое делилось бы на 6. Разделите его пополам, полученное число запомните. Теперь задуманное число разделите на 3, результат запомните. А теперь разделите задуманное число на 2. Результаты всех трех делений сложите. У вас получилось задуманное число. Почему?
Например, взяли число 72, получили три числа:
первое — 72 : 2 = 36,
второе — 72 : 3 = 24,
третье — 72 : 6 = 12.
Сложили их: 36 + 24 + 12 = 72. Получили задуманное число.
Задача 4. Возьмите любое двузначное число, которое не оканчивается нулем. Переставьте в нем цифры, получите новое число. Сложите эти два числа и разделите их на сумму цифр любого из этих чисел. Докажите, что в ответе получается 11.
Например, взяли число 53. Переставили в нем цифры, получили число 35. Сложили их и получили 35 + 53 = 88.
Сумму разделили на сумму цифр первого числа 5 + 3 = 8 (у второго она та же), получили 88 : 8 = 11.
Задача «Четвертый лишний».
В каждом ряду три числа обладают общим свойством, а одно число этим свойством не обладает. Укажите, что это за свойство и какое число лишнее.
Нестандартные задачи на деление
Задача 1. Трехметровый брусок надо разрезать на полуметровые. Сколько разрезов надо сделать?
Решение: в трехметровом бруске 300 см. Его надо разрезать на бруски длиной 50 см каждый. Получится: 300 : 50 = 6 (брусков). А сколько же надо сделать разрезов? Рассуждать будем так: чтобы разделить брусок пополам, то есть на 2 части, надо сделать один разрез, на три части — два разреза, и так далее, на шесть частей — пять разрезов. Итак, надо сделать 6-1=5 (разрезов).
Ответ: 5 разрезов.
При решении подобных задач возможны различные варианты. Рассмотрим их на следующих примерах.
Задача 2. Пятидесятиметровый шнур надо разрезать на части, длина каждой из которых 2 м. Сколько разрезов надо сделать?
Решение: 50 : 2 — 1 = 24 (разреза).
Ответ: 24 разреза.
Задача 3. Шестиметровый брус разрезали на равные части, сделав при этом 5 разрезов. Какой длины получились каждая часть?
Решение: 6 : (5 + 1) = 1 (м).
Ответ: 1 метр.
Задача 4. Вдоль участка длиной 100 м поставили столбы для ограды на расстоянии друг от друга -4 м. Сколько столбов поставили?
Решение: 100 : 4 + 1 = 25 + 1 = 26 (столбов).
Ответ: 26 столбов.
Задача 5. Вдоль прямой дороги на расстоянии 150 м поставили 51 столб. Столбы ставились на равном расстоянии друг от Друга. Каково это расстояние?
Решение: 150 : (51 — 1) = 3 (м).
Ответ: на расстоянии 3 метра друг от друга.
Задачи-ребусы.
1. Найдите цифры, обозначенные буквами А и В в примере:
Решение основано на том, что переноса единиц из одного разряда в другой нет. Значит А + В = 3.
Поскольку число не может начинаться с 3 3 нуля, то возможны случаи: А = 1, В = 2 или А = 2, В = 1, то есть
Ответ: А = 1, В = 2 или А = 2, В = 1.
Учитель, однако, может пояснить учащимся, что А = 2, В = 1 не дает принципиально нового решения. Это обстоятельство очень важно, поскольку в элементарной форме подготавливает учащихся к восприятию такого свойства, как симметричность.
После этого учащимся могут быть предложены такие задачи:
Задача 1. Найдите цифры, обозначенные буквами А, В, С в примере:
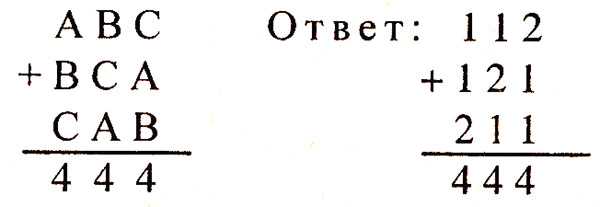
Задача 2. Какие цифры надо поставить вместо звездочек в примере?
Задача 3. Какие цифры надо поставить в примере вместо звездочек?
Задача 4. Какие цифры скрываются за звездочками?
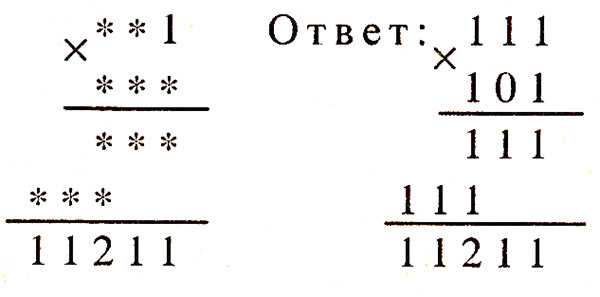
Задачи на внимание
1. Подумай и скажи — кто быстрее переплывет речку — утята или цыплята?
2. Подумай и скажи — какого цвета волосы у колобка?
3. Отгадай загадку: Лежали конфетки в кучке. Две матери, две дочки Да бабушка с внучкой Взяли конфет по штучке, И не стало этой кучки. Сколько конфет было в кучке?
4. Росли 5 берез. На каждой березе по 5 больших веток. На каждой ветке по 5 маленьких веток. На каждой маленькой ветке — по 5 яблок. Сколько всего
яблок?
5. Подумай и скажи — что помогает выжить белым медведям в пустыне, где нет воды?
6. На каких деревьях вьют свои гнезда страусы?
7. На столе лежит 2 яблока и 4 груши. Сколько всего овощей лежит на столе?
8. Подумай и скажи — кто громче рычит: тигр или буйвол?
9. Посмотрел Ваня утром в окно и говорит: — А на улице, оказывается, очень сильный ветер. Нужно теплее одеваться. Как он догадался, что на улице ветер? Что он увидел?
10. Пошли 2 девочки в лес за грибами, а навстречу 2 мальчика. Сколько всего детей идет в лес?
11. Бревно распилили на 4 части. Сколько сделали распилов?
12. У мамы есть братья Николай и Виктор, сестра Маргарита, сын Олег и дочь Мария. Сколько всего детей у мамы?
13. Шли 2 старухи в Москву, а навстречу им три старика. Сколько человек шло в Москву? (2 старухи).
14. Может ли при делении получиться ноль? (Да)
15. У прямоугольника отрезали один угол. Сколько углов стало? (5)
16. Бежала тройка лошадей. Каждая пробежала 5км. Сколько км проехал ямщик? (5км.)
17. На дереве сидело 23 птицы. Охотник прицелился, выстрелил и промахнулся. Сколько птиц осталось на дереве?
ЛОГИЧЕСКИЕ ЗАДАЧИ
У Лёвы, Гены, Васи, Толи и Миши были три барабана и две трубы.
Какой музыкальный инструмент был у каждого мальчика, если у Гены и Васи, а также у Лёвы и Толи были разные инструменты,
а у Гены и Левы – как у Миши?
На весах, которые находятся в равновесии, на одной чашке лежит 1 морковка и 2 одинаковые редиски.
На другой чашке – 2 такие же морковки и 1 такая же редиска. Что легче: морковка или редиска?
У бабушки два внука: Коля и маленький Олег. Бабушка купила им 16 конфет и сказала Коле, чтобы он дал Олегу на 2 конфеты больше, чем взял себе. Как Коля должен разделить конфеты?
Отца одного гражданина зовут Николай Петрович, а сына – Алексей Владимирович. Как зовут гражданина?
Тетрадь дешевле ручки, но дороже карандаша. Что дешевле?
Имеется перекрёсток двух дорог. Вдоль каждой из дорог, по одну сторону на этом перекрёстке надо посадить по 11 деревьев.
Каково наименьшее количество деревьев, которые можно посадить, выполняя это задание?
Какие три числа, если их сложить или перемножить, дают один и тот же результат?
Ваня живет выше Пети, но ниже Сени, а Коля живет ниже Пети. На каком этаже четырёхэтажного дома живёт каждый из них?
В семье четверо детей, им 5, 8, 13 и 15 лет, а зовут их Таня, Юра, Света и Лена.
Сколько лет каждому из них, если одна девочка ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3?
Двое подошли к реке. Лодка, на которой можно переправиться, вмещает одного человека.
И все же, без посторонней помощи, они переправились на этой лодке. Как им это удалось?
Стоят двое. Один смотрит на юг, другой на север.
Могут ли они увидеть друг друга, не поворачивая головы, не употребляя зеркал или каких – либо приспособлений?
Полтора лимона стоят полтора рубля. Сколько стоят десять лимонов?
За книгу заплатили один рубль и ещё половину стоимости книги. Сколько стоит книга?
Каждую минуту от бревна отпиливают метровый кусок. Во сколько минут распилят на такие куски бревно длиной 6 метров?
Даша и Маша получили в школе пятёрки: одна – по математике, другая – по чтению.
По какому предмету получила пятёрку Даша, если Маша получила эту оценку не по математике?
Два друга – Федя и Костя – получили в школе двойку и тройку.
Федины родители обычно ругают сына за тройки, а привыкшие к тройкам Костины родители ругают его только за двойки.
Кому попадет на этот раз, если известно, что Федя не получил тройку?
В школьном буфете Наташа, Яна и Алёна покупали пирожные – бисквитное с вареньем, бисквитное с кремом и трубочку с кремом. Кто что купил, если каждая девочка съела по одному пирожному,
Яна и Алёна любят пирожные с кремом, а Наташа и Алёна купили себе по бисквитному пирожному?
У трёх подружек – Вики, Ани и Лены – очень красивые куртки – синяя и красная с капюшонами и синяя без капюшона.
У кого какая куртка, если Аня и Лена ходят с капюшонами, а у Ани и Вики куртки синего цвета?
Бегемот тяжелее носорога, а носорог тяжелее быка. Кто из этих друзей самый лёгкий?
Вите, Пете и Андрею подарили по видеокассете: одну – с комедией, другую с веселыми мультфильмами,
а третью с фантастическим фильмом. Кто что получил в подарок, если известно, что Петя и Витя не любят смотреть мультфильмы,
а Андрей и Петя в процессе просмотра хохотали до упаду?
Три девочки – Таня, Катя и Марина – занимаются в трёх различных кружках – вышивки, танцев и хорового пения.
Катя не знакома с девочкой занимающейся танцами. Таня часто ходит в гости к девочке, занимающейся вышивкой.
Подружка Кати -–Марина, хочет в следующем году добавить к своим увлечениям занятия пением.
Кто из девочек чем занимается?
Миша, Коля и Настя решили помочь маме собрать урожай – смородину, крыжовник и вишню.
Каждый из них собирал что – то одно. Кто что собирал, если известно, что больше всего было собрано смородины,
Миша не собирал крыжовник, а Миша и Коля вдвоём набрали ягод меньше чем Настя?
Трое друзей – Игорь, Андрей и Владимир – имеют собак – овчарку, пуделя и добермана.
Игорь живет в одном подъезде с владельцем пуделя.
Доберман, выходя вечером гулять со своим хозяином, всегда очень радуется, встречая Владимира с его собакой,
но не переваривает пуделя и всегда злобно облаивает его при встрече. У кого из мальчиков какая собака?
У паука 4 пары ног, а у козлёнка 2 пары ног. На сколько ног меньше у козлёнка, чем у паука?
К числу 67 прибавить 2 однозначных числа и получить 75. Какие числа прибавили?
Разбей восемь восьмёрок на числа, которые в сумме дадут одну тысячу.
Если некоторые двузначные числа разделить на сумму его цифр, то в результате получится снова сумма цифр делимого.
Найти это число.
У Пети, Саши и Вовы было два ранца и один портфель.
У кого из мальчиков какой предмет был, если известно, что у Пети и Саши были одинаковые предметы?
У Марины, Кати и Нади было две ручки и один карандаш.
Какой предмет был у каждой девочки, если у Кати и Нади были разные предметы?
Что за число, на которое можно умножить и делить, но при этом множитель и делимое не изменяются?
На столе лежали две линейки. Жёлтая была длиннее зелёной на 2 см. Синяя короче зелёной на 3 см. Найти длину жёлтой линейки, если длина синей – 15 см.
В ряду 8 стульев. Маша села на пятое место слева, а Даша – на пятое место справа. Может быть они сели на один и тот же стул?
9 февраля был вторник. Какой день недели будет 25 февраля?
Квадрат стороной 5 см. Распилили на квадратики со стороной 1 см. Из полученных квадратов составили ленту. Какова длина ленты?
На участке дороги длиной 90 м. Школьниками поручено посадить деревья так, чтобы между ними были расстояния в 9 метров. Сколько деревьев должны посадить школьники?
10 насосов за 10 минут выкачивают 1 тонну воды. За сколько минут 20 таких насосов выкачивают 2 тонны воды?
Осёл, козёл и косолапый Мишка, за исполнение хорошей музыки, получили призы: мёд, сено и капусту.
Какой приз получил каждый музыкант, если осёл выбрал себе не сено и не капусту, а козёл тоже не взял себе капусту?
На одной чашке весов находятся две одинаковые коробки с макаронами, и стоит гиря в 4 кг., а на другой – 2 гири по 5 кг.
Весы в равновесии. Найдите массу каждой коробки.
Прямоугольник, стороны которого 8 и 5 см., разделили на одинаковые полосы шириной 1 см. Из этих полосок составили ленту. Найдите его длину.
В одном ряду 8 камешков на расстоянии 2 см. один от другого. В другом ряду 15 камешков на расстоянии 1 см. один от другого. Какой ряд длиннее
Занимательные задания повышенного уровня


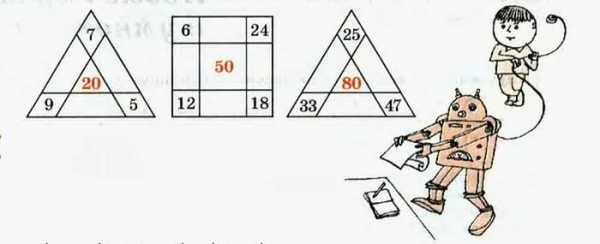


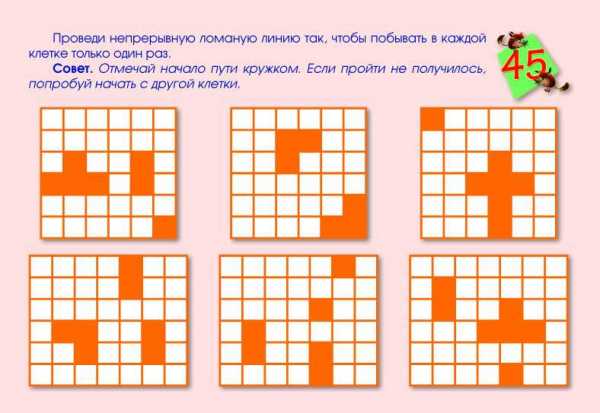




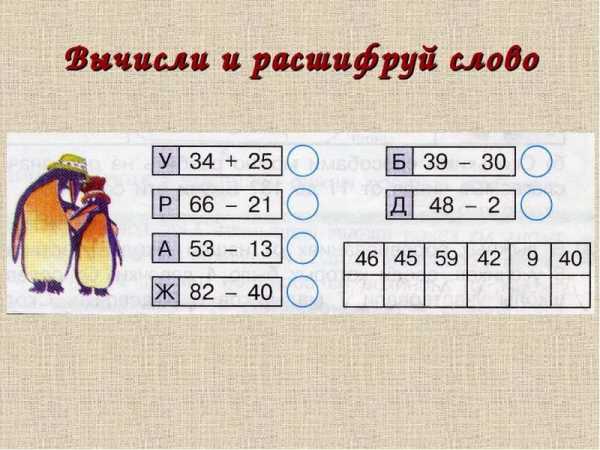


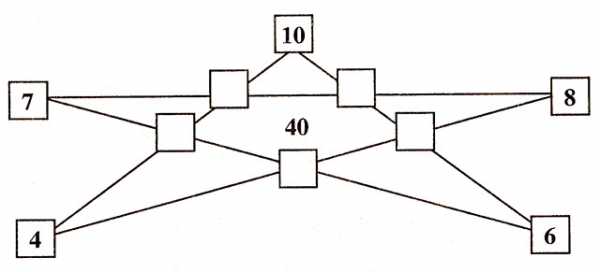
Задание: вставьте в квадраты необходимые числа таким образом, чтобы их сумма по каждой прямой равнялась числу в середине звёздочки, при этом числа не должны повторяться
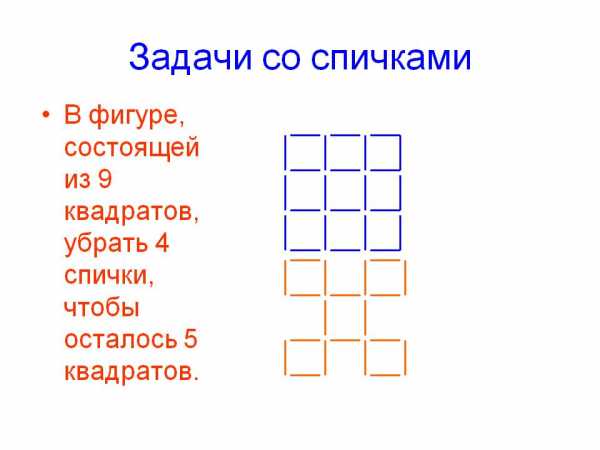
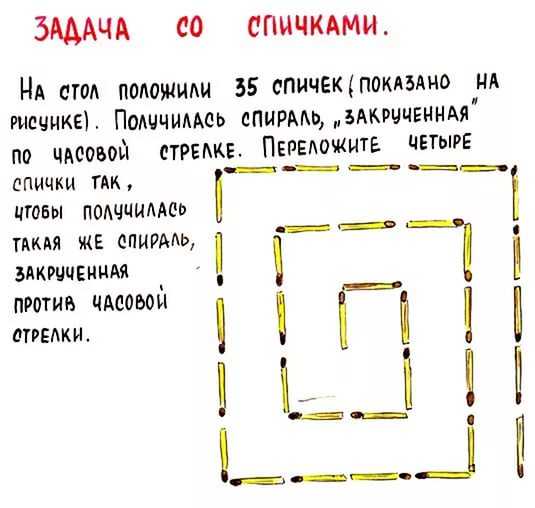
ИСПРАВЬТЕ ОШИБКУ
Возьмите 12 спичек и выложите из них «равенство»
Равенство неверное, так как получается, что 6 – 4 = 9. Переложите одну спичку так, чтобы получилось правильное равенство.
ИЗ ТРЕХ — ЧЕТЫРЕ
(шутка)
На столе лежат 3 спички. Не прибавляя ни одной спички, сделайте из трех – четыре. Ломать спички нельзя.
ТРИ ДА ДВА — ВОСЕМЬ
( шутка)
Положите на стол 3 спички и предложите товарищу добавить к ним еще 2 так, чтобы получилось восемь. Разумеется, ломать спички нельзя.
ТРИ КВАДРАТА
Из 8 палочек, четыре из которых вдвое короче остальных четырех. Составьте 3 равных квадрата.
СТАРИННЫЕ ЗАДАЧИ
ПЕРЕПРАВА ЧЕРЕЗ РЕКУ
Небольшой воинский отряд подошел к реке, через которую необходимо было переправиться. Мост сломан, а река глубока. Как быть? Вдруг офицер замечает у берега двух мальчиков, забавляющихся в лодке. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков – не больше! Однако все солдаты переправились через реку именно на этой лодке. Каким образом?
Решайте эту задачу «в уме» или практически, – используя шашки, спички, или что-либо в этом роде и передвигая их по столу через воображаемую реку.
ВОЛК, КОЗА И КАПУСТА
Это тоже старинная задача; встречается в сочинениях VIII века. Она имеет сказочное содержание.
Некий человек должен был перевезти в лодке через реку волка, козу и капусту. В лодке мог поместиться только один человек, а с ним или волк, или коза. Или капуста. Но если оставить волка с козой без человека, то волк съест козу, если оставить козу с капустой, то коза съест капусту. А в присутствии человека «никто никого не ел». Человек все-таки перевез свой груз через реку. Как он это сделал?
infourok.ru
Занимательные задачи
1 260
Занимательные задачи!
Чем хороши занимательные задачи — ими можно интересно занять детей по в дороге, по пути в школу или устроить конкурс на школьном празднике. Обратите внимание, что мало кто сможет дать правильный ответ сразу, потому не забывайте о маленьких подсказках, разгадывание задачек от этого будет не менее интересным.
Занимательные задачи по математике
1.В каждом из 4 углов комнаты сидит кошка. Напротив каждой из этих кошек сидят три кошки. Сколько всего в этой комнате кошек?
2. У отца шесть сыновей. Каждый сын имеет сестру. Сколько всего детей у этого отца?
3. В мастерской по пошиву одежды от куска сукна в 200 м ежедневно, начиная с 1 марта, отрезали по 20 м. Когда был отрезан последный кусок?
4. В клетке находятся 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось?
5. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков?
6. На одном дереве сидело 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?
7.Два землекопа за 2 часа работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 часов работы выкопали 100 м такой же канавы?
8. Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?
9. По стеблю растения, высота которого 1 м, от земли ползет гусеница. Днем она поднимается на 3 дм, а ночью опускается на 2 дм. Через сколько суток гусеница доползет до верхушки растения?
10. Есть два ведра емкостью 4 и 9 литров. Как с их помощью принести из речки ровно 6 литров воды?
Ответы:
1.4
2.Одной девочке дали клетку с кроликом.
3.9марта
4.7
5. 6 рыбаков за день едят 1 судака.
Один рыбак есть 1/6 судака в день.
10 рыбаков едят за день 10/6 судака.
10 судаков делим на 10/6 судака = 6 дней
6.Все улетели
7. 2
8. Дед, отец и внук = 2 отца и 2 сына
9.Через 7/12 суток.
10. Из полного девятилитрового ведра нужно вылить в реку 8литров воды, пользуясь ведром в 4 литра. Затем литр, оставшийся в большом ведре, нужно перелить в пустое четырехлитровое ведро. Если в него теперь добавить три литра из полного большого ведра, то в девятилитровом ведре как раз останется шесть литров воды.
Подумай и сосчитай
Чтоб одеть тепло сыночков,
Не хватает двух носочков.
Сколько же в семье сынков,
Если в доме шесть носков?
Ответ:четверо
Столько книжек у ребяток,
Сколько у Алеши пяток.
Принесла ребяткам Галя
Мячик, книжку, мишек.
Вы, ребята, посчитали,
Сколько стало книжек?
Ответ: три
******************
К трем лягушкам у болота
Прибежали два енота,
Прискакала тетя жаба
И пришла наседка Ряба.
Сколько в камышах болотных
Оказалось земноводных?
Ответ: четверо
Задачи на внимание
1. Подумай и скажи — кто быстрее переплывет речку — утята или цыплята?
2. Подумай и скажи — какого цвета волосы у колобка?
3. Отгадай загадку:
Лежали конфетки в кучке.
Две матери, две дочки
Да бабушка с внучкой
Взяли конфет по штучке,
И не стало этой кучки.
Сколько конфет было в кучке?
4. Росли 5 берез. На каждой березе по 5 больших веток. На каждой ветке по 5 маленьких веток. На каждой маленькой ветке — по 5 яблок. Сколько всего яблок?
5. Подумай и скажи — что помогает выжить белым медведям в пустыне, где нет воды?
6. На каких деревьях вьют свои гнезда страусы?
7. На столе лежит 2 яблока и 4 груши. Сколько всего овощей лежит на столе?
8. Подумай и скажи — кто громче рычит: тигр или буйвол?
9. Посмотрел Ваня утром в окно и говорит:
— А на улице, оказывается, очень сильный ветер. Нужно теплее одеваться.
Как он догадался, что на улице ветер? Что он увидел?
10. Пошли 2 девочки в лес за грибами, а навстречу 2 мальчика. Сколько всего детей идет в лес? (подсказка: 2 — остальные идут обратно)
11. В комнате горело 5 свечей. Зашел человек, потушил 2 свечи. Сколько осталось? ( подсказка: 2- остальные сгорели)
12. Бревно распилили на 4 части. Сколько сделали распилов?
13. Прочитай слова и скажи — какое слово лишнее в каждом ряду?
— диван, стул, шкаф, конура, тумбочка,
— гвоздика, ромашка, камыш, лилия, астра,
— боровик, мухомор, сыроежка, подберезовик, лисичка.
14. Подумай и скажи — сколько земли будет в яме глубиной 1 метр, длиной 1 метр и шириной 1 метр?
15. У шестилетней девочки была кошка с коротким хвостом. Она съела мышку с длинным хвостом, а мышка проглотила 2 зернышка и съела тонкий кусочек сыра. Скажи, сколько лет было девочке, у которой была кошка?
16. На одном берегу реки стоит петух, а на другом индюк. Посреди реки — островок. Кто из этих птиц быстрее долетит до островка?
17. Скажи сколько грибов можно вырастить из 5 семечек?
18. Скажи, кто обитает в море на большей глубине: щука, рак или форель?
19. Гусь на двух ногах весит 2 кг. Сколько он будет весить, стоя на одной ноге?
20. На клене 5 веток. На каждой ветке по 2 яблока. Cколько яблок на клене?
Мой блог находят по следующим фразам
xn--d1acjua1a.xn--p1ai
Задания по математике в картинках для детей 5-7 лет
Задания для детей старшей — подготовительной группы. Математическое развитие
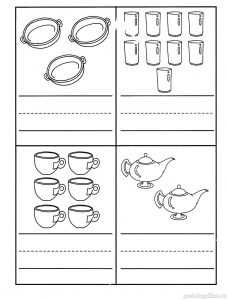
Задание 1. Считалочка на кухне
Сколько предметов в каждом прямоугольнике?
Ответ напиши словами.
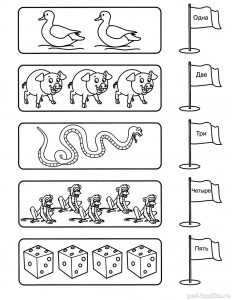
Задание 2. Считалочка
Сколько картинок в каждой рамке?
Соедини линиями рамки и соответствующие флажки
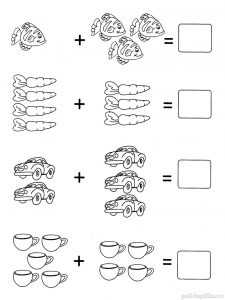
Задание 3. Веселый счет
Реши примеры
Задание 4. Фруктовый счет
Раскрась пары фруктов, сумма чисел на которых равна 9
Задание 5. Считалочка
Реши примеры.
Задание 6. Считалочка
Реши примеры
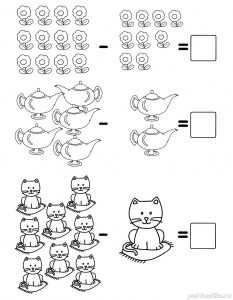
Задание 7. Большой и маленький
В каждом ряду пронумеруй картинки от самой маленькой до самой большой
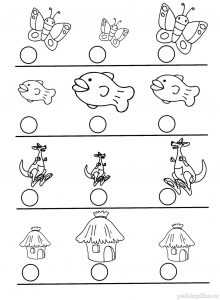
Задание 8. Вкусная считалочка
Реши примеры, используя подсказки в рамках.
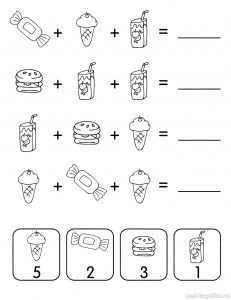
Задание 9. Считалочка
Соедини кружочек с цифрой и картинку, на которой написана такая же цифра.

Задание 10. Считалочка
Реши примеры и соедини линиями стрекоз и лягушек.

Задание 11. Считалочка
Реши примеры.
Соедини ответы с соответствующим количеством картинок
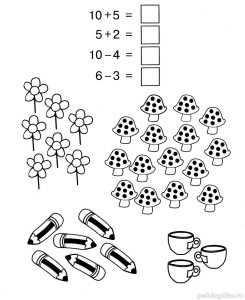
Задание 12. Кроссовки
Реши примеры и найди Мишины кроссовки.
Подсказка: ему нужна пара кроссовок, на каждой из которых в сумме получается 6
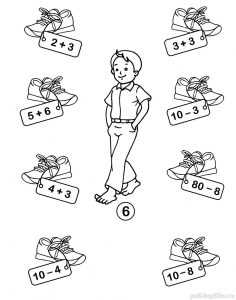
Задание 13. Веселый счет
Реши примеры и соедини их с ответами.
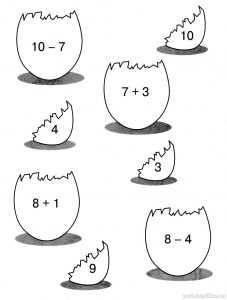
Задание 14. Считалочка
На каждом цветке раскрась красным цветом лепесток с самым большим числом и жёлтым – с самым маленьким.
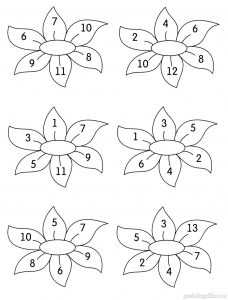
Задание 15. Облака
Сосчитай картинки в облаках.
Ответы впиши в окошки.
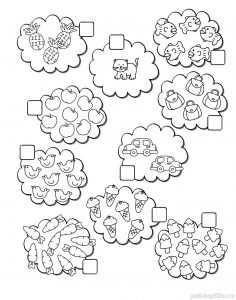
Задание 16. На дне океана
Сколько здесь морских звёзд и сколько осьминогов?
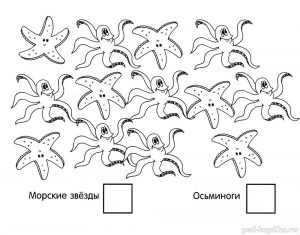
Задание 17. Считалочка
Сосчитай картинки в каждом прямоугольнике и соедини их линиями с соответствующими цифрами.
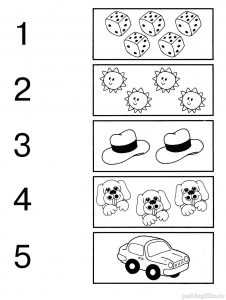
Задание 18. Большой и маленький
Раскрась больших животных и обведи маленьких

Задание 19. Воздушные шарики
Сколько воздушных шариков в каждой связке?
Задание 20. Фруктовая считалочка
Сколько здесь фруктов каждого вида?
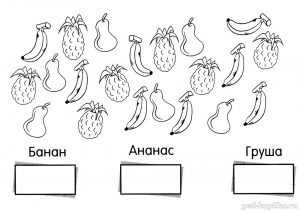
Задание 21. Считалочка
Реши примеры на яблоках и на морских звёздах.
Соедини линиями яблоки и звёзды, на которых получились одинаковые ответы.

Задание 22. Считалочка
Угадай последовательности и впиши пропущенные цифры

Задание 23. Морковка на тарелках
Нарисуй на каждой тарелке столько морковок, сколько не хватает до десяти.
Задание 24. Считалочка
Реши примеры и впиши ответы в окошки

Задание 25. Веселый счет
Раскрась три яблока так, чтобы сумма, написанная на них цифр равнялась 8.
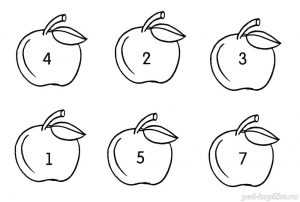
Задание 26. Считалочка
Соедини линиями прямоугольники с одинаковым количеством предметов на картинках.

Задание 27. Считалочка
Сколько картинок в каждом прямоугольнике?
Соедини их с соответствующими цифрами.
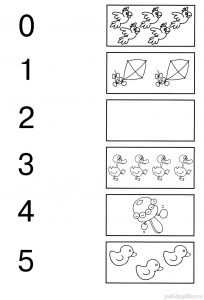
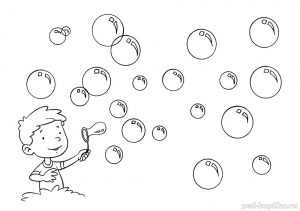
Задание 28. Мыльные пузыри
Сколько здесь мыльных пузырей?
Задание 29. Считаем палочки
Сколько палочек в каждом стаканчике с мороженым?
Ответы впиши в окошки.
Задание 30. Считалочка
Сосчитай жёлуди. Ответы впиши в окошки.
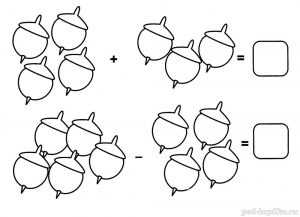
Задание 31. Воздушные змеи
Реши примеры на катушках и соедини их со змеями.
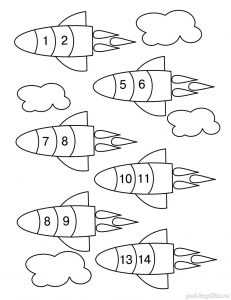
Задание 32. Ракеты
Впиши пропущенные числа.
Задание 33. Пятнистая лягушка
Сколько пятнышек разного размера на лягушке?
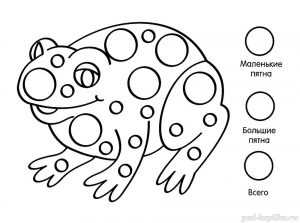
Задание 34. Олененок потерялся
Помоги оленёнку попасть к маме.
Он может идти только мимо тех листиков, на которых сумма равняется 10.
azbyka.ru
Занимательная математика: 5 секретных приемов
Воспользуйтесь нашими советами, чтобы заинтересовать изучением математики даже тех, кто уверен, что ему с лихвой хватит знаний, полученных в начальной школе!
Среди школьников и их родителей бытует мнение, что есть ученики, которые легко понимают математику, и те, кому «не дано». Так ли это на самом деле? И, если так, что делать учителю, который в идеале обязан дотянуть каждого хотя бы до троечки?
Мы считаем, что понять и полюбить математику может каждый. Конечно, кому-то это сделать значительно легче, а от кого-то потребуется немало усилий. И вот тут без дополнительной мотивации не обойтись.
Давайте разберемся, как прорекламировать математику и пробудить интерес любого ученика.
Совет 1. Приведите интересные примеры из жизни.
Докажите, что математика — наука о реальной жизни, а не об абстрактных формулах, функциях и графиках. Хотите продемонстрировать наглядную связь математики, биологии и архитектуры? Расскажите ребятам о золотом сечении.
Правило золотого сечения проявляется во всем вокруг нас: начиная от структуры ДНК и заканчивая творениями древних архитекторов, художников и композиторов или современных кутюрье и фотографов.
Совет 2. Расскажите о великих математиках.
Докажите, что математика — это наука, которую создают и развивают неординарные личности. Чтобы прочувствовать гармонию и закономерность в числах, нужно быть необычным человеком.
Пифагор
Великий мудрец и философ, известный школьникам как автор теоремы, устанавливающей соотношение между сторонами прямоугольного треугольника, был незаурядной личностью. Обосновавшись в Кротоне (одной из греческих колоний в Южной Италии), Пифагор создал тайное общество, которое фактически пришло к власти.
Кстати, в 2014 году авторитетное издание Businessinsider составило список величайших уравнений и равенств, изменивших историю. Догадались, какое равенство заслуженно получило первое место? Конечно же, теорема Пифагора!
Алан Тьюринг
Жизнь этого математика — сюжет приключенческого фильма. Он раскодировал легендарную «Энигму» — шифровальную машину немецкой армии. Коды к ней менялись каждое утро, а алгоритм кодировки был не по зубам английским математикам, инженерам связи несколько лет. Алан Тьюринг не только разгадал секрет немецкого чуда шифровальной техники, но и создал первые прообразы современных компьютеров.
Ада Лавлейс
Дочь самого Байрона и величайший математик викторианской Англии. Она ввела понятия «цикл» и «рабочая ячейка», создала первые проекты вычислительных машин. Не зря эта дама носит почетный титул первого «программиста».
Льюис Кэрролл
Этого детского писателя знают все. «Алиса в Стране чудес» и «Алиса в Зазеркалье» заняли достойное место среди шедевров мировой литературы. Но писатель в первую очередь был математиком. И даже преподавал 26 лет студентам линейную алгебру.
Григорий Перельман
Именно он решил «загадку тысячелетия», доказав теорему Пуанкаре, но остается замкнутым и не любит шума вокруг своего имени. Великий математик отказался от Премии тысячелетия размером в миллион долларов, а позднее — и от Филдсовской премии, известной также как Нобелевская премия для математиков.
Совет 3. Предложите ученикам прочитать увлекательные математические книги.
Прививать любовь и интерес к дисциплине необходимо не только на уроках. Для этого воспользуйтесь подборкой тематических, развлекательных книг для школьников разного возраста. Уверены, эти произведения будут интересны самому широкому кругу читателей.
- Владимир Левшин «Новые рассказы рассеянного магистра». Автор умеет интересно в жанре приключенческой литературы описать разделы математики. Простота подачи информации, занимательный сюжет — за это произведения В. Левшина любят школьники и взрослые.
- Эвгения Кац «Необычная математика». Эта книга — реальный конкурент учебникам по математике для 1–2 класса. Интересные задачи не потребуют помощи родителей при их решении.
- А. Звонкина «Математика и малыши». Рекомендуем школьникам младших классов и их родителям. Пусть и взрослые поймут, что математика — не только арифметические действия со статичными цифрами.
- Яков Перельман «Занимательная арифметика». Автор популярной детской литературы воспитал любовь к математике не у одного поколения школьников.
- Леонард Млодинов «(Не)совершенная случайность. Как случай управляет нашей жизнью. Эта книга просто и доступно для всех, даже для гуманитариев, объясняет теорию вероятности, показывает связь между точной дисциплиной и естественными науками.
- Иэн Стюарт «Истина и красота. Всемирная история симметрии». О связи математики с точными науками знают все. Но влияние дисциплины ощутимо в архитектуре и мировых шедеврах. Заинтересовались? Тогда советуем прочитать книгу.
- Курант Р., Роббинс Г. «Что такое математика?». Книга устраняет разрыв между сухим материалом школьных уроков математики и реальной жизнью, естественными науками.
- Н. Я. Виленкин «Функции в природе и технике». Автор подробно объясняет, как знания о функциях в реальной жизни помогают не только инженерам, но и людям самых разных профессий.
Совет 4. Расскажите ученикам о математических приложениях для смартфонов.
Они смогут играть и заниматься по ним дома или на перемене. Вы проявите себя как современного учителя, который не отстает от жизни и легко работает с современными гаджетами.
Для владельцев планшетов и смартфонов под управлением Android:
- «Математейка» поможет выучить таблицу умножения без зубрежки.
- «Математически игры» научат школьников быстро считать в уме. Для игроков предусмотрена система достижений, которая дополнительно мотивирует учеников к совершенствованию.
- «MalMath» — верный друг и помощник старшеклассника. Это приложение помогает решать задачи и подробно расписывает ход решения. Для самостоятельных и ответственных школьников «MalMath» может частично заменить репетитора по математике.
- «Пифагория» и «Пифагория 60°» заинтересуют школьников увлекательными геометрическим задачами на построение.
- «Euclidea» — это электронный сборник увлекательных интерактивных задач по геометрии. Авторы рекомендуют это приложение учителям, школьникам и всем любителям математики.
Для владельцев iPhone и iPad:
- «МатематУМ» научит школьников быстро и точно считать в уме. Регулярные занятия помогут улучшить внимательность и скорость мышления.
- «Math academy» — сборник увлекательных математических игр с приятным визуальным оформлением.
- «Правила математики» — это сборник правил, формул и теорем. Незаменимый помощник для тех, кто хочет изучить алгебру, геометрию, тригонометрию, элементы математического анализа, статистики и теории вероятности.
- «Мобильная математика» — это приложение, которым пользуются старшеклассники и студенты вузов. В приложении собраны основные формулы, а также представлены около 30 калькуляторов.
- «Пифагория», «Пифагория 60°» и «Euclidea» — это увлекательные сборники интерактивных геометрических задач на построение.
Совет 5. Участвуйте в наших конкурсах и олимпиадах по математике.
Задания наших образовательных мероприятий создают методисты с практическим опытом преподавания математики. В заданиях мы делаем упор на прикладной характер математических знаний и учитываем возрастные особенности школьников.
Организаторам дистанционных олимпиад и конкурсов мы дарим комплекты рабочих листов «Математика с Лантиком». Оцените качество наших рабочих листов прямо сейчас.
Скачать рабочие листы «Математика с Лантиком»
Скачайте рабочие листы, распечатайте их на цветном принтере и докажите, что математика — это весело и увлекательно. Ждем ваших учеников на наших образовательных мероприятиях!
Вам слово:
С грамотным использованием интересных приемов даже математика станет понятной и увлекательной. Что вы используете для повышения интереса своих учеников к дисциплине?
Рекомендуем принять участие в мероприятих ЦРТ «Мега-Талант»
Понравилась статья?
Подпишитесь и мы будем присылать вам статьи на почту
mega-talant.com
Интересные задачи по математике.
Задания «Встречи с тремя неизвестными.»
1.Расшифруйте записи в арифметических действий, в которых некоторые цифры заменены буквами (в каждой из трех записей по отдельности разные цифры заменены разными буквами, одинаковые-одинаковыми, а в первой шифровке А=Т):
а) КОРОВА+ТРАВА=МОЛОКО;
б)СТОЛ+СТУЛ=КЛАСС;
в)БЕ* РУ * 4= БУЕР
2.Рядом с большой бочкой с водой стоят два бидона. В один входит 12 литров, в другой — 17.Воду можно набирать из бочки и выливать обратно в бочку. Кто быстрее принесет нам 6 литров воды?
3.Верните сбежавшие цифры:
4.Начертите два шестиугольника, делящие плоскость на возможно большее число частей. А если дополнительно потребовать, чтобы шестиугольники были выпуклыми? Попробуйте доказать, что на большее, чем у вас, число частей разделить плоскость не удастся.
5.Нашли произведение 666 множителей, каждый из которых равен 777.Какая цифра стоит на конце?
6.В комнате 10 живых существ — людей, собак и мух, у них вместе 46 ног. У каждого человека 2 ноги, у каждой собаки 4 и у мухи 6 ног. Как это могло получиться? Найти все возможности.
7.Поле имеет форму четырехугольника. Шоссейные дороги- они идут по диагоналям- разбивают его на четыре участка. Площади трех из них- 2 гектара, 4 гектара,6 гектаров. Какой может быть площадь четвертого?
8.В одной из московских школ есть удивительный шестой класс. Судите сами. В классе 35 учеников, и все они либо играют на скрипке, либо разводят хомяков, либо плавают в бассейне «Москва», либо занимаются сразу несколькими из этих дел. Плавают или разводят хомяков 28 человек. Разводят хомяков, но не играют на скрипке 22 ученика. И тем и другим, и третьим занимаются 3 школьника. Есть пловец и скрипач, ненавидящий хомяков. Есть и такой, который не плавает, но зато прекрасный скрипач, а хомяков разводит с 1-го класса. Может быть, таких не по одному, а много. Сколько в классе скрипачей? можно ли определить ,сколько ребят разводят хомяков, а на скрипке не играют и не плавают? Если да, то сколько если нельзя определить, то почему?
Ответы «Встречи с тремя неизвестными.»
а) 186 859 + 96 959= 283 818; 385 869+ 95 969
= 481 838 ; 387 869 + 97 969= 485 838
б) 6923+6943=13 866; 6943=6923=13 866; 6523+6543=13 066; 6543+6523=13 066;
в)БУЕР- это 1972,5472 или 8632.
2.Будем производить следующий цикл действий:
а) наливаем воду в 17-ти литровый бидон;
б) наполняем из него 12-ти литровый; воду из 12-ти литрового выливаем в бочку.
в) то, что осталось в 17-ти литровом, переливаем в 12-ти литровый
Шесть раз наполнив большой сосуд, наберем в общей сложности 102 литра. Из малого бидона вода будет вылита 8 раз, всего 96 литров. Останется ровно 6 литров.
3. 7980 : 95 = 84 или 7030 : 95 = 74
4.Два шестиугольника могут разделить плоскость на 38 частей (смотреть на рисунок), а два выпуклых- только на 14.Докажите, что число частей, на которые делят плоскость два многоугольника , равно числу точек пересечения их сторон, увеличенному на 2.
5. Последняя цифра произведения определяется по последним цифрам множителей:
7*7*7*7*7*7*7*7*7*7*7*7*7,. . .
эти числа оканчиваются на 7,9,3,1,7,9,…. соотвественно, последние цифры повторяются через три на четвертую. ответ: 9.
6.Ноги естественно считать парами. Перевяжем красной ленточкой по одной паре ног у каждого из «присутствующих».Тогда неперевязанных останется 13 пар — по одной паре у каждой собаки , по две пары у каждой мухи. Понятно, что мух не больше шести. И если в комнате 1,2,3,4,5,6 мух, то собак соответственно 11,9,7,5,3,1.Первые три случая не подходят (Люди-то есть!), остальные дают три решения- 1,2,3 человека соответственно.
7. Участки можно разбить на пары не имеющих друг с другом общих сторон. Докажите, что произведения площадей участков каждой пары равны между собой. ответ: площадь четвертого участка может быть равна 4/3 га,3 га,12 га (участок, входящий в пару с четвертым, имеет площадь 6 га,4 га, 2 га соответственно) .
8. Ответ: в этом классе 12 скрипачей; плавают, но разводят хомяков 2 ученика; ребят, разводящих хомяков, но не плавающих и не играющих на скрипке, может быть 0,1,2….,22. Для наглядности полезно нарисовать три пересекающихся круга — один для скрипачей, второй- для пловцов, третий- для разводящих хомячков. Тогда плавающие скрипачи будут стоять в пересечении первого и второго округов , а 3 человека, занимающиеся всеми тремя видами полезной деятельности- в пересечении всех трех кругов и.т.д.
infourok.ru
