Цилиндр, методы чтобы находить его объём, правила перевода кубических метров в литры
Среди множества геометрических фигур часто встречается и цилиндр. Это геометрическое тело применяется в многочисленных расчётах. Согласно принятой терминологии под таким понятием принято иметь ввиду тело геометрического типа, которое в своей основе имеет поверхность. Данная поверхность представляет также цилиндрическую форму.
В литературе данная поверхность часто именуется, как поверхность бокового вида. Кроме этого, в такой фигуре есть пара поверхностей, носящих наименование оснований. Эти основания цилиндра представляют собой окружности равного диаметра. Цилиндр, в основании которого находится круг принято считать круговым.
Ещё со школьных времён знакома всем фигура цилиндра классического типа. Это и есть круговой цилиндр.
Содержание:
- Типы цилиндров
- Вычисление объёма
- Исходные данные
- Методы расчёта
- Объём в литрах
- Видео
Типы цилиндров
В математике существует несколько типов цилиндров, которые постоянно используются в геометрии.
- Цилиндр прямого типа. Это геометрическая фигура, которая имеет прямой угол между боковой поверхностью и основаниями. Такой тип самый распространённый и часто применяется в решении большого количества задач.
- Наклонный цилиндр. Исходя из основания фигуры, можно сделать вывод, что угол между боковой поверхностью и основаниями фигуры будет отличным от прямого. При этом он может колебаться в своём значении, как в большую, так и в меньшую сторону от прямого угла.
Вычисление объёма
Довольно часто для работы с цилиндрами требуется вычислить его объём. Это процедура в последнее время производится с применением вычислительной техники. Однако, чтобы провести такую процедуру необязательно использовать калькулятор и другие дополнительные методы решения поставленной задачи.
Сейчас существует несколько основных методов, которые позволяют произвести вычисление данного параметра. Это, по сути, универсальные формулы. 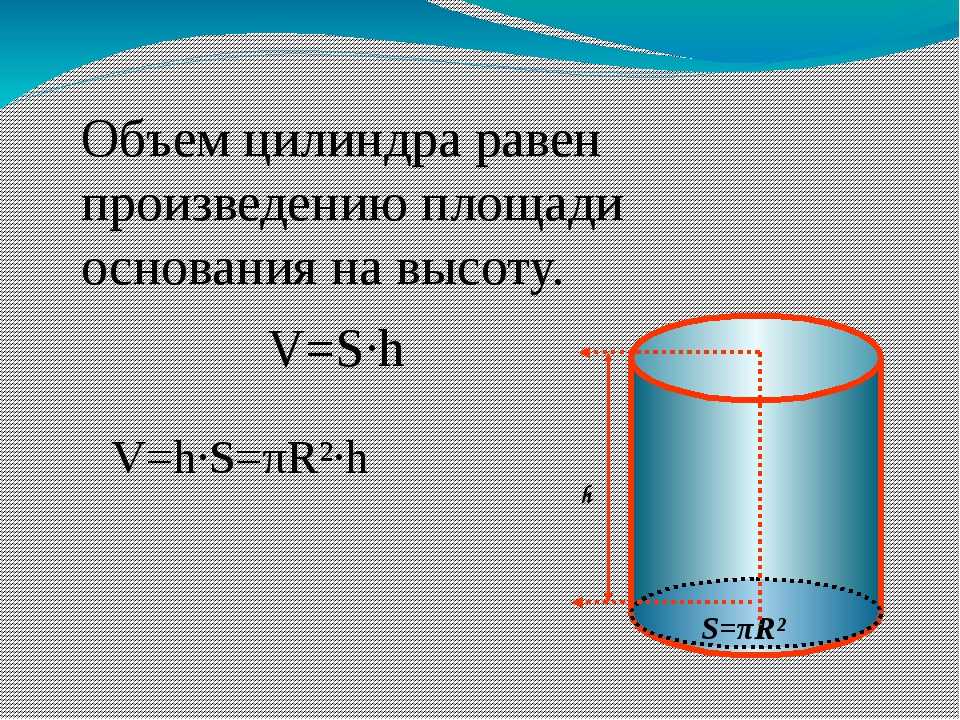 Это позволяет достигнуть ряда положительных моментов в расчётах.
Это позволяет достигнуть ряда положительных моментов в расчётах.
- Значительно сокращается время для осуществления операций подсчёта объёма.
- Уменьшается вероятность того что может быть совершена ошибка в расчётах
- Требуется для вычисления ограниченное число параметров, знание которых и даёт возможность достигать результата.
Исходные данные
Производя вычисление такого параметра, как объём, необходимо помнить, что требуется первоначальное знание параметра, который и будет исходным данным для такой процедуры.
Необходимо иметь значение высоты. Это расстояние от нижнего и верхнего основания фигуры. При этом в зависимости от типа она может определяться по-разному. В ситуации прямоугольного цилиндра высота соответствует расстоянию между основаниями фигуры. Если же он относится к наклонному типу, то расстояние будет вычисляться иным путём. Это параметр, который соответствует длине прямой проведённой под прямым углом от одного основания до плоскости, на которой лежит второе основание.
В данной формуле принято следующее обозначение при помощи переменных:
- П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
- R – Радиус окружности, лежащий в основании цилиндра.
- S — Площадь основания фигуры.
Вычисление непосредственно объёма цилиндра производится на основе стандартной формулы.
V=S*h
В данной формуле принято следующее обозначение при помощи переменных:
- S – Площадь основания цилиндра, имеющего форму круга.
- h – Высота геометрической фигуры.
- V – объём цилиндра.
- Вторым методом, позволяющим произвести вычисление объёма данной фигуры, является соотношение таких параметров, как высота цилиндра и радиуса его основания. По сути, данная формула является преобразованной формулой первого метода. В ней нет разделения на промежуточные этапы подсчёта параметров.
 2*h
2*hВ данной формуле принято следующее обозначение при помощи переменных:
- П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
- R – Радиус окружности, лежащий в основании цилиндра.
- h – Высота геометрической фигуры.
- V – Объём цилиндра.
Объём в литрах
Если говорить о нахождении объёма такой геометрической фигуры, то надо отметить что это задача не только для школьной программы. Используя приведенные ранее методы, есть возможность производить расчёты объёма ёмкости неизвестного типа.
К примеру, есть возможность вычислить объём ёмкости для полива на садовом участке. Однако есть и особенность при проведении подсчёта. Надо все значения подставлять в формулы в метрах. В результате проведения расчётом получается значение, которое будет измеряться в кубических метрах.
Однако, принято при расчётах поливных ёмкостей пользоваться измерениями в литрах.
 Для этого необходимо произвести пересчёт полученного значения объёма в литры. Это происходит на основе простого соотношения, где один кубический метр равняется 1000 литрам жидкости.
Для этого необходимо произвести пересчёт полученного значения объёма в литры. Это происходит на основе простого соотношения, где один кубический метр равняется 1000 литрам жидкости.Если вычисления происходят в сантиметрах, то и результат будет в кубических сантиметрах. Тогда надо понимать, что между кубическими сантиметрами и литрами существует чёткое соотношение. Перевод происходит путём деления полученного значения объёма на 1000. После этого данные будут представлены в литрах.
Если необходимо первоначально перевести полученный в результате вычислений параметр из кубических сантиметров в кубические метры, то достаточно произвести операцию деления. Объём делится на 1000000. Это связано с тем, что кубический метр — это куб, у которого сторона равняется 100 сантиметрам. Поэтому объём в сантиметрах будет равен произведению 100*1000*100. Соответственно это будет 1000000 сантиметров кубических.
Видео
Посмотрите, как высчитать объем цилиндра и площадь его поверхности.

объем цилиндра
Решить для объемРадиусВысотаПлощадь поверхностиБоковая поверхностьБазовая площадь
Радиус
Высота
РЕЗУЛЬТАТЫ
Заполните форму калькулятора и нажмите кнопку Рассчитать, чтобы получить результат здесь
Feedback
Этот калькулятор объема цилиндра позволяет определить объем цилиндра. Если вам нужно оценить количество воды, которая помещается в банку, чай в кружку и тому подобное, эта штуковина рассчитает все это.
Какой объем цилиндра
Цилиндр — это трехмерная труба с определенной длиной, высотой и площадью поперечного сечения. Для наглядного примера рассмотрим металлическую трубу для воды. Эта труба имеет полые цилиндрические размеры.
С другой стороны, примером для обычных цилиндрических размеров может служить цилиндрическая конфета без полой поверхности.
объем цилиндра формула — это пространство, в котором находится вещество (твердое вещество, жидкость или газ).
 2h} \)
2h} \) ‘r’ представляет радиус цилиндра.
пока
‘h’ представляет высоту цилиндра.
Это обычное уравнение объема цилиндра. Это также является формулой правильного объема цилиндра.
Как найти / рассчитать объем цилиндра
Ознакомившись с понятием объема и его формулами, вы можете легко рассчитать объем цилиндра. Однако, чтобы дать вам преимущество, мы привели два примера: расчет правого и полого цилиндров.
Правый цилиндр
Давайте сначала обсудим правильный расчет цилиндра.
Формула для этого конкретного вычисления — ортодоксальная формула, которую мы упомянули выше. Теперь давайте определимся с объемом правильного цилиндра.
• Предположим, что у вас есть цилиндр с высотой ‘h’ \ (20 \ mathrm {cm} \).
• И имеет радиус \ (2 \ mathrm {cm} \).
• Поскольку концевая основа цилиндра круглая, нам также нужен пирог, который универсален \ (3.141 \)Имея все эти значения в нашем распоряжении, мы можем начать рассчитывать объем цилиндра.

2- Мы вводим гипотетические значения в формулу. Поскольку значение пирога универсально равно 3,14, а высота полого цилиндра составляет 20 см, а внешний и внутренний радиус соответственно 5 и 4,9 см, получаем:
V (пустота) = \(3.14 \times (5-4.9) \times 20\)
3- Вычитая внутренний радиус из внешнего и умножающего пирога с произведением высоты цилиндра и разницы внешнего и внутреннего радиуса, получаем:
V (пустота) = \(3.14 \times (0.1) \times 20\)
V (полый) = \(6.28\)
4- так что объем нашего полого цилиндра \(6.28 \mathrm{cm}\).
User Ratings
- Total Reviews 0
- Overall Rating 0/5
- Stars
Your Review Will Appear Soon.
Submit Your Review Close
Reviews
No Review Yet
Please Fill aleat 1 row
Send us your feedback!
Need some help? you can contact us anytime.
Калькулятор объема цилиндра
| Сплошной или полый цилиндр
Создано Луисом Фернандо
Последнее обновление: 18 октября 2022 г.
Содержание:- Формула объема сплошного цилиндра
- Формула для расчета объема полого цилиндра
- Как использовать этот калькулятор объема цилиндра
Если вы ищете, как найти объем цилиндра, этот калькулятор объема цилиндра для вас.
Объем цилиндра — это величина, присутствующая во многих приложениях . Например, в автомобиле термин «объем двигателя » относится к объему, охватываемому поршнем в цилиндрах двигателя, умноженному на количество цилиндров.
Этот инструмент вычисляет объем цилиндра за считанные секунды. Тем не менее, в следующих разделах мы представляем формулу объема цилиндра , чтобы сделать это вручную, включая уравнение для расчета объема полого цилиндра.
Чтобы узнать больше о различных единицах измерения объема, воспользуйтесь нашим конвертером объема.
 92)\times h/4V=π×(D2−d2)×h/4
92)\times h/4V=π×(D2−d2)×h/4Как использовать этот калькулятор объема цилиндра
Для твердого цилиндра :
- Введите высоту цилиндра в Коробка «Высота». Допустим, она равна 20 см.
- Введите радиус цилиндра в поле «Радиус». Допустим, он равен 5 см.
- Объем баллона должен быть 1570,8 см 3 . Вот как вы находите объем цилиндра с помощью этого калькулятора.
Как рассчитать объем полого цилиндра :
- Введите высоту цилиндра в поле «Высота». Допустим, она равна 20 см.
- Введите внешний диаметр цилиндра в поле «Внешний диаметр». Допустим, он равен 10 см.
- Введите внутренний диаметр цилиндра в поле «Диаметр внутренний». Допустим, он равен 5 см.
- Объем цилиндра должен быть 1178,1 см 3 . Вот как вы вычисляете объем полого цилиндра с помощью этого инструмента.

Луис Фернандо
Объем цилиндра — веб-формулы
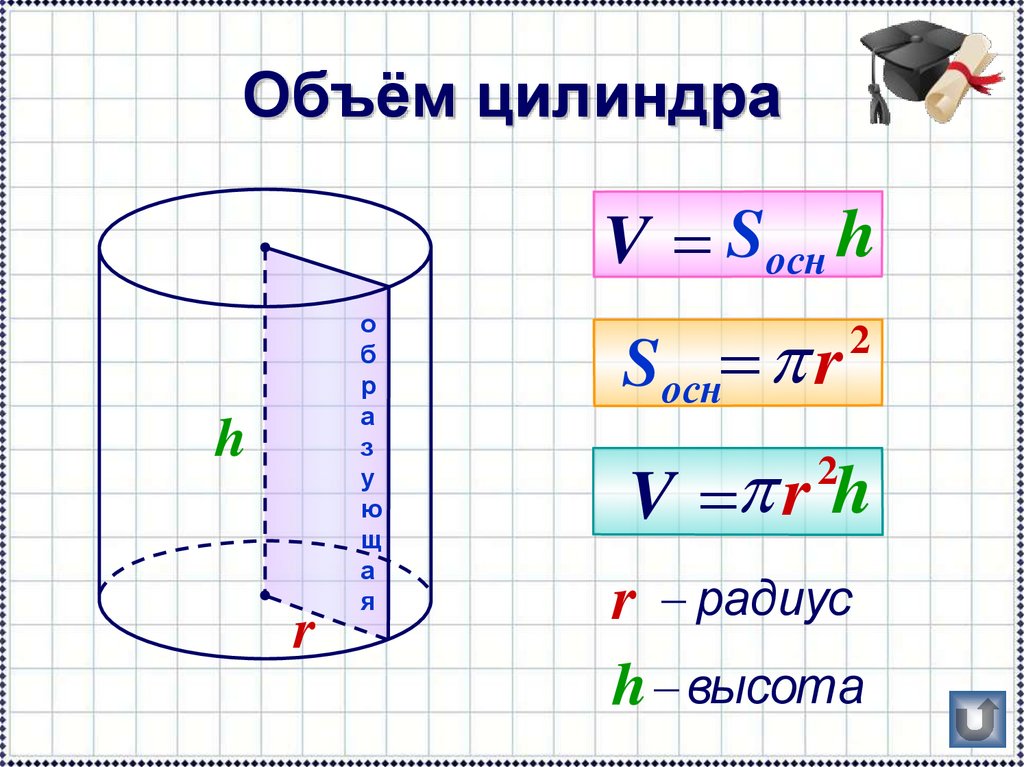
Объем цилиндра:
В геометрии цилиндр — это трехмерная фигура с круглым основанием, круглым верхом и прямыми сторонами. Это сплошная фигура, которую вы получите, если повернете прямоугольник вокруг одной из его сторон. В большинстве случаев, когда мы говорим об объеме баллона, мы имеем в виду, сколько жидкости он может вместить.Строго правильно сказать, что это « объем , окруженный цилиндром » — количество жидкости, которое он содержит. Но во многих учебниках просто говорится, что « объем цилиндра » означает то же самое.
Помните, что радиус и высота должны быть в одних и тех же единицах — при необходимости преобразуйте их.
Полученный объем будет в этих кубических единицах. Итак, если высота и радиус выражены в сантиметрах, то объем будет в кубических сантиметрах.Объем цилиндра находится путем умножения площади его вершины или основания на его высоту и определяется как: цилиндрический резервуар для хранения воды имеет внутренний радиус основания 7 м и глубину 11 м.
 Найдите вместимость бака в килолитрах (1кл = 1м 3 ).
Найдите вместимость бака в килолитрах (1кл = 1м 3 ).
Базовый радиус: р = 7 м
Высота: h = 11 м
Резервуар для воды имеет форму цилиндра. Таким образом, используя формулу объема цилиндра, мы можем найти его объем.V = π· r 2 · h
V = π· 7 2 · 11
V = 1692.46 m 3 = 1692.46 kl
Example 2: Найдите объем цилиндра, у которого радиус основания 6 см, а высота 4 см.
Решение :
Радиус основания: r = 6 см
Height: h = 4 cm
V = π· r 2 · h
V = 3.14· 6 2 · 4
V = 452.16 cm 3
Пример 3: Если вместимость цилиндрического резервуара составляет 1848 м 3 , а диаметр его основания равен 14 м, найдите глубину резервуара.
Решение :
Пусть глубина резервуара h метров. Тогда имеем:
V = π· r 2 · h
h = V / π· r 2
h = 12 м - 9012 радиус и высота 20 см и 50 см соответственно, наполнен жидкостью. Найдите высоту жидкости, если ее поместить в цилиндр с радиусом основания 10 см.
Раствор :
The volume of the vessel is:
V = π ∙ r 2 ∙ h / 3
V = π · 20 2 · 50 / 3
V = 20944 cm 3The Объем жидкости одинаков, независимо от того, находится она в сосуде или в цилиндре, поэтому имеем:
V1 = V2 , где V1 — объем сосуда, а V2 — объем, определяемый с помощью формула цилиндра.20944 = π · 10 2 · ч
ч = 20944 / ( π · 10 2 )
h = 66,67 смПример 5: Найдите объем прямоугольного цилиндра, площадь кривизны которого равна 2640 см 2
А окружность его основания 66 см.

 2*h
2*h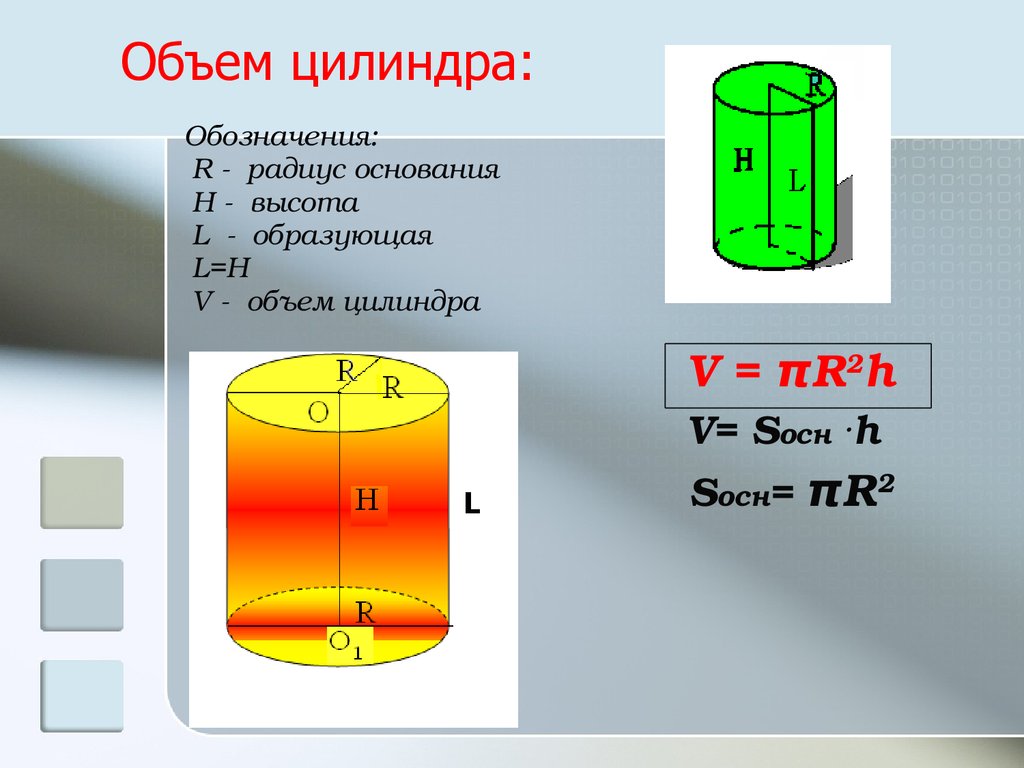 Для этого необходимо произвести пересчёт полученного значения объёма в литры. Это происходит на основе простого соотношения, где один кубический метр равняется 1000 литрам жидкости.
Для этого необходимо произвести пересчёт полученного значения объёма в литры. Это происходит на основе простого соотношения, где один кубический метр равняется 1000 литрам жидкости.
 2h} \)
2h} \) 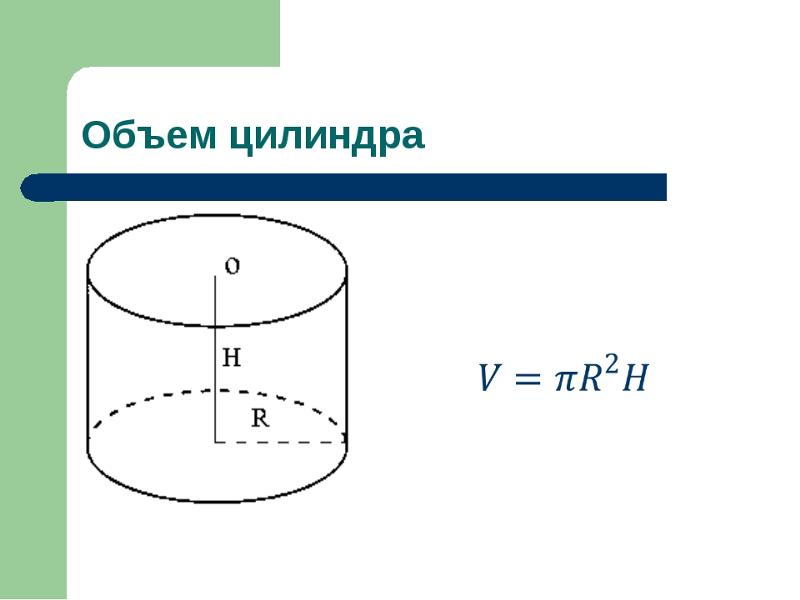
 92)\times h/4V=π×(D2−d2)×h/4
92)\times h/4V=π×(D2−d2)×h/4
 Найдите вместимость бака в килолитрах (1кл = 1м 3 ).
Найдите вместимость бака в килолитрах (1кл = 1м 3 ). 
